Hydrogen evolution reaction mechanism on Ti₃C₂ MXene revealed by in situ/operando Raman spectroelectrochemistry

Abstract

MXenes have shown great promise as electrocatalysts for the hydrogen evolution reaction (HER), but their mechanism is still poorly understood. Currently, the benchmark Ti₃C₂ MXene suffers from a large overpotential. In order to reduce this overpotential, modifications must be made to the structure to increase the reaction rate of the H⁺/e⁻ coupled transfer steps. These modifications heavily depend on understanding the HER mechanism. To remedy this, in situ/operando Raman spectroelectrochemistry combined with density functional theory (DFT) calculations are utilized to probe the HER mechanism of the Ti₃C₂ MXene catalyst in aqueous media. In acidic electrolytes, the –O– termination groups are protonated to form Ti–OH bonds, followed by protonation of the adjacent Ti site, leading to H₂ formation. DFT calculations show that the large overpotential is due to the lack of an optimum balance between O and Ti sites. In neutral electrolytes, H₂O reduction occurs on the surface and leads to surface protonation, followed by H₂ formation. This results in an overcharging of the structure that leads to the observed large HER overpotential. This study provides new insights into the HER mechanisms of MXene catalysts and a pathway forward to design efficient and cost-effective catalysts for HER and related electrochemical energy conversion systems.

---

Introduction

Environmental issues, including climate change, have led to a need for renewable fuels, such as hydrogen (H₂) fuel.^1,2 However, currently the major source of H₂ is from non-renewable sources, such as steam methane reforming, during which carbon dioxide (CO₂) is formed as a byproduct. CO₂ is considered a major contributor to negative environmental impacts including global warming.³ A method to producing renewable H₂ fuel is through the electrochemical splitting of water via the hydrogen evolution reaction (HER) electrocatalysis. This reaction provides a major upgrade in that the only reagents are water and a properly selected electrocatalyst that is able to overcome the sluggish kinetics.⁴

The current benchmark catalyst for the HER is platinum supported on carbon (Pt/C), which due to the high cost and low availability of Pt, could be limited to only small-scale H₂ productions.⁵ To this end, many research efforts have been focused on developing new catalyst systems that can reach similar performance, but at significantly lower costs. One material that has been receiving attention as of late is the special class of two-dimension (2D) transition metal-based carbide or nitride materials, known as MXenes.^6–8 These materials, commonly denoted as M_nX_n−1T_x (where M is an early transition metal, such as Ti, Mo, V, etc., X is either C and/or N, and T_x is basal plane termination groups, such as –O–, –F, and/or –OH), were first discovered in 2011 from the selective etching of the “A” layer from the parent MAX phase.⁹ The most studied and optimized MXene is the Ti₃C₂ carbide MXene, which has gained a large amount of attention due to its strong performance and ease of modification.^10–12

Regarded as the benchmark, Ti₃C₂ MXene has shown remarkable performance in energy storage and conversion.^13–15 However, it does not perform as good as one would expect in HER electrocatalysis given its high electronic conductivity and high performance in similar electrolytic systems. Although predicted to be active for HER, so far, terminated Ti₃C₂ MXene, has shown a large overpotential for HER in aqueous electrolytes.^11,16,17 The overpotential for Ti₃C₂ is nearly twice as large as that of its counterpart, Ti₄N₃ nitride MXene (0.8 V vs. 0.4 V, respectively), and much larger than that for its peer, Mo₂C carbide MXene.^12,18,19 To date, there is no report that explains the reason behind this large unexpected overpotential.

To understand and uncover the reason behind the large overpotential of Ti₃C₂ MXene in HER electrocatalysis, a true understanding of the mechanism is needed, as this will provide insight into active site location and how electron distribution is affected during reaction conditions. Currently, the HER mechanism of Ti₃C₂ MXene is unknown. There are currently no published studies that explains the mechanism of HER of Ti₃C₂ MXene. This lack of report can partially be assigned to the ill-favored large overpotential of the material. Through detailed mechanistic studies, we can provide insight into what modifications need to be made to enable lower overpotentials.

Herein, we report on the use of in situ/operando Raman spectroelectrochemistry to investigate the HER mechanism of Ti₃C₂ MXene, and explain the origin of the large overpotential. Raman spectroscopy has been employed to provide insight into the mechanism of HER for a number of materials,^20–23 but it has not been used in MXene electrocatalysis. Through in situ/operando Raman analysis, we provide reasonings for the poor performance of the Ti₃C₂ MXene for the HER process. By using in situ/operando Raman spectroelectrochemical technique, we observe the transition in functional groups and the overcharging of the Ti₃C₂ MXene material under acidic and neutral media, respectively. In situ/operando Raman analysis also provides the stability of the catalyst under these conditions through the reversibility of the changes observed after HER conditions cease.

Experimental methods

Synthesizing delaminated Ti₃C₂

Ti₃C₂ MXene (0.5 g) (NanoChemAZone 99 wt%) was intercalated with DMSO (10 mL) by stirring covered for 18 hours. After stirring, the solution was placed in a centrifuge vial, and filled with water. This mixture was then centrifuged (Thermo Scientific Sorvall ST16) at 3500 rpm (1962 RCF) for 15 minutes. The supernatant was then removed, the vial refilled with water, and centrifuged at 3500 rpm for 30 minutes. After removing the supernatant, the solution was again filled with water and centrifuged again at 3500 rpm for 30 more minutes. After this final removal of the supernatant, the precipitate was filtered on a Celgard 3501 membrane, and dried in a vacuum oven overnight at 50 °C.

Characterization

The crystalline structure of the material was analyzed using XRD (Rigaku MiniFlex 6G). Surface morphology was analyzed using SEM (FEI Quanta 600 FE-SEM courtesy of the TAMU Microscopy and Imaging Center) equipped with an energy-dispersive X-ray analyzer (EDS), and Raman spectroscopy (Renishaw inVia Qontor) equipped with a 785 nm laser, an 1800 lines per mm grating, and a 50 × L objective lens.

Electrode preparation for ex situ electrochemistry

To prepare a sample for ex situ electrochemical characterization, MXene (4 mg) was mixed into 5 wt% Nafion in ethanol (16 μL) (Fuel Cell Store) and ethanol (400 μL) (Acros Organics, 99.5+%), then sonicated for 30 minutes. This suspension (20 μL) was then dropped onto a 5 mm OD glassy carbon rotating ring disk electrode, and dried under vacuum at 50 °C for 30 minutes.

Electrode preparation for in situ electrochemistry

To prepare a sample for loading onto carbon paper (Alfa Aesar Toray Carbon Paper TGP-H-60) to be used as the working electrode, MXene (20 mg) was mixed into 5 wt% Nafion in ethanol (80 μL) and ethanol (200 μL), then sonicated for 30 minutes. This suspension (20 μL) was then dropped onto the carbon paper and dried under fume hood for 30 minutes.

Ex situ electrochemical measurements

All ex situ electrochemical measurements were conducted using a standard 150 mL RRDE cell with a rotating ring disk electrode set-up (model number AFMSRCE) connected to a Pine WaveDriver 100 potentiostat. The reference and counter electrodes were Ag/AgCl (4 M KCl) and graphite, respectively. The working electrode was rotated at a rate of 1600 rpm. All electrochemical measurements were conducted in either 0.5 M HCl or 0.5 M Na₂SO₄ for acidic or neutral conditions, respectively.

In situ/operando Raman during electrochemical measurements

In situ measurements were conducted using a three-electrode electrochemical flow cell with a quartz window from GaossUnion (Tianjin) Photoelectric Technology Company (Fig. S1, ESI†). The counter and reference electrodes were graphite and Ag/AgCl (1 M KCl), respectively. The cell was filled with either Ar-saturated 0.1 M HCl or Ar-saturated 0.5 M Na₂SO₄via the inlet port. All electrochemical tests were performed on a Metrohm AutoLab PGSTAT302N potentiostat. The potentials against reference were converted to the reversible hydrogen electrode (RHE) using E (vs. RHE) = E (vs. Ag/AgCl) + 0.235 + 0.0591 × pH. The Raman spectroscopy was collected using a Renishaw inVia Qontor microscope equipped with a 785 nm laser, a 50 × L objective lens, an 1800 lines per mm grating, and a CCD detector. Signal acquisition time for each spectrum is about 5 seconds at 5% laser power.

Computational methods

Geometry optimizations

The DFT optimized geometries were obtained using the Vienna ab initio simulation package (VASP)^24–26 with the generalized gradient approximation (GGA) exchange and correlation energy Perdew–Burke–Ernzerhof (PBE) functional,²⁷ and the projector augmented wave (PAW)^28,29 pseudopotentials. After constructing the initial unit cell structures for Ti₃C₂, Ti₃C₂O₂H₂, Ti₃C₂F₂, Ti₃C₂O₂, Ti₃C₂O(OH), the structures were relaxed by setting the electronic self-consistent convergence to 10⁻⁵ eV and allowing a preliminary optimization of the simulated structure. Next, the self-consistent electronic convergence setting was increased to 10⁻⁸ eV, and the unit cell volume and shape were fixed for further optimization. The cutoff energy of the plane-wave-basis set was 450 eV. The unit-cell structure was calculated in the Brillouin zone using a 13 × 13 × 1 mesh with the Monkhorst–Pack method.³⁰ All the atoms and degrees of freedom are allowed to relax via a conjugate gradient technique. For the further frequency calculation, we optimized the structure to the high convergence criteria until the forces on the atoms were below 10⁻⁴ eV Å⁻¹ and the energy difference between each electronic self-consistence loop below 10⁻⁸ eV. To investigate the overcharge behavior emulating different applied potentials, we added/removed an electron to the system and recalculated the Raman peak shift and intensity change for reduction and oxidation states.

Calculation of harmonic force constants

The force constants evaluation was done by creating a set of supercells with a displaced atom, and measuring the forces on all atoms, and at the same time fixing the atomic positions. After collecting all force calculation results and obtaining second- and third-order force constants parameters, we post-processed the data utilizing phonopy³¹ to do the mesh sampling for irreducible representations of the unit cell. The acidic medium was simulated by protonation of the oxygenated surface. Effects of explicit electrolyte will be reported in future work.

Calculation of IR and Raman spectrum

To calculate the IR spectrum, second- and third-order force constants, Born effective-charge tensors and irreducible representations are needed. We used the phonopy-spectroscopy software³² and Born effective-charge tensors to generate the simulated IR spectrum and peak table at room-temperature (300 K). For the Raman spectra calculation, we generate the displaced structure of Raman-intensities along Raman vibrational modes and obtain the dielectric constant for each displaced structure. Again, we use phonopy-spectroscopy with the dielectric constant of each displaced structure to generate the simulated Raman spectrum and peak table at room-temperature.

Results and discussion

Catalyst characterization

Prior to conducting the in situ/operando Raman studies, proper understanding of the material, in terms of morphology, structure, and functional groups, is needed. Fig. 1 displays the structure, scanning electron microscopy (SEM) images, X-ray diffraction (XRD), Raman, and Fourier transform infrared (FTIR) spectra, respectively, for the Ti₃C₂ MXene material being studied. Fig. 1a provides the ball-and-stick depiction of the MAX and MXene materials with mixed termination groups, based on data presented further on. The SEM images of the as-purchased MXene material (Fig. 1b) and delaminated MXene (Fig. 1c) show the expected accordion-like and few layer morphology that is expected of a multilayer and delaminated MXene material, respectively.^33–35 The estimated lateral flake size for the delaminated Ti₃C₂ MXene is approximately 5 μm, which will provide a large basal plane for the HER to take place and be studied on. The XRD data of the as-purchased material (Fig. 1d, black trace) matches published data of multilayer MXene, indicating that further delamination was necessary.^36,37 After delamination in DMSO (Fig. 1d, red trace), the XRD data shows a large shift in (002) peak to approximately 6.6°, corresponding to an interlayer spacing (d-parameter) and c-lattice parameter of 1.338 nm and 2.676 nm, respectively. These findings are in line with delaminated Ti₃C₂ materials reported in the literature.^36,37 The Raman spectroscopy (Fig. 1e) matches previously reported data and shows the possible existence of multiple functional groups for the delaminated sample.³⁸ This can be seen from the location of the A_1g Raman mode at 730 cm⁻¹. This Raman mode corresponds to out-of-plane vibrations of the sublattice carbon atoms and will change depending on the surface termination. Complete –OH termination coverage will have a peak at 684 cm⁻¹, mixed –O(OH) terminations at 708 cm⁻¹, –O– terminations at 730 cm⁻¹, and –F terminations at 694 cm⁻¹.³⁹ Due to the location of the A_1g peak, it can be determined that the predominant termination is –O–. The existence of multiple functional groups is then further corroborated by the FTIR data (Fig. 1f), which shows the existence of –OH (broad peak around 3700 cm⁻¹), –O– (small shoulder in the region of 1000 cm⁻¹), and –F (shoulder around 1100 cm⁻¹) functional groups. The peaks at ∼2100–2300 correspond to adventitious CO₂ from the atmosphere, while the peak at ∼2650 cm⁻¹ correspond to aliphatic C–H bonds from atmospheric water adsorption during measurement.

Fig. 1 (a) Stick-and-ball schematic of Ti₃C₂ MXene studied. Termination groups depicted are based on Raman and FTIR spectra. SEM images of (b) as purchased and (c) delaminated Ti₃C₂ MXene. (d) XRD spectra of multilayer Ti₃C₂ MXene (black trace) as received from company and delaminated MXene (red trace). (e) Raman spectrum of delaminated Ti₃C₂ MXene to confirm structural characteristics. (f) FTIR spectrum of delaminated MXene to confirm functional groups. XRD data collected on a zero diffraction Si plate with a well, Raman data collected using a 785 nm laser, 1800 lines per mm grating, and a 50 × L objective lens, FTIR data collected using a diamond ATR crystal.

Electrochemical properties

To gain an understanding of the electrochemical effects of the delaminated Ti₃C₂ MXene, ex situ linear sweep voltammetry (LSV) and Tafel slope analysis were performed in 0.5 M HCl and 0.5 M Na₂SO₄ electrolytes (Fig. 2). The LSV's show that the Ti₃C₂ MXene has better electrocatalytic activity in acidic media with an overpotential of −0.8 V vs. RHE compared to an overpotential of −1.25 V vs. RHE in neutral media due to the high concentration of H⁺ in the acidic media. The Tafel slope of the Ti₃C₂ MXene in acidic electrolyte was found to be 171.5 mV per decade, significantly better than the 416.4 mV per decade Tafel slope for neutral electrolyte. This is in accordance with expectations since acidic electrolyte provides a higher H⁺ concentration to enhance the HER production, whereas neutral electrolyte must rely on the splitting of water to generate protons for HER. Although these values are comparable to those previously reported for the material, they are twice as large as those reported for the counterpart Ti₄N₃ nitride MXene.^12,19 Previous studies have shown that the HER activity increases with decreasing group number, IV > V > VI; however, the Ti-based MXenes have not been able to meet this trend and are being outperformed by the Mo-based MXenes.¹⁸ It should be noted that there was no reductive activity prior to the HER onset potential in 0.5 M HCl while there was reductive activity prior to onset in 0.5 M Na₂SO₄. This reductive activity can be attributed to the splitting of water into adsorbed H* and O* on the surface, as will be discussed further below.

Fig. 2 (a) Ex situ LSV and (b) Tafel slope analysis of Ti₃C₂ MXene in 0.5 M HCl. (c) Ex situ LSV and (d) Tafel slope analysis of Ti₃C₂ MXene in 0.5 M Na₂SO₄. The LSVs were collected at 5 mV s⁻¹ at room temperature.

In situ/operando Raman analysis

We use in situ/operando Raman spectroelectrochemistry to investigate the mechanism of HER on the Ti₃C₂ MXene and provide an explanation to the large overpotential and kinetics. Raman spectroscopy is a powerful tool to probe the HER mechanism on Ti₃C₂ due to its ability to probe the structural changes in the material through its interaction with phonons. Phonons are affected by changes in the structure of the material and can be used to determine structural changes in the material through changes in the locations of Raman modes and through variation in the intensity of the Raman spectra. This becomes especially important in elucidating reaction mechanisms since the structure and surface terminations can be characterized as changes occur in real time. LSVs were used to probe the HER on Ti₃C₂ MXene, and the spectra were recorded as the potential was swept to more cathodic potentials.

Probing Ti₃C₂ HER mechanism in acidic media

The first electrolyte used to probe the HER reaction mechanism was 0.1 M HCl since it provides a large enough concentration of H⁺ for studying the HER process without creating large volumes of gas, which would interfere with the Raman data gathering. LSV paired with Raman spectroscopy provided two main sources of data that were used to characterize the material while it was swept to more cathodic potentials during the HER process. The first set of the data was the absolute intensity of the Raman spectra which would reliably change depending on the potential until bubble formation occurred. The other set of data was the location of peaks in the Raman spectra which could be tracked and directly associated with structural changes in the material. Both data were used to get insights into the mechanism of HER for the Ti₃C₂ MXene, and explain its limited performance.

We found that the absolute Raman intensity was a function of the applied potential, in that it changes in accordance with electrochemical activities during the LSV sweeps. As more negative (cathodic) potential was applied, the Raman intensity increased to a maximum peak at approximately −0.3 V (vs. RHE) and steadily decreased afterwards (Fig. 3a). This suggests that chemical effects are being experienced due to the LSV sweeping through the onset potential to initiate and maintain the formation of H₂ product. This can be visually confirmed through the direct observation of H₂ gas being formed on the material by the end of the LSV curves (Fig. S2, ESI†).

Fig. 3 (a) In situ LSV of Ti₃C₂ MXene in 0.1 M HCl. The black trace displays the current at each time and the colored traces represent the absolute intensity of significant Raman peaks as a function of time. (b) The same in situ LSV from before but shows the peak shift of the A_1g Raman mode at ∼720 cm⁻¹. The LSVs were collected at 5 mV s⁻¹ at room temperature. Raman data were collected using a 785 nm laser, 1800 lines per mm grating, and a 50 × L objective lens.

Raman intensity is directly proportional to the square of the polarizability tensor from the classical interpretation of the Raman spectra and from the Placzek approximation of the quantum mechanical approach.⁴⁰ Given the nature of the performed experiments, this polarizability tensor was the only value that was likely to change throughout. The polarizability tensor determines the magnitude of the dipole moment in multiple directions depending on the applied electric field and is a function of electron density within the material.⁴⁰ The dependence of the polarizability tensor on electron density makes it likely that the electrons flowing into the material were able to increase the magnitude of the Raman spectrum. It is also likely that the Raman intensity would be able to track the change in surface termination due to different terminations creating different structural conditions and electron distributions. Therefore, absolute intensity has been used as a measure of chemical effects in the past. Depending on relative peak heights, the Raman spectrum provides insight into the presence of complexes or into molecular concentrations in a material, meaning that the same analysis of the Raman intensity could be applied in this instance.^41,42 The changes in Raman intensity are likely attributed to charging of the material through the influx of electrons that prompt the adsorption of protons onto the MXene material.

Further fundamental insights into the mechanism of HER on Ti₃C₂ MXene is provided by probing the shifts of the main Raman bands during the in situ/operando measurements. Peak shifting in the A_1g mode of the Raman spectrum was observed and was attributed to a change in the surface termination chemistry. This can be observed over the course of multiple in situ Raman LSV experiments using the Ti₃C₂ material (Fig. 3b). During the course of this experiment, all of the LSV experiments were performed on the same flake with images showing the status of the flake before, during, and after the experiments (Fig. S2†). Each LSV that was performed showed a peak shift of the A_1g Raman mode from 735 cm⁻¹ to 715 cm⁻¹ during the course of the experiment. The peak shifting towards lower wavenumbers indicates a transition in surface termination chemistry. Before reaction conditions, the Ti₃C₂ MXene initially had a peak location of 735 cm⁻¹ in 0.1 M HCl solution. This was slightly different than the value of 730 cm⁻¹ attributed to –O– terminations but can be explained by intercalants having the ability to shift peaks slightly.³⁸ Over the course of the LSV, electrons enter the MXene material and draw H⁺ to the surface terminations. This would correspond to a shift from the –O– termination to the –O(OH) termination and is seen in the Raman spectra as the shift from 735 cm⁻¹ to 715 cm⁻¹.³⁹ Before the start of the next LSV, the peak shift realigned with the initial state at 735 cm⁻¹, indicating that the overall termination change from –O– to –O(OH) is reversible under HER conditions (Fig. 3b), consistent with a deprotonation mechanism. This transition of termination groups provides some reasoning for why the Ti₃C₂ MXene underperforms so drastically as an HER catalyst. The requirement of termination groups to transition to the –OH group, followed by deprotonation, indicates multiple steps in the HER mechanism, one of which could be the reason for the high overpotential of this material. Since a termination group change must take place before a deprotonation step prior to the formation of H₂, it is most likely that only a fraction of the material could be active towards HER at a time. It is possible that the observed limited HER activity for Ti₃C₂ MXene is due to the requirement of termination group transition from –O– to –OH groups as corroborated by theoretical predictions.¹⁹ As most Ti₃C₂ MXene materials are obtained through hydrofluoric acid (HF) etching, which results in a predominantly –F groups, they would most likely behave unfavorably towards HER.

After reaching the onset potential, the A_1g mode merges into the E_g peak at ∼680 cm⁻¹, and the absolute intensity of the Raman spectrum decreases upon approaching the 10 mA cm⁻² current density for HER (Fig. S3, ESI†). These phenomena have two possible interpretations, evolved H₂ gas interfering with the collection of Raman spectra and/or refractory effects of H₂ gas changing the path of the incident laser to minimize collection. Both explanations, while potentially valid, do not provide the complete explanation of the observed peaks merge and Raman intensity decrease, since after the LSV was stopped, the characteristic Raman spectra for Ti₃C₂ from prior to the HER experiment reappeared, despite the presence of adsorbed H₂ gas on the basal plane (Fig. 3b and S2†). The merging of the peaks and decrease in Raman intensity can most likely be ascribed to the transformation of termination groups while the material is undergoing HER. Throughout the process of HER, the –O– surface terminations adsorb H⁺ that combine with other adsorbed H⁺ to form H₂ gas. This means that following the onset of HER, the surface terminations will be a rapidly changing mixture of –O–, –O(OH), and –(OH)₂ groups, which would affect the Raman spectra. The spectrum also does not return to its absolute intensity after the experiment due to H₂ gas bubbles that remain on the basal plane. This can be proved through the return of the 730 cm⁻¹ peak since peak position is not affected by the amount of light that reaches the detector while the absolute intensity is dependent on how much light reaches the detector. Following the reaction sequence described above, the rate limiting step would be the formation of a fully protonated –OH terminated material for H₂ formation.

Probing Ti₃C₂ HER mechanism in neutral media

Given the observed results in 0.1 M HCl, in situ/operando Raman spectroelectrochemistry was then used to investigate the changes of Ti₃C₂ MXene structure in neutral conditions during HER by using 0.5 M Na₂SO₄ electrolyte. In this media, peak shifting and absolute intensity changes similar to those in 0.1 M HCl were observed (Fig. 4). Unlike 0.1 M HCl, there is no direct source of protons in solution except for the autoelectrolysis of water, meaning that the similar electronic effects had to be stemming from a different source. During the experiment, the peak for the A_1g mode shifted from 735 cm⁻¹ to 725 cm⁻¹, corresponding to the observance of reductive activity and overcharging of the termination groups as observed from DFT calculations (vide infra) (Fig. 4b). This could indicate a different HER mechanism or pathways in neutral media since the shift in Raman peak is lesser than in acidic media.

Fig. 4 (a) In situ LSV of Ti₃C₂ MXene in 0.5 M Na₂SO₄. The black trace displays the current at each time and the colored traces represent the absolute intensity of significant Raman peaks as a function of time. (b) The same in situ LSV from before but shows the peak shift of the A_1g Raman mode at ∼720 cm⁻¹. The LSVs were collected at 5 mV s⁻¹ at room temperature. Raman data were collected using a 785 nm laser, 1800 lines per mm grating, and a 50 × L objective lens.

At some point, water must be adsorbed to the surface for water splitting to occur, as this would be the only source of H⁺ for H₂ formation. We know that H₂ is formed due to the observation of bubbles on the surface of the MXene following the LSV experiment (Fig. S4, ESI†). Due to this, it is likely that the observed reductive activity and overcharging is directly related to the water splitting mechanism for Ti₃C₂ MXene. The A_1g Raman mode steadily decreases until it merges into the larger E_g peak around ∼680 cm⁻¹, but returns following the end of the experiment despite the presence of bubbles (Fig. S5, ESI†). Again, this shows that the spectral distortion following onset is not entirely due to the evolution of gas and is partially intrinsic to HER. The absolute intensity change of the Raman spectrum also follows a similar path to that in acidic media (Fig. 4a). During the overcharging of the MXene and consequential adsorption of molecules to the surface of the Ti₃C₂ MXene, the absolute intensity of the Raman spectrum increases, and then decreases following the onset potential for HER. Similar to acidic media, the absolute intensity of the Raman spectra presents a qualitative view of chemical changes for the Ti₃C₂ MXene in real time. This overcharging mechanism in neutral media partially explains the poor performance of Ti₃C₂ towards HER. This is because the material must first put enough electrons into the system to split water molecules, which then form the reactive intermediates to produce the H₂ gas.

Mechanistic insights from density functional theory (DFT)

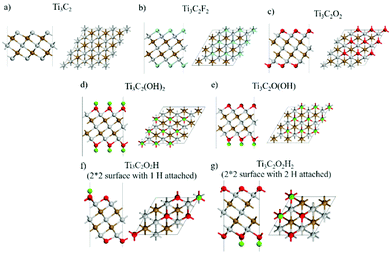
We use DFT calculations to gain further insights on the mechanism of HER on the Ti₃C₂ MXene. DFT calculations were carried out on pristine and functional group terminated MXene structures. The effect of electron transfer on the Raman intensity was corroborated by the DFT results, which provide further credence to the electronic description of the Raman intensity change. Fig. 5 illustrates the systems investigated. DFT optimizations were performed to evaluate the structures of Ti₃C₂, Ti₃C₂F₂, Ti₃C₂O₂H₂, and Ti₃C₂O₂. Absolute and relative energies reported in Table S10.† After optimization, the Raman and IR spectra were calculated using the techniques described under Computational methods.

Fig. 5 Optimized unit cell structures (represent with 3 × 3 supercell), side view, top view and its supercell structure for (a) Ti₃C₂, (b) Ti₃C₂F₂, (c) Ti₃C₂O, (d) Ti₃C₂(OH)₂, (e) Ti₃C₂O(OH). (f) and (g). Optimized cell of Ti₃C₂O₂ MXene in a 2 × 2 supercell with one (f) and two (g) H atoms attached. Color code: gray, red, brown, blue, and green represents Ti, O, C, F, and H respectively.

To emulate the effect of an applied potential, we introduced/removed one electron to the computational cell to represent reduction/oxidation conditions, respectively. After electronic distribution due to the addition/removal of 1 electron, we re-evaluate the Raman spectra and compare the changes in peaks positions and intensities in comparison with the experimental data. Although the amount of charge added/removed is arbitrary, the results illustrate the trends expected for an excess/deficiency of electrons on the surface. The c-lattice parameter varies with the surface functionalization contracting (for –F) or expanding (for –O– and –OH) with respect to the Ti₃C₂ value of 2.292 nm (Table S1, ESI†). Thus, the expanded c-parameter values best agree with the XRD value of 2.676 nm for an –O– (2.222 nm) and –OH (2.316 nm) functionalization. The calculated interlayer parameter of 1.562 nm for Ti₃C₂ contracts under functionalization, with a minimum value for –F (1.271 nm), followed by 1.301 nm for –OH termination and 1.340 nm for –O– termination. Again, the measured value (1.338 nm) is closer to that calculated for an –O– terminated surface, consistent with the conclusion from experimental findings.

Comparing the experimental –OH (broad peak around 3700 cm⁻¹), –O– (small shoulder in the region of 1000 cm⁻¹), and –F (shoulder around 1100 cm⁻¹), the DFT calculated IR spectra (Fig. S6 and Tables S2–S6, ESI†) do not show strong signal for Ti₃C₂F₂ or Ti₃C₂O₂H₂, but the result shows a broad peak signal for Ti₃C₂O₂ at ∼574 cm⁻¹ which suggests further evidence for the –O– functionalization.

The DFT Raman spectra simulated at 300 K for each neutral system is compared to those with the addition or removal of one electron (Fig. S7, ESI†). Comparing the experimental A_1g Raman peak location for functionalized Ti₃C₂ (730 cm⁻¹) with the calculated –OH, –O(OH) and –O– terminations (Table 1), the results point to Ti₃C₂O₂ at 737.05 cm⁻¹ under neutral charge as the closest peak. For the Ti₃C₂ MXene at low potential under 0.5 M Na₂SO₄ neutral electrolyte, the peak of A_1g shifted from 735 cm⁻¹ to 725 cm⁻¹_. From calculated values in Fig. S7† and Table 1, the shift is attributed to overcharging of the Ti₃C₂ MXene surface when low potentials were reached, with frequencies close to the peak calculated during the reduction process. Consistent with the in situ/operando Raman results, the A_1g Raman frequency shifted from 737.05 cm⁻¹ to 721.85 cm⁻¹ during the charging process, and the intensity significantly increased by two orders of magnitude from 0.022 × 10⁶ e² amu⁻¹ to 2.12 × 10⁶ e² amu⁻¹.

Table 1 DFT calculated Raman spectra: frequencies (ν), irreducible representation (Ir. rep.), intensity (I)

System	Oxidation			Neutral charge			Reduction
	ν [cm^−1]	Ir. rep.	I [e^2 amu^−1] × 10^−6	ν [cm^−1]	Ir. rep.	I [e^2 amu^−1] × 10^−6	ν [cm^−1]	Ir. rep.	I [e^2 amu^−1] × 10^−6
Ti3C2	606.66	Ag	0.741	626.3	Ag	0.658	624.69	Bg	5.849
	606.67	Bg	0.229	626.31	Bg	0.659	624.86	Ag	5.852
Ti3C2O2	657.72	A	561	737.05	Ag	0.022	721.85	Ag	2.120
Ti3C2F2	669.44	Ag	0.029	694.92	Ag	0.040	686.95	Ag	22.891
Ti3C2(OH)(O)				700.66	A′	0.122

---

However, when Ti₃C₂ MXene was charged in acidic 0.1 M HCl electrolytes, and during reduction, the peak shifted from ∼735 cm⁻¹ to ∼710 cm⁻¹. This shift is compared to the experimentally observed peak shift from 737 cm⁻¹ (Ti₃C₂O₂) to 700 cm⁻¹ (Ti₃C₂(OH)(O)), with peak intensity changing from 0.022 × 10⁶ e² amu⁻¹ to 0.122 × 10⁶ e² amu⁻¹ (Fig. S8, ESI†). Thus, the frequency shift between Ti₃C₂O₂ and Ti₃C₂(OH)(O) is attributed to transformation of termination groups while undergoing HER, consistent with the experimental results. Throughout the HER process, the calculated surface terminations Ti₃C₂O₂ (737.05 cm⁻¹) adsorb H⁺ and form partially hydrogenated Ti₃C₂(OH)(O) terminated surface.

Surface termination with functional groups causes structural and electronic changes. During reduction, the excess electrons induce the Ti–C bond length to decrease for the outer Ti atom for all surface terminations, indicating stronger bonds, whereas the Ti–C bond length is slightly elongated (weaker bonds) for the internal Ti in all surface terminations (Table S7, ESI†). The strengthening of the outer Ti–C bond may also affect the HER reaction. To investigate the distributions of added or removed electrons into the structure, we evaluated the Bader atomic charges on T_x (terminal functional atom), Ti₁ (outer Ti), Ti₂ (inner Ti), and C₁ atom bonded to Ti₁ (Table 2).

Table 2 Calculated atomic Bader charges (e) during oxidation (1e⁻ removed), neutral, and reduction (1e⁻ added)

Bader charge [e]
	Oxidation	Neutral	Reduction
Atom T x
Ti3C2F2	−0.585	−0.733	−0.989
Ti3C2O2H2	0.538	0.25	−0.052
Ti3C2O2	−0.828	−0.965	−1.323
Atom Ti 1
Ti3C2F2	1.725	1.37	1.244
Ti3C2O2H2	1.604	1.379	1.252
Ti3C2O2	1.809	1.571	1.511
Atom C 1
Ti3C2F2	−1.338	−1.236	−1.315
Ti3C2O2H2	−1.242	−1.282	−1.342
Ti3C2O2	−1.148	−1.233	−1.323
Atom Ti 2
Ti3C2F2	1.382	1.188	1.133
Ti3C2O2H2	1.264	1.222	1.211
Ti3C2O2	1.355	1.262	1.278

---

The main observations from Table 2 are that the added electron (reduction) goes mainly into the external functional groups (O > OH > F) with the outer Ti₁ having the second significant charge increase (smaller positive charges in the order O = OH ≫ F), whereas in C₁ and Ti₂ the changes are negligible. This high electron localization on the terminal groups and outer Ti atoms is in agreement with the in situ/operando Raman results, and is expected to influence the catalytic activity.

To get further insights into the surface reactivity, we computed the d-band center (Table 3) of the Ti atoms from the density of states (DOS) of the structures (Fig. S9, ESI†). A summary of the atomic assignments is provided in Fig. S10 (ESI†). The d-band center of the outer Ti atom in the pristine Ti₃C₂ is located at 0.06 eV in the E − E_Fermi scale (i.e., practically at the Fermi energy) and shifts to more negative energies (away from the Fermi level) as electrons are added, indicating that under a reductive environment the surface is less reactive. A similar shift occurs for the inner Ti₂. However, the values of the d-band center obtained for surface oxidation conditions suggest that reactivity would remain about the same or be slightly enhanced for these Ti atoms. For the functionalized surfaces, the values in Table 3 show the O-terminated surface having the d-band center value closest to the Fermi energy suggesting that among all systems this surface is the most reactive. Since the O atoms may act as proton receptors during HER, we also evaluated bond strengths using the crystal orbital Hamilton population (COHP) analysis, that allows computing bonding and antibonding contributions to the band-structure energy for a pair of adjacent atoms. Integrating this COHP energy function up to the Fermi level, we obtain ICOHP, an estimate of the bond strength (Table S8, ESI†). The C₁–Ti₁ bonds of C with the outer Ti become stronger with the presence of the functional groups (under reduction and neutral conditions), with the largest enhancement of the bond strength with OH-terminated surface. On the other hand, the C₁–Ti₂ bonds become much weaker. These results are in agreement with those inferred from the bond lengths in Table S7.† More importantly for the HER, the ICOHP analysis in Table S8† shows that the O–H bond strength is very strong, which may suggest a favorable proton adsorption on the O-functionalized surfaces. These results corroborate the in situ/operando Raman spectroelectrochemical results that the HER mechanism on Ti₃C₂ MXene in aqueous media involves the protonation of the O-terminated groups to –OH followed by protonation of a bare surface Ti. Afterwards, the –OH and Ti–H are deprotonated to form H₂, which then desorbs and diffuses into the electrolyte. This mechanism is further discussed in the next section on the basis of DFT reaction energies.

Table 3 DFT computed Ti d-band center location (from DOS where the Fermi value is located E − E_f = 0), and Fermi level value (E_f, eV) for each surface

System		d-band center Ti1 [eV]	d-band center Ti2 [eV]	E F [eV]
Ti3C2	Oxidation	0.048082	−0.32444	−10.9822
	Neutral	0.065577	−0.66587	−0.0684
	Reduction	−0.32717	−0.9958	1.223485
Ti3C2F2	Oxidation	0.145373	−0.13035	−8.07865
	Neutral	−0.16286	−0.39075	1.102082
	Reduction	−0.51238	−1.15572	2.778407
Ti3C2O2	Oxidation	0.675589	0.861695	−11.0379
	Neutral	0.198013	0.107459	−0.20149
	Reduction	−0.21298	−0.66974	2.087213
Ti3C2O2H2	Oxidation	0.199246	0.017371	−7.12135
	Neutral	−0.32583	−0.96638	2.529844
	Reduction	−0.56531	−1.23158	2.337724

---

Reaction thermodynamics and mechanisms

From the above experimental and theoretical evidences, we postulated the following mechanisms and evaluated them through DFT optimizations of the proposed structures and calculation of the respective reaction energies.

For a fully oxygenated surface, Ti₃C₂O₂ (Fig. 5), the O atoms are adsorbed in the hollow sites, and have three Ti neighbors. The first set of reactions, in acidic medium, involves a two-step surface protonation, where a proton is adsorbed on the surface terminal O, (step 1), and another proton onto a vacant Ti site (step 2). The first step is highly exothermic (−2.92 eV) and the second is slightly endothermic (0.05 eV). Step 3 includes bonding of the two adjacent protons and release of H₂ from the surface which is thermodynamically favorable (−1.67 eV). These steps are summarized in Fig. 6a.

Fig. 6 Schematics for HER mechanisms in (a) acidic electrolyte and (b) neutral electrolyte. In acidic electrolyte, the first H⁺/e⁻ transfer step protonates the –O– termination group into –OH. Afterwards, the next H⁺ protonates the bare Ti site. The adjacent –OH and –H* then react to form H₂ which desorbs from the surface, recreating the –O– termination. In neutral electrolytes, water is split across the –O– termination leading to protonation of two adjacent Ti sites and oxidation of the final bare Ti site. The adjacent –H termination groups then react to form H₂ which desorbs from the surface.

Acidic medium:

Ti–O–Ti + H⁺ + e⁻ → Ti–OH*–Ti (1)

Ti–OH*–Ti + H⁺ + e⁻ → Ti–OH*–Ti–H* (2)

Ti–OH*–Ti–H* → Ti–O–Ti + H₂ (3)

Additional calculations were carried out to prove that the second protonation may depend on the extent of the first protonation. In this new set of calculations, to consider the solvation effect we evaluated a hydronium ion initially located over the Ti₃C₂O₂ surface. It was shown that if naked O sites are available, the proton prefers to adsorb on the O site instead of over the Ti site. Due to this favorable adsorption, formation of a fully OH–covered surface is very likely. In the case of a completely OH-functionalized surface Ti₃C₂(OH)₂, the DFT analysis shows that H₃O⁺ is able to deprotonate over the OH site, and a water molecule is adsorbed on a nearby Ti site. The adsorbed proton (OHH*) reacts with an adjacent OH* and H₂ is observed to evolve during DFT optimization steps, leaving “naked” O* sites on the surface. After H₂ forms and drifts away from the surface, the adsorbed H₂O rotates with one of the H atoms pointing toward a “naked” O* site on the surface and adsorbs on it.

The spontaneous release of H₂ observed during the DFT optimization indicates that this reaction should be highly favorable in a fully protonated surface. However, if the concentration of OH on the surface becomes too low, we found that HER is less favorable, as protonation of the O* sites will be preferred over that of the OH* sites, thus going through the above discussed (1) to (3) steps. In summary, a high concentration of OH sites are necessary to promote H₂ evolution, and the lack of an optimum surface protonation–deprotonation balance may be the cause of the enhanced overpotential in these conditions.

The next analysis refers to reactions in neutral medium. Step (4) involves water splitting over Ti sites, and it is uphill with a reaction energy of 0.26 eV. Step (5) is also thermodynamically unfavorable (1.55 eV), and hydrogen evolution from the surface appears as the rate limiting step. These reaction steps are summarized in Fig. 6b, and the energy profiles are included in Fig. S11.†

Neutral medium:

Conclusions

We use in situ/operando Raman spectroscopy to explain the large overpotential of Ti₃C₂ MXene by probing its mechanism of HER catalysis in aqueous media. In acidic media, where the concentration of protons is high, we observe a transition of –O– terminations to –O(OH) in a proton adsorption step occurring at −0.3 V (vs. RHE) as evidenced by a peak shift in the A_1g mode. Following this, more protons from the solution are used to evolve H₂ gas past the onset potential. In neutral media, where the concentration of H⁺ is low, we observe an overcharging of the –O– surface termination during the sweep to lower potentials prior to the onset potential for HER and was corroborated through DFT analyses. Frequency shifts and changes in the intensities of the A_1g modes during the charging process was corroborated by the DFT spectra. Also, shifts obtained with a partial adsorption of H⁺ on the O-terminated surface are consistent with a protonation step during HER. Evaluation of bond strengths reveal that the reduction process substantially increases the Ti–C bond strength for the outer Ti atoms, which along with the shift of the Ti d-band center away from the Fermi level indicate a much lower reactivity during reduction, which may explain in part the large HER overpotential. Evaluation of the reaction thermodynamics in acidic medium suggests that lacking an optimum protonation/deprotonation balance on the surface may lead to enhanced overpotentials, whereas the H₂ formation/desorption step is limiting in neutral medium. We showed that we can use the absolute Raman intensity to probe the structural and chemical changes in the Ti₃C₂ MXene material, which indicate the overcharging of the material, the adsorption of molecules to the Ti₃C₂ MXene, and the evolution of products following the onset of HER. We hypothesize that the decrease in absolute intensity is through a decrease in long-range order upon the evolution of H₂ gas but needs to be developed more thoroughly through the use of X-ray absorbance spectroscopy (XAS). Future work in this area will involve using XAS to further analyze the material in acidic, neutral, and basic electrolytes.

Author contributions

Denis Johnson, Hao-En Lai, and Kyle Hansen contributed equally towards investigation and writing. Dr Perla Balbuena and Dr Abdoulaye Djire contributed equally to the supervision and reviewing & editing this manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the Department of Chemical Engineering at Texas A&M University, the College of Engineering, Dr. Mark Barteau, and the Provost for their financial support. This work was funded by Texas A&M University (TAMU), Texas A&M Engineering Experiment Station (TEES), and the Governor's University Research Initiative (GURI).

Notes and references

1. S. G. Yalew, M. T. van Vliet, D. E. Gernaat, F. Ludwig, A. Miara, C. Park, E. Byers, E. De Cian, F. Piontek and G. Iyer, Nat. Energy, 2020, 5, 794–802.
2. A. Ajanovic and R. Haas, Int. J. Hydrogen Energy, 2021, 46, 10049–10058.
3. E. Shagdar, B. G. Lougou, Y. Shuai, E. Ganbold, O. P. Chinonso and H. Tan, RSC Adv., 2020, 10, 12582–12597.
4. W. Xiao, D. Yan, Y. Zhang, X. Yang and T. Zhang, Energy Fuels, 2021, 35, 4609–4615.
5. L. Liang, H. jin, H. Zhou, B. Liu, C. Hu, D. Chen, J. Zhu, Z. Wang, H.-W. Li, S. Liu, D. He and S. Mu, J. Energy Chem., 2022, 65, 48–54.
6. C. Cui, R. Cheng, H. Zhang, C. Zhang, Y. Ma, C. Shi, B. Fan, H. Wang and X. Wang, Adv. Funct. Mater., 2020, 30, 2000693.
7. K. R. G. Lim, A. D. Handoko, L. R. Johnson, X. Meng, M. Lin, G. S. Subramanian, B. Anasori, Y. Gogotsi, A. Vojvodic and Z. W. Seh, ACS Nano, 2020, 14, 16140–16155.
8. X. Wang, C. Wang, S. Ci, Y. Ma, T. Liu, L. Gao, P. Qian, C. Ji and Y. Su, J. Mater. Chem. A, 2020, 8, 23488–23497.
9. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
10. X. An, W. Wang, J. Wang, H. Duan, J. Shi and X. Yu, Phys. Chem. Chem. Phys., 2018, 20, 11405–11411.
11. X. Li, X. Lv, X. Sun, C. Yang, Y.-Z. Zheng, L. Yang, S. Li and X. Tao, Appl. Catal., B, 2021, 284, 119708.
12. L. Huang, L. Ai, M. Wang, J. Jiang and S. Wang, Int. J. Hydrogen Energy, 2019, 44, 965–976.
13. T. B. Sobyra, T. S. Mathis, Y. Gogotsi and P. Fenter, ACS Appl. Mater. Interfaces, 2021, 13, 43597–43605.
14. A. Al-Temimy, B. Anasori, K. A. Mazzio, F. Kronast, M. Seredych, N. Kurra, M.-A. Mawass, S. Raoux, Y. Gogotsi and T. Petit, J. Phys. Chem. C, 2020, 124, 5079–5086.
15. J. Xia, S.-Z. Yang, B. Wang, P. Wu, I. Popovs, H. Li, S. Irle, S. Dai and H. Zhu, Nano Energy, 2020, 72, 104681.
16. X. Wu, Z. Wang, M. Yu, L. Xiu and J. Qiu, Adv. Mater., 2017, 29, 1607017.
17. W. Yuan and L. Cheng, in MXenes: Fundamentals and Applications, Materials Research Forum LLC, 2019, vol. 51, ch. 4, pp. 74–104.
18. Z. W. Seh, K. D. Fredrickson, B. Anasori, J. Kibsgaard, A. L. Strickler, M. R. Lukatskaya, Y. Gogotsi, T. F. Jaramillo and A. Vojvodic, ACS Energy Lett., 2016, 1, 589–594.
19. A. Djire, X. Wang, C. Xiao, O. C. Nwamba, M. V. Mirkin and N. R. Neale, Adv. Funct. Mater., 2020, 30, 2001136.
20. Y. Zhao, T. Ling, S. Chen, B. Jin, A. Vasileff, Y. Jiao, L. Song, J. Luo and S.-Z. Qiao, Angew. Chem., Int. Ed., 2019, 58, 12252–12257.
21. A. Y. Faid, A. O. Barnett, F. Seland and S. Sunde, Electrochim. Acta, 2020, 361, 137040.
22. J.-s. Zhu, H. Yang, W. Zhang, Y. Mao, S.-s. Lyu and J. Chen, Inorg. Chem. Front., 2020, 7, 1892–1899.
23. L. Zhai, T. W. Benedict Lo, Z.-L. Xu, J. Potter, J. Mo, X. Guo, C. C. Tang, S. C. Edman Tsang and S. P. Lau, ACS Energy Lett., 2020, 5, 2483–2491.
24. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
26. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
31. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
32. J. M. Skelton, L. A. Burton, A. J. Jackson, F. Oba, S. C. Parker and A. Walsh, Phys. Chem. Chem. Phys., 2017, 19, 12452–12465.
33. M. Shekhirev, C. E. Shuck, A. Sarycheva and Y. Gogotsi, Prog. Mater. Sci., 2021, 120, 100757.
34. T. S. Mathis, K. Maleski, A. Goad, A. Sarycheva, M. Anayee, A. C. Foucher, K. Hantanasirisakul, C. E. Shuck, E. A. Stach and Y. Gogotsi, ACS Nano, 2021, 15, 6420–6429.
35. B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098.
36. O. Mashtalir, M. Naguib, V. N. Mochalin, Y. Dall'Agnese, M. Heon, M. W. Barsoum and Y. Gogotsi, Nat. Commun., 2013, 4, 1716.
37. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005.
38. A. Sarycheva and Y. Gogotsi, Chem. Mater., 2020, 32, 3480–3488.
39. T. Hu, J. Wang, H. Zhang, Z. Li, M. Hu and X. Wang, Phys. Chem. Chem. Phys., 2015, 17, 9997–10003.
40. P. Bruesch, Phonons: Theory and Experiments II, Springer, 1 edn, 1986.
41. C. J. Strachan, T. Rades, K. C. Gordon and J. Rantanen, J. Pharm. Pharmacol., 2007, 59, 179–192.
42. P. Colomban and A. Slodczyk, Opt. Mater., 2009, 31, 1759–1763.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2nr00222a

‡ These authors contributed equally to this work.

---