On the problem of Dirac cones in fullerenes on gold

Abstract

Artificial graphene based on molecular networks enables the creation of novel 2D materials with unique electronic and topological properties. Landau quantization has been demonstrated by CO molecules arranged on the two-dimensional electron gas on Cu(111) and the observation of electron quantization may succeed based on the created gauge fields. Recently, it was reported that instead of individual manipulation of CO molecules, simple deposition of nonpolar C₆₀ molecules on Cu(111) and Au(111) produces artificial graphene as evidenced by Dirac cones in photoemission spectroscopy. Here, we show that C₆₀-induced Dirac cones on Au(111) have a different origin. We argue that those are related to umklapp diffraction of surface electronic bands of Au on the molecular grid of C₆₀ in the final state of photoemission. We test this alternative explanation by precisely probing the dimensionality of the observed conical features in the photoemission spectra, by varying both the incident photon energy and the degree of charge doping via alkali adatoms. Using density functional theory calculations and spin-resolved photoemission we reveal the origin of the replicating Au(111) bands and resolve them as deep leaky surface resonances derived from the bulk Au sp-band residing at the boundary of its surface projection. We also discuss the manifold nature of these resonances which gives rise to an onion-like Fermi surface of Au(111).

---

1. Introduction

Graphene is one of the most prominent 2D materials with tremendous potential for applications in electronics, optics and spintronics. In recent years, there has been a significant progress toward the creation of artificial graphene either in the form of ultra-cold atoms confined in optical lattices^1–3 or on the basis of molecular networks.^4–6 The latter could set up a pathway toward engineering synthetic graphene-like systems with unique novel properties. In particular, it was shown that CO molecules on a Cu(111) substrate create a network of hollow-site-potentials imposed onto the 2D electron gas (2DEG) of a metal surface.⁶ This potential, shaped up by muffin-tin-like spheres of electron exclusion and induced by the field of adsorbed molecules, is equivalent to a honeycomb graphene lattice and gives rise to the formation of topological Dirac cones in the surface band structure of copper. Using atomic manipulation, artificial graphene subjected to triaxial strain was created leading to the observation of Landau quantization.⁶ Such internal gauge fields are also the basis for the predicted fractionalization of electron charge⁷ and anyon formation⁸ in graphene.

Very recently, the realization of similar Dirac cones was demonstrated directly by angle-resolved photoemission (ARPES) for a molecular network of buckyball fullerenes C₆₀ deposited on the (111) faces of Cu and Au crystals.⁹ Dirac-cone-like features were observed at the corners of the mini Brillouin zone associated with fullerene superstructures which are (4 × 4) for Cu(111) and (2√3 × 2√3)R30° for Au(111). It was argued that buckyball fullerenes, similarly to CO molecules,⁶ can also impose muffin-tin-like hollow potentials on a 2DEG hosted at the noble metal surface, hence creating graphene-like band structures. While the generation of such exclusion potentials enforcing scattering of 2DEG toward honeycomb-confined lattice seems feasible in the case of strongly polar CO molecules, it can hardly be comprehended for non-polar and chemically inert C₆₀.

To tackle this controversy we performed extensive investigations of C₆₀ on Au(111) by angle- and spin-resolved photoemission and by density functional theory (DFT). Our results suggest that the realization of artificial graphene by a fullerene network may not be the only explanation for the Dirac cones reported earlier.⁹ In the following we will demonstrate that the linear bands are merely mimicking Dirac cones, and instead derive from umklapp scattering of photoelectrons on the hexagonal and perfectly periodic superlattice of fullerenes – with no need for involvement of muffin-tin-like hollow potentials and without the realization of artificial graphene. Ultimately, we can attribute the formation of false Dirac cones exclusively to the diffraction in the final state of photoemission from the 2D surface- or subsurface-localized bands of Au(111) residing at the boundaries of the surface-projected bulk sp-band.

2. Methods

The band structure of C₆₀/Au(111) was studied by angle-resolved photoemission (ARPES) at BESSY II. Band structure maps have been acquired at the endstation ARPES 1² at the beamline UE112-PGM2a using variable energy and polarization of synchrotron light. Spin-resolved measurements were conducted at the U125/2-RGBL beamline using the endstation RGBL-2. The characterization by STM was performed with an Omicron LT-STM in a separate chamber. We used polycrystalline tungsten tips prepared as described elsewhere.¹⁰

The C₆₀/Au sample was prepared in vacuo. Initially, clean Au(111) was achieved by repeated cycles of Ar⁺ sputtering at 1 kV and subsequent annealing of the Au crystal at 800 K, followed by the deposition of fullerenes from the powder heated in a molybdenum crucible. Realization of the highly ordered (2√3 × 2√3)R30° superstructure of C₆₀ required short annealing of the deposited sample at 600 K. For brevity, this superstructure will be referred to simply as (2√3) in what follows.

Density functional theory (DFT) calculations with preliminary structural optimization were performed using the VASP package¹¹ with the PAW method in the PBE approximation, DFT-D2 van der Waals interaction correction¹² and dipole correction. Band unfolding was performed using the VaspBandUnfolding code.¹³ For calculation of fullerenes on gold shown in Fig. 3 a Monkhorst–Pack grid (9 × 9 × 1) was used, without spin–orbit coupling. For the calculation of 39-layer-thick gold slab reported in Fig. 5 a (5 × 5 × 1) Monkhorst–Pack grid was used and spin–orbit coupling was included. For calculation of the 20-layer-thick gold slab shown in the ESI Fig. S1† a (13 × 13 × 1) Monkhorst–Pack grid was used and spin–orbit coupling was included. In the layer-resolved localization analysis of Au(111) bands, the possible herringbone reconstruction (22 × √3) was not taken into account. The herringbone structure was only included in the DFT analysis of the effect of its lateral superpotential on the manifold-like appearance of the Au sp-band (ESI Fig. S2†). It was modeled as relaxed 1D dislocation imposed on the top layer of a 4-layer-thick rectangular Au(111) slab with a (22 × √3) supercell. Here, spin–orbit coupling was not included.

3. Results and discussion

3.1. Apparent Dirac cones in C₆₀/Au(111)

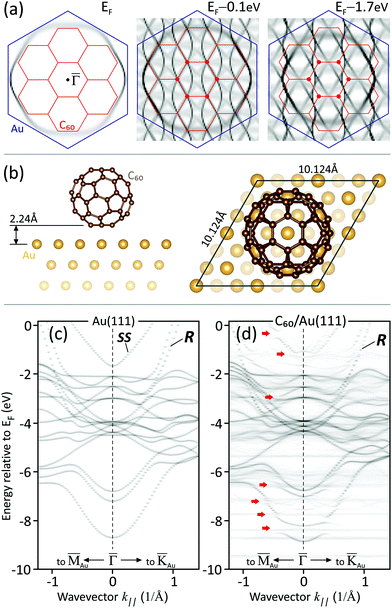
Fig. 1 shows the structural characterization of C₆₀ on Au(111). A large-scale STM image [Fig. 1(a)] shows a sub-monolayer amount of C₆₀ deposited on Au(111) and demonstrates that C₆₀ forms well-ordered molecular islands, in which nucleation seeds are at the zig-zags of the (22 × √3) herringbone reconstruction.¹⁴ Areas between islands reveal clean Au(111) with a perfectly resolved atomic lattice [Fig. 1(b)]. Zoom in of a molecular island [Fig. 1(c)] shows the highly periodic arrangement of fullerenes. Our STM data resolve the inner structure of C₆₀ formed by molecular orbitals and shows that at low temperature (80 K) most of the molecules share an identical orientation, thus creating a perfectly periodic lateral superpotential at the Au surface. Only a minor part of molecules (<30%), seen as bright protrusions, reveals an inner structure corresponding to an alternative rotational orientation of the C₆₀ cage on the Au. This, however, is not decisive for the overall coherence of the superpotential, which is substantially enhanced by freezing-out vibrations of fullerenes, also in lateral directions. Taken together, our STM results agree with earlier microscopy studies.^15–18 The formation of the (2√3) fullerene superstructure is also clearly seen in LEED [Fig. 1(d)]. Fig. 1(e) shows superstructural mini Brillouin zones (mini-BZ) of C₆₀ [red] referred to the surface Brillouin zone (SBZ) of Au(111) [blue].

Fig. 1 STM characterization of C₆₀ on Au(111) arranged in the (2√3 × 2√3)R30° superstructure at T = 80 K; (a) large-scale image showing a fullerene island and the bare Au(111) with herringbone reconstruction (see upper left area of the substrate displayed with enhanced contrast); (b) zoom-in image of bare Au(111) showing atomic resolution; (c) zoom-in image of fullerene island resolving perfectly ordered C₆₀ and inner structure of their molecular orbitals; bias voltages and tunneling currents were 2 V/0.1 nA, 0.1 V/3 nA and 1 V/2 nA for (a), (b) and (c), respectively; (d) LEED pattern revealing spots of Au(111) and fullerene superstructure at 60 eV beam energy; and (c) Brillouin zones of C₆₀ [red] and Au(111) [blue] in mutual correspondence.

Fig. 2 reports the effect of the molecular superlattice on the electronic structure of Au(111) as it appears in the full-photoemission mapping of the band structure. Fig. 2(a) and (b) compare constant energy surfaces (E_B = E_F − 0.8 eV, E_B = E_F − 0.45 eV) and Fermi surfaces (E_B = E_F) of bare Au(111) and Au(111) covered with one molecular layer of C₆₀, respectively. One sees that the extremely coherent periodic lateral potential of C₆₀ [evidenced by STM in Fig. 1(c)] results in a remarkable replication of the sp-band of Au [denoted as R in Fig. 2(a)] the contour of which, for the bare Au surface, adheres to the border of the Au(111) SBZ (the Au SBZ and mini-BZ of C₆₀ are plotted over ARPES data in the rightmost panels of Fig. 2(a) and (b) as blue and red hexagons, respectively). In the C₆₀-covered sample the replication of the sp-band R dominates the whole electronic structure and is perfectly seen in the band structure sections sliced along the traces 1 and 2 marked in Fig. 2(b) by magenta and light-blue lines, respectively. Dispersions sliced along 1 and 2 are displayed in the lower panels of Fig. 2(c) and (d). One sees that the (2√3) superpotential of fullerenes causes a repetition of the steeply dispersing Au sp-band R (see upper panels of Fig. 2(c) and (d) for reference) along both k_∥x and k_∥y directions in such a way that the replicas effectively form a set of bands resembling Dirac cones. This happens at many particular wavevectors k, though individual replica bands do not form cones in the (k_∥x, k_∥y, E) space. Cone-like features within the superstructural mini-BZ only appear as the superposition of six (in the first order of diffraction) replicated contours of the sp-band of Au. Essentially, the formation of such deceptive Dirac cones underlies the same, but much more pronounced, mechanism as that acting in silicene on Ag(111) or Au(111).^19,20 In several works on Si/Ag(111) and Si/Au(111), linearly dispersing bands were interpreted as gapped Dirac cones emerging in a honeycomb silicon lattice,^21,22 whereas the generally accepted explanation is that these states are 2D saddle-shaped band split-off from bulk sp-states of Ag, residing at the Si–Ag interface.²³ Their peculiar saddle shape was ascribed to the effect of electronic umklapp caused by the silicon superstructure.^19,20 In the present case of C₆₀ on Au(111) the situation seems to be even more straightforward, since here we deal with the exact replicas of sp-bands of Au, which are copied in k-space exactly by the highly periodic lateral superpotential of the molecular network. The importance of good fullerene ordering was evidenced by comparative photoemission mapping at low [Fig. 2(b)] and room temperature [not shown]. Indeed, at T = 16 K the constellation of replicas becomes visible up to much higher diffraction orders, and their linewidths become sharper (narrower) by 30%. This evidences the freezing out of molecular vibrational and rotational disorder and enhancement of lateral superpotential order.

Fig. 2 ARPES study of C₆₀/Au(111) performed at hν = 80 eV; (a) full photoemission mapping of the band structure of bare Au(111). Constant energy surfaces sampled at binding energies of 0.8 eV, 0.45 eV and at the Fermi level (E_F) are shown. Measurements were performed at T = 300 K; (b) same as in (a) but with the (2√3 × 2√3)R30° superstructure of C₆₀ on top and at T = 16 K. Multiple umklapp replicas of Au bands, denoted in (a) as R, translated according to the periodicity of superstructural mini-BZ of fullerenes is seen; (c) band dispersions extracted from the full photoemission maps of Au(111) [upper panel] and C₆₀/Au(111) [lower panel] along trace 1 [magenta line in (a) and (b)] and along momentum k_∥y. False Dirac cones formed by the replica of steeply dispersing and almost linear bands R are seen; (d) band dispersions extracted along trace 2 [light-blue line in (a) and (b)] and along momentum k_∥x. Also along this direction the formation of features resembling Dirac cones is observable.

Looking at the constellation of replicas of Au sp-bands in the constant energy surfaces (CESs) shown in Fig. 2(b), we argue that Dirac cones reported earlier at K̄ points of the mini-BZ of the fullerene network⁹ could emerge from the interplay of the replicas translated toward the center of the Au(111) SBZ by reciprocal lattice vectors of the fullerene superlattice. Indeed, one sees pronounced superposition features of intensity at the corners of the mini-BZ [red hexagon in Fig. 2(b)]. To simulate such a superposition effect we have developed a simple geometric model of translational replication of the Au sp-band in the (k_∥x, k_∥y, E)-space. The intensity of the band within the CESs was defined empirically in order to fit with the ARPES experiment. The first panel in Fig. 3(a) shows the Fermi surface of the reference Au band. The second and third panels present replica-molded CESs exemplarily sliced at binding energies E_B = 0.1 eV and E_B = 1.7 eV, respectively. For specific binding energies one can obtain a CES pattern in registry with the mini-BZ of C₆₀ which resemble (though not exactly reproduce) contours of Dirac cones seen earlier for C₆₀/Cu(111).⁹ We emphasize that the illumination of peculiar arc/parts of the replica and hence the overall occurrence of conical contours critically depends on the experimental geometry (the angle of light incidence, polarization of photons, and orientation of analyzer). One can therefore expect strong variations in the matrix elements of these features between different experimental setups.

Fig. 3 (a) Constant energy surfaces of Au(111) and C₆₀/Au(111) simulated by an empirical model. Replication of the Au sp-band R [left panel] according to the registry of fullerene mini-BZ (red hexagons) creates a texture of warped contours resembling Dirac cones at selected binding energies [middle and right panels]; (b) structural model of C₆₀/Au(111) used in DFT calculations; (c) band structure of bare Au(111) [3ML] calculated for reference; and (d) band structure of C₆₀/Au(111) cluster shown in (b) with the inclusion of entire fullerene molecule. The result is shown unfolded. No Dirac cones assignable to artificial graphene are observed. As compared to bare Au(111) in (c) only band gaps caused by hybridization with molecular orbitals occur as new features [red arrows].

The absence of Dirac cones and artificial graphene in the C₆₀/Au(111) system is also confirmed by our DFT calculations. We prefer performing a simulation of the entire C₆₀ molecule on Au(111) instead of muffin-tin like exclusion potentials at molecular sites⁹ (which, strictly speaking, do not reproduce a honeycomb lattice with its specific hopping integrals). The Au substrate was approximated as 3 atomic layers of Au. The structural cluster was selected in such a way that (2√3) periodicity and orientation of the fullerene network were obeyed. The system was relaxed allowing for the rotation, displacement and deformation of C₆₀. The cluster used in the calculations is shown in Fig. 3(b). The calculated band structure along the directions [capital Gamma, Greek, macron]–M̅ and [capital Gamma, Greek, macron]–K̄ of SBZ is presented in Fig. 3(d). The electronic structure of pristine Au(111) without C₆₀ is shown in Fig. 3(c) for comparison. Apart from energy gaps [red arrows] caused by hybridization between bulk and surface states of Au and the HOMO/LUMO of C₆₀, there are no noticeable differences between the band structures of Au(111) and C₆₀/Au(111). One sees that the presence of fullerenes does not lead to the generation of any new bands resembling Dirac cones. The band structure of C₆₀-covered Au(111) shown in Fig. 3(d) was unfolded according to the (2√3) periodicity of the molecular network.

3.2. Origin of the replicating Au(111) band

At this point we want to discuss the nature of the replicating Au state R which in the literature is generally acknowledged as the bulk sp-band. The assumption that apparent Dirac cones are built of replicas of the bulk bands of the substrate contradicts the observation in ref. 9 that the cones do not disperse with electron out-of-plane momentum k_z (k_⊥) upon variation of the photon energy (hν) in the ARPES experiment. Indeed, the non-dispersive behavior with k_z is naturally considered as a fingerprint of the 2D surface or interface bands. For Cu(100), on the other hand, a sharp Fermi surface feature without dispersion with k_z has been assigned to projected bulk states.²⁴ To tackle this issue we looked at the origin of the Au band R, which is the genesis of all fullerene-induced replicas seen in Fig. 2(b), and studied its dimensionality at the bare Au(111) surface. Fig. 4 shows a series of dispersions measured for photon energies hν = 55–85 eV along the direction [capital Gamma, Greek, macron]–M̅ of the Au(111) SBZ. The acquired sample spectra of both the Au(111) surface state (SS) at [capital Gamma, Greek, macron] as well as the (apparently bulk) sp-band R near M̅. Two remarkable observations are made: (1) state R is a manifold consisting of three sharp and clearly resolvable bands and (2) there is no measurable dispersion with hν (k_z) for any state in the manifold. This allows us to conclude that manifold R is not just a simple bulk sp-band, as widely believed, but might be rather a surface resonance. The narrow linewidth of the manifold bands related to the void group velocity along k_z is an additional confirmation of 2D character. The MDC width of the peaks from the manifold near the Fermi level is ∼0.025 Å⁻¹ (FWHM), which is about the same as the width of each spin-sub-band of Rashba-split Au surface state SS at [capital Gamma, Greek, macron]. The genuine bulk sp-band of Au is also seen in the measurements: it occurs as a broad and strongly dispersing with hν feature denoted in Fig. 4 as B. Since Dirac-cone-like features ascribed earlier to artificial graphene⁹ are formed by the replica of band R, it is obvious that they do not disperse with the photon energy (and k_z), since the pristine band R does not disperse itself. This underlines the fact that dispersionless behavior of the conical bands with the photon energy, shown in ref. 9 as argument toward the formation of Dirac cones, is not a strong supporting evidence.

Fig. 4 ARPES measurement of the band structure of bare Au(111) along the direction [capital Gamma, Greek, macron]–M̅ of the Au surface Brillouin zone conducted at different photon energies and T = 16 K. Neither surface state SS at [capital Gamma, Greek, macron] nor Au sp-derived band R at M̅ show a dispersion with hν (k_⊥). Band R appears almost equidistant manifold hence giving rise to an onion-like Fermi surface of Au(111). The direct-transition bulk sp-band is also seen (broad feature B) and demonstrates pronounced dispersion with hν.

It is worth noting, that the only survey of the properties of resonance band R, so far, was based on an atomic-layer-resolved analysis of spatial local density of states (LDOS) distribution of the same-type band, but in another noble metal Cu(111). In the case of the copper localization of state R in a deep subsurface with leaking to the bulk was shown.²⁵

Next, we address the nature of the band R and in particular its unexpected multi-band (manifold) appearance. We will discuss several possible physical effects (surface projection of the bulk states in ARPES, umklapp replica bands, spin-splitting, etc.) and we will try to find the most plausible origin of the band R by discounting them one by one.

The simplest explanation would be to consider R as a spectral feature occurring due to a projection of the bulk density of states (DOS) onto the Au(111) surface. Fig. 5(a) sketches an isometric view of the bulk Brillouin zone (BBZ) and bulk Fermi surface of a prototypical noble metal (such as Au).²⁶ One can see that regions of the locally enhanced density of states would occur around the perimeter of the projected bulk Fermi surface owing to the contours running nearly perpendicular to the [111] surface [bold magenta lines in Fig. 5(a)]. Such interpretation was considered for noble metals.^24,27,28 A local enhancement of the LDOS at the borders of the bulk Fermi surface projection onto Au(111) was also seen in simulations.²⁹ It is, however, difficult to corroborate the manifold nature and remarkable sharpness of the R peaks with the effect of a projection, which should ultimately integrate over the full range of wavevectors defining the outlines of the Fermi surface, hence causing substantial broadening along k_∥. The uncertainty of k_∥ in combination with non-zero k_⊥ (k_z) should also prevent umklapp replication of R by the molecular superpotential as pronounced as it is seen in the ARPES experiment [Fig. 2(b)].

Fig. 5 (a) Bulk Brillouin zone and Fermi surface of a prototypical noble metal [left panel] and their projections onto the (111) surface [right panel]. Bold magenta lines denote areas of enhanced LDOS in the surface projection; (b) layer-resolved DFT of Au(111) [39 ML] with inclusion of spin–orbit interaction. Color code denotes localization of the bands. Upper row shows constant energy surfaces covering [capital Gamma, Greek, macron], M̅ and K̄ points of SBZ, calculated for energy E_F − 1.15 eV. The SBZ border is marked by black dashed line. Onion-like arrangement of bands R (red and blue) around [capital Gamma, Greek, macron] is seen. Middle and bottom rows present band structures along [capital Gamma, Greek, macron]–K̄ and [capital Gamma, Greek, macron]–M̅ directions, respectively. Left column reports the LDOS contributions of the first surface atomic layer (“1^stAL”, red) and of 5 central atomic layers of the slab (“bulk”, blue). Middle column shows LDOS projected onto the first (red) and second (blue) atomic layers (AL). Right column presents subsurface LDOS at the second (blue) and third (green) AL; (c) wide-energy-range spin-resolved measurement passing through Au d-bands and manifold surface resonance R [green line in the inset]. Rashba-specific spin projection S_x is shown. State R appears spin-degenerate; and (d) 3D spin-resolved measurement of state R shows that the surface resonance is fully spin-degenerate.

Fig. 2(a) shows that the intensity of manifold contours is enhanced near M̅ and M̅′ points of the SBZ [dashed orange rectangular marks in Fig. 2(a)] i.e. in the regions where the L-point necks interconnecting Fermi surfaces of neighboring bulk Brillouin zones [see Fig. 5(a)] project onto the (111) surface. Indeed, the projection of the bulk L-point gaps onto the (111) surface should locally suppress the leakage of the band R into the bulk at M̅ and M̅′. Enhancement of the intensity of R at the sites of relative projected band gaps suggests that R is a surface resonance, albeit deeply leaking into the bulk of the Au crystal.

The next important question to answer is why the state R appears as a split manifold at bare Au(111). Indeed, the manifold states can contribute to the constellation and properties of the umklapp replica pattern [Fig. 2(b)]. One possible reason for the manifold appearance can be umklapp of band R on the herringbone reconstruction (22 × √3) of Au(111), as was proposed recently.³⁰ The Δk-separation between manifold bands R observed in ARPES experiment is somewhat comparable to the reciprocal lattice periodicity of the herringbone dislocation stripes. We performed DFT simulation of the effect of (22 × √3) reconstruction on the band structure of Au(111) and report the results in the ESI.† ³¹ Our DFT has in fact demonstrated replication of the resonance R, however, the spectral weight of the replica in the unfolded spectra was found to be low. This suggests faint occurrence of the replica in photoemission. Furthermore, the discrepancies between Δk-periodicities of the replica acquired by DFT and the bands of the split manifold from the ARPES experiment were found. They were as large as 20 to 30% depending on the direction of the electron wavevector ([capital Gamma, Greek, macron]–K̄ or [capital Gamma, Greek, macron]–M̅). Earlier, it was shown for the Au(111) surface state at [capital Gamma, Greek, macron] that its umklapp scattering at the (22 × √3) reconstruction leads to the Fermi surface comprising a trefoil-knot-like texture of overlapping contours of the surface state.^32,33 For the band R we could not confirm such a texture (though it cannot be fully excluded because of photoemission intensity effects and complex replica pattern [see ESI Fig. S2† ³¹]): the analysis of the ARPES maps reveals that contours of manifold bands run parallel to each other along the boundary of the surface projection of the bulk sp-band, and we do not observe crossings [Fig. 2(a)]. In such a way they create an onion-like Fermi surface of Au(111). Though we cannot decisively exclude the (22 × √3) surface reconstruction as a reason for the manifold structure of the R state, in the following we present yet another possible explanation referred to the intrinsic properties of the Au(111) band structure.

To shed more light on the nature of manifold we performed detailed DFT calculations of the band structure of Au(111) with full inclusion of spin–orbit coupling. In order to eliminate the effects of surface reconstruction from the results, the herringbone structure this time was excluded from the structural model. The layer-resolved band structure calculated for a 39 monolayer-thick slab of Au(111) is presented in Fig. 5(b). The figure shows both constant energy surfaces, revealing contours of the bands assignable to the resonance R [upper row], as well as band dispersions sampled along the high-symmetry directions of the Au(111) SBZ: [capital Gamma, Greek, macron]–K̄ [middle row] and [capital Gamma, Greek, macron]–M̅ [bottom row]. Images in the left column plot the density of states summed for the surface [red] and integrated bulk [blue]. The middle column depicts localization at the first [red] and second [blue] atomic layers. The right column shows the same, but for the second [blue] and third [green] layers in the subsurface. Layer-resolved band structures calculated for every individual atomic layer starting from the 1^st and up to the 4^th are complementary and are shown in the ESI† ³¹ with spin-polarization depicted. Both calculation schemes promote the same conclusions.

Our DFT analysis predicts R as a complex state derived from the bulk sp-band residing at the boundary of its surface projection. The resonance R comprises two components, one of which is a pure surface localized [depicted in red in panel Surface + Bulk of Fig. 5(b)], while another one is more bulk-like [blue color in panel Surface + Bulk]. The red surface-localized part of R is exclusively hosted by the first atomic layer, and its blue resonance-like part leaks into the bulk and resides deeper in the subsurface. Layer-resolved DFT data presented in the ESI† ³¹ also show that state R spin-polarized within the first atomic layer, is greatly suppressed in the second, and appears again in the third and fourth, but spin-degenerate. Such localization properties are confirmed also by layer-resolved DFT shown in Fig. 5(b). Even though in DFT the truly surface-localized component gradually decays closer to the Fermi level, for deeper layers it can be identified as the band R observed in the experiment. It is straightforwardly seen that both components of the R – surface and resonance bulk-like – disperse parallel to each other and form a manifold band structure, albeit comprising only two bands. The calculated CESs [upper row of Fig. 5(b)] show that contours of both components of R disperse parallel to each other and create an onion-like energy surface, in fair agreement with experimental CESs shown in Fig. 2(a).

Subsurface localization of R established by our layer-resolved DFT, corroborates that this state is a deep surface resonance leaking into the phase space of the bulk Au sp-band, but is nonetheless a 2D state with negligible dispersion by k_z. Sub-surface localization of R is further supported by photon-energy-dependent measurements shown in Fig. 4. Indeed, the overall photoemission intensity of manifold R grows at higher photon energies due to enhanced bulk sensitivity of photoemission, while the intensity of the surface state SS drops with increasing hν (k_z stays within a single BBZ in this range of photon energies). It is worth noting that such a projection-boundary-bound state was observed in several DFT calculations of Au(111)^34–36 but its nature and properties were not addressed.

Yet another reason for the band splitting in high spin–orbit materials (like Au) can be related to electron spin. At the surface of a high-Z metal one could, in general, expect Rashba-type spin–orbit splitting of surface bands caused by breaking of inversion symmetry. A prominent example of a Rashba effect is the Au(111) surface state at [capital Gamma, Greek, macron]^37,38 [see also the first panel in Fig. 6(a)]. When looking into the spin- and layer-resolved results of our DFT calculations shown in the ESI,† ³¹ one should not exclude a Rashba-scenario for surface resonance R. In fact, it is slightly spin polarized at the surface of Au (within the 1^st AL), while for deeper layers (e.g. 4^th) – where the inversion symmetry is recovered – it is spin degenerate. Spin polarization of R at the surface acquired by DFT³¹ reveals opposite signs for −k and +k, hence resembling a rather topological state than a Rashba-split band. Such behavior, however, could be caused by a giant Rashba effect like that known e.g. for Bi(111),³⁹ or by unconventional mirror-symmetry-driven – but trivial – Rashba splitting emerging at low-symmetry points, analogous to that observed for W(110).⁴⁰ To better understand the spin character of the surface resonance manifold we performed direct spin-resolved photoemission measurements of band R. Fig. 5(c) shows the spin-resolved spectra (energy distribution curves) of the manifold taken in a wide energy range at k_∥y = 1.12 Å⁻¹ (green line on dispersion shown in the inset). Other wavevectors k_∥y were also measured with essentially the same results. The spectrum shown in Fig. 5(c) represents an in-plane projection of spin S_x which is perpendicular to electron momentum k_∥y. This is the projection for which the expected Rashba splitting must dominate due to spin-momentum locking. One clearly observes spin polarization of Au d-bands at binding energies >1.5 eV, which also correlates with the results of our spin-resolved DFT calculations shown in the ESI.† ³¹ The peak from the band R centered at E_B ∼ 0.5 eV, however, reveals no measurable spin polarization. Fig. 5(d) shows a zoom in image of the region of the R manifold and reports 3D spin-resolved spectra acquired for spin projections S_x, S_y (in plane) and S_z (out of plane) with enhanced statistics. None of the projections reveal a detectable spin polarization. The absence of spin polarization in photoemission from R confirms that the sp-type manifold is mainly localized in the subsurface, where structural inversion symmetry is obeyed. This result clearly shows that manifold R contains no bands assignable to the spin-splitting.

Fig. 6 Effect of charge doping on the surface states of Au(111); (a) control experiment: surface doping of bare Au(111) with potassium results in significant energy shift of the Shockley-type surface state at [capital Gamma, Greek, macron]; (b and c) dispersions of pristine C₆₀/Au(111) (b) and severely doped with 2 ML of K (c) measured along trace 3 [orange line in Fig. 2(b)]. Doping has no effect on energy position of surface resonance R and their replicas. (d) Concentration of deposited K was monitored by core-level photoemission. Doping with K also has no effect on HOMO-n molecular orbitals of C₆₀ in the valence band VB (inset).

Having shown that the origin of manifold-like appearance of the R band is not related to Rashba splitting, we come back to the results of our DFT analysis and conclude on the most probable explanation of manifold, which is a localization effect. In such scenario, the band R is a deep surface resonance forming a quantum manifold of eigenstates localized at different atomic layers at and below the Au surface. This interpretation is in line with the results of our layer-resolved DFT calculations shown in Fig. 5(b). One can clearly see that in the 1^st AL the surface-localized part of state R resides at a different (smaller) k_∥ vector than its bulk-leaking resonance component in a deeper subsurface (e.g. in 3^rd or 4^th AL). Δk difference between the wavevectors extracted from DFT is about ∼0.12 Å⁻¹ which is in fair agreement with the experimentally observed separation of manifold bands of ∼0.1 Å⁻¹ (Fig. 4).

Although the manifold does not directly emerge from the electron spin, the large energy–momentum splitting between its bands and the onion-like Fermi surface caused by the specific localization could be indirectly related to the strong spin–orbit interaction in Au. Though this does not make the manifold band spin-polarized, it might have an impact on energetic degeneracy at different atomic layers of the subsurface. Indeed, our comparative measurement of the same surface resonance R in low-Z material Ag(111) [not reported here] also reveals a manifold, but with a much smaller magnitude of Δk-splitting between its sub-bands. A decisive answer on whether and to which extent the manifold splitting of R is in fact related to the spin–orbit interaction in noble metals requires further theoretical studies and should be a subject of a separate study.

Finally, we probed how fullerene-induced false Dirac cone bands shaped by the umklapp replica of surface resonance R respond to a charge doping. Earlier it was assumed⁹ that the occurrence of energy shifts of conical bands upon electron doping of C₆₀/Au(111) samples with alkali metals could serve as evidence of two-dimensionality of the cones and hence as proof of realization of artificial graphene. For instance, when potassium is deposited on bare Au(111), we observe an energy shift of the SS at [capital Gamma, Greek, macron] of up to ΔE_B ∼ 0.2 eV [Fig. 6(a)]. Though this is expectable for Shockley-type surface states sensitive to the shape of the surface potential barrier, such behavior is not expected for deep-surface-resonance-like manifold R, which is predominantly localized in the subsurface. Nevertheless, we tested doping of C₆₀/Au(111) with K. The results are presented in Fig. 6(b) and (c) for the slice of the band structure marked in Fig. 2(b) as trace 3 (orange line). Increasing concentration of potassium upon gradual deposition on the sample was monitored by core-level spectroscopy. Fig. 6(d) shows selected overview spectra with growing 3s and 3p peaks of K for gradually increasing concentrations of potassium (0.5, 1 and 2 ML). Fig. 6(b) and (c) report valence band dispersions of the bare and K-deposited (with ∼2 ML of K) sample, respectively. Neither energy shifts of conical bands, nor changes in the umklapp pattern of replicas are seen. No changes (apart from increasing background) were seen also for any lower concentration of K. Remarkably, no energy shifts of molecular orbitals (HOMO-n) of C₆₀ were observed. That, in turn, suggests that deposited K diffuses to the C₆₀/Au interface and affects neither the charge state nor the muffin-tin potential of fullerene molecules. All in all, these results indicate that surface doping is not a universally sensitive tool for probing the dimensionality of novel electronic states induced by (or in) molecular networks.

One final question to answer is whether the observed umklapp replicas (forming deceptive Dirac cones) occur in the ground state of the electronic system or are characteristic of the final state of photoemission. Here, we understand the final state exclusively as diffraction of photoelectrons emitted from the Au(111) substrate on the adsorbed array of fullerene molecules. Our ARPES experiments were conducted at photon energies between 35 and 110 eV which allows us to assume that the final-state of photoelectrons has a free-electron-like character describable by plane waves and conventional Bragg formalism. There are straightforward arguments supporting the scenario of diffraction on the molecular network. First, when looking at the multiple band replicas of state R crossing each other [Fig. 2(c) and (d), lower panels], one sees no energy gaps at the crossing points. Avoided-crossing minigaps are known for ground-state replicas and, in particular, for Dirac cones of graphene (see e.g. for graphene/Ir(111)^41,42) and they are expected to occur in the ground-state spectrum. Second, C₆₀ molecules are bonded to Au(111) covalently but relatively weakly, only through a single unoccupied orbital, the LUMO.⁴³ It is unlikely that such weak molecular superpotential would cause a strong superlattice effect on deep subsurface-localized resonance R. A more probable scenario is that the perfect pattern of replicas seen in Fig. 2(b) is caused by the diffraction of photoelectrons from band R at the molecular grid of C₆₀.

4. Conclusions

In summary, using angle-resolved photoemission we have shown that the (2√3 × 2√3)R30° molecular network of C₆₀ on Au(111) does not electronically turn the Au surface into artificial graphene, in contrast to a recent report.⁹ Instead, a highly coherent pattern of replicated Au bands occurs as a result of diffraction of the photoelectrons at the fullerene superlattice adsorbed on the Au surface. The interplay between these multiple umklapp-replicated Au bands possessing steep and nearly linear dispersion in the vicinity of the Fermi level causes the superposition intensity patterns that only resemble Dirac cones, both in constant-energy surfaces and in band dispersions. Moreover, these patterns exist in the final state (diffraction) of photoemission only.

We also analyzed the origin of Au(111) bands creating false Dirac cones by coherent replication. By means of extensive density functional theory calculations, layer-resolved localization analysis and spin-resolved photoemission we identify this state, residing at the boundary of the surface projected bulk sp-band of Au, as a deep surface resonance leaking into Au bulk. We examined why this state occur as a band manifold and gives rise to an onion-like Fermi surface. While superlattice (umklapp) effects imposed on the band structure of Au(111) by herringbone reconstruction (22 × √3), cannot be excluded decisively, the most feasible explanation comprises localization effect entailing different energies of the surface resonance bands at and below Au(111) surface. Spin-resolved measurements reveal no Rashba-like spin polarization of these states hence indicating their predominant localization in the subsurface, where structural inversion symmetry is preserved.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by ‘Impuls- und Vernetzungsfonds der Helmholtz-Gemeinschaft’ under grant no. HRSF-0067.

References

1. I. Bloch, Nat. Phys., 2005, 1, 23–30.
2. B. Wunsch, F. Guinea and F. Sols, New J. Phys., 2008, 10, 103027.
3. S.-L. Zhu, B. Wang and L.-M. Duan, Phys. Rev. Lett., 2007, 98, 260402.
4. Z. Liu, J. Wang and J. Li, Phys. Chem. Chem. Phys., 2013, 15, 18855–18862.
5. C.-H. Park and S. G. Louie, Nano Lett., 2009, 9, 1793–1797.
6. K. K. Gomes, W. Mar, W. Ko, F. Guinea and H. C. Manoharan, Nature, 2012, 483, 306–310.
7. C.-Y. Hou, C. Chamon and C. Mudry, Phys. Rev. Lett., 2007, 98, 186809.
8. B. Seradjeh and M. Franz, Phys. Rev. Lett., 2008, 101, 146401.
9. S. Yue, H. Zhou, D. Geng, Z. Sun, M. Arita, K. Shimada, P. Cheng, L. Chen, S. Meng, K. Wu and B. Feng, Phys. Rev. B, 2020, 102, 201401(R).
10. A. Varykhalov, O. Rader and W. Gudat, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115440.
11. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
12. S. Grimme, J. Comput. Chem., 2021, 27, 1787–1799.
13. Q. Zheng, VASP band unfolding, URL https://github.com/QijingZheng/VaspBandUnfolding.
14. Y. Wang, N. S. Hush and J. R. Reimers, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 233416.
15. E. I. Altman and R. J. Colton, in Characterization of the Interaction of C60 with Au(111), ed. P. Avouris, Springer Netherlands, Dordrecht, 1993, pp. 303–314.
16. L. Tang, Y. Xie and Q. Guo, J. Chem. Phys., 2021, 135, 114702.
17. H. Shin, A. Schwarze, R. D. Diehl, K. Pussi, A. Colombier, E. Gaudry, J. Ledieu, G. M. McGuirk, L. N. Serkovic Loli, V. Fournée, L. L. Wang, G. Schull and R. Berndt, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 245428.
18. M. Paßens and S. Karthäuser, Surf. Sci., 2015, 642, 11–15.
19. S. K. Mahatha, P. Moras, V. Bellini, P. M. Sheverdyaeva, C. Struzzi, L. Petaccia and C. Carbone, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201416.
20. S. K. Mahatha, P. Moras, P. M. Sheverdyaeva, V. Bellini, T. O. Menteş, A. Locatelli, R. Flammini, K. Horn and C. Carbone, J. Electron Spectrosc. Relat. Phenom., 2017, 219, 2–8.
21. W. Wang, W. Olovsson and R. I. G. Uhrberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205427.
22. Y. Feng, D. Liu, B. Feng, X. Liu, L. Zhao, Z. Xie, Y. Liu, A. Liang, C. Hu, Y. Hu, S. He, G. Liu, J. Zhang, C. Chen, Z. Xu, L. Chen, K. Wu, Y.-T. Liu, H. Lin, Z.-Q. Huang, C.-H. Hsu, F.-C. Chuang, A. Bansil and X. J. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14656.
23. D. Tsoutsou, E. Xenogiannopoulou, E. Golias, P. Tsipas and A. Dimoulas, Appl. Phys. Lett., 2021, 103, 231604.
24. O. Rader, H. Wolf, W. Gudat, A. Tadich, L. Broekman, E. Huwald, R. C. G. Leckey, J. D. Riley, A. M. Shikin, F. Matsui, H. Miyata and H. Daimon, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245104.
25. A. Winkelmann, C. Tusche, A. A. Ünal, M. Ellguth, J. Henk and J. Kirschner, New J. Phys., 2012, 14, 043009.
26. T.-S. Choy, J. Naset, S. Hershfield and C. Stanton, Bull. Am. Phys. Soc., 2000, 45(1), L36.042.
27. C. Tusche, A. Krasyuk and J. Kirschner, Ultramicroscopy, 2015, 159, 520–529.
28. F. Baumberger, T. Greber and J. Osterwalder, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195411.
29. F. Sirotti, N. Beaulieu, A. Bendounan, M. G. Silly, C. Chauvet, G. Malinowski, G. Fratesi, V. Véniard and G. Onida, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035401.
30. F. Matsui, S. Makita, H. Matsuda, T. Ueba, T. Horigome, H. Yamane, K. Tanaka, S. Kera and N. Kosugi, e-J. Surf. Sci. Nanotechnol., 2020, 18, 18–23.
31. ESI is available online, URL.†.
32. F. Reinert and G. Nicolay, Appl. Phys. A, 2004, 78, 817–821.
33. M. Dendzik, M. Bianchi, M. Michiardi, C. E. Sanders and P. Hofmann, Phys. Rev. B, 2016, 94, 201401.
34. P. M. Sheverdyaeva, R. Requist, P. Moras, S. K. Mahatha, M. Papagno, L. Ferrari, E. Tosatti and C. Carbone, Phys. Rev. B, 2016, 93, 035113.
35. R. Requist, P. M. Sheverdyaeva, P. Moras, S. K. Mahatha, C. Carbone and E. Tosatti, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045432.
36. R. Mazzarello, A. D. Corso and E. Tosatti, Surf. Sci., 2008, 602, 893–905.
37. S. LaShell, B. A. McDougall and E. Jensen, Phys. Rev. Lett., 1996, 77, 3419–3422.
38. M. Hoesch, M. Muntwiler, V. N. Petrov, M. Hengsberger, L. Patthey, M. Shi, M. Falub, T. Greber and J. Osterwalder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 241401.
39. A. Kimura, E. E. Krasovskii, R. Nishimura, K. Miyamoto, T. Kadono, K. Kanomaru, E. V. Chulkov, G. Bihlmayer, K. Shimada, H. Namatame and M. Taniguchi, Phys. Rev. Lett., 2010, 105, 076804.
40. A. Varykhalov, D. Marchenko, J. Sánchez-Barriga, E. Golias, O. Rader and G. Bihlmayer, Phys. Rev. B, 2017, 95, 245421.
41. I. Pletikosić, M. Kralj, P. Pervan, R. Brako, J. Coraux, A. T. N'Diaye, C. Busse and T. Michely, Phys. Rev. Lett., 2009, 102, 056808.
42. J. Sánchez-Barriga, A. Varykhalov, D. Marchenko, M. R. Scholz and O. Rader, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 201413.
43. I. Hamada and M. Tsukada, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245437.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1nr07981f

---