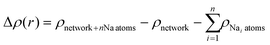Borazatruxenes as precursors for hybrid C-BN 2D molecular networks

Abstract

Synthesizing atomically thin, crystalline two-dimensional (2D) molecular materials which combine carbon with other elements is an emerging field requiring both custom-designed molecular precursors and their ability to organize into networks (hydrogen-bonded or covalent). Hybrid carbon-boron nitride (C-BN) networks face the additional challenge of needing hydrolytically-stable BN-containing molecular precursors. Here, we show that borazatruxenes (truxene-like molecules with a borazine core) and their halogenated derivatives are highly stable precursors suitable for on-surface assembly. Using scanning tunneling microscopy (STM) and density functional theory (DFT) simulations we demonstrate hierarchical H-bonded assembly based on chiral homodimers of tribromo-borazatruxenes (3Br-borazatruxenes) as building blocks for both 1D chains and 2D networks. A low-symmetry, H-bonded chiral 2D lattice forms on Au(111) from the C₃-symmetric 3Br-borazatruxenes, leading to large enantiomorphic domains that are molecularly homochiral. Such homochiral segregation is a necessary condition if chiral C-BN covalent networks are to be obtained via subsequent on-surface reactions. We show via DFT that up to two Na atoms can be trapped within the small pores of this dense lattice, while further Na atoms can adsorb on preferred network sites; this leads to hybrid Na-molecular network electronic bands with anisotropic dispersion and significant (up to hundreds of meV) bandwidths, as well as significant doping, that can engender anisotropic transport through the network. Finally, electronic structure comparisons (combining both experiment and computation) between borazatruxene, its tri-brominated derivative and truxene show that the borazine core controls the band gap increase, while also inducing C–B p_z–p_z electron delocalization that facilitates a continuous electron path across the molecule. Furthermore, as shown by DFT, the borazine core drives inter-layer B–N polar interactions that promote adsorption of BN containing molecules in a staggered configuration, a mechanism to be exploited in layer-by-layer supra-molecular assembly of novel hybrid C-BN materials.

---

1 Introduction

Replacing benzene with its inorganic counterpart, borazine (BN-), in polycyclic aromatic hydrocarbons (PAHs) gives rise to a new type of precursors suitable for the creation of two-dimensional (2D) hybrid carbon-boron nitride (C-BN) networks, such as H-bonded or covalent; the latter are an emerging class of materials which, by design, can have graphene-like properties.¹ The inclusion of borazine is expected to modulate the electronic structure and transport properties of those networks. This would mirror, for example, what occurs in 2D graphene-like sheets, where the addition of BN content increases the bandgap of the resulting 2D sheets.²

To date, only a very small number of borazine-containing molecular precursors have been synthesized because of difficult synthesis and the inherent hydrolytic instability associated with the borazine core. The field of C-BN 2D network synthesis is incipient, with only a few BN derivatives having been studied on surface to date.^3–8 B-Trimesityl-N-triphenylborazine-based precursors^5,6,8 were the first BN-containing molecules to be adsorbed on surface and formed van-der-Waals (vdW) interaction-driven assemblies on various metallic substrates (with the BN core decoupled from the surface due to their non-planarity). BN-doped hexabenzocoronene (BN-HBC), another H-terminated parent molecule, was also found to assemble via vdW interactions on Au(111).³ Neither of these molecules can however form H-bonded or covalent networks. Sanchez-Sanchez et al.⁷ have demonstrated the first and only covalent (sp²-hybridized, hence planar) C-BN network to date, via Ullmann coupling and cyclo-dehydrogenation of BN-HBC precursors on Ag(111). Finally, Beniwal et al.⁴ synthesized a buckled C-BN 2D material on Ir(111) via the dehydrogenation of sp³-hybridized BN-cyclohexane.

Here we focus on the class of borazatruxenes, where borazine constitutes the core that is connected to aromatic lobes by five member-ring bridges to create an on-surface prochiral, three-lobed planar molecule (Fig. 1 and S1†). These molecules have been recently synthesized by our group for the first time,⁹ however their electronic properties and self-assembly behaviour on surfaces have not been investigated thus far. One of their main characteristics is their strong hydrolytic stability that we believe arises from the direct connectivity of the boron atom to the aromatic rings, and on which this work sheds further light. Using a combination of scanning tunnelling microscopy (STM)-based techniques and density functional theory- (DFT-) based simulations we investigate the self-assembly of halogenated borazatruxenes into H-bonded networks and their prospective functional properties, as well as identify the fingerprints of the borazine core on electronic structure. In this way, we demonstrate the potential of borazatruxenes as building blocks for novel 2D hybrid, C-BN supramolecular materials.

Fig. 1 Low molecular coverage of 3Br-borazatruxene on Au(111). (a) Constant current STM z image of 3Br-borazatruxenes showing the co-existence of chiral (R)- and (S)- monomers, dimers and trigonal clusters. Inset: zoom on (R)- and (S)- 3Br-borazatruxenes, and a (S)- 3Br-borazatruxene trigonal assembly cluster in fcc areas with its chemical structure overlaid. Tunnelling parameters: 2 V, 0.3 nA. (b) Chemical structures of (R)- and (S)- 3Br-borazatruxenes adsorbed on the substrate in conformation A. (c) Homodimers (dark and light green frame) formed from monomers in A and B conformations (see text), and (d) heterodimers (purple and blue frame) formed from monomers in conformation A. (e) Structure of a trigonal 2D cluster, with type II halogen–halogen contacts shown with dotted lines. Atom colour coding: H, light grey; C, grey; Br, burgundy; B, pink; N: blue.

Tribromo-borazatruxene (3Br-borazatruxene) shows on-surface chirality (i.e. is a prochiral adsorbate¹⁰) – a consequence of the intramolecular connectivity of (i) the BN core to the benzene groups via a methylene bridge, and (ii) the trisubstituted Br atoms in para position to the methylene C – which could impart chirality-dependent optoelectronic properties to the resulting 2D networks. While this is exciting, molecular chirality might however hinder the formation of large, defect free network domains unless some chirality segregation mechanism operates. Furthermore, Br atoms can initiate the formation of covalent 2D C-BN molecular networks via Ullmann coupling – a generic route to covalent bonding demonstrated for other molecules.¹¹ Here we focus on the proto-stages of this process, before the Ullmann reaction has been initiated, and show that they can lead to the creation of chiral H-bonded 2D networks of 3Br-borazatruxenes.

Surprisingly, the H-bonded network formed on Au(111) does not have the C₃ symmetry of the 3Br-borazatruxene molecule, or C₆-symmetry, as was the case for other C₃-symmetric molecules,¹² but exhibits two directions of non-equivalent H bonding. We uncover a hierarchical mechanism that explains such chiral, low symmetry supramolecular assembly, where H-bonded homochiral dimers are building blocks for both 1D and 2D molecular phases. The preferential formation of chiral homodimers of 3Br-borazatruxenes is key to homochiral segregation into extended enantiomorphic domains (hundreds of nanometres in lateral size, typically) on Au(111). Homochiral segregation also implies that the covalent network domains that can form by subsequent Ullmann coupling will also be chiral, hence showing a route towards the first realization of chiral, covalently-bonded 2D materials.

As a result of the dimer-led H-bonding, the packing of 3Br-borazatruxenes in the 2D H-bonded network is tight, yielding small chiral pores (∼5 × 8 Ų), unlike in many 2D H-bonded networks known in literature.^13–15 This makes these H-bonded networks suitable for trapping of very small clusters/individual molecules or single atoms. We show via computational studies that these pores can trap up to two Na atoms, which brings the Fermi energy in the reach of the network's bands. Na-aromatic carbon hybrid bands within this low-symmetry network, hence, engender anisotropic transport; while electron delocalization can be further increased to several hundreds of meV (comparable with some of the largest values encountered in molecular networks)¹⁶ by additional Na adsorption on preferred network sites. Loading the network with an odd number of Na atoms per unit cell induces locally spin-polarised energy levels.

We also study borazatruxenes, the parent molecules (Fig. 1, 4 and S1†), as the electronic building blocks of any borazatruxene-based 2D network. In contrast with 3Br-borazatruxenes, we find that borazatruxenes do not have the ability to form H-bonded clusters or networks due to repulsive intermolecular interactions. By comparing the electronic structure of borazatruxene, its tribromo-substituted derivative, and truxene we demonstrate that the borazine ring controls the increase of the HOMO–LUMO gap, and hence, is expected to define the electronic signature of all borazatruxene-based 2D networks, in both H-bonded and covalent forms. Replacing the all-carbon core with borazine also yields unexpected electron delocalization between B and the adjacent C atom p_z orbitals showing the existence of a double bond-like interaction, which is not present in truxene for the analogous C–C bonds. This also helps stabilize the borazatruxene molecule. Finally, we show that the BN-core plays a significant role in driving polarization-led supramolecular assembly that can be exploited in the creation of multi-layered molecular materials.

2 Results and discussion

2.1 Hierarchical H-bonded assembly based on chiral homodimers

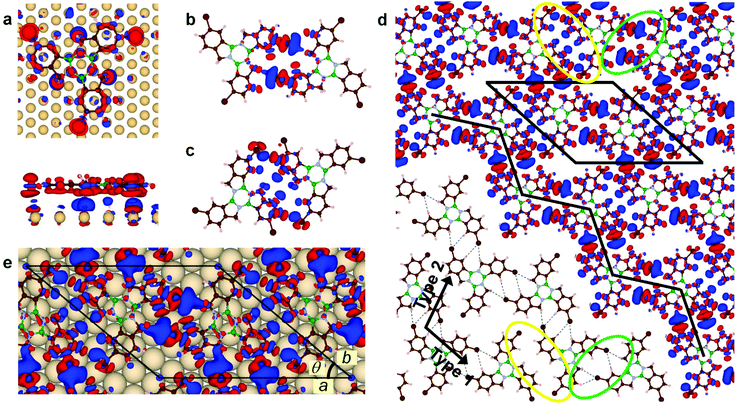
Borazatruxene and 3Br-borazatruxene molecules were synthesized as previously described by our group (Methods). The self-assembly and electronic structure studies were performed using scanning tunnelling microscopy and spectroscopy (STM/STS), and conductance (dI/dV) maps, performed at 4.5 K in ultra high vacuum (UHV) (Methods). The experiments were supported by density functional theory (DFT) simulations of charge distribution, binding energy, and electronic structure, for the individual molecules and their assemblies, in vacuum and substrate- (Au(111)) supported (Methods).

To investigate the on-surface assembly, we created both low and high molecular surface coverages. Fig. 1a shows a representative STM z image of low molecular coverage of 3Br-borazatruxene on Au(111). 3Br-borazatruxene adsorbs flat on Au(111), with tri-fold symmetry and lateral size of about 1.6 nm (Fig. S1†). The large size of its halogen groups gives it a characteristic chiral, “propeller” shape. On-surface molecular adsorption facilitates mirror symmetry breaking¹⁷ which results in both (R)- and (S)- enantiomers being adsorbed. Individual enantiomers adsorb preferentially on the fcc regions or at the herringbone elbows of the reconstructed Au(111) substrate, and in a single conformation, labelled A, with respect to the herringbone direction (see Fig. 1a and b and S2†).

In the fcc regions of the reconstructed substrate, we observed the formation of (R)–(R) and (S)–(S) homodimers, as well as (R)–(S) and (S)–(R) heterodimers (Fig. 1). A homodimer forms between two monomers of the same chirality: one in conformation A, found to be stabilized by the molecule–substrate interaction, and another in conformation B, which is 60° rotated with respect to A (Fig. 1c). The conformation B has not been observed experimentally in monomer form, in contrast to A; we rationalize this based on the non-equivalence of the atomic environment on the Au(111) surface of the two conformations as a result of the molecule's chirality (Fig. S1c†). The A–B homodimer allows the formation of two tri-furcated H bonds (dashed lines in Fig. 1c), where each of the two Br atoms of the dimer points towards the ortho aromatic C–H and methylene (CH₂) of its neighbour. Due to the orientation of the two constituent A and B conformations, the (S)–(S) and (R)–(R) homodimers assemble in two possible orientations: with their long axis at 60° and 120° with respect to the [112̄] direction (Fig. 1a and c). In contrast, heterodimers form from enantiomers, both in conformation A, and align with their axes parallel to the [112̄] direction (see Fig. 1a and d). Their assembly occurs via a single tri-furcated H-bond interaction between the halogen and ortho aromatic C–H and methylene (CH₂) atoms (dashed lines in Fig. 1d), as opposed to two in homodimers. This significantly decreases the binding energy per monomer (Fig. S3† and Fig. 3b) and makes the homodimer configuration the most stable of the two. The conformation/bonding differences between heterodimers and homodimers allow us to account for the rotation of one of the monomers during homodimer assembly: from A, the equilibrium conformation for individual monomers, to B. This non-equilibrium, B, conformation for the monomer is stabilized by the energy gain due to doubling the number of tri-furcated H bonds in homodimers compared to heterodimers. C₃-Symmetry assembly (section “Alternative H- and halogen-assisted assemblies”) of monomers with same chirality is also observed as a possible topology in the much less frequent, extended fcc areas of the herringbone elbows (Fig. 1a and e). This type of packing is based on the assembly of the monomers in their most stable, A, conformation, and could be attributed to type II halogen–halogen contacts between terminal Br atoms.^18,19

At increased molecular coverage (coverages in the 0.5–0.9 ML range were tested), the A–B homodimer proves to be the building block for assembly into higher dimensionality, chiral structures (Fig. 2), whether 1D chains or 2D network domains. We found two different ways the homodimers can assemble along the fcc regions of the herringbones, while preserving their initial orientation relative to the [112̄] direction (Fig. 2g): type 1, via two tri-furcated H bonds, similar to those observed in the dimer itself; and type 2, via two weaker, single H bonds, between Br and the aromatic H. Two types of short 1D chains can then form, inclined at different angles relative to the [112̄] direction of the herringbones: type 1, at ∼35°, and type 2, at ∼15°. The direction of 1D chain growth further allows or limits their extended formation within the confinement of one fcc herringbone region. Type 1 chains, more strongly bonded, can accommodate only 2–3 pairs of homodimers; in contrast, type 2 chains, weaker bonded, can accommodate up to five pairs of homodimers within the constraints of one fcc herringbone region. The weaker bonded chains being able to grow relatively extensively (Fig. 2a and b) suggests that the uni-directional herringbone substrate reconstruction aids their formation by stabilizing the weaker, type 2 interaction between homodimer pairs. Within the wider fcc regions that occur where the herringbones change direction, double row chains can be accommodated. Fig. 2b and c show that this can result in type 2 double chains and nucleated islands; and type 1, double zig-zag parallel chains, bonded together by the weak, type 2, H bonding; or, alternatively, assembly of hexagonal pores where the dimers are connected via type 1 H bonding only.

Fig. 2 High molecular coverage of 3Br-borazatruxene on Au(111): a homodimer-based, hierarchical self-assembly enables the formation of 2D chiral H-bonded networks with low symmetry. (a and b) Type 2 single and double 1D chains of homodimers. A nucleated type 2, 2D island is labelled with star. (c) Homodimer-based hexamer structure and a type 1 double 1D chain. (d) Large area, 2D homochiral domain; molecular coverage ∼0.7 ML. (e and f) Zoomed-in regions of (S)- (e) and (R)- (f) 2D enantiomorphic domains, respectively, with superimposed molecular patterns of type 1, zig-zag chains. Unit cell orientations, in white, show best the mirror symmetry linking the two types of domains. Alternative selection of unit cell, in blue, corresponds to simulations from Fig. 3 and S5.† All images in (a–f) are constant current STM z images. (g) Hierarchical mechanism for the formation of low symmetry 2D chiral H-bonded networks, starting from the homodimer configuration as the building block, through two types of dimer-based 1D chains (type 1 and type 2), and finally, the 2D network incorporating both types of chains. The herringbone reconstruction of Au(111) plays a role in the stabilization of both 1D and 2D structures. Atom colour coding: H, light grey; C, grey; Br, burgundy; B, pink; N: blue.

Fig. 2d–f show that, at high molecular coverage, chiral ((R)- or (S)-) 2D domains form, extending defect-free over hundreds of nanometres in lateral size. Surprisingly, despite the individual 3Br-borazatruxene molecules having C₃ symmetry, their 2D assembly on Au(111) has only inversion symmetry, and a unit cell a = 2.34 nm, b = 2.17 nm, and θ ≈ 40° (Fig. 3e). This is in contrast with other chiral molecules with C₃ symmetry, which form H-bonded 2D networks with the expected C₆ symmetry on Au(111).^12,20–22 We found that the homodimer is also the building block for the 2D networks, with type 1 homodimer chains clearly forming the zig-zag edges of the domains (Fig. S4†). Furthermore, type 2, weakly bonded chains are now an integral part of such 2D networks, where they maintain the same molecular arrangement and angle with the [112̄] herringbone direction (i.e. 15°) as for individual chains. In this 2D molecular assembly the type 1, more strongly bonded zig-zag chains, are now oriented at approximately 90° relative to the [112̄] herringbone direction. The fact that the type 2 chains do not change orientation when incorporated in the 2D network while type 1 chains do, despite their stronger bonding, suggests that the type 2 chains are the nucleation sites for the assembly of these 2D networks.

Fig. 3 Formation of 3Br-borazatruxene homodimers and low-symmetry 2D network is controlled by hydrogen bonding. Charge density difference maps, Δρ(r), for (a) R 3Br-borazatruxene molecule on a Au(111) slab plotted for an isosurface ρ(r) = 0.006 e bohr⁻³ (Δρ(r) = ρ_Au+adsorbate − ρ_Au − ρ_adsorbate). (b) Homodimer (experimentally observed) and (c) “tip-to-tip” dimer (not observed experimentally) for an isosurface ρ(r) = 0.00015 e bohr⁻³ (Δρ(r) = ρ_homodimer − ρ_monomer1 − ρ_monomer2). (d) 2D molecular network optimized in vacuum, plotted for ρ(r) = 0.00015 e bohr⁻³. Highlighted are the two possible types of H binding: type 1 (stronger binding, green), and type 2 (weaker binding, yellow). Unit cell and zig-zag, type 1 H-bonded dimer chains in black. (e) 2D molecular network on an Au(111) slab, plotted for ρ(r) = 0.00015 e bohr⁻³. Δρ(r) = ρ_network/Au − ρ_monomer1/Au − ρ_monomer2/Au + ρ_Au, so that solely the interaction between the monomers forming the 2D network is shown. Red (blue) isosurfaces correspond to electron-deficient (electron-rich) regions due to their specific interaction.

All these observations allow the formulation of a hierarchical mechanism for building 3Br-borazatruxene 1D chains and 2D networks on the Au(111) substrate. This is summarized in Fig. 2g. Initially, at low coverage, monomers are stabilized by the interaction with the substrate in a single orientation, for each chirality. Then, in a first stage of assembly, homodimers form: these are stabilized by pairs of tri-furcated H bonds between enantiomers, and constitute the building blocks for both 1D and 2D assemblies. The fact that homodimers form even at low molecular coverage further proves their thermodynamic stability as a standalone unit. In a second stage, homodimers assemble into type 2 1D chains, driven by weaker H bonding and aided by the directional, herringbone morphology of the substrate. In a third stage, as the number of homodimers in the 1D chain reaches a critical length within the herringbone regions, other homodimers start to bind perpendicular to the 1D chains, stabilized by the much stronger, double bifurcated H bonds. This leads to the emergence of type 1, zig-zag dimer chains held together by double tri-furcated bonds, which complete the build-up of the 2D network. The gain in energy due to the stronger interaction between homodimer pairs along the zig-zag direction allows the adsorption of homodimers on top of the corrugated reconstructed substrate, across the herringbones, and insures the 2D assembly of the network. (Based on this reasoning, the 2D network cannot assemble starting from the short type 1 chains confined within the fcc regions of the herringbones as seeds as in this case the weaker type 2 chains would need to cross the energy barrier created by the herringbones.) The 2D network formed has a chiral lattice, which is both based on homochiral “clusters” (here the “cluster” is a homodimer) and has homochiral molecular content¹⁰ (Fig. 2e and f). No crystalline domains with heterochiral content (at any level, “cluster” or molecular) were observed.

We support this qualitative description of the hierarchical mechanism of 3Br-borazatruxene self-assembly on the Au(111) substrate by computed charge density difference (CDD) maps of the DFT-optimized homodimer building block, as well as of the assembled 2D network in vacuum and on the substrate; along with estimations of the intermolecular binding energies and geometric parameters. Hence, we performed geometry optimization of 3Br-borazatruxene on a three layer Au(111) slab, followed by CDD maps for several cases (Methods): (i) the monomer on the substrate, (ii) the optimized homodimer in vacuum, and (iii) the 2D molecular network in both vacuum and substrate-supported. This analysis allowed us to gain a deeper understanding of the types of interactions at play within the homodimer building block, as well as within the 2D network.

Fig. 3a shows the CDD map of (R)-3Br-borazatruxene adsorbed on a three-layer Au slab, where red (blue) isodensity represents electron-deficient (electron-rich) regions due to molecule–substrate interaction. On the Au(111) substrate, the molecule becomes overall positively charged, while at the molecule–substrate interface a layer of electron excess is present known as the pillow effect.²³ 3Br-borazatruxene loses charge to the substrate mainly through its terminal halogen atoms, amounting to ∼0.15e⁻ by the Bader analysis (Methods). Due to the structure of the molecule, electrons are withdrawn from the para methylene C bridge via the aromatic system, leaving its H atoms slightly positively charged, supported by the quinod-type shape of the electron density in the aromatic regions. The benzene ring donates charge through its π system, while in the borazine ring, N electron density is donated towards the neighbouring B atoms, which furthermore loses charge to the substrate. This degree of charge exchange, together with a mean molecule-metal adsorption distance of 3.38 Å (Table 1) show that the 3Br-borazatruxenes physisorb on the Au(111) surface. This is in agreement with the computed physisorption distance of 3.6 Å of graphene on Au(111)²⁴ and other organic molecules physisorbed on Au(111),²⁵ and in contrast with systems chemisorbed on more strongly interacting substrates, such as Cu(111) or Ni(111) where this distance is ∼2 Å.²⁴

Table 1 Molecule–substrate distances and molecular dipoles normal to the surface due to on-surface adsorption

	Borazatruxene	3Br-Borazatruxene	Truxene
Central core	3.37 Å	3.38 Å	3.37 Å
Aromatic core	3.30 Å	3.37 Å	3.31 Å
μ z	−0.17D	−0.08D	−0.15D

---

We now examine the reasons behind the stabilization of the homodimer unit, which in Fig. 1 and 2 was identified as the building block across all the assemblies present on the surface. The CDD map for the optimized R-3Br-borazatruxene homodimer, in vacuum, is plotted in Fig. 3b. We find that the homodimer is stabilized by H bonding interactions in a double tri-furcated configuration: this results from the partial positive charges developing on the aromatic and methylene H atoms, as well as the electronegative character of terminal halogens. This type of bonding corresponds to a binding energy per monomer of −34.2 meV, indicative of weak H bonding.²⁶ This is consistent (Fig. S3†) with the relatively large (within the 3 to 4 Å range) intermolecular distances between Br and the methylene H atoms, or the aromatic ortho H atoms; as well as with the corresponding CH⋯Br angles, of which the largest, 138°, is with the methylene H atoms. The “tip-to-tip” homodimer configuration that binds together the homodimers within the type 2 1D chains, along the less strong binding direction in the 2D network, was also examined (Fig. 3c and S3†). The binding energy per monomer in this case is only −14.8 meV, providing the reason why this potential dimer configuration is less likely to form. In this case, there is a single Br-aromatic H bond per monomer, with an interatomic distance of ∼3 Å and a lower CH⋯Br angle, of 106.5°. To this, intermolecular repulsive interactions between facing negatively charged H atoms of the aromatic and methylene groups contribute to lowering the binding energy per monomer of this configuration (Fig. S3†).

This analysis for various contributing homodimer configurations is consistent with the picture emerging from analysing the DFT-based CDD map of the optimized 2D molecular network, first in vacuum (Fig. 3d), then supported by the Au(111) surface (Fig. 3e). As shown in Fig. 2g, the molecular network is formed from the weaker, type 2 1D chains, stabilized by herringbone surface reconstruction, and the type 1, zig-zag 1D chains running across them. For the network in vacuum we found the intermolecular interaction within the type 1, zig-zag chains to be similar to the double tri-furcated Br–H bonds within the homodimer units themselves (Fig. 3b and S3c†). Indeed, the Br-methylene-H and Br-aromatic ortho H distances and the corresponding CH⋯Br angles in the network are very similar to those in the isolated homodimer (Fig. S3c†). The weaker, type 2 1D chains are found to be stabilized by single Br-aromatic ortho H atoms, with computed Br–H interatomic distance of 3.03 Å, and substantial electron density overlap within the bond revealed by a large CH⋯Br interatomic angle of ∼168° (Fig. S3c†). The binding energy of a monomer within this in vacuum 2D network was estimated as ∼−90.7 meV, and corresponds to each monomer being involved in two tri-furcated and one simple Br–H bonds. This value compares well with adding twice the binding energy per monomer of a type 1, stabilized homodimer (Fig. 3b) with the binding energy per monomer of the “tip-to-tip” dimer (not found to form in isolation) (Fig. 3c). This validates the interpretation of the 2D network as forming via homodimer-based building blocks. The computed 2D network on the Au(111) substrate was found to preserve the two type 1 and type 2 chain directions, with several subtler differences (Fig. 3e and S5†): (i) the charge exchanged between the monomers (whether along the type 1 or type 2 chain directions) increased, leading to (ii) a strengthening of the H bonds within the type 1 dimers. The latter manifests by changes in inter-atomic distances and bond angles that favour the interaction between Br and the ortho H atoms (Fig. 3e and S5†), and (iii) an almost doubling of the binding energy per monomer, to about −158 meV. This behaviour is paralleled by an enhancement of the interfacial charge transfer (pillow) effect between the molecules and the Au(111) substrate.

2.2 Alternative H- and halogen-assisted assemblies

Fig. 2c shows another possible hierarchical H-bonded assembly based entirely on type 1 H bonding of homodimers, observed only in the fcc regions of the Au(111) substrate. This network has C₆ symmetry, with a monomer engaged in three tri-furcated Br–H bonds and −93.85 meV binding energy per monomer in vacuum (Fig. S6†). This is very close to the −90.7 meV binding energy per monomer in vacuum for the low-symmetry 2D network that dominates the H-bonded assembly on Au(111). As in that case the monomer is engaged in two tri-furcated Br–H bonds (forming type 1 chains) and one single, weaker Br–H bond, as opposed to three tri-furcated Br–H bonds in the C₆-symmetry network, it follows that the binding energy of type 1 chains in the low symmetry network is larger than for equivalent chains in the high-symmetry network. This could explain why the type 1 chains can develop perpendicular to the herringbone directions of the Au(111) surface and stabilize the low-symmetry 2D network, but not the C₆-symmetry one for which the herringbones constitute a barrier. While the herringbones facilitate the formation of type 2 homodimer chains as seeds for the low-symmetry network, as discussed in section 1, this analysis suggests that the high symmetry, C₆ network is the one that will dominate on surfaces without herring bones and moderate reactivity, such as Ag(111). Chlorinated precursors, such as 3Cl-borazatruxene are expected to provide stronger H-bonded homodimers (due to the increased electronegativity of Cl) of the same type, in case tuning of this interaction is needed.

The C₃-symmetry assembly in Fig. 1a and e involves three halogen–halogen interactions leading to −48.82 meV binding energy per monomer in vacuum (Fig. S6†). Though possible, it is the least stable of the three network assemblies encountered here.

2.3 Effect of the borazine core

A remaining question is what effect the borazine core, with its strongly polar bonds, exerts on (i) the supramolecular assembly, and (ii) the electronic properties of the assembled networks (covalent or H-bonded). To answer it, we focused on borazatruxene, the parent molecule to 3Br-borazatruxene: in this case, the Br atoms, strongly involved in H bonding, are no longer present. We studied the borazatruxene intermolecular interactions on Au(111) via STM/STS imaging at submonolayer molecular coverage; and performed DFT simulations of the single borazatruxene on a Au(111) slab, as well as of the borazatruxene homodimer in vacuum. Furthermore, we compared the borazatruxene behavior with that of its all-carbon analogue, truxene.

STM z images of submonolayer coverage of borazatruxene (Fig. 4a) and truxene (Fig. 4b) on Au(111) show, in both cases, a surface decorated with well-separated tripod-like molecules with a lateral size of ∼1.5 nm (Fig. S1†). Both molecules adsorb preferentially on the fcc substrate regions, for which adsorption energy has been previously found to be reduced compared to hcp areas.²⁷ Experimental nearest-neighbour diagrams for borazatruxenes along the fcc trenches show peaked distributions with an average pairwise distance of 1.92 ± 0.29 nm for low molecular coverage, which is reduced to 1.34 ± 0.37 nm as the coverage is increased (Fig. S7†). The adsorption of truxenes on Au(111) in a similar manner to borazatruxene is a first indication that replacing the benzene core with borazine does not impact the assembly. In fact, this type of on-surface distribution observed for both molecules is indicative of long range repulsive interaction between monomers. Such a behavior was previously attributed to molecules that became charged by electron donation to the metallic substrate,²⁸ while in other cases, e.g. hexabenzocoronenes on Au(111), intermolecular repulsive forces were induced due to partial charges present on neighbouring molecules, independent of the substrate.²⁹

Fig. 4 Long-range repulsive interaction in borazatruxenes and truxenes adsorbed on Au(111). (a and b) STM z images of borazatruxenes (−2 V, 0.2 nA) and truxenes (−2 V, 0.3 nA), respectively, at moderate molecular coverage. (c and d) Charge density difference map, Δρ(r), of borazatruxene/Au(111) and truxene/Au(111), respectively, plotted for an isosurface ρ(r) = 0.006 e bohr⁻³ (Δρ(r) = ρ_Au+adsorbate − ρ_Au − ρ_adsorbate). (e) Charge density difference map, Δρ(r), of a borazatruxene dimer in vacuum, plotted for an isosurface ρ(r) = 0.00003 e bohr⁻³ (Δρ(r) = ρ_homodimer − ρ_monomer1 − ρ_monomer2). Red (blue) isosurfaces correspond to electron-deficient (electron-rich) regions due to their specific interaction.

In our case, DFT calculations of individual borazatruxene and truxene adsorbed on a Au(111) slab showed charge transfer from the molecule to the substrate amounting to ∼0.11e⁻ for each of the systems, according to Bader analysis (Methods). Isosurfaces of charge density difference maps (Fig. 4c and d) show that both molecules become overall positively charged, while there is an excess of electrons at the interface with the substrate. This is similar to what has been observed for 3Br-borazatruxene in Fig. 3a. The CDD map of the borazatruxene on Au shows delocalization of lost electron density mainly on the p_z orbitals of the benzene rings, while for truxene there is an imbalance of charge depletion across the aromatic lobes, where less charge is lost from the C atoms shared with the five-membered rings. Replacing the all-carbon core with borazine also yields unexpected electron delocalization between B and the adjacent C atom p_z orbitals, revealing a double bond-like interaction, which is not present in truxene for the analogous C–C bonds. This is an interesting feature which should facilitate electron transport across the molecule (from the benzene groups to the BN core) and can also contribute to borazatruxene's hydrolytic stability. Computed partial charges via Bader analysis (Fig. S8†) reveal that the BN ring of borazatruxene induces strong bond polarization in the central core and adjacent B–C and N-methylene C bonds, whereas truxene shows only negligible partial charges across its structure. Hence, there is accumulation of 1e⁻ partial charge on the aromatic C due to bonding to B, which could be deemed as the reason for the unexpected electron delocalization between the two atoms. The polar nature of the borazine core means that there is also some electron donation from the substrate to the N atoms. In contrast, the all-carbon core of truxene shows depletion of charge from the entire π system.

The existence of partial positive charges on both borazatruxene and truxene due to the adsorption on the Au slab is quite intriguing since similar behavior was observed in the charge density difference map of 3Br-borazatruxene on Au(111) (Fig. 3a). The latter case demonstrated sufficiently strong attractive intermolecular interaction to create dimers even at low molecular coverage (Fig. 1a), despite the overall positive charge acquired by the individual molecules. This contrasts with the repulsive intermolecular interactions observed for the non-brominated molecules where such dimers did not form even at increased molecular coverage. Therefore, as in all three cases the individual molecules become positively charged on the substrate but only one type forms dimers while the others not, we submit that the small net negative charge transfer to the substrate has a negligible effect on the intermolecular interaction. To further support this idea, a CDD map is plotted in Fig. 4e for the borazatruxene homodimer in vacuum purposefully kept at the same BN center-to-BN center distance as the 3Br-borazatruxene homodimer analyzed in Fig. 3b. Repulsive interaction between induced partial negative charges on the terminal H atoms of the two borazatruxenes is obtained, in stark contrast with the 3Br-borazatruxene homodimer which shows attractive H bonding interaction between the two monomers.

We can thus conclude that the intermolecular interaction observed within a dimer as in Fig. 4e is the driving force for the long-range repulsive interaction observed experimentally for borazatruxene and truxene, and not the small charge transfer to the substrate invoked in the literature for many other molecular systems. The borazine core appears to have negligible influence on the supramolecular assembly in all cases as only small partial charges develop on it, as evidenced by Fig. 3b, c, and 4e. However, the borazine core in borazatruxene, via two effects (namely bond polarization in the core and with the adjacent aromatic and methylene C atoms, and charge transfer with the substrate), induces electronic delocalization from the benzene rings to the BN core through the B–C double bond-like character, which can favorably affect electron transfer across 2D networks incorporating borazatruxenes.

Whilst the study of intermolecular interactions between precursors is important for understanding the possible assembly pathways, the study of the properties of the borazatruxene molecule – the electronic and structural building block of any network – gives insight into the electronic properties of networks formed out of them. We acquired experimental STS (dI/dV) spectra which we correlated with computed electronic structure of borazatruxene on Au(111), and compared them with similar results for the all-carbon analogue truxene, and 3Br-borazatruxene. This allowed us to identify the fingerprints of the embedded borazine core.

Fig. 5a shows the total and atom-projected DoS (PDOS) as a function of energy for each of the three precursors adsorbed on a three-layer Au(111) slab (as computed at PBE + D3 level, Methods). Integrated local DoS (ILDOS) maps corresponding to the peaks of the energy-dependent DoS show the electron density distribution across the molecules for the highest-occupied molecular resonance (HOMR) and lowest-unoccupied molecular resonance (LUMR) states on Au(111) (defined by analogy with the vacuum-based HOMO and LUMO states), where the underlying Au(111) slab has been omitted for clarity. The resonances in the ILDOS maps for borazatruxene on Au(111) originated from linear superposition of various molecular orbitals of the molecule in vacuum (Fig. S9†). The computed electronic gap increases from truxene to borazatruxene due to the benzene core being replaced by the borazine: from 3.31 eV to 3.91 eV, as the HOMR state shifts downwards from −0.82 eV to −1.26 eV, and the LUMR state shifts upwards from 2.49 eV to 2.65 eV relative to the Fermi energy. The lowering of the HOMR state is a fingerprint of benzene replacement by borazine, a downward shift in the position of the valence band being observed also in the BN-doped graphene systems.² The electron density of the HOMR state is given by the 1 : 1 hybridization of the external benzenes and central benzene core π system in truxene, while for borazatruxene only the N p_z electrons participate from the core region. The LUMR state in truxene arises again from the 1 : 1 hybridization of the external benzenes and central benzene core π system, while in borazatruxene mainly the B p_z orbitals participate from the core region. In 3Br-borazatruxene we observe an overall downshift in the energy levels compared to the borazatruxene parent molecule, which is likely due to the hybridization of the aromatic π system and p_z orbitals of bromine, and differences in the electrical dipole that develops perpendicular to the molecule on the substrate compared to the borazatruxene and truxene counterparts (discussed below, Table 1). The HOMR state of 3Br-borazatruxene is found at −1.40 eV, while the LUMR at 2.31 eV, yielding an electronic gap of 3.71 eV when adsorbed on Au(111) close to that of borazatruxene. Furthermore, the HOMR state arises from the hybridization of the external benzenes with the BN core, while for the LUMR state, the p_z orbitals of B contribute more strongly than those of N.

Fig. 5 Electronic structure of borazatruxene, 3Br-borazatruxene and truxene adsorbed on Au(111). (a) Computed projected DoS (PDOS) of the three molecules adsorbed on a three layer Au(111) slab, and associated integrated local density of states (ILDOS) maps for their respective HOMR and LUMR electronic resonances. Top panel: Dashed grey line represents the total PDOS of the molecule/Au(111) states projected onto molecular states, while the atomic contributions are shown in: black – aromatic C, red – methylene C, purple – core C, blue – N, pink – B and orange – Br atoms. Bottom panel: ILDOS for various (colour-coded) energy ranges. (b) Site-dependent STS dI/dV spectra for borazatruxene, colour code matching location of the spectra on the molecule shown in inset. The spectra were staggered on the Oy axis for ease of viewing. The inset also shows the ILDOS map corresponding to the 2 eV resonance, together with the proposed corresponding locations of the points where STS was taken. Where the resonance weakens, the electron density on the ILDOS map is low. (c) 3D “DoS (energy) vs. distance” map containing 20 spectra recorded across borazatruxene/Au(111) along the black line shown at right, each spectrum being the average of three spectra; dark green: low intensity, dark pink: high intensity. Sampling points are shown with pink and green dots. Right: Computed ILDOS maps for selected energies; experimental values for the molecular resonances appear to be downshifted relative to theoretical ones (shown in brackets) by about 0.6 eV. Sampling direction is indicated by the black arrow. Sampling point 11, dark line on the LDOS map, is assigned to borazine's nitrogen site. Choice of STS conditions described in Methods.

The computed PDOS spectra were compared with experimental site-dependent dI/dV energy spectra obtained using STS (Fig. 5b), and analyzed in the context of experimentally-derived tridimensional “DOS (energy) vs. distance” maps (Fig. 5c). These sample DOS maps (as well as the site-selected DOS spectra corresponding to Fig. 5b) were obtained by deconvoluting the corresponding dI/dV spectra from the barrier transmission function using a similar procedure as in Wagner et al.³⁰ (see also Fig. S10†). The spectra recorded midway within the series show a clear resonance at ∼2 eV, which we identify as the LUMR state of the N and B of the borazine core since it is the only resonance above the Fermi energy associated with the borazine core (as seen in Fig. 5a). Compared with the computed total and atom-projected DOS energy spectrum, this indicates a downshift of the molecular energy levels by about 0.6 eV from 2.65 eV. Taking this downshift in consideration, there appears to be good agreement between the computed and the experimentally-measured energy spectra: we further assign the resonance at ∼2.6 eV measured above the aromatic lobes to the LUMR+1 state (in the simulations at ∼3.25 eV), the resonance at −1.85 eV to the HOMR state (in the simulations at ∼−1.25 eV) present on both borazine core and external benzenes, and the one at about −2.2 eV, present only on the external benzenes, to the HOMR−1 state (in the simulations at ∼−1.6 eV). Tridimensional “DOS (energy) vs. distance” maps taken between −3 and +3 eV along two different line scans across the molecule corroborate this assignment (Fig. 5c and S10a†): such maps identify regions of high electronic density across the molecule at different energies. For example, the intensity line profiles at 2 eV extracted from these maps along the two different directions across the molecule are compatible in their spatial variations with the computed ILDOS map for the various molecular resonances shown in Fig. 5(a). The ILDOS maps for selected energies (−2.4 and +2.65 eV in Fig. 5a) show that despite the borazine core being polar, a continuous path of electron delocalization traversing the molecule can be achieved.

Further simulations demonstrated that an interfacial dipole is present for both borazatruxenes and truxenes on Au(111); this decreases by half for 3Br-borazatruxene (Table 1). The geometry optimization performed for the three molecules on a three-layer Au(111) slab showed an average molecular core-substrate distance for borazatruxene and truxene of ∼3.37 Å, while the core of 3Br-borazatruxene sits slightly higher, by only 0.01 Å (Table 1). This separation distance between the molecules and the substrate points to a weak interaction, hence physisorption, with the substrate.²⁵ Even so, truxene and borazatruxene adopt a non-planar conformation, with the outer aromatic lobes bent towards the substrate and an average distance between the plane of the external benzenes and central core for borazatruxene and truxene of 0.07 and 0.06 Å, respectively. This distance is substantially smaller, of only 0.01 Å, for 3Br-borazatruxene (Table 1), due to the larger mass of terminal Br atoms compared to H in the other two molecules. Consistent with this, the angle between the plane of the central core and the outer aromatic lobes is ∼2.5° for borazatruxene and truxene, and only ∼1.7° for 3Br-borazatruxene (Fig. S11†). This misalignment between the core and outer moieties leads to a small intramolecular dipole in the z direction, perpendicular to the Au(111) surface: this was calculated to −0.17D for borazatruxene, −0.15D for truxene, and a much lower value, of −0.08D, for 3Br-borazatruxene. The existence of a normal intramolecular dipole can shift the molecular energy levels when the molecule is adsorbed on the metallic substrate, due to the change in the workfunction of the entire system.^31,32 This is what we observed in the computed DOS energy spectra of borazatruxene compared to 3Br-borazatruxene which have similar HOMR–LUMR gaps (Fig. 5a). Charge transfer from the molecule to the substrate, as shown by Bader analysis, and the surface dipole resulting from the push-back effect might also account for the observed energy level shift between borazatruxene and 3Br-borazatruxene.

The electronic density of borazatruxene has been spatially mapped via differential conductance (dI/dV) maps at constant tunneling current (Fig. 6). The spatial distribution of the electronic density of a molecule at a bias voltage corresponding to a tunneling resonance is not necessarily an image of the square of the electronic wavefunction at that energy, but its interpretation can be far more complex, as it has been demonstrated for the pentacene/Au(111) system.³³ Depending on the z position of the STM tip during dI/dV mapping of a molecule, the tip can have access to a number of molecular states and build an image of their superposition, which is challenging to account for from a computational point of view.^34,35 Therefore, in this work, we do not expect an exact one-to-one correspondence between the experimental dI/dV maps and the computed integrated local density of states (ILDOS) maps. Nevertheless, a good broad agreement between these conductance maps and the STS-based energy level and ILDOS assignment from Fig. 5 exists: (i) the map at 2.4 eV captures characteristics of the LUMR+1 state, where the electronic density is localized mainly on the aromatic lobes, and there is little intensity on the central, borazine core; (ii) at 2 eV, close to the LUMR state, the electronic density is maximum on the borazine core while showing sizeable contributions on the aromatic lobes; (iii) −2.2 eV corresponds to the HOMR−1 state, where the electronic density is essentially present only on the aromatic lobes, with no intensity on the borazine core; and, finally, (iv) −3.1 eV, which is slightly below the HOMR−2 state, yields substantial electronic density on the borazine core and the C–B bonds making a characteristic “propeller” display, with sizeable contributions also on the aromatic lobes. In general, the signature of a new resonance is a strong change/inversion in contrast when reaching the respective energy. Such contrast inversion was observed when scanning through the gap between the HOMR and HOMR−1 states of pentacene on Au(111).³³

Fig. 6 Constant current dI/dV experimental maps of borazatruxene/Au(111). Tunnelling parameters: 2.4 V, 4 nA; 2.0 V, 3 nA; −2.2 V, 3 nA; −2.5 V, 2.3 nA; −3.0 V, 6 nA; −3.1 V, 6 nA. Choice of tunnelling conditions was justified in Methods.

The comparison between borazatruxene, 3Br-borazatruxene and truxene based on constant current dI/dV experimental maps (Fig. S12†) reveals the following salient points: (i) there are similarities between borazatruxene and 3Br-borazatruxene regarding the appearance of the core and the C–B bonds, while the Br atoms introduce specific increase in the LDOS; and (ii) for truxene, there is less contrast between the central, C core and the external benzenes compared to borazatruxene, for which the borazine core acquires strong LDOS variations relative to the rest of the molecule. Fig. S13† shows narrowing of the HOMR–LUMR gap for truxene, compared to borazatruxene.

2.4 Projected functional properties: atom trapping, doping and BN-led assembly

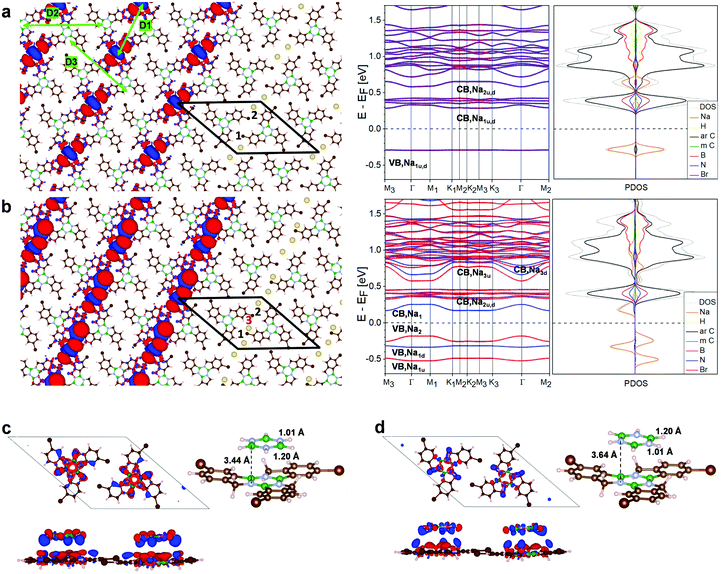
The band structure of the low symmetry, 3Br-borazatruxene H-bonded network in vacuum (Fig. S14†) shows a bandgap of 3.7 eV, and the Frontier conduction (CB_1–4) and valence bands (VB_1–5) located at +1.5 above and −2.2 eV below the Fermi energy, respectively. The full band dispersion of these Frontier states is in the 5–15 meV range, indicating only weak delocalization. A strongly dispersing group of bands (with bandwidths up to about 300 meV) is located far above, around 3 eV, the Fermi energy. The low symmetry of this network appears to be conducive to anisotropic transport once the Fermi energy can be shifted sufficiently. For this, we investigated the network's potential to trap atoms with strong donor character, such as Na.

DFT simulations showed that up to two Na atoms can be trapped within each of the pores of this network (Fig. 7a and b). One atom per pore is trapped with −0.25 eV binding energy and 1.93 Å above the average molecular plane of the network, strongly raising the Fermi energy of the network, by 1 eV, compared to the unmodified network (Fig. S15 and S17†). Energy levels become locally spin-polarized, however the network as a whole is paramagnetic as spin up, spin down and antiferromagnetic configuration have the same total energy (Fig. S16†). Trapping a second Na atom per pore increases their binding energy (to −1.07 eV for the two atoms, that includes both the interaction with the network and between the two Na atoms), the atoms being located 2 to 2.1 Å above the average molecular plane; and stabilises atom pairing with opposite spins (Fig. S15†). The small adsorption distances of the Na atoms (whether one or two in a pore), as well as the electron accumulation between the two Na atoms revealed by the CDD maps (Fig. 7a), akin to inter-atomic bonding, show that such trapping is stable. Trapping two Na atoms per pore brings the Fermi energy into close proximity, about 0.25 eV, to the Frontier conduction band (Fig. 7a), so that further tuning could then be achieved using only moderate electrostatic gating. The new Frontier conduction band in both one- and two Na atom-doped networks is the result of aromatic C–Na hybridization, and acquires ∼40 to 50 meV bandwidth (Fig. 7a and S17†). This reflects moderate but substantially increased delocalization compared to the low-lying bands of the undoped network (shown in Fig. S14†). Other anisotropic Na-derived bands, of larger, ∼70 meV bandwidth, exist at around 0.5 eV above the Fermi energy. In both one and two Na pore-trapped cases, these Na-derived bands do not intersect with others, and because they disperse only along the D2 and D3 directions (Fig. 7a and S17†) they can facilitate anisotropic transport across the network. This behavior is predicted to be further amplified when a third Na atom is adsorbed approximately in line with the first two atoms, at ∼3.3 Å relative to the network (Fig. 7b and S17†): anisotropic Na–C hybrid bands with ∼100 meV bandwidth lay now about 0.15 eV above and below the Fermi energy, while the Na–C bands at ∼0.5 eV acquire a bandwidth of almost 200 meV, which is substantial among non-covalent molecular crystals.¹⁶ Analysis of six non-equivalent adsorption sites on the network for the third Na atom (Fig. S18†) shows that the configuration from Fig. 7b is energetically preferred. In general, bands with anisotropic dispersion and sizeable bandwith are characteristic of this Na-doped network, irrespective of the adsorption site (Fig. S19†).

Fig. 7 Atom trapping, doping and BN-led molecular adsorption on the low-symmetry, 3Br-borazatruxene 2D network. (a) Pore-trapping of two Na atoms. (b) Network doped with three Na atoms: two are pore-trapped (in positions 1 and 2), the third is adsorbed (in position 3). In both (a) and (b), left: charge density difference (CDD) map, , plotted for 0.003 e bohr⁻³ isovalue. Red (blue) isosurfaces correspond to electron-deficient (electron-rich) regions due to their specific interaction. There is electron accumulation between adjacent Na atoms, indicative of “bonding” in a stable configuration. Centre: spin-resolved band structure. Na-derived hybrid bands are labelled (u, red – spin up; d, blue – spin down). ΓM₁, ΓM₂, and ΓM₃ directions in the reciprocal space correspond to the D₁, D₂ and D₃ directions in the real space (shown in (a), green, left). Right: Atomic orbital-projected density of states (PDOS) with colour-coded atomic contributions: N, blue; B, pink; H, yellow; aromatic C, black; methylene C, green; Br, red; Na, orange; total DOS, grey. (c and d) Borazine molecules stacked on the borazine (BN) cores of the 3Br-borazatruxene molecules within the 2D network: staggered in (c), eclipsed in (d). Atom colour coding: N, light blue; B, green. Left: CDD map corresponding to plotted for 0.0015 e bohr⁻³ isovalue, top and side views. Right: Related structural model of borazine adsorbed on 3Br-borazatruxene in the network.

Fig. 7c shows BN core-induced staggered adsorption of borazine (B₃N₃H₆) molecules onto the borazine cores of the 3Br-borazatruxene network, which is specific to these BN-containing molecules. The polar nature of the borazine core makes the staggered BN-NB stacking energetically more stable by −0.1 eV than the eclipsed BB-NN one (Fig. S20†). This is consistent with the binding of two stacked borazine molecules, staggered vs. eclipsed (Fig. S20†). The plane of the stacked borazine relative to the average plane of the 2D 3Br-borazatruxene network is also 0.2 Å lower in the staggered configuration compared to the eclipsed one (Fig. 7d and S20†). This example highlights an interaction specific to borazine-containing molecular precursors that could be exploited in supramolecular assembly involving the 2D 3Br-borazatruxene network to create novel multi-layered materials.

3 Conclusions

In conclusion, we studied the on-surface electronic properties and assembly of borazatruxenes, a new class of C-BN molecules. The borazatruxene molecular energy gap increases compared to the all-carbon counterpart due to the replacement of the benzene with borazine as the molecular core; this is expected to modulate the electronic properties of any network that incorporates borazatruxenes. We found double bond character between the B and C atoms in the C–B bonds. This effect stabilizes the molecule, as well as changes the electron pathways across the molecule compared to truxene. A further consequence is that, at selected energies (on both sides of the Fermi energy of the system), there is a continuous path of electron delocalization traversing the molecule; this is consequential for electron transport. The BN-core of borazatruxene-class molecules also favours staggered absorption of borazines, demonstrating a BN-core specific mechanism for supramolecular assembly in multiple layers.

A hierarchical mechanism based on chiral homodimer selection directed towards the formation of both 1D chains and 2D H-bonded networks was uncovered for 3Br-borazatruxenes on Au(111). This is key for homochiral segregation into large (hundreds of nm in lateral size) enantiopure domains. H-Bonding of 3Br-borazatruxenes shown here is primarily homodimer-led, and anisotropic in strength. The presence of the Au(111) substrate strengthens it. The network assembled on Au(111) is low symmetry (despite the 3Br-borazatruxene molecule being C₃-symmetric), with dense coverage leading to small pore sizes able to trap small size molecule/atom species. Theoretical predictions show that up to two Na atoms could be trapped within these pores, shifting the Fermi energy by more than 1 eV and inducing hybrid Na–C bands with anisotropic dispersion. Further doping with a third Na atom in a preferred configuration increases the band dispersion to several hundreds of meV, thus firmly supporting the proposal of anisotropic transport in this low symmetry H-bonded network; locally spin-polarised bands emerge depending on the Na atom loading of the network. Furthermore, the chiral H-bonded 3Br-borazatruxenes domains assembled here are sufficiently wide to be probed for potential optical activity, and suitable non-linear optical techniques are continuously improving in sensitivity (e.g. chiral nanostructures assembled on surfaces, or even single in solution, were found to induce optical rotation in second harmonic generation³⁶ or hyper-Rayleigh scattering,³⁷ respectively).

Finally, understanding the phenomena guiding the supramolecular assembly of 3Br-borazatruxene (or other halogenated borazatruxenes⁹) is essential for their successful covalent bonding into 2D C-BN covalent networks. Homochirality of such H-bonded proto networks, as in the 3Br-borazatruxene network demonstrated here, is a necessary condition for the formation of large covalent domains via subsequent reactions (as opposed to heterochirality, which could limit the spatial extension of crystalline domains); it also guarantees that the covalent domains formed will be chiral. No chiral covalent networks have been demonstrated so far and halogenated borazatruxene derivatives are well placed to enable them. The low-symmetry proto 2D H-bonded network on Au(111) shown here appears to result from the herringbone reconstruction favouring the formation of seed 1D structures around which the 2D network grows. Our observations of alternative, hexagonal-symmetry homochiral structures on the wider regions between herringbones on Au(111) suggest that on a surface devoid of herringbone reconstruction and moderate reactivity, such as Ag(111), high symmetry homodimer-based H-bonded assembly can occur, which is an avenue we are currently exploring.

4 Methods

4.1 Synthesis of molecules

Synthesis of borazatruxene and 3,8,13-tribromoborazatruxene was performed as described in Limberti et al.⁹ Truxene was purchased from the commercially available supplier Sigma Aldrich, and used without any further purification.

4.2 STM imaging, spectroscopy, and differential conductance

The experiments were performed in an Omicron qPlus LT STM/AFM microscope, at a base pressure <2 × 10⁻¹¹ mbar and 4.5 K, and using electrochemically etched W tips. The STM z imaging and differential conductance (dI/dV) maps were conducted in constant current mode. Scanning tunneling spectroscopy (STS) spectra and differential conductance maps were acquired using the lock-in technique with a frequency of 317 Hz and 20 mV rms modulation amplitude typically. The current regime for dI/dV spectroscopy and conductance maps was chosen after verifying the spectra and maps independence with current level/tip-molecule distance. The current level was maintained below the level at which molecule conformational changes were observed. In the case of the differential conductance maps conducted in constant current mode at given sample bias voltages, the current was scaled with the voltage so that the distance to the substrate above the same reference point on the Au(111) substrate remained constant across conductance maps obtained at different bias voltages. All bias voltages referred to in the manuscript are in respect to the sample. The site-dependent STS mapping along a line, as recorded in Fig. 5c and S10a,† were acquired after ensuring that there is negligible positional drift over the duration of the mapping. This was verified by imaging the position of the molecule within images before and after such mapping. The two site-dependent STS mapping lines in the two figures were chosen so as to cross the borazine ring in two close locations: attempting to intersect the N site in the first case, and the two B sites in the second case. The appearance of the STS maps/spectra obtained is consistent with the expected variation in spatial position of the 2 eV resonance along the two scan lines.

Molecules were sublimated in a preparation chamber with a base pressure <2 × 10⁻¹⁰ mbar typically, on an Au(111) substrate cleaned and reconstructed using standard sputtering/annealing procedures. Sublimation temperature was 180 °C for borazatruxene, 200 °C for 3Br-borazatruxene, and 190 °C for truxene. Prior to sublimation, molecules were thoroughly degassed for at least 12 hours.

4.3 Density functional theory calculations

These were carried out with the PWscf code implemented in the Quantum Espresso 6.3 simulation package^38,39 using a plane wave basis set up to a kinetic energy threshold of 70 Ry for the description of wavefunctions, and 440 Ry for the charge density. The projected-augmented wave method⁴⁰ was used for the description of core electrons, with pseudopotentials implemented from the PS library.⁴¹ The PBE exchange–correlation functional⁴² applied was supplied with the D3 correction⁴³ to account for dispersive interactions. Energies and geometry optimizations were converged to 10⁻⁵ eV, while forces acting on ions to below 0.001 eV Å⁻¹, respectively.

Free standing systems in vacuum such as the heterodimer and homodimers, as well as 2D networks (low-symmetry, C₃- and C₆-symmetric) were computed with 20 Å separating periodic mirror images into the z direction.

Structural optimizations of the single molecules on the Au substrate were carried out using a (6 × 3) replica of a fully optimized (1 × √3 × 3) Au(111) slab, yielding a (6 × 3√3 × 3) slab large enough to accommodate the molecule adsorption. Due to the large size of the systems, only the top Au(111) layer was allowed to relax during the optimizations, the bottom two layers being fixed at their PBE + D3 optimized bulk position of 4.13056 Å. For the structural optimization of the 3Br-borazatruxene 2D network on Au, a three layer (3√3 × 5√3) Au(111) slab was used. Due to the slight mismatch in size of the two systems, the Au(111) slab was adjusted by +0.15% in the x direction and −6.39% in the y direction in order to create a commensurate system. Due to the metallic character of these systems, a Methfessel–Paxton level broadening⁴⁴ with half width of σ = 0.2 eV was used. Reciprocal space was sampled using a 3 × 3 × 1 Monkhorst–Pack grid.⁴⁵

Projected densities of states (PDOS) plots of free-standing systems were obtained by projecting the total molecular states onto atomic orbital states of interest. For molecule/metal systems, PDOS plots were obtained by projecting the states of the combined molecule/metal system onto (i) vacuum molecular states (total PDOS) and (ii) atomic orbitals of interest (B, N, C, Br states). Integrated local density of states (ILDOS) maps are plots of spatial charge distribution evaluated by the integration of molecular states within a certain energy range, as indicated in Fig. 5a and S9.†

Interaction energies per molecule in the 2D networks are defined throughout as . Plots of charge density difference and ILDOS maps were generated using VESTA software.⁴⁶

For atomic/molecular trapping studies (such as atomic Na and B₃N₃H₆), the PBE exchange–correlation functional was supplemented with the D3 correction⁴² to account for dispersive adsorption interactions. Equations used for calculating binding energies and charge density difference maps of dopants to the network are defined in their respective figure captions.

For the C₃-symmetric 2D network case, the binding energy per molecule and CDD map has been computed as where the trimer maintains the atomic configuration of the structurally relaxed 2D trigonal system.

Charge analysis has been performed using Bader analysis algorithm. The amount of charge transferred between two interacting systems (as calculated using the Bader code developed by Henkelman et al.⁴⁷) has been computed by subtracting the charge of the individual systems in vacuum from the charge of the combined systems close together.

Author contributions

AI designed the experimental work programme and methodology, carried out the initial pump-priming of surface science and scanning probe experiments, and supervised the overall programme of work. AT performed the subsequent experimental work (except the site-dependent STS line mapping of borazatruxenes), and the computational simulations. AI and AT analysed the results and wrote the paper. GDP supervised the chemical synthesis. All authors commented on and improved the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AT acknowledges a studentship from the Engineering and Physical Sciences Research Council, UK, and the University of Bath. This research made use of the Balena High Performance Computing (HPC) Service at the University of Bath.

Notes and references

1. M. A. Springer, T. J. Liu, A. Kuc and T. Heine, Chem. Soc. Rev., 2020, 49, 2007–2019.
2. Q. Peng and S. De, Physica E, 2012, 44, 1662–1666.
3. A. Belser, K. Greulich, P. Gruninger, H. F. Bettinger, H. Peisert and T. Chasse, ACS Appl. Mater. Interfaces, 2020, 12, 19218–19225.
4. S. Beniwal, J. Hooper, D. P. Miller, P. S. Costa, G. Chen, S. Y. Liu, P. A. Dowben, E. C. Sykes, E. Zurek and A. Enders, ACS Nano, 2017, 11, 2486–2493.
5. N. Kalashnyk, P. Ganesh Nagaswaran, S. Kervyn, M. Riello, B. Moreton, T. S. Jones, A. De Vita, D. Bonifazi and G. Costantini, Chemistry, 2014, 20, 11856–11862.
6. S. Kervyn, N. Kalashnyk, M. Riello, B. Moreton, J. Tasseroul, J. Wouters, T. S. Jones, A. De Vita, G. Costantini and D. Bonifazi, Angew. Chem., Int. Ed., 2013, 52, 7410–7414.
7. C. Sanchez-Sanchez, S. Bruller, H. Sachdev, K. Mullen, M. Krieg, H. F. Bettinger, A. Nicolai, V. Meunier, L. Talirz and R. Fasel, et al. , ACS Nano, 2015, 9, 9228–9235.
8. M. Schwarz, M. Garnica, F. Fasano, N. Demitri, D. Bonifazi and W. Auwarter, Chemistry, 2018, 24, 9565–9571.
9. S. Limberti, L. Emmett, A. Trandafir, G. Kociok-Kohn and G. D. Pantoş, Chem. Sci., 2019, 10, 9565–9570.
10. S. Dutta and A. J. Gellman, Chem. Soc. Rev., 2017, 46, 7787–7839.
11. M. Lackinger, Chem. Commun., 2017, 53, 7872–7885.
12. Z. C. Yang, L. Fromm, T. Sander, J. Gebhardt, T. A. Schaub, A. Gorling, M. Kivala and S. Maier, Angew. Chem., Int. Ed., 2020, 59, 9549–9555.
13. T. Kudernac, S. Lei, J. A. Elemans and S. De Feyter, Chem. Soc. Rev., 2009, 38, 402–421.
14. A. G. Slater, P. H. Beton and N. R. Champness, Chem. Sci., 2011, 2, 1440–1448.
15. K. S. Mali, N. Pearce, S. De Feyter and N. R. Champness, Chem. Soc. Rev., 2017, 46, 2520–2542.
16. C. Winkler, F. Mayer and E. Zojer, Adv. Theory Simul., 2019, 2, 1800204.
17. K.-H. Ernst, Phys. Status Solidi B, 2012, 249, 2057–2088.
18. M. Ammon, T. Sander and S. Maier, J. Am. Chem. Soc., 2017, 139, 12976–12984.
19. J. Teyssandier, K. S. Mali and S. De Feyter, ChemistryOpen, 2020, 9, 225–241.
20. R. Gatti, J. M. MacLeod, J. A. Lipton-Duffin, A. G. Moiseev, D. F. Perepichka and F. Rosei, J. Phys. Chem. C, 2014, 118, 25505–25516.
21. T. Jasper-Tonnies, M. Gruber, S. Ulrich, R. Herges and R. Berndt, Angew. Chem., Int. Ed., 2020, 59, 7008–7017.
22. D. Cui, D. F. Perepichka, J. M. MacLeod and F. Rosei, Chem. Soc. Rev., 2020, 49, 2020–2038.
23. H. Vazquez, Y. J. Dappe, J. Ortega and F. Flores, J. Chem. Phys., 2007, 126, 144703.
24. J. Gebhardt, F. Vines and A. Gorling, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(19), 195431.
25. A. Franco-Canellas, S. Duhm, A. Gerlach and F. Schreiber, Rep. Prog. Phys., 2020, 83(6), 066501.
26. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
27. F. Hanke and J. Bjork, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235422.
28. I. Fernandez-Torrente, S. Monturet, K. J. Franke, J. Fraxedas, N. Lorente and J. I. Pascual, Phys. Rev. Lett., 2007, 99(17), 176103.
29. C. Wagner, D. Kasemann, C. Golnik, R. Forker, M. Esslinger, K. Mullen and T. Fritz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035423.
30. C. Wagner, R. Franke and T. Fritz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235432.
31. N. Koch, A. Gerlach, S. Duhm, H. Glowatzki, G. Heimel, A. Vollmer, Y. Sakamoto, T. Suzuki, J. Zegenhagen and J. P. Rabe, et al. , J. Am. Chem. Soc., 2008, 130, 7300–7304.
32. R. Otero, A. L. V. de Parga and J. M. Gallego, Surf. Sci. Rep., 2017, 72, 105–145.
33. W. H. Soe, C. Manzano, A. De Sarkar, N. Chandrasekhar and C. Joachim, Phys. Rev. Lett., 2009, 102, 176102.
34. W. H. Soe, H. S. Wong, C. Manzano, M. Grisolia, M. Hliwa, X. L. Feng, K. Mullen and C. Joachim, ACS Nano, 2012, 6, 3230–3235.
35. W. H. Soe, C. Manzano, H. S. Wong and C. Joachim, J. Phys.: Condens. Matter, 2012, 24, 354011.
36. J. T. Collins, D. C. Hooper, A. G. Mark, C. Kuppe and V. K. Valev, ACS Nano, 2018, 12, 5445–5451.
37. L. Ohnoutek, N. H. Cho, A. W. Allen Murphy, H. Kim, D. M. Răsădean, G. D. Pantoş, K. T. Nam and V. K. Valev, Nano Lett., 2020, 20, 5792–5798.
38. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901.
39. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
40. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
41. A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104.
44. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
45. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
46. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
47. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr07194g

---