Second harmonic Rayleigh scattering optical activity of single Ag nanohelices in a liquid

Abstract

Determining the chirality of molecules and nanoparticles often relies on circular dichroism and optical rotation: two chiral optical (chiroptical) effects in the linear optical regime. Although these linear effects are weak compared to nonlinear chiroptical effects, they have the advantage of being measured in isotropic liquids – free from the complications of anisotropy. Recently, a nonlinear effect: hyper-Rayleigh scattering optical activity (HRS OA) has been shown to reliably distinguish between the two chiral forms of Ag nanohelices, suspended in isotropic liquids. However, this first demonstration of HRS OA also opened new questions. For instance, at a fundamental level, it is not clear what the role of interactions between nanoparticles is. Moreover, the influence of the ultrafast pulse chirp is unknown. Here, we demonstrate HRS OA from well below two Ag nanohelices in the illumination volume, precluding any interactions. Additionally, we performed the first measurements of HRS depolarization ratios in this system and find a value of ≈1. We also show that HRS is highly robust against the chirp of the ultrafast pulses. An important reason for the strong (down to single nanohelix) sensitivity of our experiments is the large chiroptical interaction at the fundamental frequency; this point is illustrated with two sets of numerical simulations of the electromagnetic near-fields. Our results highlight HRS OA as a highly sensitive experimental method for characterization of chiral solutions/suspensions, in tiny illumination volumes.

---

1. Introduction

Because they lack mirror symmetry, chiral nano/meta-materials have promising applications in areas such as photonic devices^1–3 and nanorobotics.^4,5 The materials have also sparked discussions about hyper-sensitive chemical characterization using superchiral light.^6–8 These applications have been enabled by theoretical breakthroughs in understanding the chirality parameters for metamaterials, namely geometrical chirality⁹ and optical chirality.^10,11 However, whereas these parameters are straightforward to include within electromagnetic (e.g. constitutive) equations, they can be very difficult to measure experimentally. When assembled on thin films, chiral nano/meta-materials can exhibit extrinsic chirality,^12,13 false chirality,¹⁴ and various anisotropies^15,16 that all complicate the measurement of true chirality. Hence, highly sensitive experimental methods that can probe the chirality of nanoparticles, as they revolve and drift freely in an isotropic liquid are highly desirable.

In liquids, the characterization of chiral molecules and nanostructures is often performed through linear optical means, such as by measuring optical rotatory dispersion (ORD) and circular dichroism (CD). However, both are very weak effects and consequently require large numbers of nanoparticles in solutions/suspensions. Nonlinear chiroptical effects^17–19 are usually much more sensitive to chirality (typically 10³ times more^20,21). Nevertheless, these effects are often better suited to investigating chirality at material surfaces/interfaces (especially in solids) than in 3D isotropic liquids. Among nonlinear chiroptical effects, hyper-Rayleigh scattering optical activity (HRS OA) stands out,²² because it is both well-suited to isotropic liquids and it is highly sensitive.

Hyper-Rayleigh scattering (HRS) is an incoherent nonlinear optical process, during which light is scattered at harmonic frequencies of the incident light.^23–26 In 1979, it was theoretically predicted that optical activity should exist in HRS²⁷ and, in 2019, this effect was experimentally demonstrated for suspensions of silver nanohelices.²² Soon after, the effect was observed in chiral molecules and gold helicoids.^28,29 Recently, optical activity has also been observed in third harmonic Rayleigh scattering³⁰ and third harmonic Mie scattering.³¹

Possible interactions between individual scatterers are of fundamental importance for the origin of the HRS signal. The latter is attributed to the sum of the intensity of light scattered by individual scatterers, assuming that the scatterers are independent.³² In the first experimental observation, HRS OA was measured from an illumination volume of 10⁻¹¹ m³, where ≈100 000 nanohelices were present. For such conditions, a possible interaction between the nanohelices cannot be completely ruled out.

Here, we use HRS OA to determine the handedness of single silver nanohelices. This sensitivity is achieved by reducing the illumination volume from ≈10⁻¹¹ m³ in ref. 22 to 4 × 10⁻¹⁷ m³, here. Our results rule out interactions between nanohelices and they are in good agreement with those in ref. 22. Moreover, we present the first measurements of HRS depolarization ratios in silver nanohelices and report that their value is ≈1. We also show that HRS OA is very robust and flexible: it can be adapted to setups with optical components that greatly affect the quality of the fs pulses with no significant effect on the HRS OA results. Crucial for the single nanohelix sensitivity is the strong light–matter interaction that depends dramatically on the direction of circularly polarized light and on the chirality of the nanohelices. We illustrate this point by numerical simulations of the optical near-fields at the surface of a nanohelix, calculated with both the finite-difference time-domain (FDTD) method and the potential-based boundary element method (PB-BEM). The simulation results are provided for illumination with left and right circularly polarized light.

2. Ag nanohelices with strong chiroptical properties

The Ag nanohelices studied here are grown using nanoglancing angle deposition. The growth of individual Ag nanohelices is seeded with an array of Au nanoparticles on a Si substrate. A detailed description of the fabrication process can be found in the Methods section. Fig. 1(a) shows scanning electron microscopy images of wafers with the prepared nanohelices. The top panels of the images reveal well-formed helices with a different handedness on each of the wafers. A different view (from above the substrate) is shown in the bottom right panels to illustrate the dense surface coverage. The bottom left panels show photographs of the samples from which their surface areas are calculated. Dynamic light scattering (DLS) results from left-handed (LH) and right-handed (RH) nanohelices dispersed in aqueous trisodium citrate are shown in Fig. 1(b). The nominal dimensions for LH nanohelices are shown in the inset. The height of 110 nm is in good agreement with the DLS results.

Fig. 1 Silver nanohelices with strong chiral optical properties. (a) Scanning electron microscopy images of wafers with left-handed (LH) and right-handed (RH) silver nanohelices. Bottom left: photographs of pieces of wafers used for preparing nanohelix suspensions. The surface areas of the two wafers are ≈0.9 cm² and ≈1.1 cm². (b) Dynamic light scattering measurements of LH and RH nanohelices. The inset shows the nominal dimensions of a single LH nanohelix. (c) Extinction (absorption + scattering) spectra of suspensions of LH and RH helices in a 2 mM aqueous solution of trisodium citrate. OD: optical density. (d) Measured circular dichroism (CD) spectra of suspensions of LH and RH helices in a 2 mM aqueous solution of trisodium citrate.

The linear chiroptical properties of the nanohelices suspended in 2 mM trisodium citrate are studied by measuring spectra of extinction (which is the sum of absorption and scattering) and circular dichroism (CD). The extinction spectra of the two chiral forms, enantiomorphs, have a similar spectral shape but differ slightly in their amplitude (see Fig. 1(c)). The difference in amplitude can be caused by a different concentration of the suspensions and by a slight variation in the physical dimensions between the two enantiomorphs. The CD spectra in Fig. 1(d) exhibit a characteristic bisignate profile, with the most prominent feature situated close to 650 nm. Crucially, the CD spectra have opposite sign for the suspensions of the two enantiomorphs as expected for chiral structures that are mirror images of each other (although not perfect mirror images). The difference in the amplitude of the CD spectra can again be attributed to a slightly different concentration and morphology.

For the HRS experiments, Si wafers covered with Ag nanohelices are cut into pieces of a similar size. The bottom left parts of the images in Fig. 1(a) show photographs of the wafer pieces with LH and RH helices. The surface areas of the pieces are ≈0.9 cm² and ≈1.1 cm², respectively. Because a square of area a² has an equivalent area to an equilateral triangle with sides , the areas of the samples correspond to equilateral triangles with sides 1.44 cm and 1.59 cm, respectively. These nanohelices are arranged on the substrate in quasihexagonal arrays with a spacing of ≈90 nm. Consequently, the equilateral triangles have ≈160 187 and ≈177 093 nanohelices on each side, respectively. The total number of LH and RH nanohelices on the wafers is therefore ≈1.28 × 10¹⁰ and ≈1.57 × 10¹⁰, respectively. Each of these samples is then placed into a beaker with 1.4 mL of 1 mM trisodium citrate and sonicated. Sonication causes the nanohelices to detach from the wafer and disperse in the liquid. Assuming that all of the nanohelices disperse in the liquid during sonication, the concentrations of the suspensions are ≈9.16 × 10¹⁵ nanohelices per m³ (LH nanohelices) and ≈1.12 × 10¹⁶ nanohelices per m³ (RH nanohelices). These numbers are the upper limits of concentrations. The concentration of our samples can be lower (if some nanohelices stay on the substrate during sonication) but not higher. Based on the concentrations, we can estimate the mean inter-particle distance in the suspension. If we consider a hypothetic cubic arrangement of the nanohelices in the liquid (solely as an example of a regular lattice), the mean inter-particle distances are 4.79 μm and 4.46 μm for the LH and RH nanohelices, respectively.

3. Nonlinear optical experiments

For a single meta-molecule, the induced dipole moment in the Cartesian framework of the inset of Fig. 1(b) is:²⁶

μ_i = α_ijE_j + β_ijkE_jE_k + γ_ijklE_jE_kE_l + …, (1)

where i, j, k and l can represent any of the Cartesian directions, α is the polarizability tensor, β is the first hyperpolarizability tensor, γ is the second hyperpolarizability tensor and E_j is the electric field component at the fundamental frequency of light, along the j Cartesian direction (that can be x, y or z). The induced dipole moment per unit volume at the second harmonic can then be written as:

P_i(2ω) = χ_ijkE_j(ω)E_k(ω), (2)

where χ_ijk is the macroscopic second-order susceptibility. In isotropic media, such as achiral (meta) molecules in liquids, the average value of χ_ijk is zero. For an isotropic chiral medium though, such as an enantiopure suspension of nanohelices, χ_ijk is non-zero.

The isotropic chiral symmetry group belongs to one of the seven Curie limiting point groups of anisotropic materials.³³ In Hermann–Mauguin notations, it is represented by ∞∞. The χ_ijk tensor can be expressed as χ_ijk = χ₀ε_ijk, where ε_ijk is the Levi-Civita symbol and χ₀ is a constant.³⁴ Therefore, there are only 6 non-zero tensor elements and they are related according to χ_XYZ = −χ_YXZ = χ_ZXY = −χ_XZY = χ_YZX = −χ_ZYX.³⁵ These tensor components are tridimensional and can be referred to as chiral.

In cases where the fundamental and harmonic frequencies are far from material resonances, Kleinman symmetry applies and χ_ijk = χ_kij = χ_jki. As a result χ₀ = 0, which leads to P_i(2ω) = 0, signifying that the second harmonic generation (SHG) chiroptical effects are forbidden, with collinear beams and within the electric dipole approximation.³⁶ Even outside Kleinman conditions, due to symmetry, the last two indices of our tensor components can be exchanged, meaning that χ_XYZ = χ_XZY, χ_YXZ = χ_YZX and χ_ZXY = χ_ZYX. This relationship can be easily understood, since in our experiments, the two electric fields at the fundamental frequency are collinear. It follows again that the SHG chiroptical effects are forbidden.³⁶

For reference, chiroptical effects in isotropic chiral liquids have been observed using sum frequency generation, by means of two non-collinear beams with different frequencies, (ω₁ and ω₂) and having perpendicular polarizations.³⁷ In this case, the nonlinear polarization is given by P(2ω) = χE(ω₁) × E(ω₂).³⁸ By comparison, HRS OA is a significantly less intricate technique.

Although for SHG the average nonlinear chiroptical response is forbidden, a second harmonic signal can originate from the temporal and spatial orientational fluctuations of the (meta) molecules around this average; it is these instantaneous deviations from isotropy that cause the HRS signal.³⁹

Assuming that the scatterers do not interact, the total HRS intensity is the sum squared of the electric fields scattered by each nanohelix in the illumination volume:³²

I_HRS(2ω) = G〈β_HRS²〉I(ω)², (3)

where 〈〉 indicates orientational averaging and G is the instrumental efficiency that depends on the scattering geometry, the local field factors, the concentration and on the direction cosines.⁴⁰ To rule out interactions between nanohelices, it is convenient to measure HRS from no more than 1 nanohelix in the illumination volume.

Fig. 2(a) presents a schematic diagram of the HRS OA experimental setup. A fused quartz cuvette containing a suspension of Ag nanohelices is irradiated with circularly polarized, ultrashort, 730 nm laser pulses. The laser beam is focused into the cuvette with a long working distance microscope objective and scattered light is collected at a 90° angle to the incident beam. A bandpass filter centered at 365 nm is placed in front of the light detector to measure signal only at the HRS wavelength. A detailed description of the experimental setup is available in the Methods section.

Fig. 2 Clear circular dichroism measured in volumes containing <1 nanoparticle, on average. (a) Schematic diagram of the experimental configuration. QWP: quarter-wave plate, LP: long-pass, LWD: long working distance; BP: band pass. (b) and (c) The detected intensity of hyper-Rayleigh scattering (HRS) in suspensions of left-handed (LH) and right-handed (RH) nanohelices, respectively, in 1 mM trisodium citrate solution. The samples were illuminated with left circularly polarized (LCP) and right circularly polarized (RCP) 730 nm light. Scattered light was detected at 365 nm ± 5 nm. Each data point is an average of 6 measurements. The data points up to (and including) 7 mW were fitted with a y = Ax² function. The error bars are well within the symbol sizes. (d) Calculated HRS ellipticity for illumination with 730 nm light. The error bars are calculated from the standard errors of the measurements of HRS intensity.

To determine the number of nanohelices that interact with the incident laser beam, we need to estimate the illumination volume in the experimental setup (an approximate volume, in which the focused beam is capable of exciting nonlinear optical effects). More specifically, we can define the illumination volume as an integral of the beam cross section between ±z_R, where z_R is the Rayleigh length. Previously, the illumination volume with the same long working distance microscope objective as used here was estimated to be 30 μm³ = 3 × 10⁻¹⁷ m³ (in the shape of a rotational ellipsoid with its principal axes 2.3 μm and 11 μm long).²⁹ This number was obtained by mounting the objective onto a commercial multiphoton microscope and measuring two-photon luminescence of a 200 nm fluorescent bead. Both two-photon luminescence and HRS scale quadratically with the intensity of the fundamental beam. Therefore, the volumes in which these effects are excited are also comparable when the same objective is used. While the fluorescent bead was immobilized on a substrate and thus was surrounded by air on one side, the nanohelices float in a liquid. The difference in the refractive indices of air and the solvent affects the illumination volume, as the parameters of a Gaussian beam depend on the background refractive index, e.g. the Rayleigh length is directly proportional to the refractive index of the medium. Thus, we can correct for the change of medium by multiplying the Rayleigh length in air (5.5 μm) by the refractive index of water (1.33 at 730 nm), which gives the Rayleigh length in water (7.3 μm). Hence, the illumination volume in water has a shape of a rotational ellipsoid with its principal axes 2.3 μm and 14.6 μm long, i.e. a volume of approximately 40 μm³ = 4 × 10⁻¹⁷ m³.

Based on the concentration of the nanohelices in the suspensions (9.16 × 10¹⁵ LH nanohelices per m³ and 1.12 × 10¹⁶ RH nanohelices per m³) and the illumination volume (4 × 10⁻¹⁷ m³), the average number of nanohelices in the measured volume is calculated to be 3.7 × 10⁻¹, for LH nanohelices, and 4.5 × 10⁻¹, for RH nanohelices.

HRS intensity is measured for right circularly polarized (RCP, here defined as polarization for which the electric field of light rotates counterclockwise in a fixed plane perpendicular to the direction of propagation, when looking along the direction of propagation) and left circularly polarized (LCP) light incident on a cuvette containing a suspension of nanohelices. In Fig. 2(b) and (c), the measured intensity of HRS in suspensions of LH and RH nanohelices, respectively, is plotted as a function of incident laser power. For lower incident powers, the HRS intensity follows the expected square-law. For higher incident powers, the detected intensity deviates from the quadratic dependence. This deviation could be due to photo-induced damage to the nanohelices or due to an ultrafast dynamics process, such as hot electron generation. Importantly, a difference in HRS intensity is observed for the two incident circular polarizations.

To quantify this difference, HRS ellipticity θ_HRS is calculated using the following formula:

where I_RCP and I_LCP are HRS intensities detected under illumination with RCP and LCP light, respectively.

HRS ellipticities obtained for both enantiomorphs of the Ag nanohelices are presented in Fig. 2(d). Apart from one outlier (at 1 mW), the HRS ellipticities of the two enantiomorphs are clearly separated and have opposite signs. The HRS ellipticity appears largest for lower laser power and it remains relatively constant through the whole laser power range. Laser-induced damage is expected to melt the nanostructures, eventually transforming them into achiral spheres, whose HRS ellipticity would be zero.

The HRS ellipticity values are in good agreement with the results reported in ref. 22. However, in the previous work, the concentration of nanohelices in the illumination volume was approximately 100 000, compared to approximately 0.5 in this work. This striking difference corresponds to approximately 6 orders of magnitude.

As the concentration of the nanohelices in this work is below 1, the illumination volume is sometimes occupied by a nanohelix and sometimes empty. Considering the length of a single measurement is 30 s, Brownian motion leads to random movement of the nanohelix in the illumination volume, which results in an effective averaging of its nonlinear optical response with respect to its position and orientation within the illumination volume.

Performing HRS depolarization measurements serves to probe the degree or polarized emission from the (meta) molecules.⁴¹Fig. 3(a) shows the setup for depolarization experiments. A cuvette with a suspension of nanohelices is illuminated with S (vertically) or P (horizontally) polarized light. Following collimation by a lens, the scattered light passes through a rotating analyzing polarizer (analyzer) prior to being focused into the detector. The HRS intensity measured upon illumination at 730 nm and recorded as a function of the polarization state of the scattered light is presented in Fig. 3(b). At 0°, the analyzer is oriented along the S (vertical) direction. The empty and full symbols correspond to illumination with S and P polarized light, respectively. For incident S polarized light, the depolarization ratio is defined as 〈I^P_HRS〉/〈I^S_HRS〉, where S and P indicate the direction of polarization of the HRS light. In our measurements, for incident light polarized along S, we measure 〈I^P_HRS〉/〈I^S_HRS〉 = 77.5/78.3 = 0.99. For incident light polarized along P, we measure 〈I^S_HRS〉/〈I^P_HRS〉 = 88.3/83.5 = 1.06.

Fig. 3 Hyper Rayleigh scattering (HRS) depolarization ratios indicate that the detected light is unpolarized. (a) Schematic diagram of the experimental configuration. (b) The detected intensity of HRS from suspensions of left-handed nanohelices, as a function of analyzer rotation angle. At 0°, the analyzer is oriented along the S (vertical) polarization direction. The empty and full symbols correspond to illumination with linearly polarized light, along S (vertical) and P (horizontal), respectively. The illumination was at 730 nm and the average laser power was 14 mW.

Microscope objectives can contain a high number of lenses with different dispersion that can broaden and chirp the ultrafast pulses. To investigate this effect, we assembled an experimental setup with a single focusing lens and a laser source that provides variable group delay dispersion (GDD), see Fig. 4(a).

Fig. 4 Hyper-Rayleigh scattering optical activity (HRS OA) is very robust versus ultrafast laser chirp variations. (a) Schematic of the experimental setup. Laser beam with a varying pulse length Δt is passed through a quarter-wave plate, a long-pass filter, and a lens before reaching the cuvette filled with suspensions of Ag nanohelices. Scattered light is collected at 90° to the incident beam. A plot of HRS intensity vs. group delay dispersion (GDD) for (b) left-handed nanohelices and (c) right-handed nanohelices with both left circularly polarized (LCP) and right circularly polarized (RCP) 750 nm light. The error bars show the standard deviation of 10 measurements. (d) The HRS ellipticity for the left- and right-handed nanohelices as a function of GDD, calculated using the results in (b) and (c). The average incident laser power was 15 mW for all measurements.

Fig. 4(b) shows the HRS intensity measured when a suspension of LH nanohelices is illuminated with circularly polarized 750 nm light with varying chirp (determined by the GDD pre-set on the laser system). Results for suspensions of RH nanohelices are presented in Fig. 4(c). For both samples, the HRS intensity initially increases as the GDD is increased and then gradually declines. The observed behavior is consistent with the effect of changing incident peak power. At first, as the pre-set GDD is increased, it compensates the GDD introduced by the optical elements. The laser pulses illuminating the Ag nanohelices become shorter, which translates into a larger pulse peak power and thus stronger nonlinear emission. A further increase in the pre-set GDD leads to broadening of the laser pulses and a corresponding drop in the intensity of the nonlinear emission.

Eqn (4) can be used to calculate the HRS ellipticity as a function of the pre-set GDD (Fig. 4(d)). Remarkably, in the available GDD range, the HRS ellipticity is unaffected by the varying pulse length/chirp. Therefore, any chirp effect that the optical components might have on the laser pulses only results in a change in HRS intensity but does not affect the HRS OA.

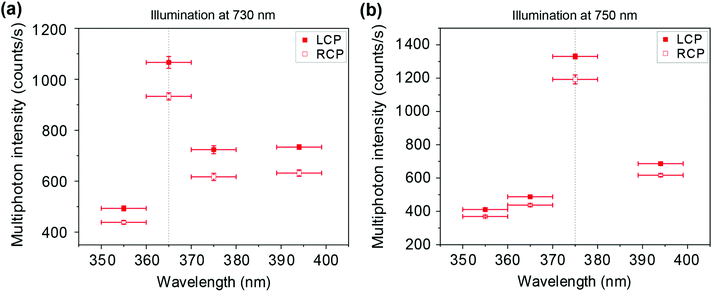
To rule out any possible confusion of the nonlinear optical effect at study here with two-photon luminescence, next we investigate the multiphoton emission spectra from our samples. Fig. 5(a) and (b) show the multiphoton emission spectra of a suspension of LH nanohelices, upon illumination at 730 nm and 750 nm, respectively. In each case, the spectra show clear emission peaks at the second harmonic, i.e., at 365 nm and at 375 nm, respectively. Thus, we can conclude that the signal detected from the samples at study is indeed HRS and not two-photon luminescence.

Fig. 5 Hyper-Rayleigh scattering signal is above the multiphoton luminescence background. Multiphoton emission spectra of a suspension of left-handed nanohelices upon illumination with left circularly polarized (LCP) or right circularly polarized (RCP) light with wavelength (a) 730 nm and (b) 750 nm. The x-error bars indicate the full-width at half-maximum of the transmission peak of the bandpass filters used. The y-error bars represent the standard deviation of 10 measurements. The average incident power was 15 mW for both wavelengths.

4. Numerical simulations

An important reason behind the large sensitivity of our measurements (down to the single nanohelix) is the strong chiroptical response of the nanohelices. The origin of this response is illustrated by the electric near-fields, calculated for a LH Ag nanohelix illuminated with LCP and RCP light propagating along the three Cartesian directions in Fig. 1(b). The problem is symmetric for the RH nanohelices. Illuminating a nanohelix that rotates freely (in suspension) within the reference frame of the lab is equivalent to a freely rotating laser beam that illuminates a fixed nanohelix (within its own reference frame).

The simulations presented in Fig. 6(a) are performed with the Lumerical FDTD software and the results in Fig. 6(b) are obtained from boundary element simulations. The details of all the numerical simulations are provided in the Methods section.

Fig. 6 A dramatic contrast in electric near-fields, depending on the direction of circularly polarized light coupling into a left-handed nanohelix, at 730 nm. (a) Electric fields obtained from (a) FDTD simulations and (b) boundary element simulations. The 6 panels in each subfigure present the amplitude of electric field in the y–z plane for left circularly polarized light (in the left panels) and right circularly polarized light (in the right panels) simulated with an incident pulse centered at 730 nm. Top, light propagating with k vector along (parallel to) the x axis; middle light propagating with k vector along the y axis; bottom, light propagating with k vector along the z axis.

In both Fig. 6(a) and (b), the amplitude of the electric field in the y–z section of the nanohelix is plotted as a color map for various illumination conditions. The left panels of the figures correspond to illumination with LCP and the right panels with RCP light. The top, middle and bottom rows show results for illumination (i.e.k vector propagating) along the x, y, and z directions, in the reference frame in Fig. 1(b).

Excellent agreement is seen between the results presented in Fig. 6(a) and (b). For illumination with k vector along the x or y directions, the electric field amplitudes around the nanohelix are not particularly sensitive to the direction of circularly polarized light. However, for illumination with k vector along the z direction, i.e., along the axis of the nanohelix, the difference is dramatic. For nanohelices freely revolving in a liquid, the orientation with respect to the incident light is assumed to be random and therefore the average response is determined by the dramatic effect observed when k is along (parallel to) the z direction. Similar trends can be observed for the magnetic near-fields that can also play a role in the HRS OA response²⁷ and for electromagnetic fields visualized in the x–z plane, see ESI.†

The origin of the HRS OA effect can be discussed in terms of Fermi's golden rule or the Purcell effect.⁴² The scattering at the second harmonic frequency depends both upon the coupling between the initial (fundamental) and final (second harmonic) states and upon the density of final (second harmonic) states. Within this context, the nanohelices can be regarded as ‘resonant cavities’. Because of the helical shape and metal nature, these structures ring; they benefit from prolonged photon lifetimes inside the ‘cavity’.

In our system, the ‘coupling’ is the frequency conversion mechanism. As can be seen from eqn (3), HRS intensity is determined by the components of the first hyperpolarizibility tensor of the nanohelices and the intensity at the fundamental frequency. The numerical simulations presented in Fig. 6 allow us to discern the contribution of the latter to the detected optical activity. As the HRS intensity is proportional to the square of intensity at the fundamental frequency, it is proportional to the fourth power of the (local) electric field. The dramatic difference in electromagnetic response at the fundamental wavelength observed in the numerical simulations, depending on the direction of circularly polarized light, thus significantly contributes to the HRS OA results in Fig. 2(d). Additionally, the results obtained in the numerical simulations, i.e., that LCP light leads to stronger local electric fields for a LH nanohelix, are in agreement with our experimental results in Fig. 2(b), where I_LCP > I_RCP (as stronger local electric fields lead to more scattering at the HRS wavelength).

Moreover, the surface plasmon resonance of the Ag nanohelices, which can be seen at 365 nm in Fig. 1(c), corresponds to an enhanced local density of states of the optical field at the second harmonic (final states, within the framework of Fermi's golden rule). As Fig. 1(d) shows, there is no significant CD in the linear optical regime at 365 nm. Therefore, the plasmon resonance contributes mainly to an increase in the intensity of the HRS signal and does not significantly affect the sign of the HRS OA. The latter is therefore determined by the sign of the geometry of the helix (hyperpolarizability) and by the difference in local field enhancements at the fundamental frequency (shown in Fig. 6).

5. Discussion and conclusion

Chiral scatterometry and circularly polarized luminescence have previously been shown to enable measurements of single chiral nanoparticles.^43–47 However, in these experiments, the nanoparticles are measured on a substrate, which can affect the results due to the fixed orientation of the nanoparticle with respect to the incident light as well as due to contributions from the substrate. By contrast, HRS OA can measure the handedness of single (on average) gold nanoparticles, in a 3D isotropic liquid.²⁹ Soon after ref. 29 was published, Sachs et al.⁴⁸ reported on time-resolved linear chiroptical measurements of freely diffusing single nanoparticles and showed that the averaged spectra are equivalent to those obtained on ensembles of nanoparticles.

Importantly, while HRS OA measured at the single nanoparticle level has been reported previously,²⁹ due to the nature of the samples studied in this work, the calculated number of nanoparticles is an absolute upper limit; i.e. any uncertainty due to experimental procedures can only lower the number of nanohelices contributing to the HRS OA signal, which would mean that the likelihood of interactions between nanohelices is even lower.

In conclusion, we demonstrate HRS OA measured in suspensions of plasmonic nanohelices with the concentration of 0.5 nanohelices in the illumination volume can reliably reveal the handedness of the nanohelices in the suspension. This concentration is well below two and therefore precludes any interactions between nanohelices during the measurements. As a consequence, the total intensity of the scattered light at the second harmonic is the sum, squared of the scattered electric fields from each individual nanohelix. We report the first measurements of HRS depolarization ratio in Ag nanohelices; the observed value is ≈1 indicating that the detected light is not polarized. The new chiroptical technique is highly robust versus dramatic variations of the chirp of the ultrafast pulses. Our experimental results and numerical simulations are in good agreement, evidencing that a strong chiroptical effect at the fundamental frequency contributes to the sensitivity of HRS OA. These results showcase HRS OA as an exquisitely sensitive optical method for characterization of chiral scatterers (nanoparticles, molecules, quantum dots, etc.) due to the strength of the effect (HRS ellipticity measured in this work is 10× larger than the ellipticity in the linear optical regime) and to the capability to measure in microscopic volumes.

6. Experimental section/methods

Fabrication of Ag nanohelices

The nano GLancing Angle Deposition (nanoGLAD) technique is used to grow three-dimensional chiral nanohelices in a manner previously reported.⁴⁹

First, a hexagonal array of 10 nm Au dots with 90 nm spacing is prepared on a 2-inch silicon wafer by block-copolymer micelle nanolithography.⁵⁰ Briefly, the block-copolymer micelles of poly(styrene)-b-poly(2-vinylpyridine) (PS units: 1056; PVP units: 495) containing Au salts in the core are formed by self-assembly in toluene and then spin-coated onto the Si wafer where the micelles form a quasi-hexagonally ordered monolayer (spacing ≈90 nm). Plasma treatment reduces the Au salts to form metallic nanodots with ≈10 nm in diameter. These act as seeds for subsequent GLAD growth.

Next, the Ag–Ti nanohelices are grown on the array of the Au dots in a GLAD system based on co-deposition from dual electron-beam evaporators with a base pressure of 1 × 10⁻⁶ mbar. The target substrate to be deposited on was cooled down to 90 K with liquid nitrogen for 1 h and positioned at 87° of the flux angle. The alloy stoichiometry was controlled by the deposition rates measured by a quartz crystal microbalance (QCM) setup for each evaporator independently. So, the helices are grown with 700 nm thickness of Ag including ca. 3% Ti through the whole body of the helices (based on the QCMs) while rotating the substrate for 720° (i.e. full rotation twice) with ca. 1 ± 0.1° nm⁻¹ of the azimuthal rotation rate per unit thickness.⁵¹ This rotation in either the clockwise or anticlockwise direction results in, respectively, the array of either the RH or LH nanohelices.

Finally, the grown Ag–Ti nanohelices are lifted off from the wafer by sonicating a piece of sample wafer (ca. 1 cm²) in an aqueous solution of 1 or 2 mM trisodium citrate for ≈5 min to prepare a stock solution.

Hyper-Rayleigh scattering experiments with fixed pulse length

The light source for the HRS experiments was a titanium:sapphire laser with 100 fs pulses and 80 MHz repetition rate. A chopper blade with 1.7% duty cycle attenuated the laser beam average power, modulating the stream of pulses at a frequency of 41 Hz, while still maintaining the peak power of pulses. Light was passed through a coated calcite polarizer and then through a superachromatic quarter-wave plate. A pair of long-pass filters (cut-on wavelength = 665 nm) removed any residual second-harmonic signal from the beam. A long-working distance microscope objective with 50× magnification focused the laser beam into a fused quartz cuvette filled with the studied samples.

The optics for collecting the scattered light was placed perpendicularly to the incident beam. On the one side of the cuvette, there was a concave mirror, and on the other side there was a plano-convex collimating lens with 25.4 mm focal length. Another plano-convex lens (focal length = 200 mm) was used to focus the collected light into a photomultiplier tube (PMT). A hard-coated bandpass filter with 10 nm full-width at half-maximum was placed in front of the PMT to filter out wavelengths other than the HRS wavelength.

The signal detected by the PMT was pre-amplified 5× before entering a photon counter. The counter was used in the gated regime, i.e., signal was counted for a specific amount of time when the chopper passes the laser beam through and for the same amount of time when the chopper blocked the beam (to estimate the number of dark and ambient counts). The integration time of a single measurement was set to 30 s.

For the depolarization experiments, the concave mirror on the side of the cuvette was removed and a coated calcite analyzing polarizer (analyzer) was placed between the collimating and focusing lens in the detection arm of the setup.

Hyper-Rayleigh scattering experiments with varying pulse length and nonlinear emission spectra

Light from a Coherent Chameleon Vision-S laser with an initial pulse length of 75 fs is modulated by an optical chopper with a 3.3% duty cycle and 43 Hz frequency. The beam was then passed through a coated calcite polarizer and an achromatic half-wave plate for power control. An achromatic quarter-wave plate was positioned after this. A long-pass filter was used to remove any light below 665 nm. The light was focused into a fused quartz cuvette containing the nanohelix samples using a coated achromatic doublet lens with a focal length of 40 mm. A plano-convex lens with a focal length of 25.4 mm was placed on one side of the cuvette, perpendicular to the incoming beam, to collimate the scattered light. The scattered light passed through a short-pass filter (cut-off wavelength of 610 nm) to remove any light scattered at the fundamental wavelength. The beam was then focused into the PMT by a plano-convex lens with a focal length of 200 mm. A hard-coated bandpass filter with a 10 nm full-width at half-maximum was placed in front of the PMT. The signal detected by the PMT was pre-amplified 5× before entering a photon counter operated under a gated counting regime. The GDD of the laser pulse was modified by adjusting the laser settings. The laser power was set to 15 mW for each GDD value.

The nonlinear emission spectra were collected in the same setup with the GDD set to 0. In these experiments, the incident wavelength was kept constant, while the bandpass filters in front of the PMT were changed to collect a spectrum.

Finite-difference time-domain (FDTD) simulations

In Fig. 6(a), the FDTD simulations were performed in Lumerical. The idealistic silver nanohelix was modelled in computer aided design (CAD) software (Autodesk Inventor) in units of mm and exported to an STL CAD file format. The STL file was then imported into Lumerical with a 10⁻⁶ geometric scaling to shrink the dimensions of the nanohelix from mm to nm units. The dimensions of the resultant geometry matched that of the studied LH nanohelix: length = 110 nm, loop diameter = 50 nm, loop pitch = 55 nm and wire diameter = 25 nm.

A Johnson and Christy material model for silver was applied to the nanohelix. The simulation domain was 1 × 1 × 1.5 μm with perfectly matched layer (PML) boundary conditions, a background refractive index of unity and initial temperature of 300 K. The elongated dimension (1.5 μm) was necessary to ensure that more than half a wavelength of space existed between the source of the light and the PML boundary along the propagation axis. A Eulerian mesh with granularity 8.5 nm was applied to the domain globally with a localized refinement region (300 × 300 × 300 nm) surrounding the nanohelix with granularity of 1 nm to enhance the fidelity of the results.

The light source was a 3.2 fs pulse formed from a pair of superimposed Bloch/periodic plane waves located 500 nm from the center of the nanohelix. The central wavelength of the plane waves was 730 nm with a full-width at half-maximum of 500 nm. The plane waves were polarized at a right angle to one another and with a phase difference of 90° to achieve circularly polarized light.

The LH nanohelix was simulated with left- and right circularly polarized light propagating for 1 ps. The pulse of circularly polarized light was simulated in three configurations; in the first two, the direction of propagation was perpendicular to the axis of the nanohelix (along the x and y axis). In the third, the direction of propagation coincided with the axis of the nanohelix. Hence a total of six simulations were executed.

Boundary element simulations

The simulations in Fig. 6(b) are performed by using a potential-based boundary element method (PB-BEM).^52–54 The PB-BEM focuses on equivalent surface sources on the boundary of a nanoscatterer. By matching the potentials on both sides of the boundary, the method provides a set of integral equations, which further discretizes the boundary with triangular patches and converts the integral equations into matrix equations. By solving the matrix equations, the method obtains the equivalent sources, and maps fields in the space. In our simulations, we consider the LH and the RH silver nanohelices immersed in vacuum and excite the structures with circularly polarized light incident along the positive x, y and z directions. The permittivity of silver is extracted from Johnson and Christy's material model data;⁵⁵ the nanohelices are discretized by 2304 triangular patches; the incident light spans from 400 nm to 1000 nm with 100 sampling points; the circularly polarized light is defined in the same way as in ref. 56; and the field is mapped at 730 nm with 81 sampling points in both y and z directions.

Data availability

All data supporting this study are openly available from the University of Bath Research Data Archive at https://doi.org/10.15125/BATH-01111

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank Prof. Peer Fischer for helpful discussions. V. K. V. acknowledges support from the Royal Society through the University Research Fellowships and the Royal Society grants PEF1\170015 and RGF\EA\180228, as well as the STFC grant ST/R005842/1 and the EPSRC grant EP/T001046/1. L. O. and V. K. V. acknowledge funding and support from the Engineering and Physical Sciences Research Council (EPSRC) Centre for Doctoral Training in Condensed Matter Physics (CDT-CMP), grant EP/L015544/1. X. Z. acknowledges funding from FWO (grant G090017N) and KU Leuven Internal Funds grants C14/19/083 and IDN/20/014.

References

1. C. Rizza, A. Di Falco, M. Scalora and A. Ciattoni, Phys. Rev. Lett., 2015, 115, 057401.
2. M. Esposito, V. Tasco, F. Todisco, M. Cuscunà, A. Benedetti, M. Scuderi, G. Nicotra and A. Passaseo, Nano Lett., 2016, 16, 5823–5828.
3. Y. Hou, H. M. Leung, C. T. Chan, J. Du, H. L.-W. Chan and D. Y. Lei, Adv. Funct. Mater., 2016, 26, 7807–7816.
4. M. J. Urban, C. Zhou, X. Duan and N. Liu, Nano Lett., 2015, 15, 8392–8396.
5. D. Schamel, M. Pfeifer, J. G. Gibbs, B. Miksch, A. G. Mark and P. Fischer, J. Am. Chem. Soc., 2013, 135, 12353–12359.
6. Y. Zhao, A. N. Askarpour, L. Sun, J. Shi, X. Li and A. Alù, Nat. Commun., 2017, 8, 14180.
7. E. Hendry, T. Carpy, J. Johnston, M. Popland, R. V. Mikhaylovskiy, A. J. Lapthorn, S. M. Kelly, L. D. Barron, N. Gadegaard and M. Kadodwala, Nat. Nanotechnol., 2010, 5, 783–787.
8. R. Tullius, A. S. Karimullah, M. Rodier, B. Fitzpatrick, N. Gadegaard, L. D. Barron, V. M. Rotello, G. Cooke, A. Lapthorn and M. Kadodwala, J. Am. Chem. Soc., 2015, 137, 8380–8383.
9. J. B. Pendry, Science, 2004, 306, 1353–1355.
10. Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901.
11. M. Schäferling, D. Dregely, M. Hentschel and H. Giessen, Phys. Rev. X, 2012, 2, 031010.
12. E. Plum, X.-X. Liu, V. A. Fedotov, Y. Chen, D. P. Tsai and N. I. Zheludev, Phys. Rev. Lett., 2009, 102, 113902.
13. A. Belardini, M. C. Larciprete, M. Centini, E. Fazio, C. Sibilia, D. Chiappe, C. Martella, A. Toma, M. Giordano and F. Buatier de Mongeot, Phys. Rev. Lett., 2011, 107, 257401.
14. L. D. Barron, Chem. Phys. Lett., 1986, 123, 423–427.
15. J. T. Collins, D. C. Hooper, A. G. Mark, C. Kuppe and V. K. Valev, ACS Nano, 2018, 12, 5445–5451.
16. D. C. Hooper, A. G. Mark, C. Kuppe, J. T. Collins, P. Fischer and V. K. Valev, Adv. Mater., 2017, 29, 1605110.
17. S. Sioncke, T. Verbiest and A. Persoons, Mater. Sci. Eng., R, 2003, 42, 115–155.
18. P. Fischer and F. Hache, Chirality, 2005, 17, 421–437.
19. K. W. Smith, S. Link and W.-S. Chang, J. Photochem. Photobiol., C, 2017, 32, 40–57.
20. T. Petralli-Mallow, T. M. Wong, J. D. Byers, H. I. Yee and J. M. Hicks, J. Phys. Chem., 1993, 97, 1383–1388.
21. J. D. Byers, H. I. Yee and J. M. Hicks, J. Chem. Phys., 1994, 101, 6233–6241.
22. J. T. Collins, K. R. Rusimova, D. C. Hooper, H.-H. Jeong, L. Ohnoutek, F. Pradaux-Caggiano, T. Verbiest, D. R. Carbery, P. Fischer and V. K. Valev, Phys. Rev. X, 2019, 9, 011024.
23. T. Verbiest, K. Clays and V. Rodriguez, Second-order Nonlinear Optical Characterization Techniques, CRC Press, 2009.
24. R. W. Terhune, P. D. Maker and C. M. Savage, Phys. Rev. Lett., 1965, 14, 681–684.
25. K. Clays and A. Persoons, Phys. Rev. Lett., 1991, 66, 2980–2983.
26. K. Clays and A. Persoons, Rev. Sci. Instrum., 1992, 63, 3285–3289.
27. D. L. Andrews and T. Thirunamachandran, J. Chem. Phys., 1979, 70, 1027.
28. D. Verreault, K. Moreno, É. Merlet, F. Adamietz, B. Kauffmann, Y. Ferrand, C. Olivier and V. Rodriguez, J. Am. Chem. Soc., 2020, 142, 257–263.
29. L. Ohnoutek, N. H. Cho, A. W. A. Murphy, H. Kim, D. M. Răsădean, G. D. Pantoş, K. T. Nam and V. K. Valev, Nano Lett., 2020, 20, 5792–5798.
30. L. Ohnoutek, H.-H. Jeong, R. R. Jones, J. Sachs, B. J. Olohan, D. M. Răsădean, G. D. Pantoş, D. L. Andrews, P. Fischer and V. K. Valev, Laser Photonics Rev., 2021, 2100235.
31. L. Ohnoutek, J.-Y. Kim, J. Lu, B. J. Olohan, D. M. Rasadean, G. D. Pantos, N. A. Kotov and V. K. Valev, Nat. Photonics, 2022, 16, 126–133.
32. E. Hendrickx, K. Clays and A. Persoons, Acc. Chem. Res., 1998, 31, 675–683.
33. A. V. Shubnikov, in Crystal Symmetries, Elsevier, 1988, vol. 16, pp. 357–364.
34. K. S. Grigoriev, V. A. Diukov and V. A. Makarov, Opt. Lett., 2020, 45, 276.
35. J. A. Giordmaine, Phys. Rev., 1965, 138, A1599–A1606.
36. R. W. Boyd, J. E. Sipe and P. W. Milonni, J. Opt. A: Pure Appl. Opt., 2004, 6, S14–S17.
37. P. M. Rentzepis, J. A. Giordmaine and K. W. Wecht, Phys. Rev. Lett., 1966, 16, 792–794.
38. R. W. Boyd, Nonlinear Optics, Academic Press, Amsterdam, 4th edn, 2019.
39. N. Matsuda, G. Olbrechts, E. J. H. Put, K. Clays and A. Persoons, Appl. Phys. Lett., 1996, 69, 4145–4147.
40. T. Verbiest, K. Clays, C. Samyn, J. Wolff, D. Reinhoudt and A. Persoons, J. Am. Chem. Soc., 1994, 116, 9320–9323.
41. R. Bersohn, Y. Pao and H. L. Frisch, J. Chem. Phys., 1966, 45, 3184–3198.
42. E. M. Purcell, Phys. Rev., 1946, 69, 681.
43. K. W. Smith, H. Zhao, H. Zhang, A. Sánchez-Iglesias, M. Grzelczak, Y. Wang, W.-S. Chang, P. Nordlander, L. M. Liz-Marzán and S. Link, ACS Nano, 2016, 10, 6180–6188.
44. J. Karst, N. Strohfeldt, M. Schäferling, H. Giessen and M. Hentschel, Adv. Opt. Mater., 2018, 6, 1800087.
45. P. Woźniak, I. De Leon, K. Höflich, C. Haverkamp, S. Christiansen, G. Leuchs and P. Banzer, Opt. Express, 2018, 26, 19275.
46. J. Karst, N. H. Cho, H. Kim, H.-E. Lee, K. T. Nam, H. Giessen and M. Hentschel, ACS Nano, 2019, 13, 8659–8668.
47. E. Vinegrad, U. Hananel, G. Markovich and O. Cheshnovsky, ACS Nano, 2019, 13, 601–608.
48. J. Sachs, J.-P. Günther, A. G. Mark and P. Fischer, Nat. Commun., 2020, 11, 4513.
49. A. G. Mark, J. G. Gibbs, T.-C. Lee and P. Fischer, Nat. Mater., 2013, 12, 802–807.
50. R. Glass, M. Möller and J. P. Spatz, Nanotechnology, 2003, 14, 1153–1160.
51. H.-H. Jeong, A. G. Mark, M. Alarcón-Correa, I. Kim, P. Oswald, T.-C. Lee and P. Fischer, Nat. Commun., 2016, 7, 11331.
52. X. Zheng, M. Kupresak, R. Mittra and G. A. E. Vandenbosch, IEEE Trans. Antennas Propag., 2018, 66, 4759–4771.
53. X. Zheng, M. Kupresak, V. V. Moshchalkov, R. Mittra and G. A. E. Vandenbosch, IEEE Trans. Antennas Propag., 2019, 67, 3948–3960.
54. X. Zheng, M. Kupresak, N. Verellen, V. V. Moshchalkov and G. A. E. Vandenbosch, Adv. Theory Simul., 2019, 2, 1900087.
55. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379.
56. J. Peatross and M. Ware, Physics of Light and Optics, Brigham Young University, 2015th edn, 2015.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr06800h

‡ These authors contributed equally to this work.

---