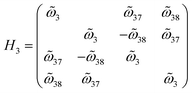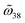A physical interpretation of coupling chiral metaatoms†
Zhaolong
Cao
,
Jianfa
Chen
,
Shaozhi
Deng
and
Huanjun
Chen
 *
*
State Key Laboratory of Optoelectronic Materials and Technologies, Guangdong Province Key Laboratory of Display Material and Technology, School of Electronics and Information Technology, Sun Yat-sen University, Guangzhou 510275, China. E-mail: chenhj8@mail.sysu.edu.cn
First published on 3rd February 2022
Abstract
The physical origins of chiroptical responses from artificial optically active media are significant for developing high-performance circular dichroism (CD) spectroscopic techniques. Here, we present a biorthogonal approach based on temporal coupled-mode theory to unravel the underlying physics of chiral metasurfaces. Equipped with physically meaningful parameters, this approach inherits the intrinsic properties of open optical cavities, including time-reversal symmetry and non-Hermitian Hamiltonians, which are found to be in excellent agreement with numerical results. Remarkably, it identifies that the intrinsic chirality of coupled chiral nanocavities arises from (i) the asymmetric coupling between interlayer cross-polarized resonant modes and (ii) a coherent interference between doubly degenerate states. Based on this formalism, a critical coupling condition capable of achieving zero transmission for circularly polarized light is proposed.
Introduction
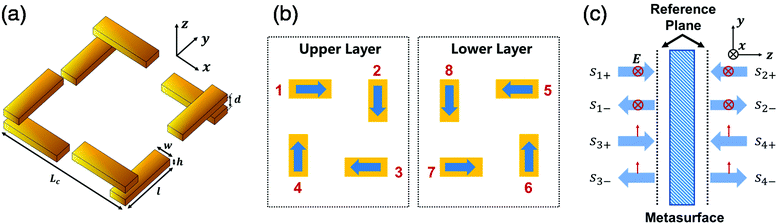
A chiral object refers to a geometrical object, or a group of points, whose mirror image (enantiomer) cannot be brought to coincide with itself.1 Although chirality is mostly associated with structural properties at its initial stage, chiral structures can manifest themselves with rich physics ranging from topological surface states2 and chiral excitonic states3 to enhanced optical chirality.4 For example, the ability of chiral media that exhibit differential responses to left circularly polarized (LCP) and right circularly polarized (RCP) lights, termed circular dichroism (CD), has been widely used as a powerful analytical tool in enantiomer characterization for centuries.5 However, the chiral-optical (chiroptical) effect is a subtle property at optical frequencies due to the weak magnetic responses of naturally occurring materials, and a medium with strong chiroptical effects is still challenging to achieve.6–10Recently, artificial metasurfaces based on plasmonic nanostructures and high-index dielectric nanoparticles have emerged as a research hotspot owing to their unprecedented capabilities for manipulating and localizing photons at a subwavelength scale.9,11,12 Various complex geometries, including split-ring resonators,13–15 gammadions,16–18 L- and S-shaped antennas,19 and nanoclusters,20–24 have been extensively studied as basic building blocks for chiral metasurfaces. Recently, giant chirality with maximum CD has been reported both theoretically25 and experimentally.15,17 However, the underlying physics governing the physical origins of chiroptical responses is still not well studied. For example, chiral plasmonic structures can be modeled with two mutually coupled harmonic oscillators from an electromagnetic perspective, which has been demonstrated to not only provide an intuitive framework but also being in qualitative agreement with experimental observations.22,26 However, this phenomenological approach, based on the coupling between resonators, is a classical analog to the constitutive relationships of optically active media.27,28 The fundamental properties of open optical systems, including time-reversal symmetry and non-Hermitian interactions, are inevitably overlooked. In contrast, temporal coupled-mode theory (CMT),29–33 a theoretical approach fruitfully employed to model optical cavities,25,34 bears great potential for solving this problem. It has been shown that CMT provides superior accuracy on the reconstruction of the far field properties from the given eigenmodes.35 However, a rigorous CMT based on the non-Hermitian interactions of optical cavities still remains unexplored. For instance, a recent CMT pre-assumes the eigenmodes of a chiral metasurface to be orthogonal and well-separated,25,34 and the physical origins of chirality, that is, how the non-Hermitian coupling between achiral nanocavities gives rise to chiral eigenmodes has not been fully investigated. As shown in Fig. 1a, the metaatom is expected to exhibit giant optical chirality owing to the optical resonance and chiral arrangements. However, the physics behind non-Hermitian interactions among 8 identical achiral nanorods contributing to optical activity is still unclear. To the best of our knowledge, a rigorous derivation that combines both physical insights and explicit expressions including eigenfrequencies, eigenmodes, radiative decay rates, etc., is still elusive.
Despite its importance, the main difficulty in applying CMT as a solid theoretical model is that it is intrinsically limited by two facts: (i) the model parameters in CMT are phenomenological quantities; and (ii) there is a lack of an intuitive but rigorous approach for obtaining non-orthogonal chiral eigenmodes. The former concern has been addressed by recent studies on the quasinormal mode (QNM) of electromagnetic systems,35–38 where the classical CMT is found to be a special form of a rigorous QNM coupling theory for the case of weak coupling and low loss.37 Here, we attempt to address the latter concern using a biorthogonal approach.39 With surprisingly high accuracy, this approach reconstructs the far-field property of a chiral metasurface with meaningful parameters while still inheriting the necessity of optical systems including time-reversal symmetry and non-Hermitian interactions. Furthermore, we identified that the optical activity originates from the asymmetric coupling between interlayer cross-polarized resonant modes and the coherent interference between doubly degenerate states. In the end, we validate our formalisms through numerical simulations and propose a critical coupling condition capable of achieving zero transmission for circularly polarized light.
Results and discussion
Non-Hermitian Hamiltonian based on CMT
We should first comment on the symmetry of the chiral metasurface. Optical chirality is a time-even and parity-odd quantity.4 However, when associated with a specific object, it could probably be intertwined with circular polarization conversion (CPC) and asymmetric transmission (AT).24,40,41 For example, two-dimensional planar metasurfaces are geometrically achiral in three dimensions,42 but they can still produce non-zero CD signals.43,44 This phenomenon, also termed 2D chirality, is reported to have no contribution to optical activities.45–47 In addition, CPC and AT effects could be absent in chiral materials (e.g., an infinite slab of Pasteur medium), suggesting that they are not the fundamental mechanism for chirality. Therefore, in order to eliminate CPC and AT effects, the chiral metasurface can be chosen to have a D4 symmetry (section S1 in the ESI†).22,25,40,48–54Fig. 1a shows an exemplary chiral metaatom. For the purpose of this study, we limited our analysis only to this configuration. CD is defined as CD = (|t+|2 − |t−|2)/(|t+|2 + |t−|2), where t± is the transmission coefficient for RCP and LCP light, respectively. Here, each nanorod represents a plasmonic nanocavity. Their positive dipole moments are defined in Fig. 1b. We should stress that the constitutional building blocks can be extended to other nanocavities such as high-index Mie resonators,11,55 split-ring resonators,14 hyperbolic cavities56etc. The metaatom is embedded in a homogeneous dielectric environment. All incoming waves are incident normally to the metasurface from both sides. ejωt time dependence for all fields is assumed throughout this paper. The period is smaller than the resonant wavelength so that only zero-order transmission/reflection is allowed. In the regime of effective medium theory, this symmetry condition is a direct analog to reciprocal (Pasteur) bi-isotropic materials.27,57We derive our equations based on temporal CMT.31 As a starting point, we first denote the incoming waves by |s+〉 = (s1+ s2+ s3+ s4+)T, where s1+(s3+) and s2+(s4+) are the x-polarized (y-polarized) light incident from −z and +z sides (Fig. 1c). Therefore, 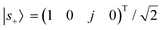 and
and 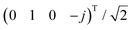 correspond to RCP incident light, and
correspond to RCP incident light, and 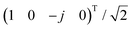 and
and 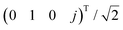 correspond to LCP incident light, respectively. Similarly, the outgoing waves are defined by
correspond to LCP incident light, respectively. Similarly, the outgoing waves are defined by 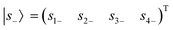 . The incoming and outgoing waves can couple through a direct pathway described by a background S-matrix C, which is unitary and symmetric for a lossless and reciprocal system in the absence of optical cavities. By properly choosing a reference input plane and considering symmetry requirements,30C takes the form (section S2 in the ESI†)
. The incoming and outgoing waves can couple through a direct pathway described by a background S-matrix C, which is unitary and symmetric for a lossless and reciprocal system in the absence of optical cavities. By properly choosing a reference input plane and considering symmetry requirements,30C takes the form (section S2 in the ESI†)
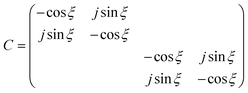 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ and jsin
ξ and jsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ being the background reflection and transmission coefficients. Once the background S-matrix, input, and output waves are defined, the dynamic equations for coupled nanocavities can be written as31
ξ being the background reflection and transmission coefficients. Once the background S-matrix, input, and output waves are defined, the dynamic equations for coupled nanocavities can be written as31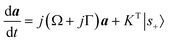 | (2.1) |
| |s−〉 = C|s+〉 + Da, | (2.2) |
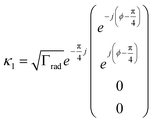 | (3) |
The phase factor π/4 in eqn (3) is due to the choice of the reference input plane in eqn (1). The physical interpretation of ϕ is a retardation coefficient for +z and −z incoming waves, which are related to the layer distance and the wavevector of incoming waves by kd = 2(ϕ − π/4). The decay matrix is defined by D = K because of time-reversal symmetry. Γrad = |κi|2/2 is the total radiative decay rate for a single cavity. The near field interactions and complex resonant frequencies of nanocavities can be represented by an 8 × 8 symmetric matrix
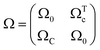 | (4.1) |
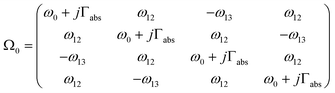 | (4.2) |
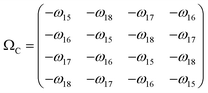 | (4.3) |
Considering both near-field and far-field interactions, the Hamiltonian of the optical system leads to the symmetric non-Hermitian matrix: H = Ω + jΓ. The off-diagonal (complex) elements of H correspond to the mutual excitation of the scattered fields between each nanocavity from the first principles of Maxwell's equations.37 As we will show later, H manifests itself with rich physics by the biorthogonal approach.
Chiral eigenmodes based on the biorthogonal approach
We start with the biorthogonal approach on the non-Hermitian H matrix. Assuming that XR is a matrix whose columns are the right eigenvectors of H, and XL is a matrix whose rows are the left eigenvectors of H, one can obtain XTL = XR and XLXR ≡ 1 (section S4 in the ESI†). Then, the general CMT equations can be reorganized by left-multiplying eqn (2.1) with XL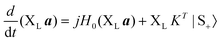 | (5.1) |
| |s−〉 = C|s+〉 + KXR(XLa) | (5.2) |
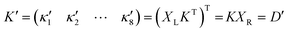 . Note that due to the non-Hermitian nature (XL+XL ≠ 1), the radiative decay rate for the ith eigenmode should be normalized by Γ′rad,i = |κi|2/(2|ai|2).
. Note that due to the non-Hermitian nature (XL+XL ≠ 1), the radiative decay rate for the ith eigenmode should be normalized by Γ′rad,i = |κi|2/(2|ai|2).
Next, we attempted to deduce the explicit equation for XL. The direct diagonalization of the 8 × 8 non-Hermitian matrix is a non-trivial task. However, a two-step diagonalization process, namely, intralayer and interlayer diagonalizations, can simplify the mathematical derivations. From a physical point of view, this is equivalent to categorizing cavity interactions into two groups: (i) nanocavities in the same layer first couple together (intralayer interaction) forming intralayer eigenmodes, and then (ii) couple to the opposite layer (interlayer interaction). Detailed derivations are given in section S5 of the ESI,† and we only list several physical implications here.
First, by performing intralayer diagonalization and reorganization, one obtains the block-diagonal Hamiltonian
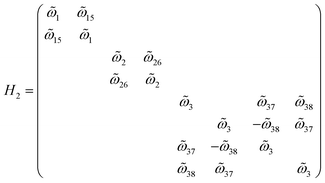 | (6) |
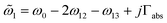 ,
, 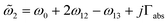 , and
, and 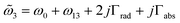 are the intralayer eigenfrequencies, and
are the intralayer eigenfrequencies, and 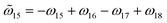 ,
, 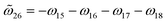 ,
, 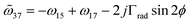 , and
, and 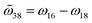 are the interlayer coupling coefficients. Therefore, the interlayer interaction can be divided into three diagonal block parts. While the first two blocks are total dark modes owing to the C4 rotational symmetry (section S5 in the ESI†), radiative modes from
are the interlayer coupling coefficients. Therefore, the interlayer interaction can be divided into three diagonal block parts. While the first two blocks are total dark modes owing to the C4 rotational symmetry (section S5 in the ESI†), radiative modes fromwill contribute to chirality.
Second, the eigenmodes of H3 are doubly degenerate. This property is of particular importance for the chiral metasurface. To understand this, we start with the explicit expression of the outgoing wave |s_〉 (section S6 in the ESI†)
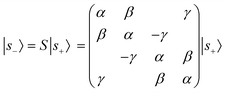 | (7) |
Third, the chiroptical response of the metasurface can be determined once the S-matrix is ready. The reflection coefficients for LCP (r−) and RCP (r+) lights are identical given by r± = α, whereas the transmission coefficients are t± = β ∓ jγ (eqn (S29)†). Therefore, according to eqn (S28.4),†γ (more specifically, the product between 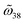 and cos
and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ) accounts for the CD responses. Apparently,
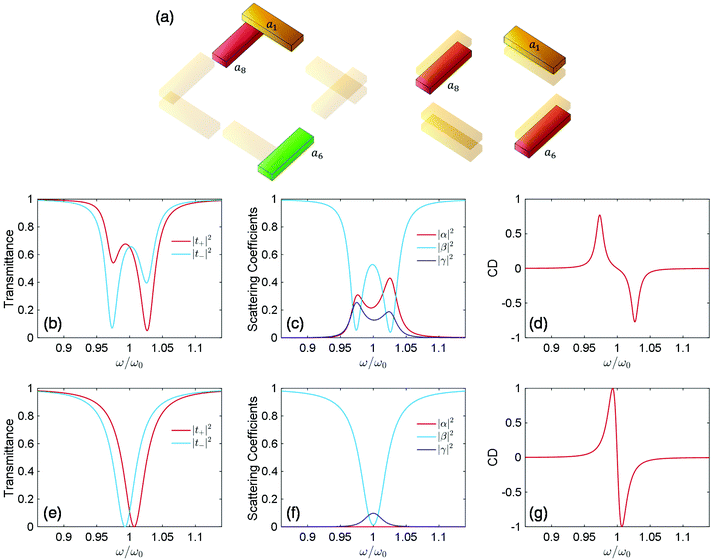
2ϕ) accounts for the CD responses. Apparently, 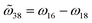 depicted in Fig. 2a is attributed to structural chirality—the asymmetric coupling from a6 and a8 to the cross-polarized a1 nanocavity. When the metaatom restores to symmetry configurations (Fig. 2a, right), a6 and a8 cancel each other, leading to negligible chirality. ϕ corresponds to the retardation effect (eqn (3)) and will be discussed later.
depicted in Fig. 2a is attributed to structural chirality—the asymmetric coupling from a6 and a8 to the cross-polarized a1 nanocavity. When the metaatom restores to symmetry configurations (Fig. 2a, right), a6 and a8 cancel each other, leading to negligible chirality. ϕ corresponds to the retardation effect (eqn (3)) and will be discussed later.
Using eqn (S28.3) and (S28.4)† and assuming negligible background reflection for subwavelength nanorods (ξ = π/2), t± can be simplified as
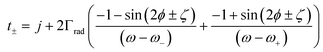 | (8) |
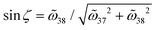 and
and 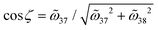 . Eqn (8) is consistent with previous results.25,34 Moreover, this formalism explicitly recovers the far-field amplitude and phase information of the system, which is crucial for explaining asymmetric chiral Fano line-shapes. Fig. 2b–d show the chiroptical behavior of an analytical metasurface with ω0 + ω13 = 1, Γrad = 0.005, Γabs = 0.003, −ω15 + ω17 = −0.022, ω16 − ω18 = −0.017 and ϕ = 1.5 rad. As expected, transmission spectra for both LCP and RCP lights exhibit Fano line-shapes (Fig. 2b) and the CD response yields characteristic bisignate signatures.
. Eqn (8) is consistent with previous results.25,34 Moreover, this formalism explicitly recovers the far-field amplitude and phase information of the system, which is crucial for explaining asymmetric chiral Fano line-shapes. Fig. 2b–d show the chiroptical behavior of an analytical metasurface with ω0 + ω13 = 1, Γrad = 0.005, Γabs = 0.003, −ω15 + ω17 = −0.022, ω16 − ω18 = −0.017 and ϕ = 1.5 rad. As expected, transmission spectra for both LCP and RCP lights exhibit Fano line-shapes (Fig. 2b) and the CD response yields characteristic bisignate signatures.
It is also noteworthy that eqn (8) predicts an isolated chiral state by evaluating the numerator
| −1 − sin(2ϕ ± ζ) = 0 | (9.1) |
| −1 + sin(2ϕ ± ζ) = 0. | (9.2) |
The above equations require that, given 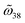 a real coefficient, ζ, or equivalently,
a real coefficient, ζ, or equivalently, 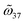 should be a real number as well. Therefore, recalling that
should be a real number as well. Therefore, recalling that  , one gets 2ϕ = nπ for all positive integers n. For the lowest order ϕ = π/2 we arrive at the assessment given by the plasmonic Born–Kuhn model:22 the isolated chiral mode is located at a quarter-wavelength layer distance (d = π/2k = λ/4). In fact, such a condition is not sufficient. By inserting ϕ = π/2 into eqn (9.1) and (9.2), one arrives at sin
, one gets 2ϕ = nπ for all positive integers n. For the lowest order ϕ = π/2 we arrive at the assessment given by the plasmonic Born–Kuhn model:22 the isolated chiral mode is located at a quarter-wavelength layer distance (d = π/2k = λ/4). In fact, such a condition is not sufficient. By inserting ϕ = π/2 into eqn (9.1) and (9.2), one arrives at sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ = ±1 and thus
ζ = ±1 and thus 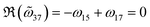 . Therefore, isolated chiral states can only be achieved when differential near field interactions from a5 and a7 to the parallel a1 nanocavity cancel each other. Considering the asymmetry positions of a5 and a7, this condition is difficult to be fulfilled. Nevertheless, Fig. 2e and f show the analytically isolated chiral condition by setting ω0 + ω13 = 1, Γrad = 0.005, Γabs = 0.01, −ω15 + ω17 = 0, ω16 − ω18 = −0.007 and ϕ = π/2. Consistent with the analysis, both |t+|2 and |t−|2 exhibit a single resonant dip and demonstrate that the metaatom resonates coherently in a single state for both LCP and RCP incoming waves.
. Therefore, isolated chiral states can only be achieved when differential near field interactions from a5 and a7 to the parallel a1 nanocavity cancel each other. Considering the asymmetry positions of a5 and a7, this condition is difficult to be fulfilled. Nevertheless, Fig. 2e and f show the analytically isolated chiral condition by setting ω0 + ω13 = 1, Γrad = 0.005, Γabs = 0.01, −ω15 + ω17 = 0, ω16 − ω18 = −0.007 and ϕ = π/2. Consistent with the analysis, both |t+|2 and |t−|2 exhibit a single resonant dip and demonstrate that the metaatom resonates coherently in a single state for both LCP and RCP incoming waves.
Numerical evaluations
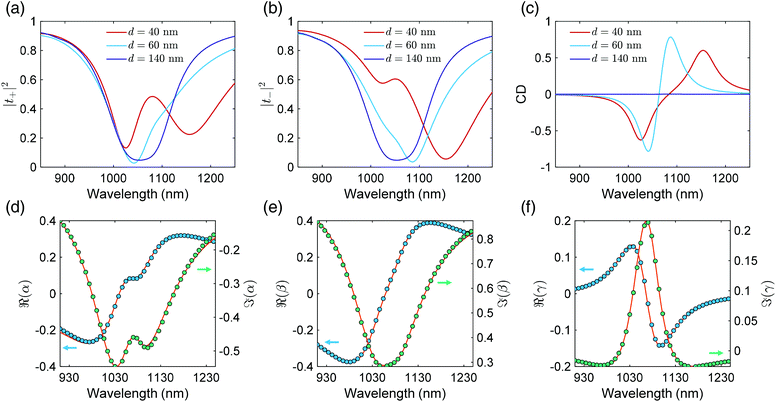
We carried out finite-difference time-domain simulations (Lumerical Inc.) to verify the validity of chiral CMT. The geometrical parameters for the metasurface are length l = 120 nm, height h = 24 nm, width w = 24 nm, and atom size Lc = 200 nm. The metaatom is arranged in a square lattice with a period P = 400 nm. The permittivity of gold is best fitted from the literature58 using the Drude model. In order to reproduce experimental conditions, the metasurface was embedded in a uniform dielectric environment with a refractive index n = 1.5.22 The S-matrix was calculated using the built-in near field to far-field algorithms, and the phase of background reflection was calibrated to π according to eqn (1).We varied the layer distance from 40 to 180 nm to facilitate different interlayer coupling strengths. Fig. 3a–c selectively show |t+|2, |t−|2 and CD spectra for strong (d = 40 nm), weak (d = 60 nm), and negligible (d = 140 nm) interlayer interactions. As expected, |t+|2 and |t−|2 for d = 40 nm exhibit two distinct resonant dips, whereas the metasurface with a distance d = 60 nm gives rise to Fano line-shapes. Moreover, the chiral response vanishes for d = 140 nm, leading to negligible CD signals. We fitted the scattering coefficients using eqn (S28)† and the results for the d = 60 nm metasurface are plotted in Fig. 3d–f (full fitting results can be found in section S8 of the ESI†). As one can see, eqn (S28)† recovers both the amplitude and phase information of the scattering coefficient with high accuracy.
We should comment that, despite the large amounts of independent parameters initially introduced in the CMT, only 7 coefficients, namely, ω0 + ω13, −ω15 + ω17, ω16 − ω18, Γrad, Γabs, ϕ, and ξ appear in the final equations. As a result, the direct fitting over 6 S-matrix spectra (real and imaginary parts of α, β, and γ) is sufficient to avoid overfitting. In addition, these parameters all provide insightful physical meanings, which can be further used to check the validity of CMT. For example, ϕ corresponds to the retardation strength within the metasurface (eqn (S15.3)†), whereas 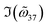 depicts the far-field interaction (eqn (S19.9)†). Their results are confirmed by Fig. 4a and b, where the fitted and analytical calculations yield almost identical values. In addition, Γabs is the non-radiative decay rate owing to the Ohmic loss of metallic nanorods.59 Therefore, if one keeps all geometrical parameters fixed but artificially reduces Drude's damping rates of gold for simulation, the resulting Γabs will be proportionally decreased as well.32,36 To elucidate this, we simulated the scattering coefficients for the d = 60 nm metasurface with 70%, 30% and 0 Drude's damping rates of its original value, and compared them with analytical CMT predictions using model parameters fitted from the full loss case. As one can see from Fig. S2† (section S9 in the ESI†), CMT predictions were found to be in excellent agreement with far-field spectra, unambiguously confirming the applicability of chiral CMT. Finally, we evaluated the near field coupling coefficient
depicts the far-field interaction (eqn (S19.9)†). Their results are confirmed by Fig. 4a and b, where the fitted and analytical calculations yield almost identical values. In addition, Γabs is the non-radiative decay rate owing to the Ohmic loss of metallic nanorods.59 Therefore, if one keeps all geometrical parameters fixed but artificially reduces Drude's damping rates of gold for simulation, the resulting Γabs will be proportionally decreased as well.32,36 To elucidate this, we simulated the scattering coefficients for the d = 60 nm metasurface with 70%, 30% and 0 Drude's damping rates of its original value, and compared them with analytical CMT predictions using model parameters fitted from the full loss case. As one can see from Fig. S2† (section S9 in the ESI†), CMT predictions were found to be in excellent agreement with far-field spectra, unambiguously confirming the applicability of chiral CMT. Finally, we evaluated the near field coupling coefficient 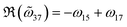 and
and 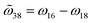 . The interaction between subwavelength nanorods can be directly calculated from the field overlapping integral among nanocavities, which is defined as,37,60
. The interaction between subwavelength nanorods can be directly calculated from the field overlapping integral among nanocavities, which is defined as,37,60
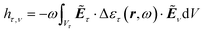 | (10) |
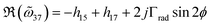 and
and 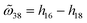 . Fig. 4c and d show the calculated near field coupling coefficient based on eqn (10). Their fitted counterparts are also superimposed for comparison. The values of both
. Fig. 4c and d show the calculated near field coupling coefficient based on eqn (10). Their fitted counterparts are also superimposed for comparison. The values of both 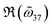 and
and 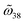 decrease with increasing layer distance. As expected, coefficients deduced from eqn (10) corroborate with the fitted values very well, again confirming the validity of the chiral CMT. We should stress that, although CMT is well-accepted as a phenomenological model, recent developments in the QNM have unveiled its solid physical foundations, where the parameters in CMT can be directly deduced from QNM information.36,60–67
decrease with increasing layer distance. As expected, coefficients deduced from eqn (10) corroborate with the fitted values very well, again confirming the validity of the chiral CMT. We should stress that, although CMT is well-accepted as a phenomenological model, recent developments in the QNM have unveiled its solid physical foundations, where the parameters in CMT can be directly deduced from QNM information.36,60–67
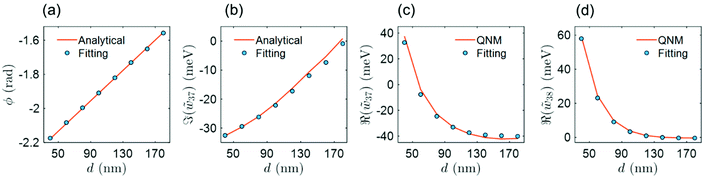 | ||
Fig. 4 Comparison between fitting parameters and analytical results. Analytical ϕ (a) and 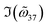 (b) from eqn (S15.3) and (S19.9)† are found to be almost identical to their fitted counterparts. In addition, the near field coupling coefficients deduced from the QNM field overlapping integral coincide well with (b) from eqn (S15.3) and (S19.9)† are found to be almost identical to their fitted counterparts. In addition, the near field coupling coefficients deduced from the QNM field overlapping integral coincide well with 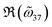 (c) and (c) and 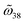 (d). (d). | ||
An important implication of the foregoing analysis is the rational design of zero transmission points for circularly polarized light. Generally speaking, the optimal CD response, defined by CD = ±1, corresponds to the zero transmission point upon either LCP or RCP excitation. Solving t± = 0 from eqn (S24) and (S25),† one arrives at
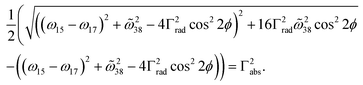 | (11) |
Eqn (11) represents the critical coupling condition for the chiral metasurface, where the absorption rate is balanced with the function of radiative and coupling coefficients. Recalling the radiative decay rate given by Γ′rad,i = |κ′i|2/(2|a′i|2), Eqn (11) deviates from the classical critical coupling condition of an individual resonator.32,33,68 In fact, this formalism is a natural consequence of Fano resonances and is of particular importance for coupled systems. As mode coupling is frequently exploited in designing high-performing metasurfaces, we envision that eqn (11) and the biorthogonal approach can serve as a guideline for designing non-Hermitian optical systems. For example, the absorption rate was calculated to be Γabs = 10.9 meV by using fitting parameters from the d = 40 nm metasurface, which is approximately 37.25% of intrinsic gold nanorods. We proceeded to verify eqn (11) by simulating the same metasurface with a reduced gold collision rate. As shown in Fig. 5a and b, transmission dips for both |t+|2 and |t−|2 spectra reached zero, and the corresponding CD signal increased from 0.63 to unity (Fig. 5c). Note that under this condition, the total radiative decay rates for chiral eigenmodes were deduced to be Γrad,+ = 52.5 meV and Γrad,− = 17.4 meV. The classical critical coupling condition is not valid for Fano resonances.
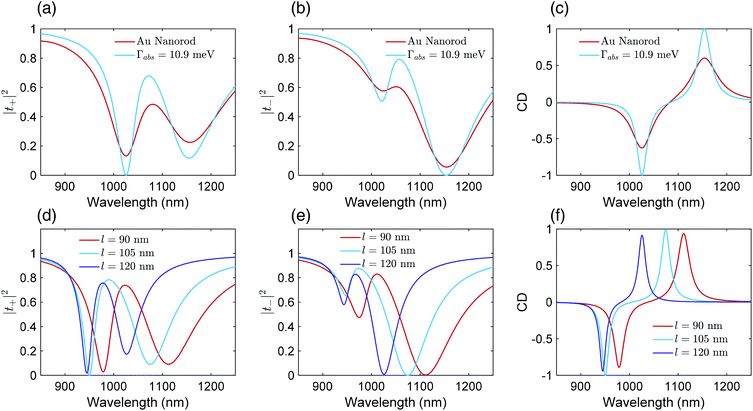 | ||
| Fig. 5 Critical coupling conditions for the zero transmission condition. Transmission dips for both (a) |t+|2 and (b) |t−|2 spectra reached zero by reducing the absorption rate of the gold nanorod to Γabs = 10.9 meV. As a result, the corresponding CD (c) increased from 0.63 to unity. (d–f) A practical silver chiral metasurface with a layer distance of d = 40 nm and an atom size of Lc = 200 nm. The rod length is scanned from l = 90 to 120 nm and the aspect ratio is kept fixed l/h = l/w = 5. The Drude permittivity used for silver is given by εAg = ε∞ + ωp2/ω(ω − jγ), with ε∞ = 3.7, ωp = 1.39 × 1016 rad s−1 and γ = 3.22581 × 1016 rad s−1. For the l = 105 nm metasurface, the fitting parameters are: ε0 + ω13 = 1.2301 eV, −ε15 + ω17 = 47.6 meV, ε16 + ω18 = 58.3 meV, Γrad = 14.3 meV, Γabs = 8.6 meV, ϕ = 2.16 rad, and ξ = 1.60 rad. The deduced Γabs from eqn (10) is 8.5 meV. Note that Γrad,+ = 45.9 meV and Γrad,− = 11.3 meV, which are also different from classical critical coupling predictions. | ||
As a proof of concept, we proceeded to design a practically chiral metasurface with zero transmission. The nonradiative dissipation rate calculated from Fig. 5c is about one-third of gold, which just coincides with silver nanorods. Assuming that the nonradiative decay rate depends primarily on the metal type and resonant frequency, it is expected to vary slowly with the geometry. Eqn (11) can be fulfilled by scanning the size of silver nanorods. Fig. 5d–f show the |t+|2, |t−|2 and CD response for the silver metasurface with different rod sizes. As expected, the zero transmission condition was achieved for length l = 105 nm, height h = 21 nm, width w = 21 nm, layer distance d = 40 nm, atom size Lc = 200 nm and period P = 400 nm.
Conclusion
In conclusion, we have proposed a generalized CMT capable of providing physical origins of chirality for coupled nanocavities. Using the biorthogonal approach, chiral CMT takes full considerations of coupled nanocavities, including non-Hermitian Hamiltonian, time-reversal symmetry, background scattering effects, physically meaningful coefficients, and geometrical symmetries. Remarkably, the closed-form expressions are found to be in excellent agreement with numerical observations. We have shown that the giant chiroptical response of a chiral metasurface is attributed to the asymmetric interlayer coupling between a6 and a8 to the a1 nanocavities and the coherent interference between doubly degenerate states. In addition, the near field coupling coefficient was demonstrated to be the QNM's field overlapping between adjacent nanocavities, which can be fine-tuned by geometry parameters and constitutional materials. As a result, the CMT approach in this study can be easily transferred to other cavity systems once (i) the mode information of the isolated constitutional cavity and (ii) coupling strength between cavities are known. As both conditions have explicit formalisms (e.g., eqn (2), (3) and (10)), we envision that CMT and this biorthogonal approach can serve as a guideline for designing novel non-Hermitian optical systems.Conflicts of interest
There are no conflicts to declare.Author contributions
Z. C., H. C., and S. D. conceived the study. Z. C. developed the theoretical model. Z. C. and J. C. performed numerical simulations. Z. C., H. C., and S. D. participated in the discussion of the data. Z. C., H. C., and S. D. supervised the project and co-wrote the manuscript with the input of all authors.Acknowledgements
The authors acknowledge Prof. Ningsheng Xu for valuable discussions and Prof. Ya-qing Bie for providing computational resources. The authors acknowledge support from the National Natural Science Foundation of China (grant no. 61905290, 61963205, and 91963205), the National Key Basic Research Program of China (grant no. 2019YFA0210203), and Guangzhou Basic and Applied Basic Research Foundation (grant no. 202102020579, 2019A1515011355, and 2020A1515011329). H. C. acknowledges the support from the Changjiang Young Scholar Program.References
- W. T. B. Kelvin, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light, Cambridge University Press, London, UK, 1904 Search PubMed.
- P. Roushan, J. Seo, C. V. Parker, Y. S. Hor, D. Hsieh, D. Qian, A. Richardella, M. Z. Hasan, R. J. Cava and A. Yazdani, Nature, 2009, 460, 1106–1109 CrossRef CAS PubMed.
- Z. R. Gong, W. Z. Luo, Z. F. Jiang and H. C. Fu, Sci. Rep., 2017, 7, 42390 CrossRef CAS PubMed.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed.
- B. Nina, N. Koji and R. W. Woody, Circular Dichroism: Principles and Applications, John Wiley & Sons, Weinheim, Germany, 2nd edn, 2000 Search PubMed.
- Y. Luo, C. Chi, M. Jiang, R. Li, S. Zu, Y. Li and Z. Fang, Adv. Opt. Mater., 2017, 5, 1700040 CrossRef.
- Z. Hu, D. Meng, F. Lin, X. Zhu, Z. Fang and X. Wu, Adv. Opt. Mater., 2019, 7, 1801590 CrossRef.
- S. Zu, T. Han, M. Jiang, F. Lin, X. Zhu and Z. Fang, ACS Nano, 2018, 12, 3908–3916 CrossRef CAS PubMed.
- Z. Cao, H. Gao, M. Qiu, W. Jin, S. Deng, K.-Y. Wong and D. Lei, Adv. Mater., 2020, 32, 1907151 CrossRef CAS PubMed.
- J. T. Collins, C. Kuppe, D. C. Hooper, C. Sibilia, M. Centini and V. K. Valev, Adv. Opt. Mater., 2017, 5, 1700182 CrossRef.
- K. Koshelev and Y. Kivshar, ACS Photonics, 2020, 8, 102–112 CrossRef.
- F. Monticone and A. Alù, J. Mater. Chem. C, 2014, 2, 9059–9072 RSC.
- D. R. Smith, J. B. Pendry and M. C. Wiltshire, Science, 2004, 305, 788–792 CrossRef CAS PubMed.
- X. Xiong, W.-H. Sun, Y.-J. Bao, M. Wang, R.-W. Peng, C. Sun, X. Lu, J. Shao, Z.-F. Li and N.-B. Ming, Phys. Rev. B, 2010, 81, 075119 CrossRef.
- S. Yang, Z. Liu, S. Hu, A. Z. Jin, H. Yang, S. Zhang, J. Li and C. Gu, Nano Lett., 2019, 19, 3432–3439 CrossRef CAS PubMed.
- E. Hendry, T. Carpy, J. Johnston, M. Popland, R. V. Mikhaylovskiy, A. J. Lapthorn, S. M. Kelly, L. D. Barron, N. Gadegaard and M. Kadodwala, Nat. Nanotechnol., 2010, 5, 783–787 CrossRef CAS PubMed.
- A. Y. Zhu, W. T. Chen, A. Zaidi, Y. W. Huang, M. Khorasaninejad, V. Sanjeev, C. W. Qiu and F. Capasso, Light: Sci. Appl., 2018, 7, 17158 CrossRef CAS PubMed.
- M. Kuwata-Gonokami, N. Saito, Y. Ino, M. Kauranen, K. Jefimovs, T. Vallius, J. Turunen and Y. Svirko, Phys. Rev. Lett., 2005, 95, 227401 CrossRef PubMed.
- T. Narushima, S. Hashiyada and H. Okamoto, ACS Photonics, 2014, 1, 732–738 CrossRef CAS.
- C. Menzel, C. Helgert, C. Rockstuhl, E. B. Kley, A. Tunnermann, T. Pertsch and F. Lederer, Phys. Rev. Lett., 2010, 104, 253902 CrossRef CAS PubMed.
- P. Banzer, P. Wozniak, U. Mick, I. De Leon and R. W. Boyd, Nat. Commun., 2016, 7, 13117 CrossRef CAS PubMed.
- X. Yin, M. Schaferling, B. Metzger and H. Giessen, Nano Lett., 2013, 13, 6238–6243 CrossRef CAS PubMed.
- M. Hentschel, M. Schaferling, B. Metzger and H. Giessen, Nano Lett., 2013, 13, 600–606 CrossRef CAS PubMed.
- M. Hentschel, M. Schaferling, T. Weiss, N. Liu and H. Giessen, Nano Lett., 2012, 12, 2542–2547 CrossRef CAS PubMed.
- M. V. Gorkunov, A. A. Antonov and Y. S. Kivshar, Phys. Rev. Lett., 2020, 125, 093903 CrossRef CAS PubMed.
- M. S. Davis, W. Zhu, J. K. Lee, H. J. Lezec and A. Agrawal, Sci. Adv., 2019, 5, eaav8262 CrossRef CAS PubMed.
- I. V. Lindell, A. H. Sihvola, S. A. Tretyakov and A. J. Viitanen, Electromagnetic Waves in Chiral and Bi-Isotropic Media, Artech House, London, 1994 Search PubMed.
- A. Lakhtakia, V. K. Varadan and V. V. Varadan, Time-Harmonic Electromagnetic Fields in Chiral Media, Lecture Notes in Physics, Springer-Verlag, 1989 Search PubMed.
- S. Fan, W. Suh and J. D. Joannopoulos, J. Opt. Soc. Am. A, 2003, 20, 569–572 CrossRef PubMed.
- H. A. Haus, Waves And Fields In Optoelectronics, Prentice-Hall, Englewood Cliffs, N.J., 1984 Search PubMed.
- W. Suh, Z. Wang and S. H. Fan, IEEE J. Quantum Electron., 2004, 40, 1511–1518 CAS.
- Z. Cao, H. Y. Lo and H. C. Ong, Opt. Lett., 2012, 37, 5166–5168 CrossRef CAS PubMed.
- Z. L. Cao, S. L. Wong, S. Y. Wu, H. P. Ho and H. C. Ong, Appl. Phys. Lett., 2014, 104, 171116 CrossRef.
- A. V. Kondratov, M. V. Gorkunov, A. N. Darinskii, R. V. Gainutdinov, O. Y. Rogov, A. A. Ezhov and V. V. Artemov, Phys. Rev. B, 2016, 93, 195418 CrossRef.
- F. Alpeggiani, N. Parappurath, E. Verhagen and L. Kuipers, Phys. Rev. X, 2017, 7, 021035 Search PubMed.
- W. Yan, R. Faggiani and P. Lalanne, Phys. Rev. B, 2018, 97, 205422 CrossRef CAS.
- C. Tao, J. Zhu, Y. Zhong and H. Liu, Phys. Rev. B, 2020, 102, 045430 CrossRef CAS.
- P. Lalanne, W. Yan, K. Vynck, C. Sauvan and J.-P. Hugonin, Laser Photonics Rev., 2018, 12, 1700113 CrossRef.
- N. Moiseyev, Non-Hermitian Quantum Mechanics, Cambridge University Press, 2011 Search PubMed.
- M. Decker, R. Zhao, C. M. Soukoulis, S. Linden and M. Wegener, Opt. Lett., 2010, 35, 1593–1595 CrossRef CAS PubMed.
- V. A. Fedotov, P. L. Mladyonov, S. L. Prosvirnin, A. V. Rogacheva, Y. Chen and N. I. Zheludev, Phys. Rev. Lett., 2006, 97, 167401 CrossRef CAS PubMed.
- M. Schäferling, Chiral Nanophotonics, Springer, 2017 Search PubMed.
- B. Semnani, J. Flannery, R. Al Maruf and M. Bajcsy, Light: Sci. Appl., 2020, 9, 23 CrossRef CAS PubMed.
- R. Knipper, T. G. Mayerhofer, V. Kopecky, U. Huebner and J. Popp, ACS Photonics, 2018, 5, 1176–1180 CrossRef CAS.
- J. Mun, M. Kim, Y. Yang, T. Badloe, J. Ni, Y. Chen, C.-W. Qiu and J. Rho, Light: Sci. Appl., 2020, 9, 139 CrossRef CAS PubMed.
- O. Arteaga, J. Sancho-Parramon, S. Nichols, B. M. Maoz, A. Canillas, S. Bosch, G. Markovich and B. Kahr, Opt. Express, 2016, 24, 2242–2252 CrossRef CAS PubMed.
- J. Sachs, J.-P. Günther, A. G. Mark and P. Fischer, Nat. Commun., 2020, 11, 4513 CrossRef CAS PubMed.
- C. Menzel, C. Rockstuhl and F. Lederer, Phys. Rev. A, 2010, 82, 053811 CrossRef.
- M. Mutlu and E. Ozbay, Appl. Phys. Lett., 2012, 100, 051909 CrossRef.
- D. Zarifi, M. Soleimani and A. Abdolali, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023204 CrossRef PubMed.
- J. Kaschke, J. K. Gansel and M. Wegener, Opt. Express, 2012, 20, 26012–26020 CrossRef PubMed.
- S.-D. Liu, J.-Y. Liu, Z. Cao, J.-L. Fan and D. Lei, Nanophotonics, 2020, 9, 3419–3434 CrossRef CAS.
- Y. Ye and S. He, Appl. Phys. Lett., 2010, 96, 203501 CrossRef.
- B. Bai, K. Ventola, J. Tervo and Y. Zhang, Phys. Rev. A, 2012, 85, 053808 CrossRef.
- R. Verre, D. G. Baranov, B. Munkhbat, J. Cuadra, M. Käll and T. Shegai, Nat. Nanotechnol., 2019, 14, 679–683 CrossRef CAS PubMed.
- Z. Zheng, N. Xu, S. L. Oscurato, M. Tamagnone, F. Sun, Y. Jiang, Y. Ke, J. Chen, W. Huang, W. L. Wilson, A. Ambrosio, S. Deng and H. Chen, Sci. Adv., 2019, 5, eaav8690 CrossRef CAS PubMed.
- R. Zhao, T. Koschny and C. M. Soukoulis, Opt. Express, 2010, 18, 14553–14567 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- R. E. Hamam, A. Karalis, J. D. Joannopoulos and M. Soljacic, Phys. Rev. A, 2007, 75, 053801 CrossRef.
- B. Vial and Y. Hao, J. Opt., 2016, 18, 115004 CrossRef.
- W. Chen, Q. Yang, Y. Chen and W. Liu, Phys. Rev. Lett., 2021, 126, 253901 CrossRef CAS PubMed.
- P. T. Kristensen, J. R. d. Lasson, M. Heuck, N. Gregersen and J. Mørk, J. Lightwave Technol., 2017, 35, 4247–4259 CAS.
- J. Ren, S. Franke and S. Hughes, Phys. Rev. X, 2021, 11, 041020 CAS.
- D. A. Powell, Phys. Rev. Appl., 2017, 7, 034006 CrossRef.
- R.-C. Ge, P. T. Kristensen, J. F. Young and S. Hughes, New J. Phys., 2014, 16, 113048 CrossRef.
- M. Benzaouia, J. D. Joannopoulos, S. G. Johnson and A. Karalis, Phys. Rev. Res., 2021, 3, 033228 CrossRef CAS.
- H. Zhang and O. D. Miller, 2020, ARXIV, 2010.08650.
- Z. Cao, L. Zhang, C. Y. Chan and H. C. Ong, Opt. Lett., 2014, 39, 501–504 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr05065f |
| This journal is © The Royal Society of Chemistry 2022 |