Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How do structural factors determine the linear and non-linear optical properties of fluorene-containing quadrupolar fluorophores? A theoretical answer†‡
Safa
Gam
 abc,
Sabri
Messaoudi
abc,
Sabri
Messaoudi
 bcd,
Jean-François
Halet
bcd,
Jean-François
Halet
 *ae and
Abdou
Boucekkine
*ae and
Abdou
Boucekkine
 *a
*a
aUniv Rennes, CNRS, Institut des Sciences Chimiques de Rennes (ISCR) – UMR 6226, F35000 Rennes, France. E-mail: Abdou.Boucekkine@univ-rennes1.fr; Jean-Francois.Halet@univ-rennes1.fr
bFaculty of Sciences of Bizerte FSB, University of Carthage, 7021 Jarzouna, Tunisia
cLaboratory of Materials, Molecules and Applications, IPEST, University of Carthage, Sidi Bou Said Road, B.P. 51, 2070 La Marsa, Tunisia
dDepartment of Chemistry, College of Science, Qassim University, Buraidah 51452, Saudi Arabia
eCNRS – Saint-Gobain – NIMS, IRL 3629, Laboratory for Innovative Key Materials and Structures (LINK), National Institute for Materials Science (NIMS), Tsukuba, 305-0044, Japan
First published on 9th June 2022
Abstract
A large series of push–push and pull–pull quadrupolar fluorophore derivatives with conjugated rods made from arylene–vinylene (PV) or arylene–ethynylene (PE) building blocks, bearing different electron-releasing or electron-withdrawing end-groups, were theoretically investigated using DFT and TD-DFT computations. These compounds, which exhibit good transparency in the visible region, are very promising for various applications, especially for optical limitation. Their absorption and photoluminescence as well as their two-photon absorption (TPA) properties in the near infrared (NIR) region were systematically investigated in order to derive structure–property relationships. The results indicate that (i) for all the studied compounds, the lowest excited state reached by the TPA is the S2 state, corresponding to the HOMO−1 to LUMO electronic transition, (ii) push–push molecules are found to be more efficient than pull–pull molecules, (iii) an increase of the strength of the donor terminal group (OPh, OMe, NH2, NPh2, and NBu2) enhances the TPA cross-section, and (iv) replacement of PV by PE always leads to an increase of TPA cross-sections in the NIR region.
Introduction
Over the years, a large number of π-conjugated organic molecules with large two-photon absorption properties have been developed.1–25 This was the case, for instance, of a series of push–push and pull–pull derivatives prepared and characterized by Mongin, Blanchard-Desce and colls,13,20,22 Jen and colls,14 Belfield and colls18,19 or Painelli and colls24 containing conjugated rods made from phenylene–vinylene (PV) or phenylene–ethynylene (PE) building blocks. More specifically, these quasi one-dimensional quadrupolar biphenyl derivatives, i.e., symmetrical conjugated molecules, bear either electron-releasing (X = OPh, OMe, NH2, NPh2, and NBu2) or electron-withdrawing (X = SO2CF3 and CN) end-groups attached at the para position to conjugated PV or PE connectors (Scheme 1). Interestingly, such elongated rod-like or banana-shaped fluorophores exhibit enhanced TPA cross-sections (σ2, expressed in GM = 1 × 10−50 cm4 s photon−1 molecule−1) in the visible red-near IR region (i.e., 700–1300 nm, a spectral window very appealing for biological applications).13,14,18,19,22 Moreover, the fluorene core exhibits high thermal and photochemical stability, making fluorene-containing compounds promising in areas such as laser applications.7,8,10,16 | ||
| Scheme 1 X-PV and X-PE series of compounds with different electron donor (X = OPh, OMe, NH2, NPh2, and NBu2) or acceptor groups (X = CN and SO2CF3). | ||
From an experimental viewpoint, it is often challenging to fully characterize the electronic processes responsible for the properties of such compounds. Fortunately, it is possible to obtain crucial information on their molecular photo-physical properties, namely those relevant to excitation and emission phenomena and the nature of the involved excited states, thanks to quantum chemical computations.26–41 In this context, we carried out standard density functional theory (DFT) and time-dependent density functional theory (TD-DFT) computations to first explore the ground state (GS) characteristics, i.e., the geometric and electronic structures of the compounds shown in Scheme 1. In the second step, we investigated their optical properties aiming to propose an assignment of the observed absorption bands and emission spectra using TD-DFT simulations. Then, we theoretically investigated their TPA properties, trying to understand and rationalize the structural origin of their large non-linear optical (NLO) responses.
It is noteworthy that systems bearing strong donor or acceptor terminal groups can also lead to a reduced fluorescence quantum yield and/or a pronounced red-shift of the one-photon absorption band.1,42 So, the aim of our work was to (i) compare the effect of the PV or PE connectors on the absorption/emission properties and on their TPA response, (ii) study the influence of the strength of the donor/acceptor terminal group on the considered properties, and (iii) evaluate the effect of the replacement of the biphenyl core by a bi-thiophene one. The purpose of these systematic structural variations was to derive complete structure–TPA relationships and to determine the appropriate combination of the core, linker (double or triple bond) and connector (PV, PE) for optimized properties of TPA/luminescence and/or TPA/transparency. Herein, we report and discuss the main results that were obtained.
Computational details
DFT and TD-DFT calculations were performed using the Gaussian 0943 and Gaussian 1644 programs. Solvent effects (toluene) were taken into account using the Polarizable Continuum Model (PCM).45–48 All the ground state (GS) geometries (thereafter S0) were optimized without any symmetry constraint and were checked to be genuine minima on the potential energy surface (PES), i.e., the computed frequencies of their normal modes of vibration were all real. Calculations were carried out employing the PBE0 functional49 and the 6-31+G(d) standard basis set. TD-DFT computations were carried out first at the same level of theory using the optimized GS geometries to investigate the absorption spectral properties of the considered molecules. It was found (vide infra) that calculations carried out at the CAM-B3LYP/6-31+G(d) level50 showed more satisfying agreement with experiments with respect to the UV-vis spectra than with respect to the PBE0/6-31+G(d) ones. The optimized geometries and vibration frequencies of the first triplet state (T1) were obtained using spin-unrestricted calculations, whereas the excited S1 state geometries were optimized using TD-DFT computations. The molecular orbitals (MO), and the simulated UV-vis and fluorescence spectra were plotted using the GaussView 5.0 program.51The TPA properties were computed using the damped cubic response theory of Lasse, Jensen and colls36 implemented in the Amsterdam Density Functional (ADF2018 and ADF2019)52,53 program packages. Unless otherwise stated, these response properties were calculated using the statistical average of orbital model exchange–correlation potentials (SAOPs) with a DZP basis set in the gas phase. Solvent effects were not included in the TPA calculations. The SAOP potential model54,55 was chosen due to its correct coulombic behavior of the potential at long distances, which is important for the description of response properties. It should be kept in mind that geometry optimizations cannot be carried out using the SAOP model and that the geometries used for the TPA calculations were those optimized at the PBE0 level in solution. Relevant SAOP/DZP MOs were plotted using the ADFView program.56
In previous studies, we showed that SAOP/DZP calculations lead to TPA cross-sections that were in satisfying agreement with the experimental measurements.57,58 The excited state lifetime was included in the theory using a damping parameter of 0.0034 atomic unit (a.u.) (∼0.1 eV or ∼800 cm−1),59 which was previously found to be suitable for TPA computations.36,60 The full TPA simulated spectra were plotted point by point after the computation of the cross-sections for different laser energies.
The TPA cross-sections (σTPA) were calculated from the imaginary part of the third-order hyperpolarizability γ as
 | (1) |
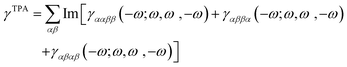 | (2) |
Results
Ground state geometries
The different possible geometric conformations of the studied compounds (Scheme 1) were first explored. They are displayed in Fig. S1 (ESI‡). Different energy minima were found for all of them (Table 1). The OPh-PV and OMe-PV molecules exhibit four thermodynamically stable forms labeled a–d that differ either by the orientation of the terminal group (OPh, OMe, respectively) or by the orientation of the two butyl groups. Forms a and b are close in energy and significantly more stable than forms c and d. This indicates that forms a and b might at least coexist in solution. Regarding NH2-PV, NPh2-PV, NPh2-PE, CN-PV and NBu2-PV, only two forms were computed to be thermodynamically stable (a and b), showing different orientations of the two butyl groups with respect to the π-conjugated backbone. Finally, for the SO2CF3-PV and SO2CF3-PE molecules, three forms were found (a, b and c with a and b very close in energy) that differ either by the orientation of the triflate terminal group (SO2CF3) and/or by the orientation of the two butyl groups. In all cases, form a is the most stable.| Compound | ΔE | |||
|---|---|---|---|---|
| Form | ||||
| a | b | c | d | |
| OPh-PV | 0.00 | 0.19 | 3.06 | 3.20 |
| OMe-PV | 0.00 | 0.25 | 3.51 | 3.25 |
| NH2-PV | 0.00 | 3.12 | ||
| NPh2-PV | 0.00 | 3.15 | ||
| NPh2-PE | 0.00 | 3.08 | ||
| NBu2-PV | 0.00 | 4.08 | ||
| CN-PV | 0.00 | 3.13 | ||
| SO2CF3-PV | 0.00 | 0.13 | 4.53 | |
| SO2CF3-PE | 0.00 | 0.17 | 4.33 | |
In the most stable configurations (form a), the two butyl groups are perpendicular to the plane of the molecules, and the peripheral arms built from the para-substituted PV or PE moieties adopt a planar structure relatively to the central fluorene core (Table S1, ESI‡). Here after, unless specified, results which are presented and discussed concern only these most stable configurations.
Absorption properties
The photo-physical properties of some of the fluorophores considered in Scheme 1, as well as their absorption and emission features including fluorescence quantum yields and lifetimes, were measured experimentally in toluene solution.13,20,22 All of them display an intense absorption in the near UV-vis blue region with typical molar extinction coefficients ranging from 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 180
000 to 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mol−1 L cm−1. TD-DFT calculations were first carried out considering the most stable form (a) of all compounds with different electron donor (X = OPh, OMe, NH2, NPh2, and NBu2) or acceptor (X = CN and SO2CF3) groups in order to assign the different absorption bands observed experimentally in toluene. Note that starting from the optimized geometries obtained at the PBE0/6-31+G(d) level, vertical TD-DFT computations were carried out using both the PBE0 and CAM-B3LYP functionals to simulate the UV-vis absorption spectra of the molecules in toluene. As can be seen for the lowest energy absorption band (Table 2), CAM-B3LYP calculations show perfect agreement with the experiments,13,20,22 whereas PBE0 overestimates systematically the experimentally measured wavelengths by ca. 50–60 nm. Thereafter, only the CAM-B3LYP results are discussed. Complete results are given in Table 3. The simulated absorption spectra of some of them (X = OPh, NH2, NPh2, CN, and SO2CF3) are shown in Fig. 1, and the molecular orbitals involved in the corresponding electronic excitations are displayed in Fig. 2–4.
000 mol−1 L cm−1. TD-DFT calculations were first carried out considering the most stable form (a) of all compounds with different electron donor (X = OPh, OMe, NH2, NPh2, and NBu2) or acceptor (X = CN and SO2CF3) groups in order to assign the different absorption bands observed experimentally in toluene. Note that starting from the optimized geometries obtained at the PBE0/6-31+G(d) level, vertical TD-DFT computations were carried out using both the PBE0 and CAM-B3LYP functionals to simulate the UV-vis absorption spectra of the molecules in toluene. As can be seen for the lowest energy absorption band (Table 2), CAM-B3LYP calculations show perfect agreement with the experiments,13,20,22 whereas PBE0 overestimates systematically the experimentally measured wavelengths by ca. 50–60 nm. Thereafter, only the CAM-B3LYP results are discussed. Complete results are given in Table 3. The simulated absorption spectra of some of them (X = OPh, NH2, NPh2, CN, and SO2CF3) are shown in Fig. 1, and the molecular orbitals involved in the corresponding electronic excitations are displayed in Fig. 2–4.
| Compound | Sn | E 0n | λ calc | f 0n | Main MO transition percentage |
|---|---|---|---|---|---|
| OPh-PV | 1 | 3.22 | 385 | 2.58 | HOMO → LUMO (87%) |
| 2 | 3.89 | 319 | 0.28 | HOMO−1 → LUMO (47%) | |
| 8 | 4.83 | 257 | 0.24 | HOMO−2 → LUMO (22%) | |
| HOMO−1 → LUMO+1 (19%) | |||||
| 17 | 5.52 | 225 | 0.32 | HOMO−4 → LUMO (25%) | |
| OMe-PV | 1 | 3.26 | 381 | 2.71 | HOMO → LUMO (87%) |
| 8 | 4.88 | 254 | 0.35 | HOMO−2 → LUMO (32%) | |
| 15 | 5.52 | 225 | 0.31 | HOMO−1 → LUMO+2 (24%) | |
| 28 | 6.10 | 203 | 0.27 | HOMO → LUMO+14 (17%) | |
| HOMO−4 → LUMO+2 (16%) | |||||
| NH2-PV | 1 | 3.20 | 387 | 2.84 | HOMO → LUMO (85%) |
| 7 | 4.72 | 262 | 0.37 | HOMO−2 → LUMO (35%) | |
| HOMO−1 → LUMO+1 (24%) | |||||
| 18 | 5.43 | 227 | 0.24 | HOMO−1 → LUMO+2 (31%) | |
| HOMO−3 → LUMO (31%) | |||||
| 27 | 5.88 | 211 | 0.15 | HOMO → LUMO+10 (31%) | |
| NPh2-PV | 1 | 3.04 | 408 | 3.10 | HOMO → LUMO (76%) |
| 2 | 3.48 | 356 | 0.17 | HOMO−1 → LUMO (48%) | |
| HOMO → LUMO+1 (38%) | |||||
| 7 | 4.27 | 290 | 0.57 | HOMO−1 → LUMO+4 (43%) | |
| 28 | 5.47 | 227 | 0.35 | HOMO−7 → LUMO (24%) | |
| HOMO−8 → LUMO+1 (16%) | |||||
| NPh2-PE | 1 | 3.25 | 382 | 3.51 | HOMO → LUMO (72%) |
| 7 | 4.33 | 287 | 0.56 | HOMO−1 → LUMO+6 (44%) | |
| 27 | 5.56 | 223 | 0.28 | HOMO−4 → LUMO (31%) | |
| 29 | 5.60 | 221 | 0.17 | HOMO−8 → LUMO (21%) | |
| HOMO−7 → LUMO+1 (17%) | |||||
| NBu2-PV | 1 | 3.05 | 407 | 2.88 | HOMO → LUMO (83%) |
| 2 | 3.59 | 345 | 0.18 | HOMO−1 → LUMO (59%) | |
| HOMO → LUMO+1 (35%) | |||||
| 19 | 5.39 | 230 | 0.25 | HOMO−4 → LUMO (28%) | |
| HOMO−1 → LUMO+2 (15%) | |||||
| 29 | 5.67 | 217 | 0.18 | HOMO−6 → LUMO (14%) | |
| CN-PV | 1 | 3.16 | 392 | 2.95 | HOMO → LUMO (86%) |
| 6 | 4.72 | 263 | 0.24 | HOMO−1 → LUMO+1 (27%) | |
| 9 | 5.13 | 242 | 0.22 | HOMO−3 → LUMO (39%) | |
| 13 | 5.52 | 225 | 0.29 | HOMO → LUMO+4 (28%) | |
| HOMO−6 → LUMO+1 (15%) | |||||
| SO2CF3-PV | 1 | 3.14 | 395 | 2.90 | HOMO → LUMO (86%) |
| 6 | 4.76 | 261 | 0.23 | HOMO−1 → LUMO+1 (29%) | |
| HOMO → LUMO+2 (22%) | |||||
| 9 | 5.11 | 243 | 0.25 | HOMO−3 → LUMO (44%) | |
| 23 | 6.15 | 202 | 0.40 | HOMO−1 → LUMO+6 (15%) | |
| SO2CF3-PE | 1 | 3.35 | 371 | 2.89 | HOMO → LUMO (84%) |
| 13 | 5.67 | 219 | 0.52 | HOMO → LUMO+4 (42%) | |
| 29 | 6.35 | 195 | 0.78 | HOMO−3 → LUMO+5 (34%) | |
| 30 | 6.39 | 194 | 0.42 | HOMO−3 → LUMO+5 (17%) |
 | ||
| Fig. 2 Frontier MO diagrams of OPh-PV (left) and NH2-PV (right) (contour isodensity values: ±0.015 (e bohr−3)1/2). Hydrogen atoms are omitted for clarity. | ||
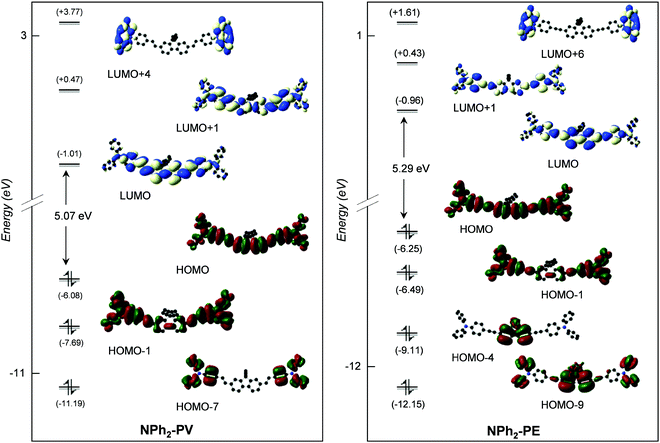 | ||
| Fig. 3 Frontier MO diagrams of NPh2-PV (left) and NPh2-PE (right) (contour isodensity values: ±0.015 (e bohr−3)1/2). Hydrogen atoms are omitted for clarity. | ||
 | ||
| Fig. 4 Frontier MO diagrams of CN-PV (left) and SO2CF3-PE (right) (contour isodensity values: ±0.015 (e bohr−3)1/2). Hydrogen atoms are omitted for clarity. | ||
As can readily be seen in Table 3, the lowest energy absorption band calculated for each compound with different donors is broad and intense with a maximum very close to the visible region, at 385 nm (f01 = 2.58), 387 nm (f01 = 2.84), 408 nm (f01 = 3.10) and 382 nm (f01 = 3.51) for OPh-PV, NH2-PV, NPh2-PV and NPh2-PE, respectively. Indeed, the absorption band energy depends very slightly upon (i) the nature of the peripheral donor groups (a small red shift is observed upon the increase of the donor properties), and (ii) the nature of the conjugated arms (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or C
C or C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) tethered to the fluorene core as can be seen comparing NPh2-PV and NPh2-PE (a small blue shift is noticed for the latter with respect to the former). Similarly, with acceptor groups, the computed lowest energy absorption band is broad and intense with a maximum very close to the visible as well at 392 nm (f01 = 2.95), 395 nm (f01 = 2.90) and 371 nm (f01 = 2.89) for CN-PV, SO2CF3-PV and SO2CF3-PE, respectively. Again, a slight blue shift is observed when the vinyl group is replaced by an ethynyl one. These little changes in the absorption band energy for these different compounds can be interpreted with a glance at the energy and nodal properties of their HOMO and LUMO which are mostly involved in the corresponding electronic excitations. They are all overall delocalized over the entire molecular π-conjugated backbone with a poor contribution of the peripheral donor/acceptor groups (see Fig. 2–4 for a few representatives and Fig. S2–S10, ESI‡). At higher energy, all compounds exhibit absorptions in the range 220–320 nm with a shoulder at a higher wavelength (Fig. 1, Table 3 and Table S2, ESI‡). These absorptions are also very slightly bathochromically or hypsochromically shifted depending on the increasing electron releasing or withdrawing properties of the para-substituent.
C) tethered to the fluorene core as can be seen comparing NPh2-PV and NPh2-PE (a small blue shift is noticed for the latter with respect to the former). Similarly, with acceptor groups, the computed lowest energy absorption band is broad and intense with a maximum very close to the visible as well at 392 nm (f01 = 2.95), 395 nm (f01 = 2.90) and 371 nm (f01 = 2.89) for CN-PV, SO2CF3-PV and SO2CF3-PE, respectively. Again, a slight blue shift is observed when the vinyl group is replaced by an ethynyl one. These little changes in the absorption band energy for these different compounds can be interpreted with a glance at the energy and nodal properties of their HOMO and LUMO which are mostly involved in the corresponding electronic excitations. They are all overall delocalized over the entire molecular π-conjugated backbone with a poor contribution of the peripheral donor/acceptor groups (see Fig. 2–4 for a few representatives and Fig. S2–S10, ESI‡). At higher energy, all compounds exhibit absorptions in the range 220–320 nm with a shoulder at a higher wavelength (Fig. 1, Table 3 and Table S2, ESI‡). These absorptions are also very slightly bathochromically or hypsochromically shifted depending on the increasing electron releasing or withdrawing properties of the para-substituent.
Emission and fluorescence
The emission spectra of part of the series (OMe-PV, NH2-PV, NPh2-PV, NPh2-PE, NBu2-PV and SO2CF3-PE) were experimentally obtained under excitation at the wavelength of maximum absorption.13,20,22 In order to investigate theoretically these emission spectra, geometries of the first singlet excited states S1 of all conformers of the whole series optimized at the CAM-B3LYP/6-31+G(d) level were considered. Results, which are given in Table 4, indicate that the computed fluorescence wavelengths of the different forms of a given compound such as forms a–d for the OPh-PV and OMe-PV molecules hardly differ. All compounds exhibit maxima emission peaks in the blue region in the range of 425–473 nm in toluene (see the computed fluorescence spectra of selected compounds in Fig. 1). As can be seen, the experimental and theoretical values are in satisfying agreement, the computed wavelengths being systematically higher than the experimentally measured ones by ca. 25 nm, the highest emission wavelength being for NBu2-PV and the lowest one for SO2CF3-PE.| Compound | Exp. | Calc. | ||||||
|---|---|---|---|---|---|---|---|---|
| λ absmax | λ emmax | Δω | Ref. | Form | λ absmax | λ emmax | Δω | |
| OPh-PV | a | 385 | 451 | 3801 | ||||
| b | 380 | 447 | 3945 | |||||
| c | 381 | 449 | 3976 | |||||
| d | 379 | 446 | 3963 | |||||
| OMe-PV | 381 | 415 | 2200 | 13 | a | 381 | 448 | 3926 |
| b | 380 | 448 | 3995 | |||||
| c | 378 | 447 | 4084 | |||||
| d | 377 | 446 | 4103 | |||||
| NH2-PV | 392 | 433 | 2400 | 13 | a | 387 | 455 | 3862 |
| b | 386 | 454 | 3881 | |||||
| NPh2-PV | 411 | 454 | 2305 | 20 | a | 408 | 471 | 3279 |
| b | 406 | 471 | 3400 | |||||
| NPh2-PE | 389 | 421 | 1954 | 22 | a | 382 | 430 | 2922 |
| b | 380 | 428 | 2951 | |||||
| NBu2-PV | 415 | 457 | 2200 | 13 | a | 407 | 473 | 3428 |
| b | 404 | 471 | 3521 | |||||
| CN-PV | a | 392 | 462 | 3736 | ||||
| b | 391 | 460 | 3839 | |||||
| SO2CF3-PV | a | 395 | 465 | 3811 | ||||
| b | 395 | 464 | 3764 | |||||
| c | 396 | 464 | 3701 | |||||
| SO2CF3-PE | 372 | 404 | 2200 | 13 | a | 371 | 426 | 3480 |
| b | 370 | 425 | 3498 | |||||
| c | 370 | 425 | 3489 | |||||
The simulated UV absorption and fluorescence emission spectra show that these molecules exhibit large Stokes shifts (Table 4), which might be due to a large difference between the Franck–Condon state and the excited state of emission of the molecules. High values of Stokes shifts ensure that there is no re-absorption of the emitted radiation. This must depend on the nature of the different electron releasing and withdrawing groups as well as the butyl groups attached to the biphenyl core. This greatly affects the intensity of absorption and emission of the target compounds resulting from a better π-extended conjugation of the synthesized compounds. The large Stokes shift provides significant information about the configuration rearrangement of molecules. This is illustrated in Fig. 5, which shows the atom-by-atom superposition of the geometry of the S0 state on the geometry of the S1 state for molecules SO2CF3-PV and SO2CF3-PE. The SO2CF3-PV molecule with the largest Stokes shift (3811 cm−1) exhibits a higher displacement of the triflate moiety (SO2CF3) and the butyl groups compared to the SO2CF3-PE molecule with a smaller Stokes shift (3480 cm−1).
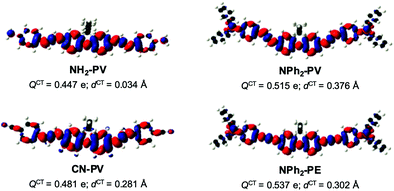
To ascertain the nature of the charge transfer induced upon excitation, the differences between the electron density of the vertical S1 state and that of the ground state S0 (Δρ(r) = ρS1(r) − ρS0(r))64 were computed to get information about the direction and the intensity of the charge transfer in these molecules. They are illustrated in Fig. 6 for NH2-PV, NPh2-PV, NPh2-PE and CN-PV.
This density difference shows a very short charge transfer distance dCT between the positive and negative charge centroids due to the symmetry of the molecules. On the other hand, the amount of charge QCT transferred between S0 and S1 is important in the four cases. Fig. 6 also clearly reveals that the charge transfer is higher in the case of the stronger electron donating terminal group NPh2 with respect to NH2, namely 0.515 e vs. 0.447 e. Interestingly, the charge transfer is larger in NPh2-PE (0.537 e) than in NPh2-PV (0.515 e). The amount of charge QCT transferred between S0 and S1 in CN-PV containing the electron acceptor terminal group CN is also important (0.481 e). This confirms that the fluorene core can also somewhat act as an electron-donating moiety depending on the peripheral counterparts.
Overall, conclusions reached for the absorption properties of this series of compounds can be extended to the emission properties, i.e., replacing a double bond by a triple bond induces a blue shift of the emission bands. On the other hand, increasing the electron releasing or withdrawing properties of the peripheral groups leads to a red shift of the emission bands, indicative of a more pronounced either core-to-periphery or periphery-to-core intramolecular charge transfer.
Another question is why does the considered series of fluorene derivatives not exhibit any phosphorescence in toluene? The relative energies of the different ground state S0, singlet excited states S1 and S2, and triplet excited state T1 were computed for the whole series. They are shown in Fig. 7 for OPh-PV, NH2-PV, NPh2-PV, and NPh2-PE. Large energy differences ranging from 0.77 to 1.07 eV are computed between S1 and T1 states for these molecules. Obviously, this large difference must prevent any intersystem crossing and consequently, phosphorescence is not observed.
 | ||
| Fig. 7 Relative energy (eV) of the excited states S1, S2 and T1 with respect to that of S0 for compounds NH2-PV, OPh-PV, NPh2-PV, and NPh2-PE computed at the CAM-B3LYP/6-31+G(d) level in toluene. | ||
Two-photon absorption
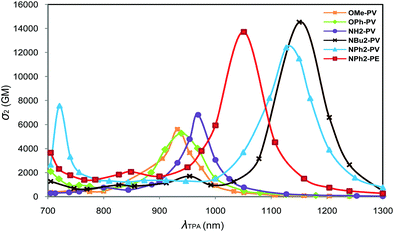
The TPA properties of the whole X-PV and X-PE series of compounds were computed at the SAOP/DZP level under vacuum. One-photon absorption (OPA) spectra were also computed at this level of theory for comparison. The geometries used for these calculations were those optimized at the PBE0/6-31+G(d) level in toluene. For quadrupolar systems, the excited S2 state is generally one-photon forbidden (or at least approximately forbidden in the case of small symmetry distortions) but is two-photon allowed. TPA energies correspond then to the half of the OPA excitation energies to the S2 state. The TPA simulated spectra, i.e., the plot of the cross-sections as a function of the laser wavelength are displayed in Fig. 8 and 9. For the whole series, the TPA-allowed excitation generally involves a HOMO−1 → LUMO transition (Fig. S11, ESI‡). Experimental13,20,22 and theoretical OPA, TPA maximum energies and cross-sections are summarized in Table 5. More detailed information (σ2, OPA and TPA energies ω) is provided in Tables S3–S26 (ESI‡). | ||
| Fig. 9 Plots of the SAOP/DZP computed TPA cross-sections σ2vs. wavelength (λTPA) for CN-PV (grey line), CN-PE (black line), SO2CF3-PV (yellow line), and SO2CF3-PE (pink line). | ||
| Compound | Exp. | Calc.d | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2λOPAmax | λ TPAmax | σ 2 | Ref. | ω OPA | ω TPA | 2λOPA | λ TPAmax1 | σ 2 | |
| a Experimental values for the TPA cross-sections were obtained via two-photon excited fluorescence (TPEF) in toluene using a mode-locked Ti:sapphire laser delivering 80 fs pulses at 80 MHz. The highest TPA cross-section was measured in the 700–1000 nm range. b TPA cross-sections were measured by using the two-photon-induced fluorescence method in toluene using a mode-locked Ti:sapphire laser delivering 120 fs pulses at 76 MHz in the wavelength range of 710–1000 nm. c TPA maximal values in dichloromethane determined by TPEF in the femtosecond regime. TPEF cross-sections were measured relative to fluorescein in 0.01 M aqueous NaOH over the range 715–980 nm, with the appropriate solvent-related refractive index corrections. d Highest TPA cross-section calculated at the SAOP/DZP level in the 700–1300 nm range. | |||||||||
| OMe-PV | 762 | 705 | 110 | 13 | 2.65 | 1.33 | 936 | 932 | 5599 |
| OPh-PV | 2.63 | 1.32 | 942 | 939 | 5266 | ||||
| NH2-PV | 784 | 705 | 400 | 13 | 2.55 | 1.28 | 972 | 969 | 6813 |
| NH2-PE | 2.79 | 1.40 | 889 | 886 | 7483 | ||||
| NBu2-PV | 830 | 740 | 1260 | 13 | 2.12 | 1.08 | 1170 | 1150 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
| NPh2-PV | — | 745 | 570 | 20 | 2.17 | 1.10 | 1142 | 1127 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
| NPh2-PE | 782 | 720 | 980 | 22 | 2.35 | 1.18 | 1056 | 1051 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 710 |
| CN-PV | 2.53 | 1.27 | 980 | 975 | 6220 | ||||
| CN-PE | 2.73 | 1.375 | 908 | 902 | 7192 | ||||
| SO2CF3-PV | 2.54 | 1.27 | 976 | 976 | 6523 | ||||
| SO2CF3-PE | 744 | 730 | 68 | 13 | 2.73 | 1.37 | 908 | 905 | 7615 |
| NBu2-PV-SO2CF3 | 2.55 | 1.28 | 972 | 969 | 3322 | ||||
| NPh2-PE-CPDT | 2.25 | 1.13 | 1102 | 1097 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
||||
As can be seen in Table 5, the computed cross-sections are much higher than the ones experimentally measured. Such a large deviation between the measured and SAOP/DZP computed TPA cross-sections is generally expected and has been discussed in the literature.57,58 Indeed, the main reason is that SAOP calculations (i) underestimate the HOMO–LUMO gaps and (ii) neglect solvent effects. Nevertheless, the theoretical results respect the trend experimentally observed for OMe-PV, NH2-PV, NPh2-PV and NBu2-PV.13,20 Additionally, the increase in intensity of the maximum TPA cross-sections is well correlated with the increase of the electron-donor properties of the end-groups, i.e., OPh-PV < OMe-PV < NH2-PV < NPh2-PV < NBu2-PV (Table 5 and Fig. 8). We note also that a red shift of both one- and two-photon absorption bands of push–push derivatives occurs, as illustrated in Fig. 8 and observed from Table 5. Moreover, as observed experimentally, comparing the computed TPA cross-sections of both NPh2-PV and NPh2-PE (6813 vs. 7483 GM) shows that replacing in the conjugated bridge a carbon–carbon double bond by a triple one slightly increases the NLO response in agreement with the experimental results.20,22 This result is also confirmed by comparing the CN-PV and CN-PE systems (6220 vs. 7192 GM).
To summarize, the extension of the π-conjugated connectors and the increase in the strength of the donor terminal groups enhance not only the photoluminescence properties, but also allow obtaining rather good two-photon absorbers on the edge of the NIR domain.
The simulated spectra obtained for the molecules containing electron-withdrawing end-groups (SO2CF3 and CN) are shown in Fig. 9. Comparable energies and intensity of the cross-sections are observed for SO2CF3-PV and CN-PV. A blue shift and a decrease of the intensity are observed relative to the molecules containing electron-releasing groups (see above). As observed earlier for the latter systems, the replacement of the vinyl group (SO2CF3-PV) by an alkyne one (SO2CF3-PE) is accompanied with a substantial blue shift and a slight increase of the TPA cross-sections in the NIR domain (Fig. 9). A similar effect is observed with the electron-withdrawing CN group. It turns out that the nature of the connector unit (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or C
C or C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) in these conjugated rods plays a non-negligible role in tuning the TPA spectra and influencing the TPA cross-section magnitude. Regardless of the nature of the end-groups (donor or acceptor), the core moiety or the length of the conjugated bridges, replacement of a double bond (C
C) in these conjugated rods plays a non-negligible role in tuning the TPA spectra and influencing the TPA cross-section magnitude. Regardless of the nature of the end-groups (donor or acceptor), the core moiety or the length of the conjugated bridges, replacement of a double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) by a triple bond (C
C) by a triple bond (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) always leads to a blue shift in energy and an increase and broadening of the TPA cross-sections in the NIR region. As a result, all fluorophores built from vinylene linkers instead of ethynylene ones exhibit lower TPA cross-sections in the whole red-NIR region. This result was not expected since higher energies gaps are often accompanied by a lowering of the cross-section. This is of particular importance when imaging applications are concerned because (i) improved penetration depth is achieved when shifting to higher wavelength (due to reduction of scattering losses) and (ii) spectral broadening offers much more flexibility in terms of two-photon excitation (allowing for a wider choice of laser sources).
C) always leads to a blue shift in energy and an increase and broadening of the TPA cross-sections in the NIR region. As a result, all fluorophores built from vinylene linkers instead of ethynylene ones exhibit lower TPA cross-sections in the whole red-NIR region. This result was not expected since higher energies gaps are often accompanied by a lowering of the cross-section. This is of particular importance when imaging applications are concerned because (i) improved penetration depth is achieved when shifting to higher wavelength (due to reduction of scattering losses) and (ii) spectral broadening offers much more flexibility in terms of two-photon excitation (allowing for a wider choice of laser sources).
We found it interesting to study the linear and non-linear optical properties of an unsymmetrical donor–bridge–acceptor molecule, namely the push–pull system NBu2-PV-SO2CF3, containing the NBu2 electron donor group on one hand and the electron acceptor SO2CF3 group on the other hand as terminal groups. The TPA spectrum of NBu2-PV-SO2CF3 exhibits a band with a maximum value at 969 nm and a cross-section at 3322 GM (Table 5 and Table S26, ESI‡). Such a push–pull system has a lower cross-section than both the pull–pull NBu2-PV (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 GM at 1150 nm) and the push–push SO2CF3-PV (6523 GM at 976 nm) species. Indeed, this confirms that quasi one-dimensional quadrupolar systems, i.e., symmetrical conjugated molecules bearing electron-releasing or electron-withdrawing end-groups, have been found to be more efficient than push–pull systems in terms of TPA.13
520 GM at 1150 nm) and the push–push SO2CF3-PV (6523 GM at 976 nm) species. Indeed, this confirms that quasi one-dimensional quadrupolar systems, i.e., symmetrical conjugated molecules bearing electron-releasing or electron-withdrawing end-groups, have been found to be more efficient than push–pull systems in terms of TPA.13
Finally, we may wonder what is the effect of the fluorene group present in all molecules that we studied on the TPA response? For that, the two phenyl groups of the NPh2-PE core were replaced by two thiophene rings (NPh2-PE-CPDT). Their TPA spectra and CAM-B3LYP/6-31+G(d) frontier MO diagrams are shown in Fig. 10 and 11, respectively, and their main photo-physical properties are given in Table 6. Corresponding SAOP/DZP frontier MO diagrams are shown in Fig. S12 (ESI‡) – they are qualitatively comparable to the CAM-B3LYP/6-31+G(d) ones. This replacement leads to a significant increase and a red shift of the TPA cross-section. As seen before, the TPA energy corresponds to half of the OPA excitation energy to state S2. For the previous quadrupolar systems, this excitation allowed by TPA generally corresponds to a HOMO−1 → LUMO transition (see Fig. S12, ESI‡). With the dithiophene core, the transition to the S2 state is HOMO → LUMO+1. The blue shift in energy observed with NPh2-PE-CPDT is due to the destabilization of the HOMO which is shifted higher in energy by 0.29 eV, with respect to that of NPh2-PE. These results demonstrate that the nature of the central conjugated core significantly influences the TPA spectra also and governs the TPA cross-section magnitude of this type of molecules.
 | ||
| Fig. 10 Plots of the SAOP/DZP computed TPA cross-sections σ2vs. wavelength (λTPA) for NPh2-PE and NPh2-PE-CPDT. | ||
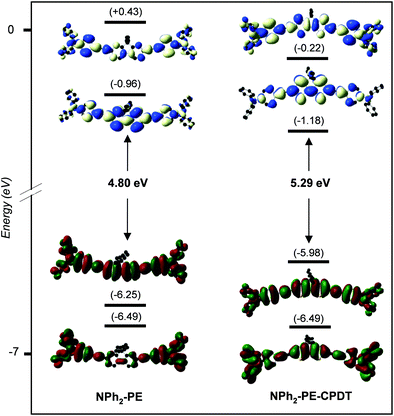 | ||
| Fig. 11 CAM-B3LYP/6-31+G(d) frontier MO diagrams of NPh2-PE (left) and NPh2-PE-CPDT (right). Contour isodensity values: ±0.015 (e bohr−3)1/2. Hydrogen atoms are omitted for clarity. | ||
| Compound | λ absmax | λ em-electmax |
E
gap
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
ω OPA | ω TPA | σ 2 |
|---|---|---|---|---|---|---|
| a CPDT = 4H-cyclopenta[2,1-b:3,4-b′]dithiophene. b The electronic gap (Egap) is calculated from the absorption and emission maxima energy difference. | ||||||
| NPh2-PE | 382 (3.25) | 430 (2.88) | 3.06 | 2.35 | 1.18 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 710 |
| NPh2-PE-CPDT | 454 (2.73) | 543 (2.28) | 2.51 | 2.25 | 1.13 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
Conclusion
This systematic theoretical study of the absorption, photoluminescence and two-photon absorption properties of a large series of quadrupolar fluorophores, made of a fluorene core bearing conjugated bridges and electron donor or acceptor end-groups, allowed us to extract some structure–property relationships of great significance for both spectral tuning and amplification of molecular TPA in the NIR spectral domain. First, their different possible geometrical configurations were optimized using DFT computations. Then, TD-DFT calculations were carried out showing absorption at low wavelengths for all compounds around 400 nm or below, due to HOMO–LUMO transition of rather large energy, with high oscillator strength in agreement with the available experimental data. The computed fluorescence wavelengths are also in good agreement with the experiments. The presence of the fluorene core and the phenylene–vinylene (PV) or phenylene–ethynylene (PE) conjugated bridges leads to high efficiency for light harvesting. The influence of each moiety constituting these quadrupolar structures (cores, linkers, connectors and end-groups) was investigated. Regarding the non-linear optical properties, the theoretical results confirm that the excited state (S2) reached by the two-photon absorption of lowest energy corresponds to the HOMO−1 → LUMO transition for all compounds. It is found that an increase of the strength of the donor terminal group (OPh, OMe, NH2, NPh2, and NBu2) enhances the TPA cross-section. Planarization of the fluorene core always leads to an increase in the TPA cross-sections. The nature of the linkers (PV or PE) and the phenylene units is of particular importance as well. Small changes in the structures may have important implications in terms of molecular engineering for specific applications, since the TPA properties (in terms of cross-sections, position of the maximum and band width), as well as the one-photon and the photoluminescence characteristics can be considerably affected. Interestingly, replacement of the fluorene core by a bithiophene one could enhance two-photon absorption. With these findings in hand, quadrupolar fluorophores, combining important peak TPA cross-sections and broad TPA bands in the whole 700–1300 nm range, could thus be obtained.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. G. and S. M. are grateful to the Tunisian Ministry of Higher Education and Scientific Research for financial support. GENCI-IDRIS and GENCI-CINES are acknowledged for computing time allocation (grant 2020-2021-080649). The authors thank Dr Olivier Mongin (University of Rennes) for his valuable comments.References
- M. Albota, D. Beljonne, J.-L. Brédas, J. E. Ehrlich, J.-Y. Fu, A. A. Heikal, S. E. Hess, T. Kogej, M. D. Levin, S. R. Marder, D. McCord-Maughon, J. W. Perry, H. Röckel, M. Rumi, G. Subramaniam, W. W. Webb, X.-L. Wu and C. Xu, Science, 1998, 281, 1653–1656 CrossRef CAS PubMed.
- L. Ventelon, L. Moreaux, J. Mertz and M. Blanchard-Desce, Chem. Commun., 1999, 2055–2056 RSC.
- M. Rumi, J. E. Ehrlich, A. A. Heikal, J. W. Perry, S. Barlow, Z. Hu, D. McCord-Maughon, T. C. Parker, H. Röckel, S. Thayumanavan, S. R. Marder, D. Beljonne and J.-L. Brédas, J. Am. Chem. Soc., 2000, 122, 9500–9510 CrossRef CAS.
- M. Blanchard-Desce, C. R. Phys., 2002, 3, 439–448 CrossRef CAS.
- O. Mongin, L. Porrès, L. Moreaux, J. Mertz and M. Blanchard-Desce, Org. Lett., 2002, 4, 719–722 CrossRef CAS PubMed.
- M. G. Silly, L. Porrès, O. Mongin, P.-A. Chollet and M. Blanchard-Desce, Chem. Phys. Lett., 2003, 379, 74–80 CrossRef CAS.
- K. D. Belfield, M. V. Bondar, A. R. Morales, O. Yavuz and O. V. Przhonska, J. Phys. Org. Chem., 2003, 16, 194–201 CrossRef CAS.
- K. D. Belfield, A. R. Morales, J. M. Hales, D. J. Hagan, E. W. Van Stryland, V. M. Chapela and J. Percino, Chem. Mater., 2004, 16, 2267–2273 CrossRef CAS.
- C. D. Entwistle and T. B. Marder, Chem. Mater., 2004, 16, 4574–4585 CrossRef CAS.
- S. Yao and K. D. Belfield, J. Org. Chem., 2005, 70, 5126–5132 CrossRef CAS PubMed.
- Z. Yuan, C. D. Entwistle, J. C. Collings, D. Albesa-Jové, A. S. Batsanov, J. A. K. Howard, N. J. Taylor, H. M. Kaiser, D. E. Kaufmann, S.-Y. Poon, W.-Y. Wong, C. Jardin, S. Fathallah, A. Boucekkine, J.-F. Halet and T. B. Marder, Chem. Eur. J., 2006, 12, 2758–2771 CrossRef CAS PubMed.
- M. Charlot, N. Izard, O. Mongin, D. Riehl and M. Blanchard-Desce, Chem. Phys. Lett., 2006, 417, 297–302 CrossRef CAS.
- O. Mongin, L. Porrès, M. Charlot, C. Katan and M. Blanchard-Desce, Chem. – Eur. J., 2007, 13, 1481–1498 CrossRef CAS PubMed.
- Y. Tian, C. Y. Chen, Y. J. Cheng, A. C. Young, N. M. Tucker and A. Y. Jen, Adv. Funct. Mater., 2007, 17, 1691–1697 CrossRef CAS.
- C. D. Entwistle, J. C. Collings, A. Steffen, L. O. Pålsson, A. Beeby, D. Albesa-Jové, J. M. Burke, A. S. Batsanov, J. A. K. Howard, J. A. Mosely, S. Y. Poon, W. Y. Wong, F. Ibersiene, S. Fathallah, A. Boucekkine, J.-F. Halet and T. B. Marder, J. Mater. Chem., 2009, 19, 7532–7544 RSC.
- K. D. Belfield, M. V. Bondar, C. O. Yanez, F. E. Hernandez and O. V. Przhonska, J. Mater. Chem., 2009, 19, 7498–7502 RSC.
- C. Katan, S. Tretiak and J. Even, Nanophotonics III, in, Proc. SPIE, ed. D. L. Andrews, J.-M. Nunzi and A. Ostendorf, 2010, vol. 7712, p. 77123D Search PubMed.
- S. Yao, H.-Y. Ahn, X. Wang, J. Fu, E. W. Van Stryland, D. J. Hagan and K. D. Belfield, J. Org. Chem., 2010, 75, 3965–3974 CrossRef CAS PubMed.
- C. D. Andrade, C. O. Yanez, L. Rodriguez and K. D. Belfield, J. Org. Chem., 2010, 75, 3975–3982 CrossRef CAS PubMed.
- C. Rouxel, M. Charlot, Y. Mir, C. Frochot, O. Mongin and M. Blanchard-Desce, New J. Chem., 2011, 35, 1771–1780 RSC.
- A. R. Morales, A. Frazer, A. W. Woodward, H.-Y. Ahn-White, A. Fonari, P. Tongwa, T. Timofeeva and K. D. Belfield, J. Org. Chem., 2013, 78, 1014–1025 CrossRef CAS PubMed.
- Z. Pokladek, N. Ripoche, M. Betou, Y. Trolez, O. Mongin, J. Olesiak-Banska, K. Matczyszyn, M. Samoc, M. G. Humphery, M. Blanchard-Desce and F. Paul, Chem. – Eur. J., 2016, 22, 10155–10167 CrossRef CAS PubMed.
- S. A. Kurhuzenkau, A. W. Woodward, S. Yao, K. D. Belfield, Y. O. Shaydyuk, C. Sissa, M. V. Bondar and A. Painelli, Phys. Chem. Chem. Phys., 2016, 18, 12839–12846 RSC.
- S. A. Kurhuzenkau, M. Y. Colon Gomez, K. D. Belfield, Y. O. Shaydyuk, D. J. Hagan, E. W. Van Stryland, C. Sissa, M. V. Bondar and A. Painelli, J. Phys. Chem. C, 2018, 122, 5664–5672 CrossRef CAS.
- J. He, F. Rauch, A. Friedrich, D. Sieh, T. Ribbeck, I. Krummenacher, H. Braunschweig, M. Finze and T. B. Marder, Chem. – Eur. J., 2019, 25, 13777–13784 CrossRef CAS PubMed.
- F. Terenziani, C. Katan, E. Badaeva, S. Tretiak and M. Blanchard-Desce, Adv. Mater., 2008, 20, 4641–4678 CrossRef CAS.
- K. A. Nguyen, P. N. Day and R. Pachter, Theor. Chem. Acc., 2008, 120, 167–175 Search PubMed.
- L. K. Yan, A. Pomogaeva, F. L. Gu and Y. Aoki, Theor. Chem. Acc., 2010, 125, 511–520 Search PubMed.
- G. L. C. Moura and A. M. Simas, J. Phys. Chem. C, 2010, 114, 6106–6116 CrossRef CAS.
- X.-T. Liu, L.-Y. Zou, A.-M. Ren, J.-F. Guo, Y. Sun, S. Huang and J.-K. Feng, Theor. Chem. Acc., 2011, 130, 37–50 Search PubMed.
- Y. Zhao, J.-F. Guo, A.-M. Ren and J.-K. Feng, Theor. Chem. Acc., 2011, 128, 265–274 Search PubMed.
- G. Argouarch, R. Veillard, T. Roisnel, A. Amar, A. Boucekkine, A. Singh, I. Ledoux and F. Paul, New J. Chem., 2011, 35, 2409–2411 RSC.
- D. W. Silverstein and L. Jensen, J. Phys. Chem., 2012, 136, 064111 CrossRef PubMed.
- I. H. Nayyar, A. E. Masunov and S. Tretiak, J. Phys. Chem. C, 2013, 117, 18170–18189 CrossRef CAS.
- M. T. Beerepoot, D. H. Friese, N. H. List, J. Kongsted and K. Ruud, Phys. Chem. Chem. Phys., 2015, 17, 19306–19314 RSC.
- H. Zhongwei, J. Autschbach and L. Jensen, J. Chem. Theory Comput., 2016, 12, 1294–1304 CrossRef PubMed.
- M. M. Alam and C. Daniel, Theor. Chem. Acc., 2016, 135, 41 Search PubMed.
- M. Abe, Y. Chitose, S. Jakkampudi, P. T. T. Thuy, Q. Lin, B. T. Van, A. Yamada, R. Oyama, M. Sasaki and C. Katan, Synthesis, 2017, 3337–3346 CAS.
- O. Sengul, E. B. Boydas, M. Pastore, W. Sharmouk, P. C. Gros, S. Catak and A. Monari, Theor. Chem. Acc., 2017, 136, 67 Search PubMed.
- M. T. Beerepoot, M. M. Alam, J. Bednarska, W. Bartkowiak, K. Ruud and R. Zaleśny, J. Chem. Theory Comput., 2018, 14, 3677–3685 CrossRef CAS PubMed.
- A. Triadon, A. N. Ndimba, N. Richy, A. Amar, A. Boucekkine, T. Roisnel, M. P. Cifuentes, M. G. Humphrey, M. Blanchard-Desce and O. Mongin, New J. Chem., 2018, 42, 11289–11293 RSC.
- S.-J. Chung, M. Rumi, V. Alain, S. Barlow, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 2005, 127, 10844–10845 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowskiand and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Wallingford, CT, 2016 Search PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. Dennington, T. Keith and J. Millam, GaussView, version 5.0, 2009 Search PubMed.
- ADF, Amsterdam Density Functional, SCM Computing & Modelling, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
- G. teVelde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. vanGisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- P. R. Schipper, O. V. Gritsenko, S. J. van Gisbergen and E. J. Baerends, J. Phys. Chem., 2000, 112, 1344–1352 CrossRef CAS.
- L. Jensen, P. T. van Duijnen and J. G. Snijders, J. Chem. Phys., 2003, 119, 12998–13006 CrossRef CAS.
- ADFGUI 2012, SCM, Amsterdam, The Netherlands, http://www.scm.com.
- A. Amar, A. Elkechai, J.-F. Halet, F. Paul and A. Boucekkine, New J. Chem., 2021, 45, 15074–15081 RSC.
- A. Amar, A. Boucekkine, F. Paul and O. Mongin, Theor. Chem. Acc., 2019, 138, 105 Search PubMed.
- L. Jensen, J. Autschbach and G. C. Schatz, J. Chem. Phys., 2005, 122, 224115 CrossRef CAS PubMed.
- H. Zhongwei, J. Autschbach and L. Jensen, J. Chem. Phys., 2014, 141, 124305 CrossRef PubMed.
- M. Göppert-Mayer, Ann. Phys., 1931, 9, 273–294 CrossRef.
- J. Pérez Moreno and M. G. Kuzyk, J. Chem. Phys., 2005, 123, 194101 CrossRef PubMed.
- J. Pérez-Moreno, K. Clays and M. G. Kuzyk, J. Chem. Phys., 2008, 128, 084109 CrossRef PubMed.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed.
Footnotes |
| † Dedicated to Dr Christian Bruneau for his important contribution to molecular chemistry. |
| ‡ Electronic supplementary information (ESI) available: Optimized geometries and Cartesian coordinates, UV-visible spectra, TD-DFT results, frontier MO diagrams, and OPA and TPA computational detailed results. See DOI: https://doi.org/10.1039/d2nj01192a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2022 |