Metathesis as an alternative synthesis route to layered sulfides A(LiZn)S₂ (A = alkali-metal) with unexpected colors

Abstract

Pure powders of Na(LiZn)S₂ can be obtained through a solid-state reaction, and A(LiZn)S₂ (A = K, Rb, Cs) result from metathesis reactions between alkali-metal chlorides and the same constituents used to prepare the Na(LiZn)S₂ powder. Hence, the metathesis reaction enables extended sulphide chemistry without the use of either H₂S gas or very reactive starting materials. By the metathesis reaction it was possible to obtain relatively pure Cs(LiZn)S₂. Trigonal Na(LiZn)S₂ and tetragonal A(LiZn)S₂ (A = K, Rb, Cs) exhibit significant structural similarities, having (LiZn)S₂ layers that are separated by alkali-metals (Na–Cs). Against expectations, Cs(LiZn)S₂ is orange red in colour, Rb(LiZn)S₂ is strongly yellow, K(LiZn)S₂ is pale yellow, and Na(LiZn)S₂ is colourless. Ultraviolet-visible spectroscopy data on Cs(LiZn)S₂ and Na(LiZn)S₂ contain several shoulders apart from apparent band-edges close to 3.3 eV. In the former, it seems as if the optical excitations range all the way into green (∼600 nm), which concurs with the observed red colour. Nuclear magnetic resonance investigations on cores ¹³³Cs, ²³Na, and ⁷Li suggest that these ions are firmly held in the atomic lattice, as judged by the resonance frequency widths and relatively long nuclear spin relaxation times (T₁), ranging from 10 to 200 seconds for ²³Na and ⁷Li. So there should be only electronic excitations in these compounds. Band-structure calculations of Li–Zn ordered versions of the lattices suggest a direct band-gap in both compounds, corresponding to an excitation from sulphur to zinc. The theoretical band-gaps amount to 2.54 eV for CsLiZnS₂ and 1.85 eV for NaLiZnS₂, and the steep edges in the density of states are found at 3.3 eV for both cases. As no Li–Zn ordering is observed by X-ray diffraction, there must be an inherent atomic disorder. By theoretical simulations, local Li–Zn anti-site orderings were introduced and the resulting electronic structure was evaluated. However, the simulated optical behaviour could only tentatively explain the spectroscopic data of Na(LiZn)S₂; the orange red colour of Cs(LiZn)S₂ must be an even more complex phenomenon, as the Li–Zn simulations were insufficient to explain the relatively strong optical activity in the range between 400 and 600 nm.

---

Introduction

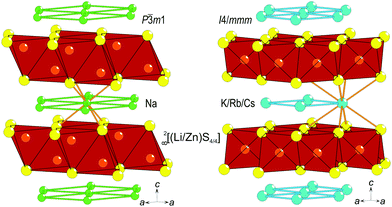
Metal oxides are dominating in the design of novel materials for optical displays, e.g. In–Sn–O compounds,¹ for optical switching like TeO₂,² and for the photocatalytic splitting of water, including for example TiO₂³ and SnO₂,⁴ wherein doping with selected cations or with crystallographic imperfections is used as a means for optimizing the optical properties, especially the band-gap. However, much less attention is given to the choice of anion. The well-known sulfide system A(LiB)S₂ (A = alkali-metal, B = Zn or Cd) has several advantageous features. First, their crystal structures are layered, either of the anti-La₂O₃ type for A = Na⁵ or of the BaZn₂P₂ type for A(LiZn)S₂ (Fig. 1) with A = K, Rb, and Cs,⁶ which is advantageous for thin-layer production applications. Second, the optical band-gaps of these sulfides are in the range needed for displays or photocatalytic activity, e.g., Na(LiCd)S₂ has been reported to have a band-gap of 2.4 eV.⁵ Third, these systems exhibit significant chemical flexibility, e.g., A can be any of the heavier alkali-metals, which affects the distance between layers in the crystal structure, and S can be substituted for Se;⁷ hence, the crystal structure can be kept fairly similar but the grade of ionicity can be chemically designed. Moreover, all systems are air-stable, water-stable, and fairly inexpensive.

Fig. 1 Structural comparison between Na(LiZn)S₂ (left, anti-La₂O₃ type) and A(LiZn)S₂ (A = K, Rb, or Cs, right, BaZn₂P₂ type). The layers of Li–Zn–S tetrahedra are highlighted and the intermediates Na and A are connected to emphasize the layered motif.

Na(LiB)S₂ (B = Zn or Cd) can be obtained by solid-state reactions,⁵ but sulfides with larger alkali-metal ions instead of Na have only been synthesized by reacting carbonates and metals in a stream of H₂S,⁶ which is a hazardous route that should not be scaled up for industrial purposes. For applications, several of the abovementioned oxides and sulfides do raise questions about environmental issues: In, Sn, Te, and Cd are generally unwanted for future applications. Therefore, we employ an alternative metathesis route to synthesize A(LiZn)S₂ (A = alkali-metal) to minimize synthesis hazards and environmental problems as well as to characterize these layered sulfides further.

Experimental

All syntheses were performed under controlled conditions inside a glove box (MBraun, Ar gas with O₂ and H₂O < 1 ppm). Na(LiZn)S₂ was prepared by homogenizing stoichiometric (1 : 1:2 : 2) amounts of Na₂S (Alfa Aesar, >99.5%), Li₂S (Alfa Aesar, 99.9%), Zn (Alfa Aesar, >98%) metal and elemental S (Alfa Aesar, 99.5%) in an agate mortar. A corundum crucible was filled with the powder mixture and subsequently placed in a silica tube before melt-sealing the tube after lowering the inner Ar pressure to about 0.2 bar. The optimized synthesis procedure involves heating up to 550 °C for 10 h before cooling at an ambient rate. For the metathesis reaction, Na₂S, Li₂S, Zn, and S were mixed with the corresponding ultra-dry halide salt (KCl – Alfa Aesar, 99.5%; RbCl – Alfa Aesar, 99%; or CsCl – Alfa Aesar, 99.9%) to cause the following reaction:

Na₂S + Li₂S + 2Zn + 2S + 2ACl → 2A(LiZn)S₂ + 2NaCl (A = K, Rb, or Cs),

which is partly driven by the higher stability of NaCl as compared to the ACl salts. These mixtures, including halide salts, were also heated in a corundum crucible inside closed silica tubes, as in the case of the solid-state reaction described above. However, the optimized temperature was close to 750 °C and the heating time was about 50 h. After the subsequent cooling at an ambient rate down to room temperature, each sample was exposed to air and washed with deionized water. All samples proved to be air and water stable for several days at ambient temperature and pressure, which also has been observed elsewhere, specifically for Na(LiZn)S₂.⁵ To investigate if the metathesis reaction was successful, a minor unwashed part of each reaction product was saved for individual examination by X-ray diffraction.

For phase identification by X-ray diffraction, a Huber G670 Guinier camera with Co-Kα radiation (λ = 1.78897 Å) was employed. High resolution X-ray diffraction data were extracted with a STOE STADI_P using a Mo-Kα₁ X-ray source (λ = 0.70926 Å) or Co-Kα radiation and Dectris Mythen 1K detectors. The WinXPOW software package⁸ was used to evaluate and compare the obtained diffraction data. A Rietveld simulation with the software JANA2006⁹ was used to confirm the crystal structure of Na(LiZn)S₂.

Scanning electron microscopy studies and basic elemental analyses were performed using a NOVA NanoSEM 200 (FEI), equipped with an EDX detector (AMETEK, Germany).

The melting behavior of Na(LiZn)S₂ was investigated with an STD Q600 simultaneous thermal analyzer from TA Instruments using a corundum crucible for the sample as well as an empty twin crucible as the reference. During heating and cooling (10° min⁻¹), the sample space was flushed with pure nitrogen (10 ml min⁻¹).

The combination of inductively coupled plasma – optical emission spectroscopy (ICP-OES, ARCOS MV from SPECTRO) was used to determine the composition of selected bulk samples. A well-defined amount of the polycrystalline sample was dissolved in a strong alkali solution during microwave heating. After the solution was cooled again, H₂O₂ was added to oxidize S²⁻ to SO₄²⁻ for 24 h before performing the analyses.

Spectra in the ultraviolet-visible (UV-Vis) range were collected in a transmission mode using a Cary 4000 UV-Vis spectrophotometer from VARIAN Inc. Each sample was homogenized with optically pure BaSO₄. An optimum signal was achieved using 10 mass% of the sample and 90 mass% BaSO₄.

Nuclear magnetic resonance spectroscopy data were obtained using an Apollo spectrometer from TECMAG using a Magnex scientific magnet with a magnetic flux density of 7.0471 T. The cores in focus were ⁷Li (I = 3/2), ²³Na (I = 3/2), and ¹³³Cs (I = 7/2). The method for determining the spin relaxation (T₁) was the free-induction-decay (FID) in the case of Li and Hahn spin-echo for the Na and Cs cores. To estimate the temperature dependence of the relaxation, spectra were obtained at room temperature (292 K) and 380 K.

Computational details

As a starting point for density functional theory (DFT) calculations, crystal structure data were taken from ref. 5 for Na(LiZn)S₂ and ref. 6 for Cs(LiZn)S₂. This was done because single crystal data provide a higher accuracy of the atomic positions. Na(LiZn)S₂ crystallizes in the trigonal space group P3̄ml (No. 164), while Cs(LiZn)S₂ crystallizes in the tetragonal I4/mmm (No. 139) space group. In each compound, Li and Zn share the same Wyckoff position with an average occupancy of 0.5. In the first step, crystal structures with ordered Li and Zn distributions and an appropriate (lower) symmetry were considered. The resulting space groups are P3m1 (No. 156) and I4̄m2 (No. 119) for the Na and Cs compounds, respectively. The atomic positions were optimized with lattice parameters kept equal to the experimental ones.^5,6 A linear tetrahedron method with Blöchl corrections was used for the k-space integration in these and all other calculations. A k-mesh with 12 × 12 × 7 intervals (12 × 12 × 12 intervals) in the Brillouin zone was chosen for the Na (Cs) compound for this step and the force threshold was set to 1 meV Å⁻¹. The details of the resulting crystal structures are provided in Appendix A, Table 3. Hereafter, we represent these ordered structures without brackets for Li–Zn, representing different Wyckoff positions for these atoms. To obtain the density of states (DOS) and the linear optical properties, denser k-meshes with 24 × 24 × 14 intervals and 24 × 24 × 24 intervals were chosen, respectively, for NaLiZnS₂ and CsLiZnS₂.

All calculations were carried out within the PBE implementation¹⁰ of generalized gradient approximation (GGA) using the Full-Potential Local-Orbital (FPLO) code,¹¹ version 18.00-52. Self-consistent calculations were carried out using scalar relativistic approximation.

To model the effects of disordered Li/Zn distribution on the electronic and optical properties, structural configurations with pseudo-random Li/Zn distribution as described in Appendix C were considered on a 2 × 2 × 2 supercell for Na(LiZn)S₂ and on a 2 × 2 × 1 supercell for Cs(LiZn)S₂. The supercell structures contain 40 atoms per unit cell for both the compounds and are considered in space group 1. These structural models also contain structures with different Li : Zn, e.g. 3 : 5, ratios in each quasi-two-dimensional (LiZn)S₂ layer. However, the stoichiometry of the compound was maintained, implying that deviations from the ordered distribution were compensated by the neighboring layer. In total, 15 configurations were obtained (labelled “Rn”) for each compound. For all the structural models, the internal parameters (atomic positions) were optimized such that the residual forces were smaller than 10 meV Å⁻¹, using a k-mesh with 12 × 12 × 6 intervals. Atomic positions are only marginally shifted with respect to the initial positions, taken from the ordered structures, due to the very similar covalent radii of Li and Zn, 0.123 and 0.125 nm, respectively. We find that the minimum Li–S distances of all pseudo-random structures differ by only up to 2.5% and the minimum Zn–S distances by up to 3.5%. The DOS and the optical properties of the pseudo-random structures were obtained on k-meshes with 18 × 18 × 9 and 17 × 17 × 10 intervals, respectively, for Na(LiZn)S₂ and Cs(LiZn)S₂.

The optical properties were studied using the complex finite-frequency dielectric function ε(ω), where ω is the angular frequency of the incident photon. The imaginary part of the dielectric function, ε₂(ω), was calculated up to ℏω = 10 eV for all the structural models using the “foptics” module of the FPLO code (plots not shown). The real part of the dielectric function, ε₁(ω), was obtained by the Kramers–Kronig transformation. The absorption coefficient was subsequently obtained using the well-known relation:¹²

α(ω) = 2^1/2(ω/c){[(Reε(ω))² + (Imε(ω))²]^1/2 − Reε(ω)}^1/2.

For supercell structures with pseudo-random Li/Zn distribution, the average dielectric function and absorption coefficient were obtained by averaging over different considered structural configurations. Ensemble averaged 〈α(ω)〉 was obtained by averaging over the ordered model structure as well as the selected supercell structures. For this, all the structural configurations were considered equally likely. Further, orientational disorder of the crystallites was accounted for by directional averaging of the absorption coefficient. It was explicitly checked that the final results for ensemble averages 〈ε(ω)〉 and 〈α(ω)〉 do not depend on the specific sequence of the ensemble averaging: alternatively, the ensemble averaging was carried out by first obtaining the ensemble and then directionally averaging 〈ε₂(ω)〉 for the ordered model structure as well as the selected supercell structures.¹³ Subsequently, 〈ε₁(ω)〉 and 〈α(ω)〉 were obtained, which were found to be numerically identical to the results obtained using the other procedure.

Results and discussion

Optimized syntheses, by either a solid-state or metathesis reaction, resulted in polycrystalline samples containing plate-like crystallites of sizes ranging from 10 μm up to about 1 mm. However, the most striking visible property was their different color when exposed to white light (black body radiation): Na(LiZn)S₂ is colorless, K(LiZn)S₂ is yellowish, Rb(LiZn)S₂ is strongly yellow, and Cs(LiZn)S₂ is orange red (Fig. 2). As the electro-positivity increases from Na to Cs, it could be expected that the ionicity should increase from Na to Cs, resulting in a larger optical band-gap. However, the observation is contrary to prediction, as the optical activity increases in the visible range, i.e. Cs(LiZn)S₂ has the strongest coloring. This unexpected coloring was the main motivation for further experiments and theoretical calculations described below.

Fig. 2 Photos of polycrystalline materials under controlled Ar atmosphere inside a glove box obtained through a light microscope. The scale bar and corresponding composition are added to each section.

Phase analyses

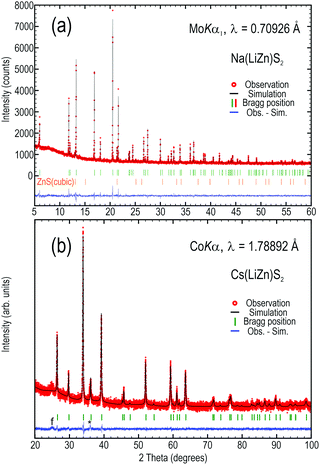
In previous attempts to prepare Na(LiZn)S₂ only a purity of 50% was reported,⁵ but here we achieved an X-ray pure sample by careful heating of stoichiometric amounts of sulfides, zinc metal, and elemental sulfur. By Rietveld refinement, the only observed secondary phase, ZnS, was estimated to constitute about 0.7 vol% of the sample (Fig. 3a). The unit cell parameters, as obtained from simulation of the powder data (Fig. 3), are a = 3.97951(6) and c = 6.7699(1) Å for Na(LiZn)S₂ and within 1% of those reported by Deng et al. for single crystal experiments (a = 3.9711(3) and c = 6.719(1) Å).⁵ For the metathesis product Cs(LiZn)S₂, the unit cell parameters are a = 4.0781(2) and c = 13.939(1) Å, which are also within 0.3% of those reported by Schmitz et al. (a = 4.092(4) and c = 13.974(8) Å).⁶ The minor discrepancies in unit cell sizes might be due to differences between single crystal and powder diffraction techniques. However, the purest samples of K(LiZn)S₂ and Rb(LiZn)S₂ still contain significant amounts of Na(LiZn)S₂ and other minority phases (data not shown), implying that the metathesis reaction was not complete. In contrast, Cs(LiZn)S₂ is relatively phase pure, in line with a complete metathesis reaction (Fig. 3b).

Fig. 3 X-Ray diffraction data of Na(LiZn)S₂ (a) with fitted Rietveld simulation and Cs(LiZn)S₂ (b) with superimposed LeBail fit, where * denotes the largest unknown intensity and f is a minor contribution from the sample holder (plastic foil).

The compounds Na(LiZn)S₂ and Cs(LiZn)S₂ were relatively phase pure, as estimated from X-ray diffraction data (Fig. 3), so these compounds were used for further analyses. The lack of super-structure reflections suggests that there are no long-range atomic ordering phenomena between Li and Zn in the (LiZn)S₂ layer, despite the possibility of formation of stripe orderings, or similar. This means, in reciprocity, that there must be random domain formation (or clustering) of Li and Zn in the (LiZn)S₂ layer, which will be very important for later discussions here.

Naturally, it can be argued that the metathesis reactions might be only partial for Cs(LiZn)S₂. However, elemental analyses on individual crystallites, by EDX analyses during scanning electron microscopy studies, and the bulk sample, done by ICP-OES analyses, support a complete metathesis reaction in forming Cs(LiZn)S₂: EDX data suggest Na_0.88(Li_xZn_1.00)S_2.12 and Cs_0.92(Li_xZn_1.08)S_2.00, when scaling the relative amounts up to a sum of 4, not counting Li as it cannot be reliably quantified by this technique. ICP-OES data, containing signals from Li, suggest Na_0.99(3)(Li_1.0(1)Zn_1.04(1))S_1.96(8) and Cs_0.95(7)(Li_1.0(1)Zn_1.06(6))S_1.9(1), when scaling to a sum of ∼5. All the observed compositions are convincingly close to the intended ones.

Thermal analyses of Na(LiZn)S₂

The difficulties in acquiring a phase pure powder from solid-state reactions become apparent when performing a thermal investigation on pure Na(LiZn)S₂ powder (Fig. 4). Up to about 800 °C, this sulfide remains stable, but a minor event at 800 °C probably indicates a phase transition and the broad endothermal peak at 875 °C is most likely the phase decomposition through peritectic melting. With peritectic melting there is also a significant weight loss that can be expected due to the relatively high vapor pressure of alkali-metal sulfides, Na_2−xLi_xS. On cooling, the sample solidifies by exerting heat in a clearly resolved double event close to 875 °C, underlining the peritectic nature of the partly decomposed, non-stoichiometric sample. The phase transition at 750 °C is probably the counterpart of the minor event at 800 °C on heating, and its hysteretic nature agrees with a phase transition of first order. These data suggest that Na(LiZn)S₂ is most successfully synthesized below 750 °C, avoiding high temperature phase transitions, decomposition, and evaporation.

Fig. 4 Differential scanning calorimetry–thermal gravimetric analysis combined data of an X-ray pure sample of Na(LiZn)S₂ (Fig. 3a). Arrows along the curves indicate how the measurement progressed. * denotes an instrumental error.

UV-Vis spectroscopy of Na(LiZn)S₂ and Cs(LiZn)S₂

The spectra of the two samples have similar basic features; both samples exhibit a steep edge that can be extrapolated to about the same optical band-gap energy (Fig. 5): Na(LiZn)S₂ – 3.41 eV and Cs(LiZn)S₂ – 3.26 eV. However, at lower energies there are several distinct differences. Na(LiZn)S₂ exhibits shoulders on the broad “tail”, close to 400 and 500 nm, while the Cs-homologue exhibits much stronger absorptions with shoulder-like features close to 400, 450, and 515 nm, of which the latter stretches up to about 650 nm. For Cs(LiZn)S₂, the strong absorption in the visible range of the light spectrum seems to correlate with the colouring shown in Fig. 1.

Fig. 5 Transmission UV-Vis spectroscopy of solid-state samples mixed with a BaSO₄ matrix. A measurement of the pure matrix, shown as a dotted line, already is subtracted from the sample measurements (black and red curves). Dashed lines represent extrapolated edge energies, while arrowheads mark shoulders on each curve.

Despite the fact that the two optically measured compounds have slight differences in crystal structures, it is not expected that the Cs-compound has stronger absorption. In contrast, any ionic Cs compound is expected to have more ionicity than the corresponding Na compound because of the higher electropositivity of Cs compared to Na. Following this argument, it could be expected that we have a larger energy gap between the valence and conduction bands in the Cs compound. However, the strong optical activity of the Cs compound indicates that this simple deduction is misleading. Naturally, minor colouring effects can arise from F-centres (trapped electrons in lattice defects), but those effects are of a much lower magnitude. To understand the situation better in these two compounds, local probe NMR spectroscopy was employed.

NMR spectroscopy of ⁷Li, ²³Na, and ¹³³Cs in Na(LiZn)S₂ and Cs(LiZn)S₂

The layered nature of the title compounds allows us to speculate about the mobility of the alkali-metal ions, especially of Na and Cs that are situated between the relatively stable (LiZn)S₂ layers. In first approximation, the relaxation time (T₁) of a nuclear spin is inversely proportional to the mobility of the atom/ion in a solid matrix, as a result of coupling to the lattice vibration. Hence, T₁ is expected also to have a typical size and temperature dependence if the compounds exhibit ion conductivity. The ⁷Li spectra (Fig. 6) reveal that Li is fairly tightly bound in both the investigated compounds; both main resonance spectra are relatively narrow and the estimated T₁ values from relaxation measurements are much larger (199 and 12 s) than what is common for Li ion conductors. For example, T₁ is 0.1–1 s for polycrystalline Li-metal¹⁴ and similarly small (0.1–1 s) for the ionic conductor Li₁₂Si₇.¹⁵ However, the Li ion seems to have more mobility in the Cs-compound, which supports the assumption that Cs is expanding the lattice and making it more ductile (softer).

Fig. 6 ⁷Li NMR spectra of Na(LiZn)S₂ (a) and Cs(LiZn)S₂ (b), with respective insets showing relaxation measurements at room temperature and estimation of T₁. The standard measurements of LiCl are added for spectral broadness comparison, and arrows indicate satellites of the main signals.

The very broad satellite intensities in the ⁷Li (I = 3/2) spectrum of Na(LiZn)S₂ (Fig. 6a) indicate that there is some disorder in the system, which might agree with the suggested atomic disorder at the Li–Zn positions. The line-width of the main intensity is 5.4 kHz (292 K) and it does not change at a higher temperature (380 K), which is in line with a rigid lattice. However, in Cs(LiZn)S₂, the central line-width is 4.3 kHz but there are clear satellites that appear with a splitting of 12 kHz (Fig. 6b). This is probably due to a second hyperfine field, indicative of more prominent ordering phenomena, although short-ranged; there might be a high abundance of next-neighboring Li–Li in the (LiZn)S₂ layer.

According to ²³Na NMR data (Fig. 7a), Na is moving more than Li as T₁ is significantly smaller. Even the two expected satellites from this I = 3/2 species are too broad to be detected. Yet, the relaxation is still too long to be comparable with typical Na–ion conductors. For example, ²³Na in β-alumina has a T₁ value of about 0.01 s.¹⁶ In contrast, ¹³³Cs has I = 7/2 and should exhibit six satellites, which are all present (Fig. 7b) although slightly asymmetric in their intensity distribution. The reasons for this asymmetry and that the main intensity is found significantly shifted from the expected frequency are not understood.

Fig. 7 ²³Na (a) and ¹³³Cs (b) NMR spectra of Na(LiZn)S₂ and Cs(LiZn)S₂, respectively. The upper inset shows relaxation measurements at room temperature and estimation of T₁. The blue vertical lines indicate where the central intensity is expected according to ω₀ = γB₀ (γ = gyromagnetic ratio). The red line in (b) is only a curve fitting (sim.). Arrows indicate satellites and Zeeman splitting.

As both NMR spectra and X-ray diffraction data suggest disorder in the (LiZn)S₂ layers, a theoretical approach was tried to understand the strange color changes when inserting different alkali-metals in position A in A(LiZn)S₂ layers.

DFT simulations of atomic disorder in Na(LiZn)S₂ and Cs(LiZn)S₂

The intrinsic Li–Zn disorder in the (LiZn)S₂ layers is reflected in the high symmetry of the space groups to describe Na(LiZn)S₂ (P3̄ml, No. 164) and Cs(LiZn)S₂ (I4/mmm, No. 139). The ordered structural models lower the symmetries to P3ml (No. 156) and I4̄m2 (no. 119), respectively. These two space groups are non-centrosymmetric due to Li–Zn ordering and keep the original unit cell size (denoted 1 × 1 × 1). This ordering results in different distributions of Li and Zn in each (LiZn)S₂ layer: in ordered NaLiZnS₂ (intentionally written without brackets for LiZn) there are alternating layers of Li and Zn, and ordered CsLiZnS₂ has two interpenetrating square lattices of either Li or Zn (Fig. 8). The band-structures for the ordered structural models are shown in Fig. 8. The smallest band-gap is found at the Γ-point for both compounds, representing a direct band-gap, which spans 1.85 eV for NaLiZnS₂ and 2.54 eV for CsLiZnS₂. In comparison, for ordered KLiZnS₂ and RbLiZnS₂ which are structurally similar to the Cs compound, however, the top of the valence band lies slightly away from Γ, leading to slightly indirect gaps, as shown in Fig. 11 (Appendix B). The band-gaps of 2.25 eV and 2.42 eV, respectively, for KLiZnS₂ and RbLiZnS₂ are in accordance with the expected increase in gap with increasing ionicity of the compounds. There are no signs of indirect band-gaps in the Na and Cs compounds, which could explain the unexpected optical activity (Fig. 2 and 5) of, especially, the latter compound. Hence, another theoretical approach was applied: several structural configurations with different Li–Zn distributions, introduced in a pseudo-random manner, were considered and the structures were allowed to “relax” by finding the energy minimum with respect to the atomic positions, but keeping the unit cell size and composition fixed. The main features of the relaxed structures can generally be described as a slightly distorted version of the starting lattices, i.e., no major changes occurred, but the resulting lattice energy decreased.

Fig. 8 The structures and Brillouin zones for NaLiZnS₂ (a) and (c) and CsLiZnS₂ (b) and (d). Band-structures along high symmetry lines for the ordered structures of (e) NaLiZnS₂ and (f) CsLiZnS₂.

Each simulation cell contains 40 atoms, i.e., close in size to the structures shown in Fig. 8, where two (LiZn)S₂ layers are involved. Crystallographically, this means that a supercell of NaLiZnS₂ contains eight unit cells (2 × 2 × 2) and a supercell of CsLiZnS₂ four unit cells (2 × 2 × 1). In addition, the simulation allowed the layers to contain different ratios of Li : Zn, like 3 : 5, but the total composition was always maintained, meaning that the neighbouring layer has a complementary composition (5 : 3). Note that these calculations are supposed to represent local domains and not complete structures. Hence, only the “local” direct band-gap is estimated in relation to the change in total energy, as compared to the ordered structures (1 × 1 × 1) shown in Fig. 8. The total energies, band-gaps, band-edge positions (the “edge position” is related to a remarkable upturn of the DOS in the lower conduction band; see Fig. 9 and the related discussion below), and Li:Zn distributions of these structure models are shown in Tables 1 and 2.

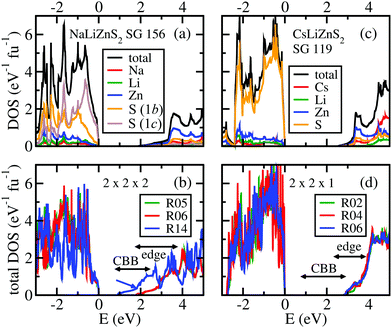Fig. 9 Density-of-states (DOS) plots of the cation ordered compounds (a and c) and of three exemplary structures with pseudo-random Li–Zn distributions (b and d) to be compared with Tables 1 and 2. CBB indicates the ranges of band-gaps within all the considered pseudo-random structures and “edge” indicates the ranges of a prominent upturn of the DOS in the lower conduction band. The atom-projected partial DOS values are also shown for the ordered compounds.

Table 1 Total energies, local band-gaps, band-edge positions, and Li:Zn distributions of ordered and pseudo-random structure models for NaLiZnS₂. All structures considered in the further evaluation show direct gaps

Model	ΔE (meV fu^−1)	Gap (eV)	Edge (eV)	Li : Zn
Colour coding agrees with the curves in Fig. 9b. “fu” is the formula unit. “Rn” denotes 15 different pseudo-random 2 × 2 × 2 structures, ordered according to their total energies.
1 × 1 × 1	0	1.85	3.3	4 : 4(4 : 4)
R01	−27	2.39	3.7	4 : 4(4 : 4)
R02	−9	2.38	3.4	4 : 4(4 : 4)
R03	1	1.97	3.2	4 : 4(4 : 4)
R04	14	1.76	2.9	3 : 5(5 : 3)
R05	30	1.78	2.9	3 : 5(5 : 3)
R06	33	1.77	2.9	3 : 5(5 : 3)
R07	38	1.71	2.8	3 : 5(5 : 3)
R08	40	1.62	2.8	3 : 5(5 : 3)
R09	44	1.61	2.7	3 : 5(5 : 3)
R10	53	1.73	2.8	3 : 5(5 : 3)
R11	54	1.71	2.8	3 : 5(5 : 3)
R12	61	1.61	2.7	3 : 5(5 : 3)
R13	213	0.84	1.8	2 : 6(6 : 2)
R14	222	0.91	1.9	2 : 6(6 : 2)
R15	521	Metal	—	1 : 7(7 : 1)

---

Table 2 Total energies, local band-gaps, band-edge positions, and Li:Zn distributions of ordered and pseudo-random structure models for CsLiZnS₂. All structures considered in the further evaluation show direct gaps

Model	ΔE (meV fu^−1)	Gap (eV)	Edge (eV)	Li : Zn
Colour coding agrees with the curves in Fig. 9d. “fu” is the formula unit. “Rn” denotes 15 different pseudo-random 2 × 2 × 1 structures, ordered according to their total energies.
1 × 1 × 1	0	2.54	3.3	4 : 4(4 : 4)
R01	11	2.79	3.6	4 : 4(4 : 4)
R02	11	2.81	3.7	4 : 4(4 : 4)
R03	30	2.73	3.7	4 : 4(4 : 4)
R04	37	2.84	3.6	4 : 4(4 : 4)
R05	49	2.70	3.8	4 : 4(4 : 4)
R06	49	2.80	3.7	4 : 4(4 : 4)
R07	55	2.65	3.6	4 : 4(4 : 4)
R08	96	2.03	2.9	3 : 5(5 : 3)
R09	105	1.85	2.4	3 : 5(5 : 3)
R10	105	2.04	2.9	3 : 5(5 : 3)
R11	121	1.98	3.0	3 : 5(5 : 3)
R12	121	1.99	2.8	3 : 5(5 : 3)
R13	122	1.97	3.0	3 : 5(5 : 3)
R14	122	1.98	2.8	3 : 5(5 : 3)
R15	323	0.82	?	2 : 6(6 : 2)

---

The total energies E_tot of the pseudo-random structures deviate from those of the ordered structure by −5 up to +100 meV atom⁻¹. These energy differences ΔE = E_tot [Rn] − E_tot[1 × 1 × 1] clearly correlate with the random distribution of the Li and Zn atoms (Tables 1 and 2). Consider first the Na-homologue (Table 1): if equal numbers of Li and Zn atoms are situated in the upper and in the lower half of the supercell (4 : 4), ΔE = −5 to 0 meV atom⁻¹; for distributions 3 : 5(5 : 3), ΔE = 3 to 12 meV atom⁻¹; for distributions 2 : 6 (6 : 2), ΔE = 40 meV atom⁻¹; and for 1 : 7(7 : 1), ΔE is about 100 meV atom⁻¹. In particular, the total energies of R13, R14, and R15 are significantly higher than those of other structures. This is probably related to a less favourable distribution of charge (Madelung energy) and/or atomic volume (strain energy). Thus, we consider R13, R14, and R15 as less probable realizations and will disregard these structures in the further analysis. Note that also the gap width and the edge position of these structures deviate essentially from those of the other structures. In particular, R15 with Li : Zn distribution of 1 : 7(7 : 1) is metallic.

On the other hand, for the Cs-homologue, the total energies of the pseudo-random structures are higher than that of the ordered structure by 2 to 60 meV per atom. The latter value is only obtained for the structure R15 with Li:Zn distribution of 2 : 6(6 : 2), which is considered as less probable realization, due to the much higher energy than those of the other structures. Hence, R15 will be disregarded in further analyses. Note that the distinction between a small DOS at the conduction band bottom and a steep edge in the Cs system is less clear than that in the Na system.

The densities of states for the ordered structural models and for several pseudo-random structural configurations are shown in Fig. 9. In all cases, the top of the valence band is dominated by sulphur states and the bottom of the conduction band by zinc states. This would mean that the electron transfer requiring the least energy is the ligand-to-metal charge transfer from sulphur to zinc. Note that in both ordered structure models the lower conduction band DOS starts with a weak tail and shows a strong upturn at 3.3 eV. The position of these upturns is close to the edge positions shown in the optical spectra (Fig. 5). In the pseudo-random structures, the edge positions are distributed (indicated by a line with arrows), as are the band-gaps.

We now turn to the consideration of the optical properties. For the supercell structures, the dielectric functions are considered excluding the three (one) members for the Na (Cs) system that were considered unlikely, as discussed above.

The fully ordered Li–Zn lattices result in rather weak absorptions that stretch into the visible range, especially far for the Na-homologue (Fig. 10a). As the crystal structures of these sulphides are anisotropic, with one unique crystallographic axis in both cases, the optical properties are displayed with xx and zz components (Fig. 10b and c): at high photon energies, the optical anisotropy is large but the effect is faint in the visible range. As the optical response depends on the joint density of states between the initial and final states, the optical absorption at higher wavelengths (lower energies) is likely proportional to the DOS at the conduction band edges for the considered ensembles since the DOS at the valence band edges is large in all cases. Further, the edge positions and the band-gap values for both the compounds, listed in Tables 1 and 2, are highly correlated. Consequently, when examining the individual optical absorptions for the different Li–Zn orderings as individual curves and as a mean (Fig. 10d and e), it is obvious that the absorption in the visible range is only slightly affected. Comparing the two homologues, and especially their ensembles and individual orderings (Fig. 10f), the strongest effect is observed in the Na-homologues which might very well explain the two shoulders in Fig. 5. On the other hand, none of the theoretically calculated optical properties, based on local Li–Zn ordering phenomena, agrees with the very strong orange red colour of Cs(LiZn)S₂. Interestingly, however, the ordered CsLiZnS₂ structure displays relatively intense features in the 250–350 nm range (Fig. 10a and c) which eventually subside due to the ensemble averaging procedure. The electronic and optical properties, while being sensitive to the choice of the functional, shows approximately a constant shift when the local density approximation (LDA) within the Perdew–Wang implementation¹⁷ is employed instead (see Appendix D for details). It is, therefore, likely that the characteristic features of the electronic and optical properties of the A(LiZn)S₂ compounds are not influenced drastically between LDA and GGA. On the other hand, it is plausible that the sample contains nano-domains with Li–Zn ordering, e.g., as phase separated regions, which would be consistent with the presence of satellite peaks in the NMR data discussed above (see Fig. 6b). A detailed characterization of the samples to rule out these possibilities is, however, beyond the scope of the present work. Another interesting possibility could be that the relative Li–Zn (anti-site) defect fraction in the Cs compound is smaller, to account for which, however, requires a weighted averaging over the considered ensembles. It should also be noted that effects beyond the Li–Zn disorder cannot be ruled out. For example, phonon-assisted indirect transitions might account for the measured edges at 3.3 eV, which coincide with the edges in the related DOS of the ordered structures.

Fig. 10 Optical properties of A(LiZn)S₂: calculated absorption coefficients, α(ω), for (a)–(c) the ordered structures (SG 156 and SG 119 for Na and Cs compounds, respectively) and (d)–(f) the ensemble averaged over all the considered structures (including the ordered structure) and directional components. The insets show a comparison of the absorption coefficients for the two compounds in the visible range.

Band-gap changes due to chemical disorder, also called band-bowing, have been observed in several other systems: ZnO–GaN,¹⁸ (1−x)ZnGeN₂−2xGaN,¹⁹ and Ni_xMg_1−xO.²⁰ In contrast, the atomic disorder in the A(LiZn)S₂ phases is not inherited by a solid solution and does not directly result in composition dependent band-bowing. Instead, the Li–Zn shared position is an intrinsic property due to the stoichiometry and the oxidation state stability of the involved elements. Hence, the amount of disorder is probably due to subtle effects like lattice strains and synthesis conditions. In the series A(LiZn)S₂, the band-gap seems to widen as the ion size on the A-site is increased based on DFT calculations and partly on measurements. The fact that the distance between (LiZn) sites increases with the size of A, should lower the Coulomb forces between the (LiZn) sites. Lower electrostatic forces allow for more Li–Zn disorder, including nano-domain formation, which also causes a stronger optical band-bowing effect. This agrees with the calculations for pseudo-random structures where the gap width shows a broader distribution in the case of the Cs compound (1.0 eV) than in the case of the Na compound (0.8 eV). A similar scenario, with anti-site defects, was suggested for the case of (ZnGe)N₂, where the band-gap was narrowed by about 0.5 eV.²¹ In theory, the band-gap can be completely closed in A(LiZn)S₂ (see for example R15 in Table 1) but the local energy increase (strain and Coulomb repulsions) for such an extreme case might be too high to be statistically relevant.

Conclusions

A solid-state reaction at moderate temperatures was enough to synthesize the first pure powders of Na(LiZn)S₂. The synthesis of this layered sulphide could also be used in combination with a salt to allow for a metathesis reaction, most successful with CsCl to result in Cs(LiZn)S₂. The strong orange red colour of the Cs-homologue proved its intrinsic property by strong absorption in a large range of the visible spectrum, as compared to the Na-homologue. Local probes indicated that Li, Na, and Cs remained firmly static in the Cs- as well as the Na-homologue. Band-structure calculations of Li–Zn ordered versions of the lattices suggest that the there is a direct band-gap in both compounds, corresponding to a charge transfer from sulphur to zinc. By theoretically simulating local Li–Zn orderings it was possible to change the size of the band-gaps in both Cs- and Na-homologues. This kind of theoretical approach makes it possible to simulate defects when trying to understand optical data in imperfect materials.

Author contributions

A. S. and S. C. performed the materials synthesis and X-ray diffraction and electron microscopy analyses. S. H. supervised the practical work of A. S. and S. C. L. G. acquired and evaluated the UV-Vis spectroscopy data. R. R. and M. R. conceptualized, performed, and analysed the DFT calculations. H.-J. G. acquired and interpreted the NMR data. M. V. conceptualized the project and composed the original draft with input from all co-authors.

Conflicts of interest

There are no conflicts to declare.

Appendix A

Table 3 Structure parameters (lattice constants a, b, c, and the atomic positions) for the ordered structural models of NaLiZnS₂ and CsLiZnS₂

A. NaLiZnS2 (SG 156, P3m1)
Param.	Value
a, b (Å)	3.9711
c (Å)	6.7186

---

Atom	Wyckoff position	Fractional coordinates
Na	1a	(0, 0, 0)
Li	1b	(1/3, 2/3, 0.3298)
Zn	1c	(2/3, 1/3, −0.4108)
S	1b	(1/3, 2/3, −0.2863)
S	1c	(2/3, 1/3, 0.2439)

---

B. CsLiZnS2 (SG 119, I4̄m2)
Param.	Value
a, b (Å)	4.092
c (Å)	13.974

---

Atom	Wyckoff position	Fractional coordinates
Cs	2a	(0, 0, 0)
Li	2c	(1/2, 0, 3/4)
Zn	2d	(1/2, 0, 1/4)
S	4e	(0, 0, 0.3432)

---

Appendix B

Fig. 11 shows the band-structures for the ordered structures of KLiZnS₂ and RbLiZnS₂. Both these compounds are structurally similar to CsLiZnS₂. The band-gaps are found to be 2.25 eV and 2.42 eV for the K and Rb compounds, respectively.

Fig. 11 The band-structures of (a) KLiZnS₂ and (b) RbLiZnS₂, featuring indirect band-gaps of 2.25 eV and 2.42 eV, respectively. The Brillouin zone is the same as that for CsLiZnS₂ (see Fig. 8). The insets show a zoomed view of the valence band maxima close to the Γ point.

Appendix C

Pseudo-random occupations of the 16 Li/Zn supercell positions were obtained as follows. In a first step, three test structures were created by filling the positions according to the series of decimals of π. Sequences of 16 numbers each were transformed into binaries n_i = (0 or 1) denoting Li and Zn, respectively. Only sequences fulfilling Σn_i = (7, 8, or 9) were considered. For cases Σn_i ≠ 8, the last appropriate binary of the sequence was switched in order to ensure the stoichiometry of the supercell. In a second step, 12 additional structures were created. To do so, a series of 20 000 real pseudo-random numbers were generated with the random number function implemented in gfortran. The first 1000 numbers were omitted to exclude initial correlations. The remaining numbers were transformed into binaries and correlation tests with neighboring binaries up to the fourth neighbor were performed. The binary series was divided into sequences of 16 numbers each and sequences not fulfilling Σn_i = 8 were excluded. The remaining first 12 sequences were used to define the occupations. For the sake of better statistics, both the three test structures and the 12 additional structures were used in the calculations.

Appendix D

Table 4 lists the electronic band gaps for the ordered structures of ALiZnS₂ obtained within local density approximation (LDA) as compared to the GGA results. Within LDA, the bandgap is found to be approximately 0.25 eV lower, while the characteristic features of the total and atom-projected densities of states as well as the optical properties only show quantitative changes. As an example, Fig. 12 shows a comparison of the absorption coefficient of the ordered structures of NaLiZnS₂ and CsLiZnS₂ obtained within LDA and GGA. Such a lowering of the bandgap arising from a near-constant shift of the conduction bands lowers the absorption onset. However, the difference in the energy of the prominent features away from the absorption edge, especially in the visible range, turns out to be insufficient to address the discrepancy between the observed and calculated optical properties, such as the sample colors, with the assumption that the two functionals lead to similar effects even for the other structural models.

Table 4 Bandgap (in eV) dependence of the ordered structures of considered systems on LDA and GGA functionals

System	GGA	LDA
NaLiZnS2 (SG 156)	1.85	1.60
KLiZnS2 (SG 119)	2.25	2.01
RbLiZnS2 (SG 119)	2.42	2.15
CsLiZnS2 (SG 119)	2.54	2.29

---

Fig. 12 Absorption coefficient for the ordered structures of Na and Cs compounds within LDA and GGA.

Acknowledgements

This work was supported by IFW Leibniz Excellence Program and German Science Foundation (DFG) through project VA831-4/1. We thank Andrea Voß for elemental analyses by ICP-OES. R. R. and M. R. are grateful to Ulrike Nitzsche for her efforts in establishing and maintaining the IFW high-performance computational environment.

References

1. R. Latz, K. Michael and M. Scherer, Jpn. J. Appl. Phys., 1991, 30, L149.
2. Y. Li, W. Fan, H. Sun, X. Cheng, P. Li and X. Zhao, J. Appl. Phys., 2010, 107, 093506.
3. A. Fujishima and K. Honda, Nature, 1972, 238, 37.
4. H. Wang and A. L. Rogach, Chem. Mater., 2014, 26, 123.
5. B. Deng, G. H. Chan, F. Q. Huang, D. L. Gray, D. E. Ellis, R. P. van Duyne and J. A. Ibers, J. Solid State Chem., 2007, 180, 759.
6. D. Schmitz and W. Bronger, Z. Anorg. Allg. Chem., 1987, 553, 248.
7. W. Bronger, H. Hardtdegen, M. Kanert, P. Müller and D. Schmitz, Z. Anorg. Allg. Chem., 1996, 622, 313.
8. STOE WinXPow, v. 2.08, STOE & Cie GmbH, Darmstadt, Germany, 2003.
9. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. – Cryst. Mater., 2014, 229, 345.
10. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
11. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743 , https://www.fplo.de/.
12. M. Dresselhaus, G. Dresselhaus, S. Cronin and A. G. S. Filho, Solid State Properties, Springer Berlin publishing, 2018.
13. Y. Perlov, H. Ebert, A. N. Yaresko, V. N. Antonov and D. Weller, Solid State Commun., 1998, 105, 273.
14. P. Heitjans and J. Kärger, Diffusion in Condensed Matter – Methods, Materials, Models, Springer-Verlag, Berlin, Heidelberg, 2005, p. 373.
15. A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018.
16. J. L. Bjorkstam and M. Villa, J. Phys., 1981, 42, 345.
17. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
18. V. S. Olsen, G. Baldissera, C. Zimmermann, C. S. Granerød, C. Bazioti, A. Galeckas, B. G. Svensson, A. Y. Kuznetsov, C. Persson, Ø. Prytz and L. Vines, Phys. Rev. B, 2019, 100, 165201.
19. T. Suehiro, M. Tansho, T. Ishigaki and T. Shimizu, Inorg. Chem., 2021, 60, 1542.
20. C. A. Niedermeier, M. Råsander, S. Rhode, V. Kachkanov, B. Zou, N. Alford and M. A. Moram, Sci. Rep., 2016, 6, 31230.
21. D. Skachkov, P. C. Quayle, K. Kash and W. R. L. Lambrecht, Phys. Rev. B, 2016, 94, 205201.

---