Transition metal dichalcogenide magnetic atomic chains

Abstract

Reducing the dimensions of a material to the atomic scale endows them with novel properties that are significantly different from their bulk counterparts. A family of stoichiometric transition metal dichalcogenide (TMD) MX₂ (M = Ti to Mn, and X = S to Te) atomic chains is proposed. The results reveal that the MX₂ atomic chains, the smallest possible nanostructure of a TMD, are lattice-dynamically stable, as confirmed from their phonon spectra and ab initio molecular dynamics simulations. In contrast to their bulk and two-dimensional (2D) counterparts, the TiX₂ atomic chains are nonmagnetic semiconductors, while the VX₂, CrX₂, and MnX₂ chains are unipolar magnetic, bipolar magnetic, and antiferromagnetic semiconductors, respectively. In addition, the VX₂, CrX₂, and MnX₂ chains can be converted via carrier doping from magnetic semiconductors to half metals with reversible spin-polarization orientation at the Fermi level. Of these chains, the MnX₂ chains exhibit either ferromagnetic or antiferromagnetic half metallicity depending on the injected carrier type and concentration. The diverse and tunable electronic and magnetic properties in the MX₂ chains originate, based on crystal field theory, from the occupation of the metal d orbitals and the exchange interaction between the tetrahedrally coordinated metal atoms in the atomic chain. The calculated interaction between the carbon nanotubes and the MX₂ chains implies that armchair (7,7) or armchair (8,8) carbon nanotubes are appropriate sheaths for growing MX₂ atomic single-chains in a confined channel. This study reveals the diverse magnetic properties of MX₂ atomic single-chains and provides a promising building block for nanoscale electronic and spintronic devices.

---

1. Introduction

Reducing the dimensionality of bulk materials has emerged as a practical route to engineer the properties of materials and create a wave of exciting research in two-dimensional (2D) materials.¹ One example is atomically thin 2D graphene, which exhibits intriguing physical properties.² Inspired by the discoveries of 2D atom-thin materials, atom-thin one-dimensional (1D) wires (or atomic chains), made from silicon,³ carbon,⁴ pnictogens,⁵ chalcogens,^6,7 iodine,⁸ metal chains,^9,10 semiconducting compounds,^11,12 metal oxides,¹³ oxyhydroxides,¹⁴ and molecular wires,^15–17 have been explored. These materials have received enormous attention for both their exotic electronic properties, such as strong quantum confinement,^18,19 novel edge states,^20,21 polarization,^22,23 and their wide array of applications in nanoconnectors,^10,24 transistors,²⁵ optoelectronics,²⁶ catalysts,^27,28 and spintronics.^15,29

Transition metal dichalcogenides (TMDs) are a class of layered van der Waals material with versatile electronic and magnetic properties.³⁰ In the past few years, 2D TMDs, which have different properties to those of bulk TMDs, have been widely investigated due to their unique combination of atomic thickness, direct band gap, strong spin–orbital coupling and enhanced catalytic properties.^30,31 Meanwhile, efforts also have been devoted to the reduction of the dimensionality of TMD materials to create atomic chains.^32,33 Experimentally, various ultrathin wires based on transition metal chalcogenides, such as transition metal monochalcogenides (TMM),^34–38 transition metal trichalcogenides (TMT),^39–41 CrSbSe₃,⁴² Mo₂S₅,²¹ Mo₅S₄,⁴³ Mo₂Se₅ ultrathin wires,²⁴ single-unit-cell Cu₉S₅ wires,⁴⁴ and segmented linear chains,²³ have been synthesized. Fascinating physical and chemical properties, such as an anisotropic optical response,³⁵ oscillating edge states,²¹ torsional waves,⁴¹ nontrivial spin-polarization,²³ and high electrocatalytic activity,⁴⁴ have been observed. Nevertheless, stoichiometric TMD atomic chains have rarely been reported.

Herein, we reported a family of stable 1D stoichiometric TMDs MX₂ (M = Ti to Mn, and X = S to Te) atomic chains via the use of first-principles calculations. Stable MX₂ atomic chains consist of a metal backbone, which is tetrahedral coordinated with a chalcogen exterior cap. The computed formation energies of these MX₂ chains are on the same order as those of their 2D counterparts. With the exception of the TiX₂ chain, the 1D MX₂ chains are either ferromagnetic (FM) or antiferromagnetic (AFM) semiconductors, depending on the occupation of metal d orbital. Meanwhile, a transition from a magnetic semiconductor to a half-metal with a tunable magnetic ground state and coupling strength can be achieved via electron or hole doping. The VTe₂ chain has a large magnetic anisotropic energy (MAE) of 3.78 meV per metal and strong inter-chain FM coupling. Finally, the MX₂ chains may possibly be realized experimentally by growing them as armchair (7,7) or armchair (8,8) carbon nanotubes (CNT). The semiconducting character of TMD atomic chains together with their tunable magnetic and electronic properties make them promising building blocks for use in optoelectronics and spintronics.

2. Results and discussion

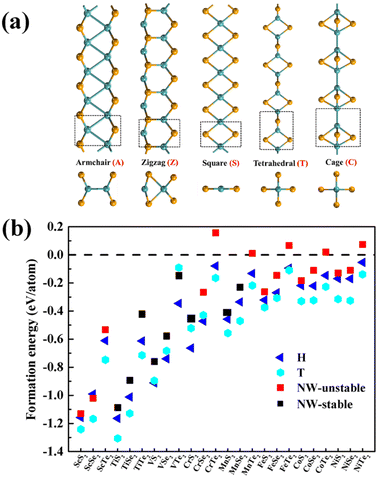
As illustrated in Fig. 1a, different configurations of 1D MX₂ (M = transition metal atoms from Sc to Ni; X = S, Se, or Te) atomic chains, including the armchair (A-type), zigzag (Z-type), planar quadrilateral (Q-type), tetrahedral (T-type), and cage-like (C-type)⁴⁵ atomic arrangements, were investigated to determine the most stable structures. The calculated energy differences between different configurations vary from 0.04 to 2.62 eV per metal atom, as summarized in Table S1 (see ESI†). According to the calculated energies, TiX₂, VX₂, CrX₂, MnS₂, MnSe₂, FeS₂, and FeSe₂ chains prefer T-type configurations, while MnTe₂, FeTe₂, ScX₂, CoX₂, ad NiX₂ chains prefer Z-type configurations. Here, only the most energy favourable configurations were considered to explore their stability. Note that the tetrahedral coordination geometry widely exists in binary compounds (e.g. the zinc blende crystals) and the repeat units have been observed in metal chalcogenide molecules and clusters.^46–50

Fig. 1 (a) Five 1D MX₂ configurations with armchair, zigzag, planar quadrilateral, tetrahedral, and cage-like atomic arrangements. Black rectangles represent the repeated unit cells. (b) The formation energies of H-phase and T-phase TMD monolayers and TMD atomic chains (NW denotes nanowire).

The optimized lattice constants range from 5.13 to 6.72 Å and from 3.19 to 4.09 Å for T-type and Z-type MX₂ atomic chains, respectively (Table S2†). The variation of the atomic radius is consistent with the calculated lattice constants. The lattice stability of the 1D MX₂ atomic chains was further investigated through phonon dispersion spectra calculations and ab initio molecular dynamics simulations (AIMD). From Fig. S1† we can see that TiX₂, VX₂, CrS₂, MnX₂, and NiTe₂ atomic chains are lattice-dynamically stable as they lack an imaginary vibrational mode. In addition, AIMD simulations were performed at a temperature of 300 K for 5 ps to check the thermodynamical stability of the MX₂ chains. A supercell containing five repeat units was used. From Fig. S2† we can see that only the T-type atomic chains, TiX₂, VX₂, CrX₂, and MnX₂, can retain their 1D lattice structures at 300 K without significant distortion and that the maximum fluctuation of the total energy is 0.06 eV per atom. This implies that their structures are thermodynamically stable at room temperature. The atomic coordinates of these nine stable chains are summarized in Table S3†.

The thermal stability of the MX₂ atomic chains can be understood using the M–X bond strength and formation energy. As summarized in Table 1, Bader charge analysis indicates that about 0.88 to 1.93 electrons are moved from the metal onto the chalcogens.⁵¹ These values are larger than those in TMM chains,⁵² resulting in smaller bond lengths between the metal and chalcogen,⁵³ and thus stronger bonding in the MX₂ chains. In addition, the average formation energies per metal atom of the MX₂ chains, defined as E_f = (E_NW(M₂X₄) − 2E(M) − 4E(X))/6, were also calculated. E_NW(MX₂), E(M), and E(X) represent the total energies of the atomic chain and the metal atoms calculated from their most stable bulk or molecular phases. The calculated values of E_f for the MX₂ atomic chains are negative, with the exception of the MTe₂ atomic chains, implying that the synthesis of MX₂ atomic chains from their bulk precursors is exothermic. The calculated E_f increases monotonically with the atomic number of the metals or X, varying from S to Te. The formation energies of nine stable T-type MX₂ chains are comparable with those of their 2D MX₂ counterparts and previously-synthesized 1D TMM and TMT wires (Fig. 1b and Tables S2 and S4†).⁵³ In particular, nine stable T-type MX₂ chains have more negative formation energies than an experimentally synthesized T-phase CrTe₂ nanosheet⁵⁴ and single-chain NWs made from W₆Te₆, VTe₃ and NbTe₃ (Fig. 1b),^38,39,53 implying that the creation of T-type MX₂ atomic chains is experimentally feasible.

Table 1 The distance between metals (D, Å), M–X bond lengths (B, Å), charge on the metal (C, e), local magnetic moment of the central metal ion (M, μ_B), ground state (GS, SC denotes semiconductor), energy gap (E_g, eV), and gap type (D and In represent direct and indirect band gap) of the TMD chains

Chains	D	B	C	M	GS	E g
TiS2	3.09	2.29	1.93	0.0	NM-SC	2.39 (D)
TiSe2	3.19	2.41	1.78	0.0	NM-SC	1.96 (D)
TiTe2	3.36	2.64	1.56	0.0	NM-SC	1.31 (D)
VS2	2.86	2.21	1.18	0.9	FM-SC	1.34 (D)
VSe2	2.95	2.35	1.37	1.0	FM-SC	0.67 (D)
VTe2	3.09	2.56	1.08	1.2	FM-SC	1.26 (D)
CrS2	2.66	2.15	1.23	2.0	FM-SC	1.32 (In)
MnS2	2.62	2.11	1.04	1.2	AFM-SC	1.64 (In)
MnSe2	2.71	2.25	0.88	1.3	AFM-SC	1.07 (D)

---

The magnetic configurations of four 1D MX₂ chains, including nonmagnetic (NM), FM, and AFM orderings, were considered when determining the magnetic ground state (Fig. S3†). As summarized in Table S5,† the TiX₂ chains have NM ground states, while the MnS₂ and MnSe₂ chains have AFM-1 ground states where the FM-AFM energy differences are equal to 540 and 709 meV per metal atom at the HSE06 level, respectively. In contrast, the VS₂, VSe₂, VTe₂, and CrS₂ chains have FM ground states with energy differences ranging from 62 to 426 meV per metal atom. The plotted spin charge density profiles in Fig. S4† reveal that the spin polarization is predominantly distributed on the central metal atom. As shown in Table 1, the local magnetic moments at the metal atom are 0.9 (VS₂), 1.0 (VSe₂), 1.2 (VTe₂), 2.0 (CrS₂), 1.2 (MnS₂), and 1.3 (MnSe₂) μ_B, respectively.

From Fig. 2 and S5† we can see that all MX₂ chains are either direct or indirect band gap semiconductors where the values of the band gap range from 0.67 to 2.39 eV, as summarized in Table 1. TiX₂ chains are NM semiconductors with a direct band gap ranging from 1.31 to 2.39 eV. The MnS₂ chain is an AFM indirect band gap semiconductor, while MnSe₂ is an AFM direct band gap semiconductor. The VX₂ and CrX₂ chains are unipolar magnetic semiconductors (UMS) and bipolar magnetic semiconductors (BMS).⁵⁵

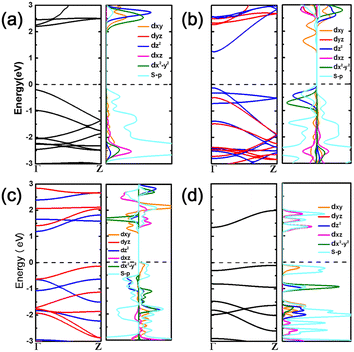Fig. 2 Electronic structures of (a) TiS₂, (b) VS₂, (c) CrS₂, and (d) MnS₂ atomic chains, respectively. The spin up and down states are indicated in red and blue colors in the band structure.

The projected density of states (PDOS) and the partial charge density of the valence band maximum (VBM) and conduction band minimum (CBM) were plotted to reveal the contributions of the metal and chalcogen atoms (Fig. 2 and S6†). The orbital energy levels and distributions indicate that the VBM and CBM of the TiX₂ chains consist of chalcogen and Ti orbitals, respectively, while the orbitals of both the chalcogens and the Cr atoms contribute to the VBM and CBM of the CrS₂ chain. Conversely, the CBM of the VX₂ chains are generated, with the exception of the VTe₂ chain which is formed from Te orbitals, from the orbitals of the chalcogens. The MnX₂ chains consist of orbitals from both the Mn and chalcogen atoms. Meanwhile, the VBM states of the VX₂ and MnX₂ chains receive contributions from both the metal and chalcogen orbitals.

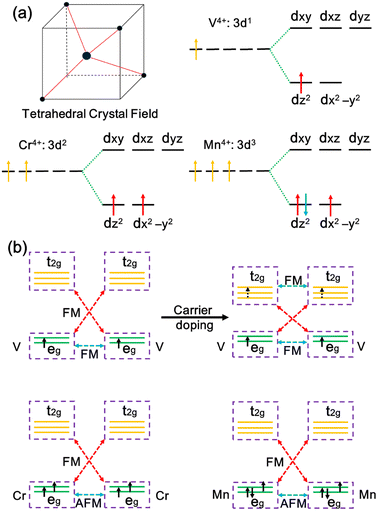
According to crystal field theory, the metal ions in MX₂ chains are tetrahedrally coordinated, and the five d orbitals will split into degenerate e_g (d_x²_−y², d_z²) and t_2g (d_xy, d_xz, d_yz) orbitals, as illustrated in Fig. 3a. Note that Ti, V, Cr, and Mn atoms in the MX₂ chains have a +4 oxidation state with their 3d electron configurations being 3d⁰, 3d¹, 3d², and 3d³, respectively. The e_g orbitals are occupied with one, two, and three electrons, generating one, two, and one unpaired 3d electrons. Thus, 1, 2, and 1 μ_B magnetic moments are located on the metals in the VX₂, CrX₂, and MnX₂ chains, respectively.

Fig. 3 (a) The tetrahedral crystal field and the 3d electron configurations of V⁴⁺, Cr⁴⁺ and Mn⁴⁺ ions. (b) Schematic representation of the 3d orbitals and magnetic exchange interactions. The blue and red dotted lines represent direct exchange and superexchange interactions, respectively.

The magnetic ground state in the MX₂ chains relies on the occupation of the metal d orbital and can be interpreted by exchange interactions between the metal ions. In the MX₂ chains, the metal–ligand–metal bonding angle varies from 74.5 to 85.0°, close to 90°, leading to the coexistence of superexchange and direct exchange interactions between the metal ions.⁵⁶ As illustrated in Fig. 3b, the lower energy e_g orbitals are half-filled while the higher energy t_2g orbitals of the Cr ion are empty. As a result, the direct exchange interaction between the half-filled orbitals is AFM, and the virtual hopping between the half-filled e_g and empty t_2g orbitals via a superexchange interaction is FM according to the Goodenough–Kanamori–Anderson (GKA) rules.^57,58 Given that the FM superexchange interaction between the half-filled e_g orbitals and empty t_2g orbitals is generally stronger than AFM direct exchange in a tetrahedral crystal, FM coupling is induced overall in the CrS₂ chain.⁵⁹ As for the VX₂ chains, in addition to the FM coupling driven by superexchange interactions, direct exchange, i.e., real hopping between partially occupied e_g orbitals, is also FM.^60,61 Therefore, FM coupling is induced in the VX₂ chains. However, the direct exchange interactions in the MnX₂ chains are enhanced because the e_g orbitals are more than half-filled and there is a decreased distance between the metal ions. Thus, the AFM coupling between the e_g orbitals dominates over the FM virtual hopping, resulting in an AFM ground state.

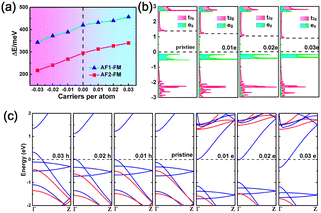
As the exchange interaction between the metal ions is related to the occupation of the metal d orbitals, the magnetic coupling strength and magnetic ground state of the MX₂ chains may be tuned by controlling the number of occupied electrons in the metal d orbitals. Next, the electronic structures and magnetic coupling tunability of MX₂ chains with carrier doping were investigated. A carrier concentration of up to 9.3 × 10¹³ cm⁻² (0.03 carriers per atom) was used, a level which is experimentally reachable.⁶² As illustrated in Fig. 4a and S7,† the VX₂, CrS₂, and MnS₂ chains retain their ground state magnetic order following carrier doping. However, an AFM to FM transition is observed in the MnSe₂ chain when doping with 0.02 or 0.03 holes per atom. In addition, the energy differences in the VX₂ chains increase monotonically with the total electron concentration, as illustrated in Fig. 4a and S7,† which can be explained by the aforementioned exchange interaction mechanism. Taking the VS₂ chain as an example, the doped electrons partially occupy the empty t_2g orbitals, as depicted in Fig. 2b. Compared with a pristine VS₂ chain, the extra FM exchange interactions between the t_2g orbitals arising from the doped electrons enlarge the energy differences between the FM and AFM states in the VS₂ chain.⁶¹ Meanwhile, the gap between the e_g and t_2g levels narrows when the VS₂ chain is doped with electrons, as illustrated in Fig. 4b, which further enhances the virtual hopping between the e_g and t_2g orbitals.⁵⁶ On the contrary, after hole injection, fewer electrons occupying the e_g orbitals weakens the strength of the FM coupling induced by superexchange and direct exchange, and thus the energy difference between the AFM and FM states is decreased. As for the CrS₂ and MnX₂ chains, the decrease in occupied electrons shrinks the AFM exchange interaction due to there being no e_g orbitals less than half-filled.

Fig. 4 (a) Energy differences between the AFM and FM configurations of the VS₂ chain following carrier injection. The injection of electrons and holes is represented by positive and negative carrier concentration values, respectively. (b) The projected density of states of a VS₂ chain with different levels of electron injection. The edges of the e_g and t_2g orbitals are shown with dashed lines, and the edge of the e_g orbitals is set as zero. (c) Band structures of a VS₂ chain with levels of carrier injection.

Fig. 4c and S8 to S10† show the band structures of the MX₂ chains doped with electrons or holes. Transitions from semiconductor to metal are observed in the carrier-doped MX₂ chains. The VX₂, CrS₂, and MnX₂ chains are transformed into half metals (HM) following carrier injection. The VX₂ chains can be converted from UMS to FM HM via carrier injection. In particular, hole (electron) doping in CrS₂ and MnS₂ chains would lead to the transition from a BMS and AFM semiconductor to a FM HM and AFM HM with reversible spin-polarization orientation, respectively. However, the MnSe₂ chain can be switched from an AFM semiconductor to an AFM HM with electron doping or doping with no more than 0.01 hole per atom. Meanwhile, a FM HM can be induced in a MnSe₂ chain by doping with 0.02 or more holes per atom. The results demonstrate the potential that MX₂ chains hold for use in electronically controlled spintronics applications.

It has been accepted that no long-range magnetic ordering can exist in infinite strictly 1D isotropic systems above 0 K.⁶³ However, thermal fluctuation is possibly blocked by strong inter-chain coupling and large magnetic anisotropic energy (MAE) and thus, long-range magnetic order could be stabilized.^15,17,29,64 For example, Pt substrate supported 1D Co atomic chains present long-range magnetic coupling below 15 K due to a large MAE of 2.0 meV per Co atom.²⁹ Our results indicate the easy axes (EA) of the MX₂ chains are parallel to the axial direction, except in the CrS₂ and MnS₂ chains where they are perpendicular to the axial direction (Table S6†). The calculated MAE values vary from 0.019 to 3.78 meV per metal. Among them, the MAE value of the VTe₂ chain reaches 3.78 meV per metal, which is larger than those of Co atomic chains²⁹ and Fe-benzenetetramine coordination polymers.⁶⁵ Furthermore, the inter-chain interactions of the MX₂ chains were also studied. As illustrated in Fig. S11,† MX₂ bundles are arranged in AA-, AB-, AC-, and AD-stacking configurations to determine the most energy favorable configuration. The total energies per metal of these bundles are summarized in Table S7.† AD-stacked MX₂ bundles are energetically preferred, with inter-chain coupling energies varying from −166 to −318 meV per metal atom and inter-chain distances ranging from 3.59 to 4.12 Å. The inter-chain coupling of VS₂, VSe₂, and CrS₂ chains are AFM with energy differences of −0.3, −20.6, and −14.4 meV per metal, respectively. Meanwhile, the VTe₂ chains are FM coupled with an FM-AFM energy difference of 27.3 meV per metal atom. This difference is distinctly larger than those of the MnH₃,¹⁵ V(Bz), and Mn(Bz) bundles,⁶⁴ indicating the feasibility of maintaining their FM order at nonzero temperatures.

Motivated by experimentally observed torsional waves in single-chain nanowires,⁴¹ here we used the TiS₂ atomic chain as a prototype to investigate the atomic and electronic structures of a twisted single chain with a variable rotation angle. Twisted nanowires with 15°, 30°, 45°, 60°, 75°, and 90° rotation angles are displayed in Fig. S12.† First, we calculated the variation of the rotation energy, i.e., E_NW(θ) − E_NW(θ = 0) as a function of the rotation angle. The results demonstrate that the total energy of the twisted TiS₂ nanowire increases monotonically with the rotation angle, and that there is a high energy barrier of 1.4 eV per metal atom between the square and tetrahedral configurations (Fig. S13†). Further, from the calculated band structures of the twisted nanowires (Fig. S14†), we can see that the direct band gap decreases from 1.40 (θ = 0) to 0.06 eV (θ = 60°) and then increases into an indirect band gap of 0.15 eV (θ = 75° and 90°), implying that the electronic structure of these nanowires is dependent on the rotation angle.

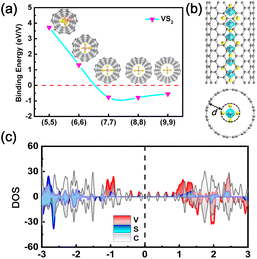
Experimentally, the MX₂ chains may be synthesized in ultra-narrow carbon nanotubes (CNTs), analogous with previously reported TMC chains.^36,38–41 Here, the suitable diameters of a CNT sheath in which to grow MX₂ chains were evaluated by plotting the variation of the binding energy E_b against the diameter of the CNT. The binding energy is defined as E_b = E_NW@CNT − E_NW − E_CNT, where E_NW, E_CNT, and E_NW@CNT are the total energies of the atomic chain, CNT, and their joint system, respectively. The lattice mismatch between the atomic chain and CNT is less than 5.5% (Table S8†). The calculated E_b decreases at first and then increases as the diameter is augmented. This behavior is attributed to the competition between the attraction and repulsion interactions between the chain and CNT (Fig. 5a and S15†). It is clear that insertion of the MX₂ chains inside (7,7) or (8,8) CNTs leads to the lowest E_b values, ranging from −0.792 to −0.698 eV per metal, which are on the same order of magnitude as that of NbSe₃ inside a CNT.⁴¹ Therefore, we believe (7,7) and (8,8) CNTs may be suitable for growing MX₂ chains inside them. As presented in Fig. S16,† the equilibrium separation d between the chains and CNTs range from 3.06 to 3.74 Å, and about 0.02 to 0.17 electrons per metal are transferred from the CNT to the chain, as shown in Fig. S17.† A smaller binding energy and larger separation between the chain and CNT than in the case of NbSe₃ suggest that the interaction between the MX₂ chains and CNT is only a van der Waals interaction.⁴¹ Both spin charge density profiles and PDOS analysis indicate that the electronic and magnetic properties of the TiX₂ and VX₂ chains are preserved inside the (7,7) and (8,8) CNTs, while a transition from a semiconductor to a HM is observed in the CrS₂, MnS₂, and MnSe₂ chains (Fig. 5b and c, S18, and S19†).

Fig. 5 (a) The evolution of binding energy with diameter of CNT. The inset shows front views of a single-chain nanowire embedded in a CNT. (b) Spin charge density distribution in the joint system with an isovalue of 1.5 × 10⁻² e bohr⁻³. (c) Projected density of states of a VS₂ single-chain encapsulated inside a CNT.

Very recently, a new type of platinum-based single-metal-atom chain (SMAC) has been fabricated in a controlled manner via a chemical vapor co-deposition method.⁶⁶ However, the synthesized Pt-based SMAC differs from our proposed MX₂ wires in terms of atomic arrangement, band structure, and magnetic properties. Firstly, although the metal ions in the T-type MX₂ chains and Pt-SMAC are both bonded with four chalcogen atoms, the metals in the MX₂ and Pt-SMAC structures have tetrahedral and square coordination symmetries, respectively. Secondly, the band structure calculations indicate that the MX₂ wires are semiconductors while a metallic behavior is observed in Pt-SMAC. Lastly, Pt-SMAC is intrinsically non-magnetic while the majority of the MX₂ wires are magnetic.

3. Conclusions

In conclusion, we have proposed a family of 1D stoichiometric transition metal dichalcogenide (TMD) atomic chains featuring magnetic properties and band gaps. Different from their bulk and 2D counterparts, the TiX₂, VX₂, CrX₂, and MnX₂ chains are nonmagnetic semiconductors, unipolar magnetic semiconductors, bipolar magnetic semiconductors, and antiferromagnetic (AFM) semiconductors, respectively. In particular, the VX₂, CrX₂, and MnX₂ chains can be converted by carrier injection from ferromagnetic (FM) or AFM semiconductors to half metals (HMs) with tunable spin-polarization orientation at the Fermi level. The diverse and tunable electronic and magnetic properties in the MX₂ chains rely on the occupation of metal d orbitals and the exchange interaction between the tetrahedrally coordinated metal atoms. Of these MX₂ chains, VTe₂ possesses the largest magnetic anisotropic energy (MAE) of 3.78 meV per metal and the inter-chain coupling is FM, revealing the potential to maintain FM ordering at nonzero temperatures. The calculated interaction between carbon nanotubes (CNTs) and the MX₂ chains reveals that armchair (7,7) or armchair (8,8) carbon nanotubes are appropriate sheaths for growing MX₂ atomic chains. In addition, both the magnetic and electronic properties of the TiX₂ and VX₂ chains were maintained inside the CNTs, while a conversion from a semiconductor to a HM is observed in the CrS₂, MnS₂, and MnSe₂ chains. The diverse and tunable electronic and magnetic properties of the MX₂ atomic single-chains make them a promising building block in the field of electronics and spintronics.

4. Methods

First-principles calculations were performed based on density functional theory as implemented in the Vienna Ab Initio Simulation Package (VASP).^67,68 The projector augmented wave (PAW) method was used,^69,70 and the generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) parametrization was adopted to deal with exchange–correlation functional.⁷¹ The cut-off energy was set to 500 eV. A vacuum space larger than 15 Å was used to eliminate interactions between the adjacent periodic images of the NWs. Brillouin zone integration was performed using a 1 × 1 × 18 Γ-centered grid. The energy and forces convergence criteria were set to 10⁻⁶ eV and 10⁻³ eV Å⁻¹. A DFT-D3 method was adopted to include a van der Waals dispersion correction for the joint systems.⁷² For accurate calculations of the electronic properties, a well-performed hybrid HSE06 functional was employed.⁷³ Unless stated otherwise, band structures, DOS, charge densities, and magnetic properties were obtained using the HSE06 functional. Spin–orbital coupling calculations were not considered during the structural relaxation but were then added into the MAE calculations by including the interaction between the electron-spin and the orbital angular momentum in the Hamiltonian. To investigate the thermodynamic stability of the designed NWs at the PBE level, the phonon calculations were performed using the PHONOPY code with a finite difference method,⁷⁴ and Ab Initio Molecular Dynamics (AIMD) simulations were simulated in the NVT ensemble using a Nosé Hoover thermostat at 300 K for 5 ps with a time step of 1 fs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (22073087, 21890751), Innovation Program for Quantum Science and Technology (2021ZD0303302), CAS Project for Young Scientists in Basic Research YSBR-004, the MOST (Grants 2016YFA0200602), the Fundamental Research Funds for the Central University, National Program for Support of Topnotch Young Professional, and the support from Super Computer Centre of the USTCSCC and SCCAS.

References

1. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926.
2. K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Stormer and P. Kim, Nature, 2009, 462, 196–199.
3. E. Do, J. W. Park, O. Stetsovych, P. Jelinek and H. W. Yeom, ACS Nano, 2022, 16, 6598–6604.
4. L. Shi, P. Rohringer, K. Suenaga, Y. Niimi, J. Kotakoski, J. C. Meyer, H. Peterlik, M. Wanko, S. Cahangirov, A. Rubio, Z. J. Lapin, L. Novotny, P. Ayala and T. Pichler, Nat. Mater., 2016, 15, 634–639.
5. M. Hart, J. Chen, A. Michaelides, A. Sella, M. S. P. Shaffer and C. G. Salzmann, Inorg. Chem., 2019, 58, 15216–15224.
6. P. V. C. Medeiros, S. Marks, J. M. Wynn, A. Vasylenko, Q. M. Ramasse, D. Quigley, J. Sloan and A. J. Morris, ACS Nano, 2017, 11, 6178–6185.
7. T. Fujimori, R. B. dos Santos, T. Hayashi, M. Endo, K. Kaneko and D. Tománek, ACS Nano, 2013, 7, 5607–5613.
8. H.-P. Komsa, R. Senga, K. Suenaga and A. V. Krasheninnikov, Nano Lett., 2017, 17, 3694–3700.
9. B. H. Hong, S. C. Bae, C.-W. Lee, S. Jeong and K. S. Kim, Science, 2001, 294, 348–351.
10. A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agraït and J. M. van Ruitenbeek, Nature, 1998, 395, 783–785.
11. D. Li, S. Hao, G. Xing, Y. Li, X. Li, L. Fan and S. Yang, J. Am. Chem. Soc., 2019, 141, 3480–3488.
12. J.-J. Zhang, J. Guan, S. Dong and B. I. Yakobson, J. Am. Chem. Soc., 2019, 141, 15040–15045.
13. Z. Zhang, T. Murayama, M. Sadakane, H. Ariga, N. Yasuda, N. Sakaguchi, K. Asakura and W. Ueda, Nat. Commun., 2015, 6, 7731.
14. S. Iijima, T. Yumura and Z. Liu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11759.
15. X. Li, H. Lv, J. Dai, L. Ma, X. C. Zeng, X. Wu and J. Yang, J. Am. Chem. Soc., 2017, 139, 6290–6293.
16. H. Sakaguchi, H. Matsumura and H. Gong, Nat. Mater., 2004, 3, 551–557.
17. M. Takahashi, P. Turek, Y. Nakazawa, M. Tamura, K. Nozawa, D. Shiomi, M. Ishikawa and M. Kinoshita, Phys. Rev. Lett., 1991, 67, 746–748.
18. F. Münning, O. Breunig, H. F. Legg, S. Roitsch, D. Fan, M. Rößler, A. Rosch and Y. Ando, Nat. Commun., 2021, 12, 1038.
19. Y. Tian, M. R. Sakr, J. M. Kinder, D. Liang, M. J. MacDonald, R. L. J. Qiu, H.-J. Gao and X. P. A. Gao, Nano Lett., 2012, 12, 6492–6497.
20. A. Murani, A. Kasumov, S. Sengupta, Y. A. Kasumov, V. T. Volkov, I. I. Khodos, F. Brisset, R. Delagrange, A. Chepelianskii, R. Deblock, H. Bouchiat and S. Guéron, Nat. Commun., 2017, 8, 15941.
21. H. Xu, S. Liu, Z. Ding, S. J. R. Tan, K. M. Yam, Y. Bao, C. T. Nai, M.-F. Ng, J. Lu, C. Zhang and K. P. Loh, Nat. Commun., 2016, 7, 12904.
22. J. Wang, S. Gudiksen Mark, X. Duan, Y. Cui and M. Lieber Charles, Science, 2001, 293, 1455–1457.
23. T. Pham, S. Oh, S. Stonemeyer, B. Shevitski, J. D. Cain, C. Song, P. Ercius, M. L. Cohen and A. Zettl, Phys. Rev. Lett., 2020, 124, 206403.
24. J. Lin, O. Cretu, W. Zhou, K. Suenaga, D. Prasai, K. I. Bolotin, N. T. Cuong, M. Otani, S. Okada, A. R. Lupini, J.-C. Idrobo, D. Caudel, A. Burger, N. J. Ghimire, J. Yan, D. G. Mandrus, S. J. Pennycook and S. T. Pantelides, Nat. Nanotechnol., 2014, 9, 436–442.
25. J.-K. Qin, P.-Y. Liao, M. Si, S. Gao, G. Qiu, J. Jian, Q. Wang, S.-Q. Zhang, S. Huang, A. Charnas, Y. Wang, M. J. Kim, W. Wu, X. Xu, H.-Y. Wang, L. Yang, Y. Khin Yap and P. D. Ye, Nat. Electron., 2020, 3, 141–147.
26. Y. Li, F. Qian, J. Xiang and C. M. Lieber, Mater. Today, 2006, 9, 18–27.
27. X.-t. Li, Y.-y. Wan and X.-j. Wu, Chin. J. Chem. Phys., 2019, 32, 267–272.
28. C. Ling, Y. Ouyang, L. Shi, S. Yuan, Q. Chen and J. Wang, ACS Catal., 2017, 7, 5097–5102.
29. P. Gambardella, A. Dallmeyer, K. Maiti, M. C. Malagoli, W. Eberhardt, K. Kern and C. Carbone, Nature, 2002, 416, 301–304.
30. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712.
31. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
32. M. Remskar, A. Mrzel, Z. Skraba, A. Jesih, M. Ceh, J. Demšar, P. Stadelmann, F. Lévy and D. Mihailovic, Science, 2001, 292, 479–481.
33. F. Cheng, H. Xu, W. Xu, P. Zhou, J. Martin and K. P. Loh, Nano Lett., 2017, 17, 1116–1120.
34. J. Kibsgaard, A. Tuxen, M. Levisen, E. Lægsgaard, S. Gemming, G. Seifert, J. V. Lauritsen and F. Besenbacher, Nano Lett., 2008, 8, 3928–3931.
35. H. E. Lim, Y. Nakanishi, Z. Liu, J. Pu, M. Maruyama, T. Endo, C. Ando, H. Shimizu, K. Yanagi, S. Okada, T. Takenobu and Y. Miyata, Nano Lett., 2021, 21, 243–249.
36. M. Nagata, S. Shukla, Y. Nakanishi, Z. Liu, Y.-C. Lin, T. Shiga, Y. Nakamura, T. Koyama, H. Kishida, T. Inoue, N. Kanda, S. Ohno, Y. Sakagawa, K. Suenaga and H. Shinohara, Nano Lett., 2019, 19, 4845–4851.
37. L. Venkataraman and C. M. Lieber, Phys. Rev. Lett., 1999, 83, 5334–5337.
38. N. Kanda, Y. Nakanishi, D. Liu, Z. Liu, T. Inoue, Y. Miyata, D. Tománek and H. Shinohara, Nanoscale, 2020, 12, 17185–17190.
39. S. Stonemeyer, J. D. Cain, S. Oh, A. Azizi, M. Elasha, M. Thiel, C. Song, P. Ercius, M. L. Cohen and A. Zettl, J. Am. Chem. Soc., 2021, 143, 4563–4568.
40. S. Meyer, T. Pham, S. Oh, P. Ercius, C. Kisielowski, M. L. Cohen and A. Zettl, Phys. Rev. B, 2019, 100, 041403.
41. T. Pham, S. Oh, P. Stetz, S. Onishi, C. Kisielowski, M. L. Cohen and A. Zettl, Science, 2018, 361, 263.
42. Y. Qu, M. Q. Arguilla, Q. Zhang, X. He and M. Dincă, J. Am. Chem. Soc., 2021, 143, 19551–19558.
43. X. Liu, T. Xu, X. Wu, Z. Zhang, J. Yu, H. Qiu, J.-H. Hong, C.-H. Jin, J.-X. Li, X.-R. Wang, L.-T. Sun and W. Guo, Nat. Commun., 2013, 4, 1776.
44. D. Yang, S. Zuo, H. Yang and X. Wang, Adv. Energy Mater., 2021, 11, 2100272.
45. R. Allmann, I. Baumann, A. Kutoglu, H. Rösch and E. Hellner, Naturwissenschaften, 1964, 51, 263–264.
46. S. C. Lee and R. H. Holm, Angew. Chem., Int. Ed. Engl., 1990, 29, 840–856.
47. D. B. Mitzi, Inorg. Chem., 2005, 44, 3755–3761.
48. M. Yuan, M. Dirmyer, J. Badding, A. Sen, M. Dahlberg and P. Schiffer, Inorg. Chem., 2007, 46, 7238–7240.
49. D. B. Mitzi, L. L. Kosbar, C. E. Murray, M. Copel and A. Afzali, Nature, 2004, 428, 299–303.
50. W. Bronger, Z. Anorg. Allg. Chem., 1968, 359, 225–233.
51. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.
52. W. Zhang, J. Wang, L. Zhao, J. Wang and M. Zhao, Nanoscale, 2020, 12, 12883–12890.
53. C. Shang, L. Fu, S. Zhou and J. Zhao, JACS Au, 2021, 1, 147–155.
54. X. Sun, W. Li, X. Wang, Q. Sui, T. Zhang, Z. Wang, L. Liu, D. Li, S. Feng, S. Zhong, H. Wang, V. Bouchiat, M. Nunez Regueiro, N. Rougemaille, J. Coraux, A. Purbawati, A. Hadj-Azzem, Z. Wang, B. Dong, X. Wu, T. Yang, G. Yu, B. Wang, Z. Han, X. Han and Z. Zhang, Nano Res., 2020, 13, 3358–3363.
55. X. Li, X. Wu, Z. Li, J. Yang and J. G. Hou, Nanoscale, 2012, 4, 5680–5685.
56. C. Huang, J. Feng, F. Wu, D. Ahmed, B. Huang, H. Xiang, K. Deng and E. Kan, J. Am. Chem. Soc., 2018, 140, 11519–11525.
57. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
58. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
59. C. Huang, J. Feng, J. Zhou, H. Xiang, K. Deng and E. Kan, J. Am. Chem. Soc., 2019, 141, 12413–12418.
60. C. Zener, Phys. Rev., 1951, 82, 403–405.
61. Y. Zhao, L. Lin, Q. Zhou, Y. Li, S. Yuan, Q. Chen, S. Dong and J. Wang, Nano Lett., 2018, 18, 2943–2949.
62. A. S. Dhoot, C. Israel, X. Moya, N. D. Mathur and R. H. Friend, Phys. Rev. Lett., 2009, 102, 136402.
63. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136.
64. H. Xiang, J. Yang, J. G. Hou and Q. Zhu, J. Am. Chem. Soc., 2006, 128, 2310–2314.
65. Y. Wan, Y. Sun, X. Wu and J. Yang, J. Phys. Chem. C, 2018, 122, 989–994.
66. S. Guo, J. Fu, P. Zhang, C. Zhu, H. Yao, M. Xu, B. An, X. Wang, B. Tang, Y. Deng, T. Salim, H. Du, R. E. Dunin-Borkowski, M. Xu, W. Zhou, B. K. Tay, C. Zhu, Y. He, M. Hofmann, Y.-P. Hsieh, W. Guo, M. Ng, C. Jia, Z. Zhang, Y. He and Z. Liu, Nature Synthesis, 2022, 1, 245–253.
67. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
68. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
69. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
70. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
71. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
72. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
73. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
74. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2na00543c

---