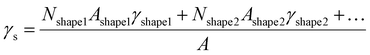Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the melting point depression, coalescence, and chemical ordering of bimetallic nanoparticles: the miscible Ni–Pt system
Evropi
Toulkeridou
a,
Joseph
Kioseoglou
 b and
Panagiotis
Grammatikopoulos
*acd
b and
Panagiotis
Grammatikopoulos
*acd
aOkinawa Institute of Science and Technology Graduate University, 1919-1 Tancha, Onna-Son, Okinawa 904-0495, Japan. E-mail: panagiotis.g@gtiit.edu.cn
bDepartment of Physics, Aristotle University of Thessaloniki, GR-54124 Thessaloniki, Greece
cDepartment of Materials Sciences and Engineering, Guangdong Technion – Israel Institute of Technology, Shantou, Guangdong 515063, China
dGuangdong Provincial Key Laboratory of Materials and Technologies for Energy Conversion, Guangdong Technion – Israel Institute of Technology, Shantou, Guangdong 515063, China
First published on 20th October 2022
Abstract
Among the properties that distinguish nanoparticles (NPs) from their bulk counterparts is their lower melting points. It is also common knowledge that relatively low melting points enhance the coalescence of (usually) nascent nanoclusters toward larger NPs. Finally, it is well established that the chemical ordering of bi- (or multi-) metallic NPs can have a profound effect on their physical and chemical properties, dictating their potential applications. With these three considerations in mind, we investigated the coalescence mechanisms for Ni and Pt NPs of various configurations using classical molecular dynamics (MD) computer simulations. Benchmarking the coalescence process, we identified a steeper melting point depression for Pt than for Ni, which indicates a reversal in the order of melting for same-size NPs of the two elements. This reversal, also evident in the nano-phase diagram thermodynamically constructed using the regular solution model, may be useful for utilising NP coalescence as a means to design and engineer non-equilibrium NPs via gas-phase synthesis. Indeed, our MD simulations revealed different coalescence mechanisms at play depending on the conditions, leading to segregated chemical orderings such as quasi-Janus core-satellite, or core–(partial) shell NPs, despite the expected theoretical tendency for elemental mixing.
Introduction
According to classical thermodynamics, melting is determined by the Gibbs free energy difference between the liquid and solid states.1 At the nanoscale, a size and a shape parameter need also be introduced to express the melting point of nanoparticles (NPs) as a function (a fraction, in principle) of that of the bulk materials. Their lower melting points are among the properties that distinguish NPs from their bulk counterparts.2,3 Indeed, the graph showing the melting point depression of Au as a function of NP diameter regularly appears at introductory nanotechnology classes4 as a typical example of a physical property within the scalable regime of the nanoworld.5One of the most characteristic consequences of the melting point depression of NPs is that it enhances their coalescence,6 an exemplar process where bulk and nano matter's behaviour differentiate not only quantitatively but also qualitatively.7 Indeed, for macroscopic objects (e.g., two solid metallic balls) to fuse together, high sintering temperatures are necessary, whereas solid metallic NPs can fully coalesce even at room temperature due to their dangling bonds and assisted by their lower melting points.6
This fundamental physical process became technologically relevant with the advent of various techniques for the gas-phase synthesis of NPs.8–10 Unlike their counterparts fabricated by chemical synthesis, NPs grown from the gas phase assume morphologies governed solely by basic physical processes. Coalescence between small (usually nascent) clusters toward bigger NPs in-flight11–13 is among the most common growth mechanisms, often dictating NP size and structure. Moreover, due to their high surface area NPs deposited on a substrate are inherently unstable and often tend to coalesce into larger NPs (a process known as Smoluchowski ripening14). This can lead to a reduction of the total surface area of, e.g., a catalytically active phase, rendering NP coalescence one of the main culprits for catalyst deactivation. As a result, a great number of studies, both experimental and theoretical, focused on NP coalescence over the past decades.15–22 Among their common findings was the effect NP coalescence can have on the chemical ordering of nanoalloys,23–26 which, in turn, can largely determine their physical and chemical properties, thus dictating their potential applications.27–30
With these considerations in mind, we investigated the coalescence mechanisms for Ni and Pt NPs using classical MD computer simulations. The Ni–Pt system, which can be employed in a wide range of industrial applications to enhance catalytic activities,31–33 is strongly miscible, as indicated by its bulk phase diagram,34 and this study complements our previous investigation of the Ag–Cu system,35 which is practically immiscible.5 Our goal was to pinpoint potential differences and/or similarities between such diametrically opposed systems (as per their mixing/demixing behaviour), which would highlight important aspects of the coalescence mechanisms.
Benchmarking the coalescence process, we identified a reversal in the order of melting for same-size NPs of the two elements. This reversal was also evident in the nano-phase diagram constructed nano-thermodynamically using the methodology by Guisbiers et al.36–38 Nano-thermodynamics39,40 is a fundamental approach that allows constructing nano-phase diagrams, considering that the limited number of atoms present in nanosystems do not guarantee the applicability of classical thermodynamics. Based on this finding, we utilised different conditions for NP coalescence and designed core–shell or (quasi-)Janus NPs, which may provide insights for the experimental fabrication of metastable miscible-yet-demixed NPs to nanoscientists and nanotechnologists working in the field of gas-phase synthesis of NPs.
Computational methods
Molecular dynamics (MD) calculations were performed with LAMMPS,41 utilising an embedded-atom method (EAM) inter-atomic potential.42,43 All the bulk Ni–Pt compounds and related NPs were formed with the use of the Density Functional Theory (DFT) based structures from the Materials Project44 and the NanomaterialsCad tool.45 For the MD simulations a default timestep size of 0.001 ps was used, and at least 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps were performed for the smallest NPs (3 nm in diameter), corresponding to a minimum 25 ns simulation time. Visualisation was performed using OVITO;46 Common Neighbour Analysis (CNA)47 using adaptive CNA (a-CNA)48 was performed within OVITO, which determines optimal cut-off radii for nearest-neighbours automatically for each individual atom in multiphase systems.
000 MD steps were performed for the smallest NPs (3 nm in diameter), corresponding to a minimum 25 ns simulation time. Visualisation was performed using OVITO;46 Common Neighbour Analysis (CNA)47 using adaptive CNA (a-CNA)48 was performed within OVITO, which determines optimal cut-off radii for nearest-neighbours automatically for each individual atom in multiphase systems.
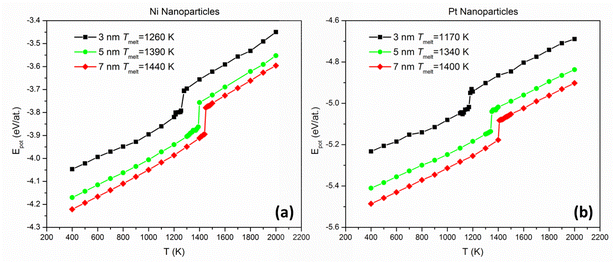
We calculated the melting temperatures of single-element Ni and Pt NPs in the size regime of interest by plotting their caloric curves using MD. Near-spherical fcc NPs were assumed, initially cut from bulk structures and relaxed statically, containing 1288 and 1435 (3 nm), 5971 and 6650 (5 nm), and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 and 18
287 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 (7 nm) Ni and Pt atoms, respectively. We equilibrated each NP at discrete temperature intervals (from 400 K up to 2000 K with a step of 100 K, implemented in the NVT ensemble) and plotted its potential energy as a function of temperature. For each distinct simulation, sufficient time was provided until the potential energy was stabilised and fluctuations subsided for at least 5 ns; the average potential energy per atom of the last 1 ns was used as a data point for each temperature of the caloric curve. A sharp increase in this plot's slope (stemming from a sudden release of heat of fusion) was a clear fingerprint of the onset of melting; thus, the meting point of each NP was determined with an accuracy of 100 K. Subsequently, nine more temperatures were examined, this time with a temperature step of 10 K, between the temperatures where the sharp slope increase was identified. Consequently, the achieved maximum accuracy of the melting point calculations is equal to 10 K.
140 (7 nm) Ni and Pt atoms, respectively. We equilibrated each NP at discrete temperature intervals (from 400 K up to 2000 K with a step of 100 K, implemented in the NVT ensemble) and plotted its potential energy as a function of temperature. For each distinct simulation, sufficient time was provided until the potential energy was stabilised and fluctuations subsided for at least 5 ns; the average potential energy per atom of the last 1 ns was used as a data point for each temperature of the caloric curve. A sharp increase in this plot's slope (stemming from a sudden release of heat of fusion) was a clear fingerprint of the onset of melting; thus, the meting point of each NP was determined with an accuracy of 100 K. Subsequently, nine more temperatures were examined, this time with a temperature step of 10 K, between the temperatures where the sharp slope increase was identified. Consequently, the achieved maximum accuracy of the melting point calculations is equal to 10 K.
The coalescence between (i) equally sized Ni and Pt NPs of various diameters (3, 5, and 7 nm) as well as between (ii) large-diameter Ni (3, 5, and 7 nm) and small-diameter Pt (1.5, 1.9, and 2.5 nm) NPs and (iii) small-diameter Ni (2.5 nm) and large-diameter Pt (7 nm) NPs was investigated at various temperatures below and in-between their estimated melting points. First, the NPs were relaxed individually at various temperatures using the canonical (NVT) ensemble. Next, they were inserted in the same simulation box at a distance just short of the cut-off radius of the inter-atomic potential (6.198 Å), and their coalescence was investigated using the microcanonical (NVE) ensemble to allow for their heating due to surface energy annihilation, according to the scheme detailed in ref. 7.
Results and discussion
1. Melting point depression
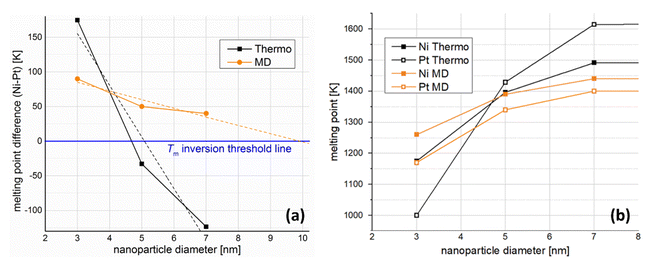
We plotted the caloric curves of Ni and Pt NPs 3, 5, and 7 nm in diameter. From the caloric curves (Fig. 1) we observe that, in the size range investigated, Pt NPs have consistently lower melting points than Ni NPs, as noted in the figure. However, it can also be seen that the difference in melting temperatures (TNimelt − TPtmelt) decreases with increasing size. This indicates that a melting point inversion threshold-size should exist, also considering that bulk Pt has a higher melting point than bulk Ni (1837 vs. 1513 K, according to previous studies utilising the same inter-atomic potential as the current study49,50).
In the regular solution model,39 the solidus–liquidus curves are given by:
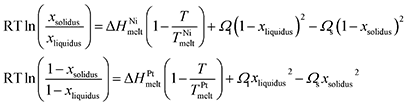 | (1) |
For specific values of T and for xsolidus and xliquidus specified from the corresponding bulk phase diagram, Ωl,∞ and Ωs,∞ can be determined by using the eqn (1). Since Ωl,∞ and Ωs,∞ are only weak functions of composition, as a first-order approximation they can be determined at the corresponding xsolidus and xliquidus at T ≅ (TNimelt + TPtmelt)/2 of their bulk phase diagram.54
For the transition from the bulk to the nanoscale phase diagrams, all the size-dependent parameters need to be re-evaluated. To do so, a linear function of 1/D, where D is the length edge of a polyhedral NP, is used:
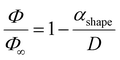 | (2) |
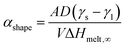 | (3) |
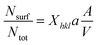 | (4) |
Combining eqn (2)–(4) we get:36
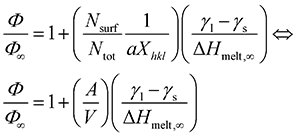 | (5) |
For every material and for different sizes we calculate:51
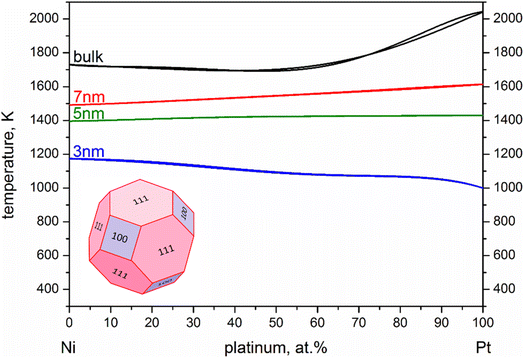
For our calculations we entered values corresponding to truncated octahedral shapes, based on the expected structures for fcc NPs of both elements (calculations based on the regular solution model51 indicated the dodecahedron shape as slightly more stable for Ni; however, we have consistently found the truncated octahedron as the equilibrium shape for similar sizes in previous MD studies55). All the values taken from literature of materials properties56,57 necessary for the calculation of the nanophase diagrams are tabulated in Table 1; a similar table containing identical values for Ni and Pt (among other elements) also exists in ref. 49, since the authors used the same literature sources. Table 2 contains all the Φ values for NPs 3, 5, and 7 nm in body diagonal. Based on these values, we constructed the nanophase diagram of Fig. 2.
| T (K) | ΔH (J mol−1) | Ω s (J mol−1) | Ω l (J mol−1) | Φ/Φ∞ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ni | Pt | Ni | Pt | Ni | Pt | Ni | Pt | Ni | Pt | |
| Bulk | 1728 | 2041 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
153![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 477 |
162![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 946 |
— | |||
| 3 nm | 1175.04 | 1000.3 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886.4 886.4 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863.3 863.3 |
104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364.36 364.36 |
75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203.7 203.7 |
110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803.3 803.3 |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843.5 843.5 |
0.68 | 0.49 |
| 5 nm | 1396.224 | 1429.05 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123.84 123.84 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 519 519 |
124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009.4 009.4 |
107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 433.9 433.9 |
131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660.4 660.4 |
114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062.2 062.2 |
0.808 | 0.7 |
| 7 nm | 1491.26 | 1614.82 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085 085 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536.47 536.47 |
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450.6 450.6 |
121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400.3 400.3 |
140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622.4 622.4 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890.3 890.3 |
0.863 | 0.791 |
Linear extrapolation of the MD plot in Fig. 3a (orange dashed line) indicates that NPs of the two elements would share the same melting temperature at size of 9.8 nm. Of course, one should note that the curve is probably not linear, which would offset the inversion point toward significantly larger sizes in reality. No matter where this point lies, however, beyond that point Pt NPs should have higher melting temperatures than Ni NPs of the same size. In a similar fashion, linear interpolation of our nano-thermodynamics results (black dashed line) indicates that Ni and Pt NPs 5.1 nm in diameter share the same melting point. Once again, linearity is a rather crude approximation, as the melting point inversion appears to happen earlier, at around 4.6 nm in diameter.
Despite the quantitative difference, which was expected due to the different implicit approximations between the two methods, both studies indicate a steeper melting point depression for Pt. This means that a melting point order inversion threshold-size exists, considering the higher melting temperature of bulk Pt compared with that of Ni, with the corresponding changes in behaviour of the coalescing system.
2. MD coalescence studies
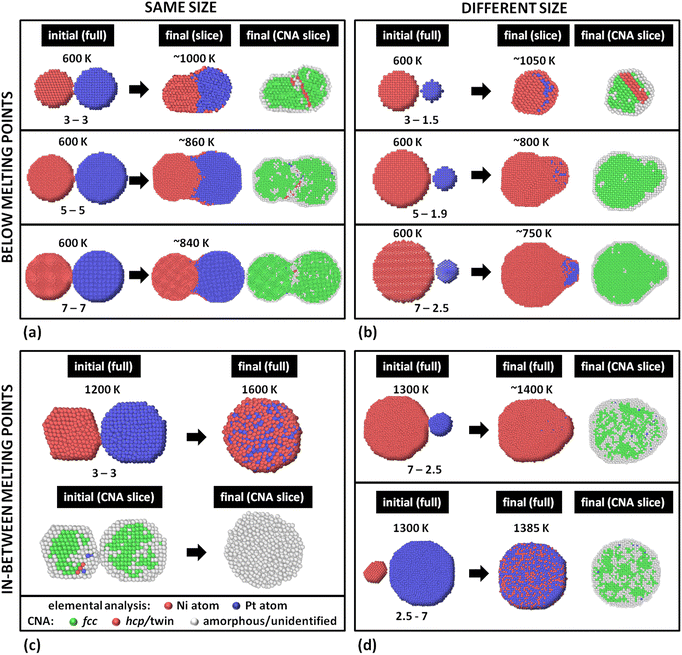
We performed coalescence studies divided in four groups. Knowing that the very end of these simulations, if prolonged enough, would contain mixed configurations in regular-shaped NPs, we stopped the runs at relatively early stages of the coalescence process (between ∼60 and 150 ns). Previous experience has shown that these configurations often resemble NPs grown by some gas-phase synthesis method8,55,58 better than equilibrium ones, due to the fast quenching experimental NPs experience while entering the deposition chamber.35 The initial and final configurations of our MD simulations of all four groups are summarised in Fig. 4.The NPs retained their crystallinity during sintering (Common Neighbour Analysis – CNA – slices). This is possible since this miscible system has a basic bulk phase diagram, which means no melting point drops are expected for intermediate alloy Ni–Pt compositions. This is in contrast to the case of eutectic systems (e.g., Ag–Cu35), where the melting point of the alloy drops near the eutectic composition, and, as a result, the alloy NPs melt at lower temperatures than the Tmelt's of their constituents. Here, the final configuration retained its fcc structure, with potential formation of a twin boundary near (but not exactly at) the original interface of the two adjacent NPs (case 3–3 nm). This relocation of the boundary within the body of one or the other NP has been explained in detail before,18 and is a result of the interfacial atoms temporarily loosening their bonds with their surrounding atoms.6
Interestingly, while in this group of simulations Pt NPs always have lower melting points than Ni NPs, Ni atoms show a tendency to diffuse more, mostly on the surface. This stems from two facts. First, the current temperature is well below either melting point, making the ΔTmelt irrelevant. Further, Pt atoms have a higher cohesive energy,59 meaning that Pt clusters behave as single cohesive objects, whereas Ni clusters resemble loosely connected collections of atoms which are easily detached to drift away. This is analogous to the behaviour of atoms in our previous study of the eutectic Ag–Cu system,35 with Cu and Ag clusters respectively corresponding to Pt and Ni clusters of the present study. According to Table 1, Ni has a lower surface energy in all crystallographic directions (100), (110), and (111), and in liquid, too; this explains the tendency for quasi-Janus structures with a Ni surface monolayer.
(1) Ni NP: 3 nm – Pt NP: 1.5 nm; at 600 K, stabilised at 1050 K.
(2) Ni NP: 5 nm – Pt NP: 1.9 nm; at 600 K, stabilised at 800 K.
(3) Ni NP: 7 nm – Pt NP: 2.5 nm; at 600 K, stabilised at 750 K.
For the duration of our simulation runs (145, 110, 85 ns, respectively), we observe the same tendency for quasi-Janus formation as with the previous group, with Ni atoms diffusing on the surface to form the external layer of the mixed NPs. Due to the size difference, the coalesced system can be better described as core-satellite. In the former case, the small Pt NP melts momentarily and wets the Ni NP, before its atoms reposition themselves within the crystalline Ni matrix. CNA indicates twinning near the interface between the Ni NP and the Pt precipitate inside it; however, the twinning does not coincide with the interface or any of the two phases, indicating that the Pt atoms aligned epitaxially with the larger Ni matrix, the stacking fault not-withstanding. The CNA of the latter two cases (5–1.9 and 7–2.5 nm) indicates that the Pt NP flattens slowly (due to the relatively low temperature), also covering the surface of the Ni NP epitaxially. No boundary is observed in the slice images.
As a result, we shifted our focus towards systems where the current temperature was above the melting point of the one NP but below that of the other, to investigate if it would be possible to wet the surface of the latter with the atoms of the former.
In the latter case, the temperature remained at similar levels (namely, 1385 K) but the coalescence mechanism was different: the mobile atoms of the molten Ni NP diffused on the surface of the large Pt NP non-hermetically encapsulating it with a surface sub-monolayer in a core@partial-shell configuration.
3. Regarding chemical ordering
Our MD study was an in silico exercise to explore the configurational variation one can generate by tuning different parameters affecting the coalescence mechanism of a fully miscible bimetallic system. To this end, we investigated the melting point inversion as a potential cause for modification of the chemical ordering of the coalesced system. Since no ΔTmelt between equal-size NPs in the diameter range we studied was pronounced enough to compensate for the heating due to surface annihilation upon coalescence, we also used the same approach for different-size NPs.Group 1 results indicate that when the current temperature is way below Tmelt the coalescence mechanism is dominated by the cohesive energies of the NPs (and their differences). Chemical ordering depends heavily on surface energies (and their differences). As our miscible system fulfils the Hume-Rothery criteria regarding crystal structure, atomic radii, valence, and electronegativity, no demixing tendencies should be expected.60 However, the significantly lower surface energy of Ni, assisted by its low cohesion, allowed Ni atoms to surface-diffuse and form a (sub)-monolayer shell. This, in principle, constitutes segregation rule #2, as defined by Guisbiers et al.38 However, it should be noted that according to that study rule #2 should become relevant if the difference between the bulk melting temperatures of the two elements is no larger than 10% of bulk TPtmelt. In this case, though, ΔTmelt = 313 K, i.e., ∼15% of bulk TPtmelt. Therefore, either the importance of the bulk Tmelt was overrated, or, possibly, the Tmelt of the actual NPs should be considered instead.
Despite their superficial similarity, there is a difference between cases 7–2.5 of Groups 2 and 4. In the former, the Pt NP retains its crystallinity throughout the whole process, whereas in the latter it temporarily melts before the energy dissipates in the system and it recrystallises. This emphasises the role of kinetics, as two phenomena happen simultaneously: wetting of Pt on Ni, and surface diffusion of Ni atoms. Their relative rates may define at any given time the oblongness of the coalesced NP or the presence/absence of a mixed phase in the Pt-rich region.
Finally, it is noteworthy that, except for the random-solution formation of Group 3 where both NPs melted, no other configuration (quasi-Janus, core-satellite, or core–shell) corresponds to equilibrium chemical ordering. Instead, all generated structures are equivalent to those of the immiscible Ag–Cu system. This is in concord with the findings of Guisbiers et al.36 for the Cu–Ni nanoalloy, another ideal substitutional solid solution system, which can form mixed or Janus NPs depending on the synthesis temperature. In conclusion, it appears that the method is insensitive to the miscibility of the system, which corresponds well to experimentally fabricated NPs from the gas phase in highly non-equilibrium conditions.
Conclusions
We investigated by classical MD the coalescence mechanisms of Ni and Pt NPs, which, in the bulk, constitute a miscible binary system. Utilising both caloric curves by MD and nano-thermodynamics, we identified an inversion in the order of the melting points of the two different-element NPs with increasing size, which meant that, in principle, we could have either type melt and wet the other, if the current temperature was chosen in-between these melting points. We identified different coalescence mechanisms at play depending on the conditions, leading to different configurations. Segregated chemical orderings were thus produced, such as quasi-Janus core-satellite, or core–(partial) shell NPs, regardless of the expected theoretical tendency for elemental mixing. In fact, the only mixed chemical ordering occurred in the only case studied where both coalescing NPs melted, allowing for their atoms to form an amorphous random solution. Simulations run at a temperature between the Tmelt's of two NPs, exploited this difference in Tmelt, as discussed above, but, for practical reasons, involved different-size NPs; it would be interesting to confirm their results with equal-size NPs, although these would involve larger NPs and elevated temperatures. Further, it is a formidable but interesting challenge for the future to reproduce specific simulated configurations experimentally utilising gas-phase synthesis, since various current experimental setups around the world facilitate good control of the growth conditions (e.g., ref. 61).Conflicts of interest
The authors declare no conflict of interest.Note added after first publication
This article replaces the version published on the 20th of October, which contained errors in eqn (1) and eqn (5).Acknowledgements
This work was supported by computational time granted from the Greek Research and Technology Network (GRNET) in the National HPC facility ARIS under the project NOUS(pr012041). Work performed at OIST (Sango HPC facility) was supported by funding from the Okinawa Institute of Science and Technology Graduate University. Work performed at GTIIT was supported by funding from the Guangdong Technion – Israel Institute of Technology.References
- M. Wautelet, On the shape dependence of the melting temperature of small particles, Phys. Lett. A, 1998, 246(3–4), 341–342 CrossRef CAS.
- D. M. Foster, Th. Pavloudis, J. Kioseoglou and R. E. Palmer, Atomic-resolution imaging of surface and core melting in individual size-selected Au nanoclusters on carbon, Nat. Commun., 2019, 10, 2583 CrossRef CAS.
- C. Zeni, K. Rossi, Th. Pavloudis, J. Kioseoglou, S. de Gironcoli, R. E. Palmer and F. Baletto, Data-driven simulation and characterisation of gold nanoparticle melting, Nat. Commun., 2021, 12, 6056 CrossRef CAS.
- R. L. Johnston, Atomic and Molecular Clusters, Taylor & Francis, London, 2002 Search PubMed.
- R. Ferrando, Structure and Properties of Nanoalloys, Elsevier, Amsterdam, 2016 Search PubMed.
- P. Grammatikopoulos, E. Toulkeridou, K. Nordlund and M. Sowwan, Simple analytical model of nanocluster coalescence for porous thin film design, Modell. Simul. Mater. Sci. Eng., 2015, 23, 015008 CrossRef CAS.
- P. Grammatikopoulos, M. Sowwan and J. Kioseoglou, Computational modeling of nanoparticle coalescence, Adv. Theory Simul., 2019, 1, 1900013 CrossRef.
- Gas-Phase Synthesis of Nanoparticles, ed. Y. Huttel, Wiley-VCH, Weinheim, 2017 Search PubMed.
- P. Grammatikopoulos, S. Steinhauer, J. Vernieres, V. Singh and M. Sowwan, Nanoparticle design by gas-phase synthesis, Adv. Phys.: X, 2016, 1, 81–100 CAS.
- L. Mädler, H. K. Kammler, R. Mueller and S. E. Pratsinis, Controlled synthesis of nanostructured particles by flame spray pyrolysis, J. Aerosol Sci., 2002, 33(2), 369 CrossRef.
- M. A. Asoro, D. Kovar, Y. Shao-Horn, L. F. Allard and P. J. Ferreira, Coalescence and sintering of Pt nanoparticles: in situ observation by aberration-corrected HAADF STEM, Nanotechnology, 2010, 21(2), 025701 CrossRef PubMed.
- T. H. Lim, D. McCarthy, S. C. Hendy, K. J. Stevens, S. A. Brown and R. D. Tilley, Real-time TEM and kinetic Monte Carlo studies of the coalescence of decahedral gold nanoparticles, ACS Nano, 2009, 3(11), 3809–3813 CrossRef.
- B. Ingham, T. H. Lim, C. J. Dotzler, A. Hemming, M. F. Toney and R. D. Tilley, How nanoparticles coalesce: an in situ study of Au nanoparticle aggregation and grain growth, Chem. Mater., 2011, 23(14), 3312–3317 CrossRef.
- C. R. Stoldt, C. J. Jenks, P. A. Thiel, A. M. Cadilhe and J. W. Evans, Smoluchowski ripening of Ag islands on Ag(100), J. Chem. Phys., 1999, 111, 5157 CrossRef CAS.
- V. Singh, P. Grammatikopoulos, C. Cassidy, M. Benelmekki, M. Bohra, Z. Hawash, K. W. Baughman and M. Sowwan, Assembly of tantalum porous films with graded oxidation profile from size-selected nanoparticles, J. Nanopart. Res., 2014, 16, 2373 CrossRef.
- G. Palasantzas, T. Vystavel, S. A. Koch and J. T. M. De Hosson, Coalescence aspects of cobalt nanoparticles during in situ high temperature annealing, J. Appl. Phys., 2006, 99, 024307 CrossRef.
- P. Grammatikopoulos, C. Cassidy, V. Singh and M. Sowwan, Coalescence-induced crystallisation wave in Pd nanoparticles, Sci. Rep., 2014, 4, 5779 CrossRef CAS PubMed.
- P. Grammatikopoulos, C. Cassidy, V. Singh, M. Benelmekki and M. Sowwan, Coalescence behaviour of amorphous and crystalline tantalum nanoparticles: a molecular dynamics study, J. Mater. Sci., 2014, 49, 3890–3897 CrossRef CAS.
- E. Goudeli and S. E. Pratsinis, Crystallinity dynamics of gold nanoparticles during sintering or coalescence, AIChE J., 2016, 62(2), 589 CrossRef CAS.
- K. Yun, J. Lee and H.-S. Nam, Effect of temperature on coalescence behaviour of unsupported gold nanoparticles, Electron. Mater. Lett., 2019, 15, 133 CrossRef CAS.
- S. Arcidiacono, N. Bieri, D. Poulikakos and C. Grigoropoulos, On the coalescence of gold nanoparticles, Int. J. Multiph. Flow, 2004, 30, 979 CrossRef CAS.
- L. M. Farigliano, S. A. Paz, E. P. M. Leiva and M. A. Villarreal, Coalescence of nanoclusters analyzed by well-tempered metadynamics. Comparison with straightforward molecular dynamics, J. Chem. Theory Comput., 2017, 13(8), 3874 CrossRef CAS.
- R. E. Palmer, R. Cai and J. Vernieres, Synthesis without solvents: the cluster (nanoparticle) beam route to catalysts and sensors, Acc. Chem. Res., 2018, 51, 2296–2304 CrossRef CAS PubMed.
- J. Vernieres, S. Steinhauer, J. Zhao, P. Grammatikopoulos, R. Ferrando, K. Nordlund, F. Djurabekova and M. Sowwan, Site-specific wetting of iron nanocubes by gold atoms in gas-phase synthesis, Adv. Sci., 2019, 6, 1900447 CrossRef PubMed.
- M. M. Mariscal, S. A. Dassie and E. P. M. Leiva, Collision as a way of forming bimetallic nanoclusters of various structures and chemical compositions, J. Chem. Phys., 2005, 123, 184505 CrossRef.
- E. Goudeli and S. E. Pratsinis, Surface composition and crystallinity of coalescing silver-gold nanoparticles, ACS Nano, 2017, 11(11), 11653 CrossRef.
- R. Ferrando, J. Jellinek and R. L. Johnston, Nanoalloys: from theory to applications of alloy clusters and nanoparticles, Chem. Rev., 2008, 108(3), 846 CrossRef PubMed.
- M. Bohra, V. Alman, A. Showry, V. Singh, R. E. Diaz, M. Sowwan and P. Grammatikopoulos, Aggregation vs. surface segregation: antagonism over the magnetic behavior of NiCr nanoparticles, ACS Omega, 2020, 5(51), 32883 CrossRef PubMed.
- A. Tricoli, M. Graf, F. Mayer, S. Kuühne, A. Hierlemann and S. E. Pratsinis, Micropatterning layers by flame aerosol deposition-annealing, Adv. Mater., 2008, 20(16), 3005 CrossRef.
- F. Yin, S. Lee, A. Abdela, S. Vajda and R. E. Palmer, Suppression of sintering of size-selected Pd clusters under realistic reaction conditions for catalysis, J. Chem. Phys., 2011, 134, 141101 CrossRef PubMed.
- Y. Chen, F. Yang, Y. Dai, W. Wang and S. Chen, Ni@Pt core–shell nanoparticles: synthesis, structural and electrochemical properties, J. Phys. Chem. C, 2008, 112, 1645–1649 CrossRef CAS.
- S. K. Ghosh, M. Mandal, S. Kundu, S. Nath and T. Pal, Bimetallic Pt–Ni nanoparticles can catalyze reduction of aromatic nitro compounds by sodium borohydride in aqueous solution, Appl. Catal., A, 2004, 268, 61–66 CrossRef CAS.
- F. Cheng, H. Ma, Y. Li and J. Chen, Ni1–xPtx (x = 0–0.12) hollow spheres as catalysts for hydrogen generation from ammonia borane, Inorg. Chem., 2007, 46, 788–794 CrossRef CAS PubMed.
- X. G. Lu, B. Sundman and J. Ågren, Thermodynamic assessment of the Ni-Pt and Al-Ni-Pt systems, CALPHAD, 2009, 33, 450 CrossRef CAS.
- P. Grammatikopoulos, J. Kioseoglou, A. Galea, J. Vernieres, M. Benelmekki, R. E. Diaz and M. Sowwan, Kinetic trapping through coalescence and the formation of patterned Ag-Cu nanoparticles, Nanoscale, 2016, 10(4), 4684 Search PubMed.
- G. Guisbiers, S. Khanal, F. Ruiz-Zepeda, J. Roque de la Puente and M. José-Yacaman, Cu-Ni nano-alloy: mixed, core-shell or Janus nano-particle?, Nanoscale, 2014, 6, 14630 RSC.
- G. Guisbiers, S. Mejia-Rosales, S. Khanal, F. Ruiz-Zepeda, R. L. Whetten and M. José-Yacaman, Gold-copper nano-alloy, “Tumbaga”, in the era of nano: phase diagram and segregation, Nano Lett., 2014, 14, 6718 CrossRef PubMed.
- G. Guisbiers, R. Mendoza-Cruz, L. Bazán-Díaz, J. J. Velázquez-Salazar, R. Mendoza-Perez, J. A. Robledo-Torres, J.-L. Rodriguez-Lopez, J. M. Montejano-Carrizales, R. L. Whetten and M. José-Yacaman, Electrum, the gold-silver alloy, from the bulk scale to the nanoscale: synthesis, properties, and segregation rules, ACS Nano, 2016, 10, 188 CrossRef PubMed.
- Q. Jiang and Z. Weng, Thermodynamics of Materials, Springer, 2011 Search PubMed.
- C. C. Yang and Y. W. Mai, Thermodynamics at the nanoscale: a new approach to the investigation of unique physicochemical properties of nanomaterials, Mater. Sci. Eng., R, 2014, 79, 1–40 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1 CrossRef.
- EAM Database Tool, https://lammps.sandia.gov/doc/Tools.html#eamdb Search PubMed.
- X. W. Zhou, R. A. Johnson and H. N. G. Wadley, Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(14), 144113 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- G. Nikoulis, P. Grammatikopoulos, S. Steinhauer and J. Kioseoglou, NanoMaterialsCAD: Flexible Software for the Design of Nanostructures, Adv. Theory Simul., 2021, 4, 2000232 CrossRef.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- J. D. Honeycutt and H. C. Andersen, Molecular dynamics study of melting and freezing of small Lennard-Jones clusters, J. Phys. Chem., 1987, 91(19), 4950–4963 CrossRef CAS.
- A. Stukowski, Structure identification methods for atomistic simulations of crystalline materials, Modell. Simul. Mater. Sci. Eng., 2012, 20, 045021 CrossRef.
- V. M. Samsonov, A. A. Romanov, A. Y. Kartoshkin, I. V. Talyzin and V. V. Puytov, Embedding functions for Pt and Pd: recalculation and verification on properties of bulk phases, Pt, Pd, and Pt-Pd nanoparticles, Appl. Phys. A: Mater. Sci. Process., 2022, 128, 826 CrossRef CAS.
- L. Koch, F. Granberg, T. Brink, D. Utt, K. Able, F. Djurabekova and K. Nordlund, Local segregation versus irradiation effects in high-entropy alloys: Steady-state conditions in a driven system, J. Appl. Phys., 2017, 122, 105106 CrossRef.
- G. Guisbiers and G. Abudukelimu, Influence of nanomorphology on the melting and catalytic properties of convex polyhedral nanoparticles, J. Nanopart. Res., 2013, 15, 1431 CrossRef.
- A. S. Barnard, Modelling of nanoparticles: approaches to morphology and evolution, Rep. Prog. Phys., 2010, 73, 086502 CrossRef.
- G. Guisbiers, R. Mendoza-Pérez, L. Bazán-Díaz, R. Mendoza-Cruz, J. J. Velázquez-Salazar and M. José-Yacamán, Size and shape effects on the phase diagrams of nickel-based bimetallic alloys, J. Phys. Chem. C, 2017, 121, 6930 CrossRef.
- L. H. Liang, D. Liu and Q. Jiang, Size-dependent continuous binary solution phase diagram, Nanotechnology, 2003, 14(4), 438 CrossRef.
- M. Bohra, P. Grammatikopoulos, R. E. Diaz, V. Singh, J. Zhao, J.-F. Bobo, A. Kuronen, F. Djurabekova, K. Nordlund and M. Sowwan, Surface segregation in chromium-doped NiCr alloy nanoparticles and its effect on their magnetic behavior, Chem. Mater., 2015, 27, 3216 CrossRef.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, The surface energy of metals, Surf. Sci., 1998, 411(1–2), 186 CrossRef.
- Springer Handbook of Condensed Matter and Materials Data, ed. W. Martienssen and H. Warlimont, Springer, Heidelberg, 2005 Search PubMed.
- P. Grammatikopoulos, Atomistic modeling of the nucleation and growth of pure and hybrid nanoparticles by cluster beam deposition, Curr. Opin. Chem. Eng., 2019, 23, 164 CrossRef.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc, 8th edn, Hoboken, NJ, 2005 Search PubMed.
- U. Mizutani, Hume-Rothery Rules for Structurally Complex Alloy Phases, CRC Press, Boca Raton, FL, 2011 Search PubMed.
- D. Llamosa, M. Ruano, L. Martínez, A. Mayoral, E. Roman, M. García-Hernández and Y. Huttel, The ultimate step towards a tailored engineering of core-shell and core-shell-shell nanoparticles, Nanoscale, 2014, 6, 13483 RSC.
| This journal is © The Royal Society of Chemistry 2022 |