Open Access Article
Open Access ArticleCarbon nanowires under compression and their vibrational anomalies†
Uri
Argaman
a and
Guy
Makov
 *ab
*ab
aMaterials Engineering Department, Ben-Gurion University of the Negev, Beer Sheva 84105, Israel. E-mail: makovg@bgu.ac.il
bIlse Katz Institute for Nanoscale Science and Technology, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel
First published on 20th May 2022
Abstract
Anomalous pressure dependence of Raman frequencies of carbon nanowires encapsulated in carbon nanotubes has been recently reported. Two hypotheses have been proposed to explain this phenomenon in linear carbon chains: softening of a carbon bond with pressure or charge transfer to the chain. However, carbon chains bend easily under stress, although stable structures under these conditions have yet to be discovered. In this study, we model linear and bent carbon nanowires under compression, including both stable and metastable structures. The structures, electronic properties, and vibrational frequencies are obtained through first-principles calculations within density functional theory. We find that polyyne, the dimerized linear ground-state structure of carbon chains at zero strain, is not stable under compression for an infinite carbon chain. Instead, the chain transforms into two possible configurations, a previously unknown three-dimensional helical shape or a two-dimensional sinusoidal shape. These structures can be modeled using an analytical atomistic force-constant model or with a continuum approach. In the continuum approach, an eigenvalue wave equation describes the energy and geometry of the chain. Moreover, this equation produces excited (metastable) structural states and can be applied to other one-dimensional systems. The wave equation formulation indicates that the much-pursued concept of Young's modulus in one-dimensional chains is ill-defined. Finally, the Raman anomaly under compression is not observed within the atomistic force-constant model contrary to assumptions in the literature. Instead, this anomaly can be understood using a model in which charge transfer between the nanotube and the nanowire occurs upon contact.
Atomic carbon wires, denoted as carbynes, are idealized, infinitely long carbon chains. Carbynes can be naturally found (e.g. in meteorites), but, in most cases, they are synthesized in a laboratory with finite length.1 There are two common finite chain allotropes:2 polyynes, with alternating single and triple carbon bonds reflected in alternating bond lengths, and cumulenes, which have one repeated double bond.1 The properties of these carbon chain structures are currently under intensive study1,3–7 along with their potential applications, such as nanoelectronics, spintronics, and nonlinear optics.1,4,5
Carbon chains can be synthesized in solution with lengths of tens of atoms before being crystallized.1 However, because of their strong reactivity, protecting them is necessary, e.g., with specific end-groups.1 As an alternative form of protection, carbon chains can be encapsulated in carbon nanotubes (CNTs),3,5 which can stabilize much longer carbon chains of up to 6000 atoms and 600 nm.5
The structure of linear carbon chains has been modeled through first-principles calculations in several studies.3,4,8 Their stable structure at low temperatures was found to be linear (polyyne) with semiconductor properties. The cumulene structure was found to be unstable with semimetallic properties. Under tension, bond length alternation (BLA) increased with strain, stabilizing the polyyne structure.9 Strain energy was found to be representable by a simple analytical atomistic force-constant model. The mechanical stability of finite polyyne chains has been considered within a continuum-mechanics-based model, and they were found to buckle beyond a critical compressive strain.10 Several studies have attempted to evaluate Young's modulus of carbon chains, leading to an unusually wide range of predicted values across two orders of magnitude between 0.3 and 32.7 GPa.11,12 The extremely large value of 32.7 GPa, approximately 32 times larger than Young's modulus of diamond, was obtained from a calculation of the tensile and bending stiffness.12 Using this approach, the authors calculated the chain radius to be 0.386 Å, which is much smaller than ∼0.7 Å, the atomic radius of carbon.
Chain length, via calculations, has been found to affect polyyne material properties strongly. In particular, increasing the chain length has been shown to reduce the BLA between single and triple carbon bonds, reduce the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap,4,5 and decrease the Raman frequency associated with the vibrations of the triple bond.13,14 All these phenomena can be understood by the increasing conjugation of the bonds with increasing polyyne length. However, it is assumed that these effects converge before a transition into a cumulene structure that has zero BLA and no bandgap.6
Recently, several studies compressed carbon chains encapsulated in CNTs under hydrostatic pressure inside diamond anvil cells and measured the Raman spectra of the chains.11,15,16 In these studies, an anomaly was observed, as the Raman frequency decreased with increasing pressure, i.e., it had a negative Grüneisen parameter. Two hypotheses have been put forward to explain this observation. The first is bond softening with pressure; for example, in ref. 11, the authors interpreted that the experimental Raman frequency softening corresponds to single-carbon-bond softening under pressure. The second hypothesis suggested that the softening can be attributed to the charge transfer from the CNT to the carbon chain.15
All these analyses assumed that the carbon chain was linear. However, it is well known that carbon chains are easily distorted from their linear form to become bent either because of the material environment, e.g., upon crystallization or external loading.17 The effects of bending on the structure have been examined;18,19 and the deviation of bond angles from 180° increases with the arc–chord ratio. The bending energy can be analytically modeled, in which a bending term with a single parameter is added to the standard harmonic terms.18 Several experimental and theoretical studies on the structure of bent carbon chains have shown that Raman frequency decreases with chain bending.18,19 Thus, a third hypothesis may be proposed stating that the bending of the carbon chains causes the observed decrease in the Raman frequency under pressure. However, the conditions for carbyne bending and for the stability of linear and bent chains have not been determined.
This study investigates the structure, stability, and Raman frequencies of linear and bent carbon chains by calculating the total energy and phonon spectra through first-principles based density functional theory (DFT). First, we show that the phonon spectrum of a linear chain exhibits imaginary frequencies under compression, indicating mechanical instability. The strain at which the instability presents itself is found to be dependent on chain length. Introducing random displacements in two and three dimensions and then minimizing the energy reveals that compressed carbon chains have either a two-dimensional sinusoidal form or a three-dimensional helical form. The bent chain structures' phonon frequencies and their strain dependence are calculated, and they indicate that the chains are dynamically stable. Subsequently, an atomistic model to describe the chain energy as a function of strain and shape is formulated. We find the conditions necessary for the stability of both finite and infinite strained linear chains, as well as the pressure dependence of the bond force constants. This model is reformulated in the continuum limit as an eigenvalue wave-equation to provide additional insight into one-dimensional chains and indicates that the concept of Young's modulus is irrelevant in one-dimensional chains. Finally, the effect of charge transfer on the aforementioned phonon spectra is considered. We conclude with a discussion on the stability of carbon chains and other one-dimensional atomic structures when compressed as well as the origin of the anomalous Raman shift under pressure.
Results and discussion
Phonon spectrum of a linear chain under strain
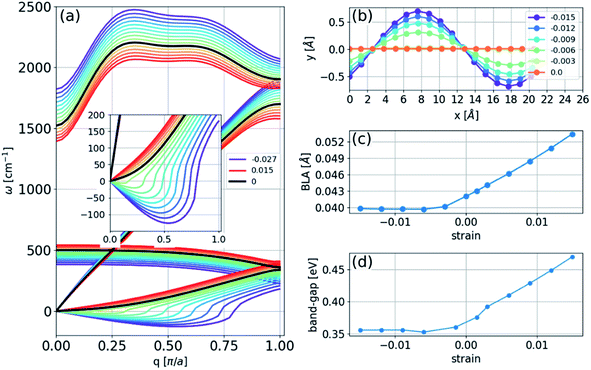
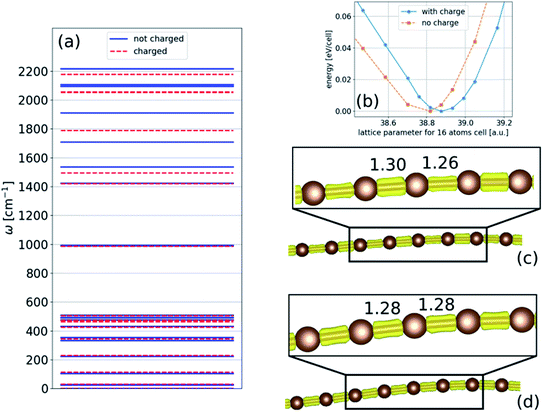
In the absence of strain and at 0 K, our density functional calculations predict that the infinite linear chain has a dimerized structure. The two-atom unit cell has bond lengths of 1.26 and 1.30 Å, which are in excellent agreement with the experimental limiting values as the chain length increases to infinity.1The phonon spectrum of a linear chain with a two-atom unit cell was calculated as a function of strain relative to the equilibrium state, and the results are presented in Fig. 1(a). The longitudinal acoustic and optical branches present high frequencies, while the transverse branches present low frequencies. The frequencies of the longitudinal acoustic branch cross over the transverse optical branch at short wavelengths. At zero strain, all the phonon frequencies are positive, and the chain is stable. This stable condition persists under tension (positive strain). The change in phonon frequencies, ω, with uniaxial strain, ε, can be represented by uniaxial mode Grüneisen parameters, which are defined as follows:
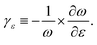 | (1) |
We found that in the linear chain, both of the transverse branches have negative values of γε at all wavelengths, as opposed to the longitudinal branches, which had positive γε values.
Consequently, upon compression, i.e., negative strain, the infinite chain is dynamically unstable, with imaginary frequencies appearing in the transverse acoustic branch, as seen in Fig. 1(a). The imaginary frequencies signify that the linear chain is not a local minimum of the Born–Oppenheimer potential energy surface and that atomic displacements perpendicular to the chain direction, i.e., bending deformations, reduce the energy. The phonon spectra under tension can be measured in principle, whereas those calculated under compression have no physical meaning in the experiments because they describe a mechanically unstable structure.
The structure of the chain under strain bending
As the infinite linear chain is not stable under compression, another stable structure must exist, which can be found by minimizing the total energy subject to suitable constraints and initial conditions in either two or three dimensions. We found two mechanically stable structures for the infinite chain: a two-dimensional sinusoidal structure in which all the atoms are on the same plane and a three-dimensional helical structure.The two-dimensional structure
To obtain the structure of an infinite chain in two dimensions, we considered unit cells of varying sizes (2 to 16 atoms in length) with PBC and introduced random displacements in two dimensions. The result of the energy minimization of the chain is a sinusoidal structure with larger amplitudes at larger strains, as illustrated in Fig. 1(b). The BLA increased in magnitude under tension, decreasing under compression until it reached a nonzero limiting value of 0.040 Å (Fig. 1(c)). This result implies that the polyyne structure remains energetically favorable even under compression, and a transition to a cumulene structure does not occur. Thus, no insulator-metal transition will occur under pressure, as shown in Fig. 1(d), which can be understood because the bandgap is correlated with the BLA (Peierls transition).Finite two-dimensional chains
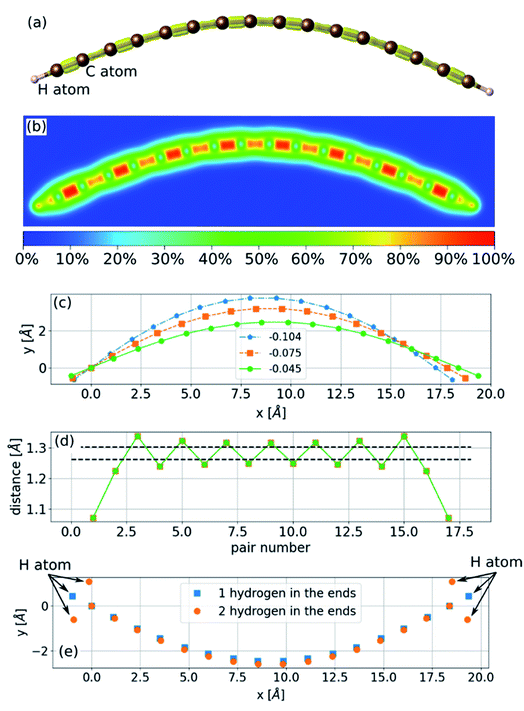
The sinusoidal structure of the infinite chain, as shown in Fig. 1, is determined by the PBC employed in the calculations and may be a good approximation for long chains. However, in experiments, chains have a finite length that can be just a few atoms long. To study the structure of finite chains under compression, we considered a chain of 16 carbon atoms terminated with a hydrogen atom at each end. The choice of termination group can affect the electronic structure and determine whether the stable structure is a polyyne or cumulene,9 but it is not expected to have a considerable effect on bending properties. As a demonstration we calculated the bending of a 16-atom carbon chain terminated either with a single hydrogen atom or two hydrogens at each end. The result is shown in Fig. 2(e) and it can be seen that the difference between the two chains is not significant. To obtain the minimum energy structure, we initiated the relaxation process from a linear structure with random displacements of the atoms in two directions and found an arc-like structure (Fig. 2). The compression has almost no effect on the bond lengths (Fig. 2(d)). As the compressive strain is increased, the amplitude of the arc increases. If the environment geometrically constrains the chain, limiting the amplitude of the arc (e.g., packing the chains into an array or encapsulating in CNTs), this structure will no longer be accessible, leading to a three-dimensional structure.Three-dimensional structure – the helix
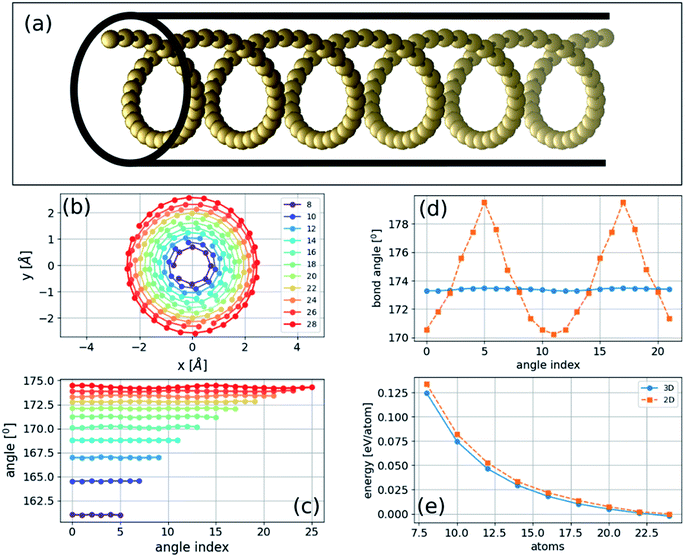
If the energy of the carbon chain is minimized after introducing random atomic displacements in three dimensions instead of two, we then obtain a novel class of three-dimensional helical structures. We consider unit cells of varying sizes from 8 to 28 atoms in length with PBC at constant strain. We find that the three-dimensional structure of a carbon chain under pressure, determined by total energy minimization, is helical (Fig. 3) that can be described as follows: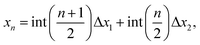 | (2) |
yn = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(kyxn), sin(kyxn), | (3) |
zn = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kzxn), cos(kzxn), | (4) |
Comparison between two- and three-dimensional structures
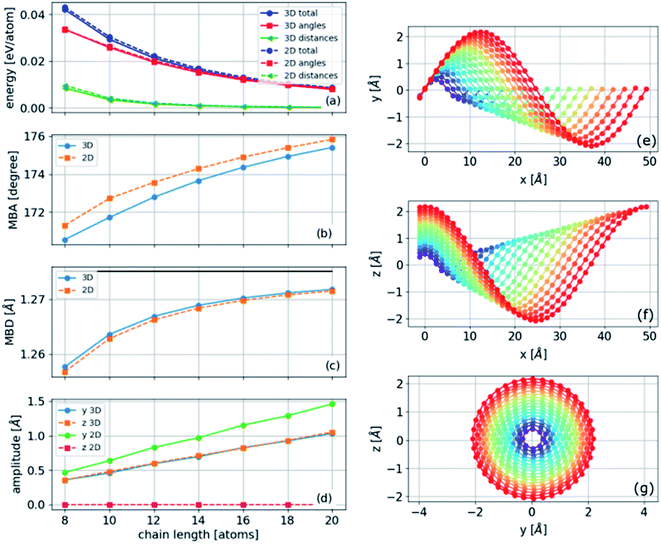
The two- and three-dimensional structures are both local minima of the Born–Oppenheimer potential energy surface (mechanically stable structures) for a fixed number of atoms. As expected, the three-dimensional structure has a slightly lower energy per atom due to the additional degree of freedom (Fig. 3(e)). The bond lengths are approximately constant in two- and three-dimensional structures and gradually become similar to the relaxed bond lengths of the chain. In contrast, the bond angles of the three-dimensional helical structure are approximately constant, whereas those of the two-dimensional sinusoidal structure exhibit considerable variation (Fig. 3(d)). This difference suggests that additional stabilization of the three-dimensional structure is obtained by reducing the bonds' angular contribution to the energy.Phonon normal modes of the bent two-dimensional structure
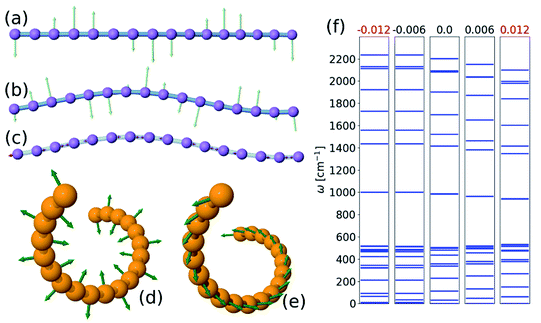
To find the vibrational properties of the carbyne chain under compression, the optical phonon frequencies are calculated at the Γ point in 16-atom unit cells as a function of strain, and the results are presented in Fig. 4(f). The positive real frequencies indicate that the two-dimensional curved chain is dynamically stable. Transverse optical phonon mode frequencies decrease with strain, i.e., they have negative-mode Grüneisen parameters, γε, whereas the lower frequency longitudinal modes present a positive γε. Furthermore, these trends are comparable to those found in the linear chain under tension, and similar results are obtained for the three-dimensional helical structure. Visualizations of selected phonon modes of the chain are shown in Fig. 4.Atomistic model for the bent chain
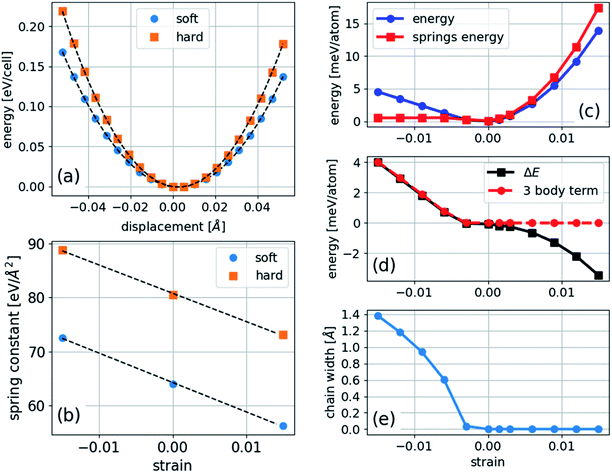
To model carbyne chains under strain, we constructed the energy from a simple harmonic model with force constants (or springs) for each bond and bending constants for each bond angle to represent the three-body angular terms as follows: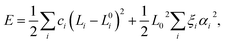 | (5) |
In the case of polyyne carbon chains, there are two force constants, c1 and c2, representing the alternating bonds and one bending parameter, ξ, whereas in cumulene chains there is only one force constant and one bending parameter. A parabolic fit of the energy can determine the force constants as a function of longitudinal atomic displacement in the absence of bending, in which just one bond is altered. This procedure can be computationally achieved using a four-atom unit cell: …C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C. In which, either only the two central atoms adjacent to the triple bond are displaced, or only the two atoms at both ends are displaced. Such a calculation is performed for several strains, and the results are shown in Fig. 5. We found that the values of the force constants for the triple (hard) and single (soft) bonds are 80.5 and 63.9 eV Å−2, respectively. Both force constants have a linear dependence on the strain with similar slopes of −547 and −527 eV Å−2 for the soft and hard bonds, respectively. This result contradicts the assumption made in ref. 11 that only the soft bond force constant changes with pressure.
C–C. In which, either only the two central atoms adjacent to the triple bond are displaced, or only the two atoms at both ends are displaced. Such a calculation is performed for several strains, and the results are shown in Fig. 5. We found that the values of the force constants for the triple (hard) and single (soft) bonds are 80.5 and 63.9 eV Å−2, respectively. Both force constants have a linear dependence on the strain with similar slopes of −547 and −527 eV Å−2 for the soft and hard bonds, respectively. This result contradicts the assumption made in ref. 11 that only the soft bond force constant changes with pressure.
To determine the bending parameter, the difference between the calculated total energy and the modeled harmonic energy under compression is fitted to eqn (5), and the results are presented in Fig. 5. The anharmonic deviation present in a linear chain under compression (Fig. 5(c) and (d)) is much smaller in bending under compression because the bonds are nearly relaxed to their unstrained lengths. The value of ξ for the carbon nanochain is 1.56 eV Å−2, which is approximately 45 times smaller than that of the average force constant, meaning that the chain is much softer toward bending than stretching. Our calculated value of ξ agrees with the value of 1.77 eV Å−2 calculated for finite carbon chains,18 which validates the generality of this model.
Dispersion relation for the linear chain – analytical stability condition – infinite chains
The dispersion relation of the phonons in an infinite chain with two bond types is given as follows (see ESI† for full derivation):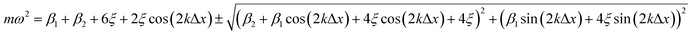 | (6) |
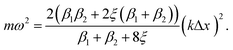 | (7) |
Both β1 and β2 are either positive, negative, or zero, as determined by the strain. At small compressive strains (negative β1 and β2), the long-wavelength limit exhibits instability with a negative numerator and positive denominator in eqn (7), yielding a bent chain. Thus, the infinite chain will not be stable under any compression. Moreover, the instability in this limit is also obtained in DFT calculations, as shown in Fig. 1.
For completeness, we also determine the dispersion relation for cumulenes, an infinite chain with one type of bond. The dispersion relation of the transverse acoustic branch of this chain is (see ESI†):
mω2 = 2β + 6ξ − 2(β + 4ξ)cos(Δx × k) + 2ξ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2Δx × k), cos(2Δx × k), | (8) |
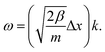 | (9) |
Thus, similar to a chain with two types of bonds, this infinite linear chain is not stable under any compression, and the frequency becomes imaginary when Δx < L0. In the long-wavelength limit, where instability is present, the bending term has no effect because ω does not depend on ξ.
At zero strain, the linear term vanishes, the sound velocity is zero, and the transverse acoustic branch has a nonlinear shape (non-Debye form) similar to the acoustic branch of graphene (Fig. 6(a)). To obtain the long-wavelength limit under these conditions, we expand eqn (8) to the fourth-order in Δx × k as follows:
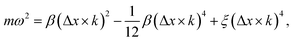 | (10) |
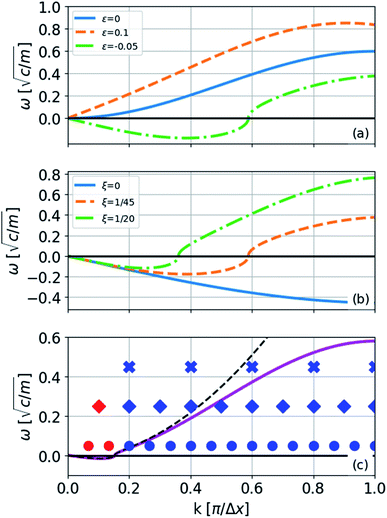 | ||
| Fig. 6 Phonon spectrum of the transverse normal mode (eqn (8)) of the model represented in eqn (5) with one type of bond: (a) ξ = (1/45)c with different strains indicated in the legend; (b) a strain of −0.05 and different values of ξ in units of c; (c) a strain of −0.005; the dashed line is ω approximated by a fourth-order expansion of ω2, the solid line is the exact expression, and the markers are the k-levels for 6-, 11-, and 16-atom chains from top to bottom (eqn (13)). | ||
To see the effect of the bending term on stabilizing the finite linear chain under strain to the leading order, we use the expansion of ω2 to the fourth-order in eqn (10). Within this approximation, the condition for stability for a given value of k is
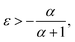 | (11) |
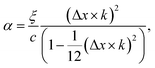 | (12) |
The instability of an infinite chain with increasing compression is illustrated in Fig. 6(a). As the bending parameter ξ increases relative to the force constant c, for example, in other materials, the chains become more stable (Fig. 6(b)). If ξ = 0, the chain is not stable with respect to any transverse displacement under compression because the harmonic term is determined only by the distances between the atoms.
The equations of motion for finite and infinite chains are the same, whereas their boundary conditions are different. Thus, we can apply the dispersion relation of an infinite chain to a finite chain by selecting only discrete values of the wavevector, k, to obtain the discrete normal modes of the finite chain.
Applying the boundary conditions of a standing wave, the allowed values of k are given by the following relation:
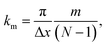 | (13) |
The condition for stability is that all the frequencies are real. Because the imaginary frequencies of the transverse acoustic branch are present in the long wavelength limit (as explained above and shown in Fig. 6), the condition for stability is that the smallest positive allowed value of k (m = 1 in eqn (13)) has a real frequency. From this consideration and eqn (12), we obtain
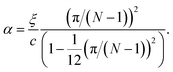 | (14) |
In the limiting case where α = 0, which occurs if there is no resistance to bending (ξ = 0), the condition for stability is ε > 0. In real chains where ξ ≠ 0, α is determined by the length of the chain, N, and the chain can be stably compressed with a negative ε up to a threshold value of −α/(α + 1). This result means that compressed, finite, linear chains are stable if the strain is small enough and the chain is short enough.
The atomistic model solution
The polyyne carbon–chain bending model presented in eqn (5) with two force constants and one bending parameter under a constant strain of −0.04 is numerically solved for finite chains of varying lengths. A gradient-based minimization algorithm is applied to minimize the energy in two and three dimensions. The results are presented in Fig. 7. A helical structure is obtained, as can be seen in Fig. 7(e) and (f). In the limit of long chains, the MBA approaches 180°, and the MBD approaches the mean relaxed bond distance, as shown in Fig. 7(b)–(d). Furthermore, the amplitude increases linearly with chain length at constant strain (Fig. 7(d)).The energies of the three-dimensional structures are slightly lower than those of the two-dimensional structures, consistent with the ab initio results (Fig. 7(a)). Moreover, the most significant contribution to the energy was the angular component (the second term in eqn (5)). As the angles were approximately constant in the three-dimensional structure and varied in the two-dimensional structure (Fig. 4(d) and similar results obtained from the analytical model below), we conclude that the lower energy in the three-dimensional structure is determined by the constant angle distribution that cannot be achieved in two dimensions.
Continuum approach
The stationary structures of carbon chains under compression can be described in a continuum model, similar to an elastic rod. In this approach, we consider harmonic and bending forces derived from the two terms in eqn (5), which act on an infinitesimal length of the chain. These two forces have opposite signs that cancel each other out at mechanical equilibrium as follows: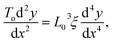 | (15) |
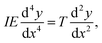 | (16) |
Consequently, we can identify the atomic bending parameter ξL03 with the continuum product of the moment of inertia, I, and Young's modulus, E. This analogy resolves an ongoing controversy over the value of Young's modulus in carbon chains. Comparing the two equations shows that the question is undefined and that atomistic properties are determined by the product IE and not via Young's modulus by itself. This problem leads to the wide range of values, between 0.3 and 32.7 GPa for Young's modulus, as mentioned in the introduction, because different calculations make different assumptions regarding the cross section of the nanowire, which is not a well-defined quantity.
The equilibrium equation can be transformed to yield a wave equation (ESI† for the derivation):
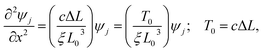 | (17) |
This wave equation is an eigenvalue equation where the eigenvalues and eigenfunctions determine the geometry of the chain by the compression parameter ΔL and the curvatures, respectively. This equation can also describe a dimerized chain where c is the average value of the spring constants (more details below).
This equation can describe both two- and three-dimensional structures. In two dimensions, it is analogous to the time-independent Schrödinger equation for a free particle. However, in three-dimensions, the eigenvalues along the y and z directions are restricted to be the same because they are both determined by the tension, unlike the Schrödinger equation for a free particle. Consequently, the periods in both directions are equal.
The solutions of the wave equation in two-dimensions, similar to a particle in a box, are
ψ(x) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(kx + ϕ), sin(kx + ϕ), | (18) |
ψy(x) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(kx), sin(kx), | (19) |
ψz(x) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(kx + ϕ), ϕ ≠ 0. sin(kx + ϕ), ϕ ≠ 0. | (20) |
In PBC, with ψj(x = 0) = ψj(x = NΔx)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and ψj′(x = 0) = ψj′(x = NΔx), representing an infinite chain, only an integer number of periods is allowed (n = 1, 2, 3,…). This wave equation indicates that at a fixed compression, there exist excited configurational states of the chain, n > 1, commonly referred to as metastable states.
and ψj′(x = 0) = ψj′(x = NΔx), representing an infinite chain, only an integer number of periods is allowed (n = 1, 2, 3,…). This wave equation indicates that at a fixed compression, there exist excited configurational states of the chain, n > 1, commonly referred to as metastable states.
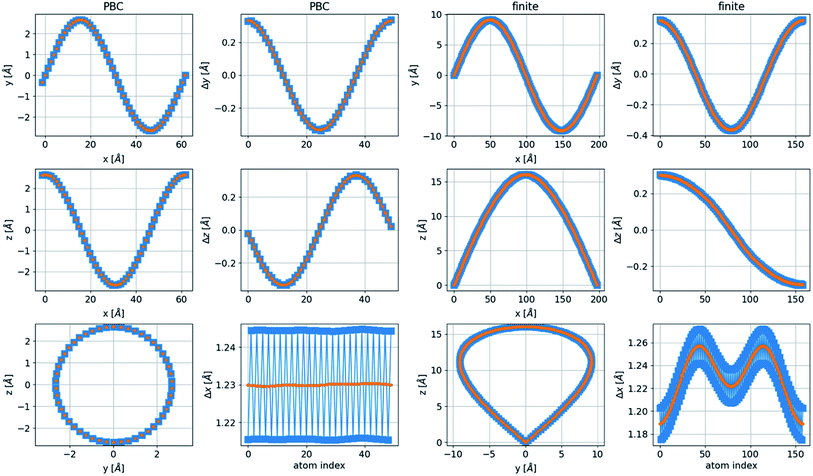
In finite boundary conditions (FBC), with ψj(x = 0) = 0 and ψj(x = NΔx) = 0, representing a finite, free chain, an integer number of half periods (n = 1/2, 1, 3/2,…) is allowed for the two-dimensional structures. In the three-dimensional case, the additional boundary condition is ψj′(x = 0) = ψj′(x = NΔx) ≠ 0, where j′ ≠ j, which allows only an integer number of periods in the additional dimension. Thus, the ground state of the finite three-dimensional chain corresponds to n = 1/2 in one transverse dimension and n′ = 1 in the other transverse dimension. This structure has a nonequal x separation to create a bond length very close to the relaxed distance, as shown in Fig. 8, together with a geometrical description of a chain in PBC. This structure with unequal periods has a noncircular cross-section.
The bent chain structures are stabilized mainly by the energy of the bond force constants. Thus, the bond length 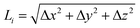 is very close to the relaxed value, L0, and where Δy and Δz are approximately proportional to the derivatives dy/dx and dz/dx (exactly proportional where Δx is constant), respectively, as shown in Fig. 8. In the case where the periods are the same along both the y and z directions with a π/2 phase difference, y(x) = A
is very close to the relaxed value, L0, and where Δy and Δz are approximately proportional to the derivatives dy/dx and dz/dx (exactly proportional where Δx is constant), respectively, as shown in Fig. 8. In the case where the periods are the same along both the y and z directions with a π/2 phase difference, y(x) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(kx), z(x) = A
sin(kx), z(x) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kx), and Δy2 + Δz2 = A2. Then both Δx and
cos(kx), and Δy2 + Δz2 = A2. Then both Δx and 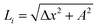 are constant. However, in a structure with unequal periods, Δy2 + Δz2 is no longer constant. Since Li remains constant from the same considerations, Δx cannot be constant, as shown in Fig. 8. Although the dimerization of the polyyne structures cannot be directly inserted into the wave equation, taking the average of the force constants and relaxed distances is a valid approach, as shown in Fig. 8.
are constant. However, in a structure with unequal periods, Δy2 + Δz2 is no longer constant. Since Li remains constant from the same considerations, Δx cannot be constant, as shown in Fig. 8. Although the dimerization of the polyyne structures cannot be directly inserted into the wave equation, taking the average of the force constants and relaxed distances is a valid approach, as shown in Fig. 8.
We assume that the solutions to the wave equation14 increase in energy with an increasing number of periods, n. To establish this assumption, we calculate the energy explicitly by the following procedure: (1) PBC or FBC determine the discrete wavenumber k, (2) substitute eqn (18) or (19) and (20) into eqn (17) to obtain ΔL (from the substitution of eqn (19) and (20) in (17) we obtain the same ΔL), and (3) calculate the two contributions of the energy using eqn (5) with the continuum approach (ESI†). These two contributions are
| Espringsn = Esprings1n4, | (21) |
| Ebendingn = Ebending1n2, | (22) |
The energy can also be obtained numerically from the atomistic model. Thus, we validate the results for the energy, as shown in Fig. 9. Under FBC, the lowest-energy two-dimensional structure has n = 1/2, while in three dimensions, n = 1 in one transverse dimension and n = 1/2 in the other. Thus, the ground state of a finite chain under compression is a two-dimensional arc-shaped structure.
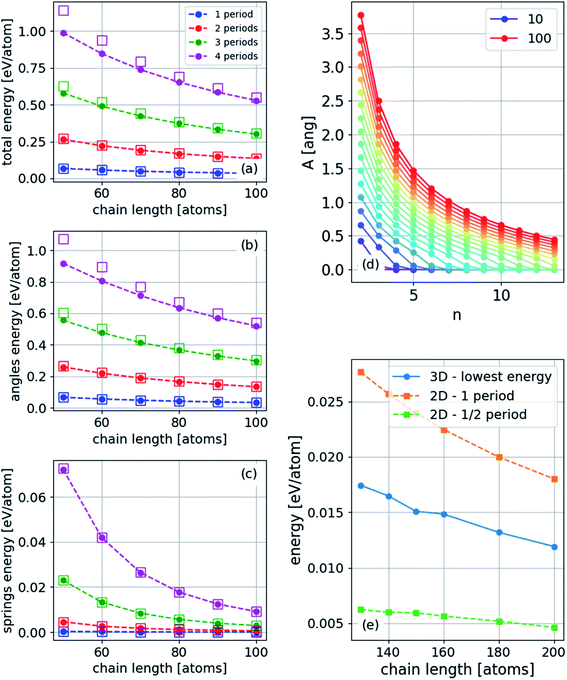 | ||
| Fig. 9 (a) Total, (b) angle (bending), and (c) harmonic energy for three-dimensional structures with PBC for different numbers of periods (wavelengths) in the unit-cell. The squares are determined using eqn (21) and (22), where Esprings1 and Ebending1 were obtained from the energies of a single period. (d) Amplitude, A, for PBC for different chain lengths indicated in the legend (atoms) and different excited states, n, and (e) energy for a finite chain: two lowest energy states for two-dimensional structure and the lowest three-dimensional structure (the geometry of this structure is shown in Fig. 10). | ||
The ground state under FBC of the chain is an arc-shaped two-dimensional structure (n = 1/2), and therefore it is the most probable structure to obtain in an experiment. The nonequal periods' three-dimensional structure (n = 1/2 along y and n = 1 along z) is the first excited state. However, the energy difference depends on the length of the chain and on the strain. As the chains become longer and the strain becomes smaller, the energy difference decreases as shown in Fig. 7. Furthermore, in the high excited states, at constant strain, the amplitude is considerably smaller, as shown in Fig. 9(d).
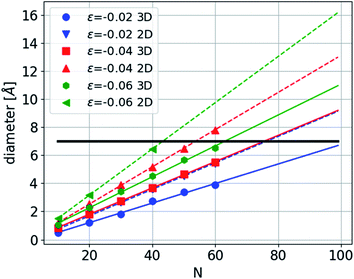
Under compression, the CNT can remain straight or it can collapse. This buckling depends on the diameter of the CNT and the number of walls22,23 and is affected by the presence of chain filling.24,25 Here we consider the case in which the CNTs remain straight. Where the carbon chain is confined in a CNT (Fig. 4), the amplitude is constrained to be smaller than the CNT's radius. Under sufficient compression, the amplitude of the arc of the bent carbon chain becomes larger than the diameter of the tube. Thus, the carbon chain must be in one of the excited states—either in three- or two dimensions. The first accessible states with increasing deformation are the excited states of the 2D sine with shorter periodicities. However, after two or three such excitations another alternative emerges and that is the formation of a helix structure with a longer period, i.e. in a lower excited state, but with the same strain. Further compression requires that the chain occupy higher excited configurational states, thus increasing the number of contact points with the CNT.
As a concrete example we present a calculation of the diameter of the 2D sine-wave and the 3D helix structures as a function of the period length and strain in a CNT with 0.7 nm diameter (Fig. 10). At −0.02 strain the diameter of the 2D sine reaches the CNT diameter and therefore the period must decrease. At approximately half the period the 2D structure can continue until a strain of 0.04. At this point an alternative may be considered, the 3D helix with the same strain but a longer period by approximately 50%. The energy of this structure will be lower than that of the 2D structure as can be seen from the results above in Fig. 7. Of course, in an experimental situation the strain might be constrained because of the technical details of the experiments, like solidification of the pressure transmitting medium and the axial elastic modulus of the CNT. However, large strains of the carbon chain in the CNT can still be achieved through bending.
Charge transfer
If the carbon chain is linear at a sufficiently small length and strain, the frequency of the optical modes increases with increasing compression, as shown in Fig. 1. The high-frequency modes do not anomalously decrease with compression if the chain is bent, as shown in Fig. 4. Thus, the Raman anomaly observed experimentally in carbon nanowires encapsulated inside CNTs under compression cannot be explained by a force constant model of the nanowire (like the models introduced in ref. 11).However, an alternative explanation is charge transfer between the CNT and the wire. It has been shown that in linear carbon wires encapsulated inside CNTs, charge transfers from the CNT to the wire and reduces the Raman frequency.7 Furthermore, charge transfer was found in other systems between the molecular fillers and the CNTs.26,27
Under compression, it is reasonable that more charge will transfer to the nanowire because it becomes wider (more bent). Thus, the effect of charge transfer in chains under compression is examined with respect to both structural relaxation and phonon calculations, and the results are presented in Fig. 11. For simplicity, we only consider the two-dimensional structure. Similar to linear chains, we found that phonon frequencies decrease as the charge is transferred to the chain. This reduction is because of (i) the change in the lattice parameter, as shown in Fig. 11(b), and (ii) the reduction in the BLA, which can reach the polyyne–cumulene transition, as shown in Fig. 11(c) and (d). These results suggest that the decrease in frequency may continue until the polyynes–cumulenes transition.
Conclusions
We found that an infinite linear chain is not stable under any compression using both ab initio calculations and an atomistic model. This instability results in new structures having two configurations: a two-dimensional sine-like shape and a three-dimensional helical structure. The ground-state is a two-dimensional structure in FBC and three-dimensional in PBC. Furthermore, we found meta-stable structures which are similar to the ground-state structures with shorter wavelengths. These structures can be described in a continuum formulation using a wave equation that also reveals the existence of excited configurational states (meta-stable states), which can be attained in experiments in which the carbon chain is confined inside a CNT. This wave equation can also be used in other systems if the atomic interactions can be described with two- and three-body terms. The wave equation formulation also indicates that the concept of Young's modulus for one-dimensional chains is ill-defined, thus explaining the wide range of values proposed. The BLA reaches a constant value as a function of compression strain, and the polyyne–cumulene transition does not occur because of bending (neglecting the effects of the environment on the chain). The bond force constants determine the chain's resistance to strain under tension and the bending constants when under compression. However, finite linear chains can be stable under small compressions if the chain is sufficiently short. Based on the above results, we have demonstrated that the proposed explanation of the Raman anomaly based on the softening of the harmonic force constant model in the case of a linear chain11 is not valid. Furthermore, the Raman frequency does not decrease with the increasing compression of a bent chain. For carbon chains confined in CNTs, we suggest that the chain occupies periodic excited configurations under compression, increasing the contact between the chain and the CNT. Furthermore, a charge transfer from the CNT to the chain reduces the phonon frequency in both linear and bent chains and is most likely the mechanism responsible for the observed Raman anomaly.Methods
First-principles based DFT calculations were performed using the plane-wave pseudopotential method in the Quantum Espresso simulation package.28 The chains were modeled using a unit cell with periodic boundary conditions (PBC) along the chain and with vacuum spacing in two dimensions normal to the chain or three dimensions in the case of finite chains. Ultrasoft pseudopotentials from the GBRV set29 and GGA-PBE exchange–correlation energy function were employed.30 The number of k-points in the periodic direction in a two-atom unit cell was 40. In large supercells, this number was reduced inversely proportional to the increased cell size. The cutoff energies were 40 Ry for the plane-wave expansion of the wave function and 200 Ry for the density and potential functions. Phonons were calculated within the density-functional-perturbation theory approach,31 as implemented in the Quantum Espresso package.Conflicts of interest
There are no conflicts to declare.References
- J. A. Januszewski and R. R. Tykwinski, Synthesis and properties of long [n]cumulenes, Chem. Soc. Rev., 2014, 43, 3184 RSC.
- A. Milani, et al., Semiconductor-to-Metal Transition in Carbon-Atom Wires Driven by sp2 Conjugated End Groups, J. Phys. Chem. C, 2017, 121, 10562–10570 CrossRef CAS.
- K. Zhang, Y. Zhang and S. Shi, A review of linear carbon chains, Chin. Chem. Lett., 2020, 31, 1746–1756 CrossRef CAS.
- E. Buntov, et al., Structure and Properties of Chained Carbon: Recent Ab Initio Studies, C—J. Carbon Res., 2019, 5, 56 CrossRef CAS.
- C. S. Casari and A. Milani, Carbyne: from the elusive allotrope to stable carbon atom wires, MRS Commun., 2018, 8, 207–219 CrossRef CAS.
- S. Heeg, et al., Carbon Nanotube Chirality Determines Properties of Encapsulated Linear Carbon Chain, Nano Lett., 2018, 18, 5426–5431 CrossRef CAS PubMed.
- M. Wanko, et al., Polyyne electronic and vibrational properties under environmental interactions, Phys. Rev. B, 2016, 94, 195422 CrossRef.
- U. Argaman, D. Kartoon and G. Makov, Driving forces behind the distortion of one-dimensional monatomic chains: Peierls theorem revisited, Phys. Rev. B, 2018, 98, 165429 CrossRef.
- V. I. Artyukhov, M. Liu and B. I. Ya, Mechanically Induced Metal−Insulator Transition in Carbyne, Nano Lett., 2014, 14, 4224–4229 CrossRef CAS PubMed.
- I. E. Castelli, P. Salvestrini and N. Manini, Mechanical properties of carbynes investigated by ab initio total-energy calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 214110 CrossRef.
- K. Sharma, et al., Anharmonicity and Universal Response of Linear Carbon Chain Mechanical Properties, Phys. Rev. Lett., 2020, 125, 105501 CrossRef CAS PubMed.
- M. Liu, et al., Carbyne from First Principles: Chain of C Atoms, a Nanorod or a Nanorope, ACS Nano, 2013, 7(11), 10075–10082 CrossRef CAS PubMed.
- A. Milani, et al., First-principles calculation of the Peierls distortion in an infinite linear carbon chain: the contribution of Raman spectroscopy, J. Raman Spectrosc., 2008, 39, 164–168 CrossRef CAS.
- Md. M. Haque, et al., Vibrational and NMR properties of polyynes, Carbon, 2011, 49, 3340–3345 CrossRef.
- W. Q. Neves, et al., Effects of pressure on the structural and electronic properties of linear carbon chains encapsulated in double wall carbon nanotubes, Carbon, 2018, 133, 446–456 CrossRef CAS.
- N. F. Andrade, A. L. Aguiar, Y. A. Kim, M. Endo, P. T. C. Freire, G. Brunetto, D. S. Galvao, M. S. Dresselhaus and A. G. Souza Filho, Linear Carbon Chains under High-Pressure Conditions, J. Phys. Chem. C, 2015, 119(19), 10669–10676 CrossRef CAS.
- A. Lucotti, et al., Evidence for Solution-State Nonlinearity of sp-Carbon Chains Based on IR and Raman Spectroscopy: Violation of Mutual Exclusion, J. Am. Chem. Soc., 2009, 131, 4239–4244 CrossRef CAS PubMed.
- Y. H. Hu, Bending Effect of sp-Hybridized Carbon (Carbyne) Chains on Their Structures and Properties, J. Phys. Chem. C, 2011, 115, 1843–1850 CrossRef CAS.
- A. Lucotti, et al., Bent polyynes: ring geometry studied by Raman and IR spectroscopy, J. Raman Spectrosc., 2012, 43, 95–101 CrossRef CAS.
- X. Fan, et al., Atomic Arrangement of Iodine Atoms inside Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2000, 84(20), 4621 CrossRef CAS PubMed.
- L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics Vol 7: Theory and Elasticity, Pergamon Press, 1959 Search PubMed.
- Y. Magnin, et al., Collapse phase diagram of carbon nanotubes with arbitrary number of walls. Collapse modes and macroscopic analog, Carbon, 2021, 178, 552–562 CrossRef CAS.
- T. F. T. Cerqueira, Density-functional tight-binding study of the collapse of carbon nanotubes under hydrostatic pressure, Carbon, 2014, 69, 355–360 CrossRef CAS.
- C. Bousige, et al., Superior carbon nanotube stability by molecular filling:a single chirality study at extreme pressures, Carbon, 2021, 183, 884–892 CrossRef CAS.
- A. C. Torres-Dias, et al., Chirality-dependent mechanical response of empty and water-filled single-wall carbon nanotubes at high pressure, Carbon, 2015, 95, 442–451 CrossRef CAS.
- R. S. Alencar, Raman resonance tuning of quaterthiophene in filled carbon nanotubes at high pressures, Carbon, 2021, 173, 163–173 CrossRef CAS.
- L. Alvarez, et al., High-pressure behavior of polyiodides confined into single-walled carbon nanotubes: A Raman study, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205403 CrossRef.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- K. F. Garrity, et al., Pseudopotentials for high-throughput DFT calculations, Comput. Mater. Sci., 2014, 81, 446 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Baroni, et al., Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematical derivation of the dispersion relation of both chains with one type of bond and two types of bonds; the derivation of the wave equation in the continuum approach; the derivation of the formula for the energy in the continuum approach. See https://doi.org/10.1039/d2na00027j |
| This journal is © The Royal Society of Chemistry 2022 |