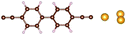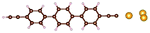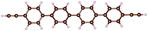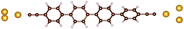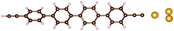Electronic transport through single-molecule oligophenyl-diethynyl junctions with direct gold–carbon bonds formed at low temperature

Abstract

We report on the first systematic transport study of alkynyl-ended oligophenyl-diethynyl (OPA) single-molecule junctions with direct Au–C anchoring scheme at low temperature using the mechanically controlled break junction technique. Through quantitative statistical analysis of opening traces, conductance histograms and density functional theory studies, we identified different types of junctions, classified by their conductance and stretching behavior, for OPA molecules between Au electrodes with two to four phenyl rings. We performed inelastic electron tunneling spectroscopy and observed the excitation of Au–C vibrational modes confirming the existence of Au–C bonds at low temperature and compared the stability of molecule junctions upon mechanical stretching. Our findings reveal the huge potential for future functional molecule transport studies at low temperature using alkynyl endgroups.

---

1. Introduction

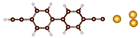
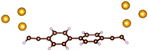
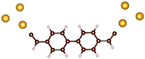
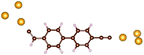
Charge transport studies through different functional molecules with high stability and robustness are key for the development of molecular electronics.^1,2 Usually, the molecule is chemically functionalized with an endgroup responsible for bridging between electrodes and forming single-molecule junctions.^3–6 Endgroups with sufficiently strong bonding, long stretching distance and electronically transparent nature are ideal candidates for molecular electronic devices. To study the in-depth electronic and magnetic transport properties of different functional molecules, the ability to form single-molecule junctions which are stable at low temperature and in vacuum are also of particular interest for choosing endgroups. Thiols (–SH),^7,8 amines (–NH₂),^9–11 cyanides (–CN),⁸ pyridines^4,12 are among the most commonly used endgroups for their coupling strengths and known contact geometries. Recently, there is surging interest on the line of establishing direct gold–carbon (Au–C) covalent bonds to achieve highly conducting molecular junctions.^{13–15,17–21} Initial studies with Au–C bonded single-molecule junctions were observed by Venkataraman's group on methylene terminated oligophenyls and polymethylene chains which shows near resonant transport and enhanced conductance compared to other endgroups.¹³ Hong et al. characterized the (oligo)-phenylene-ethynylene (OPE) derivatives using Raman scattering⁴ and Arasu et al. proposed bipodal platforms based on biphenylene with two Au–C bonds which show very stable and electronically transparent properties of Au–C anchoring scheme.²⁰ The direct Au–C bond formation can be experimentally realized using highly toxic SnMe₃ linkers, which cleave off on contact with Au electrodes^13,14,21 and also with in situ cleavage of trimethylsilyl group attached to alkynyl moiety using tetrabutylammonium fluoride.⁴ Recently, another binding mechanism based on alkynyls forming direct Au–C bonds without the need for any precursors was reported.²² So far, all these experiments have been performed in solution at room temperature. Characterizations with photoemission spectroscopy have shown that it is also possible to form Au–C bonds in ultrahigh vacuum conditions.²³ However, to the best of our knowledge, a detailed characterization of single-molecule junctions with direct Au–C covalent σ bonds at low temperature under vacuum conditions has not been realized so far. Since the Au–C anchoring scheme is already known to be a good alternative for the widely used thiol endgroups in many functional single-molecule studies including thermopower measurements¹⁵ and molecular devices used for spintronic measurements¹⁶ at room temperature, it is important to reveal whether they can be formed under non-standard conditions as well. In particular when long-lived junctions are necessary, low-temperature measurements are helpful. This will also allow to study the junctions' electronic transport and vibrational properties in detail by virtue of the lower thermal noise, thereby providing important information to the identification of the junctions' geometries.

Here we report the first systematic study of single-molecule junctions with Au–C anchoring units at low temperature, down to 4.2 K. We have used oligophenyl-diethynyl molecules with alkynyl endgroups which we denote as OPAn (n = 2, 3, 4); n represents the number of phenyl units as shown in Fig. 1. Since these have been already reported to form molecule junctions at ambient conditions,²² they represent an ideal platform for a comparison of conductance and for further characterization. We find that the resulting molecular junctions are reproducible over several weeks at 4.2 K. Our mechanically controlled break junction (MCBJ) setup at low temperature offers the stability to carry out advanced experiments like inelastic electron tunneling spectroscopy (IETS), which besides the high junction stability requires the high energy resolution provided by the low temperature. Although IETS observations are known for several other anchoring groups,^24–26 an experimental characterization of vibrational modes from single-molecule junctions with Au–C linkers is still unknown. Thus, with the help of IETS at low temperature, we confirmed the excitation of the Au–C vibron modes, as a signature for successful Au–C bond formation and giving insight into the junction characteristics upon stretching by using the variation of different vibrational modes. In order to get a theoretical understanding of the IET spectra, quantum-chemical calculations using density functional theory (DFT) for the isolated molecules and tight-binding density functional theory (DFTB) calculations for both isolated and gold-coordinated molecules were also performed (see computational details in the ESI†).

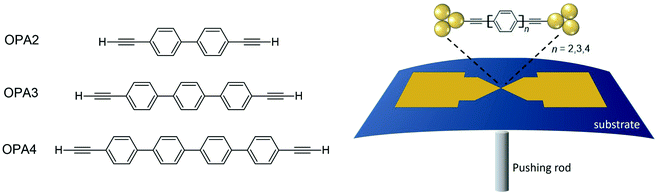Fig. 1 Molecules used for the current study are shown on the left and the mechanically controlled break junction (MCBJ) schematics is shown on the right.

2. Experimental section and characterization measurements

We prepared 5 mM of OPAn molecule solutions using dichloromethane (DCM) as solvent under a nitrogen atmosphere. The detailed NMR characterization of the molecules is given in the ESI.† We observed that the yield of molecular junctions formed with lower concentrations is very small, see Fig. S1 in the ESI.† These freshly prepared molecular solutions were dropcasted at room temperature on a free-standing Au bridge on a bronze substrate fabricated using electron beam lithography and dry etching.^27,28 When brought into contact with Au electrodes, the hydrogen atoms at the outer ends of the molecule cleave off and direct Au–C bond formation can take place.²⁹ This method avoids any need for additional precursors leaving toxic groups in the solution. Single-molecule junctions are formed using the mechanically controllable break junction (MCBJ) technique, a schematic of which is shown in Fig. 1. We dried the samples in nitrogen flow, cooled them down and broke the Au wires in cryogenic vacuum at low temperature by bending the substrate in the MCBJ mechanics. Electrical transport measurements were carried out at 4.2 K. Because of the purely mechanical drive, the opening speed is limited to about one opening trace per ≈10 min, which then limits the maximum number of opening traces that can be recorded in a reasonable time span to a few hundreds. First, we open and close the samples to form Au contacts and molecule junctions repeatedly. The conductance G is measured using the current and voltage ratio at fixed bias voltage across the junctions. The evolution of G during this process is evaluated as a function of displacement between the Au electrodes. From these data, we construct so-called one-dimensional (1D) conductance histograms using logarithmic binning of these opening conductance traces. We used different numbers of bins to calculate the 1D histograms and found that the peak positions are independent of the choice of the bin size (for examples see Fig. S2 in the ESI†).

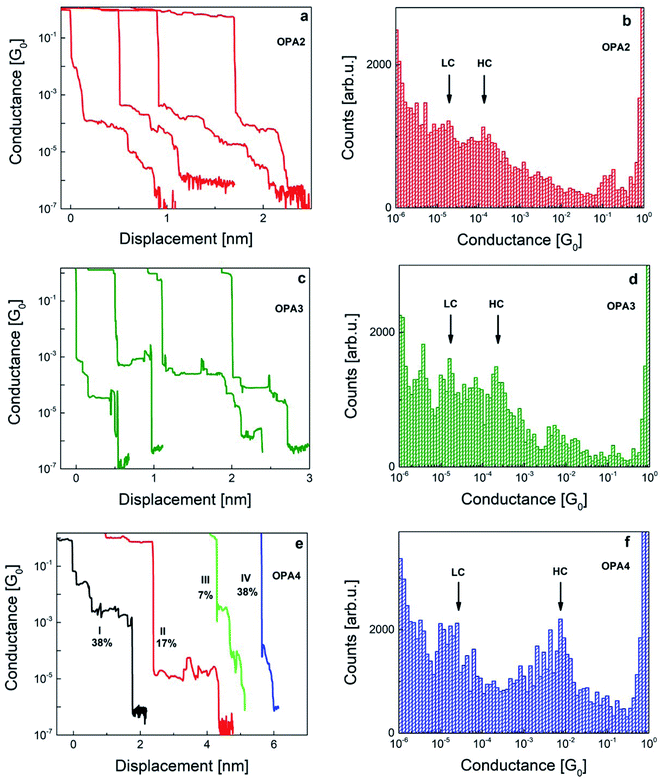
Fig. 2 shows typical individual traces obtained for each species under study. The noise floor of the measurement unit is below 10⁻⁶G₀ with the conductance quantum G₀ = 2e²/h. Au single-atom contacts form on every opening trace confirmed by the plateau formation at 1 G₀. After breaking the Au–Au contacts, we observed conductance plateaus at different G for the different molecules. These plateaus are attributed to molecular junctions formed between the sharp Au electrodes with R–C≡C–H as endgroup where R denotes the rest of the OPAn chain. The length of plateaus increases with molecular length, although there are some exceptions which we will discuss in the next paragraph. Upon further stretching of the junctions, their conductance finally drops to the noise level signaling the breaking of the junction, then forming a vacuum tunneling contact. The molecule junctions are visible on opening traces even after more than one week of measurements from the same device under test. The nominal length of fully stretched Au–OPAn–Au junctions corresponds to 1.2, 1.6 and 2.1 nm, for n = 2, 3, and 4, respectively.²² The uncertainty in the determination of the plateau length in our MCBJ molecular junctions is estimated to be in the order of 30%. We therefore mainly discuss relative length variations between the molecules. In addition, we study the IET spectra of individual junctions by using a lock-in technique in a bias range from −300 to 300 mV and an AC modulation voltage of 3 mV. These measurements also show the robustness of a single junction over longer periods of time. More details and a comparison between the lock-in measured and numerically derived IET spectra (Fig. S4) can be found in the ESI.†

Fig. 2 Examples of opening traces with molecular plateaus and 1D histograms observed for OPA2 (a and b), OPA3 (c and d) and OPA4 (e and f), respectively, measured at low temperature with an applied bias voltage of 100 mV. The displacement is measured as the inter-electrode distance upon stretching the junction. Maxima of histograms are labeled as HC and LC for higher and lower conductance, respectively. The probability of each type of traces observed for OPA4 is also shown. The opening traces in (a, c, and e) are offset horizontally for clarity.

3. Results and analysis

Fig. 2 shows examples of typical opening traces and corresponding 1D histograms obtained from 300–500 traces measured at 100 mV bias voltage applied to OPAn molecules at low temperature. We have labeled maxima with higher conductance as HC and lower conductance as LC in the histograms. Two-dimensional (2D) histograms of the same data are given in Fig. S3 in the ESI.† These histograms are constructed without any data selection.

The opening traces and histograms of all three molecules are in common that they feature multiple steps and peaks, respectively. The peaks are superimposed over a broad background and increasing counts towards small G. The latter was observed already in the room temperature measurements²² which have been recorded with much higher statistics based on several thousand opening traces per species. This observation suggests that the background is an intrinsic property of the Au–OPAn–Au junction formation and not an artefact of the limited number of opening traces available in the present study. Multiple histogram peaks are also known from gold–thiol bonds where they are attributed to different binding patterns of the sulfur atom to a single, a pair or a triangle of Au atoms.³⁰ The histogram background arises from opening traces featuring many small steps and varying conductance, which hints toward multiple possibilities of junction geometries and which we therefore attribute to junctions in which only one end of the molecule is attached via a Au–C bond, while the other one is physisorbed at different positions of the counter electrode. This observation is different from the room-temperature experiments²² in which the background was caused by rather smooth opening traces that were therefore assigned to open junctions. In view of our results we suspect that also those smooth traces might indicate single-bonded junctions, the lifetime of which is, however, too short to give rise to a step in the opening trace. Beside the background signal present for all three species, we also observe marked differences between the species, which we will discuss below.

The majority of the opening traces in OPA2 has flat plateaus near 10⁻⁴G₀ with a length of 0.2–0.5 nm. We have also observed slanted plateaus of length up to 1.5 nm starting at conductance values slightly higher than 10⁻⁴G₀ and decreasing conductance upon stretching before finally breaking to the noise level. We are attributing the latter to the presence of dimerized OPA2 systems in the junctions (OPA2–OPA2) resulting of alkynes homocoupling and the possibility of having a part of the molecule lying over the electrode surfaces as sometimes observed for long molecules.^31–33 The histogram of OPA2 has one shoulder (HC) around 2 × 10⁻⁴G₀ and another (LC) around 3 × 10⁻⁵G₀ (Fig. 2b), similarly to ref. 22 where also two broad peaks were observed the positions of which, however, were depending on the molecular concentration. In addition the histogram shows a peak around 0.2 G₀ which is often observed for short molecules and which might indicate the formation of disordered Au–Au contacts.²⁷

OPA3 shows pronounced flat plateaus between 10⁻³G₀ and 10⁻⁴G₀ of length 0.6 to 1 nm as shown in Fig. 2c. We assign these plateaus to a single OPA3 molecule bridged between Au tips. The conductance of OPA3 molecular plateaus is slightly higher than that of OPA2 which is in agreement with the reported room temperature studies.²² The OPA3 histogram has a maximum near 3.5 × 10⁻⁴G₀ (HC) and the probability of stretched junctions extends until 10⁻⁵G₀ (LC) (Fig. 2d). The molecular yield for OPA3 is 38%. Beside the two maxima labeled as HC and LC, the histogram of OPA3 shows additional peaks at very low conductance (G < 10⁻⁵G₀). Also in ref. 22 the onset of such a low-conductance peak was observed for OPA3 but not discussed. We attribute these to different junction binding configurations and also to the presence of molecular chains of OPA3 units. The latter are also evident from the long plateau length upon stretching towards lower conductance. The probability of these traces is much higher for OPA3 compared to OPA2 and OPA4 thereby leading to a substantial background signal. Finally there is a small maximum around 10⁻²G₀, which by inspection of the individual opening traces can be attributed to very short plateaus in many traces. The assignment of these steps to particular configurations is not straightforward. We argue that multi-molecule contacts could play a role.

Interestingly in the OPA4 histogram, we have observed a peak at unusually high conductance around 7.5 × 10⁻³G₀ which was not observed at room temperature. The second maximum at 3 × 10⁻⁵G₀ which we denote as LC in Fig. 2f occurs at a similar position than the single peak observed at room temperature and which is identified as the most probable conductance of a single-molecule junction. To understand the origin of the unusual HC peak better, we have carried out measurements on multiple samples and statistically evaluated 515 opening traces. We have observed a rich manifold of molecular traces and classified them into four main categories based on the conductance and length of the plateaus and we calculated the percentage of their appearance. Typical examples for each category are shown in Fig. 2e and more individual examples for each category can be found in Fig. S8 in the ESI.† 38% of traces fall into category I having a plateau lengths from 2 to 3 nm and conductance between 10⁻²G₀ and 10⁻³G₀. We suspect that junctions with several molecules aligned in parallel or π–π stacking of molecules give rise to these traces.³⁴ Type II traces are defined as having a conductance around 10⁻⁵G₀ and a plateau length up to 2 nm which agrees with the molecule junction conductance found in previous studies at ambient conditions.²² These are found in 17% abundance in our analysis. Type III traces have flat plateaus both at higher (10⁻³G₀) and lower conductance (10⁻⁵G₀) with a total plateau length around 0.5 nm which occur at a low probability of 7% indicating some molecular junctions which are not well connected to the electrodes and break apart easily upon stretching. Still this category seems to reflect a transition from the plateaus in type I to the ones in type II traces. The last category of traces are slanted plateaus (type IV) starting at 10⁻⁴G₀ which are found with 38% abundance in our study, which we attribute to junctions with molecules chemically bonded to one electrode only. We note that type IV traces are found in measurements of OPA2 and OPA3 as well and contribute to the broad background in the histogram. We have also looked at the evolution of the relative abundance of the various types of traces for OPA4 with time and found no particular trend. This indicates that the different types of traces are not caused by training or aging effects due to the mechanical deformation, but reveal different types of junction geometries or binding schemes which are possible to form under the measurement conditions. To further characterize the exact configuration of each type of traces in both HC and LC regimes, we would require detailed molecular dynamics investigations and quantitative knowledge about the conductance for the different configurations possible within the junction which is beyond the scope of the current study.

Summarizing this study, we observed an increase in the HC conductance as the number of phenyl groups increases which is different from the usual trend of exponential decay of conductance with molecular length for hydrocarbon molecules with off-resonant transport.³⁵ A similar comparison study using acetylene-terminated oligophenylenes in scanning-tunneling-microscope-based break junctions with Au and Ag electrodes also showed a decrease in conductance with molecular length and an even higher conductance for Ag–C than for Au–C bonded junctions.³⁶ The puzzle of the length dependence is resolved by the analysis of the opening traces by which we assigned the LC peak to the single-molecule junction for OPA4, while it is the HC for OPA2 and OPA3. This assignment indicates a non-exponential, but still decreasing conductance with length as was previously found for OPAn junctions at room temperature.²² The authors also noted a pronounced variation of the most probable conductance on the concentration of the molecular solution, suggesting that in their study, the formation of molecule junctions connected in parallel might have played a role. In our case, the higher concentration of molecular solution used may have affected this behavior especially in the case of OPA4, although the junction formation probability was minimal for lower concentration (see Fig. S1 in the ESI†).

We have calculated the transmission spectra of Au–OPAn–Au junctions using DFT in combination with nonequilibrium Green's functions (computational details are given in the ESI†). For the chemical anchoring, the terminal carbon has been positioned in top coordination on the Au (111) electrode surface (Fig. S11 in the ESI†). The corresponding transmission spectra are given in Fig. S12.† The calculated conductance is about 2 orders of magnitude higher than the experimental single-molecule junction peak for the symmetric OPA2, OPA3 and OPA4 junctions, as expected for this level of theory for most stable coordination.^37,38 In order to evaluate the homocoupling that has been observed experimentally in some studies,^32,33 the OPA2–OPA2 junction was also added to the series and turns out to have a conductance value intermediate between OPA3 and OPA4. Thus the possibility of dimerization resulting of alkyne homocoupling cannot be excluded. Such dimerization is surely occurring for OPA3 and for OPA4, but the resulting lengths of the dimeric systems especially for OPA4 diminishes their probability to form molecular junctions via the present MCBJ method.

We provide further evidence for the Au–C linked molecular junctions at low temperature by analyzing the most prominent vibrational modes found in these molecular devices. The IET spectrum is defined as (d²I/dV²) normalized with the differential conductance dI/dV to be able to compare spectra gathered from junctions with different conductance. We measured the spectra over a fixed bias range of −300 mV to 300 mV and symmetrized using the simple formula y = [f(x) − f(−x)]/2, to suppress contributions that might arise from conductance fluctuations or other phenomena, since the IET spectrum is expected to be symmetric. We directly measured IETS for OPA3 and OPA4 junctions with conductance around 10⁻³G₀ using a lock-in amplifier. In the case of OPA2, the IET spectrum was numerically derived from the dI/dV curve of a HC junction, due to the limited lock-in sensitivity in this conductance range (see ESI† for comparison with numerical derivative and lock-in measurement).

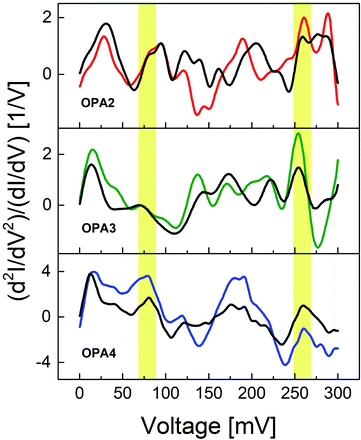
Fig. 3 compares typical examples of experimental and symmetrized IETS from 0–300 mV from a single junction for each OPAn molecule. Previous studies of surface enhanced Raman characterizations on molecular systems involving Au–C covalent bonds determined the Au–C stretch near 46–52 mV.^19,39 Later, Giuseppe et al. using first principle simulations of IETS in metal–molecule junctions, found a signature of the Au–C stretch vibration mode near 60–70 mV.⁴⁰ Our OPAn devices show characteristic bands around 60–75 mV, which we attribute to the longitudinal vibrations of the Au–C bond. This mode is absent in the IETS of thiol-linked diphenylacetylene (tolane) which consists of two phenyl rings connected by a C≡C moiety (Fig. S6 in the ESI†). The C≡C stretching mode is also observed in all our molecular junctions at 250–270 mV (ref. 19) as shown in Fig. 3. In addition to that, we observed the typical Au phonon mode near 10–20 mV,⁴¹ ring breathing near 140–160 mV and typical ring vibrations at 190–220 mV in all molecules.^42–44 We have carried out the IETS measurements on multiple HC junctions and the phonon modes are found to be prevalent even after averaging over all the measured spectra, see Fig. S5 in the ESI.† We have also shown additional examples of individual IETS from OPA3 and OPA4 (Fig. S7 in the ESI†) to show the robustness of these modes across different junctions. This strong signature of Au–C and C≡C vibration modes thus provides a direct evidence for the existence of stable Au–C linked molecular junctions at low temperature. Due to the limited resolution of the IETS at low conductance, we were only able to study the IETS in the HC regime of the OPAn junctions.

Fig. 3 Comparison of experimental inelastic electron tunneling spectra (IETS) for OPA2, OPA3 and OPA4 are shown with red, green and blue curves, respectively. Symmetrized IETS spectra calculated for each molecular junction as y = [f(x) − f(−x)]/2 are shown as black lines in each figure. The yellow regions indicate the typical energies of Au–C vibrons (in 60–75 mV) and of the C≡C stretching mode (250–275 mV).

In order to get a detailed understanding of IETS and the junction configurations, we have also carried out DFT simulations of the density of vibrational states of OPA2 and OPA3 together with the simulated infrared and Raman spectra (Fig. S9†). The vibrational modes are in good agreement with the available experimental data (calculated C≡C stretching mode = 265 meV for the two compounds, IR experimental C≡C frequency = 261 meV for OPA2 and OPA3).⁴⁵ DFT phonon calculations of the entire molecular junctions could not be performed because of excessive memory requirements. DFTB calculations were thus performed. The C≡C stretching modes are slightly overestimated compared to DFT (≈20 meV) mostly because of the optimized C≡C bonds are slightly longer at the DFTB level. Although the overall density of vibrational state spectra is in really good agreement between DFT and DFTB results (Table 1). This supports the validity of the qualitative trends which can be obtained by DFTB. The vibrational study was extended to Au-coordinated molecules by employing a cluster-type model, i.e., by coordinating the terminal carbon atoms to Au₃ clusters. Additionally to a carbon–gold coordination at both ends of the molecule (A), a single coordination to one of the electrodes was also considered (B). Alternative scenarios were considered for OPA2: an arrangement in which the terminal hydrogens do not leave upon binding (C); the same arrangement considering that hydrogen migration occurs to the adjacent carbons (D); a non-symmetrical configuration with case A on one side and case C on the other side (E); single gold-coordination as in case B but considering that the terminal hydrogen would have been removed during the process (F) (Table 1). The geometries of all the arrangements were fully optimized at the DFTB level. The vibrational signature of the Au–C (molecule) binding is calculated in the range 30–50 eV for the whole series, a value probably underestimated (due to the cluster-type model) but in line with IETS results, reinforcing the chemical anchoring scheme. It has to be noted that these low-energy vibrational modes are a collective motion of atoms involving gold atoms and most of the carbon atoms of the molecules. The study of the results in Table 1 reveals that the C≡C bond vibrational modes are lowered by roughly 10 meV when the terminal carbon is substituted by Au₃ (OPAn-A). The Au₃–C≡C vibrational signature is found at roughly 275 meV in this case. The calculated density of vibrational modes of the (OPA2)₂-A system reported in Fig. S10† reveals that this peak is well-separated from the rest of the vibrational modes (same result for OPA3-A and OPA4-A). The experimental IET spectra for the HC regime junctions show essentially this signature.

Table 1 DFTB calculated energies of the characteristic vibrational modes (meV) and their localization for OPA2, OPA2–OPA2, OPA3 and OPA4 molecules and coordinated to two Au₃ clusters at both ends (A), coordinated to one Au₃ cluster (B). DFT energies are given in parenthesis. (DFT-simulated Raman and IR spectra are given in Fig. S8). For OPA2, different scenarios were added (see text)

	Coordination	Molecule length (nm)	Au–C	C≡C	C=C–H
OPA2		1.46	—	283 (265)	—
OPA2-A		1.24	38	275	—
OPA2-B		1.35	26	275, 283	—
OPA2-C		1.39	43	249	—
OPA2-D		1.16	43	—	220
OPA2-E		1.21	48	275	219
OPA2-F		1.25	27	274, 267	—
(OPA2)2		2.84	—	283, 290	—
(OPA2)2-A		3.02	42	275, 290	—
OPA3		1.90	—	283 (265)	—
OPA3-A		1.68	40	275	—
OPA3-B		1.78	37.3	275, 283	—
OPA4		2.32	—	283 (265)	—
OPA4-A		2.11	38	275	—
OPA4-B		2.21	36.5	275, 283	—

---

Interestingly, the IETS of OPA2 in this region shows at least two peaks (Fig. 3). Several scenarios were considered to explain this feature. First, if only one end of the molecule was chemically anchored (case B and F), the calculated vibrational signatures are made of two distinct vibrational C≡C modes separated by less than 10 meV. The presence of the C≡C–H stretching above 400 meV as shown in Fig. S8† would allow to give some hints to this hypothesis but unfortunately this part of the IETS spectrum cannot be accessed experimentally because of stability issues under high bias. Nevertheless, since the IETS were done for the HC regime junctions, the calculated substantial drop in the conductance for single-gold-coordinated systems rule out this possibility.

Ref. 22 dealing with ambient condition MCBJs measurements of the OPAn series suggested the sp²-hybridized carbon to explain the unusual ordering in the conductance when increasing the number of phenyl groups as well as the presence of two distinct preferred conductance values. We performed the vibrational study of the arrangement C, D and E to study this possibility (Table 1). The vibrational signature of a C≡C around 275 meV disappears and the C=C vibrational modes is much lower in energy, 250 meV in case C down to 220 meV for case D and E (in the same region than the phenyl vibrational region). This result does not satisfactorily explain the IETS measurements. We also investigated the possibility of the presence of a dimer OPA2–OPA2 resulting from C–C coupling. As already mentioned, this reaction was observed experimentally for OPA3 on Ag (111) metallic surfaces.⁴⁶ Au is also able to induce the same reaction as recently reported for phenylacetylene homocoupling.³⁸ The (OPA2)₂ vibrational signature in the region around 275 meV consists of two distinct peaks separated by 15 meV and is due to the terminal vibrational motion of the C≡C and the C≡C–C≡C central units of the molecule. This could explain the more structured IETS peaks for some of the experimental OPA2 spectra.

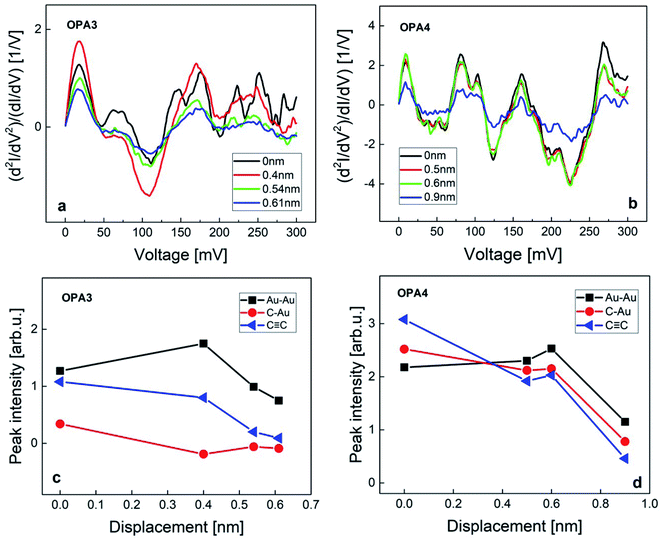
To further study the contact geometries and the evolution of these junctions upon stretching, we have compared the IET spectra from the HC regime of OPA3 and OPA4. Fig. 4 shows the IET spectra measured for increasing stretching distance starting from the initial formation of an OPA3 and OPA4 molecule junction. We have analyzed the changes in peak intensities of the Au–Au, Au–C and C≡C modes upon stretching. For OPA3, the amplitude of the Au–C phonon mode is considerably lower compared to the other modes and to the Au–C mode of the other molecules, (see Fig. S5 in ESI† for comparison of averaged IETS) which suggests only a weak bond, or a bond on only one side may have formed. Upon stretching the junction, we also found that the amplitudes of the Au–C and C≡C modes clearly reduce, supporting this interpretation (Fig. 4). In the case of OPA4, the amplitudes of these vibrational modes are observed to be large compared to other phonon modes until around 0.6 nm. The IET spectra tend to be stable with minimal changes of the Au–C mode and a significant change in the C≡C mode which corroborates the strong bonding between the Au and the end-standing C atom. A drastic decrease in vibrational excitations after this point is assigned to the rupture of the junction. The stretching distance and stability of IETS aligns with the observed average plateau length in our trace analysis. The initial enhancement of the Au phonon mode upon stretching is attributed to the formation of an atomic chain due to weak bonding strength of Au–Au atoms,⁴⁷ as also observed in the Au–thiol junctions.²⁴ These findings further confirm the presence of molecular junctions using Au–C covalent bonding at low temperature. Said that, a detailed future research on the LC regime of these molecules is required to completely understand the nature of bond formation and contact geometries in these systems.

Fig. 4 IETS spectra measured for different stretching displacements in the HC regime of OPA3 (a) and OPA4 (b) molecule junctions. Evolution of peak intensities observed for Au–Au, Au–C and C≡C vibrational modes from the same contact for OPA3 (c) and OPA4 (d) is also shown.

4. Conclusions

To conclude, we have developed single molecular junctions using direct Au–C covalent bonding at low temperature using OPAn chains. The chemical binding between Au and C and the current path through the molecular backbone were proven by a detailed study of the inelastic electron tunneling spectra of single-molecule junctions in combination with a detailed phonon mode analysis using DFT calculations. Both the Au–C vibron mode and the C≡C bands and their development upon stretching the junction provide further evidence to our analysis. We demonstrated the presence of molecular junctions between Au electrodes using conventional conductance histograms revealing several peaks for all molecules corresponding to different binding configurations. The study clearly shows that although all three molecules belong to the same class of molecular wires with the same endgroups, the actually formed junctions can be quite different and may have different formation yield. Although our assignment of certain opening traces to particular junction configurations differs, in particular for the longest molecule OPA4, there are striking similarities between the room temperature and low temperature junction formation, which is not the case for the most common endgroups, amines and thiols in combination with Au electrodes. We thus conclude that the direct Au–C bond formation seems to work similarly at low temperature as at ambient conditions, making this bonding scheme a useful testbed for incorporating and studying functional elements at various conditions. This binding scheme enables studying novel phenomena in single-molecule junctions which occur only at low temperature and that require strong electronic coupling. Our study also demonstrates the importance of the combination of complementary measurement techniques to elucidate the real nature of molecular junctions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank M. Hybertsen, A. Erbe, T. Huhn and the members of the SFB767 discussion group for fruitful interaction and A. Fischer, M. Hagner, S. Haus, J. Maier and R. Sieber for technical support. We acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG – German Research Foundation) through SFB767. Also, we gratefully acknowledge the support of the following institutions: the French “Centre National de la Recherche Scientifique” (CNRS), the University of Rennes 1, the National Fund for Scientific Research (FNRS, Belgium). K. C. and V. D. acknowledge support by the “Grand équipement national de calcul intensif (GENCI)” through HPC resources of CINES, IDRIS and TGCC (grants 2020/2 021-A0080800649/A0100800649). J. C. is a research director of the Belgian National Fund for Scientific Research (FNRS).

References

1. A. Nitzan, Electron Transport in Molecular Wire Junctions, Science, 2003, 300(5624), 1384–1389,  DOI:10.1126/science.1081572.
2. H. Song, M. A. Reed and T. Lee, Single Molecule Electronic Devices, Adv. Mater., 2011, 23(14), 1583–1608,  DOI:10.1002/adma.201004291.
3. V. Kaliginedi, A. Rudnev, P. Moreno-García, M. Baghernejad, C. Huang, W. Hong and T. Wandlowski, Promising Anchoring Groups for Single-Molecule Conductance Measurements, Phys. Chem. Chem. Phys., 2014, 16(43), 23529–23539,  10.1039/c4cp03605k.
4. W. Hong, D. Z. Manrique, P. Moreno-García, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, Single Molecular Conductance of Tolanes: Experimental and Theoretical Study on the Junction Evolution Dependent on the Anchoring Group, J. Am. Chem. Soc., 2012, 134(4), 2292–2304,  DOI:10.1021/ja209844r.
5. F. Chen, X. Li, J. Hihath, Z. Huang and N. Tao, Effect of Anchoring Groups on Single-Molecule Conductance: Comparative Study of Thiol-, Amine-, and Carboxylic-Acid-Terminated Molecules, J. Am. Chem. Soc., 2006, 128(49), 15874–15881,  DOI:10.1021/ja065864k.
6. T. Hines, I. Díez-Pérez, H. Nakamura, T. Shimazaki, Y. Asai and N. Tao, Controlling Formation of Single-Molecule Junctions by Electrochemical Reduction of Diazonium Terminal Groups, J. Am. Chem. Soc., 2013, 135(9), 3319–3322,  DOI:10.1021/ja3106434.
7. Z. Huang, F. Chen, P. A. Bennett and N. Tao, Single Molecule Junctions Formed via Au-Thiol Contact: Stability and Breakdown Mechanism, J. Am. Chem. Soc., 2007, 129(43), 13225–13231,  DOI:10.1021/ja074456t.
8. L. A. Zotti, T. Kirchner, J. C. Cuevas, F. Pauly, T. Huhn, E. Scheer and A. Erbe, Revealing the Role of Anchoring Groups in the Electrical Conduction through Single-Molecule Junctions, Small, 2010, 6(14), 1529–1535,  DOI:10.1002/smll.200902227.
9. L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Single-Molecule Circuits with Well-Defined Molecular Conductance, Nano Lett., 2006, 6(3), 458–462,  DOI:10.1021/nl052373.
10. S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Amine - Gold Linked Single-Molecule Circuits: Experiment and Theory, Nano Lett., 2007, 7(11), 3477–3482,  DOI:10.1021/nl072058i.
11. M. S. Hybertsen, L. Venkataraman, J. E. Klare, A. C. Whalley, M. L. Steigerwald and C. Nuckolls, Amine-Linked Single-Molecule Circuits: Systematic Trends across Molecular Families, J. Phys.: Condens. Matter, 2008, 20(37), 374115,  DOI:10.1088/0953-8984/20/37/374115.
12. E. S. Tam, J. J. Parks, W. W. Shum, Y. W. Zhong, M. B. Santiago-Berríos, X. Zheng, W. Yang, G. K. L. Chan, H. D. Abruña and D. C. Ralph, Single-Molecule Conductance of Pyridine-Terminated Dithienylethene Switch Molecules, ACS Nano, 2011, 5(6), 5115–5123,  DOI:10.1021/nn201199b.
13. Z. L. Cheng, R. Skouta, H. Vazquez, J. R. Widawsky, S. Schneebeli, W. Chen, M. S. Hybertsen, R. Breslow and L. Venkataraman, In situ Formation of Highly Conducting Covalent Au-C Contacts for Single-Molecule Junctions, Nat. Nanotechnol., 2011, 6(6), 353–357,  DOI:10.1038/nnano.2011.66.
14. W. Chen, J. R. Widawsky, H. Vázquez, S. T. Schneebeli, M. S. Hybertsen, R. Breslow and L. Venkataraman, Highly Conducting π-Conjugated Molecular Junctions Covalently Bonded to Gold Electrodes, J. Am. Chem. Soc., 2011, 133(43), 17160–17163,  DOI:10.1021/ja208020j.
15. J. R. Widawsky, W. Chen, H. Vázquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Length-Dependent Thermopower of Highly Conducting Au-C Bonded Single Molecule Junctions, Nano Lett., 2013, 13(6), 2889–2894,  DOI:10.1021/nl4012276.
16. F. Bejarano, I. J. Olavarria-Contreras, A. Droghetti, I. Rungger, A. Rudnev, D. Gutiérrez, M. Mas-Torrent, J. Veciana, H. S. J. Van Der Zant, C. Rovira, E. Burzurĺ and N. Crivillers, Robust Organic Radical Molecular Junctions Using Acetylene Terminated Groups for C-Au Bond Formation, J. Am. Chem. Soc., 2018, 140(5), 1691–1696,  DOI:10.1021/jacs.7b10019.
17. P. Pla-Vilanova, A. C. Aragonès, S. Ciampi, F. Sanz, N. Darwish and I. Diez-Perez, The Spontaneous Formation of Single-Molecule Junctions via Terminal Alkynes, Nanotechnology, 2015, 26(38), 381001,  DOI:10.1088/0957-4484/26/38/381001.
18. A. M. Ricci, E. J. Calvo, S. Martin and R. J. Nichols, Electrochemical Scanning Tunneling Spectroscopy of Redox-Active Molecules Bound by Au-C Bonds, J. Am. Chem. Soc., 2010, 132(8), 2494–2495,  DOI:10.1021/ja907867b.
19. W. Hong, H. Li, S. X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, Trimethylsilyl-Terminated Oligo(Phenylene Ethynylene)s: An Approach to Single-Molecule Junctions with Covalent Au-C σ-Bonds, J. Am. Chem. Soc., 2012, 134(47), 19425–19431,  DOI:10.1021/ja307544w.
20. N. P. Arasu and H. Vázquez, Direct Au-C Contacts Based on Biphenylene for Single Molecule Circuits, Phys. Chem. Chem. Phys., 2018, 20(15), 10378–10383,  10.1039/c8cp00613j.
21. F. Schwarz, G. Kastlunger, F. Lissel, H. Riel, K. Venkatesan, H. Berke, R. Stadler and E. Lörtscher, High-Conductive Organometallic Molecular Wires with Delocalized Electron Systems Strongly Coupled to Metal Electrodes, Nano Lett., 2014, 14(10), 5932–5940,  DOI:10.1021/nl5029045.
22. I. J. Olavarria-Contreras, M. L. Perrin, Z. Chen, S. Klyatskaya, M. Ruben and H. S. J. van der Zant, C-Au Covalently Bonded Molecular Junctions Using Nonprotected Alkynyl Anchoring Groups, J. Am. Chem. Soc., 2016, 138(27), 8465–8469,  DOI:10.1021/jacs.6b03383.
23. A. Batra, G. Kladnik, N. Gorjizadeh, M. Steigerwald, C. Nuckolls, S. Y. Quek, D. Cvetko, A. Morgante and L. Venkataraman, Trimethyltin-Mediated Covalent Gold-Carbon Bond Formation, J. Am. Chem. Soc., 2014, 136(36), 12556–12559,  DOI:10.1021/ja5061406.
24. Y. Kim, H. Song, F. Strigl, H. F. Pernau, T. Lee and E. Scheer, Conductance and Vibrational States of Single-Molecule Junctions Controlled by Mechanical Stretching and Material Variation, Phys. Rev. Lett., 2011, 106(19), 2–5,  DOI:10.1103/PhysRevLett.106.196804.
25. J. G. Kushmerick, J. Lazorcik, C. H. Patterson, R. Shashidnar, D. S. Seferos and G. C. Bazan, Vibronic Contributions to Charge Transport across Molecular Junctions, Nano Lett., 2004, 4(4), 639–642,  DOI:10.1021/nl049871n.
26. Y. Kim, T. J. Hellmuth, M. Bürkle, F. Pauly and E. Scheer, Characteristics of Amine-Ended and Thiol-Ended Alkane Single-Molecule Junctions Revealed by Inelastic Electron Tunneling Spectroscopy, ACS Nano, 2011, 5(5), 4104–4111,  DOI:10.1021/nn200759s.
27. T. Böhler, A. Edtbauer and E. Scheer, Conductance of Individual C₆₀ Molecules Measured with Controllable Gold Electrodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(12), 1–5,  DOI:10.1103/PhysRevB.76.125432.
28. T. Böhler, J. Grebing, A. Mayer-Gindner, H. V. Löhneysen and E. Scheer, Mechanically Controllable Break-Junctions for Use as Electrodes for Molecular Electronics, Nanotechnology, 2004, 15(7), S465,  DOI:10.1088/0957-4484/15/7/054.
29. P. Maity, S. Takano, S. Yamazoe, T. Wakabayashi and T. Tsukuda, Binding Motif of Terminal Alkynes on Gold Clusters, J. Am. Chem. Soc., 2013, 135(25), 9450–9457,  DOI:10.1021/ja401798z.
30. C. Li, M. Chen, I. Pobelov, T. Wandlowski, A. Bagrets, A. Arnold and F. Evers, Charge Transport in Single Au–Alkanedithiol–Au Junctions: Coordination Geometries and Conformational Degrees of Freedom, J. Am. Chem. Soc., 2008, 130(1), 318–326,  DOI:10.1021/ja0762386.
31. S. Martín, I. Grace, M. R. Bryce, C. Wang, R. Jitchati, A. S. Batsanov, S. J. Higgins, C. J. Lambert and R. J. Nichols, Identifying Diversity in Nanoscale Electrical Break Junctions, J. Am. Chem. Soc., 2010, 132(26), 9157–9164,  DOI:10.1021/ja103327f.
32. B. Cirera, Y. Q. Zhang, J. Björk, S. Klyatskaya, Z. Chen, M. Ruben, J. V. Barth and F. Klappenberger, Synthesis of Extended Graphdiyne Wires by Vicinal Surface Templating, Nano Lett., 2014, 14(4), 1891–1897,  DOI:10.1021/nl4046747.
33. F. Mohammadparast, A. P. Dadgar, R. T. A. Tirumala, S. Mohammad, C. O. Topal, A. K. Kalkan and M. Andiappan, C-C Coupling Reactions Catalyzed by Gold Nanoparticles: Evidence for Substrate-Mediated Leaching of Surface Atoms Using Localized Surface Plasmon Resonance Spectroscopy, J. Phys. Chem. C, 2019, 123(18), 11539–11545,  DOI:10.1021/acs.jpcc.8b12453.
34. T. Fu, S. Smith, M. Camarasa-Gómez, X. Yu, J. Xue, C. Nuckolls, F. Evers, L. Venkataraman and S. Wei, Enhanced Coupling through π-Stacking in Imidazole-Based Molecular Junctions, Chem. Sci., 2019, 10(43), 9998–10002,  10.1039/c9sc03760h.
35. S. Y. Quek, H. J. Choi, S. G. Louie and J. B. Neaton, Length Dependence of Conductance in Aromatic Single-Molecule Junctions, Nano Lett., 2009, 9(11), 3949–3953,  DOI:10.1021/nl9021336.
36. S. Li, H. Yu, X. Chen, A. A. Gewirth, J. S. Moore and C. M. Schroeder, Covalent Ag-C Bonding Contacts from Unprotected Terminal Acetylenes for Molecular Junctions, Nano Lett., 2020, 20(7), 5490–5495,  DOI:10.1021/acs.nanolett.0c02015.
37. V. K. Kanuru, G. Kyriakou, S. K. Beaumont, A. C. Papageorgiou, D. J. Watson and R. M. Lambert, Sonogashira Coupling on an Extended Gold Surface in vacuo: Reaction of Phenylacetylene with Iodobenzene on Au(111), J. Am. Chem. Soc., 2010, 132(23), 8081–8086,  DOI:10.1021/ja1011542.
38. C. Sánchez-Sánchez, F. Yubero, A. R. González-Elipe, L. Feria, J. F. Sanz and R. M. Lambert, The Flexible Surface Revisited: Adsorbate-Induced Reconstruction, Homocoupling, and Sonogashira Cross-Coupling on the Au(100) Surface, J. Phys. Chem. C, 2014, 118(22), 11677–11684,  DOI:10.1021/jp501321u.
39. L. Laurentius, S. R. Stoyanov, S. Gusarov, A. Kovalenko, R. Du, G. P. Lopinski and M. T. McDermott, Diazonium-Derived Aryl Films on Gold Nanoparticles: Evidence for a Carbon–Gold Covalent Bond, ACS Nano, 2011, 5(5), 4219–4227,  DOI:10.1021/nn201110r.
40. G. Foti, H. Vázquez, D. Sánchez-Portal, A. Arnau and T. Frederiksen, Identifying Highly Conducting Au-C Links through Inelastic Electron Tunneling Spectroscopy, J. Phys. Chem. C, 2014, 118(46), 27106–27112,  DOI:10.1021/jp5077824.
41. T. Frederiksen, M. Paulsson, M. Brandbyge and A. P. Jauho, Inelastic Transport Theory from First Principles: Methodology and Application to Nanoscale Devices, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(20), 1–22,  DOI:10.1103/PhysRevB.75.205413.
42. C. R. Arroyo, T. Frederiksen, G. Rubio-Bollinger, M. Vélez, A. Arnau, D. Sánchez-Portal and N. Agraït, Characterization of Single-Molecule Pentanedithiol Junctions by Inelastic Electron Tunneling Spectroscopy and First-Principles Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(7), 4–8,  DOI:10.1103/PhysRevB.81.075405.
43. M. Kula, J. Jiang and Y. Luo, Probing Molecule-Metal Bonding in Molecular Junctions by Inelastic Electron Tunneling Spectroscopy, Nano Lett., 2006, 6(8), 1693–1698,  DOI:10.1021/nl060951w.
44. M. Paulsson, T. Frederiksen and M. Brandbyge, Inelastic Transport through Molecules: Comparing First-Principles Calculations to Experiments, Nano Lett., 2006, 6(2), 258–262,  DOI:10.1021/nl052224r.
45. L. Liu, Z. Liu, W. Xu, H. Xu, D. Zhang and D. Zhu, Syntheses, Optical and Electrochemical Properties of 4,4′-Bis-[2-(3,4-Dibutyl-2-Thienylethynyl)] Biphenyl and Its Oligomers, Tetrahedron, 2005, 61(15), 3813–3817,  DOI:10.1016/j.tet.2005.01.133.
46. C. Sánchez-Sánchez, N. Orozco, J. P. Holgado, S. K. Beaumont, G. Kyriakou, D. J. Watson, A. R. Gonzalez-Elipe, L. Feria, J. Fernández Sanz and R. M. Lambert, Sonogashira Cross-Coupling and Homocoupling on a Silver Surface: Chlorobenzene and Phenylacetylene on Ag(100), J. Am. Chem. Soc., 2015, 137(2), 940–947,  DOI:10.1021/ja5115584.
47. N. Agraït, C. Untiedt, G. Rubio-Bollinger and S. Vieira, Onset of Energy Dissipation in Ballistic Atomic Wires, Phys. Rev. Lett., 2002, 88(21), 4,  DOI:10.1103/PhysRevLett.88.216803.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00650a

---