Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Engineering plastic phase transitions via solid solutions: the case of “reordering frustration” in ionic plastic crystals of hydroxyquinuclidinium salts†
Samet
Ocak
a,
Rebecca
Birolo
b,
Gianluca
Carì
a,
Simone
Bordignon
b,
Michele R.
Chierotti
 *b,
Dario
Braga
*b,
Dario
Braga
 a,
Roberto
Gobetto
a,
Roberto
Gobetto
 b,
Tommaso
Salzillo
b,
Tommaso
Salzillo
 *cd,
Elisabetta
Venuti
*cd,
Elisabetta
Venuti
 c,
Omer
Yaffe
c,
Omer
Yaffe
 d and
Simone
d'Agostino
d and
Simone
d'Agostino
 *a
*a
aDepartment of Chemistry “Giacomo Ciamician”, The University of Bologna, Via F. Selmi, 2, 40126 Bologna, Italy. E-mail: simone.dagostino2@unibo.it
bDepartment of Chemistry and NIS Centre, The University of Turin, Via P. Giuria 7, 10125 Torino, Italy. E-mail: michele.chierotti@unito.it
cDepartment of Industrial Chemistry “Toso Montanari”, The University of Bologna, Viale del Risorgimento 4, 40124, Bologna, Italy. E-mail: tommaso.salzillo@unibo.it
dDepartment of Chemical and Biological Physics, Weizmann Institute of Science, Rehovot 76100, Israel
First published on 13th May 2022
Abstract
A family of salts of R-(+)-(3)-hydroxyquinuclidinium [QH]+, with SO42−, BPh4−, BF4− and PF6− counter-anions, have been prepared by the metathesis of [QH]Cl and metal salts of the corresponding anions. Solid solutions of formula [QH](PF6)x(BF4)1−x for x = 0.9, 0.8, 0.7 have also been obtained. The crystalline materials have been investigated by a combination of solid-state techniques, including variable temperature XRD, thermal analyses, multinuclear (11B, 13C, 15N, 19F, and 31P) solid-state NMR spectroscopy, variable temperature wideline 19F T1 relaxation measurements, and micro-Raman spectroscopy to investigate their thermal stability and phase transition behaviors. It has been shown that the salts [QH]PF6 and [QH]BF4 undergo an order–disorder solid–solid phase transition to plastic phases, whereas [QH]2SO4·H2O and [QH]BPh4 do not display any plastic phase transition. Doping [QH]BF4 into the [QH]PF6 lattice up to 30% results in the formation of a solid solution that is plastic in an expanded thermal range, thanks to a phenomenon that we describe here for the first time as “reordering frustration”.
Design, System, ApplicationIonic plastic crystalline materials (IPCs) are being actively explored for their potential applications in batteries, NLO, and solid-state electrolytes in fuel cells. IPCs feature long-range crystalline order while their components remain disordered locally, providing, thus, diffusion of ions through an otherwise rigid crystal typical of ordered structures. Upon applying a suitable stimulus (pressure or heating), it is possible to “switch” between the static and dynamic states. The primary strategy for achieving fine control over the transition temperature and type relies on ionic metathesis to replace anions or cations, whereas, a new one based on the formation of crystalline solid-solutions can be exploited. In this work we study the effect that various combinations of cation and anions have on plastic transitions, as well as the possibility of obtaining control over the transitions thanks to solid solutions. Interestingly, solid-solution “kills” the reversible transition and makes the solids permanently disordered. Thus, the system experiences an effect described here as reordering frustration. We believe that this work can potentially contribute to developing solid-state electrolytes working on a broader range of temperatures. |
1. Introduction
Plastic crystals (PCs) are materials characterized by long-range crystalline order while their components remain disordered locally.1–4 Most chemical species of spherical, cylindrical, and disk-like shapes5–11 are prone to display reorientation processes around their center of mass when they feature low steric hindrance within the crystal packing, giving thus plastic phases.1,12 This often results in high mechanical plasticity;13 hence, the term “plastic crystal” introduced by Timmermans12 many decades ago. Depending on the nature of the components (molecules or ions), PCs further divide into two broad families, namely neutral and ionic plastic crystals.1,2 Studies on PCs show that they undergo at least one solid–solid transition, from an ordered, or static (glassy), to a dynamically disordered (plastic) phase and vice versa, upon applying a suitable stimulus, i.e., pressure or heating,1,12,14,15 (see Scheme 1). In general, plastic phases tend to display highly symmetrical crystal lattices such as cubic or hexagonal.12,16 However, it remains somewhat challenging to predict a priori which combination of molecules, or ions might generate systems able to give plastic phases.In the last decades, PCs have received much attention in the fields of materials for electronics,17–21 magnetics,16,22 barocalorics,23–25 and non-linear optics,26 owing to the potentiality arising from their remarkable properties.
In particular, ionic PCs stand out as potential candidates for solid-state electrolytes in fuel cells, batteries, and capacitors since they have thermal stability, neglectable volatility, and extraordinary plasticity that decreases the contact problems between electrolyte and electrodes during volume changes.1,27,28 Moreover, they exhibit assessable ionic conductivities in the solid state activated by the reorientational motions of molecules and ions.5,29
The main strategies currently in use to realize ionic PCs rely either on acid–base reactions or on ionic metathesis to replace anions or cations. The size and symmetry effect of the counter-anion on this matter has been discussed by Mochida et al.16 and Makhlooghiazad et al.30,31 It is mentioned that, for a given cation, the transition temperature decreases with increasing anion size.
Another way to obtain ionic PCs is from crystalline solid solutions32–34 with components mutually miscible and fulfilling the prerequisite conditions for forming a solid solution proposed by Kitaigorodsky.34 The potential of solid solutions as a tool for modifying the physicochemical properties of materials has been recently highlighted in several studies, and among others modulation of the thermosalient effect,35 enantioselectivity,36–38 polymorphic transition,39,40 and melting point34,41,42 have been reported.
Concerning PCs, this approach would offer, in principle, also the possibility of achieving a fine control over the temperature and type of transition.43–47 Notwithstanding the great potential, no systematic and detailed investigations have been carried out on the relationships between PCs and solid solutions, and the way they can affect the transition temperature and type, hence the need to pursue research in this direction.
The aim of this work was essentially twofold. First, we were interested in investigating the counter-anion dependence of the plastic phase transitions in a series of R-(+)-(3)-hydroxyquinuclidinium salts [QH]X. By varying size, shape, and charge of the anion, we expected to obtain different behaviors in terms of plastic phase transition and type. Second, we wanted to explore the possibility of preparing crystalline solid solutions, studying how the composition of the resulting materials further affects the phase transition compared to the pure parent systems.
To this end, we synthesized a series of [QH]X salts with various counter-anions, including the tetrahedral anions sulfate (SO42−), tetraphenylborate (BPh4−), tetrafluoroborate (BF4−), and the octahedral hexafluorophosphate (PF6−), see Scheme 2, by the metathesis of [QH]Cl using metal salts of the corresponding anions. A combination of solid-state techniques, including variable temperature XRD, thermal analyses, multinuclear (11B, 13C, 15N, 19F and 31P) solid-state NMR spectroscopy, variable temperature wideline 19F T1 relaxation measurements and micro-Raman spectroscopy, was used to elucidate crystal structures and phase transition behavior of the so-obtained materials.
 | ||
| Scheme 2 Molecular structures of the ions chosen as components for the preparation of [QH]X salts and binary crystalline solid solutions. | ||
All reactions afforded the desired products as anhydrous salts of general formula [QH]X (X = BPh4−, PF6− and BF4−), except for the sulfate, which was instead obtained as mono-hydrate, [QH]2SO4·H2O. The latter salt was also the only one obtained as a polycrystalline powder, and its structure was solved from powder diffraction data. It is also the only system not showing structural changes, with the exception of a reversible dehydration/rehydration process following the heating/cooling cycle. In [QH]BPh4, the [QH]+ cation was found to undergo a reorientational flip-flop motion over two positions, and that could be frozen out on lowering the temperature at approximately 100 K via a second-order transition.
On the other hand, the [QH]BF4 and [QH]PF6 salts exhibit reversible transitions at or above room temperature (TC = 308 and 298 K, respectively), affording genuine and highly symmetrical plastic phases.
To achieve a fine control over the transition temperature, we explored the possibility of obtaining binary solid solutions of these latter two salts by applying the crystal engineering principles.48–50 Unlike other similar reported systems,43–45 [QH]PF6 and [QH]BF4 lattices did not result fully miscible as they afforded stable binary solid solutions [QH](PF6)x(BF4)1−x only for x = 0.9, 0.8, 0.7; other molar fractions with x < 0.7 gave deliquescent materials.
The most remarkable finding, however, was the observation that the solid solutions were already in their plastic phase at RT, and no transition to ordered or semi ordered, namely a structure that feature disorder only for one component (anion or cation), phases was detected on lowering the temperature.
This behavior was unexpected and could be interpreted as a direct consequence of the parent compounds' structural diversity of the anions, their non-isomorphism, and ion mobility, which is not enough to allow complete anion migration within the crystal. These factors prevent the solid solutions from rearranging either to the respective parent compounds lattices, eventually separating out, or to a new phase in which BF4− and PF6− would occupy well-defined crystallographic positions. In fact, this appears to leave the system permanently disordered and experiencing, as a consequence, a sort of reordering frustration, and, to the best of this authors' knowledge, the [QH](PF6)x(BF4)1−x (x > 0.7) system represents the first example of a crystalline material with a relatively simple composition showing such a behavior.
Variable temperature (VT) solid-state NMR and micro-Raman measurements were instrumental for the elucidation of the dynamics within the materials. VT 19F T1 relaxation profiles, as well as the extracted activation energies, are in perfect agreement with the results obtained from other techniques: the reversible phase transition of [QH]PF6 and [QH]BF4 salts is detected, while no change in mobility for the [QH](PF6)0.9 (BF4)0.1 binary solution is observed.
VT micro-Raman measurements confirm the absence of the typical disordered–ordered or disordered-semi ordered phase transitions which characterize the plastic crystals. The band broadening of the molecular vibrations of the anion and cation, evidence of the reorientational motion, remains substantially unaltered even at 80 K in the solid solution, while the pure system [QH]PF6 undergoes a reversible disordered-semi ordered phase transition with high hysteresis close to ambient conditions.
2. Experimental
Synthesis
All reactants and reagents were purchased from Sigma-Aldrich and used without further purification. Reagent grade solvents and bi-distilled water were used.The salts [QH]2SO4·H2O, [QH]PF6, and [QH]BF4 were obtained using the same procedure, based on the anion exchange reaction between the (R)-3-hydroxlyquinuclidinol hydrochloride, [QH]Cl, and the appropriate halide abstraction reagent (Ag2SO4, AgPF6, and AgBF4). In a typical procedure, 100 mg (0.06 mmol) of [QH]Cl was dissolved in a beaker with 3 mL of the appropriate solvent (both ethanol or water equally work) and left under stirring at RT. Then, the stoichiometric amount of halide abstraction reagent was dissolved in another beaker with ca. 3 mL of solvent, the resulting solution was added dropwise to the solution of [QH]Cl and left under stirring until the byproduct AgCl crashed out from the solution. The precipitates were filtered off, and the resulting solutions were left to slowly evaporate to afford the growth of diffraction quality crystals of the desired products, see Table S1.† The salt [QH]BPh4 was synthesized via a modification of the procedure reported above, 100 mg (0.06 mmol) of [QH]Cl was dissolved under stirring at RT in 3 mL of H2O, then a stoichiometric amount of NaBPh4 was added dropwise. The resulting solution was left under stirring and afforded the desired product as a white precipitate which was recovered via suction filtration and washed abundantly with water (10 × 2 mL). Slow evaporation at RT of dimethylformamide (DMF) solution afforded diffraction quality crystals of [QH]BPh4. For the preparation of the binary solid solutions [QH](PF6)x(BF4)1−x (x = 0.9, 0.8, 0.7) the same procedure was applied. The reactants AgPF6 and AgBF4 were weighed in the proper stoichiometric ratio (see Table S1†), dissolved in ca. 5 mL of water and added to 100 mg (0.06 mmol) of [QH]Cl. The white precipitate was removed, and the resulting solutions were left to slowly evaporate at RT. Polycrystalline samples were obtained upon complete evaporation of the solvent. The stoichiometric ratio of the binary solid solution [QH](PF6)0.9(BF4)0.1 was confirmed by 19F direct excitation SSNMR (see below). Integration of the signals at 69.7 ppm (PF6) and −149.8 ppm (BF4−) yields a ratio of 0.93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.07. The composition of the corresponding sample is, thus, reasonably approximated as [QH](PF6)0.9(BF4)0.1.
0.07. The composition of the corresponding sample is, thus, reasonably approximated as [QH](PF6)0.9(BF4)0.1.
Single crystal X-ray diffraction (SCXRD)
Single-crystal data for all salts (except [QH]2SO4·H2O, whose structure was solved from powder XRD data; see below) were collected on an Oxford X'Calibur S CCD diffractometer equipped with a graphite monochromator (Mo-Kα radiation, λ = 0.71073 Å) and with a cryostat Oxford CryoStream800. Subsequent structure solution and refinement were performed using the HKLF4 file containing non-overlapped reflections. The structures were solved by intrinsic phasing with SHELXT51 and refined on F2 by full-matrix least squares refinement with SHELXL52 implemented in the Olex2 software.53 All non-hydrogen atoms were refined anisotropically applying the rigid-body RIGU restraint.54 HOH and HNH atoms were either directly located or, when not possible, added in calculated positions; HCH atoms for all compounds were added in calculated positions and refined riding on their respective carbon atoms. Data collection and refinement details are listed in Table S2.† The Mercury55 program was used to calculate intermolecular interactions and for molecular graphics. CCDC numbers 2155973–2155977.For ϕ-scan experiments, a fresh single crystal specimen of [QH]PF6 was selected and mounted on the diffractometer. Goniometer angles (θ, k, ω, ϕ) were set at 0° and detector distance at 45 mm, and then ϕ was moved by 1° during the exposure time (20 s). Unit cell determinations at RT and 320 K were performed and corresponded to those of the salt [QH]PF6 at RT and HT, respectively.
Powder X-ray diffraction (PXRD)
For phase identification and variable temperature X-ray powder diffraction purposes, measurements were performed on a PANalytical X'Pert Pro automated diffractometer equipped with an X'Celerator detector in Bragg–Brentano geometry, using Cu-Kα radiation (λ = 1.5418 Å) without monochromator in the 2θ range between 3° and 50° (continuous scan mode, step size 0.0167°, counting time 19.685 s, soller slit 0.04 rad, antiscatter slit 1/2, divergence slit 1/4, 40 mA 40 kV) and with an Anton-Paar TTK 450 + LNC. The program Mercury55 was used for the calculation of powder XRD patterns on the basis of single-crystal data collected in this work. Chemical and structural identities between bulk materials and single crystals were always verified by comparing experimental and calculated powder diffraction patterns. For Pawley refinement and structural solution from powder data purposes, diffractograms in the 2θ range 3–70° (step size, 0.026°; time/step, 200 s; 0.02 rad soller; V × A 40 × 40) were collected on a Panalytical X'Pert PRO automated diffractometer equipped with a PIXcel detector in transmission geometry (capillary spinner), using Cu-Kα radiation (λ = 1.5418 Å) without monochromator in the 2θ range between 3° and 70° (continuous scan mode, step size 0.0260°, counting time 889.70 s, soller slit 0.02, antiscatter slit ¼, divergence slit ¼, 40 mA × 40 kV). 6 patterns were recorded and summed to enhance the signal to noise ratio. For Pawley refinements, diffractograms were analyzed with the software TOPAS4.56 For the structural solution of [QH]2SO4·H2O, powder diffraction data were analyzed with the software EXPO2014,57 which is designed to analyze both monochromatic and non-monochromatic data. Selected peaks were chosen in the 2θ range 5–50°, and a monoclinic cell (see Table S2†) was found using the algorithm N-TREOR09.58 The structure was solved by simulated annealing employing fragments retrieved from the CCDC,59 and refined as a rigid body with the software EXPO2014.57 A shifted Chebyshev function with 10 parameters and a Pearson VII function were used to fit background and peak shape, respectively. An overall thermal parameter for all the atoms was adopted. Refinement converged with GOF = 1.2, Rwp = 6.9%, Rp = 5.3%. See Fig. S1† for the pattern difference plot.Thermogravimetric analysis (TGA)
TGA analyses were performed with a PerkinElmer TGA-7. Each sample, contained in a platinum crucible, was heated in a nitrogen flow (20 cm3 min−1) at a rate of 5 K min−1, up to decomposition. Samples weights were in the range 5–10 mg.Differential scanning calorimetry (DSC)
Calorimetric measurements were performed with a PerkinElmer DSC-7 equipped with a PII intracooler. Temperature and enthalpy calibrations were performed using high-purity standards (n-decane, benzene, and indium). Heating of the aluminum open pans containing the samples (3–5 mg) was carried out at 5 K min−1 in the temperature range 243–473 K under N2 atmosphere. Entropy changes were estimated by dividing the enthalpy changes by the transition temperature.Hot stage and cross-polarized optical microscopy (HSM-CP)
Hot stage experiments were carried out using a Linkam TMS94 device connected to a Linkam LTS350 platinum plate and equipped with polarizing filters. Images were collected with a NIKON DS FI3 camera, from an Olympus BX41 stereomicroscope.Solid-state NMR (SSNMR)
Raman spectroscopy
Raman measurements were performed with a custom-built system based on a 1000 mm focal length Horiba FHR-1000 dispersive spectrometer. Ultra-low frequency (ULF) range was reached by using in the optical setup notch filters from ONDAX allowing the access till the THz region (<150 cm−1). Excitation was provided from a 632.8 nm He–Ne gas laser, a wavelength with enough lower energy to avoid the electronic excitation of the system and with a nominal power of 35 mW. Neutral optical density filters were used to reduce the impinging power at less than 1 mW to avoid sample damage. The laser was focused on the sample by an optical microscope Zeiss Axio equipped with a long-distance 50× objective which allow a nominal spatial resolution of about 2 microns. The combination of the 632.8 nm excitation line, the use of a holographic grating with 1800 gr mm−1 coupled with a 1024 × 256 pixels CCD detector gave a maximum spectral resolution just below 1 cm−1. Variable temperature Raman spectra were collected by Janis ST-500 continuous flow microscopy cryostat between 403 K and liquid nitrogen temperature in inert atmosphere conditions heating and cooling with a 2 K min−1 rate.3. Results and discussion
The following section has been organized as follows: (I) structural and thermal features of the salts, (II) solid solutions, and (III) spectroscopic investigation to facilitate the description of the experimental results.The salts: [QH]2SO4·H2O, [QH]BPh4, [QH]PF6, and [QH]BF4
The structure of the first compound of the series, [QH]2SO4·H2O, had to be determined from powder data since all crystallization experiments were fruitless, and only polycrystalline samples could be obtained. The [QH]2SO4·H2O crystallizes at room temperature in the monoclinic space group P21 (see Table S2† for details). As reported in Fig. 1, water molecules interact with one [QH]+ cation [N–H⋯Ow = 2.917(6) Å] and bridge the SO42− anions [O—Hw⋯O = 2.598 (5)–2.629(2) Å], while cations interact with the anions through a multitude of charge-assisted hydrogen bonds: N–H⋯O [2.808(1), 2.932(5) Å] and O–H⋯O [2.463(3) Å]. The electrostatic compression61–63 between oppositely charged ions combined with the strength and high directionality coming from the nature of hydrogen bonds leads to the formation of relatively shorter bonds in anion–cation interactions.Thermal analysis indicates a weight loss of ca. 5% as the only occurring process, compatible with the evaporation of water (see Fig. S2†). This behavior is also proven by the VT powder XRD results shown in Fig. S3.† There is a phase change associated with the dehydration of the salt; however, no plastic transition was detected for this compound, not even when the same experiments were carried out in the absence of air to avoid water reuptake from the moisture.
The salt [QH]BPh4 presents the largest anion amongst those studied in this series and crystallizes in the orthorhombic space group P212121 (see Table S2† for details). Structural analysis reveals that the [QH]+ cations fit the cavities resulting from the [BPh4]− anion arrangement (Fig. 2), and at RT they feature a disorder over two positions (flip-flop motion) that can be “frozen out” in only one as the anionic hosting cage is made tighter by decreasing the temperature down to 100 K (Fig. 2) as shown by the collection of an additional dataset. Since this transition does not lead to a crystal symmetry change, the motion at RT might occur between two slightly non-equivalent positions. On lowering the temperature, the cavity size‡ decreases, from 168 Å3 to 152 Å3 (ca −9%), resulting in short contacts between cations and anions; consequently, one position becomes preferred over the other. The behavior of the crystal structure of [QH]BPh4 was further explored at higher temperatures. However, no plastic phase was detected with neither variable temperature powder XRD nor thermal techniques (Fig. S4 and S5†).
[QH]BF4 has the smallest anion size among the compounds studied in this work and crystallizes directly in the plastic phase at RT. Therefore, it is an appropriate example of the effect of the anion size on plastic phase transition temperature compared to [QH]BPh4. The DSC results show a reversible phase transition with peaks at around 298 K and 248 K upon heating and cooling, respectively, with a hysteresis of ca. 50 K, ΔH of 3.6 kJ mol−1, and ΔS of 12.1 J mol−1 K−1 (see Fig. S6†). Although the RT structure could not be solved because of the severe disorder, structural solution could be attained from data measured at LT (200 K), i.e., below transition temperature (Fig. 3). At LT, the salt crystallizes in the orthorhombic space group P212121 (see Table S2† for details), in which cations and anions form 1D charge-assisted hydrogen bonded chains through anion–cation O–H⋯F [2.837(7) Å] and cation–cation N–H⋯O [2.817(7) Å] interactions along the b-axis (Fig. 3). The electrostatic repulsion between the cation pairs is counterbalanced by the charge delocalization which strengthens the bonds and shortens the interaction distances, with the counterions stabilizing the net electrostatic forces;64–66 VT powder XRD was applied to monitor the plastic transition (Fig. 3), which turned out to be fully reversible.
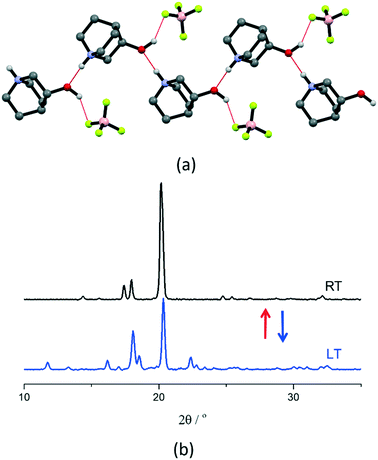 | ||
| Fig. 3 (a) Intermolecular interactions in crystalline [QH]BF4 at LT (200 K), and (b) VT powder XRD patterns recorded at LT (blue line) and at RT (black line) for a polycrystalline sample of [QH]BF4. | ||
Compound [QH]PF6 shows the most interesting thermal behavior among the whole series of salts examined in this study. The salt crystallizes in the tetragonal space group P41212 (see Table S2† for details) with two [QH]+ cations and two PF6− anions in the asymmetric unit. At RT, both anions feature crystallographic disorder over two positions with occupancy ratios of ca. 60/40 and 20/80, likely due to the flip-flop motion of the PF6− units around one F—P—F axis (Fig. 4). Therefore, this phase can be considered as a semi ordered crystal structure. To investigate the type of disorder affecting the PF6− anions, we carried out a variable-temperature single-crystal XRD experiment. Unfortunately, the sample started crumbling on cooling; consequently, no further structural analysis could be performed. To this end, the spectroscopic techniques were instrumental in elucidating what type of disorder affects the anions (vide infra).
 | ||
| Fig. 4 Intermolecular interactions in crystalline [QH]PF6 at RT (left), and detail showing the flip-flop motion of the PF6− around one F—P—F axis (right). HCH atoms are omitted for clarity. | ||
Similarly, to the tetrafluoroborate salt at LT, within crystalline [QH]PF6, cations and anions are involved in 1D charge-assisted hydrogen-bonded chains through the O–H⋯F [3.23(3)–2.959(6) Å] and N–H⋯O [2.856(7), 2.882(7) Å] interactions along the a-axis-direction (Fig. 4).
Experimental powder XRD patterns, recorded at RT, match well with the simulated one from the single crystal structure, revealing the high crystallinity and purity of the phase (Fig. S8†). TGA analysis shows that the salt is stable up to ca. 473 K. At the same time, DSC indicates a reversible phase transition around 308 K (heating cycle) with a ΔH of 8.2 kJ mol−1, ΔS of 26.4 J mol−1 K−1, and with ca. 20 K of hysteresis (see Fig. S9†).
To gain insights about the structural characteristics of the high-temperature phase, both VT single-crystal and powder XRD experiments were performed.
In agreement with the DSC data, upon increasing the temperature up to 320 K, [QH]PF6 single crystals undergo a transition from the semi ordered tetragonal phase to a plastic phase (Fig. 5a), which is cubic as expected for PCs.1,12 Furthermore, as confirmed by recording the ϕ-scans XRD pattern (Fig. S10†), the retainment of the crystal's outer shape, as well as the reversible birefringence loss and regain accompanying the RT ⇆ HT transition (Fig. 5c), indicate that such a transformation takes place in a single-crystal to single-crystal (SCSC) fashion. However, the severe disorder affecting the [QH]+ cations within the plastic phase made it impossible to fully solve and refine the model. This is a common feature of PCs; when all the possible degrees of freedom are activated, the orientationally disordered molecules/ions assume an almost perfect isotropic spherical shape, which is often impossible to fully model.1,12
The powder pattern recorded at 320 K shows fewer peaks with respect to that at RT (Fig. 5b). This result accounts for the increase in symmetry accompanying the transition to a plastic phase, and agrees with what is reported in the literature for analogous salts.10,44,45 Additionally, the excellent match with the pattern simulated from the single-crystal structure at 320 K reveals the quantitative conversion to the plastic phase (Fig. S11†).
Solid solutions between [QH]PF6 and [QH]BF4
Ordered phases of [QH]PF6 and [QH]BF4 exhibit similar packing arrangements (i.e. they are almost isostructural) and undergo a transition to a plastic phase at the temperatures of ca. 308 K and 298 K, respectively. On the other hand, the two salts are not isomorphous in their ordered phases, and probably they are not even in the plastic phases. Additionally, the two anions possess diverse shapes and different volumes accounting for 53.4 Å3 (tetrahedral) and 73.0 Å3 (octahedral) for BF4− and PF6−, respectively.67,68 These differences appear to violate the key prerequisite for the formation of a solid solution laid out by Kitaigorodsky,32,33i.e. structural similarity in terms of size and shape. Pure components should, ideally, be (i) isomorphous, or at least isostructural, and (ii) display a difference less than 15% in size and shape. In our case, [QH]PF6 and [QH]BF4 partially satisfies the first prerequisite while leaving the second utterly unfulfilled with a ca. 30% difference. The [QH]BF4 salt is also affected by deliquescence, which makes working with this material challenging.Aware of such differences and non-optimal conditions for solid solution formation, we deliberately blended the two salts (see Experimental section) to investigate the possibility of obtaining binary mixed-systems, and to study the effect of the composition on the temperature and type of transition.
Polycrystalline samples for the obtained binary systems were analyzed by powder XRD. The diffraction patterns of the compounds [QH](PF6)x(BF4)1−x with x = 0.9, 0.8, and 0.7 are all similar to that of pure [QH]PF6 at HT (above transition temperature), suggesting that BF4− anions randomly substitute for PF6− ones, leading to the formation of solid solutions based on the cubic plastic phase structure (Fig. 6a). On the other hand, for all the other compositions, with x < 0.7, samples were far too hygroscopic and were difficult to analyze.
Based on a comparison of the unit cell volumes extracted from Pawley refinements, the two salts are indeed miscible, affording crystalline phases that follow Vegard's rule69 in the examined composition range, namely x = 0.7–1 (Fig. 6b).
The DSC traces of each new crystalline phase, measured in the range 243–423 K, do not show any peak of the two reagents, confirming that the two salts successfully merged into a unique phase, and no peak for the solid solution samples was observed (Fig. S12†). This result is somehow unexpected and sharply contrasts with other reported similar systems forming solid solutions and exhibiting a regular trend of the transition temperature as a function of the composition.43–45
To investigate the unexpected behavior of [QH](PF6)x(BF4)1−x, VT powder XRD experiments were carried out up to the instrumental limit of 123 K. Still, also in this case, no changes in the diffraction patterns were detected on decreasing the temperature (Fig. S13†). Thus, we investigated the slow kinetics for the reverse transition (plastic crystal to ordered crystal). A polycrystalline sample of [QH](PF6)0.9(BF4)0.1 was split, the two fractions kept at RT and 273 K, respectively, and powder XRD patterns were measured every week for a period of ca. one month. Even after such a long time, the plastic crystal phases still existed that rules out the occurrence of kinetic factors for the missing transformation.
To the best of these authors' knowledge, the missed reordering transition can be interpreted only as a direct consequence of the parent compounds' structural diversity in terms of anion size/shape and their non-isomorphism, as anticipated above, and lack of ion mobility. Although within plastic phases ions possess high mobility compared to their ordered counterparts, they do not attain a degree of freedom that would allow them to flow over the entire crystal. This prevents, de facto, the solid solutions from rearranging either to their parent compounds' ordered structures, separating out, or to a new ordered phase in which BF4− and PF6− occupy well-defined crystallographic positions. Therefore, the mixed systems remain disordered, experiencing what we have called a phenomenon of reordering frustration.
To gain further insights into the lattice dynamics of the [QH]+ salts and solid solutions and prove our hypothesis, we performed a combined spectroscopic study.
Solid-state NMR
The 13C, 15N and 31P CPMAS, 19F and 11B MAS spectra fully confirm the purity of the salts and their high degree of crystallinity. The 13C CPMAS spectra (Fig. 7; chemical shifts in Table S3†) of [QH]BF4, [QH]PF6 and [QH](PF6)0.9(BF4)0.1 are almost superposable, highlighting the similarity of their short-range structures, whereas the presence of several aromatic signals and their spinning sideband patterns indicates a higher rigidity of the [QH]BPh4 system. This difference can be easily ascribed to the size and steric hindrance of the BPh4− anion with respect to the smaller BF4− and PF6− anions.The 15N CPMAS spectra (Fig. S14†) and the chemical shift values reported in Table S4† are very similar and typical of protonated aliphatic amines.70 The 19F MAS spectrum of [QH]BF4 (Fig. S15†) shows an intense singlet at −149.8 ppm, while the 19F SSNMR signal of the PF6− ion at 69.7 ppm in [QH]PF6 is a doublet, due to the 31P–19F J-coupling (729.8 Hz). The same 1P–19F J-coupling is measured in the 31P CPMAS spectrum (Fig. S16†), where the expected septuplet is observed. Interestingly, although quadrupolar, no spinning sidebands are present in the 11B MAS spectra of [QH]BF4 and [QH](PF6)0.9(BF4)0.1 (Fig. 8) suggesting a fast-isotropic motion. On the other hand, their presence in the case of the sample having BPh4− as anion confirms the absence of fast motion for this bulky system.
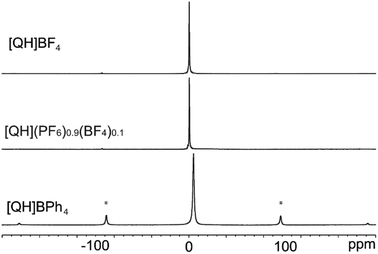 | ||
| Fig. 8 11B (128.38 MHz) MAS spectra of [QH]BF4, [QH](PF6)0.9(BF4)0.1 and [QH]BPh4 acquired at 12 kHz (room temperature). Asterisks indicate the presence of spinning sidebands. | ||
While the 11B spectra provide qualitative information only, to perform an in-depth analysis on the plastic phase transition, low-resolution 19F spin–lattice relaxation times, T1, studies have been conducted. Indeed, it is known that the T1 relaxation times provide an experimental route to evaluate the molecular motions in the solid state.71,72 The Bloembergen, Purcell and Pound theory73,74 allows obtaining information on the mobility of the system according to eqn (1):
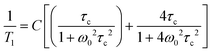 | (1) |
| τc = τ0eEa/RT | (2) |
Considering that H⋯F distances fall in the range 3.13(1)–2.95(1) Å and that the F⋯F distance is ca. 2.2 Å, as measured from the structures, the F–H dipolar interaction can be safely neglected if one considers the inverse dependence on the sixth power of the interatomic distances. Therefore, with this approximation it is possible to easily derive the activation energy from the equation mentioned above. More specifically, plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T1versus 103/T, the activation energy Ea can be obtained from the slope of the line. Fig. 9 reports the 19F ln
T1versus 103/T, the activation energy Ea can be obtained from the slope of the line. Fig. 9 reports the 19F ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T1 profiles of the [QH]PF6, [QH]BF4 and [QH](PF6)0.9(BF4)0.1 samples versus 103/T (K−1) as measured at 564.69 MHz over a range of temperatures from 213 to 353 K by the inversion recovery technique.
T1 profiles of the [QH]PF6, [QH]BF4 and [QH](PF6)0.9(BF4)0.1 samples versus 103/T (K−1) as measured at 564.69 MHz over a range of temperatures from 213 to 353 K by the inversion recovery technique.
 | ||
| Fig. 9 Variation of 19F T1 relaxation times with inverse temperature T−1 for (a) [QH]PF6, (b) [QH]BF4 and (c) [QH](PF6)0.9(BF4)0.1. | ||
The profile of the plotted line for the PCs is significantly different over the observed temperature range: the binary solution [QH](PF6)0.9(BF4)0.1 shows a constant slope, due to the presence of a single activation energy, while [QH]PF6 and [QH]BF4 display a point of discontinuity respectively around 313 and 298 K, where the slope changes. We can thus surmise that the phase transition observed in the DSC measurements must be related to the presence of two regimes of motion characterized by different τc correlation times in the 19F T1 profile of [QH]PF6 and [QH]BF4. Interestingly, such a behaviour is not observed for [QH](PF6)0.9(BF4)0.1, in agreement with the absence of transition. The calculated activation energies are shown in Table 1.
| Salt | Activation energy (kJ mol−1) |
|---|---|
| [QH]PF6 | 5.8 (for T > 308 K) |
| 6.8 (for T < 308 K) | |
| [QH]BF4 | 4.3 (for T > 298 K) |
| 6.5 (for T < 298 K) | |
| [QH](PF6)0.9(BF4)0.1 | 6.8 |
The measured Ea values are in the range currently found for the PF6− group rotation in the solid state in other systems, as reported, for example, by Burbach et al.76 It is possible to observe a small but significant variation of the activation energy for the [QH]PF6 and [QH]BF4 salts. These values confirm what has already been assessed: the activation energy decreases at temperatures over 313 K for [QH]PF6 and over 298 K for [QH]BF4, demonstrating the conversion to a phase characterized by higher mobility in both cases. The difference in the activation energy values, before and after the phase transition temperature, is slightly higher for the [QH]BF4 system.
The [QH]PF6 phase transition can also indirectly be observed by the peak narrowing at higher temperatures in the 19F MAS static spectra, which corresponds to a larger mobility of the system. On the other hand, for the [QH](PF6)0.9(BF4)0.1 system there is no signal width variation on increasing temperatures (Fig. S17†).
Micro-Raman spectroscopy
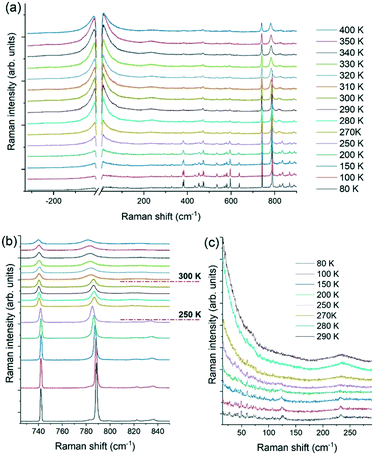
VT micro-Raman spectroscopy also provides valuable insights into understanding the plastic phase transition. It allows studying the molecular and lattice dynamics, where the former property probes the effect of the dynamic disorder of the cation and the anion on the intramolecular vibrations. At the same time, the latter gives information on the crystal symmetry changes which accompany such transitions.14,77 The temperature-dependent Raman spectra of a [QH]PF6 crystal in the wavenumber range of interest are presented in Fig. 10, which includes the anti-Stokes scatterings for the low-frequency region.Focusing on the intramolecular range (>250 cm−1, Fig. 10b), two main features are representative of the spectrum: the peak centered at 741 cm−1, assigned to the symmetric stretching of the PF6− anion,78–80 and that centered at 788 cm−1, characteristic of the [QH]+ cation and assigned to the C—N—C and C—C—C stretching modes.81 Based on these bands, In Fig. 10b two phase transitions can be identified, one at nearly RT, in agreement with what observed by thermal analyses (vide supra), and another around 250 K. Both transitions show significant hysteresis depending on the specimen. By lowering the temperature below 300 K, the characteristic band of the [QH]+ sharpens and shifts toward higher energy because of the reduced re-orientational disorder of the cation in the unit cell. On the contrary, no effect is observed on the full width at half-maximum (FWHM) of the PF6− stretching vibration peak at 741 cm−1, apart from what expected as a result of the cooling down, signature that the re-orientational disorder of the anion is not involved in this phase transition.
In the second sudden spectral change in the range 730–850 cm−1 at 250 K (Fig. 10b), the [QH]+ vibrational band shifts to lower energy while the PF6− symmetric stretching band sharpens and shifts on the red. In the course of this phase transition, the crystal changes its morphology dramatically and breaks, but no more spectra changes take place on decreasing the temperature down to 80 K. Information about the symmetry change that the system undergoes with temperature can be inferred from the analysis of the spectral features that probe the lattice dynamics.
Low-frequency Raman spectroscopy is indeed a consolidated technique to probe the lattice dynamics of molecular materials and lately has been applied to the study of systems which show dynamic re-orientational disorder.14 The Raman modes observed in the low-frequency range (<250 cm−1) hold the character of lattice phonons or vibrations, in which the molecules oscillate as a whole around the lattice equilibrium positions. These modes are therefore dependent on the intermolecular force field77,82 and can be used to detect even slight changes in crystal symmetry. In fact, measurements over this range have been applied extensively to investigate polymorphism and phase transitions in molecular crystals, relying on each lattice's unique dynamics.83–85 Recently, the approach has also been effectively used to revisit the pressure-induced phase transition in adamantine derivatives, which display plastic crystals characteristics.14
The low-frequency range for [QH]PF6 at high temperature is dominated by the diffuse Rayleigh wing (RW) centered at ω = 0, the frequency of the exciting laser. This feature is attributed to the re-orientational molecular motions paradigmatic of a disordered system and can thus be ascribed to the dynamic disorder of cations and anions in the unit cell. As both kinds of ions lack a specific orientation inside the unit cell, the lattice phonon pattern gets washed away in the averaged cubic structure (Fig. 10a). In correspondence of the phase transition near RT, the cation slows down in its re-orientational motion, and finally gets frozen in a specific configuration; in contrast, the anion PF6− is still represented by an averaged position of its motion around one F—P—F axis, as depicted in Fig. 4. The reduced disorder results in the broadening and intensity dropping of the RW as well as in the appearance of the Boson peak centered at around 240 cm−1 (Fig. 10c) which has been reported to demonstrate the presence of semi ordered phases.14 The lattice phonon pattern changes again suddenly below 250 K, with finally the complete disappearance of the RW at 80 K. The formation of an ordered structure is revealed by the resolution of the Boson peak into the sharp features lying below 250 cm−1. Below 100 cm−1 the lattice phonon pattern and some peaks of the air overlap, as reported in Fig. S18.† By comparison with the spectrum in the Fig. S18,† some other modes are still recognizable, while the RW appears to have negligible intensity at low T. The lattice phonons are usually more intense than the intramolecular vibrations and in the present case this unusually low intensity could be the result of the mosaicity of the specimen, which displays many and very small crystal domains.
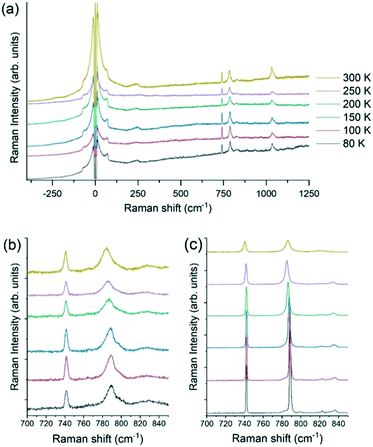
Contrariwise, the Raman spectra of the solid solution [QH](PF6)0.9(BF4)0.1, reported in Fig. 11, do not show any phase transition, but a persistence of both the central peak even at 80 K and the broadening of the two characteristic peaks of the anion PF6− and the cation [QH]+ at 741 and 788 cm−1, respectively. The slight spectral shift of the intramolecular vibration towards higher energy is ascribable to the effect of the temperature. The Raman measurements thus confirm the absence of any disordered-semi ordered or disordered–ordered phase transition in the solid solutions, in agreement with the XRD and NMR findings.
Conclusions
Crystals possessing components in rapid motion, i.e. plastic crystals, are at the forefront of the research on material sciences and for the development of solid-state molecular machines.1,3,4 A promising approach envisages the modification of the molecular dynamics by acting on the choice of the molecular fragments/ions used as building blocks whose re-orientational motion can be triggered thermally. The final goal would be the development of stimuli-responsive materials. In view of this, it would be highly desirable to achieve fine control over the transition temperatures as well, and in this regard the solid solution32–34 approach has proved to be a promising strategy.43–45With this in mind, we have reported here the results of our studies on the solid-state dynamics in a series of R-(+)-(3)-hydroxyquinuclidinium salts, [QH]X, with various counter-anions (SO42−, BPh4−, BF4−, and PF6−). All salts have been crystallized as anhydrous forms with general formula [QH]X (X = BPh4−, PF6− and BF4−) except for the sulfate, which was obtained as mono-hydrate, [QH]2SO4·H2O.
The sulfate salt does not show any structural change, except for a reversible dehydration/rehydration process following the heating/cooling cycle, whereas in [QH]BPh4, the [QH]+ cation was found to undergo a re-orientational flip-flop motion over two positions, that could be frozen out on lowering the temperature. Interestingly, the [QH]BF4 and [QH]PF6 salts exhibit reversible transitions at or just above room temperature, affording genuine and highly symmetrical plastic phases.
However, the most remarkable findings were observed on solid solutions of formula [QH](PF6)x(BF4)1−x: (i) unlike other similar reported systems,43–45 the two salts are not fully miscible in the whole range of composition and only up to 30% of [QH]BF4 can be “dissolved” into the [QH]PF6 lattice, and (ii) solid solution formation “kills” the reversible nature of the plastic transition, making, de facto, these solids dynamically disordered in their plastic phases permanently, or at least up to the lowest detectable limit of 80 K. This behavior was somewhat unexpected.
All these findings have been corroborated by multinuclear solid-state NMR (13C, 15N and 31P CPMAS, 19F and 11B MAS) and micro-Raman measurements. In particular, VT 19F T1 relaxation profiles allowed obtaining the activation energies associated to the molecular mobility.
The synergy between spectroscopic and XRD techniques allowed us to rationalize this behavior. As a direct consequence of the parent compounds' structural diversity of the anions, their non-isomorphism, and reduced ion mobility, the plastic phases are prevented from rearranging either to the respective parent compounds lattices or to new phases.
To the best of these authors' knowledge, this system represents the first example of a crystalline material showing such behavior, that we have described here for the first time as “reordering frustration”.
Further research is ongoing to characterize and study the ion conduction of such materials, as well as to extend the same synthetic approach to other systems, and explore how the ions' structural diversity and size may affect the formation of solid solutions and plastic transitions in terms of temperature and type.
Author contributions
SO, GC, RB, SB: experimentation and data collection; SD, MRC, TS conceptualization, manuscript preparation; and supervision; DB, RG, OY, and EV, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
SO, GC, SD, DB, TS and EV acknowledge financial support from the University of Bologna (RFO Scheme) and PRIN 2020. TS thanks the European co-financing project FSE REACT EU - PON R&I 2014-2020 and Prof. Aldo Brillante for the fruitful and helpful discussions. OY acknowledges funding from European Research Council (850041 - ANHARMONIC).Notes and references
- S. Das, A. Mondal and C. M. Reddy, Chem. Soc. Rev., 2020, 49, 8878–8896 RSC.
- J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8 CrossRef CAS.
- S. D. Karlen and M. A. Garcia-Garibay, Top. Curr. Chem., 2005, 262, 179–227 CrossRef CAS.
- P. Naumov, D. P. Karothu, E. Ahmed, L. Catalano, P. Commins, J. Mahmoud Halabi, M. B. Al-Handawi and L. Li, J. Am. Chem. Soc., 2020, 142, 13256–13272 CrossRef CAS PubMed.
- J. Luo, O. Conrad and I. F. J. Vankelecom, J. Mater. Chem. A, 2013, 1, 2238–2247 RSC.
- K. Pogorzelec-Glaser, A. Rachocki, P. Ławniczak, A. Łapiński and J. Tritt-Goc, Solid State Ionics, 2012, 227, 96–101 CrossRef CAS.
- A. Ggor, A. Piecha, R. Jakubas and A. Miniewicz, Chem. Phys. Lett., 2011, 503, 134–138 CrossRef.
- C. K. Yang, W. N. Chen, Y. T. Ding, J. Wang, Y. Rao, W. Q. Liao, Y. Xie, W. Zou and R. G. Xiong, J. Am. Chem. Soc., 2019, 141, 1781–1787 CrossRef CAS PubMed.
- D. Braga, G. Cojazzi, D. Paolucci and F. Grepioni, Chem. Commun., 2001, 803–804 RSC.
- P. F. Li, Y. Y. Tang, Z. X. Wang, H. Y. Ye, Y. M. You and R. G. Xiong, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- J. N. Sherwood, The Plastically Crystalline State: Orientationally Disordered Crystals, J. Wiley & Sons, cop., 1979 Search PubMed.
- R. Brand, P. Lunkenheimer and A. Loidl, J. Chem. Phys., 2002, 116, 10386–10401 CrossRef CAS.
- A. Mondal, B. Bhattacharya, S. Das, S. Bhunia, R. Chowdhury, S. Dey and C. M. Reddy, Angew. Chem., Int. Ed., 2020, 59, 10971–10980 CrossRef CAS PubMed.
- T. Salzillo, A. Girlando and A. Brillante, J. Phys. Chem. C, 2021, 125, 7384–7391 CrossRef CAS.
- L. Fornasari, A. Olejniczak, F. Rossi, S. d'Agostino, M. R. Chierotti, R. Gobetto, A. Katrusiak and D. Braga, Chem. – Eur. J., 2020, 26, 5061–5069 CrossRef CAS PubMed.
- T. Mochida, M. Ishida, T. Tominaga, K. Takahashi, T. Sakurai and H. Ohta, Phys. Chem. Chem. Phys., 2018, 20, 3019–3028 RSC.
- Q. Pan, Y. A. Xiong, T. T. Sha and Y. M. You, Mater. Chem. Front., 2021, 5, 44–59 RSC.
- Y. Y. Tang, P. F. Li, W. Q. Liao, P. P. Shi, Y. M. You and R. G. Xiong, J. Am. Chem. Soc., 2018, 140, 8051–8059 CrossRef CAS PubMed.
- J. Harada, Y. Kawamura, Y. Takahashi, Y. Uemura, T. Hasegawa, H. Taniguchi and K. Maruyama, J. Am. Chem. Soc., 2019, 141, 9349–9357 CrossRef PubMed.
- J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata and T. Inabe, Nat. Chem., 2016, 8, 946–952 CrossRef CAS PubMed.
- Y. Zhang, M. A. Hopkins, D. J. Liptrot, H. Khanbareh, P. Groen, X. Zhou, D. Zhang, Y. Bao, K. Zhou, C. R. Bowen and D. R. Carbery, Angew. Chem., Int. Ed., 2020, 59, 7808–7812 CrossRef CAS PubMed.
- H. Kimata, T. Sakurai, H. Ohta and T. Mochida, ChemistrySelect, 2019, 4, 1410–1415 CrossRef CAS.
- J. Li, D. Dunstan, X. Lou, A. Planes, L. Mañosa, M. Barrio, J. L. Tamarit and P. Loveras, J. Mater. Chem. A, 2020, 8, 20354–20362 RSC.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S. I. Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510 CrossRef CAS PubMed.
- A. Aznar, P. Lloveras, M. Barrio, P. Negrier, A. Planes, L. Mañosa, N. D. Mathur, X. Moya and J. L. Tamarit, J. Mater. Chem. A, 2020, 8, 639–647 RSC.
- Z. Sun, T. Chen, X. Liu, M. Hong and J. Luo, J. Am. Chem. Soc., 2015, 137, 15660–15663 CrossRef CAS PubMed.
- H. Zhu, D. R. MacFarlane, J. M. Pringle and M. Forsyth, Trends Chem., 2019, 1, 126–140 CrossRef CAS.
- J. M. Pringle, P. C. Howlett, D. R. MacFarlane and M. Forsyth, J. Mater. Chem., 2010, 20, 2056–2062 RSC.
- S. Horike, D. Umeyama, M. Inukai, T. Itakura and S. Kitagawa, J. Am. Chem. Soc., 2012, 134, 7612–7615 CrossRef CAS PubMed.
- A. Basile, M. Hilder, F. Makhlooghiazad, C. Pozo-Gonzalo, D. R. MacFarlane, P. C. Howlett and M. Forsyth, Adv. Energy Mater., 2018, 8, 1–20 Search PubMed.
- F. Makhlooghiazad, J. Guazzagaloppa, L. A. O'Dell, R. Yunis, A. Basile, P. C. Howlett and M. Forsyth, Phys. Chem. Chem. Phys., 2018, 20, 4721–4731 RSC.
- M. Lusi, CrystEngComm, 2018, 20, 7042–7052 RSC.
- M. Lusi, Cryst. Growth Des., 2018, 18, 3704–3712 CrossRef CAS.
- E. Schur, E. Nauha, M. Lusi and J. Bernstein, Chem. – Eur. J., 2015, 21, 1735–1742 CrossRef CAS PubMed.
- E. Nauha, P. Naumov and M. Lusi, CrystEngComm, 2016, 18, 4699–4703 RSC.
- T. Rekis, A. Berziņš, I. Sarceviča, A. Kons, M. Balodis, L. Orola, H. Lorenz and A. Actiņš, Cryst. Growth Des., 2018, 18, 264–273 CrossRef CAS.
- T. Rekis, S. D'Agostino, D. Braga and F. Grepioni, Cryst. Growth Des., 2017, 17, 6477–6485 CrossRef CAS.
- A. Grandeury, E. Condamine, L. Hilfert, G. Gouhier, S. Petit and G. Coquerel, J. Phys. Chem. B, 2007, 111, 7017–7026 CrossRef CAS PubMed.
- A. Delori, P. Maclure, R. M. Bhardwaj, A. Johnston, A. J. Florence, O. B. Sutcliffe and I. D. H. Oswald, CrystEngComm, 2014, 16, 5827–5831 RSC.
- R. W. Smith, W. N. Mei, J. W. Flocken, M. J. Dudik and J. R. Hardy, Mater. Res. Bull., 2000, 35, 341–349 CrossRef CAS.
- A. K. S. Romasanta, D. Braga, M. T. Duarte and F. Grepioni, CrystEngComm, 2017, 19, 653–660 RSC.
- H. Li and M. Li, J. Mater. Res., 2011, 26, 997–1005 CrossRef CAS.
- S. D'Agostino, L. Fornasari, F. Grepioni, D. Braga, F. Rossi, M. R. Chierotti and R. Gobetto, Chem. – Eur. J., 2018, 24, 15059–15066 CrossRef PubMed.
- S. D'Agostino, L. Fornasari and D. Braga, Cryst. Growth Des., 2019, 19, 6266–6273 CrossRef.
- K. Matsumoto, R. Nonaka, Y. Wang, G. Veryasov and R. Hagiwara, Phys. Chem. Chem. Phys., 2017, 19, 2053–2059 RSC.
- K. Gesi, J. Phys. Soc. Jpn., 1993, 62, 3805–3808 CrossRef CAS.
- J. G. Aston, Pure Appl. Chem., 1961, 2, 231–240 CrossRef CAS.
- D. Braga, F. Grepioni, L. Maini and S. D'Agostino, IUCrJ, 2017, 4, 369–379 CrossRef CAS PubMed.
- D. Braga, F. Grepioni, L. Maini and S. d'Agostino, Eur. J. Inorg. Chem., 2018, 2018, 3597–3605 CrossRef CAS.
- G. R. Desiraju, IUCrJ, 2016, 3, 1–2 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- A. Thorn, B. Dittrich and G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 448–451 CrossRef CAS.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. Van De Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- A. Altomare, C. Cuocci, C. Giacovazzo, A. Moliterni, R. Rizzi, N. Corriero and A. Falcicchio, J. Appl. Crystallogr., 2013, 46, 1231–1235 CrossRef CAS.
- A. Altomare, C. Giacovazzo and A. Guagliardi, J. Appl. Crystallogr., 2000, 1180–1186 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- V. Hronský, Acta Electrotech. Inf., 2013, 13, 95–98 Search PubMed.
- D. Braga, C. Bazzi, F. Grepioni and J. J. Novoa, New J. Chem., 1999, 23, 577–579 RSC.
- D. Braga, L. Maini, F. Grepioni, A. De Cian, O. Félix, J. Fischer and M. W. Hosseini, New J. Chem., 2000, 24, 547–552 RSC.
- J. D. Dunitz, A. Gavezzotti and S. Rizzato, Cryst. Growth Des., 2014, 14, 357–366 CrossRef CAS.
- E. D'Oria and J. J. Novoa, CrystEngComm, 2004, 6, 367–376 RSC.
- D. Braga, F. Grepioni and J. J. Novoa, Chem. Commun., 1998, 1959–1960 RSC.
- S. G. Dash and T. S. Thakur, Phys. Chem. Chem. Phys., 2019, 21, 20647–20660 RSC.
- M. Yamada, H. Hagiwara, H. Torigoe, N. Matsumoto, M. Kojima, F. Dahan, J. P. Tuchagues, N. Re and S. Iijima, Chem. – Eur. J., 2006, 12, 4536–4549 CrossRef CAS PubMed.
- A. R. Koh, B. Hwang, K. Chul Roh and K. Kim, Phys. Chem. Chem. Phys., 2014, 16, 15146–15151 RSC.
- A. R. Denton and N. W. Ashcroft, Phys. Rev. A, 1991, 43, 6 CrossRef PubMed.
- R. Gobetto, C. Nervi, E. Valfrè, M. R. Chierotti, D. Braga, L. Maini, F. Grepioni, R. K. Harris and P. Y. Ghi, Chem. Mater., 2005, 17, 1457–1466 CrossRef CAS.
- S. Aime, R. Gobetto, A. Orlandi, D. Braga and F. Grepioni, Inorg. Chem., 1991, 30, 951–956 CrossRef CAS.
- S. Aime, L. Cordero, R. Gobetto, D. Braga, F. Grepioni, S. Righi and S. Sostero, Inorg. Chem., 1992, 31, 3054–3059 CrossRef CAS.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- R. Kubo and K. Tomita, J. Phys. Soc. Jpn., 1954, 9, 6 CrossRef.
- M. E. Di Pietro, F. Castiglione and A. Mele, J. Mol. Liq., 2021, 322, 114567 CrossRef CAS.
- G. Burbach, N. Weiden and A. Weiss, Z. Naturforsch. A, 1992, 47, 689–701 CrossRef CAS.
- A. Brillante, I. Bilotti, R. G. Della Valle, E. Venuti and A. Girlando, CrystEngComm, 2008, 10, 937–946 RSC.
- R. W. Berg, Raman spectroscopy and ab-initio model calculations on ionic liquids, 2007, vol. 138 Search PubMed.
- E. R. Talaty, S. Raja, V. J. Storhaug, A. Dölle and W. R. Carper, J. Phys. Chem. B, 2004, 108, 13177–13184 CrossRef CAS.
- M. Boumediene, B. Haddad, A. Paolone, M. Drai, D. Villemin, M. Rahmouni, S. Bresson and O. Abbas, J. Mol. Struct., 2019, 1186, 68–79 CrossRef CAS.
- N. A. Wojcik, D. A. Kowalska, M. Trzebiatowska, E. Jach, A. Ostrowski, W. Bednarski, M. Gusowski, P. Staniorowski and A. Cizman, J. Phys. Chem. C, 2021, 125, 16810–16818 CrossRef CAS.
- T. Salzillo, A. Giunchi, L. Pandolfi, A. Brillante and E. Venuti, Isr. J. Chem., 2021, 61, 650–667 CrossRef CAS.
- T. Salzillo, A. Giunchi, M. Masino, N. Bedoya-Martĺnez, R. G. Della Valle, A. Brillante, A. Girlando and E. Venuti, Cryst. Growth Des., 2018, 18, 4869–4873 CrossRef CAS.
- J. Socci, T. Salzillo, R. G. Della Valle, E. Venuti and A. Brillante, Solid State Sci., 2017, 71, 146–151 CrossRef CAS.
- T. Salzillo, E. Venuti, C. Femoni, R. G. Della Valle, R. Tarroni and A. Brillante, Cryst. Growth Des., 2017, 17, 3361–3370 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of synthesis, thermal analysis, VT-powder XRD, SS-NMR and micro-Raman spectra. CCDC 2155973–2155977. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2me00040g |
| ‡ Evaluated by running the display-void algorithm implemented in Mercury81 on the relative CIF-files obtained by erasing the cation coordinates. |
| This journal is © The Royal Society of Chemistry 2022 |