Rationally designed foldameric adjuvants enhance antibiotic efficacy via promoting membrane hyperpolarization

Abstract

The negative membrane potential of bacterial cells influences crucial cellular processes. Inspired by the molecular scaffold of the antimicrobial peptide PGLa, we have developed antimicrobial foldamers with a computer-guided design strategy. The novel PGLa analogues induce sustained membrane hyperpolarization. When co-administered as an adjuvant, the resulting compounds – PGLb1 and PGLb2 – have substantially reduced the level of antibiotic resistance of multi-drug resistant Escherichia coli, Klebsiella pneumoniae and Shigella flexneri clinical isolates. The observed antibiotic potentiation was mediated by hyperpolarization of the bacterial membrane caused by the alteration of cellular ion transport. Specifically, PGLb1 and PGLb2 are selective ionophores that enhance the Goldman–Hodgkin–Katz potential across the bacterial membrane. These findings indicate that manipulating bacterial membrane electrophysiology could be a valuable tool to overcome antimicrobial resistance.

---

Design, System, Application

The strong hydrophobic interaction between the amphipathic helices and the lipid components is essential to disrupt bacterial membrane integrity, a mechanism involved in the direct antimicrobial effect. We aimed to scale down the hydrophobic stabilization of the helix-membrane interaction and thereby promote selective ion transport through the intact membrane. We performed structure-based rational modifications of the parent antimicrobial peptide PGLa at sites interacting with the bacterial membrane. A rational, computer-assisted backbone homologation design approach was applied to modify the secondary structure of PGLa, and thereby its ion transport properties. We have developed beta-amino acid-containing antimicrobial peptide mimetics that can hyperpolarize the bacterial membrane by generating Goldman–Hodgkin–Katz potential. This effect leads to the bacteria's resensitization against conventional antibiotics. The unnatural amino acids also improve proteolytic resistance, which can help overcome the traditional drawback of antimicrobial peptides. Our work reveals that designing molecular systems interfering with bacterial electrophysiology can effectively combat antimicrobial resistance.

Introduction

Generating a transmembrane electrochemical gradient across the bacterial cell membrane plays a crucial role in essential cellular processes, such as ATP synthesis,¹ cell division,² membrane transport,³ motility,^4,5 pH homeostasis^6,7 and dynamic bacterial communication.^8,9 Accordingly, dysfunction of membrane bioenergetics appears to be a critical factor in bacterial cell death. Strikingly, dysregulated membrane potential and perturbation of pH homeostasis also appear to play a critical role in antibiotic induced lethality.^10–12 These findings suggest that antibiotic action could be improved by simultaneously targeting bacterial membrane potential during antibiotic treatment. The impact of membrane depolarization on antibiotic efficacy is relatively well-described.^13,14 Indeed, new antibiotics like daptomycin and telavancin act via permeabilizing and depolarizing the bacterial membrane.^15–18 In contrast, the impact of membrane hyperpolarization on antibiotic susceptibility is largely unknown. Recent studies indicate that certain inorganic compounds (e.g. gold nanoparticles) and antimicrobial peptides (AMPs) exert their bactericidal effects through hyperpolarization rather than depolarization of the bacterial membrane.^19–22 Intriguingly, Staphylococcus aureus mutants with a deficient potassium transport system were demonstrated to display a higher membrane potential and sensitivity towards AMPs.²³ Moreover, upon lethal stress with ribosome targeting antibiotics, growth-defective Bacillus subtilis cells exhibit a transient increase in membrane potential (hyperpolarization), followed by cell death.²⁴

Based on these considerations, we aimed to design novel peptide-based antimicrobial adjuvants that act primarily through inducing membrane hyperpolarization. We hypothesized that, when used in combination, such compounds would decrease the level of antibiotic resistance of multidrug-resistant pathogens. We focused on cationic AMPs for several reasons. AMPs frequently display synergism when combined with clinically relevant antibiotics, and antibiotic-resistant bacteria often show collateral sensitivity to these molecules.^25–28 It has also been demonstrated that resistance evolution against certain AMPs is limited.^29,30 Therefore, AMPs are a promising class of compounds that could potentially be employed in combination with antibiotics for the treatment of bacterial infections.^26,31 Given their broad spectrum of activity, much effort has been made to find potential novel antibacterial drug candidates among AMPs. Even though sceptics have raised concerns regarding low peptide stability and potential toxicity in vivo,^32,33 it is possible to develop peptide-based compounds with improved stability and activity, and reduced toxicity.^30,34

PGLa is a promising AMP that could serve as a starting point to design antimicrobial agents for combination therapy.²⁵ PGLa belongs to the magainin peptide family isolated from the skin surface of frogs. The strong hydrophobic interaction between the amphipathic helix and the lipid components is essential to disrupt bacterial membrane integrity, a mechanism involved in PGLa's direct antimicrobial effect. At low concentrations, however, PGLa permeabilizes the bacterial membrane and affects osmoregulation without forming pores in the membrane.³⁵ Indeed, both molecular dynamics simulations and confocal microscopy experiments suggest that PGLa can translocate through the membrane prior to pore formation.³⁶ Based on these findings, we hypothesized that at sub-inhibitory concentrations PGLa may simultaneously perturb ion homeostasis and bacterial membrane potential. If it were so, PGLa derivatives with improved properties could potentially be employed as adjuvants to re-sensitize antibiotic-resistant bacteria towards the available antibacterial agents.

Based on the molecular scaffold of PGLa, we designed new peptidomimetic foldamers that potentiate antibiotic activity against antibiotic-resistant bacteria and simultaneously display improved resistance to human proteases. We aimed to scale down the hydrophobic stabilization of the helix-membrane interaction in PGLa molecules, and thereby promote selective ion transport through the intact membrane. We performed structure-based rational modifications of PGLa at sites interacting with the bacterial membrane. The resulting PGLa analogues, PGLb1 and PGLb2 meet the following criteria: i) adopt a stable α-helix mimetic conformation, ii) its hydrophobic packing at the helix-membrane interface is altered, and iii) its Lys-type side-chains are retained to ensure electrostatic interactions with the membrane. These compounds display strong synergism with antibiotics, such as nalidixic acid and ampicillin against a range of pathogenic bacteria, driven by sequence-dependent hyperpolarization of the bacterial cell membrane.

Results and discussion

Molecular dynamics-assisted rational design of PGLa analogues

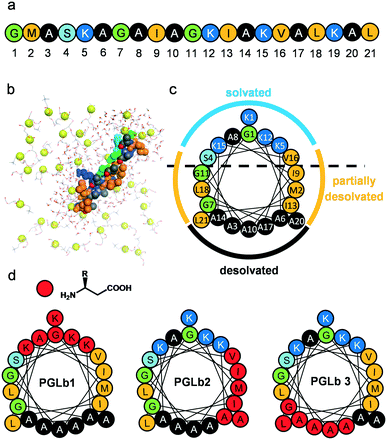
PGLa has the propensity to fold into an amphiphilic helix upon interaction with bacterial membranes. Using molecular dynamics (MD) simulations, we modelled the sequential membrane-induced folding of PGLa to identify the key amino acid residues involved in this process.

The simulations have revealed a complex and dynamic interplay between PGLa and the bacterial membrane, modelled with a lipid composition of DOPC/DOPG 8 : 2 (Fig. 1b). In particular, after the initial interactions of PGLa's side chains with the membrane within the first 500 ns, a nucleated stepwise folding process starts at the N-terminal part of PGLa molecules. This process includes three main consecutive folding steps involving the following peptide segments (Fig. S1†): Gly1–Gly7 (segment 1), Ala8–Lys15 (segment 2) and Val16–Leu21 (segment 3). Each folding step is separated by a few hundreds of nanoseconds and is coupled to the desolvation of key amino acid residues, including A3, A6, G7, A10, I13, A14, A17, A20 and L21. As might be expected, the local desolvation process substantially decreases the number of contacting water molecules (Fig. S2†).

Fig. 1 Structures of PGLa and the designed foldamers. The sequence of PGLa (a) PGLa in parallel orientation with the membrane surface. Yellow spheres indicate the phosphorus atoms of the lipid, surrounding waters are drawn with ball and stick model. (b) Helix wheel representation of PGLa and the different solvation states of residues along the helix surface. (c) Positions of modifications (homologous α → β³ amino acid replacements) are marked with red circles for the three designed foldamers: PGLb1, PGLb2, and PGLb3 (d).

In summary, the model indicates that the helix surface of PGLa can be dissected into three major areas (Fig. 1c): (i) fully desolvated hydrophobic residues responsible for the closely packed contacts with the interior of the bacterial membrane (Ala face), (ii) fully solvated residues with mostly basic side chains (cationic face), and (iii) partially solvated hydrophobic residues (partially solvated face).

PGLa-membrane interactions demand that the peptidic helix attains both parallel and tilted orientations within the membrane interior relative to the membrane surface.³⁷ Accordingly, we aimed to stabilize the helix formation of the peptide upon interaction with the bacterial membrane, and simultaneously decrease side chain packing density along the hydrophobic faces of the helix by backbone homologation. It is well established that α → β-amino acid replacements positioned evenly along the heptad repeat pattern of α-helices maintain the helical structure,³⁸ while α → β amino acid replacements at residues in close contact with the target generally disrupt the interaction.³⁹ Backbone homologation approach led to foldameric AMPs with tunable and improved properties.^40–42 Taken together, we designed and synthesized backbone homologated sequences(Fig. 1d and S3†) PGLb1 (cationic face), PGLb2 (partially solvated face) and PGLb3 (hydrophobic face).

Next, we tested whether these molecules retained the capacity to form helix upon membrane interaction. For this purpose, the circular dichroism (CD) spectrum of each molecule was recorded in the presence and absence of large unilamellar vesicles (LUVs) containing 1,2-dioleoyl-sn-glycero-3-phosphocholine/1,2-dioleoyl-sn-glycero-3-phosphoglycerol (DOPC/DOPG), which are regularly employed as a model for biological membranes.⁴³ All sequences displayed a random coil curve in the absence of LUVs (Fig. S4a†). The addition of 1 mM LUV resulted in marked changes of the CD curves for all compounds (Fig. S4b†). The CD curve of PGLa was characteristic of α-helix molecules, while in the case of PGLa analogues, the U-shaped CD fingerprints were replaced by a cotton-effect with the negative lobe at around 205 nm. These patterns are indicative of the helix formation of α/β-sequences.⁴⁴ These results suggest that backbone homologation had no major impact on membrane-induced folding of the PGLa analogues. Of note, PGLb3 had no antibacterial activity against E. coli BW25113, and therefore it was excluded from further investigations.

Synergism is prevalent between foldamers and antibiotics

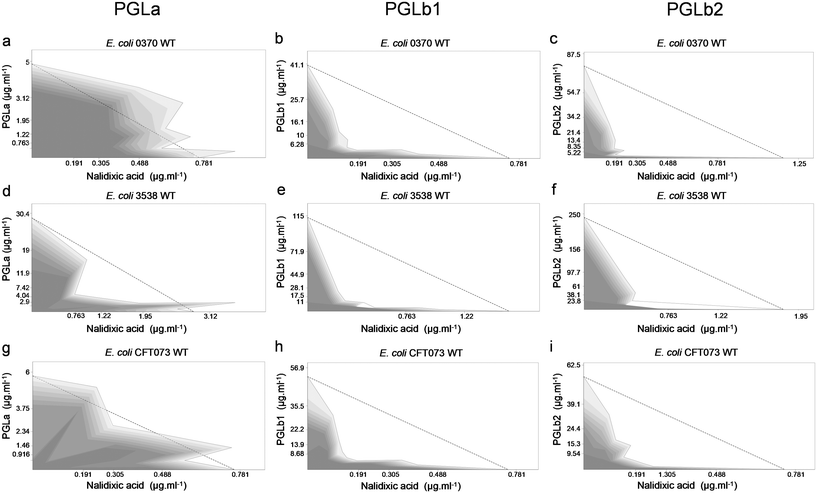
To investigate the antimicrobial effects of PGLa, PGLb1 and PGLb2, these compounds were systematically screened against three E. coli clinical isolates and their corresponding antibiotic-resistant variants. These compounds were found to exert a relatively weak antibacterial activity characterized by minimal inhibitory concentrations (MIC) in the range of 2.5 to 200 μg ml⁻¹ (Table S1†).

Next, we investigated whether these compounds act additively or synergistically in combinations with ampicillin and nalidixic acid. Nalidixic acid is a DNA synthesis inhibitor, while ampicillin targets the bacterial cell wall. We tested the impact of foldamer/antibiotic combinations on the growth rates of multiple E. coli isolates. The Loewe additivity model was used to assess drug–drug interactions, as this model estimates interactions based on deviation from the case of applying the drug by itself.⁴⁵ PGLb1 and PGLb2 induced strong synergism, while PGLa acted mainly additively with these antibiotics (Fig. 2, S5 and Table S2†). Remarkably, these patterns were evident both in antibiotic-sensitive and multidrug-resistant strains of E. coli (Table S2†).

Fig. 2 Peptide–nalidixic acid interactions. Combination effect of PGLa, PGLb1 or PGLb2 with nalidixic acid against the wild-type E. coli 0370 (a–c), E. coli 3538 (d–f), and E. coli CFT073 (g–i) strains. Dashed line represents no interaction calculated based on the Loewe additivity model (see Experimental section). Growth rate is represented in the combination space by the shade of the grey colour, with darker shades denoting higher growth rates.

Foldamers restore antibiotic activity in antibiotic-resistant bacteria

Based on the above results, we hypothesized that PGLb1 and PGLb2 could effectively target drug-resistant pathogenic bacteria when used in combination with antibiotics. To investigate this issue, we used clinical isolates of E. coli, K. pneumoniae and S. flexneri, all of which display clinically significant levels of resistance against nalidixic acid. PGLb1 and PGLb2 were administered at sub-inhibitory concentrations, i.e., at a dosage that permitted the growth of the isolates when the compound was used alone.

When used in combination with antibiotics, PGLb1 and PGLb2 substantially decreased resistance against nalidixic acid in all three bacterial species (Fig. 3). Next, we investigated the antimicrobial effects of moxifloxacin-PGLb1 and moxifloxacin-PGLb2 combinations against moxifloxacin-resistant strains of Enterobacter cloacae, Acinetobacter baumannii, and K. pneumoniae. Again, we found that PGLb1 and PGLb2 substantially decreased the level of resistance against moxifloxacin in all three species (Fig. S6†). We conclude that when co-administered with topoisomerase inhibitor antibiotics (such as moxifloxacin or nalidixic acid), PGLb1 and PGLb2 substantially reduce the level of antibiotic resistance in vitro. The same findings held when E. coli strains harbouring a single resistance mutation in the antibiotic target gene (gyrA) were targeted (Fig. S7†).

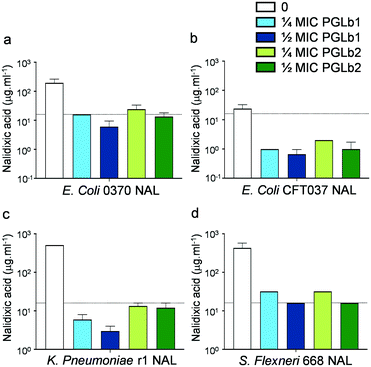Fig. 3 Impact of sub-inhibitory concentrations of foldamers on antibiotic activity against nalidixic acid-resistant bacteria. The MIC of nalidixic acid (NAL) was assessed in E. coli clinical isolates 0370 (a) and CFT073 (b), K. pneumoniae r1 (c) and S. flexneri 668 (d) strains, all of which are resistant to NAL, in the presence of 1/2 × MIC and 1/4 × MIC of the peptide against each strain*. When applied alone, neither of these peptide concentrations interfered with the growth of any of the strains. Dashed line represents resistance breakpoint for NAL (i.e. 16 mg l⁻¹) suggested by the CLSI (Clinical Laboratory Standards Institute).⁴⁴ Data are based on at least two biological replicates.

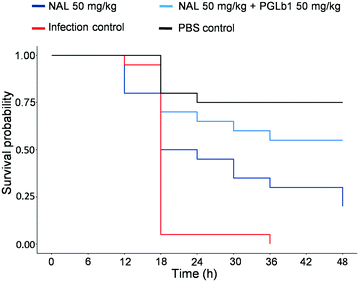
The above findings were corroborated by in vivo studies, via infecting the larvae of the greater wax moth Galleria mellonella with a clinical E. coli strain resistant to nalidixic acid. G. mellonella infection models utilized for testing bacterial infectivity and compound efficacy are rapidly gaining popularity due to the great reproducibility of test results and the lack of ethical concerns.^46,47 This established infection model was used to evaluate synergism between nalidixic acid and PGLb1 via assessing their effect on the survival of host larvae. When used alone, PGLb1 had no impact on the survival of G. mellonella (P = 0.37). In contrast, when used in combination with nalidixic acid, PGLb1 significantly enhanced the larvae's survival upon bacterial infection (Fig. 4). This finding indicates that PGLb1 can restore the antibacterial activity of nalidixic acid in vivo, hence it can increase the survival rate of G. mellonella. In Conclusion, the peptide PGLb1 shows promising results in terms of potentiating the effects of co-administered antibiotics.

Fig. 4 Co-administration of PGLb1 and nalidixic acid in vivo. Cell death kinetics of E. coli CFT073 resistant to nalidixic acid, over 48 hours. The phosphate buffered saline (PBS) control group received one injection of sterile phosphate buffered saline, while the other groups were infected with approximately 2 × 10⁷E. coli cells. The infection control group received no further treatment, while the other two groups were treated with 50 mg kg⁻¹ nalidixic acid or 50 mg kg⁻¹ nalidixic acid + 50 mg kg⁻¹ PGLb1, respectively. Animals treated with nalidixic acid and PGLb1 in combination showed a significantly higher survival rate than those treated with nalidixic acid alone (P = 0.02) experiments were performed in two biological replicates, with 10 animals per treatment group, hence each curve represents 20 animals.

Foldamers induce hyperpolarization of the bacterial membrane

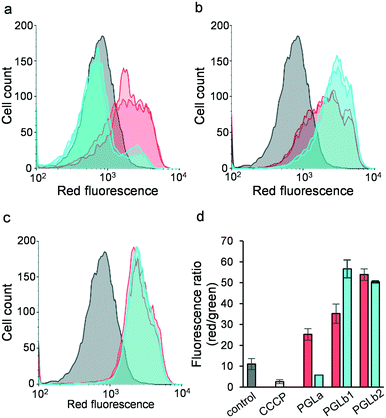
Based on their suggested mechanism of action, we hypothesized that PGLb1 and PGLb2 restore antibiotic activity by interfering with the bacterial membrane potential. To test this hypothesis, we measured the changes in membrane potential of E. coli cells in response to PGLa, PGLb1 or PGLb2, each administered individually at sub-inhibitory concentrations. The membrane potential was determined by flow cytometric analysis using the membrane potential sensitive dye DiOC₂(3).⁴⁸ To avoid any potential bacterial cell death associated with DiOC₂(3), all measurements were run after 15 or 30 minutes of incubation (Fig. 5). When applied at sub-inhibitory concentrations, PGLb1 and PGLb2 induced substantial and sustained hyperpolarization of the bacterial membrane, while PGLa had only a relatively mild and transient effect on membrane polarity. Intriguingly, there was no sign of membrane depolarization under PGLb1 or PGLb2 stress during the entire course of the experiment, indicating that these molecules do not induce membrane rupture or ion depletion when applied at sub-inhibitory concentrations. In contrast, PGLa depolarized the bacterial membrane after 30 minutes of incubation.

Fig. 5 Flow cytometric membrane polarization assay (BacLight) carried out in E. coli. Bacterial cells were stained with the fluorescent membrane potential indicator dye diOC₂(3). Flow cytometry histograms for the red channel are shown in panels a) PGLa, b) PGLb1 and c) PGLb2 after 15 minutes (red) and 30 minutes (blue) of incubation; control cells are plotted in grey. d) Ratio of red and green fluorescence recorded for cells treated with the peptides and the membrane depolarizing proton ionophore CCCP. A decrease in the ratio corresponds to depolarization, while an increased ratio corresponds to a hyperpolarized membrane potential. Red and blue bars represent measurements after 15 and 30 minutes of incubation, respectively.

Foldamers induce the Goldman–Hodgkin–Katz (GHK) potential via selective ion transport

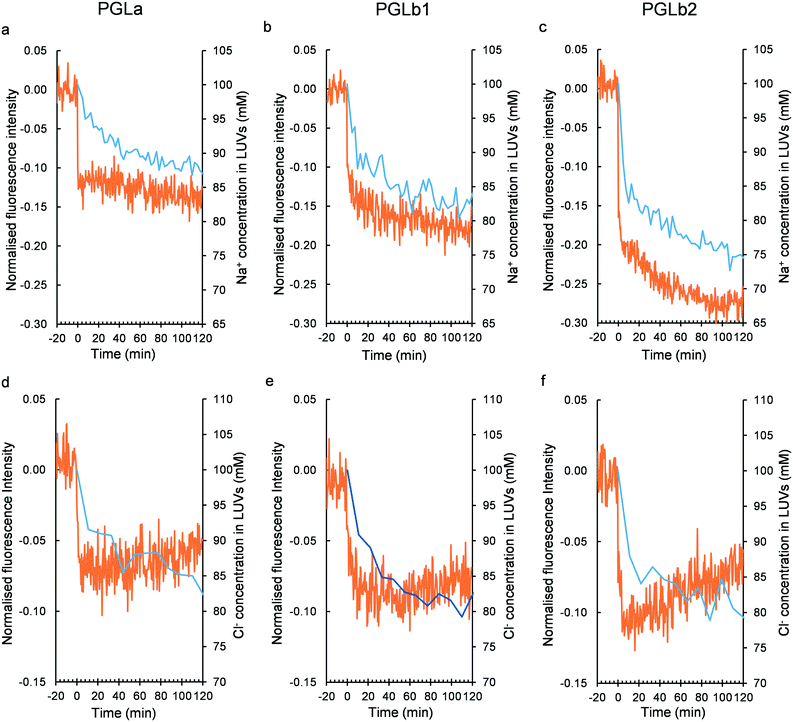
Next, we investigated the molecular mechanisms that could underlie membrane hyperpolarization induced by PGLb1 and PGLb2. Theoretically, the initial binding of the cationic regions of these molecules to the negatively charged bacterial membrane may shift the static component of the membrane potential. Alternatively, PGLb1 and PGLb2 may act as selective ion transporters that shape the Goldman–Hodgkin–Katz (GHK) potential. Of note, the dynamic Goldman–Hodgkin–Katz (GHK) potential is driven by differential ion permeabilities, as well as by active ion transport across the bacterial membrane.⁴⁹

To assess these potential molecular mechanisms, a voltage-sensitive dye (oxonol VI)⁵⁰ was utilized in an established large unilamellar vesicle (LUV) system with the composition of DOPC/DOPG 7 : 3. The experimental setup was validated by using valinomycin, a K⁺-selective ionophore. Upon establishing a K⁺ (outside)/Na⁺ (inside) ion gradient across the vesicle's bilayer surface, we found that valinomycin decreased the dye's fluorescence level by promoting a positive (inside) GHK potential (Fig. S8†). The decreasing fluorescence level of the dye indicates an elevated positive inside membrane potential in this LUV system. Upon adding PGLa, PGLb1 and PGLb2 without establishing a K⁺/Na⁺ ion gradient, only minor changes in the fluorescence level were observed (Fig. S10†). This suggests that these compounds have only a relatively small impact on the static component of the membrane potential. In contrast, when a K⁺/Na⁺ ion gradient was established prior to adding PGLb1 or PGLb2 to the medium, these sequences induced a rapid and marked drop in fluorescence level (Fig. 6). This finding indicates the presence of a significant positive inside GHK potential in the LUV model, facilitated by a K⁺-selective ion transport. The positive potential can be controlled by the outside K⁺ concentration corroborating the GHK origin of membrane polarization (Fig. S10†). A similar change in membrane potential was observed when an anion gradient (Cl⁻ inside and NO₃⁻ outside) was introduced into the LUV samples, indicating the ability of the sequence to conduct both cations and anions with differential permeabilities. Taken together, these findings support that the studied sequences induce membrane hyperpolarization via selective ion transport.

Fig. 6 Membrane polarization and ion transport assessments in the LUV model. Peptide-induced membrane potential (red curve) and intravesicular Na⁺ concentration (blue curve) changes in the Na⁺/K⁺ exchange experiments (100 mM NaCl in the intra- and 100 mM KCl in the extravesicular space) upon adding PGLa (a), PGLb1 (b) and PGLb2 (c). Peptide-induced membrane potential (red curve) and intravesicular Cl⁻ concentration (blue curve) changes in the Cl⁻/NO₃⁻ exchange experiments (100 mM NaCl in the intra- and 100 mM NaNO₃ in the extravesicular space) upon adding PGLa (d), PGLb1 (e) and PGLb2 (f). The normalized relative fluorescence level for the membrane potential-dependent dye oxonol VI was monitored. A negative change indicates a positive potential inside. The ion concentrations were determined by ²³Na and ³⁵Cl NMR assays. To distinguish between the external and internal ion signals, NMR chemical shift reagents 1 mM Dy(PPP)₂⁷⁻ for ²³Na, and 4 mM Co(NO₃)₂ for ³⁵Cl were utilized.

Next, we further elaborated in detail how PGLa and the corresponding analogues shape ion transport across the membrane. Specifically, time-dependent Na⁺/K⁺ and Cl⁻/NO₃⁻ exchanges were monitored by detecting ²³Na and ³⁵Cl NMR signals⁵¹ in the LUV-based membrane model. Upon adding the test compounds, we observed Na⁺/K⁺ and Cl⁻/NO₃⁻ exchanges across the LUV's bilayer surface (Fig. 6). In contrast, no transport of shift reagents (Dy³⁺ or Co²⁺) was detected, nor did the size distribution of LUV changed according to dynamic light scattering (Fig. S11–S14†). The affinity and stoichiometry for peptide-ion interactions were in line with their ability to transport ions (Fig. S15–S17†). These findings indicate that PGLa, PGLb1, and PGLb2 shape the flux of single charged ions only, without rupturing the membrane in the LUV model when applied at low (sub-inhibitory) concentrations.

Stability and toxicity analyses

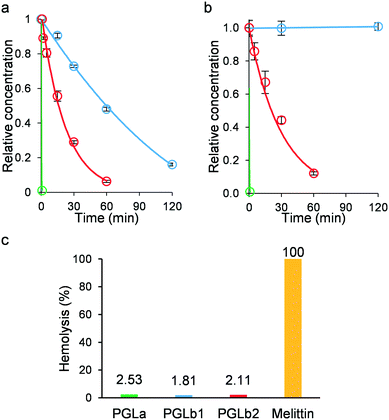
Regarding the clinical application of peptide-based antibacterial drugs, at least two general concerns arise: the issue of low stability in the presence of human protease enzymes and potential toxicity. Indeed, PGLa contains numerous lysine molecules, almost evenly distributed along the peptide sequence, which could render PGLa an ideal target for human trypsin and proteinase K, a broad-spectrum serine protease. However, introducing a non-natural β-amino acid into PGLa could improve resistance of PGLb1 and PGLb2 to human proteases. As expected, PGLa was rapidly decomposed in the presence of both enzymes (Fig. 7a and b), while the half-lives of PGLb1 and PGLb2 were substantially improved under the same conditions. Finally, we performed a haemolysis assay on human red blood cells using standard protocols (Fig. 7c), and found that neither PGLb1 nor PGLb2 had a significant haemolytic effect (<5% haemolysis). These results are promising, thus future studies should investigate the stability and potential toxicity of these peptidomimetics in more details.

Fig. 7 Protease stability and toxicity assays. a) Stability of PGLa (green), PGLb1 (blue) and PGLb2 (red) against trypsin. b) Stability of PGLa (green), PGLb1 (blue) and PGLb2 (red) against proteinase K. c) Haemolytic activity of PGLa (green), PGLb1 (blue) and PGLb2 (red) at 500 μg ml⁻¹ concentration compared to melittin at 50 μg ml⁻¹ concentration.

Conclusions

The global rise of multidrug-resistant bacteria has rendered several existing antibiotics ineffective. Several prior works showed that AMPs in combination with antibiotics could potentially be employed to effectively target multidrug-resistant bacterial pathogens of critical clinical importance.^25–28,52

In this work, we have focused on a rational, computer-assisted backbone homologation design approach to modify the secondary structure of PGLa, and thereby its ion transport properties. When administered at sub-inhibitory concentrations, PGLb1 and PGLb2 induced an up to 128-fold decrease in the antibiotic resistance level of E. coli, K. pneumoniae and S. flexneri clinical isolates. PGLb1 and PGLb2 appear to be stable against human proteases, and preliminary tests have revealed no toxicity in human red blood cells. These results are promising, and suggest that upon further chemical optimization, such compounds could be used as adjuvants capable of selectively potentiating antibiotic activity against antibiotic-resistant bacteria. Clearly, future studies should investigate the stability, potential toxicity, and in vivo effects of these peptidomimetics in far more details.

Our work has some other, broader implications for antibiotic research. PGLb1 and PGLb2 act as selective ion transporters that shape the Goldman–Hodgkin–Katz (GHK) potential. Specifically, they are selective towards K⁺ over Na⁺, and this selectivity leads to sustained hyperpolarization of the bacterial membrane. In parallel, we observed a selective transport of Cl⁻ ions across the membrane, a pattern that might contribute to the development of the excessive negative membrane potential. The observed ion selectivity of PGLb1 and PGLb2 is all the more surprising, as most AMPs exert their antimicrobial effects via non-selective membrane rupture resulting in membrane depolarization, rather than membrane hyperpolarization. Our work also indicates that, by computer-assisted rational design, it is possible to design peptide-based selective ionophores which could be utilized to effectively target antibiotic-resistant bacteria. We note, however, that by reducing respiration and consequent depolarization of the membrane, pathogenic bacteria can enter into a persistent state wherein they can better survive lethal antibiotic stress.⁵³ In the future, we aim to investigate whether membrane hyperpolarization induced by PGLa analogues could be utilized in combinational antibiotic/foldamer treatment strategies to eliminate resistant bacterial subpopulations in vivo.

The exact mechanistic link between membrane hyperpolarization and antimicrobial effects remains to be elucidated. We have revealed synergism between PGLa analogues and antibiotics belonging to the penicillin and quinolone families. Despite major differences in their molecular mechanism of action, the uptake of these antibiotics is facilitated by the outer membrane porin OmpF.^54,55 Outer membrane porins are generally voltage-controlled,⁵⁶ raising the possibility that hyperpolarization modulates antibiotic susceptibility via modulating porin activity. In summary, our work demonstrates that it is feasible to rationally design new peptidomimetic foldamer antimicrobials that induce hyperpolarization of the bacterial membrane via a controlled biophysical mechanism, capable of enhancing the sensitivity of multi-drug resistant bacteria towards existing antimicrobial compounds.

Experimental section

Molecular dynamic simulations

The initial, extended structure of PGLa (G1-M2-A3-S4-L5-A6-G7-A8-I9-A10-G11-K12-I13-A14-K15-V16-A17-L18-K19-A20-L21-NH₂) was built up by means of the tleap leap module of AMBER16 (ref. 57) program package. The structure obtained was solvated with TIP3P⁵⁸ water model and appropriate number of chlorine ions (e.g. 5) was added also ensuring the electro-neutrality of the system. The ff03.r1 forcefield parameter set⁵⁹ was assigned for the peptide and hydrogen mass repartition⁶⁰ was applied, as well. For this structure 800 ns long molecular dynamics simulation was performed in order to obtain the initial structure for membrane simulation with the following protocol. In the first step the structure was minimized, and two, consecutive NVT simulation was conducted at 10 and at 303 K, with a duration was 20 ps for each step. In the next step 200 ps long NPT calculation was conducted in order to equilibrate the density of the system and finally we applied again the NVT ensemble. The temperature was kept constant using Langevin dynamics⁶¹ and in the NPT step Berendsen barostat was used⁶² and the cut-off value was set to 10 Å.

Mixed DOPC/DOPG membranes (80 : 20 ratio) was constructed by means of the CHARMGUI web server.⁶³ 80 lipids were used as a model membrane resulting in 1 : 80 peptide : lipid ratio. The generation was repeated 3 times in order to obtain different surface distribution of different membrane components. Finally the chirality of the DOPG headgroups was changed randomly for each structure 3 times resulting DOPG(S) : DOPG(R) 50 : 50 ratio, and altogether 9 lipid systems. The number of water molecules per lipid monomer was >50 in each case and due to the anionic nature of DOPG 16 Na⁺ were added to the systems, as well.

The 9 lipid systems were equilibrated using the protocol described in the LIPID14 article.⁶⁴ The difference was in the applied pressure scaling, where we used semi-isotropic scaling, and the surface tension value was set to 0 dyn per cm and we applied the hydrogen mass repartition⁶⁰ here as well. The last structure of the 125 ns calculation was used in the final lipid–peptide system preparation. Peptide structures were placed at least 20 Å from the membrane-water interface and additional water molecules were added also around the peptide. The number of atoms in final systems size varied between 29 586 and 32 805, and a stepwise equilibration and production protocol was used for investigating the folding process of PGLa at the membrane-water interface.

Due to the complex nature of the system, we started the simulation with a three-step minimization protocol. In the first step, only the position of the H-atoms was optimized, heavy atoms were restrained with a force constant of 10 kcal mol⁻¹ Å⁻². In the second step, water molecules and ions were optimized, and an unrestrained optimization was performed in the last step. Thereafter the systems were heated in two steps: from 10 K to 100 K in 20 ps and from 100 K to 303 K in 100 ps using NVT ensemble and restraining the lipids and peptide. After the NVT calculation we turned to NPT calculations, the length of which varied between 375 and 1125 ns. Temperature and pressure regulation was the same as those applied for the pure lipid simulations.

Peptide synthesis and purification

All starting materials were commercially available. Peptides PGLa, PGLb1, PGLb2 and PGLb3 were synthesized by SPPS using Fmoc-chemistry. Tentagel R RAM resin was used as solid support and COMU was used as coupling reagent. Couplings were performed for 90 minutes with 5-equivalent amino acid excess for α-, and for 180 minutes with 3-equivalent for β-residues. Peptides were cleaved with TFA/water/D,L-dithiothreitol/triisopropylsilane (90 : 5 : 2.5 : 2.5) and precipitated in ice-cold diethyl ether. The resin was washed with acetic acid and water and was subsequently filtered and lyophilized. The peptides were purified with RP-HPLC on a C18 column (Phenomenex Luna, 250 × 10 mm). The HPLC eluents were (A) 0.1% TFA in water and (B) 0.1% TFA and 80% ACN in water, with a gradient from 30% to 60% B over 60 min, at a flow rate of 4 ml min⁻¹. Purity was confirmed by analytical RP-HPLC and ESI-MS measurements.

Peptide content study

Peptide contents⁶⁵ of PGLa and analogues was measured with NanoDrop (UV-vis spectrophotometer) from Thermo Scientific™ using direct absorbance at 205 nm. Samples were dissolved in water (as buffers used in other studies show high absorbance at same wavelength). For measurements 2 μL of sample were pipetted directly on the sample pedestal. A205 direct absorbance pre-program in NanoDrop One was used for scanning. Absorbance was measured at various dilutions and data generated within a linear range for absorbance versus concentration were averaged (Table S4†).

Preparation of large unilamellar vesicles (LUVs) of DOPC : DOPG

LUVs were prepared following a standard literature method.⁶⁶ 20 mM DOPC/DOPG – LUVs containing 100 mM NaCl in the intravesicular and 100 mM NaNO₃ in the extravesicular space were prepared by mixing DOPC and DOPG in molar ratio of 7 : 3 from chloroform stocks in a clean and dry round bottom flask. A thin film of DOPC/DOPG was obtained by purging nitrogen gas for 30 min over the chloroform solution. It was then kept under reduced pressure for 48 hours to remove residual chloroform from the film. Then, the film was hydrated with 20 mM HEPES buffer, pH 7.2 containing 100 mM NaCl on a shaker for at 4 °C to get multilamellar vesicles. After 1 hour, the suspension was passed through 12 cycles of freeze–thaw to break multilamellar vesicles. The vesicles were then extruded through an extruder with pore size of 200 nm from T&T Scientific Corporation lipids for 21-times at 4 °C. To remove unencapsulated NaCl from the lipid suspension, the suspension was filtered 6 times through 0.5 ml 10 kDa amicon from Merck Millipore (at 12 000 rpm for 60 min), each time adding fresh 20 mM HEPES buffer, pH 7.2, containing 100 mM NaNO₃. Removal of extravesicular chloride was confirmed by NMR. The final volume was adjusted using 20 mM HEPES buffer pH 7.2, containing 100 mM NaNO₃. The LUVs with 100 mM KCl in the extravesicular space were prepared in the same way, except for the removal of unencapsulated NaCl and adjustment of final volume, which was done with 20 mM HEPES buffer, pH 7.2, containing 100 mM. Lipid concentration was verified by a colorimetric assay.⁶⁷

NMR measurements

Na⁺/K⁺ exchange was measured with 100 mM NaCl in the intravesicular and 100 mM KCl in the extravesicular space of the LUVs, while Cl⁻/NO₃⁻ exchange was measured with 100 mM NaCl in the intravesicular and 100 mM NaNO₃ in the extravesicular space. Dy(PPP)₂⁷⁻ and Co(NO₃)₂ were used as ²³Na and ³⁵Cl chemical shift reagents outside, respectively.^68,69 The experimental setup was further validated by a selective anionophore prodigiosine (Fig. S12†),⁶⁶ and a membrane disrupting agent Triton-X (Fig. S13†). All spectra were recorded on a Bruker Ascend 500 spectrometer with a 5 mm BBO Prodigy Probe at 310 K. ²³Na NMR: operating at 132.3124 MHz, spectral width 9091 Hz, 64 data points, relaxation delay 0.1 s, ninety-degree pulse 10 μs. 0.5 μL 1 M Dy(PPP)₂⁷⁻ were added to 500 μL LUV suspension as a shift reagent in each sample. ³⁵Cl NMR: operating at 49.0091 MHz, spectral width 10 000 Hz, 3000 data points, relaxation delay 0.1 s, ninety-degree pulse 20 μs. 2 μL 1 M Co(NO₃)₂ were added to 500 μL LUV suspension as a shift reagent in each sample.

Membrane potential measurements on LUVs

Fluorescent measurements were carried out using an Optima Fluostar plate reader. The excitation wavelength was set to 580 nm (slit width 10 nm) and the emission wavelength to 640 nm (slit width 10 nm). 0.2 mM LUVs containing 100 mM NaCl in the intravesicular and either 100 mM KCl or 100 mM NaNO₃ in the extravesicular space (diluting from the corresponding 20 mM LUV stock) was used for the measurements. 1 mg ml⁻¹ [3.16 mM] oxonol VI stock in ethanol was freshly diluted before measurement in the corresponding buffer to get the final concentration of 0.45 μM in the plate. Required volumes of LUVs and oxonol VI were mixed just before the scan. 290 μl aliquots of the LUVs and oxonol VI mix were measured into Nunc 96-well transparent flat-bottom plates, with 3 parallels. 10 μl of peptide stock solutions (half-MIC value) were added with multi-channel pipette after the fluorescence flatlined (typically 40 minutes). Valinomycin stock solution was 1.8 mM in ethanol, which was diluted to 0.45 μM in the same buffer as before. Fluorescence response of buffer addition was used as background. Measurements were done at 37 °C temperature control. The fluorescence intensity was normalized by (F − F₀)/F₀, where F is average intensity of the peptides and valinomycin cells respectively and F₀ is the average intensity of the buffer cells.

Membrane potential assay

A previously described protocol⁷⁰ was used to determine the change in transmembrane potential for wild-type E. coli BW25113 strain upon AMP treatment. BacLight™ Bacterial Membrane Potential kit (Invitrogen) was used to perform the membrane potential assay. This assay is based on a fluorescent membrane potential indicator dye that emits green fluorescence in all bacterial cells and the emission shifts to red in the cells that maintain a high membrane potential. The resulting ratio of red/green fluorescence provides a measure of membrane potential. Prior to the measurement bacterial cells were grown overnight in minimal salt (MS) medium at 30 °C with shaking at 200 rpm. The overnight grown cultures were diluted into fresh MS medium and grown further until cell density reached OD₆₀₀ 0.5–0.6. The grown cultures were diluted to 10⁶ cells per mL in filtered PBS buffer. Diluted cells were incubated with a sub-MIC concentration of the tested peptides (PGLa, PGLb1 and PGLb2) for 15 and 30 minutes at 37 °C. Following incubation, 5 μl of 3 mM DiOC₂(3) was added to each sample tube containing 500 μl of bacterial suspension. Control populations treated with cyanide-m-chlorophenylhydrazone (CCCP, a chemical inhibitor of proton motive force) were used as an experimental control. Red to green fluorescence values of the samples were measured using fluorescence activated cell sorter (BD Facscalibur).

Antibiotics

The following antibiotics were used in this study: ampicillin, nalidixic acid (NAL) and moxifloxacin (MOX). Nalidixic acid was purchased from Fluka, Hungary. Ampicillin and moxifloxacin were purchased from Sigma-Aldrich. Fresh antibiotic solutions were prepared from powder stocks on a weekly basis, kept at −20 °C and filter sterilized before use.

Strains

E. coli K-12 BW25113 was used as the wild-type strain. The three E. coli uropathogen clinical isolates (0370, 3538, CFT073) before and after adaptation to nalidixic acid (NAL) and ampicillin, the K. pneumoniae r1 and the S. flexneri 668 clinical isolates and their NAL evolved strains were kindly provided by Morten Sommer, Technical University of Denmark, Hørsholm. The pathogen strains Enterobacter cloacae BAA2341, K. pneumoniae ATCC700603 and Acinetobacter baumannii BAA1605, were purchased from Microbiologics, Hungary.

Medium

As a general rule minimal salts medium optimized for AMPs was used for the combination and antibiotic susceptibility testing on the E. coli uropathogen clinical isolates (0370, 3538, CFT073) and the K. pneumoniae r1.⁷¹ The medium contained 1 g l⁻¹ (NH₄)₂SO₄, 3 g l⁻¹ KH₂PO₄ and 7 g l⁻¹ K₂HPO₄ supplemented with 0.1 mM MgSO₄, 0.54 μg ml⁻¹ FeCl₃, 1 μg ml⁻¹ thiamine hydrochloride, 0.2% Cas amino acids and 0.2% glucose. Minimum inhibitory concentrations of antibiotics and peptides against all other strains were performed using Muller-Hinton II broth.

MIC measurements

MICs were determined using a standard serial broth dilution technique.⁷² Experiments on the impact of PGLa, PGLb1 and PGLb2 co-treatment on antibiotic-resistance levels used 2-times serial dilution of antibiotic and an inoculum of 5 × 10⁵ bacteria per ml as suggested by the Clinical and Laboratory Standards Institute (CLSI) guidelines. To avoid possible edge effects, rows A and H contained only media devoid of cells. The environment during incubation was also set to minimize evaporation and hence edge effects. After 18 h of incubation at 37 °C, raw A_{600 nm} values were measured in a Biotek Synergy microplate reader. MIC was defined by a cut-off A_{600 nm} value (mean + 2 s.d. of A_{600 nm} values of bacteria-free wells containing only growth medium).

Antibiotic-peptide combination screens

Experiments were conducted on E. coli uropathogen clinical isolates (0370, 3538, CFT073) to two different antibiotics (nalidixic acid and ampicillin). Drug interaction was defined as deviation from non-interaction under the Loewe additivity model,⁴⁵ which assumes that a drug does not interact with itself. We followed a previously published protocol⁷³ with two important modifications. First, instead of examining all pairwise combinations of a predefined number of linearly increasing concentration points, we focused on a set of different antibiotic-peptide relative concentration ratios and their dilution series. This setup enabled us to efficiently sample the most informative regions of the two-dimensional concentration space. Second, we inferred drug interactions based on concentration combinations that led to 90% growth inhibitions. This enabled an especially robust detection of growth inhibition for AMPs, which often exhibit steep dose–response curves that hinder precise measurement of, say, 50% inhibition concentrations. As a first step, for each single agent (antibiotic and peptide alike), a 1.6-fold, eight-step dilution series was prepared with dose points determined based on the MIC of the agents. The concentration range for each agent was between 10.5 times lower and 2.6 times higher than the MIC of the strain. Then, for each antibiotic peptide pair we set up a 96-well plate as follows: we defined 7 different antibiotic/peptide relative concentration ratios (7 : 1, 3 : 1, 5 : 3, 1 : 1, 3 : 5, 1 : 3, 1 : 7) and generated dilution series thereof across the plate. As a result, each plate contained dilution series of seven antibiotic/peptide ratios, dilution series from the given antibiotic or peptide alone, four bacteria-free wells (no growth control) and four wells containing only medium without any drugs (growth control). Combination screen plates were inoculated with 5 × 10⁴ cells per well from overnight culture (grown at 30 °C, with shaking at 300 rpm). The culture volume was 100 μl. Assay plates were incubated at 30 °C with shaking at 300 rpm and bacterial growth was monitored by measuring the A_600nm of the liquid cultures after 24 h. We chose an incubation time of 24 hours in order to be able to discern condition-specific fitness defects from general costs of resistance of the antibiotic-resistant strains.

To assess antagonism and synergy between pairs of antibiotics and peptide in the sensitive wild type and in the antibiotic-resistant strains, we used the Loewe additivity model⁴⁵ which assumes that a drug does not interact with itself. To identify interactions for each pair of antibiotics and peptide we first calculated relative inhibition values based on the initial A_600nm (maximum inhibition) and the average A_600nm of antibiotic-free control wells (maximum growth). Then, we identified those two concentration points for each antibiotic/peptide ratio where the inhibition of the growth was just above and below 90%, respectively. By fitting a linear model between these two concentration points we could interpolate the dosages for each antibiotic/peptide ratio that were responsible for the 90% growth inhibition (90% effective dosage: EC90%). Based on the Loewe model from the EC90% values of the single agents, we then calculated the theoretical EC90% dosages for each of the seven antibiotic/peptide ratios. Geometrically, the theoretical EC90% based on the Loewe model can be represented as a straight line between the EC90% of the single agents in the two-dimensional linear concentration space. Deviation of the shape of the lines connecting the experimentally measured EC90% from linearity indicates either synergy (concave isoboles) or antagonism (convex isoboles). For each of the seven antibiotic/peptide ratios we defined the expected and the experimentally measured EC90% values. The combination index was calculated as: (theoretical EC90%)/(experimental EC90%) for each antibiotic/peptide ratio (CI_r). The combination index for a given antibiotic and peptide pair was defined as the average of the combination index of the seven antibiotic/peptide ratios (mean(CI_r1,CI_r2…,CI_r7)). Where multiple independent experimental runs were available, we calculated the average value of the measured combination indexes. Measurement errors of interaction screens were estimated from two independent experimental runs of 24 combinations by calculating the pooled variance (standard deviation) of the combination indexes of the replicate experiments. The cut-off values were defined as 1.95 × s.d. value of the combination index. The cut-off values were as follows: combination index ≥ 1.14 for antagonism; combination index ≤ 0.86 for synergism; and 0.86 < combination index < 1.14 for no interaction.

In vivo experiments

Age and weight defined TruLarv™ Galleria mellonella caterpillars were obtained in bulk from BioSystems Technology (University of Exeter, Exeter, United Kingdom) and stored at 15 °C in absence of food. E. coli CFT073 nalidixic acid resistant line was grown overnight in Mueller-Hinton II broth and washed twice in sterile phosphate buffered saline (PBS). In the case of every experiment, treatment solutions were injected into the hemocoels of the larvae via the first left proleg (bacteria) and the second right proleg (antibiotics) using 10 μl Hamilton syringes (Reno, Nevada, U.S.A.). Larvae were incubated in petri dishes lined with filter paper at 37 °C for 48 h and survival was documented every 6 hours. Insects were considered dead if they failed to respond to touch. In order to with the aim of establishing the inoculum required to kill G. mellonella over 48 hours, 10 caterpillars were inoculated with 10 μl of bacterial suspensions containing 10³, 10⁴, 10⁵, 10⁶ and 10⁷ CFU/larva of bacteria in PBS. CFU number was verified by viable bacterial counts on Mueller-Hinton II agar. Based on this preliminary experiment 10⁷ was determined as the ideal inoculum size to kill G. mellonella larvae. The toxicity of both nalidixic acid and peptide PGLb1 were observed by injecting 10–10 larvae with 10, 25, 50, 100 and 200 mg per body weight kg of the compounds, respectively. Nalidixic acid showed no toxicity on higher concentration, while PGLb1 showed moderate toxicity above the 10 mg per body weight kg dose (+20–50% death compared to the control group). Nalidixic acid and PGLb1 monotherapy and nalidixic acid+ PGLb1 combination therapy were tested by first injecting the larvae with E. coli CFT073 nalidixic acid resistant line, then the appropriate antibiotic treatment. Monotherapies were tested with 10, 25, 50 and 100 mg per body weight kg doses. Nalidixic acid at 50 mg per body weight kg improved survival by approximately 25%, while PGLb1 in monotherapy did not improved survival in any tested concentrations. Finally, in the case of combination therapy, nalidixic acid had been used at a fixed 50 mg per body weight kg concentration, while PGLb1 was added at 25, 50 and 100 mg per body weight kg, respectively. Among those experimental setups, adding 50 mg per body weight kg peptide PGLb1 provided the best results.

Hemolysis assay

Human red blood cells (hemoglobin concentration (Hb) 150–160 g L⁻¹) were collected from apparently healthy patients in EDTA tubes. 600 μL of EDTA-blood were washed in TBS buffer (10 mM TRIS, 150 mM NaCl) and centrifuged at 1500g for 1 min until the supernatant became colourless/colourless. The final pellet was diluted to 5 mL with TBS buffer. Hundred microliters of this cell suspension were pipetted into sterile Eppendorf tubes together with twofold serial dilutions of each compound to a final volume of 200 μl. Final concentrations ranged between 2500–9.75 μg mL⁻¹. Following incubation for one hour at 37 °C, samples were centrifuged at 1500g for 1 min to precipitate the red blood cells. All supernatants were transferred to sterile 96-well plates for the measurement of their direct optical density (OD) at 565 nm wavelength (Multiskan FC microplate reader, Thermo Scientific). Melittin (Bachem) at concentration of 50 μg mL⁻¹ and TBS were used as positive (100% hemolysis) and negative (no hemolysis) controls, respectively. Haemolytic effect of each peptide at each concentration was calculated as follows: hemolysis effect = (compound OD_565nm − TBS OD_565nm) × 100/(Melitin OD_565nm − TBS OD_565nm).

Protease resistance assay

Experiments with proteinase K were measured in 50 mM TRIS pH 7.5, with 100 μM peptide and 25 μg mL⁻¹ enzyme concentrations. 50 μL of the mixture was diluted into 450 μL 2.5% TFA solution to quench the degradation. Experiments with trypsin were measured in 50 mM TRIS pH 7.8, with 500 μM peptide and 100 μg mL⁻¹ enzyme concentrations. 20 μL of the mixture was diluted into 480 μL 2.5% TFA solution to quench the degradation. Samples were taken from the reaction mixtures at 0, 5, 15, 30, 60 and 120 minutes. For PGLb1, the experiment was extended for 24 hours. Reverse phase – high performance liquid chromatography – mass spectrometry (RP-HPLC-MS) measurements were run using Phenomenex Widepore C18 column (250 × 4.6 mm). Peak areas were calculated with the default setting of the ICIS algorithm.

Data availability

All the necessary data were provided in ESI.†

Author contributions

K. N. B. prepared LUV. G. O. synthesized all studied materials. K. N. B. and A. H. design experiment, data analysis and carried out NMR measurements. K. N. B. and G. O. measured membrane polarization. A. M. designed and performed in vitro combination experiments, R. S. and L. D. carried out in vitro antibacterial experiments., L. N. and B. J. carried out computational analysis. P. S. performed the in vivo studies. A. D. and P. K. J. carried out flow cytometric membrane polarization assay. I. F. and D. K. carried out protease stability and toxicity assays. C. P. and T. A. M. wrote the paper with input from all co-authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The study was supported by the following research grants: European Research Council H2020-ERC-2014-CoG 648364-Resistance Evolution (CP); European Research Council H2020-ERC-2019-PoC 862077-Aware (CP), ELKH Lendület Programme LP-2017-10/2020 (CP); ‘Élvonal’ Programme KKP 126506 of the National Research, Development and Innovation Office, Hungary (CP), National Laboratory of Biotechnology Grant NKFIH-871-3/2020 (CP), GINOP-2.3.2-15-2016-00014 (EVOMER) (CP, TAM), GINOP-2.3.2-15-2016-00020 (MolMedEx TUMORDNS) (CP), and NKFI PD 116222 (AM), NKFI K134754 (TAM), Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT (TAM). The authors thank Dora Bokor, PharmD, for proofreading the manuscript.

References

1. P. C. Maloney, E. R. Kashket and T. H. Wilson, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 3896–3900.
2. H. Strahl and L. W. Hamoen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12281–12286.
3. R. J. Poole, Annu. Rev. Plant Physiol., 1978, 29, 437–460.
4. J. B. Miller and D. E. Koshland, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 4752–4756.
5. S. Nakamura and T. Minamino, Biomolecules, 2019, 9, 279–302.
6. E. Padan, D. Zilberstein and S. Schuldiner, Biochim. Biophys. Acta, Rev. Biomembr., 1981, 650, 151–166.
7. T. A. Krulwich, G. Sachs and E. Padan, Nat. Rev. Microbiol., 2011, 9, 330–343.
8. D.-Y. D. Lee, A. Prindle, J. Liu and G. M. Süel, Cell, 2017, 170, 214–214.e211.
9. A. Prindle, J. Liu, M. Asally, S. Ly, J. Garcia-Ojalvo and G. M. Süel, Nature, 2015, 527, 59–63.
10. I. L. Bartek, M. J. Reichlen, R. W. Honaker, R. L. Leistikow, E. T. Clambey, M. S. Scobey, A. B. Hinds, S. E. Born, C. R. Covey, M. J. Schurr, A. J. Lenaerts and M. I. Voskuil, mSphere, 2016, 1, e00176-16.
11. C. R. MacNair and E. D. Brown, MBio, 2020, 11, e01615-20.
12. H. AlRabiah, J. W. Allwood, E. Correa, Y. Xu and R. Goodacre, PLoS One, 2018, 13, e0200272.
13. G. N. Bruni and J. M. Kralj, eLife, 2020, 9, e58706.
14. M. A. Farha, C. P. Verschoor, D. Bowdish and E. D. Brown, Chem. Biol., 2013, 20, 1168–1178.
15. A. Muthaiyan, J. A. Silverman, R. K. Jayaswal and B. J. Wilkinson, Antimicrob. Agents Chemother., 2008, 52, 980–990.
16. C. S. Lunde, S. R. Hartouni, J. W. Janc, M. Mammen, P. P. Humphrey and B. M. Benton, Antimicrob. Agents Chemother., 2009, 53, 3375.
17. N. N. Mishra, A. S. Bayer, T. T. Tran, Y. Shamoo, E. Mileykovskaya, W. Dowhan, Z. Guan and C. A. Arias, PLoS One, 2012, 7, e43958.
18. D. L. Higgins, R. Chang, D. V. Debabov, J. Leung, T. Wu, K. A. Krause, E. Sandvik, J. M. Hubbard, K. Kaniga, D. E. Schmidt, Q. F. Gao, R. T. Cass, D. E. Karr, B. M. Benton and P. P. Humphrey, Antimicrob. Agents Chemother., 2005, 49, 1127–1134.
19. N. Miyazawa, M. Hakamada and M. Mabuchi, Sci. Rep., 2018, 8, 3870–3870.
20. W. F. Porto, L. Irazazabal, E. S. F. Alves, S. M. Ribeiro, C. O. Matos, Á. S. Pires, I. C. M. Fensterseifer, V. J. Miranda, E. F. Haney, V. Humblot, M. D. T. Torres, R. E. W. Hancock, L. M. Liao, A. Ladram, T. K. Lu, C. de la Fuente-Nunez and O. L. Franco, Nat. Commun., 2018, 9, 1490.
21. M. Yasir, D. Dutta and M. D. P. Willcox, Sci. Rep., 2019, 9, 13267.
22. W. Y. Li, N. M. O'Brien-Simpson, J. Tailhades, N. Pantarat, R. M. Dawson, L. Otvos, E. C. Reynolds, F. Separovic, M. A. Hossain and J. D. Wade, Chem. Biol., 2015, 22, 1250–1258.
23. C. M. Gries, J. L. Bose, A. S. Nuxoll, P. D. Fey and K. W. Bayles, Mol. Microbiol., 2013, 89, 760–773.
24. D.-Y. D. Lee, L. Galera-Laporta, M. Bialecka-Fornal, E. C. Moon, Z. Shen, S. P. Briggs, J. Garcia-Ojalvo and G. M. Süel, Cell, 2019, 177, 352–360.e313.
25. V. Lazar, A. Martins, R. Spohn, L. Daruka, G. Grezal, G. Fekete, M. Szamel, P. K. Jangir, B. Kintses, B. Csorgo, A. Nyerges, A. Gyorkei, A. Kincses, A. Der, F. R. Walter, M. A. Deli, E. Urban, Z. Hegedus, G. Olajos, O. Mehi, B. Balint, I. Nagy, T. A. Martinek, B. Papp and C. Pal, Nat. Microbiol., 2018, 3, 718–731.
26. L. Lin, P. Nonejuie, J. Munguia, A. Hollands, J. Olson, Q. Dam, M. Kumaraswamy, H. Rivera, R. Corriden, M. Rohde, M. E. Hensler, M. D. Burkart, J. Pogliano, G. Sakoulas and V. Nizet, EBioMedicine, 2015, 2, 690–698.
27. K. R. Baker, B. Jana, A. M. Hansen, H. M. Nielsen, H. Franzyk and L. Guardabassi, Front. Cell. Infect. Microbiol., 2019, 9, 236.
28. Q. Li, R. Cebrian, M. Montalban-Lopez, H. Ren, W. H. Wu and O. P. Kuipers, Commun. Biol., 2021, 4, 31.
29. R. Spohn, L. Daruka, V. Lazar, A. Martins, F. Vidovics, G. Grezal, O. Mehi, B. Kintses, M. Szamel, P. K. Jangir, B. Csorgo, A. Gyorkei, Z. Bodi, A. Farago, L. Bodai, I. Foldesi, D. Kata, G. Maroti, B. Pap, R. Wirth, B. Papp and C. Pal, Nat. Commun., 2019, 10, 4538.
30. I. Nicolas, V. Bordeau, A. Bondon, M. Baudy-Floc'h and B. Felden, PLoS Biol., 2019, 17, e300033.
31. D. Pletzer, S. C. Mansour and R. E. W. Hancock, PLoS Pathog., 2018, 14, e1007084.
32. N. J. Afacan, A. T. Y. Yeung, O. M. Pena and R. E. W. Hancock, Curr. Pharm. Des., 2012, 18, 807–819.
33. M. D. Seo, H. S. Won, J. H. Kim, T. Mishig-Ochir and B. J. Lee, Molecules, 2012, 17, 12276–12286.
34. M. D. T. Torres, C. N. Pedron, Y. Higashikuni, R. M. Kramer, M. H. Cardoso, K. G. N. Oshiro, O. L. Franco, P. I. Silva, F. D. Silva, V. X. Oliveira, T. K. Lu and C. de la Fuente-Nunez, Commun. Biol., 2018, 1, 221.
35. M. Hartmann, M. Berditsch, J. Hawecker, M. F. Ardakani, D. Gerthsen and A. S. Ulrich, Antimicrob. Agents Chemother., 2010, 54, 3132–3142.
36. F. Parvez, J. M. Alam, H. Dohra and M. Yamazaki, Biochim. Biophys. Acta, Biomembr., 2018, 1860, 2262–2271.
37. E. Glattard, E. S. Salnikov, C. Aisenbrey and B. Bechinger, Biophys. Chem., 2016, 210, 35–44.
38. L. M. Johnson and S. H. Gellman, Methods Enzymol., 2013, 523, 407–429.
39. W. S. Horne and S. H. Gellman, Acc. Chem. Res., 2008, 41, 1399–1408.
40. E. A. Porter, X. Wang, H. S. Lee, B. Weisblum and S. H. Gellman, Nature, 2000, 405, 298.
41. E. A. Porter, B. Weisblum and S. H. Gellman, J. Am. Chem. Soc., 2002, 124, 7324–7330.
42. G. N. Tew, R. W. Scott, M. L. Klein and W. F. Degrado, Acc. Chem. Res., 2010, 43, 30–39.
43. J. Sarkis and V. Vié, Front. bioeng. biotechnol., 2020, 8, 270.
44. W. S. Horne, J. L. Price, J. L. Keck and S. H. Gellman, J. Am. Chem. Soc., 2007, 129, 4178–4180.
45. S. Loewe, Arzneim. Forsch., 1953, 3, 285–290.
46. M. F. Pereira, C. C. Rossi, G. C. da Silva, J. N. Rosa and D. M. S. Bazzolli, Pathog. Dis., 2020, 78, ftaa056.
47. C. J.-Y. Tsai, J. M. S. Loh and T. Proft, Virulence, 2016, 7, 214–229.
48. D. Novo, N. G. Perlmutter, R. H. Hunt and H. M. Shapiro, Cytometry, 1999, 35, 55–63.
49. J. M. Benarroch and M. Asally, Trends Microbiol., 2020, 28, 304–314.
50. H. J. Apell and B. Bersch, Biochim. Biophys. Acta, Biomembr., 1987, 903, 480–494.
51. Y. Lyu, N. Xiang, X. Zhu and G. Narsimhan, J. Chem. Phys., 2017, 146, 155101.
52. F. Reffuveille, C. de la Fuente-Nunez, S. Mansour and R. E. W. Hancock, Antimicrob. Agents Chemother., 2014, 58, 5363–5371.
53. N. Verstraeten, W. J. Knapen, C. I. Kint, V. Liebens, B. Van den Bergh, L. Dewachter, J. E. Michiels, Q. Fu, C. C. David, A. C. Fierro, K. Marchal, J. Beirlant, W. Versées, J. Hofkens, M. Jansen, M. Fauvart and J. Michiels, Mol. Cell, 2015, 59, 9–21.
54. F. Yoshimura and H. Nikaido, Antimicrob. Agents Chemother., 1985, 27, 84.
55. K. Hirai, H. Aoyama, T. Irikura, S. Iyobe and S. Mitsuhashi, Antimicrob. Agents Chemother., 1986, 29, 535.
56. G. Bainbridge, I. Gokce and J. H. Lakey, FEBS Lett., 1998, 431, 305–308.
57. D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, University of California, San Francisco, 2016.
58. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
59. Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. M. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. M. Wang and P. Kollman, J. Comput. Chem., 2003, 24, 1999–2012.
60. C. W. Hopkins, S. Le Grand, R. C. Walker and A. E. Roitberg, J. Chem. Theory Comput., 2015, 11, 1864–1874.
61. T. Schlick, Molecular Modeling and Simulation, Springer, 2002.
62. H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
63. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.
64. C. J. Dickson, B. D. Madej, A. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879.
65. N. J. Anthis and G. M. Clore, Protein Sci., 2013, 22, 851–858.
66. N. Akhtar, A. Saha, V. Kumar, N. Pradhan, S. Panda, S. Morla, S. Kumar and D. Manna, ACS Appl. Mater. Interfaces, 2018, 10, 33803–33813.
67. J. C. M. Stewart, Anal. Biochem., 1980, 104, 10–14.
68. A. R. Waldeck and P. W. Kuchel, Biophys. J., 1993, 64, 1445–1455.
69. Y. Shacharhill and R. G. Shulman, Biochemistry, 1992, 31, 6272–6278.
70. V. Lazar, G. P. Singh, R. Spohn, I. Nagy, B. Horvath, M. Hrtyan, R. Busa-Fekete, B. Bogos, O. Mehi, B. Csorgo, G. Posfai, G. Fekete, B. Szappanos, B. Kegl, B. Papp and C. Pal, Mol. Syst. Biol., 2013, 9, 700.
71. V. Lázár, A. Martins, R. Spohn, L. Daruka, G. Grézal, G. Fekete, M. Számel, P. K. Jangir, B. Kintses, B. Csörgő, Á. Nyerges, Á. Györkei, A. Kincses, A. Dér, F. R. Walter, M. A. Deli, E. Urbán, Z. Hegedűs, G. Olajos, O. Méhi, B. Bálint, I. Nagy, T. A. Martinek, B. Papp and C. Pál, Nat. Microbiol., 2018, 3, 718–731.
72. I. Wiegand, K. Hilpert and R. E. Hancock, Nat. Protoc., 2008, 3, 163–175.
73. M. Cokol, H. N. Chua, M. Tasan, B. Mutlu, Z. B. Weinstein, Y. Suzuki, M. E. Nergiz, M. Costanzo, A. Baryshnikova, G. Giaever, C. Nislow, C. L. Myers, B. J. Andrews, C. Boone and F. P. Roth, Mol. Syst. Biol., 2011, 7, 544.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1me00118c

‡ These authors contributed equally to this work.

---