DOI:
10.1039/D2MA00438K
(Paper)
Mater. Adv., 2022,
3, 6237-6245
Dependence of defect structure on In concentration in InGaN epilayers grown on AlN/Si(111) substrate†
Received
20th April 2022
, Accepted 21st June 2022
First published on 21st June 2022
Abstract
InGaN epilayers with different indium concentrations have been grown on a 100-nm-thick AlN/n-Si(111) template using plasma assisted molecular beam epitaxy. The sample with the lowest indium (In) content is found to exhibit the highest crystallinity. Furthermore, the types as well as the densities of the threading dislocations in InGaN have been analyzed via high resolution X-ray diffraction measurements. The InGaN epilayers have been described as mosaic crystals, which are characterized by biaxial strain, hydrostatic strain, and mean tilt and twist angles. It is observed that the biaxial strain increases with increasing indium content and the hydrostatic strain decreases with increasing indium content in the films. The twist and tilt angles have also been correlated with the edge and screw dislocation densities, respectively. Furthermore, it has been concluded that point defects dominate in samples with a lower In content whereas trench defects and sub-interfacial extended defects dominate in samples with a higher In content.
Introduction
In recent years, InGaN-based devices have garnered tremendous research interest due to the possibility of extensive band gap engineering through modulation of the In-to-Ga ratio, thereby covering a large range of wavelengths. Therefore, InGaN epitaxial layers have shown high demands in optoelectronic devices such as light-emitting diodes (LEDs), lasers, optical communications and in photodetection.1–9 However, the industrialization of InGaN-based devices with larger In contents still faces some challenges imposed by the inherent material properties.10–13 Firstly, as the In content is increased, the mismatch to GaN also increases, which results in a higher strain in these ternary alloys.14,15 Secondly, GaN and InN have a large difference in their thermal stabilities. InN starts to dissociate at ∼500 °C,16 which is well below the ideal growth temperature for GaN (∼700 °C) in molecular beam epitaxy.17 Hence, to achieve high In concentrations, the substrate temperature must be kept below 500 °C, which eventually reduces the mobility of Ga adatoms on the substrate surface. This leads to the formation of 3D islands, resulting in a high surface roughness along with an inhomogeneous composition in the alloy.12,18–20 Moreover, at the temperatures typical for InGaN growth, the desorption rate of In is lower than the decomposition rate of In–N bonds, making the accumulation of In droplets on the substrate surface unavoidable.21,22 The majority of InGaN ternary alloys are predicted to be thermodynamically unstable and show a tendency towards clustering and phase separation.23 Therefore, a good-quality InGaN layer needs an appropriate substrate temperature along with proper In incorporation to avoid the phase separation. Therefore, it is very important to understand the strain and compositional effects in these ternary alloys, for improving device quality for a better performance.
However, extensive studies have been carried out for the growth of InGaN epilayers on a GaN buffer layer to obtain a better crystalline quality for solid-state lighting applications such as LEDs, laser diodes and photodetectors.1,2,5,24,25 However, the GaN buffer layer does not meet the need for using the InGaN epilayer in broad band semiconductor–insulator–semiconductor (S–I–S) photodetection applications. For broad band S–I–S photodetector applications, it is required to have an insulating layer in between two semiconductors.26,27 If we consider the insulating layer to be AlN from III-nitride materials, then it is necessary to understand the growth mechanism of the InGaN epilayer on AlN directly. Recently, Hu et al.28 reported the application of LEDs using the AlN buffer layer, although that study shows the use of a GaN buffer layer on top of the AlN layer, and they did not grow the InGaN layer directly on the AlN layer. Therefore, it is necessary to understand the types of strain and defects present in the InGaN epilayers with different indium fractions on the AlN epilayer.
In this study, three InGaN epilayers with different indium concentrations have been grown on a 100-nm-thick AlN/n-Si(111) template using plasma assisted molecular beam epitaxy (PAMBE). It was important to check the qualities of the InGaN epitaxial layers with increasing indium content on the AlN template and the resulting mosaic structure characteristics such as the biaxial strain, hydrostatic strain, tilt angle, twist angle and dislocation densities, which were investigated via high-resolution X-ray diffraction measurements. Moreover, field emission microscopy, atomic force microscopy and photoluminescence measurements were also introduced to study the surface and optical properties. It was found that the biaxial strain increases with increasing indium content, and the hydrostatic strain decreases with increasing indium content in the films. Furthermore, it has been concluded that point defects dominate in lower indium content samples, and trench defects and sub-interfacial extended defects dominate in higher indium content samples.
Growth conditions, sample preparation and experimental details of InGaN epilayers
Three InGaN epitaxial layers with different indium fractions were grown using plasma assisted molecular beam epitaxy (PAMBE) on 100-nm-thick AlN/n-Si(111) templates. During the growth of sample A, the In and Ga effusion cell temperatures were kept at 770 °C and 880 °C, respectively, and the corresponding beam equivalent pressure (BEP) values were maintained at 1.69 × 10−7 and 1.26 × 10−7 mbar, respectively. On the other hand, for samples B and C, the In effusion cell temperature was reduced to 750 °C and the corresponding BEP was maintained at 1.13 × 10−7 mbar. Moreover, the only difference in growth conditions between sample B and sample C is that Si doping was introduced in sample C and, consequently, a lower indium fraction (In ≈ 10%) in sample C was achieved compared with sample B (In ≈ 22%), and details of these doping mechanisms are described elsewhere.26,29 Furthermore, the substrate temperature for all three samples was kept constant at 550 °C. The N2 flow rate and plasma power for all three samples were kept constant at 1 SCCM and 350 W, respectively. During growth, the plasma pressure was maintained at 6 × 10−5 mbar and all samples were grown for 3 h without any intermediate steps. Structural characterization via strain and lattice constant measurements was carried out using a high-resolution X-ray diffractometer (HRXRD) (Bruker D8 discover) with CuKα1 (1.54056 Å) radiation. The thickness, surface morphologies and roughness of the films were characterised using field-emission scanning electron microscopy (FESEM) and atomic force microscopy (AFM).
Results and discussions
The HRXRD 2θ–ω scan in the (0002) direction and the full width at half maxima (FWHM) of samples A–C are presented in Fig. 1(a) and Fig. 1(b), respectively. All three samples (A–C) show strong peaks of the 0002 reflections along with the substrate peaks. It can be seen from Fig. 1(a) that sample A has a higher In concentration than samples B and C, and that sample B has a higher In concentration than that of sample C. The higher order 2θ–ω and rocking curve scans of the symmetric (0004) and (0006) planes are shown in Fig. S1 (ESI†). Similarly, the 2θ–ω and rocking curve scans of the asymmetric (105) and (205) planes for all three samples are shown in Fig. S2 (ESI†). Consequently, the 2θ peak values of the symmetric reflections of all three samples along with the (0002) reflections are presented in Table 1. This table also shows the FWHM values from rocking curve scans of the three samples corresponding to all reflections. Moreover, the values of the asymmetric reflections such as (105) and (205) for the three samples are presented in Table 2. The values of the inclination angles (χ) are displayed in Table 3 for the asymmetric planes.
 |
| | Fig. 1 (a) HRXRD scans of the InGaN epilayers along the (0002) plane. (b) Rocking curve measurements for the InGaN epilayers of the (0002) planes. | |
Table 1 Parameters obtained from symmetric HRXRD scans
|
|
Symmetric planes |
(0002) |
(0004) |
(0006) |
| Sample A |
HRXRD peak position (2θ) in degrees |
33.34 |
70.08 |
118.69 |
| FWHM (ω) in degrees |
1.31 |
1.74 |
1.34 |
| Sample B |
HRXRD peak position (2θ) in degrees |
33.65 |
70.65 |
120.44 |
| FWHM (ω) in degrees |
0.77 |
1.05 |
0.97 |
| Sample C |
HRXRD peak position (2θ) in degrees |
34.01 |
71.48 |
122.38 |
| FWHM (ω) in degrees |
0.55 |
0.58 |
0.51 |
Table 2 Parameters obtained from asymmetric HRXRD scans
|
|
|
(105) |
(205) |
| Sample A |
HRXRD peak position (2θ) in degrees |
100.16 |
128.34 |
| FWHM (ω) in degrees |
1.41 |
1.52 |
| Sample B |
HRXRD peak position 2θ) in degrees |
101.36 |
130.05 |
| FWHM (ω) in degrees |
1.02 |
1.418 |
| Sample C |
HRXRD peak position (2θ) in degrees |
102.72 |
132.62 |
| FWHM (ω) in degrees |
0.84 |
1.34 |
Table 3 Values of inclination angles of asymmetric planes
|
|
Asymmetric planes |
Inclination angle (χ) in degrees |
| Sample A |
(105) |
20.7693 |
| (205) |
37.1804 |
| Sample B |
(105) |
20.6635 |
| (205) |
37.0266 |
| Sample C |
(105) |
20.5337 |
| (205) |
36.8374 |
It can be seen from Tables 1 and 2 that the FWHM values of sample C are smaller than those of sample A and sample B for every symmetric and asymmetric plane, which indicates the better crystalline quality of sample C. In addition, sample A shows the spinodal decomposition in the (0002) reflection, which is due to the presence of the higher indium content in sample A. This is also supported by photoluminescence (PL) measurements, which are shown in Fig. 2 for samples A–C.
 |
| | Fig. 2 Photoluminescence spectra of InGaN epilayers. | |
The indium concentration for all the samples was calculated using Vegard's law.26,29 The indium concentration values were found to be 26%, 22% and 10% for samples A, B, and C, respectively. The FESEM images of the top surface and cross-sectional views of samples A–C are shown in Fig. 3.
 |
| | Fig. 3 Top surface FESEM images of (a) sample A, (b) sample B, and (c) Sample C. (d) Cross-sectional FESEM images of sample A, (e) sample B, and (f) sample C. Parts b, c, e and f are reproduced with permission from ref. 29. | |
It can be seen that sample C, with the lower indium content, has a smooth and planar surface. On the other hand, a large number of pits can be observed in sample B, although the remaining surface shows a planar nature. By contrast, the FESEM image of sample A shows quite a rough surface compared with the other two samples. Furthermore, Fig. 3(a) suggests an initial 3D growth mechanism in the InGaN epilayer. Therefore, with increasing indium concentration, the growth mode gradually shifts from a 2D to 3D mode due to the increase in lattice mismatch with the underlying AlN layer. Similarly, the AFM images of samples A–C are shown in Fig. 4. The values of the thickness and surface roughness are displayed in Table 4.
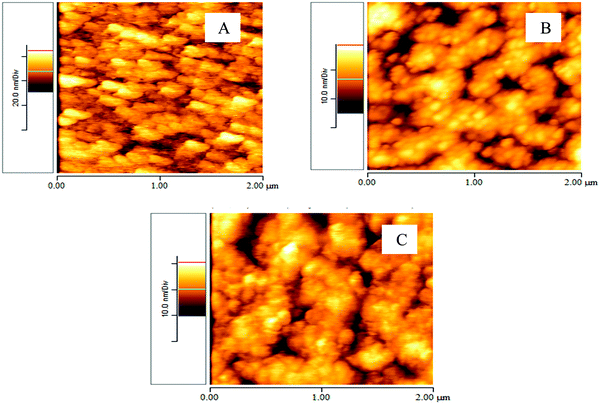 |
| | Fig. 4 AFM images of (A) sample A, (B) sample B, and (C) sample C. Parts B and C are reproduced with permission from ref. 29. | |
Table 4 Values obtained from FESEM and AFM measurements
|
|
Thickness from FESEM cross-section (nm) |
AFM rms roughness (nm) |
| Sample A |
127 |
5 |
| Sample B |
150 |
3.8 |
| Sample C |
110 |
3.2 |
The values in Table 4 indicate that the roughness of sample C is lower compared with the other samples. The low roughness and the smoother surface in sample C indicate that, due to the presence of the lower indium fraction, the degree of lattice crystalline quality is increased. It is well known that a higher indium fraction in the InGaN lattice decreases the quality of the InGaN epilayers and as well as greater defects and higher strain values being observed. On the other hand, it has been observed from the HRXRD, FESEM and AFM studies that the quality of sample A is very poor compared with samples B and C. Furthermore, sample A shows a split in the (0002) reflection, which could indicate either short-range spinodal decomposition or long-range phase separation, or simply the partial strain relaxation of some parts of the InGaN layer. Moreover, the short-range spinodal decomposition or long-range phase separation is also supported by the PL spectrum as shown in Fig. S3 (ESI†). Furthermore, it can be seen from Fig. S3 (ESI†) that sample A has a hump around 31.3 degrees in the HRXRD pattern, which is just the InN (0002) reflection peak in the sample. Hence, sample A is not suitable for optoelectronic device applications and was excluded from further analysis. We subsequently took samples B and C for further investigations such as XPS studies to verify the indium concentration, and the results are shown in Fig. S4 (ESI†).
The nature of the biaxial strain of the InGaN layer on the GaN layer has been reported in many studies,30–33 but the behaviour with the AlN layer remains to be understood. Therefore, to further investigate the strain, stress and dislocation densities of these InGaN layers, further analysis was carried out using the HRXRD data. The in-pane and out-of-plane lattice parameters a and c, respectively, were determined using the following relationship for the hexagonal system34
| |  | (1) |
where
dhkl is the interplanar spacing between two planes. Values of
dhkl were measured using Bragg's law, taking the higher order reflections such as
d004,
d006 for the symmetric planes and
d105,
d205 for the asymmetric planes. Moreover, the in-plane and out-of-plane strain,
εa and
εc, respectively, can be described as
| |  | (2) |
| |  | (3) |
where
a0 and
c0 are the relaxed lattice parameters for the InGaN epilayers. The relaxed lattice parameters were obtained using Vegard's law, which is given as
| | | c0 = (1 − x)cGaN0 + cInN0 | (4) |
| | | a0 = (1 − x)aGaN0 + aInN0 | (5) |
where
x is the indium fraction,
cGaN0and
aGaN0 are the strain-free lattice parameters for GaN, and
cInN0 and
aInN0 are the strain-free lattice parameters for InN.
13
However, InGaN layers grown using the MBE technique contain a lot of defects and dislocation densities due to several reasons, such as doping, lattice mismatch and the different thermal expansion coefficient from the underneath substrate layer. Because of these reasons there could be contraction and expansion in the lattice constants, which leads to biaxial compressive or tensile strain in the layer. Furthermore, the measured in-plane (εa) and out-of-plane (εc) strain comprises two components, one is biaxial strain, and the other is hydrostatic strain. These are given by the following equations as34,35
where
ε(bi)a and
ε(bi)c are the in-plane and out-of-plane biaxial strain, respectively. The parameter
εhy is the hydrostatic strain, which is described by the following equation
34,35| |  | (8) |
| |  | (9) |
where
ν is the Poisson ratio and
c13 and
c33 are the elastic constants of the InGaN layers. The values of the elastic constants were obtained from Vegard's law, which is described by the following relations:
| | | c13 = (1 − x)cGaN13 + xcInN13 | (10) |
| | | c33 = (1 − x)cGaN33 + xcInN33 | (11) |
where
cGaN13and
cGaN33 are the elastic constants of bulk GaN, and
cInN13 and
cInN33 are the elastic constants of bulk InN.
13
The values of the in-plane stress (σin) can be derived in terms of the biaxial strain and elastic constants and are given by34,35
| | 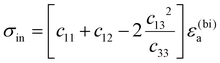 | (12) |
where
c11 and
c12 are the elastic constants of the corresponding InGaN layers, and the obtained values are discussed in terms of the relations below given:
| | | c11 = (1 − x)cGaN11 + xcInN11 | (13) |
| | | c12 = (1 − x)cGaN12 + xcInN12 | (14) |
where
cGaN11 and
cGaN12 are the elastic constants of bulk GaN, and
cInN11 and
cInN12 are the elastic constants of bulk InN.
36 The values of the characteristic parameters for the samples are presented in
Table 5.
Table 5 Characteristic parameters for all the InGaN samples
|
|
Sample B |
Sample C |
|
c (Å) |
5.3266 |
5.2747 |
|
a (Å) |
3.2432 |
3.2126 |
|
c
0 (Å) |
5.2990 |
5.2368 |
|
a
0 (Å) |
3.2659 |
3.2241 |
|
ε
a
|
−6.9506 × 10−3 |
−3.567 × 10−3 |
|
ε
c
|
5.208 × 10−3 |
7.237 × 10−3 |
|
ε
(bi)
a
|
−7.839 × 10−3 |
−7.083 × 10−3 |
|
ε
(bi)
c
|
4.3196 × 10−3 |
3.721 × 10−3 |
|
ε
hy
|
8.884 × 10−4 |
3.516 × 10−3 |
|
ν
|
0.216 |
0.208 |
|
c
13 (GPa) |
100.58 |
101.9 |
|
c
33 (GPa) |
365.18 |
386.9 |
|
c
11 (GPa) |
335.32 |
352.6 |
|
c
12 (GPa) |
130.6 |
133 |
|
σ
in (GPa) |
−3.218 |
−3.059 |
Generally, biaxial strain in the epilayers appeared due to lattice mismatch and the different lattice expansion coefficients between the sample layer and the substrate, but on the other hand, hydrostatic strain in the layer appeared due to the doping and defects.34,35 It is seen from Table 5 that, for the samples, the values of the measured in-plane stain (εa) and the biaxial strain (ε(bi)a) are negative in nature; therefore, it can be suggested that the in-plane strain values are compressive in nature, i.e., the in-plane lattice constants are decreased from the relaxed lattice constants. Consequently, the values of the out-of-plane strain parameters (εc, ε(bi)c) are positive in nature, i.e., the out-of-plane lattice constants are increased from the relaxed values. This behaviour of the lattice constants changed the hexagonal unit cell from its relaxed condition, and is depicted in Fig. 5. It is found that the biaxial strain value in samples B and C increases (greater negative value) with increasing indium content in the InGaN epilayer. There have been various literature reports that the in-plane strain increases with increasing indium fraction in InGaN lattices.28,30,37–40 Hence, we can expect that the number of defects will also be enhanced with increasing in-plane strain as well as with increasing indium content. Moreover, the reason behind the increasing number of defects is that the increased strain in any layer must be relaxed to minimize the formation energy by some means, and defects are the best possible way to relax the high strain in an any epilayer, which is why if an epilayer contains a high level of strain then there is a high probability of a large number of defects present in that material to minimize the formation energy. Furthermore, several types of defects, such as V-type defects, trench defects and sub-interfacial extended-type defects, can appear due to the higher indium content and biaxial compressive strain in the material. However, recent studies have suggested that V-type defects are mostly kinetically driven and cannot be related to the higher indium content and with biaxial compressive strain.15,41–43 On the other hand, it has been suggested that trench defects and sub-interfacial extended-type defects can be related to a higher indium content and as well as to biaxial compressive strain.15,41,42,44 But some reports still suggest the dependency of V-type defects on a higher indium content and as well as on compressive strain.37,39,45 In our FESEM results also (Fig. 3), it can be seen that there is no sign of V-pits in sample C, but as the In fraction is increased the V-type pits are observed in sample B. Therefore, the dependency of V-type defects on the indium fraction is still a matter of debate. On the other hand, the large difference between the covalent radii of In (rIn = 0.144 nm), Ga (rGa = 0.126 nm) and N (rN = 0.07 nm) could be the reason for the high in-plane compressive strain in the samples with increasing indium content, although by contrast, it can be seen that the hydrostatic strain decreases with increasing indium content. It has already been discussed that the hydrostatic strain originates due to doping and defects such as point defects.34,35 There are several types of point defect present in InGaN lattices, such as substitutional defects (InGa, InN, GaN, NGa), interstitial defects (Ini, Gai, Ni) and vacancy-type defects (VIn, VGa, VN). Now, the hydrostatic strain depends on the measured in-plane (εa) and out-of-plane (εc) strain, as shown in eqn (8). The value of εa increases with increasing indium content but the value of εc decreases with increasing indium content (Table 5). Therefore, the influence of the out-of-plane strain (εc) dominates over the in-plane strain (εa) in the case of hydrostatic strain (εhy) for the InGaN layers grown on AlN templates. Hence, in this present case, it can be stated that εc is a measure of point defects in the InGaN epilayers. Thus, it can be said that biaxial strain due to trench defects and sub-interfacial extended-type defects in the InGaN lattices increased with increasing indium fraction, and that hydrostatic strain due to point-type defects in the InGaN lattices decreased with increasing indium fraction. Therefore, we suggest that, in our case, point-type defects dominate in the lower indium fraction sample C and trench or sub-interfacial extended-type defects dominate in the higher indium fraction sample B. Moreover, values of the in-plane stress (σin) were calculated using eqn (12) for all three samples. In the samples it is seen that the value of the in-plane stress increases with increasing indium content in a similar way as the in-plane biaxial strain increases, and this is to be expected because the in-plane stress is directly proportional to the in-plane biaxial strain of the sample (eqn (12)).
 |
| | Fig. 5 (a) Schematic of a hexagonal unit cell under relaxed and strain conditions. (b) W–H plot for sample B, and (c) W–H plot for sample C. | |
Next, the mosaic structure of the InGaN films was investigated via HRXRD rocking curve experiments, i.e., ω scan measurements. Due to the large lattice mismatch between InGaN and the AlN template layer, a number of misoriented islands or sub-grains form at the heterostructure interface, giving rise to a mosaic structure. Therefore, the angle due to the out-of-plane rotation of these islands with respect to the surface normal is known as the tilt angle and, similarly, the angle due to the in-plane rotation with respect to the surface normal is known as the twist angle. Consequently, threading dislocation densities (TDs) become introduced by the process of coalescence at the heterojunction to bring close the misoriented sub-grains and, as a result, TDs become a strong measure of the mosaic structure in InGaN lattices.46–49 Values of the tilt and twist angles can be calculated from the FWHM values of the symmetric and asymmetric planes, respectively.34,46–48 However, to calculate precisely the tilt angle from symmetric planes, it is convenient to use the Williamson–Hall (W–H) plot. The plot of (β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ) vs. (sin
θ/λ) vs. (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ) is known as the W–H plot, where β is the FWHM of each symmetric reflection (0002, 0004, 0006) and θ is the Bragg angle and λ is the wavelength of the X-ray source. The W–H plot gives a straight line, and from the slope of the straight line the tilt angle can be evaluated, and the intercept with the y-axis gives the lateral coherence length. The W–H plots for samples B and C are shown in Fig. 5. On the other hand, the twist angle can be calculated by plotting the FWHM data of the asymmetric reflections (10 × 5, 20 × 5, 20 × 4, etc.) with the inclination angle χ, and with suitable fitting, the angle that is derived at χ = 90° can be considered as the twist angle. But in our case, obtaining the peaks for the asymmetric reflection planes greater than χ = 40° was very difficult. This might be because of the quality of the InGaN epilayers that were grown directly on the AlN layer, which had a large lattice mismatch. So far, preferably, most of the InGaN layers were grown either on a GaN epilayer or on a GaN buffer layer to obtain a high crystalline quality and also to obtain a reduced lattice mismatch compared with AlN. Therefore, we considered the FWHM values as the twist angle, which were derived at the largest possible inclination angle, as also suggested by Heinke et al.50 In our present case, we took the FWHM values of 20 × 5 reflections as the twist angle and the corresponding inclination angles varied from χ = 37° to χ = 40° for all three samples. Hence, after evaluating the tilt and twist angles, the TDs can be calculated as they are directly proportional to the tilt and twist angles according to the expressions given below, where these equations are for random distributions of dislocation densities:34,45,47
θ/λ) is known as the W–H plot, where β is the FWHM of each symmetric reflection (0002, 0004, 0006) and θ is the Bragg angle and λ is the wavelength of the X-ray source. The W–H plot gives a straight line, and from the slope of the straight line the tilt angle can be evaluated, and the intercept with the y-axis gives the lateral coherence length. The W–H plots for samples B and C are shown in Fig. 5. On the other hand, the twist angle can be calculated by plotting the FWHM data of the asymmetric reflections (10 × 5, 20 × 5, 20 × 4, etc.) with the inclination angle χ, and with suitable fitting, the angle that is derived at χ = 90° can be considered as the twist angle. But in our case, obtaining the peaks for the asymmetric reflection planes greater than χ = 40° was very difficult. This might be because of the quality of the InGaN epilayers that were grown directly on the AlN layer, which had a large lattice mismatch. So far, preferably, most of the InGaN layers were grown either on a GaN epilayer or on a GaN buffer layer to obtain a high crystalline quality and also to obtain a reduced lattice mismatch compared with AlN. Therefore, we considered the FWHM values as the twist angle, which were derived at the largest possible inclination angle, as also suggested by Heinke et al.50 In our present case, we took the FWHM values of 20 × 5 reflections as the twist angle and the corresponding inclination angles varied from χ = 37° to χ = 40° for all three samples. Hence, after evaluating the tilt and twist angles, the TDs can be calculated as they are directly proportional to the tilt and twist angles according to the expressions given below, where these equations are for random distributions of dislocation densities:34,45,47
| |  | (15) |
| |  | (16) |
Here,
ρscrew and
ρedge are the screw and edge dislocation densities, respectively,
βtilt and
βtwist are the tilt and twist angles respectively,
bscrew is the Burgers vector along [0001] and
bedge is the Burgers vectors along
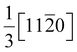
. The obtained values of
βtilt,
βtwist,
ρscrew and
ρedge are presented in
Table 6.
Table 6 Values of tilt, twist, screw and edge threading dislocation densities for InGaN samples
|
|
β
tilt
|
β
twist
|
ρ
screw (cm−2) |
ρ
edge (cm−2) |
| Sample B |
1.069 |
1.418 |
9.26 × 1013 |
4.39 × 1014 |
| Sample C |
0.489 |
1.34 |
1.97 × 1013 |
3.99 × 1014 |
It is seen that edge TDs are greater compared with screw TDs for both samples B and C. Furthermore, both TDs were increased with increasing indium content, indicating the greater number of defects and the decreasing crystalline quality with increasing indium fraction. Moreover, the obtained results of TDs are in good agreement with the strain calculations as well as the FESEM and AFM measurements with increasing indium content. We also carried out asymmetric reciprocal space mapping (RSM) to verify the defect densities, which is represented in Fig. 6. From the asymmetric RSM images, it can be observed that sample C has the lesser mosaicity and compositional inhomogeneity compared with sample B, as the RSM of sample C is highly symmetric compared with sample B. Therefore, it may be noted that the calculated defect densities in Table 6 are well supported by the RSM results.
 |
| | Fig. 6 Reciprocal space map around the (105) reflection for (a) sample B and (b) sample C. Qx and Qz are the reciprocal space vectors in Å−1. | |
Hence, it is seen from the above extensive calculations that the growth of the InGaN epilayer directly on a 100-nm-thick AlN layer shows good results in terms of the crystalline quality, despite of having a large lattice mismatch. In particular, for sample B, it is observed that despite having a moderately large indium fraction (In ≈ 22%) compared with sample C (In ≈ 10%), sample B still shows a good crystalline quality for future device applications, such as green LEDs, visible-range photodetectors, etc. Furthermore, sample B needs extensive future research on the green gap issue in LED devices. On the other hand, sample C is the better candidate for Si-based S–I–S photodetection applications in the broad band range. It is necessary to have a good-quality InGaN layer on the AlN epilayer, which has been achieved by sample C.26 Therefore, we suggest that a good quality of InGaN epilayers can also be achieved with different indium concentrations on an AlN epilayer, despite having large a lattice mismatch, and this work opens up a new research area of growing InGaN epilayers on AlN templates for future device applications.
Conclusion
In conclusion, InGaN epilayers with different In concentrations have been grown on AlN/Si(111), and it has been observed that the crystalline and optical quality of the InGaN layers increases with decreasing In content. Extensive high-resolution X-ray diffraction measurements have been performed to calculate the various mosaic characteristics, such as the bi-axial strain, hydrostatic strain, stress and threading dislocation densities. A fundamental correlation between the tilt and twist angles has been established. This work opens up a new avenue to growing high-quality InGaN epilayers on AlN for future optoelectronic device applications.
Author contributions
Prof. S. B. Krupanidhi, Prof. K. K. Nanda and A. M. C. generated the idea and designed experiments. A. M. C. performed experiments. A. M. C., D. K. S. and B. R. prepared the manuscript. All authors participated in the discussion of experimental results and revision of the manuscript.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
A. M. C. is thankful to Prof. G. S. Bandyopadhyay and Prof. S. Gangopadhyay, principal and head of the Department of Physics, respectively from Syamsundar College, University of Burdwan. D. K. S. is thankful to Council of Scientific and Industrial Research, Government of India, New Delhi for providing senior research fellowship. Prof. S. B. Krupanidhi acknowledges the INSA senior scientist fellowship.
References
- F. A. Ponce and D. P. Bour, Nitride-Based Semiconductors for Blue and Green Light-Emitting Devices, Nature, 1997, 386(6623), 351–359 CrossRef CAS.
- Z. L. Li, P. T. Lai and H. W. Choi, A Reliability Study on Green InGaN-GaN Light-Emitting Diodes, IEEE Photonics Technol. Lett., 2009, 21(19), 1429–1431 CAS.
- I. Akasaki, Fascinating Journeys into Blue Light (Nobel Lecture), Ann. Phys., 2015, 527(5–6), 311–326 CrossRef CAS.
- R. Dahal, B. Pantha, J. Li, J. Y. Lin and H. X. Jiang, InGaN/GaN Multiple Quantum Well Solar Cells with Long Operating Wavelengths, Appl. Phys. Lett., 2009, 94(6), 2007–2010 CrossRef.
- K. Zhang, H. Liang, D. Wang, R. Shen, W. Guo, Q. Deng, Y. Liu, X. Xia, Y. Luo and G. Du, The Properties of Reversed Polarization Yellow InGaN-GaN MQWs in p-Side down Structure Grown by Metal-Organic Chemical Vapor Deposition on Sapphire Substrate, Phys. E, 2014, 64, 57–62 CrossRef CAS.
- J. Liu, H. Liang, X. Xia, Y. Liu, J. Liu, Q. Abbas, R. Shen, Y. Luo, Y. Zhang and G. Du, Indium Incorporation Induced Morphological Evolution and Strain Relaxation of High Indium Content InGaN Epilayers Grown by Metal-Organic Chemical Vapor Deposition, Cryst. Growth Des., 2017, 17(6), 3411–3418 CrossRef CAS.
- E. Matioli, C. Neufeld, M. Iza, S. C. Cruz, A. A. Al-Heji, X. Chen, R. M. Farrell, S. Keller, S. DenBaars and U. Mishra,
et al., High Internal and External Quantum Efficiency InGaN/GaN Solar Cells, Appl. Phys. Lett., 2011, 98(2), 2009–2012 CrossRef.
- A. M. Chowdhury, D. K. Singh, B. Roul, K. K. Nanda and S. B. Krupanidhi, Overcoming the Challenges Associated with the InN/InGaN Heterostructure via a Nanostructuring Approach for Broad Band Photodetection, ACS Appl. Electron. Mater, 2021, 3(9), 4243–4253 CrossRef CAS.
- T. Walther, H. Amari, I. M. Ross, T. Wang and A. G. Cullis, Lattice Resolved Annular Dark-Field Scanning Transmission Electron Microscopy of (Al, In)GaN/GaN Layers for Measuring Segregation with Sub-Monolayer Precision, J. Mater. Sci., 2013, 48(7), 2883–2892 CrossRef CAS.
- E. Arslan and M. K. Ozturk, Evolution of the Mosaic Structure in InGaN Layer Grown on a Thick GaN Template and Sapphire Substrate, J. Mater. Sci.: Mater. Electron., 2013, 24(11), 4471–4481 CrossRef CAS.
- O. Ambacher, Growth and Applications of Group III-Nitrides, J. Phys. D. Appl. Phys., 1998, 31(20), 2653 CrossRef CAS.
- F. K. Yam and Z. Hassan, InGaN: An Overview of the Growth Kinetics, Physical Properties and Emission Mechanisms, Superlattices Microstruct., 2008, 43(1), 1–23 CrossRef CAS.
- S. Pereira, M. R. Correia, E. Pereira, K. P. O’Donnell, E. Alves, A. D. Sequeira, N. Franco, I. M. Watson and C. J. Deatcher, Strain and Composition Distributions in Wurtzite InGaN/GaN Layers Extracted from X-Ray Reciprocal Space Mapping, Appl. Phys. Lett., 2002, 80(21), 3913–3915 CrossRef CAS.
- I. H. Ho and G. B. Stringfellow, Solid Phase Immiscibility in GaInN, Appl. Phys. Lett., 1996, 69(18), 2701–2703 CrossRef CAS.
- S. L. Rhode, W. Y. Fu, M. A. Moram, F. C.-P. Massabuau, M. J. Kappers, C. McAleese, F. Oehler, C. J. Humphreys and R. O. Dusane, and S. S. Structure and Strain Relaxation Effects of Defects in InxGa1 − xN Epilayers, J. Appl. Phys., 2014, 116(10), 103513 CrossRef.
- Q. Guo, O. Kato and A. Yoshida, Thermal Stability of Indium Nitride Single Crystal Films, J. Appl. Phys., 1993, 73(11), 7969–7971 CrossRef CAS.
- M. Kumar, B. Roul, T. N. Bhat, M. K. Rajpalke, P. Misra, L. M. Kukreja, N. Sinha, A. T. Kalghatgi and S. B. Krupanidhi, Improved Growth of GaN Layers on Ultra Thin Silicon Nitride/Si (1 1 1) by RF-MBE, Mater. Res. Bull., 2010, 45(11), 1581–1585 CrossRef CAS.
- Y. Zhang, X. Zhou, S. Xu, Z. Wang, Z. Chen, J. Zhang, J. Zhang and Y. Hao, Effects of Growth Temperature on the Properties of InGaN Channel Heterostructures Grown by Pulsed Metal Organic Chemical Vapor Deposition, AIP Adv., 2015, 5, 12 Search PubMed.
- A. Senichev, B. Dzuba, T. Nguyen, Y. Cao, M. A. Capano, M. J. Manfra and O. Malis, Impact of Growth Conditions and Strain on Indium Incorporation in Non-Polar m-Plane (10 1 0) InGaN Grown by Plasma-Assisted Molecular Beam Epitaxy, APL Mater., 2019, 7, 12 Search PubMed.
- Y. S. Chen, C. H. Liao, C. T. Kuo, R. C. C. Tsiang and H. C. Wang, Indium Droplet Formation in InGaN Thin Films with Single and Double Heterojunctions Prepared by MOCVD, Nanoscale Res. Lett., 2014, 9(1), 1–12 CrossRef PubMed.
- R. Kour, S. Arya, S. Verma, A. Singh, P. Mahajan and A. Khosla, Review—Recent Advances and Challenges in Indium Gallium Nitride (InxGa1−xN) Materials for Solid State Lighting, ECS J. Solid State Sci. Technol., 2020, 9(1), 015011 CrossRef CAS.
- N. Sinha, B. Roul, S. Mukundan, G. Chandan, L. Mohan, V. M. Jali and S. B. Krupanidhi, Growth and Electrical Transport Properties of InGaN/GaN Heterostructures Grown by PAMBE, Mater. Res. Bull., 2014, 61, 539–543 CrossRef.
-
H. Morkoç and H. Morkoç, Handbook of Nitride Semiconductors and Devices, Wiley-VCH, 2008 Search PubMed.
- C. A. M. Fabien, A. Maros, C. B. Honsberg and W. A. Doolittle, III-Nitride Double-Heterojunction Solar Cells with High In-Content InGaN Absorbing Layers: Comparison of Large-Area and Small-Area Devices, IEEE J. Photovoltaics, 2016, 6(2), 460–464 Search PubMed.
- Q. Zheng, M. Peng, Z. Liu, S. Li, R. Han, H. Ouyang, Y. Fan, C. Pan, W. Hu and J. Zhai,
et al., Dynamic Real-Time Imaging of Living Cell Traction Force by Piezo-Phototronic Light Nano-Antenna Array, Sci. Adv., 2021, 7(22), 1–9 Search PubMed.
- A. M. Chowdhury, G. Chandan, R. Pant, B. Roul, D. K. Singh, K. K. Nanda and S. B. Krupanidhi, Self-Powered, Broad Band, and Ultrafast InGaN-Based Photodetector, ACS Appl. Mater. Interfaces, 2019, 11(10), 10418–10425 CrossRef CAS PubMed.
- A. M. Chowdhury, R. Pant, B. Roul, D. K. Singh, K. K. Nanda and S. B. Krupanidhi, Double Gaussian Distribution of Barrier Heights and Self-Powered Infrared Photoresponse of InN/AlN/Si(111) Heterostructure, J. Appl. Phys., 2019, 126(2), 025301 CrossRef.
- H. Hu, S. Zhou, H. Wan, X. Liu, N. Li and H. Xu, Effect of Strain Relaxation on Performance of InGaN/GaN Green LEDs Grown on 4-Inch Sapphire Substrate with Sputtered AlN Nucleation Layer, Sci. Rep., 2019, 9(1), 1–9 CrossRef PubMed.
- A. M. Chowdhury, B. Roul, D. K. Singh, R. Pant, K. K. Nanda and S. B. Krupanidhi, Temperature Dependent “S-Shaped” Photoluminescence Behavior of InGaN Nanolayers: Optoelectronic Implications in Harsh Environment, ACS Appl. Nano Mater., 2020, 3(8), 8453–8460 CrossRef CAS.
- L. Görgens, O. Ambacher, M. Stutzmann, C. Miskys, F. Scholz and J. Off, Characterization of InGaN Thin Films Using High-Resolution X-Ray Diffraction, Appl. Phys. Lett., 2000, 76(5), 577–579 CrossRef.
- M. D. McCluskey, Van de Walle, C. G. Romano, L. T. Krusor and B. S. Johnson, N. M. Effect of Composition on the Band Gap of Strained InxGa1−XN Alloys, J. Appl. Phys., 2003, 93(7), 4340–4342 CrossRef CAS.
- T. Böttcher, S. Einfeldt, V. Kirchner, S. Figge, H. Heinke, D. Hommel, H. Selke and P. L. Ryder, Incorporation of Indium during Molecular Beam Epitaxy of InGaN, Appl. Phys. Lett., 1998, 73(22), 3232–3234 CrossRef.
- F. A. Ponce, S. Srinivasan, A. Bell, L. Geng, R. Liu, M. Stevens, J. Cai, H. Omiya, H. Marui and S. Tanaka, Microstructure and Electronic Properties of InGaN Alloys, Phys. Status Solidi, 2003, 240(2), 273–284 CrossRef CAS.
- M. A. Moram and M. E. Vickers, X-ray Diffraction of III-Nitrides, Reports Prog. Phys., 2009, 72(3), 036502 CrossRef.
- V. S. Harutyunyan, A. P. Aivazyan, E. R. Weber, Y. Kim, Y. Park and S. G. Subramanya, High-Resolution X-ray Diffraction Strain – Stress Analysis of GaN/Sapphire Heterostructures, J. Phys. D. Appl. Phys., 2001, 34(10A), A35 CrossRef CAS.
- A. F. Elastic Wright, Properties of Zinc-Blende and Wurtzite AIN, GaN, and InN, J. Appl. Phys., 1997, 82(6), 2833–2839 CrossRef CAS.
- T. L. Song, Strain Relaxation Due to V-Pit Formation in In XGa 1-XN/GaN Epilayers Grown on Sapphire, J. Appl. Phys., 2005, 98(8), 084906 CrossRef.
- L. T. Romano, B. S. Krusor, M. D. McCluskey, D. P. Bour and K. Nauka, Structural and Optical Properties of Pseudomorphic InxGa1-XN Alloys, Appl. Phys. Lett., 1998, 73(13), 1757–1759 CrossRef CAS.
- C. Bazioti, E. Papadomanolaki, T. Kehagias, T. Walther, J. Smalc-Koziorowska, E. Pavlidou, P. Komninou, T. Karakostas, E. Iliopoulos and G. P. Dimitrakopulos, Defects, Strain Relaxation, and Compositional Grading in High Indium Content InGaN Epilayers Grown by Molecular Beam Epitaxy, J. Appl. Phys., 2015, 118, 15 CrossRef.
- S. Pearton, GAN and ZNO-Based Materials and Devices, Springer Ser. Mater. Sci, 2012, 156, 1 Search PubMed.
- S. L. Sahonta, M. J. Kappers, D. Zhu, T. J. Puchtler, T. Zhu, S. E. Bennett, C. J. Humphreys and R. A. Oliver, Properties of trench defects in InGaN/GaN quantum well structures, Phys. Status Solidi A, 2013, 210(1), 195–198 CrossRef CAS.
- J. Bruckbauer, P. R. Edwards, T. Wang and R. W. Martin, High Resolution Cathodoluminescence Hyperspectral Imaging of Surface Features in InGaN/GaN Multiple Quantum Well Structures, Appl. Phys. Lett., 2011, 98(14), 141908 CrossRef.
- J. Gruber, X. W. Zhou, R. E. Jones, S. R. Lee and G. J. Tucker, Molecular Dynamics Studies of Defect Formation during Heteroepitaxial Growth of InGaN Alloys on (0001) GaN Surfaces, J. Appl. Phys., 2017, 121(19), 195301 CrossRef CAS PubMed.
- F. C.-P. Massabuau, S.-L. Sahonta, L. Trinh-Xuan, S. Rhode, T. J. Puchtler, M. J. Kappers and C. J. Humphreys, and R. A. O. Morphological, Structural, and Emission Characterization of Trench Defects in InGaN/GaN Quantum Well Structures, Appl. Phys. Lett., 2012, 101(21), 212107 CrossRef.
- D. Won, X. Weng and J. M. Redwing, Effect of Indium Surfactant on Stress Relaxation by V-Defect Formation in GaN Epilayers Grown by Metalorganic Chemical Vapor Deposition, J. Appl. Phys., 2010, 108, 9 CrossRef.
- M. E. Vickers, M. J. Kappers, R. Datta, C. McAleese, T. M. Smeeton, F. D. G. Rayment and C. J. Humphreys, In-Plane Imperfections in GaN Studied by X-ray Diffraction, J. Phys. D: Appl. Phys., 2005, 38(10A), A99 CrossRef CAS.
- S. Christiansen, M. Albrecht and H. P. Strunk, Defect Structure of Epitaxial GaN Films Determined by Transmission Electron Microscopy and Triple-Axis X-Ray Diffractometry, Philos. Mag. A, 1998, 77(4), 1013–1025 Search PubMed.
- H. Heinke, V. Kirchner, S. Einfeldt and D. Hommel, X-Ray Diffraction Analysis of the Defect Structure in Epitaxial GaN, Appl. Phys. Lett., 2000, 77(14), 2145–2147 CrossRef CAS.
- B. Moran, F. Wu, A. E. Romanov, U. K. Mishra, S. P. Denbaars and J. S. Speck, Structural and Morphological Evolution of GaN Grown by Metalorganic Chemical Vapor Deposition on SiC Substrates Using an AlN Initial Layer, J. Cryst. Growth, 2004, 273(1–2), 38–47 CrossRef CAS.
- H. Heinke, V. Kirchner, S. Einfeldt and D. Hommel, Analysis of the Defect Structure of Epitaxial GaN, Phys. Status Solidi A, 1999, 176(1), 391–395 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: HRXRD scans of higher order symmetric and asymmetric planes and XPS spectra of the samples. See DOI: https://doi.org/10.1039/d2ma00438k |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Deependra Kumar
Singh
*ab,
Deependra Kumar
Singh
 a,
Basanta
Roul
ac,
K. K.
Nanda
*ade and
S. B.
Krupanidhi
*a
a,
Basanta
Roul
ac,
K. K.
Nanda
*ade and
S. B.
Krupanidhi
*a









![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ) vs. (sin
θ/λ) vs. (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ) is known as the W–H plot, where β is the FWHM of each symmetric reflection (0002, 0004, 0006) and θ is the Bragg angle and λ is the wavelength of the X-ray source. The W–H plot gives a straight line, and from the slope of the straight line the tilt angle can be evaluated, and the intercept with the y-axis gives the lateral coherence length. The W–H plots for samples B and C are shown in Fig. 5. On the other hand, the twist angle can be calculated by plotting the FWHM data of the asymmetric reflections (10 × 5, 20 × 5, 20 × 4, etc.) with the inclination angle χ, and with suitable fitting, the angle that is derived at χ = 90° can be considered as the twist angle. But in our case, obtaining the peaks for the asymmetric reflection planes greater than χ = 40° was very difficult. This might be because of the quality of the InGaN epilayers that were grown directly on the AlN layer, which had a large lattice mismatch. So far, preferably, most of the InGaN layers were grown either on a GaN epilayer or on a GaN buffer layer to obtain a high crystalline quality and also to obtain a reduced lattice mismatch compared with AlN. Therefore, we considered the FWHM values as the twist angle, which were derived at the largest possible inclination angle, as also suggested by Heinke et al.50 In our present case, we took the FWHM values of 20 × 5 reflections as the twist angle and the corresponding inclination angles varied from χ = 37° to χ = 40° for all three samples. Hence, after evaluating the tilt and twist angles, the TDs can be calculated as they are directly proportional to the tilt and twist angles according to the expressions given below, where these equations are for random distributions of dislocation densities:34,45,47
θ/λ) is known as the W–H plot, where β is the FWHM of each symmetric reflection (0002, 0004, 0006) and θ is the Bragg angle and λ is the wavelength of the X-ray source. The W–H plot gives a straight line, and from the slope of the straight line the tilt angle can be evaluated, and the intercept with the y-axis gives the lateral coherence length. The W–H plots for samples B and C are shown in Fig. 5. On the other hand, the twist angle can be calculated by plotting the FWHM data of the asymmetric reflections (10 × 5, 20 × 5, 20 × 4, etc.) with the inclination angle χ, and with suitable fitting, the angle that is derived at χ = 90° can be considered as the twist angle. But in our case, obtaining the peaks for the asymmetric reflection planes greater than χ = 40° was very difficult. This might be because of the quality of the InGaN epilayers that were grown directly on the AlN layer, which had a large lattice mismatch. So far, preferably, most of the InGaN layers were grown either on a GaN epilayer or on a GaN buffer layer to obtain a high crystalline quality and also to obtain a reduced lattice mismatch compared with AlN. Therefore, we considered the FWHM values as the twist angle, which were derived at the largest possible inclination angle, as also suggested by Heinke et al.50 In our present case, we took the FWHM values of 20 × 5 reflections as the twist angle and the corresponding inclination angles varied from χ = 37° to χ = 40° for all three samples. Hence, after evaluating the tilt and twist angles, the TDs can be calculated as they are directly proportional to the tilt and twist angles according to the expressions given below, where these equations are for random distributions of dislocation densities:34,45,47

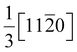 . The obtained values of βtilt, βtwist, ρscrew and ρedge are presented in Table 6.
. The obtained values of βtilt, βtwist, ρscrew and ρedge are presented in Table 6.


