Open Access Article
Open Access ArticleComputational discovery of spin-polarized semimetals in spinel materials†
Shenda
He‡
ab,
Ruirong
Kang‡
ab,
Pan
Zhou
 *a,
Zehou
Li
b,
Yi
Yang
*b and
Lizhong
Sun
*a,
Zehou
Li
b,
Yi
Yang
*b and
Lizhong
Sun
 ab
ab
aHunan Provincial Key laboratory of Thin Film Materials and Devices, School of Materials Science and Engineering, Xiangtan University, Xiangtan 411105, China. E-mail: zhoupan71234@126.com
bSchool of Materials Science and Engineering, Xiangtan University, Xiangtan 411105, China. E-mail: yangyi@xtu.edu.cn
First published on 18th May 2022
Abstract
Materials with spin-polarized electronic states have attracted a huge amount of interest due to their potential applications in spintronics. Based on first-principles calculations, we study the electronic characteristics of a series of AB2X4 chalcogenide spinel structures and propose two promising candidates, VZn2O4 and VCd2S4, that are spin-polarized semimetal materials. Both of them have ferromagnetic ground states. Their bands near the Fermi level are completely spin-polarized and form two types of nodal rings in the spin-up channel, and the large gaps in the spin-down channel prevent the spin-flip. Further symmetry analysis reveals that the nodal rings are protected by the glide mirror or mirror symmetries. Significantly, these nodal rings connect with each other and form a nodal chain structure, which can be well described using a simple four-band tight-binding (TB) model. The two ternary chalcogenide spinel materials with a fully spin-polarized nodal chain can serve as a prominent platform in the future applications of spintronics.
1 Introduction
Since the discovery of topological insulators, topological states of matter have attracted a lot of interest because of their extraordinary transport, magnetic, and optical properties.1–8 Topological semimetals are materials that exhibit nontrivial band crossings near the Fermi level and can be classified according to the dimension and distribution of the crossing points: nodal points (zero-dimensional), nodal lines and nodal rings (one-dimensional), and even nodal surfaces (two-dimensional).8–13 Interestingly, the nodal line can be twisted into a number of shapes, resulting in more complicated topological phases such as nodal chain, Hopf-link states, and nodal-net.14–17Topological semimetals have already been identified in a series of materials, including IrF4,18 Ba3Si4,19 carbon networks,14 and β-cristobalite BiO2.20 The majority of them, however, are nonmagnetic, whereas magnetic semimetals appear to exhibit exotic features such as tunable nodal points and the anomalous Hall effect. Initially the pyrochlore iridate AIr2O7 (A is Y or a rare-earth element) was proposed to be a magnetic topological semimetal,21 and later the ferromagnetic (FM) material HgCr2Se4 was proposed to be a novel Weyl semimetal.22 Soon after, HgCr2Se4 has been experimentally confirmed as a half-metal by Guan et al.23 Recently, more materials having magnetic topological properties have been proposed. For example, LiV2F6 has been theoretically demonstrated to be a Weyl monoloop half-semimetal,24 and Li3 (FeO3)225 has been proposed as a half-semimetal material with two independent Weyl loops. The Dirac line-nodal half-semimetal penta-X2Y (X = N, C and Y = B, C, P) was proposed,26 and CaFeO3 was theoretically predicted to have line-surface electronic states.9 Type-II spin-polarized nodal lines exist in quasi-two-dimensional compounds X2YZ4 (X = K, Cs, Rb, Y = Cr, Cu, Z = Cl, F),27 and nodal points, lines, and surfaces coexist in quasi-one-dimensional compounds XYZ3 (X = Cs, Rb, Y = Cr, Cu, Z = Cl, I).28 The spin-polarized Dirac point, triply degenerate nodal point, nodal loops, and nodal surface coexist in the anti-ferromagnetic (AFM) electride Ba4Al5·e−.29
Due to its various applications, the ternary chalcogenide spinel family is well-known and has been extensively researched for decades.17 They have a face centered cubic structure and are represented as AB2X4, where A and B are metal atoms that center the X (chalcogens) tetrahedrons and octahedrons, respectively. Almost all main group and transition metal elements may be synthesized in a stable spinel form, resulting in a diverse range of elemental compositions, electronic configurations, and valence states.30,31 Due to these features, the spinel has a wide range of magnetic, electrical, optical, and catalytic properties.32–36 Until now, a series of spinel materials, including HgCr2Se4, VMg2O4, LiV2O4, FeAl2O4, and NiAl2O4,22,37–39 have been theoretically predicted to have the fully spin polarized electronic states. Transition metal spinels always have various tunable magnetic properties, which is significant for spintronic applications. Their established synthesis technology lends themselves to spintronic studies as well. Therefore, exploring ideal spinel structures with fully spin-polarized electronic states is beneficial for spintronic experimental research and potential applications.
In this work, we find two spinel structures, VZn2O4 and VCd2S4, which have completely spin-polarized electronic states near the Fermi level. In their spin-up channel, they have a series of band crossings that belong to two different types of nodal rings and are protected by mirror or gliding mirror operations. We discovered that these rings form a chain-like structure. The nontrivial topological properties of the nodal chains are confirmed by the surface states. Only small gaps are opened after considering spin–orbit coupling (SOC). Hence, our work reveals a promising material platform for studying the fundamental physics of the fully spin-polarized nodal-chain, which also possesses great potential for future spintronic applications.
2 Method
The first-principles calculations were performed by using the Vienna Ab initio Simulation Package (VASP) within the framework of density functional theory (DFT).40–42 In our calculations, we used the projector augmented wave (PAW) method and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation interaction within generalized gradient approximation (GGA).40,43–45 The cutoff energy was set to 600 eV and a 15 × 15 × 15 Γ-centered k-point mesh was used. The force and energy convergence criteria were set to −0.001 eV Å−1 and 10−7 eV, respectively. The phonon dispersion was obtained by using the PHONOPY code.46 Because of the Coulomb interaction effects, the GGA+U method was applied within the rotationally invariant DFT+U approach proposed by Dudarev et al.47 and the effective U value (Ueff = U – J) for V was set to 4 eV. The Wannier90 and WannierTools packages48,49 were used to construct the maximally localized Wannier functions (MLWFs) for the energy bands close to the Fermi level and to calculate the local band gap and surface states, respectively.3 Results and discussion
3.1 Materials discovery
In this paper, we examine a series of spinel materials with the chemical formula AB2X4, where B can be Ag, Cu, Cd, Al, Ga, Ti, Ni, Ge, Hg, In, Zn or Y, A is the element of V, Mn, Fe, or Co, and X is O or S. Because most synthesized spinels have FM ground states, we first relaxed the crystal structures and calculated their band structures in the FM state. Table S1, ESI,† summarizes their lattice constants, magnetic moments, and spin-polarized properties. According to their band structures, the most promising candidates with spin-polarized semimetal states are VZn2O4 and VCd2S4. Therefore, we mainly study these two materials.3.2 Magnetic properties and structural stability of VZn2O4 and VCd2S4
The crystal structures of VZn2O4 and VCd2S4 are shown in Fig. 1(a) and (b), respectively. The V atoms are centered in the O tetrahedron, and Zn or Cd atoms are located at the centers of the O octahedron. Both of them belong to the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227). Their lattice constants are 8.534 Å and 10.778 Å, respectively. According to Bader charge analysis,50 the O atom gains 1.12(0.84)|e|, the V atom loses 1.97(1.54)|e|, and the Zn(Cd) atom loses 1.25(0.92)|e|. Therefore, the charge transfer from V to O is greater than that in Zn(Cd). We have further confirmed their magnetic ground states by computing the energies of the FM and AFM configurations, as shown in Fig. S1, ESI.† The results show that the FM configuration is the most stable, with an energy of 70.3(86.2) meV per V atom lower than that of the AFM state in VZn2O4 (VCd2S4). The magnetic moment per primitive cell in the FM ground state is 2 μB, which is primarily contributed by V atoms with a low-spin electronic configuration (V↓↓↑). Therefore, all of the material properties listed below are calculated from their FM ground states.
m (No. 227). Their lattice constants are 8.534 Å and 10.778 Å, respectively. According to Bader charge analysis,50 the O atom gains 1.12(0.84)|e|, the V atom loses 1.97(1.54)|e|, and the Zn(Cd) atom loses 1.25(0.92)|e|. Therefore, the charge transfer from V to O is greater than that in Zn(Cd). We have further confirmed their magnetic ground states by computing the energies of the FM and AFM configurations, as shown in Fig. S1, ESI.† The results show that the FM configuration is the most stable, with an energy of 70.3(86.2) meV per V atom lower than that of the AFM state in VZn2O4 (VCd2S4). The magnetic moment per primitive cell in the FM ground state is 2 μB, which is primarily contributed by V atoms with a low-spin electronic configuration (V↓↓↑). Therefore, all of the material properties listed below are calculated from their FM ground states.
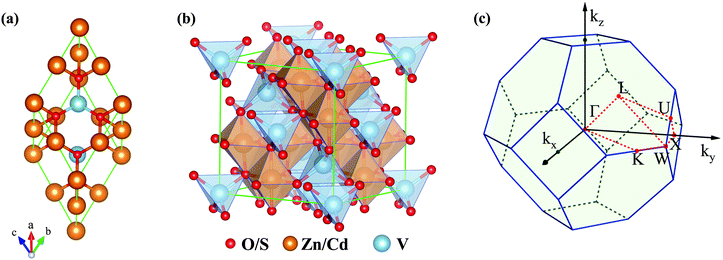 | ||
| Fig. 1 (a) Primitive cell and (b) conventional cell of VZn2O4 and VCd2S4. (c) BZ and the corresponding high-symmetry paths in the first Brillouin zone. | ||
Despite the fact that a large number of similar materials with the same crystal structure have been synthesized, the two spinel materials have yet to be synthesized in experiments. We will investigate their stability with the experimentally synthesized spinel material in the following section. To demonstrate their stability, we firstly calculate the cohesive energies (Ec) of VZn2O4 and VCd2O4. The results are 4.23 eV per atom and 2.86 eV per atom, respectively. In addition, we also calculate the Ec of experimentally synthesized ZnV2O4.51 The value is 3.72 eV per atom, which is comparable to those of our structures, indicating that they have the potential to be synthesized. The phonon dispersions are calculated as well, and the results are shown in Fig. 2(a) and (b). The absence of imaginary frequency reveals that they are kinetically stable. Their first-principles molecular dynamics (MD) simulations are performed by using a 2 × 2 × 2 supercell [see Fig. 2(c) and (d)]. The evolutions of total energies prove that the two materials are thermodynamically stable. Furthermore, as shown in Table S2, ESI,† the linear elastic constants and Young's moduli computed using the stress vs. energy method meet the Born–Huang criteria (C11 − C12 > 0, C11 + 2C12 > 0, C44 > 0),52 indicating that they are mechanically stable.
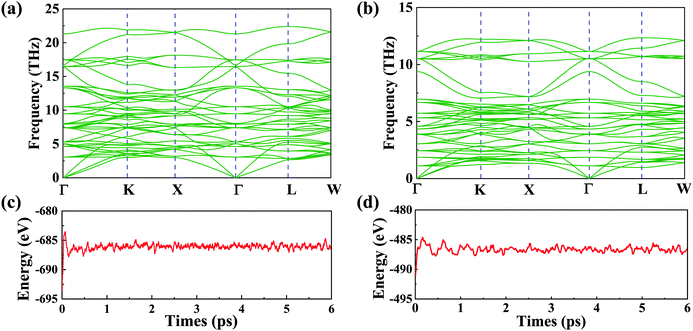 | ||
| Fig. 2 Phonon dispersions (a) for VZn2O4 and (b) for VCd2S4. Their energy evolutions obtained by MD at 300 K for 6 ps (1 fs per step) are shown in (c) and (d), respectively. | ||
3.3 Electronic properties
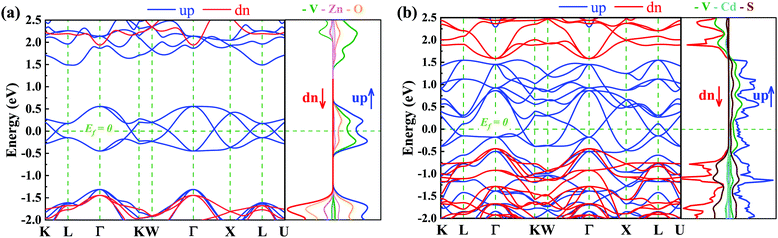
Here we focus on the electronic properties of VZn2O4 and VCd2S4. Their band structures without SOC are depicted in Fig. 3. Both of their electronic states near the Fermi level are entirely spin-polarized. The bands in the spin-up channel cross the Fermi level and show metallic properties, while the bands in the spin-down channel exhibit insulating characteristics with a large gap of 3.38 eV in VZn2O4 and 2.02 eV in VCd2S4. The bands around the Fermi level have hourglass dispersion along the high symmetry lines and form many crossing points. Their total and projected density of states are also shown in Fig. 3(a) and (b), respectively, and the results demonstrate that V atoms contribute the majority of their half-metallic bands near the Fermi level.The orbital-resolved band structures in Fig. 4(a) indicate that the V-dz2 and V-dx2−y2 orbitals contribute the most to the conduction-band minimum (CBM) and valence-band maximum (VBM) of VZn2O4, but there are more orbitals that contribute to the low-energy electronic states of VCd2S4 [see Fig. S2(a), ESI†]. The local band gaps between the CBM and VBM are calculated (as shown in Fig. 4 for VZn2O4 and Fig. S2, ESI,† for VCd2S4). It can be seen that the band crossings are not isolated, and they combine to form two different types of closed loops. We use the abbreviation NR1 to represent the nodal ring that includes the crossing points on the paths of Γ–K, W–Γ, and Γ–X and centers around the Γ point in the kz = 0 plane. On the other hand, NR2 represents the nodal ring centered around the X point in the Γ–X–L plane. Although a band crossing appears in the L–K path, it seemingly belongs to a new nodal ring in the L–Γ–K plane, which also contains the crossing in the Γ–K path. After analyzing the symmetry property of the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, we discover that the L–Γ–K and Γ–X–L planes are equivalent, and the new nodal ring is equivalent to NR2.
m, we discover that the L–Γ–K and Γ–X–L planes are equivalent, and the new nodal ring is equivalent to NR2.
In order to decide whether the nodal rings are accidental or symmetry-protected, we further analyze their symmetries by calculating the irreducible representations (irreps) of the Bloch states around these crossing points (as shown in Fig. S3, ESI†). As a result, we find that the NR1 in the kz =0 plane is under the protection of the glide mirror operation Gz:(x, y, z) → (x + 1/4, y + 3/4, −z + 1/2), which can be verified by the corresponding opposite sign of glide eigenvalues. Similarly, the NR2 in the Γ–X–L plane is protected by the mirror operation G![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01:(x, y, z) → (z, y, x) (Fig. S3, ESI†). The glide or mirror eigenvalues are used to illustrate the formation of hourglass dispersion in the planes of Γ–K–W–X and Γ–X–U–L [see Fig. S4, ESI†]. These two planes are invariant planes of Gz:(x, y, z) → (x + 1/4, y + 3/4, −z + 1/2) and G
01:(x, y, z) → (z, y, x) (Fig. S3, ESI†). The glide or mirror eigenvalues are used to illustrate the formation of hourglass dispersion in the planes of Γ–K–W–X and Γ–X–U–L [see Fig. S4, ESI†]. These two planes are invariant planes of Gz:(x, y, z) → (x + 1/4, y + 3/4, −z + 1/2) and G![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01:(x, y, z) → (z, y, x), respectively. The eigenvalues of the corresponding operations can then be used to label the Bloch states in these two planes. Here we use the representative paths W–Γ and X–L to demonstrate them. As shown in Fig. S4(b), ESI,† the four bands around the Fermi level form an hourglass dispersion. According to the ‘Bilbao Crystallographic Server’53 website's little group representation of the space group Fd
01:(x, y, z) → (z, y, x), respectively. The eigenvalues of the corresponding operations can then be used to label the Bloch states in these two planes. Here we use the representative paths W–Γ and X–L to demonstrate them. As shown in Fig. S4(b), ESI,† the four bands around the Fermi level form an hourglass dispersion. According to the ‘Bilbao Crystallographic Server’53 website's little group representation of the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, only two two-order single-values representations exist at W (W1 and W2). However, there are four one-order (Γ+1, Γ−1, Γ+2, and Γ−2), two two-order (Γ+3 and Γ−3), and four third-order (Γ+4, Γ−4, Γ+5, and Γ−5) single-valued representations at Γ. Using the wavefunctions from VASP, we find that the representations at W (Γ) are W1 and W2 (Γ+3 and Γ−3) and all of them are double-degenerate. Because the W–Γ is located on the invariant plane, the glide eigenvalues must be
m, only two two-order single-values representations exist at W (W1 and W2). However, there are four one-order (Γ+1, Γ−1, Γ+2, and Γ−2), two two-order (Γ+3 and Γ−3), and four third-order (Γ+4, Γ−4, Γ+5, and Γ−5) single-valued representations at Γ. Using the wavefunctions from VASP, we find that the representations at W (Γ) are W1 and W2 (Γ+3 and Γ−3) and all of them are double-degenerate. Because the W–Γ is located on the invariant plane, the glide eigenvalues must be 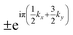 [where (kx, ky, kz) is the fractional coordination of the k-points on the Γ–K–W–X plane], which indicate that the sign of the eigenvalues would be changed when k moves from W to Γ. By replacing the coordinates with the above eigenvalues, we obtain the glide eigenvalues at W and Γ, as shown in Fig. S4(b), ESI.† Because the double-degenerate states have opposite signs at W, the degenerate states at Γ have the same glide eigenvalues. Because the band evolution along W–Γ must be smooth, the two eigenspaces must be exchanged, resulting in hourglass dispersion. A similar argument can be applied to X–L with the operator of G
[where (kx, ky, kz) is the fractional coordination of the k-points on the Γ–K–W–X plane], which indicate that the sign of the eigenvalues would be changed when k moves from W to Γ. By replacing the coordinates with the above eigenvalues, we obtain the glide eigenvalues at W and Γ, as shown in Fig. S4(b), ESI.† Because the double-degenerate states have opposite signs at W, the degenerate states at Γ have the same glide eigenvalues. Because the band evolution along W–Γ must be smooth, the two eigenspaces must be exchanged, resulting in hourglass dispersion. A similar argument can be applied to X–L with the operator of G![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01. However, because this operation does not involve fractional translation, the eigenvalues in the whole plane must be +1 or −1.
01. However, because this operation does not involve fractional translation, the eigenvalues in the whole plane must be +1 or −1.
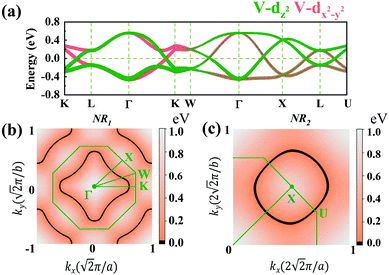
Due to the cubic symmetry of the two materials, other equivalent rings can appear on the equivalent planes, for example, similar nodal rings NR1 can appear in the planes of kx = 0, ky = 0. Surprisingly, we find that NR1 and NR2 are not isolated but share the same nodal points in the paths of Γ–K and Γ–X, and form a chain-like band crossing structure in BZ in the spin-up channel, as shown in Fig. 5(a).
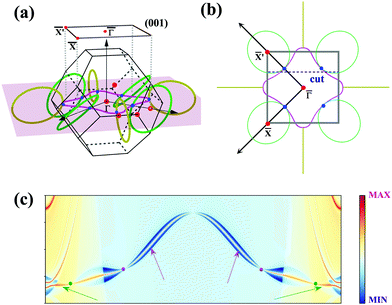
To further illustrate the topological properties of the nodal chain, we calculated the Berry phase with the help of MLWFs. As shown in Fig. S5, ESI,† the Berry phase is π (0) if the k-loop passes through NR1 or NR2 (NR1 and NR2), which are the typical characteristics of a nodal chain. Nodal chains that are topologically protected always lead to nontrivial surface states. The 2D projection of bulk BZ onto the (001) plane and the related high-symmetry points are shown in Fig. 5(a). Fig. 5(b) shows the projection of a portion of the nodal rings. We chose a path cut in the projected 2D BZ to investigate the nontrivial surface states, and the electronic local density states are shown in Fig. 5(c). The surface states demonstrate that the nodal chain's two types of nodal lines are topologically nontrivial.
Recently, several spinels with nodal net states have been proposed. Here we compare their nodal states with VZn2O4 and VCd2S4, including LiV2O4, FeAl2O4 and NiAl2O4, MgV2O4 and Mg2VO4.37,39,54 They have a half-semimetal electronic state near Ef, which is the same as our two materials. When compared to the nodal lines in VZn2O4 or VCd2S4, the size of NR2 for LiV2O4 is clearly different, resulting in the band crossing of the Γ–K path disappearing and the band structure also being different. Despite the fact that FeAl2O4 and NiAl2O4 have been proposed as having nodal chain states, the energy ranges of their band crossings near Ef are too broad and are disadvantageous to analyze the topological characters and surface states. However, the dispersion of the crossing points for VZn2O4 and VCd2S4 is small, making experimental detection much easier. The magnetic ground state of MgV2O4 is AFM, with spin-polarized flat band states under a ferromagnetic state, as opposed to our ferromagnetic ground states and half-metallic nodal chains. Because Mg2VO4 has a similar atomic occupation to our two materials, its nodal chain is similar to our two materials.
3.4 Tight-binding model
In this section, we construct a tight-binding model based on the Slater–Koster method55 to understand the formation of the nodal chain. As observed in the orbital-projected band structures without SOC, the dx2−y2 and dz2 orbitals of V atoms contribute the most to the four isolated bands around the Fermi level for VZn2O4. Therefore, we use them as the basis to construct a four-band tight-binding model. A Hamiltonian considering the d–d hopping until the next-nearest neighbor is given by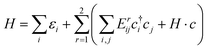 | (1) |
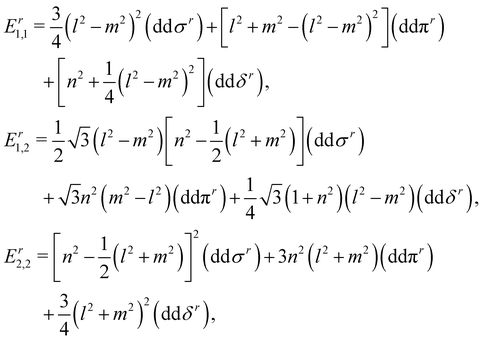 | (2) |
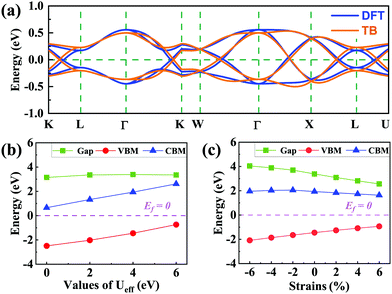
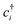 (cj) is the creation (annihilation) operator of electrons at site i (j). Enij is the n-hopping coefficient between the ith and jth sites. l, m, and n represent the directional cosine of Rij along the three directions x, y, and z, respectively. ddσ, ddπ, and ddδ are independent parameters in the SK method. Because of the double degenerate energy bands along the L–Γ path, the on-site energies of the dx2−y2 and dz2 orbitals must be equal. Besides, after considering the concrete structure of VZn2O4, we find that ddσ1 vanishes in the final expressions of hopping parameters. As a result, there are six independent parameters in the TB model. After fitting the first-principles energy bands, we obtain the values of these parameters, and they are listed in Table 1. The band structures computed by the TB model Hamiltonian correspond well with those derived using DFT, as shown in Fig. 6(a). Further calculations reveal that the TB model shares the same topological properties with the MLWFs.
(cj) is the creation (annihilation) operator of electrons at site i (j). Enij is the n-hopping coefficient between the ith and jth sites. l, m, and n represent the directional cosine of Rij along the three directions x, y, and z, respectively. ddσ, ddπ, and ddδ are independent parameters in the SK method. Because of the double degenerate energy bands along the L–Γ path, the on-site energies of the dx2−y2 and dz2 orbitals must be equal. Besides, after considering the concrete structure of VZn2O4, we find that ddσ1 vanishes in the final expressions of hopping parameters. As a result, there are six independent parameters in the TB model. After fitting the first-principles energy bands, we obtain the values of these parameters, and they are listed in Table 1. The band structures computed by the TB model Hamiltonian correspond well with those derived using DFT, as shown in Fig. 6(a). Further calculations reveal that the TB model shares the same topological properties with the MLWFs.
| Onsite energy | ε | 0.012 eV |
| Nearest neighbor | ddπ1 | −1.097 eV |
| ddδ1 | 1.869 eV | |
| ddσ2 | −0.555 eV | |
| Next nearest neighbor | ddπ2 | −0.045 eV |
| ddδ2 | 0.257 eV |
3.5 Robust semimetal states and the effect of SOC
Because the spinels have not been synthesized, there are no experimental data about their electronic structures. Here we investigate how electronic correlations affect the half-semimetal states. The energy band structures and the evolution of the VBM, CBM and gaps with the Ueff range from 0 to 6 eV are calculated, as shown in Fig. S6, ESI,† and Fig. 6(b). When the Ueff value increases, the energy values of the VBM and CBM increase, but the band gaps of spin-down bands do not change significantly. Moreover, the crossing points remain around the Fermi level with varying Ueff. The results reveal that the half-semimetal characters are insensitive to electron correlation.Finally, we examine how the external strain and SOC affect the energy band structures of these two materials. As shown in Fig. 6(c), the band gaps of the spin-down bands become smaller with increasing lattice constants, but they are still insulated and the semimetal states around the Fermi level are still well preserved (Fig. S7, ESI†). The band structures with SOC are presented in Fig. S8 (ESI†). We find that all opened gaps are below 10 meV, which means they can always be neglected at room temperature.
4 Conclusion
In conclusion, we proposed two spinel materials with nontrivial spin-polarized semimetal states: VZn2O4 and VCd2S4. Both of them have FM ground states and are kinetically and mechanically stable. The band crossings around the Fermi level belong to two kinds of fully spin-polarized hourglass nodal rings and they are, respectively, protected by the glide operation Gz and mirror operation G![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01 (or their equivalent operations). The nontrivial properties are also verified by their nontrivial surface states. Remarkably, we find that the two kinds of nodal rings link together and form a chain-like structure. When SOC is included, negligible gaps are opened for the semimetal states. The band crossings are also well retained under various Ueff values and external strains. These two spinel materials provide an excellent platform for studying the topological semimetal states of ferromagnetic systems.
01 (or their equivalent operations). The nontrivial properties are also verified by their nontrivial surface states. Remarkably, we find that the two kinds of nodal rings link together and form a chain-like structure. When SOC is included, negligible gaps are opened for the semimetal states. The band crossings are also well retained under various Ueff values and external strains. These two spinel materials provide an excellent platform for studying the topological semimetal states of ferromagnetic systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11804287 and 11574260), the Hunan Provincial Natural Science Foundation of China (2019JJ50577, 2021JJ30686, and 2019JJ60006) and the Postgraduate Scientific Research Innovation Project of Hunan Province (CX20210623).Notes and references
- M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X. L. Qi and S. C. Zhang, Science, 2007, 318, 766–770 CrossRef PubMed.
- C. Lei, S. Chen and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27224–27230 CrossRef CAS PubMed.
- Y. Tokura, K. Yasuda and A. Tsukazaki, Nat. Rev. Phys., 2019, 1, 126–143 CrossRef.
- R. Yu, W. Zhang, H. J. Zhang, S. C. Zhang, X. Dai and Z. Fang, Science, 2010, 329, 61–64 CrossRef CAS PubMed.
- C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei and L. L. Wang, et al. , Science, 2013, 340, 167–170 CrossRef CAS PubMed.
- A. A. Zyuzin, S. Wu and A. A. Burkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165110 CrossRef.
- N. Nagaosa, T. Morimoto and Y. Tokura, Nat. Rev. Mater., 2020, 5, 621–636 CrossRef CAS.
- X. Zhang, Z. M. Yu, Z. Zhu, W. Wu, S. S. Wang, X. L. Sheng and S. A. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 235150 CrossRef CAS.
- R. W. Zhang, D. S. Ma, J. M. Zhang and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 195115 CrossRef CAS.
- W. Wu, Y. Liu, S. Li, C. Zhong, Z. M. Yu, X. L. Sheng, Y. Zhao and S. A. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 115125 CrossRef CAS.
- Q. F. Liang, J. Zhou, R. Yu, Z. Wang and H. Weng, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 085427 CrossRef.
- Z. Yan, R. Bi, H. Shen, L. Lu, S. C. Zhang and Z. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 041103 CrossRef.
- A. A. Soluyanov, D. Gresch, Z. Wang, Q. Wu, M. Troyer, X. Dai and B. A. Bernevig, Nature, 2015, 527, 495–498 CrossRef CAS PubMed.
- Z. Li, Y. Xie, P. Y. Chang and Y. Chen, Carbon, 2020, 157, 563–569 CrossRef CAS.
- R. Bi, Z. Yan, L. Lu and Z. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 201305 CrossRef.
- W. Chen, H. Z. Lu and J. M. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 041102 CrossRef.
- L. Li, X. Kong and F. M. Peeters, Carbon, 2019, 141, 712–718 CrossRef CAS.
- T. Bzdušek, Q. Wu, A. Rüegg, M. Sigrist and A. A. Soluyanov, Nature, 2016, 538, 75–78 CrossRef PubMed.
- J. Cai, Y. Xie, P. Y. Chang, H. S. Kim and Y. Chen, Phys. Chem. Chem. Phys., 2018, 20, 21177–21183 RSC.
- S. M. Young, S. Zaheer, J. C.-Y. Teo, C. L. Kane, E. J. Mele and A. M. Rappe, Phys. Rev. Lett., 2012, 108, 140405 CrossRef CAS PubMed.
- X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205101 CrossRef.
- G. Xu, H. Weng, Z. Wang, X. Dai and Z. Fang, Phys. Rev. Lett., 2011, 107, 186806 CrossRef PubMed.
- T. Guan, C. Lin, C. Yang, Y. Shi, C. Ren, Y. Li, H. Weng, X. Dai, Z. Fang, S. Yan and P. Xiong, Phys. Rev. Lett., 2015, 115, 087002 CrossRef PubMed.
- R.-W. Zhang, X. Zhou, Z. Zhang, D.-S. Ma, Z.-M. Yu, W. Feng and Y. Yao, Nano Lett., 2021, 21, 8749–8755 CrossRef CAS PubMed.
- C. Chen, Z. M. Yu, S. Li, Z. Chen, X. L. Sheng and S. A. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 075131 CrossRef.
- L. Wang, L. Jin, G. Liu, Y. Liu, X. Dai and X. Zhang, Appl. Mater. Today, 2021, 23, 101057 CrossRef.
- T. He, X. Zhang, L. Wang, Y. Liu, X. Dai, L. Wang and G. Liu, Mater. Today Phys., 2021, 17, 100360 CrossRef CAS.
- T. He, Y. Liu, L. Tian, X. Zhang, W. Meng, X. Dai and G. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 085135 CrossRef CAS.
- W. Meng, X. Zhang, Y. Liu, X. Dai and G. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 104, 195145 CrossRef CAS.
- M. G. Brik, A. Suchocki and A. Kaminska, Inorg. Chem., 2014, 53, 5088–5099 CrossRef CAS PubMed.
- C. Biagioni and M. Pasero, Am. Mineral., 2014, 99, 1254–1264 CrossRef.
- Z. Yue, Z. Hou, F. Yun, P. Liu, G. Yang, A. Bake, W. Zhao, D. Cortie, C. Shu and S. Hu, et al. , J. Mater. Chem., 2021, 9, 8874–8881 CAS.
- J. H. Lee, Y. W. Noh, I. S. Jin, S. H. Park and J. W. Jung, J. Mater. Chem., 2019, 7, 7288–7298 CAS.
- X. Huang, J. Y. Zhang, M. Wu, S. Zhang, H. Xiao, W. Han, T. L. Lee, A. Tadich, D. C. Qi and L. Qiao, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 115301 CrossRef CAS.
- L. I. Granone, A. C. Ulpe, L. Robben, S. Klimke, M. Jahns, F. Renz, T. M. Gesing, T. Bredow, R. Dillert and D. W. Bahnemann, Phys. Chem. Chem. Phys., 2018, 20, 28267–28278 RSC.
- C. Dong, Z. Qu, Y. Qin, Q. Fu, H. Sun and X. Duan, ACS Catal., 2019, 9, 6698–6710 CrossRef CAS.
- H. Zhang, X. Zhang, T. He, X. Dai, Y. Liu, G. Liu, L. Wang and Y. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 155116 CrossRef CAS.
- W. Jiang, H. Huang, F. Liu, J.-P. Wang and T. Low, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 121113 CrossRef CAS.
- H. Zhang, X. Zhang, Y. Liu, X. Dai, G. Chen and G. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 195124 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- Q. Wu, S. Zhang, H. F. Song, M. Troyer and A. A. Soluyanov, Comput. Phys. Commun., 2018, 224, 405–416 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- F. K. Butt, C. Cao, R. Ahmed, W. S. Khan, T. Cao, N. Bidin, P. Li, Q. Wan, X. Qu and M. Tahir, et al. , CrystEngComm, 2014, 16, 894–899 RSC.
- M. Born, K. Huang and M. Lax, Am. J. Phys., 1955, 23, 474 CrossRef.
- M. I. Aroyo, J. Perez Mato, D. Orobengoa, E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS.
- J. G. Azadani, W. Jiang, J.-P. Wang and T. Low, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 155144 CrossRef CAS.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498–1524 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Information of all spinels considered. Magnetic configurations and elastic constants. Orbital resolved bands and local gap distribution of VCd2S4. Eigenvalues of symmetry operations. Berry phase of the TB model. Energy band structures of VZn2O4 with different Hubbard U values, strains and SOC. See DOI: https://doi.org/10.1039/d2ma00107a |
| ‡ These two authors equally contributed to this work. |
| This journal is © The Royal Society of Chemistry 2022 |