Three-dimensional heating and patterning dynamics of particles in microscale acoustic tweezers

Abstract

Acoustic tweezers facilitate a noninvasive, contactless, and label-free method for the precise manipulation of micro objects, including biological cells. Although cells are exposed to mechanical and thermal stress, acoustic tweezers are usually considered as biocompatible. Here, we present a holistic experimental approach to reveal the correlation between acoustic fields, acoustophoretic motion and heating effects of particles induced by an acoustic tweezer setup. The system is based on surface acoustic waves and was characterized by applying laser Doppler vibrometry, astigmatism particle tracking velocimetry and luminescence lifetime imaging. In situ measurements with high spatial and temporal resolution reveal a three-dimensional particle patterning coinciding with the experimentally assisted numerical result of the acoustic radiation force distribution. In addition, a considerable and rapid heating up to 55 °C depending on specific parameters was observed. Although these temperatures may be harmful to living cells, counter-measures can be found as the time scales of patterning and heating are shown to be different.

---

1 Introduction

The active manipulation of biological cells and other corpuscular components of biological fluids by means of sound waves has recently attracted significant interest in biology and medicine. It provides a versatile toolset for precise, contactless, label-free, and biocompatible micromanipulation. This is of particular interest for point-of-care applications.^1–6 The utilization of the acoustophoretic effect has been demonstrated for diverse biomedical engineering applications, including focusing of cells to enable a high-throughput analysis^7,8 and separation of different cell species^9–11 or exosomes¹² from whole blood to implement a cell-level therapy. Moreover, three-dimensional trapping and the precise control of the position was shown for particles and cells^13–15 as well as for much larger living microorganisms.¹⁶

In general, acoustic tweezers rely on the coupling of ultrasonic waves to the cell suspension, thereby inducing mainly two forces: i) the body force caused by the absorption of acoustic energy in the fluid yielding a steady flow known as acoustic streaming, and ii) the acoustic radiation force (ARF) caused by acoustic scattering at suspended objects.^17–20 The latter is of special interest for the active manipulation of cells, i.e. moving them relative to the surrounding fluid, even though the acoustic streaming also transfers momentum to the cells by the drag force. For this, an appropriate ratio between the acoustic wavelength and the size of cells has to be chosen, where the latter is typically in the micrometer range or even smaller. Acoustic tweezers based on the primary excitation of bulk acoustic waves (BAW) are generally limited to larger wavelengths. They were particularly demonstrated for cell sorting, mostly combined with a microfluidic flow-through system.^21–24 In contrast, acoustic tweezers based on the primary excitation of surface acoustic waves (SAW) allow efficient manipulation with even smaller acoustic wavelengths. Moreover, complex acoustic fields can be realized by superposition of several SAWs facilitating a more precise cell manipulation, e.g. the separation and trapping even of single cells.^13,25–27 However, both types of acoustic tweezers finally rest upon the radiation of bulk waves into the fluid, accompanied by the transfer of acoustic energy from the active surface to the cell suspension in the microfluidic chamber.

The lateral distribution of the mechanical vibration at the surface-fluid interface is the most crucial parameter for the intended actuation. The determination of the displacement amplitude at the surface-fluid interface has already been an essential part of many investigations of the acoustophoretic effect.^28,29 However, it remains challenging because the interface under investigation is hardly accessible for experimental methods if a fluid (or any other material) is in contact with the substrate surface. Thus, the amplitude of the displacement was mostly determined either by measurements in absence of surface loading^14,30–36 or by numerical simulations.^{14,29,37–41} The former approach does not yield the real amplitude because acoustic attenuation and diffraction caused by the radiation of a bulk wave into the attached material cannot be determined in this way. The latter approach requires a well-defined interface as well as the knowledge of effective material properties. Moreover, numerical simulations based on the commonly used finite element method (FEM) require large computational resources. Thus, they are limited to small volumes or have to be reduced to two spatial dimensions and are not able to completely cover all aspects of real setups.^42–45

Besides the transfer of momentum, the acoustic energy is mainly dissipated due to the viscous attenuation of the bulk wave and thereby heating the fluid. This issue, also known as the acoustothermal effect, is of special importance for acoustophoretic cell manipulation since cells are very sensitive against elevated temperature and large temperature gradients. For instance, mammalian cells can be seriously harmed, if the temperature exceeds 43 °C, and denaturation of lots of proteins generally occurs at temperatures above 45 °C.⁴⁶ On the other hand, acoustically induced heating can also be used for active temperature control of cells and protein suspensions.^47,48 An increase of temperature due to the acoustothermal effect has to be considered anyhow, what recently came into the focus of interest.^49–51 So far, experimental investigations of acoustically induced heating in acoustofluidic systems were carried out either by invasive techniques, like thermocouples or resistance thermometers,^52–54 or by noninvasive techniques, e.g. thermography using an infrared camera.^{27,47,55–59} The former techniques are not suitable for microfluidics due to the large sensing element with respect to the volume under investigation. The main drawback of infrared thermography is that it is limited to surfaces and it is not possible to measure inside the fluid with high spatial resolution. A common technique for measurements inside the fluid is the laser induced fluorescence technique, usually applied for microscopic flows using two dissolved fluorescent dyes.^60,61 This technique enables high temporal and high spatial resolution within a two-dimensional plane. However, in microfluidics usually volume illumination is applied. Hence, dye molecules outside the focus plane contribute to the fluorescence intensity signal, which biases the temperature measurements particularly when temperature gradients in out-of-plane direction exist.⁶²

Microacoustic tweezers pose specific challenges with respect to the experimental investigation of acoustophoretic and acoustothermal effects, since small acoustic wavelengths involve relatively large spatial gradients of potential quantities, e.g. sound pressure and temperature. These difficulties increase for standing waves due to the sub-wavelength node/anti-node periodicity of the acoustic field. Hence, advanced noninvasive experimental methods providing a high spatial resolution are required to gain more detailed insight into the fluid volume as well as to enable a reliable analysis of the mechanical and thermal impact on cells during acoustophoretic manipulation.

Here, we present a comprehensive approach for detailed investigations of the involved acoustophoretic and acoustothermal effects based on noninvasive experimental methods. Investigations are exemplarily performed for an acoustic tweezer setup driven by a two-dimensional standing surface acoustic wave field (Fig. 1). The optical access necessary for the applied methods is realized through the substrate (Fig. 1a). The surface normal displacement amplitude of the SAW at the substrate-fluid interface is experimentally determined using a conventional laser Doppler vibrometer (LDV) specifically adapted for transmission measurements through the crystalline substrate.⁶³ The BAW field inside the fluid is determined by a numerical simulation with the measured SAW field used as boundary condition. This combination allows for a more accurate and realistic determination of the acoustic field inside the chamber. Moreover, the particles suspended in the fluid help to demonstrate acoustic trapping and serve as tracer particles for three-dimensional measurements of position and temperature. The volumetric measurement of particle positions is realized by applying the astigmatism particle tracking velocimetry (APTV).⁶⁴ The combination of APTV with luminescence lifetime imaging (LLI) furthermore enables the simultaneous measurement of the temperature of the particles.⁶⁵ A comparison of the acoustic field and the positions of trapped particles, measured in all three dimensions, is illustrated in Fig. 1c. Besides the position, the temperature of the particles provides high-resolution localized information about heating due to the acoustothermal effect even for highly dynamic processes (Fig. 1d). Hence, by measuring all important quantities in situ, unique findings on the highly dynamical behavior of the acoustophoretic motion and temperature of trapped particles, dependencies between the actual acoustic fields and particle positions as well as inherent energy conversion processes and heating effects can be revealed.

Fig. 1 a) Experimental investigations are realized with optical transmission through the substrate material. b) The acoustofluidic device consists of the SAW chip with an arrangement of interdigital transducers (IDTs) and the chamber confining the fluid with suspended particles. The origin of the coordinate system coincides with the lateral center of the chamber and z = 0 at the substrate-fluid interface. c) The parallel measurement of acoustic fields with the subsequent estimation of the acoustic radiation force distribution (illustrated as isosurface) as well as of particle positions and according temperature enables high-resolution, three-dimensional observation of the acoustophoretic and the acoustothermal effect. d) This approach even allows for the investigation of transient processes, i.e. the temporal variation of particle positions and temperature.

2 Experimental

2.1 Acoustic tweezer setup

2.1.1 Surface acoustic wave device. The SAW device was fabricated on a 128° rotated Y-cut of lithium niobate (LiNbO₃) single crystal substrate. This material is typically employed for SAW-driven microfluidics due to the relatively high electroacoustic coupling coefficient. Four interdigital transducers (IDTs) with solid electrodes were arranged at the top side of the double side polished substrate. One pair of opposing IDTs is arranged to excite SAW propagating in x direction whereas the other pair is oriented orthogonal to this (y direction). The distance between opposing IDTs equals 3.2 mm. All IDTs have the same aperture (1.2 mm) while the period as well as the number of electrode finger pairs were adapted for both orientations, in order to achieve impedance matching at a common resonance frequency of 32.4 MHz.³⁶ The IDT electrodes were patterned using laser direct writing photolithography and subsequent deposition of titanium (5 nm) and aluminum (295 nm) followed by a lift-off process. An additional passivation layer (500 nm SiO₂) was deposited on the complete structure in order to protect the electrodes from corrosion and to improve the adhesion of the microfluidic chamber.

2.1.2 Microfluidic chamber. The microfluidic chamber with an inner lateral size of 1.2 mm × 1.2 mm and a height of 88 μm was fabricated from polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) by mold-assisted casting using a silicon master. The outer dimensions of the PDMS structure are 20 mm × 22 mm with a height of 5 mm. The cured PDMS structure and the SAW device were subsequently bonded after previous UV/ozone activation of both surfaces to be connected. The center of the microfluidic chamber was aligned to the center between the four IDTs.

2.1.3 Particles and fluid. Particles used for acoustophoretic trapping were made from polymethylmethacrylate (PMMA) with a diameter of 10 μm and contained the temperature sensitive phosphorescent dye europium(III) thenoyltrifluoroacetonate (EuTTa, 360/615 nm, Surflay Nanotec GmbH). The fluid in which the particles were suspended was a glycerol–water mixture with a concentration of 55% w/w, yielding a density of 1.135 g cm⁻³ at 25 °C.⁶⁶ Thus, the mismatch with respect to the density of the particles (1.18 g cm⁻³) was low enough to avoid strong sedimentation, while offering sufficient acoustic contrast in order to induce an appropriate radiation force for manipulation.

2.1.4 Electric operation and fluid supply. The SAW device together with the attached PDMS structure was mounted on a custom-built holder, to ensure proper electrical connection of the IDTs as well as the fluid supply via inlets and outlets. Moreover, the holder was equipped with a hole, to allow optical access to the substrate-fluid interface and the fluid volume inside the chamber by transmission through the substrate material from the bottom side (cf.Fig. 1a). The SAW device was electrically characterized by means of S-parameter measurements using a vector network analyzer (VNA, E5071C, Keysight Technologies). Besides checking for proper operation of the device, the electric transmission coefficients, which were determined for each pair of opposing IDTs, made it possible to estimate the energy transferred to the microfluidic structure, i.e. PDMS and fluid. For operation during particle experiments, a signal generator with an integrated power amplifier (PowerSAW, SAW Generator BSG-F20, BelektroniG) was used. This device has two signal output ports maintaining user-defined amplitudes, frequencies and phase relations. Accordingly, two additional power splitters (SYPS-2-52HP+, Mini-Circuits) were used to connect each IDT pair to one of the output ports of the PowerSAW generator. The fluid was supplied by either a syringe pump (Nemesys 290N, Cetoni) for measurements of particle trapping and temperature distribution or a peristaltic pump (ISM 597, Ismatec) during SAW wave field measurements.

2.2 Measurement of displacement amplitude at the substrate-fluid interface

The lateral distribution of the surface normal displacement amplitude u(x, y) at the substrate-fluid and the substrate-PDMS interface was measured using a conventional ultrahigh-frequency laser Doppler vibrometer (LDV, UHF-120, Polytec). For this purpose, the standard LDV setup was adapted in order to enable optical transmission measurement through the birefringent LiNbO₃ substrate.^63,67 A linear polarizer was inserted in the optical beam path of the LDV to suppress one of the laser beams originating from birefringence. Moreover, the influence of effects based on different indices of refraction as well as complex parasitic acousto-optic modulation due to passage of the crystal had to be compensated by post-processing.⁶³

The laser beam of the LDV was focused on the interface under investigation using a microscopic objective lens (Mitutoyo, M Plan APO 20×, NA = 0.42) yielding normally a spot of <2.5 μm in diameter and a depth of field equal to 1.6 μm. The complete interface area of 3.2 mm × 3.2 mm was scanned with a lateral resolution of Δx = Δy = 10 μm, yielding a total measurement duration of approximately 130 hours. A constant flow of particle-free fluid was maintained during LDV measurement, to ensure conditions comparable to APTV measurements as well as to avoid the accumulation of gas bubbles inside the chamber.

2.3 Numerical simulation of the sound pressure and the acoustic radiation force

The high-frequency acoustic pressure p_f(x, y, z) in the fluid was computed with the help of the finite element method (FEM) in the frequency domain using a combination of Matlab and Comsol Multiphysics 3.5a. The computational domain included the fluid-filled chamber surrounded by PDMS from all sides but the bottom (z = 0). The latter is the substrate-fluid interface. The material constants of the fluid are given in Table S1.† The dimensions of the chamber correspond to those of the experimental setup (see subsection 3.1 “Acoustic fields and particle patterning”). The transverse BAW in the PDMS was neglected, since the corresponding transverse phase velocity is very small.^68–72 Thus, the PDMS was considered mechanically as a fluid with a sound velocity of 1076 m s⁻¹ and a density of 970 kg m⁻³. In order to reduce the computational effort, waves transmitted from the fluid to the PDMS were assumed not to return because of the strong attenuation in PDMS and sufficiently thick walls of the actual structure. Correspondingly, the effective wall thickness was set to 110 μm (approximately twice the sound wavelength in the fluid at 32.4 MHz) and an additional attenuation was introduced, in order to have the walls acting as perfectly matched layers (PML).^73,74 In other words, on the one hand, the boundary conditions requiring the continuity of the pressure and velocity at the fluid-PDMS interfaces were ensured (, where p_c is the pressure in the PDMS, ρ_f is the fluid density, ρ_c is the PDMS density, is the derivative along the normal to an interface) and hence, the waves reflected from the fluid-PDMS interfaces were present in the fluid. On the other hand, there were no waves reflected from the external interfaces of the PDMS structure. In order to check the absence of such waves, we performed a series of test computations in which we increased the wall thickness. No marked changes of the pressure in the fluid were observed in the case of thicker walls. Note that the “operational principle” of PML and some subtleties of its implementation in FEM are comprehensively discussed by Jin⁷⁵ as applied to electromagnetic waves but all aspects touched in this book are straightforwardly applicable to acoustic waves as well.

In our model the waves in the fluid are generated by the surface normal displacements at the substrate-fluid interface u(x, y), which are considered to be known in the course of computations. Namely, the displacements u(x, y) were obtained by LDV measurements. In turn, displacements at the vertexes of the FEM mesh at the corresponding face of the computation domain were determined by interpolating the experimental values u(x, y) measured at a set of points at the fluid-substrate contact (see subsection 2.2). As a result, the boundary condition at the substrate-fluid interface z = 0 was set , where ω is the frequency. This condition guarantees the equality of the normal velocity in the fluid at the surface z = 0 to the normal velocity of the substrate surface v_sz = iωu(x, y). Finally, the acoustic radiation force (ARF) acting on particles was calculated by an analytic expression derived in Settnes and Bruus,⁷⁶ see also Nama et al.⁷⁷

The influence of temperature on the BAW field in the fluid was considered by using effective material parameters for the fluid for different temperatures (Table S1†). Hence, a constant temperature was assumed for the whole fluid volume, i.e. local variations were not considered. The ARF was calculated for temperatures of 40 °C, 50 °C (mean temperature for steady-state experiments with acoustic power P_ac = 160 mW) and 60 °C in order to investigate the influence of temperature on the BAW field. The obtained results indicate a relevant variation in the magnitude of ARF, whereas the effect on the relative location of ARF minima (nodal positions) is minor and thus, almost negligible with regard to particle patterning.

2.4 Particle position and temperature measurement

2.4.1 Measurement setup. For the measurement of the particle position and temperature, the complete acoustofluidic setup was placed on top of an inverse microscope (Axio Observer 7, Zeiss GmbH) equipped with a long working distance Plan-Neofluar objective (M20×, NA = 0.4, Zeiss GmbH). A high-power LED with a central wavelength of 365 nm (Solis365C, Thorlabs Inc.) was used to illuminate the PMMA particles containing the temperature sensitive phosphorescent dye. To discriminate between illumination and phosphorescence of the particles' dye, the microscope was equipped with a long-pass dichroic mirror (86-330, Edmund Optics) and a long-pass filter (FELH0550, Thorlabs Inc.) with a cut-on wavelength of 409 nm and 550 nm, respectively. The microscope was further equipped with an adjustable linear polarization filter (Zeiss GmbH) to suppress the extraordinary ray caused by the birefringence of lithium niobate. To induce astigmatism in the detection path, a cylindrical lens with a focal length of f_cy = 250 mm was placed approximately 40 mm in front of the sensor of the camera (Imager sCMOS, LaVision GmbH), causing different magnifications in the x and y direction and, therefore, elliptically shaped particle images depending on their z position within the measurement volume. In order to relate the elliptical shape of the particle images to the z position of the corresponding particles, in situ calibration measurements were done with the same particles sedimented on the substrate (LiNbO₃) surface. To pretend different depth positions, the microscope objective was precisely moved in the z direction, yielding particle images at well-known depth-positions taking into account the changed height scale resulting from a different index of refraction of the fluid. In this way, the three-dimensional particle position within the measurement volume can be measured with very high precision, yielding standard deviations of about σ_x,y ≈ 0.1 μm and σ_z < 1 μm over the entire field of view, employing the Euclidean distance approach.^78,79 The depth of the measurement volume was larger than the height of the microfluidic chamber, while the field of view amounted to approximately 830 μm × 835 μm, which was smaller than the width of the microfluidic chamber.

In the present study, the combination of astigmatism particle tracking velocimetry (APTV) and luminescence lifetime imaging (LLI) was utilized, i.e. not only the shape but also the decay time of luminescent light emission needs to be determined from the elliptical particle images.⁶⁵ Thus, simultaneous measurements of the acoustically induced particle patterning and temperature within the microfluidic chamber can be realized. For the precise measurement of the decay time, a laser with a very short pulse duration and a high-speed camera are usually applied.⁶⁵ However, the high energetic laser light heats the small amount of fluid within the microfluidic chamber additionally, causing a systematic uncertainty of the temperature measurement. To enable reliable temperature measurements with the low power LED and the sCMOS-camera of the APTV setup, the timing sequence for the temperature determination has been adapted from short to long time LED pulse excitation. Details can be found in the ESI.† A careful temperature calibration was performed with the elaborated timing sequence. For this purpose, a temperature calibration chamber was used, which consisted of a thin PDMS gasket in between the LiNbO₃ chip at the bottom side and a Peltier element at the top side. Almost identical optical conditions have been used with this calibration setup as compared to the actual experiments, while the temperature of the fluid with suspended particles inside the gasket could precisely be controlled and monitored. To determine the calibration curve, calibration measurements were performed by gradually increasing the temperature from 12.5 °C to 50 °C with equidistant temperature steps of 2.5 K.

2.4.2 Measurement procedure. For the SAW device presented herein, the SAW wavelength is much larger than the diameter of the particles, causing particle agglomerates at nodal positions when a high particle concentration is applied. However, APTV relies on the tracking of individual particles. Therefore, the particle concentration applied during the experiments was chosen to be relatively low, yielding only a few nodal positions being occupied by single particles within the microfluidic chamber. In order to realize measurements of particle position and temperature distribution over the entire fluid volume, measurements were done in a repeated manner with several experimental runs. Experiments were conducted carefully by following a consistent protocol to ensure constant experimental conditions. Regardless of the actual measurement done, each experimental run started with (re-)filling the microfluidic chamber with particle suspension through three inlets, in order to obtain randomly distributed particles over almost the entire microfluidic chamber. Fluid inlets/outlets were closed and a time of 15 minutes was waited, to ensure the sedimentation of all particles to the substrate surface due to the higher density of the particles in comparison to the surrounding fluid. In order to synchronize the APTV system and the PowerSAW-Generator, the trigger output signal of the PowerSAW-Generator was used to start the optical measurements.

The experiments can be subdivided into two categories: measurements at (i) steady-state and (ii) transient state. The frequency of the PowerSAW-Generator was set to 32.4 MHz for all experiments whereas differences in the timing scheme and measurement duration existed. For (i) an electric power P_el = 650 mW was set to both coupled channels of the PowerSAW-Generator. The power was kept constant for the entire duration of each experimental run of about 350 s. The position and temperature measurements started 300 s after the beginning of the SAW excitation, hence, at the very end of the experimental run. After this time, steady-state conditions exist, meaning that all particles are trapped in their final positions and no significant change of temperature is expected anymore. Within the remaining time (50 s), double-frame images were taken with a frame rate of 10 Hz, starting at the center of the microfluidic chamber and subsequently at four measurement positions slightly decentered by 360 μm in the x direction and 390 μm in the y direction, in order to cover the entire microfluidic chamber. Therefore, for each experimental run 500 double-frame images were obtained for position and temperature measurements of the trapped particles. In total, 40 experimental runs were done for a total electric input power of P_el = 2 × 650 mW. In order to study also the influence of power on the temperature increase, measurements have been repeated at nine different power levels. For each power level, four experimental runs were conducted as mentioned above, with the measurement volume located at the center position of the microfluidic chamber. To investigate acoustophoresis and temperature rising during transient state (ii), the measurement procedure was slightly adapted, meaning that the duration of SAW excitation was limited to 60 s only, and the measurement of the particle position and temperature was started two seconds before the power was applied. Within the total measurement duration of 62 s, double-frame images were captured with, again, a frame rate of 10 Hz. While the first 20 double-frame images contain particle images from particles in quiescent fluid without the influence of the acoustic field, the subsequent 600 images taken allow for a detailed study of the acoustophoretic motion of the particles and the temperature evolution during the transient state applying APTV and LLI analysis.

The double-frame images were pre-processed with an in-house Matlab script to detect and validate individual particle images. For each particle image detected, the corresponding three-dimensional particle position and temperature have been determined as described in the ESI.† In the case of steady-state, most of the particles were trapped in pressure minima during the entire measurement time, i.e. particles have been detected for at least 100 times within one experimental run depending on their position relative to the field of view. All estimated positions and temperature values have been time-averaged, yielding a mean three-dimensional position and temperature of each individual particle. Besides this temporal averaging, ensemble averaging was applied for all experimental runs using the same conditions. In the case of nodal positions being occupied by particles within several experimental runs, these data were eventually grouped together to obtain one position and temperature value of all particles at one nodal position.

3 Results and discussion

3.1 Acoustic fields and particle patterning

Acoustic fields inside the microfluidic chamber comprise the SAW field at the substrate-fluid interface and the BAW field in the fluid originating from the radiation of acoustic energy from the substrate surface. Fig. 2 shows the lateral distribution of the surface-normal SAW amplitude u(x, y) at the substrate-fluid interface determined in presence of the fluid-filled microfluidic chamber using the in situ LDV measurement method.⁶³ The SAW field shows a complex two-dimensional standing-wave pattern of amplitude minima and maxima (2DsSAW) arising from the superposition of four SAWs. In other words, both one-directional standing SAWs (1DsSAW in x and y direction) interfere with each other. The measured periodicity of surface corrugation in both directions is 56 μm (in x direction) and 61 μm (in y direction), respectively. This corresponds to half of the particular SAW wavelengths at a frequency of 32.4 MHz. Moreover, the SAW field shows a regular pattern, namely, the amplitude maxima are well-defined and almost uniformly distributed over the entire surface area. However, there are slight deviations at the edges due to the limited aperture of the interdigital transducers (IDTs) that equals the lateral dimensions of the chamber. The maximum amplitude is observed at 0.2 mm < |x| ≤ 0.4 mm and |y| < 0.4 mm originating from SAW diffraction, which is clearly distinct along the y direction, whereas it does not occur to the same degree for propagation along the x direction at 32.4 MHz. The resultant nonuniform SAW diffraction for both directions is caused by the anisotropic acoustic behavior of LiNbO₃ as well as by the different number of electrode pairs (at constant aperture) of the IDTs that are required in order to match frequencies and electric impedances for both directions.

Fig. 2 Surface normal displacement amplitude u(x, y) (magnitude in pm) at the substrate-fluid interface (z = 0) measured with a laser Doppler vibrometer (LDV) at 32.4 MHz. The y coordinate is parallel to the X direction of the 128° rotated Y-cut LiNbO₃ crystal while the x coordinate corresponds to X + 90° direction.

The BAW field is given by the volumetric distribution of sound pressure inside the fluid. The sound pressure (time-averaged value) was calculated based on the measurement data of the complex SAW displacement amplitude, i.e. magnitude and phase, followed by a calculation of the ARF acting on 10 μm particles (see subsection 2.3). The particle size-to-wavelength ratio indicates that acoustophoresis is mainly provoked by ARF rather than by acoustic streaming.^76,77 Besides, optical observation of particles inside the chamber and subsequent APTV analysis yields the three-dimensional position of particles. Once power is applied to the IDTs and acoustic fields are consequentially formed, particles are eventually arranged at distinct constant (steady-state) three-dimensional positions in the chamber. According to the result of the measurement with APTV depicted in Fig. 3a, these positions occur across the entire width of the chamber. However, only two particle position levels can be determined in vertical direction under the experimental conditions described in subsection 2.4.2, see Fig. 3b. In order to compare the three-dimensional locations of the particles with the experimentally assisted numerical result of the ARF in detail, the following discussion is subdivided into vertical and lateral direction.

Fig. 3 a) Three-dimensional particle distribution determined by the astigmatism particle tracking velocimetry (APTV) measurement. b) The histogram of the z_p positions of all particles indicates two levels of height at mean values of z̄_p = 5.2 μm and z̄_p = 26.3 μm and according standard deviations of σ_z̄p = 0.46 μm and σ_z̄p = 2.63 μm, respectively. c) Cross-sectional view of the vertical component F_z of the acoustic radiation force (calculated with material properties for 50 °C, Table S1†) at y = 70 μm. The dashed lines indicate the two nodal levels at z = 26 μm and z = 58 μm. Positions of particles located at the first and second particle levels are represented by circular markers for direct comparison purposes. Note that the (x̄_p, z̄_p) positions of all particles are shown independently from their ȳ_p positions, and the marker size does not correspond to the actual particle size (10 μm). The diamond-shaped markers correspond to particle positions found in an additional experiment conducted under different initial conditions, to prove the existence of the third particle level located at the second nodal level (for details see ESI†).

Fig. 3c shows an exemplary cross-sectional view of the vertical component of the radiation force F_z, which is aligned in parallel to the z coordinate of the setup. This cross-sectional view is representative for the whole area of the chamber with regard to the presence of two nodal levels at z = 26 μm and z = 58 μm that are characterized by converging F_z yielding local minima of ARF. Hence, particles were expected to be found at both nodal levels, which was confirmed for the lower nodal level by a mean particle level of z̄_p = 26.3 μm measured with APTV. However, no particles were found at the higher nodal level (z = 58 μm) with the measurement procedure described above. In order to prove the existence of the second nodal level and to validate the numerical result, an additional experiment was conducted without a 15 minutes waiting time after (re-)filling the chamber with particle solution. As not all particles were sedimented, another mean particle position level of z̄_p = 58.6 μm was found, which agrees well to the the second nodal level. Details about the additional experiment can be found in ESI.† Besides particle positions at the two nodal levels, an initially unexpected mean particle level was observed at z̄_p = 5.2 μm (Fig. 3a and b), where the ARF is directed toward the substrate surface (F_z < 0, cp. Fig. 3c).

In between the areas of local maxima of ARF (z < 10 μm, F_z < 0), there also exist relevant lifting forces with F_z > 0 that move particles to higher positions where they are subsequently trapped at the first nodal level at z = 26 μm. Note also that the distribution width of particles' z position at z̄_p = 26.3 μm is larger as compared to z̄_p = 5.2 μm (Fig. 3b) due to the balance of opposing vertical forces that slightly varies with the lateral position. However, this is not relevant if particles are present in close vicinity to the substrate surface. The particles are arranged only in the lower half of the chamber volume owing to the experimental starting condition. Particles were sedimented at the substrate surface after refilling of the chamber in order to ensure reproducible conditions for every experimental run of the particle position measurement. However, two distinct particle levels exist, in which the second particle level coincides with the first nodal level of the acoustic field. The mean particle positions z̄_p and their standard deviations σ_z̄p are also affected by the measurement procedure, consisting of several experimental runs, traversing of the measurement volume, and subsequent stitching to enable particle position measurements over the entire microfluidic chamber with 1.2 mm in width. Due to this large region of interest and traversing of the measurement volume, the error of the mean particle position and standard deviation increase during steady state measurements. Therefore, a mean particle position of slightly smaller than 5 μm has been estimated for a part of the particles within the first particle level close to the substrate even though the particle diameter is about 10 μm in size. In addition, a very slight difference of the mean particle position occurs between the results obtained during steady state and transient state, as the latter was conducted without traversing the measurement volume along the entire chamber width.

Besides the particle arrangement at distinct levels, a characteristic lateral particle patterning is observed, which is induced by the lateral distribution of the ARF, often expressed as acoustic force potential (so-called Gor'kov potential) (Fig. 4). Particles are generally expected to be located at positions of acoustic force potential wells of oval shape situated in between neighboring maxima.⁸⁰ In fact, the particle positions obtained from APTV measurement confirm that all single particles are arranged at distinct areas. The result depicted in Fig. 4b agrees with the smeared potential wells that can be expected from previous investigations,⁸⁰ for the case of the superposition of two orthogonal waves of same frequency but different amplitude like in the case given here.

Fig. 4 a) Particle positions (x_p, y_p) at the second particle level with z̄_p = 26.3 μm plotted versus the lateral distribution of the normalized acoustic force potential, calculated with material properties for 50 °C. b) Detail view of Fig. 4a. Arrows indicate the acoustic radiation force direction within the corresponding lateral plane.

Explanations for the lateral particle arrangement induced by the acoustic field exemplarily given for the second particle level z̄_p = 26.3 μm, basically also hold true for the first level z̄_p = 5.2 μm (Fig. S3, ESI†). However, there is one major difference. Particles arranged close to the substrate were not trapped at a real nodal level of the acoustic field, even though they are laterally patterned by the ARF. In contrast, particles arranged at the first nodal level (i.e. the second particle level at z = 26 μm) as well as at the second nodal level (i.e. third particle level at z = 58 μm) were vertically trapped by converging F_z (cf.Fig. 3c) well above the substrate surface. In the latter cases, there exists a balance between ARF and gravitational force trapping particles at stable z̄_p positions even though they slightly vary within the lateral plane, which can also be seen from the standard deviation σ_z̄p ≈ 2.63 μm for z̄_p = 26.3 μm that is almost six times larger as compared to the first particle level (cf.Fig. 3b).

Finally, the periodicity of the particle patterns given by Δx̄_p = 57.3 μm and Δȳ_p = 61.5 μm is in reasonable agreement with the periodicity of the lateral distribution of the SAW displacement amplitude (56 μm in x direction and 61 μm in y direction), and of the resultant ARF in both directions.

3.2 Energy transfer and heating effects

The radiation of a bulk wave into the microfluidic structure, i.e. PDMS chamber and fluid, accompanies a transfer of acoustic energy from the surface wave to the microfluidic structure. The overall transfer of energy, starting from the electric input energy applied to the IDTs, followed by dissipation and parasitic effects, finally yielding the acoustic energy transmitted to the microfluidic structure has to be carefully evaluated.⁸¹ For the particular setup used for experimental investigations, losses due to electrical dissipation are minor. However, a relevant part of the electric input energy is reflected due to the high reflection coefficient of IDTs (|S₁₁| = 0.77, which corresponds to −2.2 dB for both directions at 32.4 MHz, see frequency dependent reflection and transmission coefficients in Fig. S2, ESI†). The mechanical energy transmitted by each IDT is converted to periodic vibrations of the surface that finally superimpose to an acoustic wave propagating along the surface. However, due to the utilization of uniform, solid-electrode IDTs, only half of the total acoustic energy is directed toward the center of the SAW device and subsequently applied to the microfluidic structure. The other half is directed away from the chamber, i.e. is no more available for fluidic actuation.

Furthermore, the SAW attenuates while propagating along the interface between substrate and microfluidic structure due to the radiation of acoustic energy. The resultant SAW attenuation was determined at 32.4 MHz based on two different methods: i) the evaluation of the decay of the surface normal displacement amplitude of the SAW, and ii) the evaluation of the difference of electrical transmission.⁶³ The decay of the displacement amplitude was obtained from LDV measurement data for every single SAW propagating towards the center of the device (exemplarily shown in Fig. 5a). As a result, the SAW amplitude is decreased by 16 dB (x direction) and 17 dB (y direction) during transmission of the fluid and the chamber (both PDMS walls). The frequency dependent electrical transmission coefficient |S₂₁|(f) of both pairs of opposing IDTs was measured in presence of the microfluidic structure, both for the empty and the fluid-filled chamber, as well as for the bare surface, i.e. in absence of the microfluidic structure (Fig. S2, ESI†). The resulting differences Δ|S₂₁| at 32.4 MHz in relation to the bare surface are shown for y direction in Fig. 5b. The corresponding values for fluid-filled chamber are 15 dB (x direction) and 16.9 dB (y direction), respectively. The SAW attenuation obtained by means of both methods reasonably agrees for y direction, whereas a slight deviation is observed for x direction. Nevertheless, the variance for both propagation directions is minor and can be attributed to slightly different SAW polarizations.

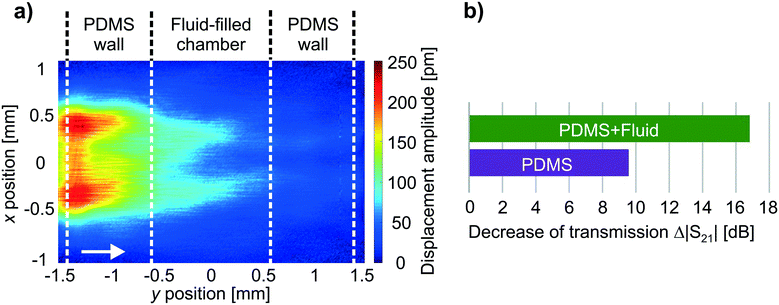Fig. 5 a) SAW displacement amplitude of a traveling SAW in presence of the microfluidic structure on the substrate surface. Note that the SAW field of the traveling SAW (excited by one IDT, arrow indicates propagation direction) is extracted from 2DsSAW at 32.4 MHz (cf.Fig. 2). b) The decrease of the electrical transmission Δ|S₂₁| is exemplarily shown for y direction at a frequency of 32.4 MHz. The difference Δ|S₂₁| is evaluated in relation to the bare substrate surface (no microfluidic structure present, i.e. Δ|S₂₁| = 0 dB) for both, the empty (PDMS) and the fluid-filled (PDMS + fluid) chamber.

The energy transferred to the microfluidic structure can be estimated based on above considerations and the experimentally determined SAW attenuation. According to this, 12.5% of the electric input power P_el was subsequently transferred as acoustic power P_ac to the microfluidic structure, more precisely, to the fluid-filled chamber that is attached to the substrate in the area given by |x| ≤ 1.4 mm and |y| ≤ 1.4 mm, respectively. This energy transfer gives rise to a temperature increase of the fluid due to viscous attenuation of the BAW in the fluid as well as diffusive and hydrodynamic heat transfer, e.g. from the PDMS structure that is heated up as well.^47,49 Under steady-state conditions and by applying an overall electric power of P_el = 1.3 W (P_ac = 160 mW), a significant increase of particle temperature was observed yielding temperatures of the particles ranging from 43 °C to 55 °C, see Fig. 6.

Fig. 6 Three-dimensional particle distribution determined by astigmatism particle tracking velocimetry (APTV). The color of the circular markers represents the temperature of the trapped particles obtained from the combination of APTV with luminescence lifetime imaging (LLI).

Apart from the power applied, the temperature also depends on the position of the particles. In general, particles at the center of the chamber show higher temperature as compared to those located at the edges of the chamber and thus are closer to the PDMS walls. However, maxima of the measured temperature do not directly coincide with those of the amplitude of the SAW at 0.2 mm < |x| ≤ 0.4 mm and |y| ≤ 0.4 mm (cf.Fig. 2). The mean temperature determined by averaging over all particles is about 50 °C. This temperature information was already employed by means of the temperature-dependent material parameters used for the calculation of sound pressure and ARF. Besides an increasing temperature towards the lateral center of the microfluidic chamber, a temperature difference between both particle position levels can be determined, as shown by the histograms of the temperatures measured at both particle position levels (Fig. 7a). While the mean temperature close to the substrate was determined to be 49.8 °C, the mean particle temperature at the second particle position level was about 50.8 °C. Thus, the temperature of the fluid increases from the substrate surface to the top of the microfluidic chamber.

Fig. 7 a) Temperature distribution at the first and second particle position level evaluated for all lateral particle positions. b) Increase of temperature (mean value and standard deviation averaged over all particles) as a function of the acoustic power P_ac applied to the microfluidic structure.

In situ measurements of the SAW field and the subsequent estimation of the acoustic power transferred to the fluid-filled microfluidic chamber, as well as in situ measurements of the temperature of the particles for different power levels, demonstrate the direct correlation between temperature of acoustically trapped particles and acoustic power for the first time. The mean temperature increase ΔT_s at steady-state increases with power as depicted in Fig. 7b. An almost linear increase of the temperature as a function of the acoustic power P_ac transferred to the microfluidic structure was observed. The corresponding proportionality factor determined by linear regression is 0.153 K mW⁻¹. Note that this value is valid only for the current setup due to specific energy transfer characteristics, such as the IDT-substrate combination, the geometrical dimensions of the microfluidic structure and material properties. However, a tremendous increase of the temperature ΔT_s of the trapped particles was obtained even for a comparably low acoustic power P_ac. Moreover, the temperature measurements indicate a nonuniform temperature distribution in the chamber providing even more detailed information about the thermal impact during acoustophoretic manipulation.

3.3 Transient processes

In addition to the investigations performed under steady-state conditions, the acoustophoretic particle motion and the evolution of the temperature of the particles were studied during the start-up phase of particle trapping, i.e. starting with the formation of acoustic fields. Particles initially were sedimented on the substrate surface before switching on the SAW and trapping the particles at two distinct particle position levels of height. The z positions of two particles captured during a period of 60 seconds after starting SAW excitation are depicted in Fig. 8a. One particle is lifted to the particle position level very close to the substrate surface (blue curve), whereas the second particle is lifted to the first nodal level (red curve). The latter corresponds to the particle trajectory shown in Fig. 1d. The change of particle positions immediately takes place after starting excitation of the SAW and is completed after approximately one second, whereas the maximum acceleration was 0.4 mm s⁻². Afterward, the particles' z positions remain almost constant, i.e. the particles do not move in height. According to the inset of Fig. 8a, the elevation of the particle trapped close to the substrate surface is about 0.6 μm, which was found to be representative for all sedimented particles trapped in the first particle position level (Fig. S4, ESI†). Hence, particles within the first particle position level were not trapped directly on the substrate surface where a local pressure minimum exists, but slightly above. The reason for the slight levitation of particles is a complex interaction of forces acting on the particles. Besides ARF and gravitational force, there also exists fluid streaming caused by the electroacoustic field above the substrate material.^41,77,82Fig. 8a further reveals that the particles were locally trapped by the acoustic field once they reached at a certain height. However, a larger variation of the z position of the particle at the second particle position level can be determined, indicating a remaining particle motion of the particle. This might be attributed to a decrease of the local ARF with increasing distance from the substrate surface as well as to the influence of acoustic streaming even though ARF is dominant. Moreover, spatial and temporal changes of temperature also affect the acoustic field resulting in a slight deviation of nodal positions of acoustic force magnitude. While the acoustic radiation force decreases with increasing distance to the substrate surface, the acoustically induced fluid flow increases in terms of convection rolls caused by Eckart streaming, depending on the actual position of the particle within the microfluidic chamber.^41,77,83 In general, the acoustically induced patterning of particles occurs quite fast. For all acoustic power levels applied, a mean transition time for the particles inside the microfluidic chamber of about 1.2 s was estimated, which subtly decreased with increasing power levels (Fig. S5, ESI†).

Fig. 8 a) Time-resolved measurement of the position of two different particles, determined during the start-up phase of particle trapping. One particle is trapped at the first particle level, i.e. in close vicinity to the substrate surface (blue curve), and the other one at the first nodal level (cf.Fig. 3). SAW excitation started at t = 2 s. b) Increase of temperature ΔT over time for different acoustic power P_ac. c) Temperature increase ΔT is normalized to the temperature increase at the end of transient process ΔT_e. d) Characteristic rise times of temperature increase during transition-state for different acoustic power levels. The times τ_0.63 and τ_0.95 correspond to a temperature increase of 63% and 95% of steady-state temperature increase ΔT_s, respectively.

Besides the particle motion, the temperature of the particles was also measured for the transient-state. The evolution of the temperature increase ΔT measured for different power levels is depicted in Fig. 8b. As soon as the SAW excitation starts, the temperature increases rapidly and approaches almost steady-state conditions within the duration of measurement (60 s) as depicted in Fig. 8b. The transient process is characterized by an exponential increase within the very first seconds, followed by a linear increase. However, small differences occur in the temporal behavior when normalizing the temperature increase ΔT by the temperature increase ΔT_e measured at the end of the transient process (Fig. 8c). In order to estimate the time scale of the heating process, the measured temperature increase was fitted by a model function. This model function consists of an exponential and a linear term to consider the different temporal behavior of the temperature increase. Two characteristic times were determined for all acoustic power levels applied: the first τ_0.63 at 63% and the second τ_0.95 at 95% of the steady-state temperature ΔT_s. According to the result depicted in Fig. 8d, the time needed to reach 63% of the steady-state temperature was about two seconds only, whereas the temperature reaches steady-state conditions (95%) after 20 seconds and even later. This large difference between both times confirms the different evolution of the temperature increase during the transient state, i.e. a very fast exponential increase immediately after starting SAW excitation, subsequently followed by a linear increase (see also ESI† Movie S1 for particle's trajectory and temperature evolution). In addition, the higher the acoustic power level applied, the faster the heating process. While steady-state conditions (95%) were established within 40 seconds at an acoustic power level of about P_ac = 60 mW, only 24 seconds were needed at an acoustic power level of about P_ac = 160 mW. Regardless of the time considered, the results demonstrate a very fast temperature response of the microfluidic setup.

4 Conclusions

In situ investigations of the acoustophoretic and acoustothermal effects have been performed for a 3D acoustic tweezer setup based on a 2D standing surface acoustic wave field. For this, laser Doppler vibrometry (LDV), astigmatism particle tracking velocimetry (APTV) and luminescence lifetime imaging (LLI) were combined and applied under comparable experimental conditions. In addition to experiments, the sound pressure in the fluid and the acoustic radiation force acting on suspended particles were determined numerically using the surface normal displacement amplitude measured at the fluid-substrate interface. This holistic approach reveals the complexity of acoustofluidic interaction in real devices and, for the first time, delivers a deep insight into acoustophoresis and issues of energy conversion, including dissipation that leads to significant heating. Moreover, the dynamics of transient processes, e.g. resultant particle trajectories and temperature rise starting with the formation of the acoustic fields, were observed with a high spatial and temporal resolution. In principle, the approach presented here can be adapted to every kind of acoustofluidic setup.

Acoustophoresis

The three-dimensional measurement of particle positions confirmed the trapping of particles due to acoustophoresis. The direct comparison of particle positions and the volumetric distribution of acoustic radiation force yields reasonable agreement revealing that particles were arranged at positions where the acoustic radiation force is at minimum. Particles were located at two distinct levels of height. The upper particle level coincides with a real nodal level of the acoustic field. In contrast, the lower particle level in close vicinity to the substrate is mainly provoked by the vertical component of radiation force directed toward the substrate. However, the particles were slightly lifted by approximately 0.6 μm away from the surface. The lateral particle patterning at both levels was shown to resemble the standing acoustic wave field pattern originally induced by the two-dimensional standing SAW field at the substrate-fluid interface. The actual lateral position of particles is governed by acoustic potential wells depending in shape and strength on the ratio of interfering SAW fields. Within this study, only the acoustic radiation force was considered, which is reasonable for the large wavelength and particle size used here. However, drag force exerts on the particles due to a fluid flow induced by the acoustic streaming effect, which may cause particles to be displaced from locations predicted solely by considering the acoustic radiation force. The smaller the acoustic wavelength and the particles, the larger the influence of the fluid flow. In this case, the impact of acoustic streaming on acoustophoresis has to be considered in greater detail, including measurements of the streaming velocity of the fluid.

Thermoacoustics

In addition to the spatial position, the temperature of the acoustically trapped particles was directly measured for the very first time. Moreover, the acoustic power actually applied to the microfluidic structure (PDMS and fluid) was estimated from the electrical input power based on considerations of transfer, reflection and parasitic radiation of energy. As a result, a maximum particle temperature of 55 °C was observed under steady-state conditions, even though a comparably low acoustic power of 160 mW was applied. The temperature increase linearly scales with the acoustic input power. This fundamental relationship has already been reported in different studies based on theoretical and experimental investigations, even though the relationship was given by the electric power applied or from other considerations.^49,52,53,55 In contrast, in situ experimental investigations performed in the present study allow a precise determination of the acoustic power applied to the microfluidic structure, which is effectively relevant for heating. A specific rise of 0.153 K mW⁻¹ was obtained, which is valid only for the setup presented herein. For instance, using water only as fluid, which has a lower viscosity compared to the mixture of water and glycerol used herein, a lower temperature rise has to be expected. Besides the overall temperature increase, temperature gradients were measured not only in lateral,⁵¹ but also in vertical direction, as merely predicted by simulations in a microchannel so far.⁴⁹ However, a significant temperature increase was observed even in close vicinity to the substrate surface that was not reported so far. A characteristic lateral temperature distribution was found with a pronounced maximum at the center of the chamber due to a maximum of the acoustic energy density.⁴⁹ However, the measured slight local variations of the SAW amplitude due to acoustic diffraction have not been reproduced in the temperature of the particles. This is not surprising, as the local temperature rise is not only affected by the attenuation of the acoustic wave in the fluid but also by heat conduction and convection. The latter originates from a fluid motion characterized by streaming rolls in between pressure minima and close to the side walls (also known as Eckart streaming) induced by standing wave and traveling wave components of the 2DsSAW field.^41,49,83,84

Dynamics of acoustophoresis and thermoacoustics

In addition to investigations under steady-state conditions, i.e. a constant power input over time, the transient behavior was investigated. For this purpose, the trajectory and the temperature evolution of particles were simultaneously tracked starting with the formation of the acoustic field inside the microfluidic chamber. Besides very fast trapping of particles within approximately one second, characterized by a three-dimensional particle trajectory toward a certain nodal position, a rapid temperature rise occurred during the initial phase. The temporal increase of temperature is characterized by an exponential phase at the very beginning followed by an almost linear phase. Particle patterning takes place within the order of 1 s, whereas the final (steady-state) temperature is reached within the order of 10 s. Hence, acoustophoretic and acoustothermal effects are characterized by different time scales. These different time scales can be exploited to elaborate strategies allowing the patterning of cells with a reduced thermal load, e.g. by applying a pulsed SAW excitation to limit the temperature increase.^53,55

Besides those strategies, further experimental investigations are required, particularly including the measurement of the fluid flow induced by the acoustic streaming effect, which affects the actual particle position and causes mechanical stress on cells. For this purpose, the astigmatism particle tracking velocimetry setup needs to be extended to allow the measurement of both, the position of the acoustically trapped particles as well as the velocity of the fluid flow. In principle, the measurement of the velocity and temperature distributions of the fluid enables the experimental investigation of cell acoustophoresis and heating, i.e. particles are no more mandatory then for experimental investigations. Following this route, detailed knowledge can be gained to answer still open fundamental questions of microscale acoustofluidics, in particular, the controversial issue of non-invasive treatment and biocompatibility.

Author contributions

J. K., R. W., H. S., C. C. contributed to the conceptualization of the research project. J. K., R. W., Z. D., V. V. K. developed the methodology. Z. D., J. K. implemented the measurement on particle location and temperature. V. V. K., R. W. implemented the characterization of acoustic field. A. N. D. worked on the FEM Computations. Z. D., V. V. K., J. K., R. W. realized the visualization of the results. C. C., H. S. supervised the research project. Z. D., V. V. K., R. W., J. K. wrote the original draft of the manuscript. And all authors were involved in the reviewing and editing of the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors are grateful to Christian Koppka, Manuela Breiter, Joachim Döll, David Schreier and Arne Albrecht from the Center of Micro- and Nanotechnology (ZMN) at Technische Universität Ilmenau as well as to Dina Bieberstein and Andreas Büst from Leibniz Institute for Solid State and Materials Research Dresden for their support during fabrication of the acoustic tweezer setup. Funding: Z. D., J. K. and C. C. received funding from German Research Foundation under grant CI 185/6-1. V. V. K., R. W., A. N. D. and H. S. received funding from German Research Foundation under grant SCHM 2365/17-1. The work of A. N. D. was also supported by the Ministry of Science and Higher Education of the Russian Federation within the State assignment FSRC “Crystallography and Photonics”, RAS in part of preparing publication.

References

1. J. Hultström, O. Manneberg, K. Dopf, H. M. Hertz, H. Brismar and M. Wiklund, Ultrasound Med. Biol., 2007, 33, 145–151.
2. D. Baresch, J.-L. Thomas and R. Marchiano, Phys. Rev. Lett., 2016, 116, 024301.
3. A. Ozcelik, J. Rufo, F. Guo, Y. Gu, P. Li, J. Lata and T. J. Huang, Nat. Methods, 2018, 15, 1021–1028.
4. S.-H. Hong, J.-B. Gorce, H. Punzmann, N. Francois, M. Shats and H. Xia, Sci. Adv., 2020, 6, eaaz9386.
5. Z. Ao, H. Cai, Z. Wu, J. Ott, H. Wang, K. Mackie and F. Guo, Lab Chip, 2021, 21, 688–699.
6. G. Simon, C. Busch, M. A. B. Andrade, J. Reboud, J. M. Cooper, M. P. Y. Desmulliez, M. O. Riehle and A. L. Bernassau, Biomicrofluidics, 2021, 15, 014105.
7. M. E. Piyasena, P. P. Austin Suthanthiraraj, R. W. J. Applegate, A. M. Goumas, T. A. Woods, G. P. López and S. W. Graves, Anal. Chem., 2012, 84, 1831–1839.
8. V. Romanov, G. Silvani, H. Zhu, C. D. Cox and B. Martinac, Small, 2021, 17, 2005759.
9. P. Augustsson, C. Magnusson, M. Nordin, H. Lilja and T. Laurell, Anal. Chem., 2012, 84, 7954–7962.
10. P. Li, Z. Mao, Z. Peng, L. Zhou, Y. Chen, P.-H. Huang, C. I. Truica, J. J. Drabick, W. S. El-Deiry, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4970–4975.
11. C. Richard, A. Fakhfouri, M. Colditz, F. Striggow, R. Kronstein-Wiedemann, T. Tonn, M. Medina-Sánchez, O. G. Schmidt, T. Gemming and A. Winkler, Lab Chip, 2019, 19, 4043–4051.
12. M. Wu, Y. Ouyang, Z. Wang, R. Zhang, P.-H. Huang, C. Chen, H. Li, P. Li, D. Quinn, M. Dao, S. Suresh, Y. Sadovsky and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10584–10589.
13. D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686.
14. F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li, L. Ren, J. Liu, J. Yang, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1522–1527.
15. T. D. Nguyen, V.-T. Tran, S. Pudasaini, A. Gautam, J. M. Lee, Y. Q. Fu and H. Du, Adv. Eng. Mater., 2021, 23, 2001377.
16. C. Chen, Y. Gu, J. Philippe, P. Zhang, H. Bachman, J. Zhang, J. Mai, J. Rufo, J. F. Rawls, E. E. Davis, N. Katsanis and T. J. Huang, Nat. Commun., 2021, 12, 1118.
17. T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506.
18. H. Bruus, Lab Chip, 2012, 12, 1014–1021.
19. S. Liang and W. Chaohui, J. Appl. Phys., 2018, 123, 044504.
20. J. Guo, Y. Kang and Y. Ai, J. Colloid Interface Sci., 2015, 455, 203–211.
21. M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991.
22. A. Urbansky, P. Ohlsson, A. Lenshof, F. Garofalo, S. Scheding and T. Laurell, Sci. Rep., 2017, 7, 17161.
23. Z. Ma, Y. Zhou, F. Cai, L. Meng, H. Zheng and Y. Ai, Lab Chip, 2020, 20, 2947–2953.
24. K. Yiannacou and V. Sariola, Langmuir, 2021, 37, 4192–4199.
25. X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109.
26. L. Ren, S. Yang, P. Zhang, Z. Qu, Z. Mao, P.-H. Huang, Y. Chen, M. Wu, L. Wang, P. Li and T. J. Huang, Small, 2018, 14, e1801996.
27. M. Baudoin, J.-L. Thomas, R. A. Sahely, J.-C. Gerbedoen, Z. Gong, A. Sivery, O. B. Matar, N. Smagin, P. Favreau and A. Vlandas, Nat. Commun., 2020, 11, 4244.
28. J. Shi, D. Ahmed, X. Mao, S.-C. S. Lin, A. Lawit and T. J. Huang, Lab Chip, 2009, 9, 2890–2895.
29. F. Guo, P. Li, J. B. French, Z. Mao, H. Zhao, S. Li, N. Nama, J. R. Fick, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2014, 112, 43–48.
30. T. D. Nguyen, V. T. Tran, Y. Q. Fu and H. Du, Appl. Phys. Lett., 2018, 112, 213507.
31. Z. Tian, S. Yang, P.-H. Huang, Z. Wang, P. Zhang, Y. Gu, H. Bachman, C. Chen, M. Wu, Y. Xie and T. J. Huang, Sci. Adv., 2019, 5, eaau6062.
32. G. Greco, M. Agostini, I. Tonazzini, D. Sallemi, S. Barone and M. Cecchini, Anal. Chem., 2018, 90, 7450–7457.
33. C. Witte, J. Reboud, R. Wilson, J. M. Cooper and S. L. Neale, Lab Chip, 2014, 14, 4277–4283.
34. R. Weser, A. N. Darinskii, M. Weihnacht and H. Schmidt, Ultrasonics, 2020, 106, 106077.
35. R. W. Rambach, J. Taiber, C. M. L. Scheck, C. Meyer, J. Reboud, J. M. Cooper and T. Franke, Sci. Rep., 2016, 6, 21980.
36. R. Weser, A. Winkler, M. Weihnacht, S. Menzel and H. Schmidt, Ultrasonics, 2020, 106, 106160.
37. J. Lei, M. Hill and P. Glynne-Jones, Lab Chip, 2014, 14, 532–541.
38. P. Hahn, I. Leibacher, T. Baasch and J. Dual, Lab Chip, 2015, 15, 4302–4313.
39. N. R. Skov, P. Sehgal, B. J. Kirby and H. Bruus, Phys. Rev. Appl., 2019, 12, 044028.
40. J.-C. Hsu and C.-L. Chao, J. Appl. Phys., 2020, 128, 124502.
41. C. Devendran, T. Albrecht, J. Brenker, T. Alan and A. Neild, Lab Chip, 2016, 16, 3756–3766.
42. P. B. Muller, R. Barnkob, M. J. H. Jensen and H. Bruus, Lab Chip, 2012, 12, 4617–4627.
43. S. Karthick and A. K. Sen, Phys. Rev. Appl., 2018, 10, 034037.
44. Z. Ni, C. Yin, G. Xu, L. Xie, J. Huang, S. Liu, J. Tu, X. Guo and D. Zhang, Lab Chip, 2019, 19, 2728–2740.
45. A. N. Darinskii, M. Weihnacht and H. Schmidt, Lab Chip, 2016, 16, 2701–2709.
46. M. Wiklund, Lab Chip, 2012, 12, 2018–2028.
47. B. H. Ha, K. S. Lee, G. Destgeer, J. Park, J. S. Choung, J. H. Jung, J. H. Shin and H. J. Sung, Sci. Rep., 2015, 5, 11851.
48. Y. Ding, K. A. Ball, K. J. Webb, Y. Gao, A. DAlessandro, W. M. Old, M. H. B. Stowell and X. Ding, Small, 2020, 16, 2003506.
49. P. K. Das, A. D. Snider and V. R. Bhethanabotla, Phys. Fluids, 2019, 31, 106106.
50. V. Levario-Diaz, P. Bhaskar, M. Carmen Galan and A. C. Barnes, Sci. Rep., 2020, 10, 8493.
51. M. Cui, M. Kim, P. B. Weisensee and J. M. Meacham, Lab Chip, 2021, 21, 2534–2543.
52. S. Ito, M. Sugimoto, Y. Matsui and J. Kondoh, Jpn. J. Appl. Phys., 2007, 46, 4718–4722.
53. J. Kondoh, N. Shimizu, Y. Matsui, M. Sugimoto and S. Shiokawa, Sens. Actuators, A, 2009, 149, 292–297.
54. G. Werr, Z. Khaji, M. Ohlin, M. Andersson, L. Klintberg, S. Searle, K. Hjort and M. Tenje, J. Micromech. Microeng., 2019, 29, 095003.
55. R. J. Shilton, V. Mattoli, M. Travagliati, M. Agostini, A. Desii, F. Beltram and M. Cecchini, Adv. Funct. Mater., 2015, 25, 5895–5901.
56. T. Zheng, C. Wang, Q. Hu and S. Wei, Appl. Phys. Lett., 2018, 112, 233702.
57. Y. Wang, Q. Zhang, R. Tao, D. Chen, J. Xie, H. Torun, L. E. Dodd, J. Luo, C. Fu, J. Vernon, P. Canyelles-Pericas, R. Binns and Y. Fu, Sens. Actuators, A, 2021, 318, 112508.
58. L. Li, E. Wu, K. Jia and K. Yang, Lab Chip, 2021, 21, 3184–3194.
59. M. Mehmood, T. N. Chaudhary, S. Burnside, U. Khan, R. Y. Fu and B. Chen, Exp. Therm. Fluid Sci., 2022, 133, 110580.
60. V. K. Natrajan and K. T. Christensen, Meas. Sci. Technol., 2008, 20, 015401.
61. M. Kim and M. Yoda, Exp. Fluids, 2010, 49, 257–266.
62. J. Massing, D. Kaden, C. J. Kähler and C. Cierpka, Meas. Sci. Technol., 2016, 27, 115301.
63. R. Weser and H. Schmidt, J. Appl. Phys., 2021, 129, 244503.
64. C. Cierpka, R. Segura, R. Hain and C. J. Kähler, Meas. Sci. Technol., 2010, 21, 045401.
65. J. Massing, C. J. Kähler and C. Cierpka, Exp. Fluids, 2018, 59, 163.
66. L. Negadi, B. Feddal-Benabed, I. Bahadur, J. Saab, M. Zaoui-Djelloul-Daouadji, D. Ramjugernath and A. Negadi, J. Chem. Thermodyn., 2017, 109, 124–136.
67. F. Kiebert, S. Wege, J. Massing, J. König, C. Cierpka, R. Weser and H. Schmidt, Lab Chip, 2017, 17, 2104–2114.
68. Z. Liu, X. Zhang, Y. Mao, Y. Y. Zhu, Z. Yang, C. T. Chan and P. Sheng, Science, 2000, 289, 1734–1736.
69. T. Still, M. Oudich, G. K. Auerhammer, D. Vlassopoulos, B. Djafari-Rouhani, G. Fytas and P. Sheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094102.
70. I. D. Johnston, D. K. McCluskey, C. K. L. Tan and M. C. Tracey, J. Micromech. Microeng., 2014, 24, 035017.
71. J. K. Tsou, J. Liu, A. I. Barakat and M. F. Insana, Ultrasound Med. Biol., 2008, 34, 963–972.
72. R. H. Pritchard, P. Lava, D. Debruyne and E. M. Terentjev, Soft Matter, 2013, 9, 6037–6045.
73. J.-P. Berenger, J. Comput. Phys., 1994, 114, 185–200.
74. User's guide COMSOL Multiphysics®, Comsol AB, Stockholm, Sweden software.
75. J. Jin, The Finite Element Method in Electromagnetics, Wiley-IEEE Press, 2nd edn, 2002, p. 784.
76. M. Settnes and H. Bruus, Physical Review E, 2012, 85, 016327.
77. N. Nama, R. Barnkob, Z. Mao, C. J. Kähler, F. Costanzo and T. J. Huang, Lab Chip, 2015, 15, 2700–2709.
78. C. Cierpka, M. Rossi, R. Segura and C. J. Kähler, Meas. Sci. Technol., 2010, 22, 015401.
79. J. König, M. Chen, W. Rösing, D. Boho, P. Mäder and C. Cierpka, Meas. Sci. Technol., 2020, 31, 074015.
80. S. Oberti, A. Neild and J. Dual, J. Acoust. Soc. Am., 2007, 121, 778–785.
81. A. Winkler, R. Brünig, C. Faust, R. Weser and H. Schmidt, Sens. Actuators, A, 2016, 247, 259–268.
82. A. N. Darinskii, M. Weihnacht and H. Schmidt, J. Appl. Phys., 2018, 123, 014902.
83. R. Barnkob, N. Nama, L. Ren, T. J. Huang, F. Costanzo and C. J. Kähler, Phys. Rev. Appl., 2018, 9, 014027.
84. S. Sachs, M. Baloochi, C. Cierpka and J. König, Lab Chip, 2022, 22, 2011–2027.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00200k

---