Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterization of nanoparticle size distributions using a microfluidic device with integrated optical microcavities†
Kiana
Malmir
 a,
William
Okell
a,
Aurélien A. P.
Trichet
b and
Jason M.
Smith
a,
William
Okell
a,
Aurélien A. P.
Trichet
b and
Jason M.
Smith
 *ab
*ab
aOxford University, Department of Materials, University of Oxford, Parks Road, Oxford OX1 3PH, UK. E-mail: kianamalmir@gmail.com
bOxford HighQ Ltd, Centre for Innovation and Enterprise, Begbroke Science Park, Oxford OX5 1PF, UK
First published on 10th August 2022
Abstract
We introduce a method for analyzing the physical properties of nanoparticles in fluids via the competition between viscous drag and optical forces in a microfluidic device with integrated optical microcavities. The optical microcavity acts as a combined optical trap and sensor, such that the time duration of individual particle detection events can be used as a measure of particle size via a parameter which represents the dielectric polarizability per unit radius. Characterization of polymer particles with diameters as small as 140 nm is reported, below that used in previous optical sorting approaches and in the size range of interest for nanomedicine. This technique could be applied in combination with other analytic techniques to provide a detailed physical characterization of particles in solution.
1 Introduction
The characterization of nanoparticles in solution is of increasing importance for applications in biomedical, environmental, and materials sciences.1–5 In particular, the engineering of nanoparticles for use in medical applications such as drug delivery requires accurate characterization of the physical and chemical characteristics of particles within the fluid medium. The efficient clinical drug delivery systems need to accurately control drug release. The ability of nanomedicine to reach the target organ can be determined by its particle size, and concentration. Therefore, characterizations of nanocarriers such as nanoparticles are crucial to controlling their desired effects.6 For instance, investigation of the size and loading properties of lipid nanoparticle vehicles containing silencing RNA (siRNA), is of increasing importance for future studies of dynamics with single-particle resolution.7There are a number of methods to characterize nanoparticles at the single-particle level with high resolution. Electron microscopy or scanning probe microscopy can provide accurate information on the shape of the nanoparticles.8,9 For example, Atomic Force Microscopy (AFM) technique can characterize nanoparticles with the size range of 1–20 nm in dry and liquid states.10,11 Although AFM has high compatibility with different samples and measurement environments, it is limited due to the need for sample preparation. Namely, the samples need to be deposited on a hard substrate.11 Methods based on light-scattering and diffusion have been also developed to characterize the suspended nanoparticles in a fluid. These techniques are the common techniques for determining the size and the shape of nanoparticles.
Particle size and size distribution are readily measured using light scattering techniques. Dynamic Light Scattering (DLS)12 is fast and sensitive to particles as small as 5 nm, but provides limited resolution for polydisperse samples where larger particles dominate the scattered signal.13,14 Nanoparticle Tracking Analysis (NTA) and Tunable Resistive Pulse Sensing (TRPS) provide single particle measurements of particle size allowing for more reliable measurement of size distributions.11,15–21 Optical microscopy cannot measure the size of individual biological nanoparticles but combination of NTA with surface-sensitive optical imaging allows us to accurately quantify the size of biological nanoparticles attached to lipid bi-layers.22 Also, particle size, shape and orientation can be determined by measuring optical cross-sections of nanoparticles in wide field extinction microscopy for different light wavelengths and excitation polarization.8 Flow cytometry (FCM) is another well-established method to characterize individual cells and particles.23,24 FCM is a flow-based method to detect size of polydisperse, heterogeneous, or mixed samples and concentrations by measuring the properties of scattered light or fluorescence associated with the cells.25
Beyond particle size, centrifugation techniques allow direct measurement of the mass density of particle ensembles.26,27 New optical techniques have recently emerged which measure the composition of individual particles via the dielectric polarizability, a parameter which depends on both particle volume and dielectric constant and can in some cases provide a proxy for particle mass.28 Such measurements are made more challenging by the rapid Brownian motion of the particles in the bulk fluid. There exist several solutions to this problem such as using hydrodynamic forces on nanoparticles to induce their drift in the flow direction. While the movement perpendicular to the flow remains random, the size of the nanoparticles can be accurately measured by quantifying the deterministic and random components of the movement,22 as well as analyzing the thermal motion of nanoparticles in an array of electrostatics traps.29 Another approach is to trap the nanoparticle in an optical microcavity to allow prolonged measurement,30 a technique that can provide independent measurements of size and polarizability on a particle-by-particle basis.31 The use of optical gradient forces for the sorting and trapping micron-sized particles in a flowing fluid is also well-established.32–34 This work builds on30,35 by introducing a controlled fluid flow through the microcavity, such that the trap duration is determined by the competition between the optical forces and viscous drag. Since the optical force is proportional to the dielectric polarizability of the particle and the viscous drag force is proportional to its hydrodynamic radius, the balance between them is determined by the polarization per unit radius, a new parameter which can be combined with others to provide comprehensive characterization methodologies.
2 Method
The equation of motion for a spherical particle with polarizability α in a viscous fluid flowing at uniform velocity![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) 0 and illuminated with an optical field of intensity distribution I(
0 and illuminated with an optical field of intensity distribution I(![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) ) is
) is | (1) |
![[W with combining low line]](https://www.rsc.org/images/entities/i_char_0057_0332.gif) (t) is a time-varying normally distributed random vector36 where t is time. Within the dipole approximation the polarizability is
(t) is a time-varying normally distributed random vector36 where t is time. Within the dipole approximation the polarizability is | (2) |
It can be seen from eqn (1) and (2) that for a given optical intensity distribution I(![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) ) and flow velocity
) and flow velocity ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) 0, the balancing of the optical force with the drag force due to the flowing fluid is achieved for a threshold value, βT, of the parameter
0, the balancing of the optical force with the drag force due to the flowing fluid is achieved for a threshold value, βT, of the parameter
 | (3) |
Apparatus which allows the rate of trapping events (Γtrap) to be detected as a function of the flow speed or optical power can therefore be used to determine the distribution N(β) by differentiating the measured trapping rate with respect to βT,
 | (4) |
The thermal motion of the particle introduces a random element to the time a particle spends in the mode for values of β close to the threshold and is therefore a source of broadening of the distribution function.
The geometry of our measurement apparatus is depicted in Fig. 1(a). A plano-concave microcavity generally consist of two separate mirrors facing each other where one mirror can move independently.35,37–41 This type of microcavities supports a standing wave optical mode comprising five antinodes of light of wavelength λ = 640 nm with a mode width of less than 1 μm. The fluid flow direction is perpendicular to the optical axis. For this cavity mode, I(![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) ) can be expressed approximately as a standing wave of a Gaussian beam with cylindrical symmetry about the axis,
) can be expressed approximately as a standing wave of a Gaussian beam with cylindrical symmetry about the axis,
 | (5) |
As a particle passes through the cavity mode, its presence is detected by a spectral shift in the resonance which is proportional the mode intensity at the position of the particle. The resultant signal can therefore be modelled using a Monte Carlo approach based on eqn (1) to simulate the motion of the particle through the device. We define transverse axes x and y such that ρ2 = x2 + y2 and select x as the direction of fluid flow. Particles are ‘launched’ starting from a position 1 μm upstream of the cavity mode (x = −1 μm) with selected values of position (y, z), fluid flow rate v and optical power P. Fig. 1(b and c) show example trajectories for a particle of diameter 200 nm and with flow speed v = 100 μm s−1. Fig. 1b shows an example trajectory of a particle that is not trapped by the mode at P = 10 mW, while Fig. 1c shows a similar particle being trapped when P is increased to 20 mW. To determine a trapping probability, trapping was defined to have occurred if the particle did not pass x = 1 μm within a time equal to 10 μm divided by the flow speed. For a given choice of v and P the initial position (y, z) was varied and the trapping probability (based on 100 repetitions per position) was established to produce a distribution map (Fig. 1d). It was found that within the range of parameters used the trapping probability was independent of the initial z position and so the trapping cross section σ was defined by integrating the distribution map with respect to y only. The trapping rate Γ is then given by the product of the trapping cross section, the cavity length (L), the flow speed (v) and nanoparticle concentration per unit volume in the fluid (CNP):
| Γ = σLvCNP. | (6) |
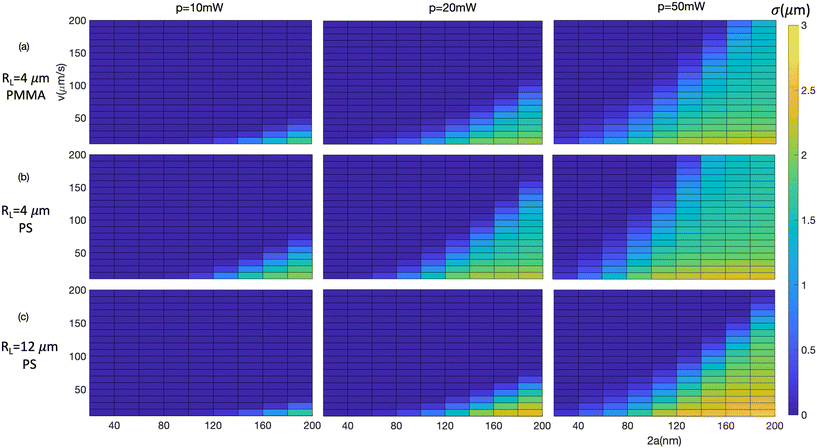
Fig. 2 shows the simulated variation of σ with several experimental parameters, as a series of false colour-scale plots. Each plot shows the dependence on flow speed v and particle diameter 2a; maps are generated for optical powers of P = 10 mW, 20 mW and 50 mW (columns) and for two different mirror radii of curvature (RL) and particle refractive index (np) (rows). The general result is as expected – that small particles in a rapidly flowing fluid (upper left of maps) do not trap, while larger particles in a slow flow speed show substantial trapping cross sections of order 2 μm. The striking feature of these maps is that in each case the boundary between the region with no trapping and the region where trapping occurs is reasonably sharp, such that at a given flow speed σ rises from zero to around 1.5 μm within an increase in particle diameter of about 20 nm. It is this sharp boundary that provide a basis for using the method for quantitative measurement.
The location of this boundary within the map depends on the values of the fixed parameters P, w0 and np. As expected the boundary moves to smaller particle sizes and higher flow speeds for increasing P and np and for decreasing w0. Within each plot the quadratic dependence of the threshold speed on particle radius given in eqn (3) can be seen, and the sensitivity to refractive index is shown by the comparison of PS and PMMA in Fig. 2a and b. The dependence on fixed experimental parameters indicates the ability to tune the measurement to different particles. The value of β that balances the maximum trapping force with the flow force is found to be
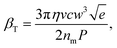 | (7) |
3 Experimental results
In the experiments, nanoparticle solutions of concentration 1011 ml−1 were pumped through a microfluidic flow cell with integrated microcavity measurement system. Here we used RL = 12 μm and L = 1.5 nm. A constant differential pressure of 2 mbar was established using a hydrostatic flow regulator,42 resulting in a peak flow speed of ∼50 μm s−1. Single nanoparticles passing through the microcavity register as discrete ‘events’ the duration of which is our primary indicator for trapping. Based on the flow speed alone we expect events due to particles that flow freely through the cavity mode to display durations of about 20 ms, and so we define a trapping event as one with duration exceeding 200 ms preceded by a period exceeding 100 ms with no observed mode shift.Fig. 3a shows exemplar mode shift events highlighting both trapped and non-trapped particles.
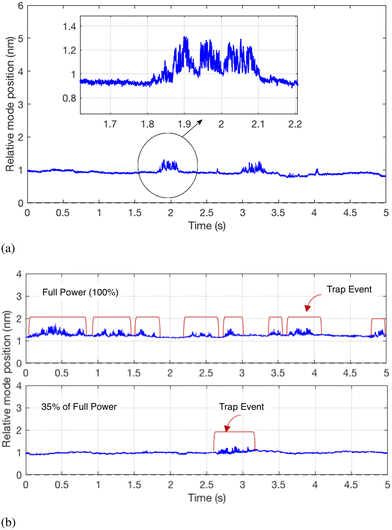 | ||
| Fig. 3 Example experimental data showing single particle events. (a) Prolonged mode shift of a trapped particle (b) the effects of laser power on the number of trapping events. | ||
An important consideration for the pressure-driven flow used here is that the flow speed is not uniform but follows a parabolic profile across the flow channel cross section, with zero flow rate at the mirror surfaces. We select the mirror separation such that five anti-nodes of the optical field lie within the flow channel, whereby we expect about two-thirds of the recorded events to result from the anti-nodes nearest the centre of the flow channel. The parabolic flow profile is included in the simulation to ensure accurate comparison with experimental data.
The distribution N(β) for particles in a solution is measured by sweeping the magnitude of the optical force via the laser power while maintaining a constant flow speed. Fig. 3b shows broadly how the number of trap events can be seen to increase with increased laser power.
Fig. 4 and 5 compare experimental (upper row) and simulated (lower row) data for the trapping behaviour as a function of laser power, with each panel comparing two different nanoparticle samples. Sub-figures (a) and (c) show raw data in which the laser power is swept and the rate of trap events is recorded, while sub-figures (b) and (d) show the derivative of these raw data with respect to power which represents a measure of the distribution N(β).
The experimental data in Fig. 4a and 5a show clear steps in trap rate with laser power, agreeing well with the simulations. The effect of the parabolic flow can be seen by a small increase in trap rate at laser powers below the main step, consistent with the lower threshold of trapping for the slower moving particles close to the mirrors.
Fig. 4a and b show that PS particles of diameter 140 nm and 175 nm are clearly resolved by the technique. The 140 nm particles require about double to power of the 175 nm particles to be trapped, such that the threshold power for trapping scales as ∼a3 in contrast to eqn (3). This dependency suggests that these experiments are in a regime where the trap time is determined more by the thermal energy than by the fluid flow. The full-width-at-half-maxima of the peaks in Fig. 4b reveals a sizing resolution of about 10 nm. Fig. 5a and b show similarly that PS (np = 1.59) particles of diameter 187 nm and PMMA (np = 1.49) particles of size 196 nm are easily distinguished, the PMMA particles requiring a high laser power from trapping despite being slightly smaller. The full-width-at-half-maxima of the peaks in Fig. 5b reveals a refractive index resolution of 0.03 RIU. We note that the resolution of the technique could in principle be increased significantly by increasing both the intracavity power and flow speed. An estimate of the quality factor of the measurement is provided by the optical trap strength: the ratio of the depth of the trap to the thermal energy,
 | (8) |
4 Conclusion
While based on single particle measurements, the technique as presented provides only ensemble data in the form of the distribution N(β). Adaptations could in principle measure β for each particle, potentially by sweeping the trap power during the trapping event. Such developments would be valuable in extending the range of parameters that can be measured on single particles. For example the maximum mode shift provides a measure of the polarizability of each particle30 and so could be combined with β to yield both particle radius and refractive index.The measured distribution N(β) provided by this method can be used to establish sample-to-sample variations in particle size and composition, complementary with other analytic techniques. Since the data recorded contains further information beyond the duration of trap events it is also possible to use this method as part of a wider technique to provide independent measurements of size and composition parameters.
The use of higher average intracavity powers would facilitate higher resolution measurements and measurement of smaller particles. One approach to this would be a configuration in which the trapping laser is ‘always on’ such that the peak power and average power are equal. Eqn (7) reveals that a factor of 50 increase in P would lead to a concomitant reduction in βT, such that particles about seven times smaller would be trapped. Equivalently a larger quality factor Q ∼ 100 might be achieved by simultaneously increasing the flow speed to around 1.5 mm s−1 to provide a resolution to particle size of below 1 nm or to refractive index of order 10−3 RIU. An additional benefit of the increased flow speed would be that each trap measurement would take only a few milliseconds to record.
Additional improvements might be achieved by pumping the particles through the cavity using dielectrophoresis, which is capable of establishing a uniform flow rate across the flow channel. The technique might also be used to measure thermophoretic effects that result from particle heating and can provide information on particle thermal conductivity43,44 or ionic shielding.45
As discussed in our previous work,35 open-access microcavity is a promising method for lab-on-a-chip applications. The proposed technique based on these type of cavities allows us to effectively evaluate the size distribution of particles in a fluid if particles of known composition are taken with different sizes. Thus, this technique is a promising method to find the range of needed power and flow rate to overcome the Brownian force, and to trap nanoparticles. This result has motivated us to study other methods to increase the average interactivity power, e.g., illuminating the cavity with a light source that provides constant optical injection. Not only this method can measure the size of particles, but also it is sensitive to the refractive index of particles so that we can measure the polarizability of particles as well. The magnitude of the resonance shift reveals the particle polarizability, providing a useful fingerprint that is sensitive to the material composition of the nanoparticle. The technique, therefore, allows the differentiation of particles of similar size, as we showed by the distinction of polystyrene and PMMA particles. Therefore, our method can be used to give a measure of composition such as those used in drug loading for nanomedicine. As a result, this method can be a powerful technique to characterize nanoparticles in a solution in applications where we need high-resolution measurements at the level of single molecule detection, showing a major breakthrough in nanoparticle characterization.
A Appendix
A.1 Gaussian beam parameters
The plano-concave optical microcavity is characterized by the cavity length L and the radius of curvature of the concave mirror RL. The Rayleigh range zR of the confined mode is then | (A.1) |
 | (A.2) |
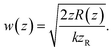 | (A.3) |
The intensity distribution for the resonant cavity mode supported between opposing concave and planar mirrors given in eqn (5) is determined as the sum of two Gaussian beams propagating in opposite directions, I = nmε0c∣Ei + Er∣2, where the incident (Ei(ρ, z)) and reflected (Er(ρ, z)) waves are given by:46
 | (A.4) |
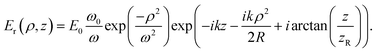 | (A.5) |
A.2 Balancing optical and flow forces
The maximum optical force is obtained by establishing the maximum value of using the mode intensity in eqn (5). This maximum force opposing the drag force due to the fluid flow occurs at
using the mode intensity in eqn (5). This maximum force opposing the drag force due to the fluid flow occurs at  , y = 0, z = 0 at which point
, y = 0, z = 0 at which point  . Substitution of this expression into the optical force term in eqn (1) and equating with the viscous drag force due to fluid flow yields eqn (7). This condition corresponds approximately to the potential energy profile shown in red in Fig. 6, where the potential gradient tends to zero at the downstream side of the cavity mode.
. Substitution of this expression into the optical force term in eqn (1) and equating with the viscous drag force due to fluid flow yields eqn (7). This condition corresponds approximately to the potential energy profile shown in red in Fig. 6, where the potential gradient tends to zero at the downstream side of the cavity mode.
 | ||
| Fig. 6 Total potential energy along the axis (x, 0, 0) for a PS particle diameter of 200 nm with no flow (blue curve) and with a flow speed of 100 μm s−1 (red curve). | ||
A.3 Monte Carlo simulation
Based on eqn (1) and (5), and the selection of the x axis as the flow, the equations for incremental movements of a particle in the Cartesian coordinate system are: | (A.6) |
 | (A.7) |
 | (A.8) |
 | ||
| Fig. 7 The mode shift of a PS particle with diameter of 200 nm with a fluid flow speed of 50 μm s−1 and intracavity powers of (a) 2 mW and (b) 20 mW. | ||
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by Oxford HighQ and the University of Oxford.Notes and references
- C. A. Barrios, Anal. Bioanal. Chem., 2012, 403, 1467–1475 CrossRef CAS PubMed.
- X. Chen, H. Guan, Z. He, X. Zhou and J. Hu, Anal. Methods, 2012, 4, 1619–1622 RSC.
- K. Malmir, H. Habibiyan and H. Ghafoorifard, Opt. Commun., 2016, 365, 150–156 CrossRef CAS.
- K. Malmir, H. Habibiyan and H. Ghafoorifard, Optik, 2020, 216, 164906 CrossRef CAS.
- N. Malmir and K. Fasihi, J. Mod. Opt., 2017, 64, 2195–2200 CrossRef CAS.
- F. Caruso, T. Hyeon and V. M. Rotello, Chem. Soc. Rev., 2012, 41, 2537–2538 RSC.
- A. Kamanzi, Y. Gu, R. Tahvildari, Z. Friedenberger, X. Zhu, R. Berti, M. Kurylowicz, D. Witzigmann, J. A. Kulkarni and J. Leung, et al. , ACS Nano, 2021, 15, 19244–19255 CrossRef CAS PubMed.
- L. M. Payne, W. Albrecht, W. Langbein and P. Borri, Nanoscale, 2020, 12, 16215–16228 RSC.
- M. M. Modena, B. Rühle, T. P. Burg and S. Wuttke, Adv. Mater., 2019, 31, 1901556 CrossRef PubMed.
- K.-T. Liao, J. Schumacher, H. J. Lezec and S. M. Stavis, Lab Chip, 2018, 18, 139–152 RSC.
- Y. Seo and W. Jhe, Rep. Prog. Phys., 2007, 71, 016101 CrossRef.
- J. Stetefeld, S. A. McKenna and T. R. Patel, Biophys. Rev., 2016, 8, 409–427 CrossRef CAS PubMed.
- S. Soares, J. Sousa, A. Pais and C. Vitorino, Front. Chem., 2018, 6, 360 CrossRef PubMed.
- S. Mourdikoudis, R. M. Pallares and N. T. Thanh, Nanoscale, 2018, 10, 12871–12934 RSC.
- A. Surrey, D. Pohl, L. Schultz and B. Rellinghaus, Nano Lett., 2012, 12, 6071–6077 CrossRef CAS PubMed.
- E. Orlova and H. R. Saibil, Chem. Rev., 2011, 111, 7710–7748 CrossRef CAS PubMed.
- E. Nakamura, N. A. Sommerdijk and H. Zheng, Acc. Chem. Res., 2017, 50, 1795–1796 CrossRef CAS PubMed.
- V. Filipe, A. Hawe and W. Jiskoot, Pharm. Res., 2010, 27, 796–810 CrossRef CAS PubMed.
- C. Troiber, J. C. Kasper, S. Milani, M. Scheible, I. Martin, F. Schaubhut, S. Küchler, J. Rädler, F. C. Simmel and W. Friess, et al. , Eur. J. Pharm. Biopharm., 2013, 84, 255–264 CrossRef CAS PubMed.
- N. C. Bell, C. Minelli and A. G. Shard, Anal. Methods, 2013, 5, 4591–4601 RSC.
- C. Haiden, T. Wopelka, M. Jech, F. Keplinger and M. J. Vellekoop, Langmuir, 2014, 30, 9607–9615 CrossRef CAS PubMed.
- S. Block, B. J. Fast, A. Lundgren, V. P. Zhdanov and F. Höök, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- P. C. Simons, S. M. Young, M. B. Carter, A. Waller, D. Zhai, J. C. Reed, B. S. Edwards and L. A. Sklar, Nat. Protoc., 2011, 6, 943–952 CrossRef CAS PubMed.
- G. Grégori, V. Patsekin, B. Rajwa, J. Jones, K. Ragheb, C. Holdman and J. P. Robinson, Cytometry, Part A, 2012, 81, 35–44 CrossRef PubMed.
- S. Zhu, L. Ma, S. Wang, C. Chen, W. Zhang, L. Yang, W. Hang, J. P. Nolan, L. Wu and X. Yan, ACS Nano, 2014, 8, 10998–11006 CrossRef CAS PubMed.
- A. G. Shard, K. Sparnacci, A. Sikora, L. Wright, D. Bartczak, H. Goenaga-Infante and C. Minelli, Anal. Methods, 2018, 10, 2647–2657 RSC.
- C. Minelli, A. Sikora, R. Garcia-Diez, K. Sparnacci, C. Gollwitzer, M. Krumrey and A. G. Shard, Anal. Methods, 2018, 10, 1725–1732 RSC.
- G. Young, N. Hundt, D. Cole and P. Kukurra, Science, 2018, 360, 423–427 CrossRef CAS PubMed.
- N. Mojarad and M. Krishnan, Nat. Nanotechnol., 2012, 7, 448–452 CrossRef CAS PubMed.
- A. Trichet, P. Dolan, D. James, G. Hughes, C. Vallance and J. Smith, Nano Lett., 2016, 16, 6172–6177 CrossRef CAS PubMed.
- https://www.oxfordhighq.com .
- K. Ladavac, K. Kasza and D. G. Grier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 010901 CrossRef CAS PubMed.
- M. P. MacDonald, G. C. Spalding and K. Dholakia, Nature, 2003, 426, 421–424 CrossRef CAS PubMed.
- P. T. Korda, M. B. Taylor and D. G. Grier, Phys. Rev. Lett., 2002, 89, 128301 CrossRef PubMed.
- A. Trichet, J. Foster, N. Omori, D. James, P. Dolan, G. Hughes, C. Vallance and J. Smith, Lab Chip, 2014, 14, 4244–4249 RSC.
- G. Volpe and G. Volpe, Am. J. Phys., 2013, 81, 224–230 CrossRef CAS.
- L. Giriunas, et al. , J. Appl. Phys., 2018, 124, 025703 CrossRef.
- Z. Geng, et al. , Phys. Rev. Lett., 2020, 124, 153603 CrossRef CAS PubMed.
- Z. Geng, K. Peters, A. Trichet, K. Malmir, R. Kolkowski, J. Smith and S. Rodriguez, 2019, preprint arXiv:1911.00463, DOI:10.48550/arXiv.1911.00463.
- K. Peters, Z. Geng, K. Malmir, J. Smith and S. Rodriguez, 2020, preprint arXiv:2008.11615, DOI:10.48550/arXiv.1911.00463.
- K. Peters, et al. , Phys. Rev. Lett., 2021, 126, 213901 CrossRef CAS PubMed.
- Datasheet, OB1–4 channels microfluidic flow controller Search PubMed.
- G. McNab and A. Meisen, J. Colloid Interface Sci., 1973, 44, 339–346 CrossRef CAS.
- R. T. Schermer, et al. , Opt. Express, 2011, 19, 10571–10586 CrossRef CAS PubMed.
- S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682 CrossRef CAS PubMed.
- P. Zemánek, A. Jonáš, L. Šrámek and M. Liška, Opt. Commun., 1998, 151, 273–285 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00180b |
| This journal is © The Royal Society of Chemistry 2022 |


![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif)
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif)