 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An image-to-answer algorithm for fully automated digital PCR image processing†
Zhiqiang
Yan‡
 a,
Haoqing
Zhang‡
a,
Haoqing
Zhang‡
 a,
Xinlu
Wang
a,
Martina
Gaňová
b,
Tomáš
Lednický
a,
Xinlu
Wang
a,
Martina
Gaňová
b,
Tomáš
Lednický
 b,
Hanliang
Zhu
b,
Hanliang
Zhu
 a,
Xiaocheng
Liu
a,
Marie
Korabečná
c,
Honglong
Chang
a,
Xiaocheng
Liu
a,
Marie
Korabečná
c,
Honglong
Chang
 a and
Pavel
Neužil
a and
Pavel
Neužil
 *a
*a
aSchool of Mechanical Engineering, Department of Microsystem Engineering, Northwestern Polytechnical University, 127 West Youyi Road, Xi'an, Shaanxi 710072, P.R. China. E-mail: pavel.neuzil@nwpu.edu.cn
bCentral European Institute of Technology, Brno University of Technology, Purkyňova 656/123, 612 00, Brno, Czech Republic
cInstitute of Biology and Medical Genetics, First Faculty of Medicine, Charles University and General University Hospital in Prague, Albertov 4, 128 00 Prague, Czech Republic
First published on 24th February 2022
Abstract
The digital polymerase chain reaction (dPCR) is an irreplaceable variant of PCR techniques due to its capacity for absolute quantification and detection of rare deoxyribonucleic acid (DNA) sequences in clinical samples. Image processing methods, including micro-chamber positioning and fluorescence analysis, determine the reliability of the dPCR results. However, typical methods demand high requirements for the chip structure, chip filling, and light intensity uniformity. This research developed an image-to-answer algorithm with single fluorescence image capture and known image-related error removal. We applied the Hough transform to identify partitions in the images of dPCR chips, the 2D Fourier transform to rotate the image, and the 3D projection transformation to locate and correct the positions of all partitions. We then calculated each partition's average fluorescence amplitudes and generated a 3D fluorescence intensity distribution map of the image. We subsequently corrected the fluorescence non-uniformity between partitions based on the map and achieved statistical results of partition fluorescence intensities. We validated the proposed algorithms using different contents of the target DNA. The proposed algorithm is independent of the dPCR chip structure damage and light intensity non-uniformity. It also provides a reliable alternative to analyze the results of chip-based dPCR systems.
Introduction
The polymerase chain reaction (PCR) method was initially developed for enzymatic deoxyribonucleic acid (DNA) amplification using thermal cycling. It allowed further qualitative characterization of the amplified DNA fragments,1 especially for gene mutation analysis and the detection of polymorphic DNA sequences. The PCR technique evolved with the introduction of intercalating dyes or target sequence hybridization with fluorescently labeled probes, leading to real-time monitoring of reaction kinetics and subsequent quantitative analysis of nucleic acids in samples, known as real-time or quantitative PCR (qPCR).2,3 It was then further developed and, with the advent of micromachining and miniaturization, the hand-held qPCR for point-of-care applications was introduced.4The development of the microfluidics technique enabled new digital PCR (dPCR) technology, a variant of end-point detection PCR techniques. A compartmentalized sample forms a binary system of thousands or millions of subsamples, each containing a single copy or no copy of the target DNA.5 This technique allows absolute quantification of selected target DNA sequences and, most importantly, performs multiplex PCR with minimal interaction between different targets,6 distinguishing rare DNA targets from abundant ones.7 The compartmentalization of the original sample is achieved either by filling predefined partitions forming a chip-based dPCR (cdPCR)8 or by forming individual droplets as microreactors of a droplet-based dPCR (ddPCR).9,10 The PCR protocol is then conducted with several thermal cycles (typically between 40 and 45), and the fluorescence amplitude (F) from each well or droplet (partition) is determined once the protocol is completed for either single DNA target11 or several DNA targets thus performing target multiplexing.12
The partitions with amplified targets are defined as positive partitions (PW), exhibiting an increased value of F when compared with the original value. The partitions without targets, defined as negative partitions (NW), show significantly lower F values. Image processing methods, including a series of image corrections and F value analysis, determine the reliability of the dPCR results.13 In this study, we mainly discuss cdPCR-based image processing, typically determining partition positions, error correction, and subsequent F extraction.
Current techniques to determine partition positions are based on pattern recognition, chip structure, or alignment marks.14 A passive reference dye is added to the dPCR master mix to provide the background fluorescence signal, help the software recognize PW and NW in the chip, and improve statistical precision.15 The pattern recognition method identifies the partitions with fluorescence using a machine-learning algorithm,16 a region-growing algorithm,17 and a clustering algorithm.18–20 However, chip defects, such as dust and scratches, often result in bright image areas incorrectly identified as PW, while the partitions not filling the sample may be identified as NW, affecting the result's accuracy.
The chip structure-based partition positioning method excludes false recognition as only the fluorescence in each partition's area is captured.15,21,22 This method utilizes the chip's design to determine the position of all partitions, removing fixed pattern noise in the image caused by dust or defects. Recently, we proposed a method using the chip's alignment marks to determine the partition locations by capturing them using a bright-field imaging method, registering their centers, and then capturing the partition area by fluorescence imaging in six blocks, followed by image-stitching and subsequent image processing.23
The chip structure-based partition positioning method improves recognition precision. However, feature structure damage, such as missing alignment marks, affects the accuracy of partition position determination. In addition, this method does not consider chip illumination inhomogeneity.21
Once the partitions are recognized, the F values are extracted, and a fixed F (FT) threshold is defined to distinguish PW from NW.24–26 However, the chip illumination non-uniformity and the emitted F value affect the reliability of the extracted results.27
The adaptive FT method reduces the influence of light non-uniformity.28 First, the image is split into several segments, assuming that each segment's light distribution is uniform. Each segment's threshold is then defined, and the PW number is counted in each segment. Alternatively, a machine-learning algorithm determines whether partitions with fluorescence are PW or NW.29
Additionally, the details of image processing algorithms in commercial dPCR systems are not available to users; thus, it is impossible to elaborate on their merits or demerits. Only a few papers have described chip-based image processing methods based on deep learning.30 However, it requires a high computer configuration level and an extensive training dataset, making detection complex and time-consuming. Previous research has proposed a random background transfer-based image processing algorithm to simplify the training dataset significantly, as it only requires three experimental images.31 However, it is used in augmenting images to lower the effect of uneven illumination rather than to remove it.
Here, we develop an image-to-answer processing algorithm that requires only a single fluorescence image capture using a dPCR chip. The process eliminates capturing a set of bright field images, registering the chip location, capturing a set of fluorescence images, stitching them together, and then processing them as previously required.23 Moreover, the proposed method simplifies the image processing procedure as it does not rely on a training dataset. Additionally, we implement several image-related error corrections, making this proposed dPCR image processing method versatile. Furthermore, we locate the partitions' positions using a new method combined with pattern recognition and chip structure, providing an option to help identify the location of the partitions in the chip. Together with the previously published method of dPCR image emulation,32 both works complement each other for dPCR image emulation and processing.
Materials and methods
dPCR chips
We utilized a 9 × 9 mm2 dPCR chip with 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 partitions, each with a target diameter of 50 μm split into six blocks, designed using the script-based Nanolithography Toolbox,33,34 a family of dPCR chips with the same previously described size and basic structure.23 The dPCR chip was made of Si using a single lithography step, followed by deep reactive ion etching with a target depth of 30 μm.
448 partitions, each with a target diameter of 50 μm split into six blocks, designed using the script-based Nanolithography Toolbox,33,34 a family of dPCR chips with the same previously described size and basic structure.23 The dPCR chip was made of Si using a single lithography step, followed by deep reactive ion etching with a target depth of 30 μm.
The chip was first immersed in H2SO4/H2O2 (piranha) with a 96%/30% concentration and a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio solution at a temperature of ≈120 °C for ≈10 min. This piranha solution treatment demineralizes organic materials, removing all traces of previous dPCR experiments and making the dPCR chip reusable. This treatment also forms OH− groups at the Si surface, making it hydrophilic. The prepared PCR master mix subsequently filled the partitions in the dPCR chip, and the chip was sealed with a microscope cover glass of ≈10 × 10 mm2 and ≈170 μm in size and thickness, respectively. The cover glass was spincoated with ≈50 μm polydimethylsiloxane and then coated with ≈2 μm thick parylene C by physical vapor deposition.
1 ratio solution at a temperature of ≈120 °C for ≈10 min. This piranha solution treatment demineralizes organic materials, removing all traces of previous dPCR experiments and making the dPCR chip reusable. This treatment also forms OH− groups at the Si surface, making it hydrophilic. The prepared PCR master mix subsequently filled the partitions in the dPCR chip, and the chip was sealed with a microscope cover glass of ≈10 × 10 mm2 and ≈170 μm in size and thickness, respectively. The cover glass was spincoated with ≈50 μm polydimethylsiloxane and then coated with ≈2 μm thick parylene C by physical vapor deposition.
The dPCR hardware
We designed a fluorescence imaging system using a fluorescein isothiocyanate (FITC) cube from an optical microscope (Fig. 1A). The cube was mounted on an X–Y stage with a light-emitting diode (LED) with a principal wavelength and a maximum power of 470 nm and 30 W, respectively; the optical power was controlled by an LED controller using the pulse-width modulation (PWM) method. A commercial complementary metal-oxide semiconductor (CMOS) single-lens reflex (SLR) camera, with a 35 × 24 mm2 full-frame and 20.2 Mpixel imager size, can capture images with 16- or 8-bit gray-scale resolution. In this study, we operated the images with 16-bit resolution, which is 256 times more precise than 8-bit resolution. The camera, with a 180 mm focal length macro lens and 3.5 minimum aperture, set to 8.0, one extension tube with a total length of 150 mm, and a 1.4× telephoto image enhancer, was attached to the cube via a tube spacer.The dPCR chip was placed under the cube's center on a brass plate. The plate was soldered onto a thermoelectric cooler (TEC) powered by electrical current pulses from an H-bridge system (Fig. 1B). The TEC was fixed to the top of a copper cooler mounted on a Z-stage and located on two sliders, making chip filling and replacement more convenient. The dPCR chip was placed in a brass holder on top of the TEC to fix the chip's location (Fig. 1B inset), protecting the sealed chip from accidental movement. The holder also allowed fast heat transfer from the TEC to the solution in the partitions during thermal cycling. The brass plate's thermal cycling was monitored with a Pt100 temperature sensor. The temperature was controlled using the PWM method, allowing proportional, integrative, and derivative methods to control the dPCR chip's temperature from a personal computer. We used the same setup as before for verification of the dPCR image generation method.32
DNA template and PCR protocol
The chip was filled with a ≈0.15 μM concentration fluorescein solution, which had ≈0.17 ± 0.01 (mean ± standard deviation from three experiments) of the F value of a double-stranded DNA amplicon in the presence of EvaGreen after 40 cycles of PCR, determined using a commercial qPCR system (ESI† section A). First, the chip photograph was used as an input calibration dPCR chip image. Then, we chose a synthesized hepatitis B virus gene as a DNA template.35 The amplicon length was 102 base pairs (bp), and the template and primer sequences are given in Table 1.| DNA template | CGCTGAATCCTGCGGACGACCCTTCTCGGGGTCGCTTGGGACTCTCTCGTCCCCTTCTCCGTCTGCCGTTCCGACCGACCACGGGGCGCACCTCTCTTTACGCGGACTCCCCGTCTGTGCCTTCTCATCTGCCGGACCGTGTGCACTTCGCTTCACCTCTGC |
| Forward primer | 5′-GTCGCTTGGGACTCTCTC-3′ |
| Reverse primer | 5′-GCAGATGAGAAGGCACAGA-3′ |
The PCR master mix consisted of ≈0.96 μL Taq polymerase, ≈5 μL buffer, ≈1 μL of forward and reverse primers with a final concentration of ≈100 nM, ≈0.4 μL fluorescein in a concentration of ≈0.15 μM helping to increase the contrast between PW and NW, ≈1.2 μL EvaGreen, ≈1 μL DNA template, ≈0.94 μL bovine serum albumin at a concentration of 20 mg mL−1 and ≈13.5 μL deionized H2O. The polymerase concentration was increased due to the unfavorable surface-to-volume ratio.36
We performed a three-step PCR protocol, a hot start to activate the polymerase at a set temperature of 95 °C for 60 s followed by 40 PCR cycles, consisting of the following steps: denaturation at a set temperature of 95 °C for 15 s, annealing at 56 °C for 20 s, and elongation at 72 °C for 30 s.
Principle of the method
We used a single fluorescence image to automatically determine the copy number (cn) of targets in a dPCR chip. The image processing algorithm included system calibration and fluorescence analysis (Fig. 2). The algorithm workflow is shown in ESI† section B.We determined a series of image correction algorithm parameters, including radial lens distortion correction coefficient k, image skew angle θ, and light non-uniformity correction mask A. These parameters were used to correct the dPCR chip's fluorescence image after DNA amplification. Point of note: these correction operations are optional; some can be skipped because optical systems with acceptable global non-uniformity do not require correction.
System calibration
The image processing algorithm started with several pre-processes from the acquired calibration dPCR chip fluorescence image. First, the original image's Canon raw 2 (CR2) format was converted into tag image file format (TIFF), maintaining 16-bit resolution. Then, the background area of the image was cropped so that the only area of the dPCR chip with partitions remained, and the red, green, and blue (RGB) image was converted into the gray-scale format.Image conversion
Radial distortion can be caused by the lens,37,38 including barrel and pincushion types, and is a common form of image error that negatively affects the determination of partition positions. If such a lens is used, correction of this distortion is essential. Therefore, we mainly used a commercial SLR camera with automated lens recognition and a barrel distortion correction program. However, if the image is captured using a different camera, such as a smartphone camera, the k implementation algorithm should be employed (Fig. S2†). Details of this algorithm are shown in ESI† section C.Detection of partitions and image skew correction
The camera is always rotated (skewed) by an unpredictable value of θ when taking a fluorescence image of the dPCR chip (Fig. 3A), as it is impossible to place the dPCR chip under the camera with a value of θ = 0°. If the rotation angle is not compensated, the subsequent location correction is affected, leading to a false recognition. The image skew correction allows the subsequent algorithm to detect the image boundary easily. Also, the chip layout we processed was based on an array with a hexagonal pattern rather than a square. This pattern makes chip boundary recognition more complicated if the skew is still present. We proposed a fast Fourier transform (FFT)-based skew correction algorithm (Fig. 3B) to determine the image's θ value. This algorithm started with partition detection using a circle Hough transform (CHT) (Fig. 3B, I1),39,40 determining the circle indexed i with a radius ri and center location (xi, yi) defined by the pixel coordinate (Fig. 3A). The partitions' radius and layout are two essential parameters for the dPCR chip image processing we describe in our work. Because we used the dPCR chip we designed and fabricated, we had access to these vital design parameters. Should we process somebody else's design, we first need to extract these parameters, which is not difficult using modern optical microscopes with size measurement.Afterward, I1 was converted into a binary image I2 (Fig. 3B). The gray level with a radius of three pixels in the circle areas centered at (xi, yi) was set to 1, and the gray level in other areas was set to 0. This method removed the non-uniformity of subsequently used spectrum image I3. Thus, we did not need to use a multi-level segmentation algorithm. We then applied 2D FFT and generated the spectrum image I3; the gray value of each pixel showed periodicity at a unique frequency and direction (Fig. 3B).
We decreased the contrast of I3 and binarized the generated spectrum image with an empirical threshold value of 0.5. Subsequently, a line Hough transform (HTM) was employed to detect the first eight distinct lines on I3. The median rotation angle of these lines was regarded as θ in the fluorescence image.
Finally, we rotated the original fluorescence image to get the skew-corrected image Irot (Fig. 3C). The partitions' previously detected center position was also updated using a transform formula:
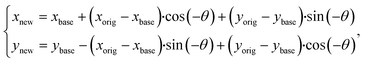 | (1) |
After that, we verified the algorithm to determine the θ value of the dPCR chip image, using a series of emulated images (Fig. 3D) with predefined θ values from −14° to 14°.32 These emulated images contained different normalized F values, such as partitions with 80% defined as PW with DNA, and a lower level of 30%, representing NW and unfilled (empty) partitions. A comparison between a predefined angle in an emulated image and the calculated angle extracted from it is shown in Table 2. The mean value of the absolute residual angle was only 0.0057°; this was considered an acceptable value for the subsequent image processing algorithm.
| Predefined θ (°) | −14 | −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 |
| Detected θ (°) | −14.00 | −13.00 | −11.99 | −11.01 | −10.00 | −9.00 | −8.00 | −7.00 | −6.01 | −5.01 |
| Predefined θ (°) | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
| Detected θ (°) | −4.01 | −3.00 | −2.00 | −0.99 | 0 | 0.99 | 2.00 | 3.00 | 3.99 | 5.00 |
| Predefined θ (°) | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | — |
| Detected θ (°) | 6.00 | 6.99 | 7.99 | 8.99 | 9.99 | 11.01 | 12.00 | 13.00 | 14.00 | — |
Location correction
Some partitions, especially the ones near the chip corners, were not detected using the CHT method (Fig. 3E) due to fabrication defects on the chip and incomplete filling of the chip with the solution. Therefore, we proposed a 3D projection transformation method based on an automatic partition location correction algorithm to locate all partitions on the chip.We analyzed the image processed by the CHT method, locating the upper, lower, left, and right boundary partitions. First, we searched for characteristics of partitions neighboring the analyzed partition. Once we found that the analyzed partition had no neighbors on the left-hand side, the partition was regarded as a potential left boundary partition. Thus, the four boundary lines were fitted to the corresponding potential boundary partitions using the random sample consensus (RANSAC) method.41 This method fitted lines on the boundaries, eliminating wrongly identified boundary partitions (ESI† section D).
Next, the coordinates of the four corner points such as top left, top right, bottom left, and bottom right were calculated as cross points of the four boundary lines (Fig. 3F). These four corner points were used as control points to calculate the 3D projection transformation matrix from the chip image to a predefined chip structure. Finally, the positions of all partitions were calculated by performing inverse 3D projection transformations (Fig. 3G) (ESI† section E).
Global non-uniformity corrections
Non-uniform illumination on dPCR chips negatively affects the precise detection of F values. In addition, illumination non-uniformity could result in overlapping fluorescence distribution of PW and NW, making it difficult to distinguish the two types. Moreover, the fluorescence system readout might not report uniform detection across the imaging device; these global non-uniformities should be corrected.A dPCR illumination system was proposed to reduce the influence of light non-uniformity based on the improved illumination setup.27 However, the demonstrated device did not completely eliminate the related problem. Therefore, we proposed a global non-uniformity correction algorithm, making a mask from a set of images of a dPCR chip filled with fluorescein solution, a method similar to the fixed pattern noise reduction utilized in infrared focal plane arrays.42 This algorithm automatically generates a correction mask and suppresses global non-uniform illumination.
We used two methods: the first was based on the approximation of non-uniformity by a 3D parabolic function extracted from a set of images, and the second was by the smoothing method. The first steps were almost identical in both methods; generating the correction mask was the only difference.
The correction algorithm's first step was to extract F values in each partition. Here, we averaged the gray value in the circle area defined by the center locations (xi, yi) and mean radius r = ri to obtain value Fi. This gray value was used to quantify the F values of partition i. Afterward, the relative F values FiN of partition i were calculated for each partition. As for the PW, FiN was calculated by dividing Fi by the mean value of positive partitions F2, while for the negative partitions, the FiN value was set to 1.
The FiN was affected by structure defects, incomplete filling, and image noise caused by optical system. We employed a median fitting method to smooth FiN in the partitions i. The filtered gray value was set to the median gray value in the partitions, including its neighbor partitions and itself. Finally, a 3D map (Fig. 4A, S1) showed the illumination intensity distribution on the chip, constructed based on FiN and the partitions' location.
Method 1: 3D parabolic function fitting method
This method was conducted by performing a surface function fitting on the 3D map of S1 using the function:f(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y) = P00 + P10x + P01y + P20x2 + P11xy + P02y2, y) = P00 + P10x + P01y + P20x2 + P11xy + P02y2, | (2) |
After obtaining the polynomial surface function, a correction mask matrix with the same size fluorescence image was generated by calculating f(x, y) in each pixel (x, y) (Fig. 4A, M1). This matrix is used to correct the subsequent actual dPCR fluorescence image by dividing its gray value in each pixel. It should also be noted that the non-uniformity of fluorescence intensity is caused by many factors, including non-uniform illumination, non-uniform film coating, and unpredictable image random noise. Therefore, this 2D parabola fitting method is designed only for systematic errors, such as non-uniform illumination and fluorescence capture. This method cannot correct other defects, such as random glass coating non-uniformity.
Method 2: the image smoothing method
We performed surface adjacent pixel smoothing and created a 3D map, exhibiting non-uniformity caused by uneven illumination, fluorescence imaging, and the parylene coating of the glass coverslip. First, we performed a Gauss filtering algorithm to smooth the light non-uniformity mask S1 initially extracted from the fluorescein-filled chip using a set standard deviation of 20 pixels (Fig. 4A, S3). Then, a correction mask M2, similar to M1, was generated by extracting a relative gray value on S3 in each pixel (x, y). The smoothing method was used for mask smoothing while preserving its intact edges.We calculated the averaged non-uniformity index M to quantify the effect of our non-uniformity correction algorithm, as described below:
 | (3) |
| Original image | Corrected image using method 1 | Corrected image using method 2 | |
|---|---|---|---|
| M (%) | 3.44 | 0.95 | 0.40 |
| σ (pixel) | 7.96 | 3.20 | 1.55 |
| Correction rate of M (%) | — | 72.38 | 88.37 |
| Correction rate of σ (%) | — | 59.80 | 80.53 |
The adjacent smoothing method is significantly better than the 3D parabolic function fitting, but it is specific to the glass used for the experiment. The first method based on 3D surface fitting is less precise but more universal.
We combined feature-based and chip-structure-based methods to locate all partitions on the chip. The chip was filled with fluorescein solution with a concentration of ≈0.15 μM having ≈17% of F values of a PCR master mix after completion of PCR. We first captured the chip's fluorescence image using a 20.2 Mpixel commercial camera and close lookup lens. Next, CHT method was performed to detect partitions with F values in the detectable range in the captured image. Then, we determined the image barrel distortion and corrected it. The image's skew angle was found using the FFT method. Using the extracted partitions' locations, we determined the coordinates of the four corners (control points). Finally, we performed a 3D projection transformation using these control points and the known design to locate all partitions, including those with F values out of range. According to our experiment, all partitions on the chip were located with accuracy better than ≈5 μm.
Subsequently, we performed either 3D surface fitting to create a mask or formed the mask by direct 3D smoothing and generated a non-uniformity correction mask for both methods. Applying this mask lowered the non-uniformity by ≈72.4% and 88.4% using 3D parabolic surface fitting and adjacent smoothing, respectively. This technique was applied before in conjunction with DNA melting curve analysis for dPCR chip temperature non-uniformity determination.43
Here we conducted the following measurements to recognize and identify both NW and PW: adding the fluorescein with a concentration of ≈0.15 μM in the dPCR master mix, capturing the dPCR image using 16-bit resolution, and performing global non-uniformity corrections to reduce the non-uniform F value distribution of both PW and NW on the chip, thus inhibiting the false identification caused by non-uniform illumination.
Results and discussion
Copy number calculation methods
We created a histogram of an average gray-scale value extracted from each partition, using the image with 16-bit gray-scale resolution with a BIN number of 256. A histogram from extracted F values may show several clusters by adjusting the image contrast, even with a single target.44 An ideal histogram of dPCR results based on a single target test consists of two major clusters, one having a lower F value representing the NW and the other with a higher F value representing the PW. Thus, the Gauss distribution function can be used to fit these clusters in a histogram: | (4) |
 | (5) |
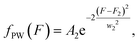 | (6) |
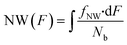 | (7) |
 | (8) |
Unfortunately, there is a chance that multiple targets can land in the same partitions.45 In this case, the data extraction described above using two Gauss distribution functions would not yield correct results. The probability P(k) of having k targets in a partition is given by Poisson distribution:23
 | (9) |
The total number of partitions (N) is defined as the sum of NW and PW:
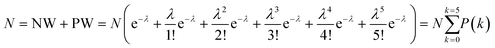 | (10) |
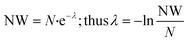 | (11) |
 | (12) |
Experimental results
First, we filled a dPCR chip with fluorescein as a calibration chip (Fig. 5A) and created a fluorescence non-uniformity correction mask for the subsequent calibration (Fig. 5B).We used our dPCR chip with 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 wells each with a diameter set to 50 μm and loaded with PCR master mix ≈1.56 μL, having different values of cn, corresponding to the calculated λ (λC) values of 0.1, 0.2, 0.3, 0.4, 0.7, and 0.8. We then placed the dPCR chip on the built setup and performed dPCR protocols once for each λC value. Once the thermal cycling was completed, we captured a fluorescence image at room temperature, with an LED excited to 80% of its maximum power and the following parameters: exposure time of 30 s with the camera speed set to the international standard organization (ISO) 200, inhibiting the noise from the environment and improving the contrast between PW and NW. Here, we used a dPCR chip image with a λC value of 0.3 as an example (Fig. 5C).
448 wells each with a diameter set to 50 μm and loaded with PCR master mix ≈1.56 μL, having different values of cn, corresponding to the calculated λ (λC) values of 0.1, 0.2, 0.3, 0.4, 0.7, and 0.8. We then placed the dPCR chip on the built setup and performed dPCR protocols once for each λC value. Once the thermal cycling was completed, we captured a fluorescence image at room temperature, with an LED excited to 80% of its maximum power and the following parameters: exposure time of 30 s with the camera speed set to the international standard organization (ISO) 200, inhibiting the noise from the environment and improving the contrast between PW and NW. Here, we used a dPCR chip image with a λC value of 0.3 as an example (Fig. 5C).
The image was first corrected with the known k, θ, and A values determined from step 1 (Fig. 5D). Then, the location and radius of the partitions were extracted from the image. Next, the four corner points and coordinates of all partitions were located (Fig. 5E), and all partition locations were subsequently corrected based on the chip design (Fig. 5F). Finally, each partition's F values (Fi) were extracted, and the histogram was built and used to calculate the cn of the DNA targets (Fig. 5G).
Finally, we determined the number of PW and NW based on the histogram and used a derived Poisson distribution eqn (11) to obtain the extracted values (λE) (Table 4) to validate the proposed algorithm. The error in λ in the table was defined as the percentage of the difference between λC and λE. The images and extracted histograms are shown in ESI† section F.
| Calculated λC (copies per partition) | 0.1 | 0.2 | 0.3 | 0.4 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|
| Calculated percentage of PW number (%) | 9.52 | 18.13 | 25.92 | 32.97 | 50.34 | 55.07 |
| Extracted λE (copies per partition) | 0.105 | 0.173 | 0.237 | 0.347 | 0.564 | 0.676 |
| Extracted percentage of PW number (%) | 9.87 | 15.92 | 20.16 | 26.24 | 39.47 | 46.01 |
| Error in λ (%) | 0.49 | 2.67 | 6.31 | 5.33 | 13.58 | 12.41 |
The experimental result showed that our algorithm obtained quantitative data corresponding to the expected values. However, imperfect loading of the sample into the chip and some evaporation during thermal cycling led to significant error, primarily due to the concentrated sample filling the chip.23 Furthermore, the gap between the calculation and extraction widened with the amount of cn filling the chip.
Additionally, we also used our dPCR chip with 139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896 wells each with a diameter set to 20 μm and loaded with PCR master mix with a cn value of 2310, corresponding to the λC value of 0.1 as well as the PW percentage of ≈9.5%.23 We performed the dPCR protocol four times. We captured fluorescence images of four blocks of the chip and processed the data using the proposed algorithm (Fig. 6A). We extracted the λE value of 0.08 ± 0.02 from the histograms based on extracted data with an error of ≈20% between λC and λE (Fig. 6B). The relatively high error was due to each partition's limited pixel numbers. These results could be improved by using an image with more pixels (ESI† section G).
896 wells each with a diameter set to 20 μm and loaded with PCR master mix with a cn value of 2310, corresponding to the λC value of 0.1 as well as the PW percentage of ≈9.5%.23 We performed the dPCR protocol four times. We captured fluorescence images of four blocks of the chip and processed the data using the proposed algorithm (Fig. 6A). We extracted the λE value of 0.08 ± 0.02 from the histograms based on extracted data with an error of ≈20% between λC and λE (Fig. 6B). The relatively high error was due to each partition's limited pixel numbers. These results could be improved by using an image with more pixels (ESI† section G).
Finally, we used images extracted from commercial dPCR chips (ThermoFisher Quantstudio 3D) after thermal cycling to validate the algorithm, corresponding to the original cn values of 2 and 20, each experiment was performed once. We processed captured images, built histograms, and calculated the cn values. The results with errors are shown in Table 5. Chip images are shown in ESI† section H.
| Calculated cn | 2 | 20 |
|---|---|---|
| Calculated percentage of PW number (%) | 0.04 | 0.41 |
| Extracted cn | 2 | 14 |
| Extracted percentage of PW number (%) | 0.04 | 0.29 |
| Error in cn (%) | 0 | 30% |
Conclusion
This study proposed an image-to-answer algorithm for dPCR image processing. The algorithm automatically locates partitions, extracts F values, and analyzes them. It includes two major parts: extraction of partition locations and subsequent F value analysis. We used the Hough transform to identify partitions in images of dPCR chips, the 2D Fourier transform to rotate the images, and the 3D projection transformation to locate and correct the positions of all partitions. We then calculated the average F values of each partition and generated a 3D fluorescence intensity distribution map of the images. We subsequently corrected the fluorescence non-uniformity between partitions based on the map and achieved statistical results of partition fluorescence intensities. Finally, we performed dPCR and processed the chip images to verify the proposed algorithm. The experimental result showed that our algorithm obtained quantitative data corresponding to expected values.Nevertheless, some steps of this algorithm are optional, such as image skew and light non-uniformity correction, and can be omitted if the error they cause is insignificant. Moreover, imaging at higher magnification would make the image processing more precise. We adopted image utilization of ≈1/3 of a field of view 20.2 Mpixel imager. There is certainly room for improvement in utilizing more pixels, such as a 2× optical magnifier or smaller CMOS imager. However, as previously described, once the chip no longer fits into the CMOS imager's field of view, field stitching is required.
The proposed algorithm is designed independent of the dPCR chip structure damage and light intensity non-uniformity. Therefore, it provides a reliable alternative when analyzing the results of chip-based dPCR systems. Furthermore, compared with a conventional image processing algorithm, our algorithm is designed to process dPCR images with known defects, such as a damaged chip structure, incomplete chip filling, assembly error, and light non-uniformity. This characteristic might be beneficial for realizing a versatile dPCR platform, especially for future chip-based platforms.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Haoqing Zhang, Zhiqiang Yan, Xinlu Wang, and Pavel Neužil were supported by grant no. 2018YFE0109000 from the Ministry of Science and Technology of the P.R. of China. Marie Korabečná was supported by grant no. LTACH19005 from the Ministry of Education, Youth, and Sports of the Czech Republic and grant no. RVO-VFN 64165 from the Ministry of Health of the Czech Republic. We also acknowledge the Ph.D. student Chao Zhang and Prof. Feng Xu from Xi'an Jiaotong University, Xi'an, P.R. China, for providing images of the QuantStudio 3D dPCR chips.References
- K. Mullis, F. Faloona, S. Scharf, R. Saiki, G. Horn and H. Erlich, Cold Spring Harbor, 1986 Search PubMed.
- R. Higuchi, C. Fockler, G. Dollinger and R. Watson, Bio/Technology, 1993, 11, 1026–1030 CAS.
- H. Zhu, H. Zhang, Y. Xu, S. Laššáková, M. Korabečná and P. Neužil, BioTechniques, 2020, 69, 317–325 CrossRef CAS PubMed.
- H. Zhu, H. Zhang, S. Ni, M. Korabečná, L. Yobas and P. Neuzil, TrAC, Trends Anal. Chem., 2020, 130, 115984 CrossRef CAS PubMed.
- B. Vogelstein and K. W. Kinzler, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9236 CrossRef CAS PubMed.
- H. Zhang, Z. Yan, X. Wang, M. Ganova, M. Korabecna, S. Laššáková, H. Chang and P. Neuzil, ACS Omega, 2021, 6, 22292–22300 CrossRef CAS PubMed.
- J. F. Huggett, C. A. Foy, V. Benes, K. Emslie, J. A. Garson, R. Haynes, J. Hellemans, M. Kubista, R. D. Mueller, T. Nolan, M. W. Pfaffl, G. L. Shipley, J. Vandesompele, C. T. Wittwer and S. A. Bustin, Clin. Chem., 2013, 59, 892–902 CrossRef CAS PubMed.
- A. M. Thompson, A. Gansen, A. L. Paguirigan, J. E. Kreutz, J. P. Radich and D. T. Chiu, Anal. Chem., 2014, 86, 12308–12314 CrossRef CAS PubMed.
- A. C. Hatch, J. S. Fisher, A. R. Tovar, A. T. Hsieh, R. Lin, S. L. Pentoney, D. L. Yang and A. P. Lee, Lab Chip, 2011, 11, 3838–3845 RSC.
- J. Madic, A. Zocevic, V. Senlis, E. Fradet, B. Andre, S. Muller, R. Dangla and M. E. Droniou, Biomol. Detect. Quantif., 2016, 10, 34–46 CrossRef CAS PubMed.
- A. Lievens, S. Jacchia, D. Kagkli, C. Savini and M. Querci, PLoS One, 2016, 11, e0153317 CrossRef CAS PubMed.
- M. Gaňová, H. Zhang, H. Zhu, M. Korabečná and P. Neužil, Biosens. Bioelectron., 2021, 181, 113155 CrossRef PubMed.
- L. Cao, X. Cui, J. Hu, Z. Li, J. R. Choi, Q. Yang, M. Lin, L. Ying Hui and F. Xu, Biosens. Bioelectron., 2017, 90, 459–474 CrossRef CAS PubMed.
- A. Petrov and S. Shams, J. VLSI Signal Process. Syst. Signal Image Video Technol., 2004, 38, 211–226 CrossRef.
- K. A. Heyries, C. Tropini, M. VanInsberghe, C. Doolin, I. Petriv, A. Singhal, K. Leung, C. B. Hughesman and C. L. Hansen, Nat. Methods, 2011, 8, 649–651 CrossRef CAS PubMed.
- Z. Wang, B. Zineddin, J. Liang, N. Zeng, Y. Li, M. Du, J. Cao and X. Liu, Comput. Methods Programs Biomed., 2013, 111, 189–198 CrossRef PubMed.
- Y. H. Yang, M. J. Buckley, S. Dudoit and T. P. Speed, J. Comput. Graph. Stat., 2002, 11, 108–136 CrossRef.
- G. Shao, D. Li, J. Zhang, J. Yang and Y. Shangguan, PLoS One, 2019, 14, e0210075 CrossRef CAS PubMed.
- L. Qin, L. Rueda, A. Ali and A. Ngom, Appl. Bioinf., 2005, 4, 1–11 CrossRef CAS PubMed.
- G. Shao, T. Li, W. Zuo, S. Wu and T. Liu, PLoS One, 2015, 10, e0133025 CrossRef PubMed.
- B. Belean, M. Borda, B. Le Gal and R. Terebes, Comput. Med. Imaging Graph., 2012, 36, 419–429 CrossRef PubMed.
- B. Belean, R. Terebes and A. Bot, Med. Biol. Eng. Comput., 2015, 53, 99–110 CrossRef PubMed.
- C. Tan, X. Chen, F. Wang, D. Wang, Z. Cao, X. Zhu, C. Lu, W. Yang, N. Gao, H. Gao, Y. Guo and L. Zhu, Analyst, 2019, 144, 2239–2247 RSC.
- J. Tanaka, T. Nakagawa, A. Shiratori, Y. Shimazaki, C. Uematsu, M. Kamahori, T. Yokoi, K. Harada and Y. Kohara, Sci. Rep., 2019, 9, 2626 CrossRef PubMed.
- C. Liu, W. Zhou, T. Zhang, K. Jiang, H. Li and W. Dong, J. Bioinf. Comput. Biol., 2018, 16, 1850003 CrossRef CAS PubMed.
- L. Miotke, B. T. Lau, R. T. Rumma and H. P. Ji, Anal. Chem., 2014, 86, 2618–2624 CrossRef CAS PubMed.
- S. Zhou, T. Gou, J. Hu, W. Wu, X. Ding, W. Fang, Z. Hu and Y. Mu, Biosens. Bioelectron., 2019, 128, 151–158 CrossRef CAS PubMed.
- Z. Wu, Y. Bai, Z. Cheng, F. Liu, P. Wang, D. Yang, G. Li, Q. Jin, H. Mao and J. Zhao, Biosens. Bioelectron., 2017, 96, 339–344 CrossRef CAS PubMed.
- K. Perez-Toralla, I. Pereiro, S. Garrigou, F. Di Federico, C. Proudhon, F.-C. Bidard, J.-L. Viovy, V. Taly, S. J. S. Descroix and A. B. Chemical, Sens. Actuators, B, 2019, 286, 533–539 CrossRef CAS.
- Z. Hu, W. Fang, T. Gou, W. Wu, J. Hu, S. Zhou and Y. Mu, Anal. Methods, 2019, 11, 3410–3418 RSC.
- Z. Beini, C. Xuee, L. Bo and W. Weijia, IEEE Access, 2021, 9, 74446–74453 Search PubMed.
- H. Zhang, Z. Yan, X. Wang, M. Gaňová, M. Korabečná, P. Zahradník, H. Chang and P. Neuzil, Sens. Actuators, B, 2022, 358, 131527 CrossRef CAS.
- K. C. Balram, D. A. Westly, M. Davanco, K. E. Grutter, Q. Li, T. Michels, C. H. Ray, L. Yu, R. J. Kasica and C. B. Wallin, J. Res. Natl. Inst. Stand. Technol., 2016, 121, 464–476 CrossRef CAS PubMed.
- H. Zhang, J. Pekárek, J. Feng, X. Liu, H. Li, H. Zhu, V. Svatoš, I. Gablech, P. Podešva and S. Ni, J. Vac. Sci. Technol., B, 2020, 38, 063002 CrossRef CAS.
- H. Zhang, M. Ganova, Z. Yan, H. Chang and P. Neuzil, ACS Omega, 2020, 5, 30267–30273 CrossRef CAS PubMed.
- J. Hoffmann, M. Trotter, F. von Stetten, R. Zengerle and G. Roth, Lab Chip, 2012, 12, 3049–3054 RSC.
- N. T. Vo, R. C. Atwood and M. Drakopoulos, Opt. Express, 2015, 23, 32859–32868 CrossRef PubMed.
- J. H. Brito, R. Angst, K. Köser and M. Pollefeys, presented in part at the Proc. IEEE Conf. Comput. Vis. Pattern Recognit., June 2013, 2013, vol. 23–28 Search PubMed.
- M. A. Khorshidi, P. K. P. Rajeswari, C. Wählby, H. N. Joensson and H. Andersson Svahn, Lab Chip, 2014, 14, 931–937 RSC.
- M. Vaithiyanathan, N. Safa and A. T. Melvin, PLoS One, 2019, 14, e0215337 CrossRef PubMed.
- M. A. Fischler and R. C. Bolles, Commun. ACM, 1981, 24, 381–395 CrossRef.
- J. Pekárek, R. Prokop, V. Svatoš, I. Gablech, J. Hubálek and P. Neužil, Sens. Actuators, A, 2017, 265, 40–46 CrossRef.
- M. Gaňová, X. Wang, Z. Yan, H. Zhang, T. Lednický, M. Korabečná and P. Neužil, RSC Adv., 2022, 12, 2375–2382 RSC.
- I. Banerjee, S. G. Aralaguppe, N. Lapins, W. Zhang, A. Kazemzadeh, A. Sönnerborg, U. Neogi and A. Russom, Lab Chip, 2019, 19, 1657–1664 RSC.
- J. Nectoux, Mol. Diagn. Ther., 2018, 22, 139–148 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1lc01175h |
| ‡ These two authors contributed equally, and both are considered as first authors. |
| This journal is © The Royal Society of Chemistry 2022 |






