Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Out-of-plane faradaic ion concentration polarization: stable focusing of charged analytes at a three-dimensional porous electrode†
Beatrise
Berzina‡
a,
Sungu
Kim‡
ab,
Umesha
Peramune
a,
Kumar
Saurabh
b,
Baskar
Ganapathysubramanian
 b and
Robbyn K.
Anand
b and
Robbyn K.
Anand
 *a
*a
aThe Department of Chemistry, Iowa State University, 2415 Osborn Drive, 1605 Gilman Hall, Ames, Iowa 50011-1021, USA. E-mail: rkanand@iastate.edu
bThe Department of Mechanical Engineering, Iowa State University, 2043 Black Engineering, 2529 Union Drive, Ames, Iowa 50011-2030, USA
First published on 4th January 2022
Abstract
Ion concentration polarization (ICP) accomplishes preconcentration for bioanalysis by localized depletion of electrolyte ions, thereby generating a gradient in electric field strength that facilitates electrokinetic focusing of charged analytes by their electromigration against opposing fluid flow. Such ICP focusing has been shown to accomplish up to a million-fold enrichment of nucleic acids and proteins in single-stage preconcentrators. However, the rate at which the sample volume is swept is limited, requiring several hours to achieve these high enrichment factors. This limitation is caused by two factors. First, an ion depleted zone (IDZ) formed at a planar membrane or electrode may not extend across the full channel cross section under the flow rate employed for focusing, thereby allowing the analyte to “leak” past the IDZ. Second, within the IDZ, large fluid vortices lead to mixing, which decreases the efficiency of analyte enrichment and worsens with increased channel dimensions. Here, we address these challenges with faradaic ICP (fICP) at a three-dimensional (3D) electrode comprising metallic microbeads. This 3D-electrode distributes the IDZ, and therefore, the electric field gradient utilized for counter-flow focusing across the full height of the fluidic channel, and its large area, microstructured surface supports smaller vortices. An additional bed of insulating microbeads restricts flow patterns and supplies a large area for surface conduction of ions through the IDZ. Finally, the resistance of this secondary bed enhances focusing by locally strengthening sequestering forces. This easy-to-build platform lays a foundation for the integration of enrichment with user-defined packed bed and electrode materials.
Introduction
Biomarkers that serve as indicators for disease detection are often present at a low concentration (fM–pM) and therefore, require preconcentration prior to analysis. Electrokinetic methods of analyte preconcentration are advantageous for integration into lab-on-chip (LOC) devices because they provide efficient transport of charged species in small sample volumes.1 Over the past two decades, electrokinetic methods of focusing that employ ion concentration polarization (ICP) and faradaic ICP (fICP) have been developed for enrichment and separation of a wide range of disease biomarkers, including nucleic acids,2–4 proteins,5,6 enzymes,7,8 exosomes,9 and biological cells10,11 and for separations in complex biofluids.12 There have been reports of concentration enrichment ranging from 102-fold for simple devices to even 109-fold for multistage hierarchical preconcentrators that sweep a large fluid volume.2 Despite the success of these preconcentration methods, some aspects remain challenging.13 Many existing ICP-based preconcentrators operate at >100 V, which hinders integration into portable devices. Further, improvement of volumetric throughput,2,14,15 integration with downstream analysis,16–19 and the development of strategies to decrease fluidic instability are active areas of research.20,21 Fluidic instability (evidenced by size and magnitudes of vortex flow near the electrode), which is caused by steep gradients in electrolyte concentration and electric field strength and exacerbated by increased device dimensions, leads to unwanted mixing, ultimately limiting sensitivity.Both ICP and fICP accomplish localized depletion of the ions of the background electrolyte (BGE). A key feature of the ion depleted zone (IDZ) is its low ionic conductivity, which leads to a strong local enhancement of the electric field and formation of an extended electric field gradient, along which charged species can be focused based on their migration against opposing convection (Scheme 1b).22,23 Depletion of BGE ions can proceed via faradaic (charge transfer) reactions that occur at an electrode – a process called faradaic ICP (fICP) (Scheme 1a).24 fICP is analogous to ICP driven by selective charge transport at a permselective membrane with the exception that the local concentration of the BGE is modulated by charge transfer reactions. fICP has been demonstrated as an alternative to conventional ICP for separation of particles,25,26 modulation of dielectrophoretic force,11 and enrichment of charged species for analysis,24,27–30 where the latter has been carried out in paper-based analytical devices.31 In these applications, electrochemical reactions are most commonly facilitated by a bipolar electrode (BPE).32–34Scheme 1a depicts a well-characterized route to fICP that proceeds via base neutralization of buffer ions comprising the BGE in a microfluidic channel with an embedded planar electrode. Here, at the planar electrode, water is reduced to generate OH−, which goes on to generate uncharged species (tris(hydroxymethyl)aminomethane, (Tris)) by accepting a proton from the BGE cation (TrisH+). The removal of ions of the BGE results in a local decrease in ionic strength and creation of an IDZ, which can propagate several hundred microns upstream of the electrode. This cathodic reaction is coupled to an oxidation reaction at anodic driving electrodes located several millimeters away in the device reservoirs (‘+’ signs, Scheme 1a). This configuration is similar to that reported previously, for ion depletion carried out at a single permselective membrane-coated electrode in ‘half-cell’ ICP.35 A key advantage of fICP over ICP by ion permselection is that charge transfer resistance, instead of the ionic resistance of a membrane, dictates the required potential bias and is often lower, allowing a smaller power supply or batteries to be used.
Existing fICP preconcentrators have used thin film electrodes to facilitate electrochemical reactions that generate an IDZ. However, in a tall microchannel or under rapid fluid flow, the IDZ does not extend the full height of the microchannel from the planar electrode, and therefore, a fraction of the analyte escapes, carried over the IDZ by convection (Scheme 1d). This phenomenon decreases the efficiency of enrichment.27 In prior reports, this challenge has been addressed by decreasing the microchannel height and increasing the applied electric field to augment the IDZ size.24 However, these approaches sacrifice volumetric throughput and are limited by gas bubble formation, respectively. In a device employed for desalination by ICP, MacDonald and coworkers achieved throughput of up to 20 μL min−1 by using an out-of-plane device, in which a vertical nanoporous membrane was integrated into the wall of a microchannel, thereby increasing the exposed area available for ion transport.14 Based on this result, we anticipated that a 3D electrode (Scheme 1e) could enhance analyte retention in fICP.
Fluidic instability is another key limitation to increased volumetric throughput. When the channel cross section becomes large, mixing driven by fluid vortices drastically decreases the efficiency of enrichment and separation. To understand how to mitigate this detrimental process, several research groups have proposed theoretical models describing mechanisms for vortex formation. These models indicate that the dominant mechanism can vary based on the critical dimensions of the microchannel and the concentration of the BGE.36 Experimental approaches have been developed to limit vortex formation, including geometric restriction of the fluid in microslits,20 creation of an alternate current path through the IDZ by coating the channel with a highly conductive polymer,21 and addition of microposts to augment surface conduction within the IDZ.20 For these reasons, we anticipated that an additional bed of insulating microbeads, positioned within the IDZ would promote fluidic stability (Scheme 1f).
Chang and coworkers have further demonstrated that increased surface area of a permselective membrane leads to smaller vortices due to a decrease in the current density.37 Another recent approach is to microstructure the surface of the ion selective membrane.38 In 2018, de Valença et al. demonstrated that the applied potential that is required to start and sustain electroconvection is strongly affected by the geometry of a membrane, indicating that the position and size of vortices can be controlled.38 A reduction in the resistance of approximately 50% was demonstrated when using membranes with step structures (100 to 400 μm) close in size to the dimensions of the mixing layer, resulting in more confined vortices with less lateral motion in comparison to flat membranes. These smaller vortices can prevent the development of larger instabilities. This behavior can be recognized by a signature alteration to the shape of a current–voltage curve (CVC) – the mitigation of mass transfer limiting behavior.25Scheme 1c illustrates that at low voltages, current increases linearly with the applied potential bias showing ohmic behavior (i). A further increase in applied voltage leads to ion depletion at the cathodic microband, and the current reaches a limiting value that is reflected by a sharp decrease in the slope of the CVC (ii). Here, increasing voltage leads to growth of the resistive IDZ, preventing further gains in current. At high voltages, rapid vortex flow is initiated within the IDZ leading to increased slope of the CVC, called the overlimiting region (iii). Microstructuring mitigates limiting behavior by nucleating small, rapid vortices, which facilitate transport of BGE ions across the IDZ.
In this paper, we describe out-of-plane fICP, in which electrokinetic enrichment of charged analytes is driven by a 3-dimensional (3D) flow-through electrode comprising a bed of metallic beads. This approach combines the design principles from the aforementioned studies to achieve stable, high-throughput preconcentration of charged analytes. Specifically, we demonstrate that a flow-through 3D electrode, comprising a bed of Ag-coated microbeads overlying an Au microband (‘Ag/Au’, Scheme 2c), generates an IDZ, leading to an electric field gradient distributed across the entire cross section of a microchannel. In this system, IDZ formation at the 3D electrode is driven by neutralization of a buffer cation by electrochemically generated OH−. The formation of small, non-disruptive fluid vortices is supported by the microstructure of this bead bed and its large surface area, which supports decreased current density. To further restrict vortex growth, we employ a secondary bead bed comprised of polystyrene carboxylate (PSC) beads, located upstream of the 3D electrode (‘PSC/Ag/Au’, Scheme 2d). This secondary bed geometrically confines fluid laminae and enhances surface conduction of ions from the bulk solution to the electrode. We compare these device designs to one having a conventional planar Au electrode (‘Au’, Scheme 2b). We first evaluate the enrichment of a small molecule fluorophore and a dye-linked protein, at a planar Au electrode, and verify the presence of three distinct regimes in the CVC, thereby confirming the fICP mechanism. Second, the rate and morphology of IDZ growth, current transients, and the shape of the CVCs are compared for the Au, Ag/Au, and PSC/Ag/Au devices. These experiments show that the bead bed(s) facilitate formation of both an IDZ that fills the channel cross section and small fluid vortices that support overlimiting current without disruption of analyte focusing. Next, we observed that the rate of enrichment of a small molecule fluorophore is greater in both bead bed designs but more dramatically for the PSC/Ag/Au – a result, which is attributed to the higher electric field strength and fluid velocity within the resistive PSC bead bed. Finally, we support these findings with the results of numerical simulations, which show that a 3D-electrode i) generates an IDZ that extends the full depth of the channel, while a planar electrode does not, ii) better retains charged species upstream of this junction, and iii) constrains the size of fluid vortices overlying the Au microband electrode. A key point is that, based on the mechanism of enhancement and prior studies of biomolecule focusing by ICP and fICP,2–11 these observed gains are expected to be generalizable to charged biomarkers (indeed, we are currently pursuing such applications). This platform lays a foundation for further advancements because it utilizes off-the-shelf microbeads, which make its construction straightforward and lend versatility to its composition and function. These advancements are significant because they address the most pressing challenges to the application of ICP-based preconcentrators to bioanalysis.
Results and discussion
Characterization of faradaic ion concentration polarization at a planar electrode
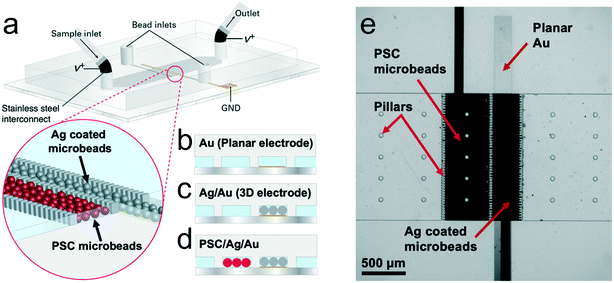
Prior to evaluating enrichment, we characterized formation of an IDZ by faradaically-driven acid–base neutralization of buffer ions at a planar electrode (Schemes 1a and 2b) in our microfluidic device. These experiments were carried out in a device comprising a microchannel (1.48 mm wide, 40.0 μm tall, 11.0 mm long) with a planar Au electrode (100 μm wide) embedded centrally. Stainless steel interconnects with 1.0 mm outer diameter fitted in the inlet and outlet were utilized to apply a voltage (V+) vs. ground at the planar electrode. In this device, the presence or absence of an IDZ was determined in three distinct BGE solutions: Tris·HClO4 (40.0 mM, pH 8.3), KNO3 (10.0 mM) and phosphate buffer (10.0 mM), each spiked with two fluorescent tracers (10.0 μM BODIPY2− and 300 nM dye-linked albumin (Texas Red BSA)). First, we evaluated the current voltage curves (CVCs) obtained when a series of voltages was applied. The details of this experiment are included in the ESI.† Fig. S1† is a plot of the CVCs obtained for these three solutions. Ohmic, limiting, and overlimiting regions, corresponding to three distinct slopes were observed only in the Tris buffer solution. This result supports the proposed mechanism because the electrolyte ions of the other two BGE solutions, K+, Na+, NO3− and HPO42−/H2PO4−, do not react with OH− generated at the planar electrode to form an uncharged product as does TrisH+. For example, upon reaction with OH−, H2PO4− becomes the more highly charged species HPO42−.We next evaluated the distribution of two anionic fluorescent tracers (BODIPY2− and dye-linked albumin (Texas Red BSA)) in these solutions under conditions appropriate for electrokinetic enrichment. First, the channel was filled with the BGE, and then a constant flow rate of 100 nL min−1 was established by a syringe pump connected to the inlet reservoir. Next, a voltage bias of V+ = 6.0 V was applied between a driving electrode in the microchannel inlet and outlet and a wire lead connected to the Au microband. Finally, a series of fluorescence micrographs was obtained to monitor the distribution of the tracers. Fig. 1a and b are fluorescence micrographs obtained following 10 min of enrichment of these tracers in the Tris buffer. These species accumulated upstream of the microband, indicating that an IDZ and electric field gradient have formed. Since each tracer is focused at an axial location at which its electrophoretic and convective velocities are equal, but opposite, BODIPY2−, which has a higher electrophoretic mobility, forms an enriched plug further upstream than does the dye-linked albumin (Fig. 1c), the mobility of which is minorly impacted by Texas Red, a zwitterion. Focusing of these species by fICP was not observed in KNO3 or phosphate buffer solutions. A key point is that BODIPY2− has an electrophoretic mobility (2.11 × 10−4 cm2 V−1 s−1)39 that is similar to that of nucleic acids (2 – 3 × 10−4 cm2 V−1 s−1, depending on ionic strength),40 and therefore, the degree to which it is enriched and the location at which it focuses approximate the performance of our device for nucleic acid preconcentration and separation from other sample components (e.g., albumin). Such a separation has been reported previously by Ouyang et al.41 who utilized pressure modulation at the device inlet to push dye-linked albumin past the locally enhanced electric field. Similarly, a balance favoring convection led to the narrow width of the enriched plug of BSA shown in Fig. 1c and the significant red fluorescence downstream of the electrode (∼50% that of upstream intensity).
We next investigated CVC characteristics obtained at a planar Au electrode as a function of the concentration of Tris buffer. Resistance dictated by ion transport to the electrode can be observed in a CVC.37,42,43Fig. 1d shows CVCs obtained in 10.0, 40.0 and 100.0 mM Tris buffer under low flow conditions (10 nL min−1) in a device with a planar Au microband. After establishing flow, a voltage bias (V+) was applied at the inlet/outlet versus ground at the Au microband and then swept (0.25 V every 0.33 s) to 15 V. Each curve exhibits clear variations in the slope that delineate the three characteristic regimes (compare to Scheme 1c). A shift in the onset of limiting and overlimiting behavior to higher voltages is observed with increasing Tris buffer concentration, which is in qualitative agreement with previously published results for the CVC characteristics observed during ICP at nanoporous membranes and nanochannels.42,43
3D structures for fICP
Next, we compared the size and morphology of an IDZ formed at this planar Au electrode to those generated at a three-dimensional electrode in the absence (Ag/Au) and presence (PSC/Ag/Au) of an additional bed of insulating beads. Previous studies have shown that microstructured ion selective features with increased conductive or geometric heterogeneities reduce the limiting-current window, and have localized space charge regions that can sustain corner vortex pairs, and moreover, show increased ion flux and an enhanced electric field gradient.37,44It was anticipated that placing conductive Ag beads on top of the planar Au electrode would create a 3D flow-through electrode, and that extension into the z-direction would distribute the electric field gradient to the full channel height. Ag-coated microspheres (10–20 μm diameter) are commercially available and the potential for water reduction (to generate OH−) is comparable on Ag and Au (Fig. S6, ESI†). Further, PSC microspheres (20 μm diameter) were expected to confine the vortices and to facilitate surface conduction of ions to the electrode. To test these hypotheses, a 300 μm-wide bed of Ag beads (aligned over the Au microband) and a 500 μm-wide bed of PSC beads were defined by rows of narrowly spaced posts (20.0 μm-wide posts with 10.0 μm gaps). The projected area and shape of the IDZ, as visualized with an anionic tracer (BODIPY2−), was then monitored over time within the three device architectures under continuous slow fluid flow.
In these experiments, first, the channel was filled with a solution of 10.0 μM BODIPY2− in 40.0 mM Tris buffer. Second, the device was conditioned under an applied voltage of V+ = 3.0 V and a flow rate of 200 nL min−1. Then, a flow rate of 10 nL min−1 was established and allowed to equilibrate for 10 min. Finally, V+ = 5.0 V was applied between the inlet/outlet and the embedded Au microband (cathode), and the resulting ion depletion was monitored. Fig. 2a–c are a series of fluorescence micrographs showing the distribution of the tracer, at t = 0, 5, 20, and 30 s following application of this voltage in the planar Au (Fig. 2a), Ag/Au (Fig. 2b), and PSC/Ag/Au (Fig. 2c) devices. Under this condition of slow or no externally applied fluid flow, the IDZ is expected to extend symmetrically from the embedded cathode. Based on qualitative evaluation of these micrographs, the planar Au device exhibits larger fluid vortices, indicated by a larger radius of curvature in the distorted IDZ boundary (Fig. 2a). In the Ag/Au device (Fig. 2b), smaller vortices are observed (many vortices with small radius of curvature) and the IDZ boundary has a more uniform shape. In the PSC/Ag/Au device (Fig. 2c), the IDZ boundary had a stable, plug-like shape, and it was maintained within the secondary bead bed over the duration of the experiment. This attribute is significant because propagation of the IDZ boundary complicates the alignment of an enriched plug of analyte to a detector or other functional device component (e.g., droplet generator).
Based on measurements of the projected area of the IDZ (Fig. 2d), the onset time for outward IDZ growth is earlier for Ag/Au (1 s) versus the planar Au system (5 s). We attribute this lag to the time required for the IDZ to extend to the full height of the channel (z-direction) before propagating upstream and downstream from the electrode. The IDZ growth over time for the PSC/Ag/Au was comparable to the Ag/Au system (compare black and red traces, Fig. 2d). An increase in the time to the initiation of ion depletion (to ∼2 s) is attributed to an increase in the electrical and fluidic resistance of the device due to the volume occupied by the PSC beads. IDZ growth was also investigated under an applied potential of 7.0 and 10.0 V (Fig. S2†) for all device designs. With increased potential, more rapid IDZ growth is observed and the difference in IDZ growth rate between device designs diminishes. Further stabilization of the IDZ can be achieved by flanking the 3D electrode from both sides with PSC bead beds (Fig. S3†). However, by adding a tertiary bead bed, the overall resistance of the device increases, requiring higher voltage and applied pressure, with minimal benefit.
To clarify the role of the metallic beads, we evaluated a control, in which PSC beads overlaid the Au planar electrode (PSC/Au device). Fig. S5a† is a series of fluorescence micrographs showing initiation of fICP under continuous slow flow (10 nL min−1). These results show smaller vortices than the Au device but a less symmetrical boundary than the Au/Ag device. Measurements of the projected area of the IDZ (Fig. S5b†) show that the onset time for outward IDZ growth is intermediate for PSC/Au (3 s) to that observed for the Ag/Au (1 s) and planar Au (5 s) systems. This result indicates that IDZ growth is expedited by both a decrease in fluid volume (PSC or Ag beads occupy space) and by increased active area of the electrode (only Ag beads).
Comparison of current transients and CVCs for the three device architectures
We next evaluated the impact of Ag and PSC microbeads on the electrochemical response obtained following application of a constant voltage (current transients) and a voltage sweep (CVCs). Fig. 3a shows current transients obtained for all three device architectures. Full experimental details are included in the ESI.† Briefly, the microchannel was filled with 40.0 mM Tris buffer and the device was conditioned under an applied voltage of V+ = 3.0 V and a flow rate of 200 nL min−1. Then, a flow rate of 10 nL min−1 was established and allowed to equilibrate for 10 min. Finally, the current was monitored following application of V+ = 7.0 V (for results at V+ = 5.0 V and 10.0 V, see Fig. S4†). The current transient obtained with the planar Au device (blue line, Fig. 3a) shows a stepwise decay, while both 3D-structured devices exhibit gradual decay (red and black lines, Fig. 3a). We attribute this stepwise decay to initial growth of the IDZ in the z-direction from the planar electrode until the IDZ contacts the channel ‘ceiling’, which leads to a sudden increase in resistance (drop in current at approx. t = 5 s). An important point is that contact of the IDZ to the ‘ceiling’ can be disrupted at higher flow rates. Fig. S5c† compares these results to current transients obtained for the PSC/Au control, for which stepwise decay occurs at t = 3 s. This result agrees with the observed onset of IDZ propagation (Fig. S5b†). A key point is that the current and rate of IDZ growth is lower for the PSC/Au control than for either of the other two cases due to the high electrical resistance and electrochemically inert nature of the PSC beads.Next, CVCs were obtained for these device architectures, and the onset potentials and slopes (conductance) of the ohmic, limiting and overlimiting regimes were compared. The same procedure for device preparation as described in the preceding paragraph was employed, and then, a voltage sweep (0.25 V steps every 0.33 s) was applied and the current monitored. In the planar Au device, three distinct regimes are observed in the CVC (blue line, Fig. 3b). In the Ag/Au device (red line, Fig. 3b), there is a direct transition from the ohmic to overlimiting regime. Such an absence of limiting behavior has been demonstrated previously in an ICP-based preconcentrator having nanoslit structures.37 A secondary bead bed (PSC/Ag/Au device) yields a comparable CVC to the Ag/Au device, but the currents are shifted lower due to increased overall resistance (black line, Fig. 3b). Finally, in the PSC/Au control, an earlier and abbreviated limiting current regime was observed when compared to the planar Au system (Fig. S5d,† blue and red trace), while the Ag/Au system shows a direct transition from the ohmic to overlimiting regime (black trace). Based on these results we conclude that the PSC beads reach a mass transport limit more rapidly because the limited interstitial fluid volume is more readily depleted of electrolyte ions. Earlier onset of overlimiting behavior (alternative routes of cation transport to the electrode) in the presence of these negatively charged beads may be attributed to enhanced ion conduction along bead surfaces, enhanced electroosmotic flow, and decreased diffusion length scales between beads. However, the direct transition from ohmic to overlimiting behavior observed at the 3D electrode (Ag/Au case) is characteristic of ICP at a microstructured junction (electrode or membrane) attributed to facile nucleation of fluid vortices.
Enrichment of charged species under constant flow
Having demonstrated the electronic and fluidic properties of these systems, we compared their ability to enrich charged analytes. In these experiments, first, the channel was filled with 0.1 μM BODIPY2− in 20.0 mM Tris buffer, under constant flow at 100 nL min−1. This buffer concentration was selected to decrease the risk of gas bubble formation at the electrode while providing sufficient “contrast” in ionic strength along the IDZ boundary to generate a steep electric field gradient.45 Then, a potential of V+ = 7.0 V was applied between both driving electrodes and the Au microband. Fig. 4a and b are fluorescence micrographs showing the enrichment of BODIPY2− in the PSC/Ag/Au device obtained at t = 5 min and 15 min after applying the voltage. Fluorescence micrographs of the enriched plug in the Au and Ag/Au devices are shown in Fig. S7.† The tracer accumulates within the secondary bead bed, leading to a local increase in fluorescence intensity. The enriched plug has a flat profile indicative of suppressed vortices.Fig. 4c is a plot of enrichment factor (EF) as a function of time observed in the three device architectures. These results indicate that higher EF (up to 115-fold within 15 min) can be obtained by employing the PSC/Ag/Au device, in comparison to Au or Ag/Au, for which EFs of 30- and 40-fold were obtained, respectively. The increased enrichment observed with the addition of a Ag bead-bed electrode to the Au microband is attributed to the full height of the electrode and its stabilization of the IDZ. This difference is expected to become more dramatic as the height of the microchannel (here, 40 μm) or the average velocity of bulk fluid flow is increased such that, at a planar electrode, contact between the IDZ and the “ceiling” becomes disrupted. Furthermore, if device channel width and flow rate are doubled (3.0 mm and 200 μL min−1 respectively), the overall enrichment rate (0.10-fold/s) is comparable to the rate observed in narrower (1.48 mm wide) device (0.11-fold/s, Fig. S8†), thus indicating the out-of-plane fICP is scalable.
The PSC/Ag/Au device yields a still greater increase in the rate of enrichment for three reasons. First, the PSC bead bed provides fluidic stabilization within the entire IDZ volume by geometric restriction of vortices and by the conduction of cations along the charged surface of the beads through the IDZ. Second, both the fluid velocity and the electric field are enhanced in the bead-occupied channel segment due to its increased fluidic and electrical resistance. Finally, dispersion is expected to be mitigated by the beads. These last two conclusions are supported by horizontally aligned normalized intensity profiles for all three device architectures (Fig. 4d). The PSC/Ag/Au device exhibited a narrower peak profile (blue line), while planar Au and Ag/Au device architectures yeilded a broader, tailing peak, approximately double the width of the enriched plug formed in the PSC/Ag/Au device.
Simulation of charged species transport during fICP at planar and 3D porous electrodes
To investigate the principles underlying the observed effect of the Ag microbeads on device performance, we simulated charged species transport, electric field distribution, and fluid flow by numerically solving the Navier–Stokes and Poisson–Nernst–Planck (NS–PNP) equations for a model of fICP in the planar Au and Ag/Au systems. The non-dimensional forms of the NS–PNP equations are as follows. | (1) |
| Poisson (P): −2Λ2∇2∅ = ρe | (2) |
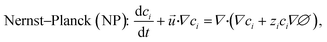 | (3) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , p, ∅, ci, zi are fluid velocity, pressure, electric potential, concentration of species i, and valence of species i, respectively. κ is the electrohydrodynamic coupling constant.46
, p, ∅, ci, zi are fluid velocity, pressure, electric potential, concentration of species i, and valence of species i, respectively. κ is the electrohydrodynamic coupling constant.46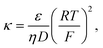 | (4) |
 | (5) |
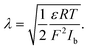 | (6) |
 is the ionic strength of the bulk electrolyte.
is the ionic strength of the bulk electrolyte.
The Navier–Stokes (NS) eqn (1) describes conservation of fluid momentum with an additional body force term from the local electric field. Eqn (2) is the Poisson equation (P) describing the relationship between charge density and the resulting electric field. The Nernst–Planck (NP) equation represents mass conservation of the ionic species driven by convection, diffusion, and electromigration. The fully coupled NS–PNP equations were numerically solved using the finite element method (FEM). The geometry and mesh are depicted in Fig. S9.†
The details of the material properties and non-dimensional parameters are provided in ESI.†
The details of the numerical methods and validation can be found in our previous study.47 In short, NS and PNP were solved in a block iterative manner, and iterated until self-consistency within each timestep was achieved (flowchart, Fig. S10†). For the NS equation, the non-linear convection term was linearized. A 2nd order accurate backward differential formula (BDF 2) was used for discretizing the time dependent terms. Following standard strategy, a variational multiscale method (VMS)48 was used for the NS equation.49 For the PNP equation, a streamline upwind Petrov–Galerkin (SUPG) style stabilizer was adopted for the convection and electric migration terms. In addition, we utilize an octree based adaptive mesh generator that enables massive parallelization and complex geometry.50,51
No-slip boundary conditions for fluid flow were applied for all solid surfaces in the domain. An electric potential was applied to the inlet (∅ = V+) and the electrodes (planar and Ag microbeads, ∅ = 0). Mass transport across the liquid-PDMS boundary was assumed to be zero. The reaction rate at the electrode surface is faster than mass transport, and therefore, the cation is completely depleted on those surfaces, (c1 = 0). This assumption simplified the simulation while allowing us to ascertain the impact of the packed bed on the system. The simulation was performed for conditions modeling a volumetric flow rate of 100 nL min−1 and applied potential of 7 V versus ground at the embedded electrode. Table S2† details the boundary conditions used.
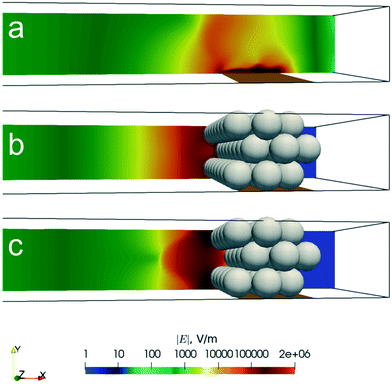
Fig. 5 illustrates the flow structures obtained in the simulation results. The complex packed bed geometry generated a locally enhanced electric field by fICP, thereby creating vortices just upstream of the electrode within the IDZ. Prior work by de Valença et al. showed that microstructuring at an ion permselective membrane led to the formation of vortices having more well-defined and uniform size, less lateral vortex movement, and a more stable mixing layer than was observed at a flat membrane.38 We anticipated that microstructuring at the electrode surface would accomplish a similar outcome.
 | ||
Fig. 5 Surface plot of the simulated magnitude of the fluid velocity (|![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) |) in the packed bed of the Ag/Au device. Fluid vortices were generated due to the high local electric field generated by fICP. |) in the packed bed of the Ag/Au device. Fluid vortices were generated due to the high local electric field generated by fICP. | ||
Fig. 6 is a side view comparison of the flow streamlines and vorticity in the presence (Ag/Au) and absence (Au device) of the packed bed. Without Ag microbeads, a single strong and large vortex was formed above the planar electrode (Fig. 6a). On the other hand, the flow structure with Ag microbeads varied across the lateral dimension, depending on the local ‘microstructure’ of the microbeads.
In Fig. 6b, the streamline and the vorticity were extracted from a vertical plane that cuts through the center of the microbeads in the first row of the bed. We see vorticity generated close to (and at) the particle surface (Fig. 6b, z = 0.25 of channel width), which is then transported in the lateral direction, as seen in Fig. 6c. In Fig. 6c, streamlines and vorticity were extracted from a vertical plane that passes between two microbeads. Here, we clearly see vortex formation, however, the size and the magnitude were significantly smaller than those observed in the absence of microbeads. Moreover, the vortices seen in Fig. 5 and 6b are small, uniform in size and paired. Therefore, the simulation results confirm that the microstructured electrode limits vortex formation, which is consistent with the reduced vortex size and uniform mixing layer thickness observed experimentally in the Ag/Au device (Fig. 2b).
Next, we investigated the impact of the Ag microbeads on the electric field. A surface plot of the magnitude of the electric field strength obtained by simulation is shown in Fig. 7. Without added Ag microbeads, a high electric field was achieved only at the bottom of the channel (Fig. 7a). In contrast, with added Ag microbeads, a strong electric field was uniformly distributed across the entire channel height. These simulation results are significant because the electric field distribution is an indicator of enrichment performance. ICP enrichment is achieved by countering convective transport by the locally enhanced electric field within the IDZ. Therefore, a higher electric field results in greater enrichment. Without microbeads, the lower electric field above the electrode could lead to poor enrichment performance and the loss of low mobility analytes. The added Ag microbeads work as an extentsion of the electrode in the z-direction, which successfully counters convection; thus, results in higher EF.
Fig. S11† shows the distribution of ionic strength in the simulated devices with the planar (Fig. S11a†) and microstructured 3D (Fig. S11b†) electrodes. The ionic strength is near to that of the bulk fluid at the upstream boundary of the simulated domain and transitions abruptly to an IDZ within approx. 100 μm of the planar electrode. However, in the device with conductive microbeads, the vortices create inroads for cation transport to the electrode, which can be observed as narrow extensions of bulk ionic strength across the IDZ. This enhanced mass transport is what facilitates direct transition from ohmic to overlimiting regimes.
In combination, the results indicate that 1) the microbeads facilitate nucleation of small, rapid vortices (microstructured 3D electrode) and restrict their growth (secondary bead bed) and 2) the microbeads support the formation of an IDZ and associated high electric field over the full channel height, which could lead to reduced loss of anions over the junction. Analytes possessing lower mobilities are anticipated to “leak” over the junction to a greater extent, and therefore, the added coverage afforded by a 3D electrode is critical to achieve efficient enrichment. We anticipate that this advantage will allow the channel cross-sectional area and the volume of sample that is swept for the analyte to be increased further.
Conclusions
In this article, we have reported several key findings. First, we demonstrated out-of-plane fICP, which employs a 3D flow-through electrode to distribute the IDZ across the entire channel cross section. This result is important because the full-height IDZ mitigates analyte loss and it allows the channel cross section to be increased further to sweep a larger sample volume. Second, we achieved a more uniform IDZ boundary by influencing vortex flow through several mechanisms: (i) the increased surface area of the electrode, (ii) formation of small, non-disruptive vortices at the microstructured surface, and a secondary bed of insulating beads to facilitate surface conduction of ions and geometric restriction of vortices. In combination, these advancements allow for more stable enrichment of charged analytes – higher EFs are achieved with the addition of a Ag bead bed, and more dramatically improved in the device having a secondary bead bed (PSC/Ag/Au). We anticipate that this approach will allow an increase in the sample volume that can be swept by faradaic electrokinetic preconcentrators to accumulate the target species. In this way, flow-through 3D structures have the potential to broaden the impact of ICP and fICP for chemical separations. A key point is that by leveraging packed beds of microbeads, this platform offers a route to incorporate a wide range of electrode and membrane materials to serve as the junction and a range of geometries, charges, and chemistries for intermolecular interactions at the upstream bed. Furthermore, the secondary bead bed provides an attractive avenue for incorporation of a biorecognition agent for in situ biosensing by colorimetric or electrochemical routes for diagnostic test development, which is the focus of ongoing studies in our laboratory.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
Funding for this research was provided by an NSF CAREER grant awarded by the Chemistry Directorate Chemical Measurement and Imaging Program under award number 1849109.References
- M. C. Breadmore, Electrophoresis, 2007, 28, 254–281 CrossRef CAS PubMed.
- W. Ouyang and J. Han, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16240–16249 CrossRef CAS PubMed.
- H. Song, Y. Wang, C. Garson and K. Pant, Anal. Methods, 2015, 7, 1273–1279 RSC.
- S. A. Hong, Y.-J. Kim, S. J. Kim and S. Yang, Biosens. Bioelectron., 2018, 107, 103–110 CrossRef CAS PubMed.
- Y. C. Wang, A. L. Stevens and J. Han, Anal. Chem., 2005, 77, 4293–4299 CrossRef CAS PubMed.
- L. F. Cheow and J. Han, Anal. Chem., 2011, 83, 7086–7093 CrossRef CAS PubMed.
- H. L. Jeong, B. D. Cosgrove, D. A. Lauffenburger and J. Han, J. Am. Chem. Soc., 2009, 131, 10340–10341 CrossRef PubMed.
- L. F. Cheow, A. Sarkar, S. Kolitz, D. Lauffenburger and J. Han, Anal. Chem., 2014, 86, 7455–7462 CrossRef CAS PubMed.
- S. Marczak, K. Richards, Z. Ramshani, E. Smith, S. Senapati, R. Hill, D. B. Go and H. C. Chang, Electrophoresis, 2018, 39, 2029–2038 CrossRef CAS PubMed.
- R. Kwak, S. J. Kim and J. Han, Anal. Chem., 2011, 83, 7348–7355 CrossRef CAS PubMed.
- R. K. Anand, E. S. Johnson and D. T. Chiu, J. Am. Chem. Soc., 2015, 137, 776–783 CrossRef CAS PubMed.
- B. Berzina and R. K. Anand, Anal. Chem., 2018, 90, 3720–3726 CrossRef CAS PubMed.
- B. Berzina and R. K. Anand, Anal. Chim. Acta, 2020, 1128, 149–173 CrossRef CAS PubMed.
- B. D. MacDonald, M. M. Gong, P. Zhang and D. Sinton, Lab Chip, 2014, 14, 681–685 RSC.
- V. A. Papadimitriou, L. I. Segerink and J. C. T. Eijkel, Anal. Chem., 2020, 92, 4866–4874 CrossRef CAS PubMed.
- S. A. Hong, Y. J. Kim, S. J. Kim and S. Yang, Biosens. Bioelectron., 2018, 107, 103–110 CrossRef CAS PubMed.
- H. Lee, J. Choi, E. Jeong, S. Baek, H. C. Kim, J. H. Chae, Y. Koh, S. W. Seo, J. S. Kim and S. J. Kim, Nano Lett., 2018, 18, 7642–7650 CrossRef CAS PubMed.
- C. Zhang, G. Sun, S. Senapati and H. C. Chang, Lab Chip, 2019, 19, 3853–3861 RSC.
- Z. Yin, Z. Ramshani, J. J. Waggoner, B. A. Pinsky, S. Senapati and H. C. Chang, Sens. Actuators, B, 2020, 310, 127854 CrossRef CAS.
- K. Kim, W. Kim, H. Lee and S. J. Kim, Nanoscale, 2017, 9, 3466–3475 RSC.
- J. Kim, I. Cho, H. Lee and S. J. Kim, Sci. Rep., 2017, 7, 1–12 CrossRef PubMed.
- T. A. Zangle, A. Mani and J. G. Santiago, Chem. Soc. Rev., 2010, 39, 1014 RSC.
- A. Mani, T. A. Zangle and J. G. Santiago, Langmuir, 2009, 25, 3898–3908 CrossRef CAS PubMed.
- R. K. Anand, E. Sheridan, K. N. Knust and R. M. Crooks, Anal. Chem., 2011, 83, 2351–2358 CrossRef CAS PubMed.
- C. D. Davies, E. Yoon and R. M. Crooks, ChemElectroChem, 2018, 5, 877–884 CrossRef CAS.
- C. D. Davies and R. M. Crooks, Chem. Sci., 2020, 11, 5547–5558 RSC.
- D. Hlushkou, R. K. Perdue, R. Dhopeshwarkar, R. M. Crooks and U. Tallarek, Lab Chip, 2009, 9, 1903–1913 RSC.
- R. K. Perdue, D. R. Laws, D. Hlushkou, U. Tallarek and R. M. Crooks, Anal. Chem., 2009, 81, 10149–10155 CrossRef CAS PubMed.
- K. N. Knust, E. Sheridan, R. K. Anand and R. M. Crooks, Lab Chip, 2012, 12, 4107 RSC.
- U. Tallarek, R. K. Perdue, R. M. Crooks, D. Hlushkou and D. R. Laws, Anal. Chem., 2009, 81, 8923–8929 CrossRef PubMed.
- X. Li, L. Luo and R. M. Crooks, Anal. Chem., 2017, 89, 4294–4300 CrossRef CAS PubMed.
- R. M. Crooks, ChemElectroChem, 2016, 3, 357–359 CrossRef CAS.
- L. Koefoed, S. U. Pedersen and K. Daasbjerg, Curr. Opin. Electrochem., 2017, 2, 13–17 CrossRef CAS.
- S. E. Fosdick, K. N. Knust, K. Scida and R. M. Crooks, Angew. Chem., Int. Ed., 2013, 52, 10438–10456 CrossRef CAS PubMed.
- R. Kwak and J. Han, J. Phys. Chem. Lett., 2018, 9, 2991–2999 CrossRef CAS PubMed.
- W. Ouyang, Z. Li, X. Ye and J. Han, Nanoscale, 2018, 10, 15187–15194 RSC.
- G. Yossifon, P. Mushenheim, Y. C. Chang and H. C. Chang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 1–13 Search PubMed.
- J. De Valença, M. Jõgi, R. M. Wagterveld, E. Karatay, J. A. Wood and R. G. H. Lammertink, Langmuir, 2018, 34, 2455–2463 CrossRef PubMed.
- V. A. Papadimitriou, L. I. Segerink and J. C. T. Eijkel, Lab Chip, 2019, 19, 3238–3248 RSC.
- E. Stellwagen and N. C. Stellwagen, Biophys. J., 2020, 118, 2783–2789 CrossRef CAS PubMed.
- W. Ouyang, Z. Li and J. Han, Anal. Chem., 2018, 90, 11366–11375 CrossRef CAS PubMed.
- I. Rubinstein and L. Shtilman, J. Chem. Soc., Faraday Trans. 2, 1979, 75, 231–246 RSC.
- G. Yossifon, P. Mushenheim, Y. C. Chang and H. C. Chang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 1–9 CrossRef PubMed.
- J. Balster, M. H. Yildirim, D. F. Stamatialis, R. Ibanez, R. G. H. Lammertink, V. Jordan and M. Wessling, J. Phys. Chem. B, 2007, 111, 2152–2165 CrossRef CAS PubMed.
- R. K. Anand, E. Sheridan, D. Hlushkou, U. Tallarek and R. M. Crooks, Lab Chip, 2011, 11, 518–527 RSC.
- C. L. Druzgalski, M. B. Andersen and A. Mani, Phys. Fluids, 2013, 25, 0804 Search PubMed.
- S. Kim, R. K. Anand and B. Ganapathysubramanian arXiv preprint, 2020, arXiv:2010.08778.
- T. J. Hughes, G. R. Feijóo, L. Mazzei and J. B. Quincy, Comput. Methods Appl. Mech. Eng., 1998, 166, 3–24 CrossRef.
- T. Tezduyar and S. Sathe, Journal of Computational and Applied Mechanics, 2003, 4, 71–88 Search PubMed.
- M. Ishii, M. Fernando, K. Saurabh, B. Khara, B. Ganapathysubramanian and H. Sundar, Int. Conf. High Perform. Comput. Netw. Storage Anal. SC, 2019, pp. 1–61 Search PubMed.
- S. Kumar, M. Ishii, M. Fernando, B. Gao, K. Tan, M.-C. Hsu, A. Krishnamurthy, H. Sundar and B. Ganapathysubramanian arXiv preprint, 2021, arXiv:2108.03757.
Footnotes |
| † Electronic supplementary information (ESI) available: Device designs and fabrication; verification of the mechanism of fICP; collection of current transients and current–voltage curves (CVCs); measurement of the onset potential of water reduction on several distinct electrode materials; electrokinetic enrichment of charged species; scalability of the device; computational method for charged species transport simulation. See DOI: 10.1039/d1lc01011e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |