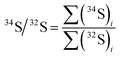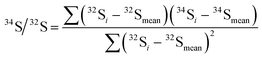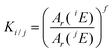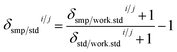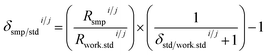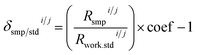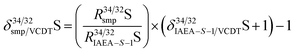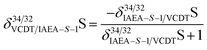Data processing made easy: standalone tool for automated calculation of isotope ratio from transient signals – IsoCor†
Received
15th June 2022
, Accepted 14th September 2022
First published on 15th September 2022
Abstract
Despite numerous advantages offered by hyphenation of chromatography and electrokinetic separation methods with multicollector (MC) ICP-MS for isotope analysis, the main limitation of such systems is the decrease in precision and increase in uncertainty due to generation of short transient signals. To minimize this limitation, most authors compare several isotope ratio calculation methods and establish a multi-step data processing routine based on the precision and accuracy of the methods. However, to the best of our knowledge, there is no universal data processing tool available that incorporates all important steps of the treatment of the transient signals. Thus, we introduce a data processing application (App) IsoCor that facilitates automatic calculation of isotope ratios from transient signals and eases selection of the most suitable method. The IsoCor App performs baseline subtraction, peak detection, mass bias correction, isotope ratio calculation and delta calculation. The feasibility and reliability of the App was proven by reproducing the results from isotope analysis of three elements (neodymium, mercury and sulfur) measured on-line via hyphenated systems. The IsoCor App provides trackability of the results to ensure quality control of the analysis.
Introduction
Hyphenation of chromatography and electrokinetic separation methods with multicollector (MC) ICP-MS has been successfully implemented in recent years for the on-line isotope analysis of archeological,1 environmental,2–4 nuclear,5,6 and biological samples.7 Performing on-line isotope analysis via hyphenated separation systems enables the investigation of isotope fractionation of a target analyte/elemental species by separating it from matrix and/or from other analytes/elemental species. Moreover, on-line separation of different elemental species of the target element makes the species-specific isotope analysis possible by eliminating the contribution of non-fractionating species without performing laborious off-line sample preparation.8,9 The depth of the information about isotope fractionation of the element is substantially increased by studying target species, which allows to address questions like provenance determination, geochronological dating, medical diagnosis and environmental pollution monitoring. The hyphenated systems introduce the possibility to analyse several species within one run, drastically decrease analysis time, increase sample throughput, and minimize “human error”.3,10
However, the main limitation of on-line isotope analysis with hyphenated systems is the decrease of the precision due to generation of short transient signals.11 There are several reasons that cause the decrease in precision: (i) transient signals occur in a certain time window of several seconds, thus the total measurement time as well as the commonly applied integration time are considerably lower compared to a continuous sample introduction of several minutes, (ii) the transient signals comprise peak shapes with substantial variations in intensity, thus the weights of points are not equal, (iii) depending on the separation technique, the injected amount of sample might be significantly lower than the amount of sample processed with off-line separation, thus the signal intensity of the respective isotopes are generally low with hyphenated systems. To minimize these limitations, along with optimization of measurement parameters, a robust data processing strategy is highly needed.
Three methods for the calculation of an isotope ratio from raw transient signals are compared in the literature to achieve the desired precision:12 point-by-point (PBP), peak area integration (PAI) and linear regression slope (LRS). The calculation formulae of the methods are given in the Materials and methods section below. During the method development of on-line isotope analysis, testing these isotope ratio calculation methods is a step generally included to establish the most robust and accurate data processing routine. Fassbender et al.9 evaluated the PAI, PBP and LRS methods for isotope analysis of sulfur species with Capillary Electrophoresis/MC-ICP-MS (CE/MC-ICP-MS). They found that the delta values obtained by the PAI method agreed best with the results from off-line separation and, thus, concluded that the PAI method is more reliable compared to the two other isotope ratio calculation methods (PBP, LRS). Horst et al.13 tested the PAI and LRS methods for the isotope analysis of volatile aliphatic compounds with Gas Chromatography/MC-ICP-MS (GC/MC-ICP-MS); they concluded that the LRS method was robust towards background noise and selected it for their further investigations. More examples of the isotope ratio calculation methods used for the on-line isotope analysis are given in Table 1.
Table 1 Isotope ratio measurement methods for transient signals from MC-ICP-MS coupled with various separation techniques. External reproducibility corresponds to standard deviation 1s
| Separation technique |
Isotope ratio calculation method |
Isotope ratio (delta) |
External reproducibility |
Ref. |
| Tested |
Selected |
| LC |
PAI, LRS, PBP |
LRS |
i
Nd/144Nd; i = {142, 143, 145, 146, 148, 150} |
<0.2‰ (2s, N = 6) |
6
|
| ITP* and CE |
PAI, LRS |
LRS |
i
Nd/144Nd; i = {142, 143, 145, 146, 148, 150} |
<0.2‰ (2s, N = 3) |
17
|
| CE |
PAI, LRS, PBP |
PAI |
34S/32S (δ34S) |
<1.3‰ (2s, N = 3) |
9
|
| GC |
PAI, LRS, PBP |
LRS |
i
Hg/198Hg; (δi/198Hg); i = {199, 200, 201, 202} |
<0.5‰ (2s, N = 25) |
15
|
| GC |
PAI, LRS |
LRS |
37Cl/35Cl (δ37Cl) |
<0.2‰ (s, N = 4-34) |
13
|
When transient signals are acquired, the systematic increase or decrease of isotope ratio might occur leading to isotope ratio drift. Krupp and Donard14 listed several reasons causing this drift: overall instrumental mass bias, change of the concentration of the analyte, change of the matrix during elution, isotopic fractionation during separation. Many of these factors are hardly to be corrected for by mathematical means. Therefore, systematic approaches are needed to identify the individual source(s) of drift or/and to eliminate the factors such that they play no role in the occurrence of the drift. A most common cause of the drift is the amplifier time constant difference between Faraday cups. Several studies15,16 calculated the constants then applied mathematical correction upon isotope ratio calculation. Examples of the approaches of compensating for the drift are discussed in the Results and discussion section.
Epov et al.18,19 created a data processing scheme for species-specific isotope analysis of mercury species with GC/MC-ICP-MS that can be adapted to other on-line isotope analysis. The scheme includes the correction for polyatomic or isobaric interferences, isotope ratio calculation, mass bias correction (also known as instrumental isotope fractionation correction) and relative isotope ratio (delta) calculation. To the best of our knowledge, there is no universal data processing tool integrating these steps into a convenient and versatile workflow. The tool used by most authors is Microsoft® Excel®, but it does not have functions to perform the steps of data processing scheme automatically, thus steps like peak detection and background correction are usually done manually. This is not only time consuming, but also causes inconsistency of data processing between samples and, consequently, worsens measurement precision. Several groups developed and shared Visual Basic code20 and Matlab script21 to facilitate the data processing routine, however, one needs to have knowledge of programming languages to benefit from these codes.
In the present paper, we introduce IsoCor, an easy-to-use standalone, free-access application (App) for automated calculation of isotope ratio from transient signals generated via MC-ICP-MS coupled on-line with separation techniques. The IsoCor App performs baseline subtraction, peak detection, mass bias correction, isotope ratio calculation and delta calculation. The interface is user friendly and allows modification of main parameters to enable a detailed investigation of the raw data. We demonstrate the feasibility and reliability of IsoCor by reprocessing the transient signals from recent publications measured by various authors.
Materials and methods
Materials: datasets
The IsoCor App was developed and tested using three datasets from published results from three different separation systems: sulfur isotopes measured with CE/MC-ICP-MS,9 mercury isotopes measured with GC/MC-ICP-MS15 and neodymium isotopes measured with Liquid Chromatography/MC-ICP-MS (LC/MC-ICP-MS).6 The values obtained with IsoCor were compared to the values from the original publication calculated with Microsoft® Excel®. We consider in this context results which agree within 1s as equal. The comparison of the performance of both tools is given in the Results and discussion section. The schematic data processing workflow of each dataset is given in the ESI† (Fig. S1). All three datasets contain three peaks in each run, where the middle peak corresponds to the sample bracketed by two standard peaks (Fig. 1) according to the sample standard bracketing (SSB) approach.
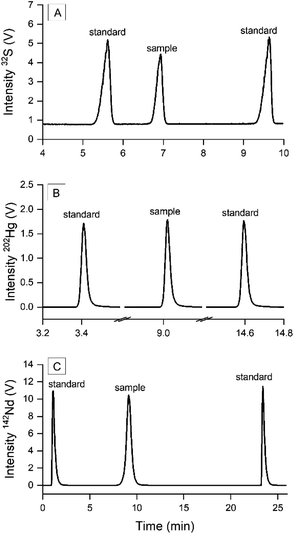 |
| | Fig. 1 Transient signals generated by hyphenated systems. (A) S measured with CE/MC-ICP-MS where standard and sample were injected in-run via a multiple-injection protocol,9 (B) Hg measured with GC/MC-ICP-MS where sample and standard were measured separately and combined as one run,15 and (C) Nd measured with LC/MC-ICP-MS where sample eluted from chromatographic column was bracketed with post-column injected standard.6 | |
Sulfur_CE/MC-ICP-MS dataset.
Species-specific isotope analysis of sulfur was done by separating sulfate SO42− from other sulfur species in river water using CE, then measuring two S isotopes (32S, 34S) on-line with MC-ICP-MS. The mass bias correction and delta δ34S calculations were done by SSB approach: the standard solution was injected into the CE before and after the sample with the novel multiple-injection protocol to obtain three peaks within one run (Fig. 1A).
Mercury_GC/MC-ICP-MS dataset.
Species-specific isotope analysis of mercury was conducted by separating Hg(II) and MeHg in the standard solutions using GC and subsequently measuring five Hg isotopes on-line with MC-ICP-MS. A T-piece connector was placed between the GC and ICP torch to continuously nebulize Tl solution for optimizing the system parameters and monitor the mass bias. The correction factor found with the 205Tl/203Tl measurement was used to correct mass bias caused by plasma instabilities during the chromatographic run. The calculation of relative isotope ratios of Hg ((δi/198Hg); i = {199, 200, 201, 202}) was done via SSB approach, where three GC runs were required to obtain the sample run bracketed with two separate standard runs. As IsoCor requires the sample and standard peaks to be uploaded within one run, thus one sample run was combined with two bracketing standard runs into a single file (Fig. 1B).
Neodymium_LC/MC-ICP-MS dataset.
Neodymium was separated from other lanthanides using LC in the simulated representative solutions of nuclear fission products. Guéguen et al.6 developed a new mass bias correction protocol called intra injection SSB, where the standard solution JNdi-1 was injected before and after the sample using a secondary chromatographic pump placed after the column to obtain all peaks within one run while maintaining the perfect matrix match between the sample flow and standard flow (Fig. 1C). The authors calculated the following ratios: iNd/144Nd; i = {142, 143, 145, 146, 148, 150}.
Methods: data processing workflow
We adapted the data processing workflow recommended by Epov et al.18,19 consisting of five steps (Fig. 2): import, processing, isotope ratio calculation, delta calculation and export. Each step is discussed in detail below. The data processing script was developed with R open-source language (https://www.r-project.org/) and implemented as a standalone App using Shiny package (https://shiny.rstudio.com/). The App is available viahttps://bam.de/IsoCor. We included detailed help on each step inside the App for a satisfying user experience. For routine use, the App can be downloaded as an R package from CRAN (https://cran.r-project.org/) and run locally. Moreover, all functions are available on GitHub (https://github.com/cran/IsoCor) to allow modification of codes and integration into alternative data processing workflows.
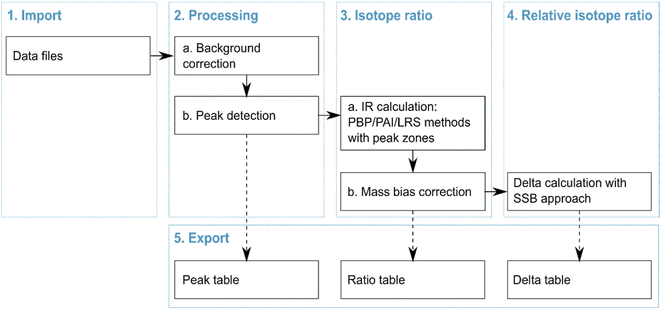 |
| | Fig. 2 Data processing workflow of IsoCor. | |
Step (1) Raw data import.
The App supports text files with different extensions (.exp, .csv, and .txt). Each data file should contain at least three columns, one for the separation run time duration and two more columns for the intensities of the two isotopes under investigation. The calculation of isotope ratio is done for one pair of isotopes at once.
Step (2) Processing.
Baseline estimation and baseline subtraction are critical steps in isotope ratio measurements. The same method should be applied to standard and sample peaks to ensure accurate calculation of results. When dealing with transient signals, several approaches are implemented to perform background correction:19 correction of the electronic noise by performing series of measurement, correction of the instrumental background by subtracting the baseline found by averaging the points before and/or after the peak, or not performing any background correction. In IsoCor we included several approaches to correct the instrumental background. The baseline estimation methods are implemented using R-package MALDIquant22 that offers four algorithms, namely “SNIP”,23 “TopHat”,24 “ConvexHull”25 and moving median. Along with baseline estimation, MALDIquant functions were used for peak maxima detection and signal smoothing.
Peak detection method was adapted from N. Dyson26 and Ricci et al.27 Firstly, the algorithm finds the peaks' maxima, then the rate of intensity change is evaluated based on the slope of a five-point linear regression. The start of the consecutive increase of the slope values is assigned as the beginning of the peak, and similarly, the end of the consecutive decrease of the slope values is the ending of the peak. The peak boundaries are defined using the intensity of the main isotope (denominator on the isotope ratio formula) and obtained retention times are applied to the secondary isotope (numerator on the isotope ratio formula) signal. The peak boundaries are visualized along with the chromatogram on the App interface and are automatically updated upon parameter modifications by the user. The user-changeable parameters include Signal-to-Noise Ratio (SNR) and smoothing via the Savitzky–Golay method.28 The SNR parameter helps to avoid the determination of small peaks of no interest, and the smoothing parameter minimizes intensity fluctuations within the peak. It is important to note that smoothing is only applied for background correction and peak detection steps, while non-smoothed intensities are used for isotope ratio calculation.
To increase the accuracy of the results, several authors12,29 suggested selecting specific zones of the peak rather than the full peak for isotope ratio calculation with PAI and PBP methods. They found that 90–95% of the peak with the PAI method resulted in better accuracy than 100% of the peak, whereas the peak zone for the PBP method was selected based on the stability of the points. Our tool allows for selecting specific zones of the peak. Specified zones contain only intensities that are selected relative to the peak maxima. For example, when the zone is set to 90%, then all intensities that are equal or higher than 10% of the peak maxima are used for the isotope ratio calculation (Fig. 3).
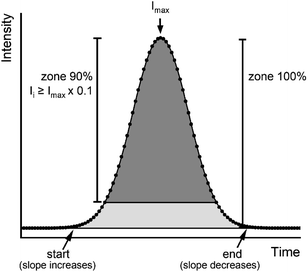 |
| | Fig. 3 Determination of the peak and the peak zones. | |
Step (3) Isotope ratio.
(a) Isotope ratio calculation.
The IsoCor App calculates isotope ratio using three methods (PAI, LRS and PBP) and generates a detailed table containing the isotope ratio values for each peak calculated for all combinations of available methods and user-selected zones. The PAI method calculates ratio of peak areas of the isotopes according to eqn (1), the LRS method finds the slope of the best linear fit between the intensities of two isotopes according to eqn (2), the PBP method finds the median of the individual isotope ratios calculated throughout the peak by arranging the values in ascending order and selecting the middle point. The App performs background correction for the PBP and PAI methods, while it uses raw intensities for the LRS method.30 The PBP method is usually carried out by averaging individual isotope ratios. This approach, however, is considered to show poor performance by several groups6,29,31 compared to the other two methods presumably because it is susceptible to higher uncertainty caused by outliers and isotope ratio drift. Considering this, it is preferable to use the median instead of the mean, which is the function implemented in IsoCor, because it provides more accurate results, and it is more robust towards outliers that usually correspond to individual isotope ratios calculated on the shoulders of the peak.| | 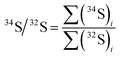 | (1) |
| | 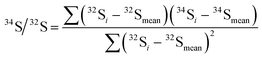 | (2) |
(b) Mass bias correction.
In IsoCor the mass bias correction of the measured isotope ratios Rmeasured is performed according to eqn (3), where K is a mass bias correction factor. The calculation of K is carried out using one of the three equations32,33 that is selectable by the user: linear equation (eqn (4)), Russel's equation (eqn (5)) or exponential equation (eqn (6)), where f is the time dependent mass bias coefficient that is found separately for each peak, and Ar(iE) and Ar(jE) are the atomic weights of two isotopes under consideration. The f values in the selected K equation should be calculated manually by the user for each peak from the isotope ratio of the continuously introduced internal standard using the values associated with the elution window of each peak. If the instrument is ensured of performing stable measurements between the peaks, then the mass bias correction step can be skipped during the data processing workflow with the K values set to 1 by default.| | | Rcorrected = Rmeasured × K | (3) |
| | | Ki/j = 1 + f(Ar(iE) − Ar(jE)) | (4) |
| | 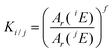 | (5) |
| | | Ki/j = ef(Ar(iE)−Ar(jE)) | (6) |
Step (4) Relative isotope ratio (delta).
Delta calculation is performed based on the SSB approach, where the standard is measured before and after the sample to find relative differences of isotope ratios of the sample Rsmpi/j and the standard Rstdi/j determined in Step (3) (eqn (7)). The examples of the implementation of the SBB approach are shown in Fig. 1. When reporting delta values, it is advised to provide the values relative to the primary isotope reference material, which is the scale defining standard and which often is represented by a certified reference material (CRM). Due to scarcity and expensive price of CRMs, most laboratories use working standards during SSB measurements. In this case, the delta value of the sample measured relative to the working standard δsmp/work.stdi/j needs to be converted to the delta value relative to the CRM δsmp/stdi/j using the delta value of the CRM measured relative to the same working standard δstd/work.stdi/j (eqn (8)).34 The delta value of the sample measured relative to the working standard δsmp/work.stdi/j can be expressed by the isotope ratio of the sample Rsmpi/j and isotope ratio of the working standard Rwork.stdi/j to obtain eqn (9). In IsoCor, we use eqn (10) for delta calculation to include the possibility to perform delta scaling by user-provided scaling coefficient coef into the App. When no scaling of delta is needed, then coef is set to 1 which simplifies the formula to (eqn (7)).| |  | (7) |
| | 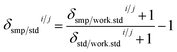 | (8) |
| | 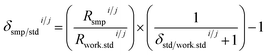 | (9) |
| | 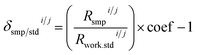 | (10) |
Step (5) Export.
As shown in Fig. 2, the IsoCor App allows for exporting three tables generated during each step of the data processing workflow. The peak table contains details of the detected peaks in each imported data file: retention time, boundaries, type (sample, standard or discard) and parameters of the mass bias correction. The ratio table consists of columns with the isotope ratios found for each peak using the three isotope ratio calculation methods (PAI, LRS and PBP) with user-selected zones, and columns containing the respective delta values. The delta table is only generated when several data files are imported into the App. In this case, IsoCor treats these files as replicate measurements and calculates mean and standard deviation (1s) of delta values found with each method with the user-selected zones. The plot of delta values on the right side of the table allows the user to have a visual comparison of the isotope ratio calculation methods allowing a quick selection of the suitable one. The tables contain all the parameters used during the data processing workflow, thus ensuring trackability and transparency of the results.
Results and discussion
Sulfur_CE/MC-ICP-MS dataset
The authors9 of the Sulfur_CE/MC-ICP-MS dataset assessed the isotope ratio calculation methods with 100% zone of the peak. They concluded that the PAI method is the most suitable one for their application. Moreover, the selection of the PAI method was reinforced by its possibility to correct systematic isotope ratio drift. Apart from the systematic drift, the isotope analysis of sulfur suffers from high background.35 Thus, the authors9 performed background correction by averaging points before and after each peak and subtracting the average baseline from the peak intensity on point-by-point basis. During our data processing with IsoCor, we found that the background correction with the “CorvexHull” method works best for the current dataset.
When conducting isotope analysis of sulfur, the delta should be reported relative to VCDT (Vienna Cañon Diablo meteorite) scale using the CRM IAEA-S-1 as recommended by IUPAC to enable comparability between the laboratories.33 Thus, the scaling coefficient coef from eqn (10) was set to 0.9997 calculated according to eqn (11) where δ34/32IAEA−S−1/VCDTS = −0.000336 The modification of eqn (9) to eqn (11) can be explained by the scaling of δ34/32VCDT/IAEA−S−1S to δ34/32IAEA−S−1/VCDTS using eqn (12).
| | 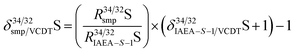 | (11) |
| | 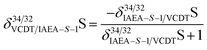 | (12) |
The values calculated with IsoCor agree with the values published by the authors9 within 1s range (Fig. 4). Improvement of the precision of the delta values calculated with IsoCor can be explained by the selection of a more appropriate background correction method.
 |
| | Fig. 4 Comparison of the δ34/32S values between the original publication9 and IsoCor for different River water samples measured with CE/MC-ICP-MS. The isotope ratio calculation method was PAI with 100% peak. Error bars represent external precision as s for N = 3. Explanation of the sample names can be found in the original publication. | |
Mercury_GC/MC-ICP-MS dataset
During the data processing step of the species-specific isotope analysis of Hg with GC/MC-ICP-MS, the authors15 evaluated two parameters (calculation method and number of acquisition points) to find the most suitable method for the isotope ratio calculation. To reproduce results from the original publication, we calculated the delta values with three methods using 45–100% zones of the Hg(II) peak. The mass bias correction of the peaks was achieved via Russel's equation (eqn (5)): first, we calculated f from isotope ratios of 205Tl/203Tl, which was continuously added as internal standard, for each peak using Microsoft® Excel®; then, we pasted the f values to the IsoCor App. As delta was measured relative to NIST RM 8610, the coef in eqn (10) was set to 1 without performing any delta scaling. The results of the two sources agree within 1s range for δ199/198Hg values (Fig. 5). The delta values of other Hg isotopes also agree within 1s range (Fig. S2†). Slight difference of the delta values calculated with IsoCor can be explained by the different criteria used for selection of the peak boundaries.
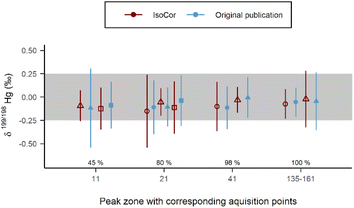 |
| | Fig. 5 Comparison of the δ199/198Hg values between the original publication15 and IsoCor from isotope analysis with GC/MC-ICP-MS. Shape of the point indicates isotope ratio calculation method: circle (○) is LRS, triangle (△) is PAI, square (□) is PBP. Error bars represent external precision as s for N = 8. Optimal external precision as s of ±0.25‰ is highlighted. The percentage values above the x-axis represent the taken peak zones. | |
Neodymium_LC/MC-ICP-MS dataset
The authors6 of the Neodymium_LC/MC-ICP-MS dataset calculated six isotope ratios of Nd using LRS, PBP and PAI methods. They used the raw intensities for all three calculation methods, as the influence of the background correction was found to be negligible. According to the conclusion from the original publication, the LRS method performed better with full 100% zone of the peak, whereas PAI and PBP worked best with 95% zone of the peak and the LSR method was chosen to be suitable for the application. To evaluate the performance of IsoCor we uploaded .csv files of six repetitive runs from the LC/MC-ICP-MS measurement. The raw isotope ratios were calculated with LRS, PAI and PBP methods with 100% and 95% zones similar to the authors' selection. Then the ratio table generated by the App was exported for further processing.
Unlike previous two datasets where the SSB method was used to calculate delta, this dataset used the SSB method for mass bias correction of the sample to calculate conventional isotope ratio of Nd. This application of SSB method is not included in the IsoCor App, thus the mass bias correction step was performed outside the App using R: the f values for Russel's equation were calculated from the isotope ratios of the bracketing standards using the results measured with TIMS37 as a reference; then, K found according to the eqn (5) was multiplied to the raw isotope ratios of the sample. The comparison between the results from the original publication and the results calculated with IsoCor are shown in Fig. 6 for six isotope ratios of Nd. The agreement between the values within 1s range shows that IsoCor yields similar results to previously published calculations. The high discrepancy of 143Nd/144Nd and 150Nd/144Nd values calculated with the PBP method can be explained by different approaches used: IsoCor selects the median of the PBP values, whereas in the original publication the mean of the PBP values was calculated. The mean typically is much more affected by extreme outliers as might occur at the edges of the peak compared to the median.
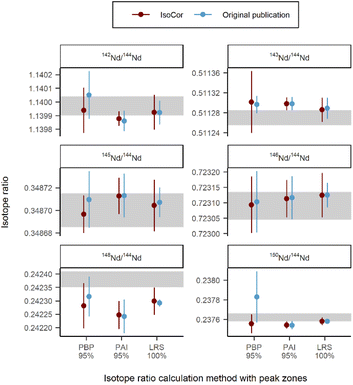 |
| | Fig. 6 Comparison of the isotope ratio results between the original publication6 and IsoCor for different Nd isotopes determined via LC/MC-ICP-MS. The off-line results measured via MC-ICP-MS with continuous sample introduction are highlighted in grey. Error bars represent external precision as s for N = 6. | |
Comparison of datasets
When developing (species-specific) on-line isotope analysis methods with MC-ICP-MS coupled on-line with separation techniques, two main issues arise: optimization of the separation parameters to ensure compatibility with MC-ICP-MS and optimization of the isotope ratio calculation method to achieve the desired accuracy with transient signals. With IsoCor, the resolution of the latter issue is facilitated. The characteristic of the elution peaks (height, width, number of acquisition points, shape) may vary depending on characteristics of the separation system (Table 2), the amount of the isotopes in the sample, and the abundances of the measured isotopes. As shown in Fig. 1, the peaks generated with GC are the narrowest compared to LC and CE peaks. Usually, the GC/MC-ICP-MS parameters are specifically optimized to increase the peak width to obtain more acquisition points per peak. However, the authors of the Mercury_GC/MC-ICP-MS dataset selected a short integration time of 0.131s to record more acquisition points (≈140) per peak for narrow GC peaks to achieve the desired external precision. With LC, the duration of the peak elution can be optimized to exceed one minute, thus a higher integration time than GC can be selected.
Table 2 Comparison of peak characteristics of the datasets
| Dataset |
Number of points for 100% peak zone |
Average elution/migration duration of the peak, s |
Intensity at peak maxima of the most abundant isotope, V |
Concentration of the element in the sample |
Volume of injection, μL |
| Sulfur_CE/MC-ICP-MS |
231 ± 23 |
≈30 |
≈4.5 (32S) |
14 mg L−1 |
0.35 |
| Mercury_GC/MC-ICP-MS |
141 ± 4 |
≈20 |
≈1.8 (202Hg) |
250 ng g−1 |
2 |
| Neodymium_LC/MC-ICP-MS |
150 ± 69 |
≈100 |
≈12 (142Nd) |
500 ng g−1 |
1 |
The LRS method was the method of choice for the authors of Neodymium_LC/MC-ICP-MS and Mercury_GC/MC-ICP-MS datasets, whereas PAI was found to be suitable for the processing of Sulfur_CE/MC-ICP-MS dataset. The LRS method is favoured by researchers based on several advantages:17 ease of calculation due to the omission of background correction step, natural weighing of the points when constructing the regression line, the possibility to apply the SSB method with different concentrations of sample and bracketing standard. However, one should note that the LRS method assumes a stable baseline during the elution of the peak, and it is not robust against prominent systematic drift. The PBP method is compromised by isotope ratio drift, which might not be fully compensated for when using the median. The PAI method is not biased by the systematic drift when using 100% zone of the peak. However, the height of the standard and sample peaks should be the same to ensure the same background correction when calculating delta with isotope ratios from the PAI method.
The authors of the datasets applied several approaches to correct for an isotope ratio drift. When measuring sulfur with CE/MC-ICP-MS, the authors reported presence of the drift that might be caused by different amplifier time constants of the Faraday cup detectors or slight fractionation within the CE capillary. The automatic time-lag correction of the Neptune Plus instrument did not eliminate the drift, thus the authors selected PAI with 100% zone to correct for the drift. The authors of the Mercury_GC/MC-ICP-MS dataset assumed that the isotope ratio drift was caused by the different amplifier time constants of the individual collectors and calculated the constants for each cup by minimizing the squared sum of residuals of the linear regression applied to calculate the isotope ratio. The drift correction improved the internal precision of the delta values calculated with LRS and PBP methods, but external precision of the delta values remained similar to the ones calculated with the uncorrected signal. The authors of the Neodymium_LC/MC-ICP-MS dataset studied the cause of the isotope ratio drift and reported that both mass dependent LC column fractionation and different amplifier time constants were causing this phenomenon. They applied PAI and LRS methods along with instrumental mass bias correction to compensate for the drift. Current version of the IsoCor App does not include a step for isotope ratio drift correction. Once relations of isotope ratio drifts and detector time lag have been established and the correction approaches for detector time lag have been agreed upon it can be implemented in the software package.
Conclusion
IsoCor fills the gap in software solutions to automate common steps in the calculation of isotope ratio from transient signals. The App has a user-friendly interface that does not require knowledge of any programming language and the App is open access. The common steps include baseline correction, peak detection, isotope ratio calculation, mass bias correction and delta calculation. The performance evaluation of IsoCor using three datasets showed that our App is reliable and applicable for the isotope ratio calculation from transient signals of diverse hyphenated MC-ICP-MS setups. The App generates detailed tables to ease investigation of the data and improves reproducibility and trackability of the results, which might be helpful during quality assurance and validation of the methods. Application of identical parameters for all runs minimizes “human error”. Moreover, the App can be used during quantification analysis using isotope dilution method performed with on-line hyphenated separation systems.
Isotope analysis with on-line hyphenated separation systems is a relatively new area of research, thus most papers published on this topic demonstrate the application of the methods using standard solutions. However, we expect that our modular open-source tool IsoCor can be easily extended to include further processing steps (multiple linear regression,38 detector time lag correction,16etc.) and handle also more complex samples. Thus, becoming a useful tool in standardization and wider application of (MC-) ICP-MS.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank S. Fassbender, S. Queipo-Abad and H. Isnard for their kindness to share raw transient signal data files with us. We thank the German Research Foundation (DFG) for funding to DT (ME 3685/5-1, project number: 440953647).
References
- P. Alvarez Penanes, M. Moldovan, A. Mederos, P. Martín-Ramos and J. I. García Alonso, J. Anal. At. Spectrom., 2021, 36, 1694–1703 RSC.
- A. Rua-Ibarz, E. Bolea-Fernandez, A. Maage, S. Frantzen, M. Sanden and F. Vanhaecke, Environ. Sci. Technol., 2019, 53, 1776–1785 CrossRef CAS.
- M. Martinez, J. I. Garcia-Alonso, C. Parat, J. R. Encinar and I. L. Hecho, Anal. Chem., 2019, 91, 10088–10094 CrossRef CAS PubMed.
- W. Said-Ahmad, K. Wong, M. McNall, L. Shawar, T. Jacksier, C. Turich, A. Stankiewicz and A. Amrani, Anal. Chem., 2017, 89, 3199–3207 CrossRef CAS PubMed.
- E. Dupuis, H. Isnard, C. Evette and F. Chartier, Talanta, 2020, 219, 121345 CrossRef CAS PubMed.
- F. Guéguen, H. Isnard, A. Nonell, L. Vio, T. Vercouter and F. Chartier, J. Anal. At. Spectrom., 2015, 30, 443–452 RSC.
- L. Rodas Sanchez, P. Rodriguez Gonzalez and J. I. Garcia Alonso, Anal. Chim. Acta, 2021, 1170, 338606 CrossRef CAS PubMed.
- J. Karasiński, C. T. Nguyen-Marcińczyk, M. Wojciechowski, E. Bulska and L. Halicz, J. Anal. At. Spectrom., 2020, 35, 560–566 RSC.
- S. Fassbender, K. Rodiouchkina, F. Vanhaecke and B. Meermann, Anal. Bioanal. Chem., 2020, 412, 5637–5646 CrossRef CAS.
- A. Gourgiotis, G. Manhes, B. Martelat and H. Isnard, J. Anal. At. Spectrom., 2017, 32, 1428–1434 RSC.
- I. Gunther-Leopold, B. Wernli, Z. Kopajtic and D. Gunther, Anal. Bioanal. Chem., 2004, 378, 241–249 CrossRef.
- P. Rodriguez-Gonzalez, V. N. Epov, C. Pecheyran, D. Amouroux and O. F. Donard, Mass Spectrom. Rev., 2012, 31, 504–521 CrossRef CAS PubMed.
- A. Horst, J. Renpenning, H. H. Richnow and M. Gehre, Anal. Chem., 2017, 89, 9131–9138 CrossRef CAS PubMed.
- E. M. Krupp and O. F. X. Donard, Int. J. Mass Spectrom., 2005, 242, 233–242 CrossRef CAS.
- S. Queipo-Abad, P. Rodriguez-Gonzalez and J. I. G. Alonso, J. Anal. At. Spectrom., 2019, 34, 753–763 RSC.
- A. Gourgiotis, S. Bérail, P. Louvat, H. Isnard, J. Moureau, A. Nonell, G. Manhès, J.-L. Birck, J. Gaillardet, C. Pécheyran, F. Chartier and O. F. X. Donard, J. Anal. At. Spectrom., 2014, 29, 1607–1617 RSC.
- B. Martelat, L. Vio, H. Isnard, J. Simonnet, T. Cornet, A. Nonell and F. Chartier, J. Anal. At. Spectrom., 2017, 32, 2271–2280 RSC.
- V. N. Epov, P. Rodriguez-Gonzalez, J. E. Sonke, E. Tessier, D. Amouroux, L. M. Bourgoin and O. F. Donard, Anal. Chem., 2008, 80, 3530–3538 CrossRef CAS PubMed.
-
V. N. Epov, S. Berail, C. Pécheyran, D. Amouroux and O. F. X. Donard, in Isotopic Analysis: Fundamentals and Applications Using ICP-MS, ed. F. Vanhaecke and P. Degryse, Wiley-VCH, Weinheim, 2012, ch. 17, pp. 495–518 Search PubMed.
- A. Amrani, A. L. Sessions and J. F. Adkins, Anal. Chem., 2009, 81, 9027–9034 CrossRef CAS PubMed.
- A. Horst, H. Holmstrand, P. Andersson, A. Andersson, D. Carrizo, B. F. Thornton and O. Gustafsson, Rapid Commun. Mass Spectrom., 2011, 25, 2425–2432 CrossRef CAS PubMed.
- S. Gibb and K. Strimmer, Bioinformatics, 2012, 28, 2270–2271 CrossRef CAS.
- C. G. Ryan, E. Clayton, W. L. Griffin, S. H. Sie and D. R. Cousens, Nucl. Instrum. Meth. B, 1988, 34, 396–402 CrossRef.
- M. van Herk, Pattern Recognit. Lett., 1992, 13, 517–521 CrossRef.
- A. M. Andrew, Inform. Process. Lett., 1979, 9, 216–219 CrossRef.
-
N. Dyson, Chromatographic Integration Methods, Thomas Graham House, Cambridge, 1990 Search PubMed.
- M. P. Ricci, D. A. Merritt, K. H. Freeman and J. M. Hayes, Org. Geochem., 1994, 21, 561–571 CrossRef CAS PubMed.
- A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS.
- V. N. Epov, S. Berail, M. Jimenez-Moreno, V. Perrot, C. Pecheyran, D. Amouroux and O. F. Donard, Anal. Chem., 2010, 82, 5652–5662 CrossRef CAS.
- J. Fietzke, V. Liebetrau, D. Günther, K. Gürs, K. Hametner, K. Zumholz, T. H. Hansteen and A. Eisenhauer, J. Anal. At. Spectrom., 2008, 23, 955–961 RSC.
- F. Guéguen, A. Nonell, H. Isnard, L. Vio and F. Chartier, Talanta, 2017, 162, 278–284 CrossRef PubMed.
-
J. Irrgeher, J. Vogl, J. Santner and T. Prohaska, in Sector Field Mass Spectrometry for Elemental and Isotopic Analysis, ed. T. Prohaska and J. Irrgeher, The Royal Society of Chemistry, Cambridge, 2015, ch. 8, pp. 126–151 Search PubMed.
-
J. Meija, L. Yang, Z. Mester and R. E. Sturgeon, in Isotopic Analysis: Fundamentals and Applications Using ICP-MS, ed. F. Vanhaecke and P. Degryse, Wiley-VCH, Weinheim, 2012, ch. 5, pp. 113–137 Search PubMed.
- J. Vogl, O. Rienitz, A. Pramann and L. Flierl, Geostand. Geoanal. Res., 2022 DOI:10.1111/ggr.12450.
- P. Phukphatthanachai, U. Panne, N. Jakubowski and J. Vogl, J. Anal. At. Spectrom., 2018, 33, 90–101 RSC.
- T. B. Coplen and H. R. Krouse, Nature, 1998, 392, 32 CrossRef CAS.
- S. Wakaki and T. Tanaka, Int. J. Mass Spectrom., 2012, 323–324, 45–54 CrossRef CAS.
- J. Ángel Rodríguez-Castrillón, S. García-Ruiz, M. Moldovan and J. Ignacio García Alonso, J. Anal. At. Spectrom., 2012, 27, 611–618 RSC.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Jochen
Vogl
b,
Jochen
Vogl
 a and
Björn
Meermann
a and
Björn
Meermann
 *a
*a