Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Local excitation and valley polarization in graphene with multi-harmonic pulses
Ulf
Saalmann
and
Jan Michael
Rost

Max Planck Institute for the Physics of Complex Systems, Nöthnitzer Str. 38, 01187 Dresden, Germany. E-mail: us@pks.mpg.de; rost@pks.mpg.de
First published on 16th June 2022
Abstract
We elucidate the mechanism of strong laser pulse excitation in pristine graphene with multi-harmonic pulses, linearly polarized parallel to the line connecting the two different Dirac points in the Brillouin zone and with a maximal vector potential given by the distance of those points. The latter two conditions have emerged from our previous work [Kelardeh et al., Phys. Rev. Res., 2022, 4, L022014] as favorable for large valley polarization. We introduce a novel compacted representation for excitation, locally resolved in the initial conditions for the crystal momenta. These maps are our main tool to gain insight into the excitation dynamics. They also help with understanding the effect of dephasing. We work out why a long wavelength and a moderate number of overtones in the harmonic pulse generate the largest valley polarizations.
1 Introduction
Illuminating condensed-matter targets with intense short pulses affects non-linear photo-absorption which depends crucially on the band structure of the system and is commonly probed by high-harmonic generation.1,2 Pioneering work has shown that the basics of the ensuing electron dynamics follows a similar two-step process in reciprocal space,3,4 as is familiar from atoms and molecules in real space. Firstly, a valence electron tunnels at the gap to the energetically closest conduction band appearing there with wave vector k. Subsequently, the wave vector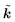 moves on the conduction band driven by the lasers’s vector potential A according to
moves on the conduction band driven by the lasers’s vector potential A according to 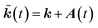 . Owing to the gap, electronic transitions back to the valence band are exponentially suppressed.
. Owing to the gap, electronic transitions back to the valence band are exponentially suppressed.
This is not the case for gapless 2D systems such as graphene, rendering the ensuing (coherent) excited electron dynamics potentially more complicated. Moreover, dephasing may alter the final excitation for laser pulses longer than the coherence time. Physical properties of interest are the excitation probability and valley polarization.5–8 The latter quantifies the difference of excitation originating from initial wave-vectors in the first Brillouin zone (BZ) belonging to the domains of the two Dirac points K and K′ of the vanishing gap. These two domains of triangular shape form a unit cell of the BZ, well adapted to describe valley polarization, see Fig. 1. Valley polarization (VP), detectable via even harmonics,6 has generated considerable interest, since it promises a means of storing and manipulating quantum information by phase changes only, although this is still quite a distant goal.8
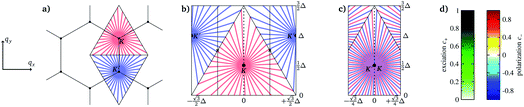 | ||
| Fig. 1 Sketch for the compact representation of the triangular q-domains around K and K′, which we will use below. We fold the Voronoi triangles into a rectangle (a → b). Then the two outer rectangles, confined by the dotted lines, are overlaid with the inner ones (b → c) by a π-rotation around the center between K and K′, marked with crosses. Since the dynamics are symmetric with respect to the dashed line, we use the left part for presenting the local excitation c+(q) and the right part for the local polarization c−(q), respectively. The probabilities c± are defined below in eqn (5), their corresponding color scales are given in the right panel of d. The momenta are given in terms of Δ = |K − K′|, the distance between the K-points. | ||
In recent work,9 we have shown that laser fields of sufficient strength to affect excitation, can be chosen such that transitions between bands occur in graphene essentially only close to the Dirac points. Hence, band transitions happen at instants of time when the intense pulse driven electron wave vector ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) passes by K or K′ leading to a sequence of (coherent) electron amplitudes in the conduction band.
(t) passes by K or K′ leading to a sequence of (coherent) electron amplitudes in the conduction band.
As an immediate consequence and in contrast to common belief, linearly polarized pulses can generate substantial valley polarization for a gapless system9 under two conditions: (i) the linear polarization is parallel to the difference vector Δ = K − K′ of the two Dirac points and the vector potential A0 is of the order of the distance 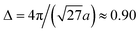 a.u. between the two Dirac points, where a = 1.43 Å is the nearest-neighbor C–C spacing in graphene. (ii) The pulse couples differently to electrons at K and K′. This requires an asymmetry† in the driving pulse which is, from a theoretical point of view, most simply achieved with a half cycle pulse.9 A sufficiently short pulse also ensures that dephasing does not play a role. Experimentally, such pulses can be generated thanks to recent experimental advances,10,11 requiring, however, special equipment. With one notable exception,12 to the best of our knowledge pristine (gapless) graphene exposed to light polarized in the graphene plane has only been investigated with linear polarization perpendicular13,14 to Δ or with ultrashort circular pulses, where the vector potential’s component parallel to Δ was symmetric,14,15 with |max{AΔ(t)}| = |min{AΔ(t)}|. These kind of pulses cannot generate VP.
a.u. between the two Dirac points, where a = 1.43 Å is the nearest-neighbor C–C spacing in graphene. (ii) The pulse couples differently to electrons at K and K′. This requires an asymmetry† in the driving pulse which is, from a theoretical point of view, most simply achieved with a half cycle pulse.9 A sufficiently short pulse also ensures that dephasing does not play a role. Experimentally, such pulses can be generated thanks to recent experimental advances,10,11 requiring, however, special equipment. With one notable exception,12 to the best of our knowledge pristine (gapless) graphene exposed to light polarized in the graphene plane has only been investigated with linear polarization perpendicular13,14 to Δ or with ultrashort circular pulses, where the vector potential’s component parallel to Δ was symmetric,14,15 with |max{AΔ(t)}| = |min{AΔ(t)}|. These kind of pulses cannot generate VP.
In the following, we investigate the interplay of coherent dynamics and dephasing in graphene as a gapless system with a multi-harmonic pulse whose characteristics in terms of pulse shape, pulse length and wavelength can be systematically changed, while maintaining a basic asymmetry of the pulses to enable valley polarization. The main quantities which will provide detailed insight are local probabilities, resolved w. r. t. the initial conditions in the Brillouin zone. We will analyze excitation and valley polarization. To this end we calculate the time-dependent density matrix in a two-band approximation with a phenomenological dephasing rate γ and we introduce a compact graphical representation for the local probabilities. If the laser pulses are intense as in our case, the two-band approximation is confirmed to provide an excellent description.14 The model is briefly described in Section 2, where we also explain the multi-harmonic pulse and illustrate with an example, the basic light-driven electronic excitation dynamics.
Section 3 presents the results for different numbers of overtones in the pulses and uncovers how excitation and valley polarization depend on the parameters of the pulse, elucidating how intense pulses steer electrons in graphene. Section 4 uses excitation distributions in connection with the compacted local probabilities to work out the differences between coherent and dephased dynamics and to identify those initial conditions in the unit cell which mainly contribute to excitation and/or VP. The paper ends with a short summary in Section 5. We use atomic units, unless stated otherwise.
2 Prerequisites
2.1 Graphene dynamics including dephasing
The time-dependent Hamilton matrix for the well known two-band approximation for graphene reads in reciprocal space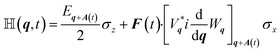 | (1) |
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) in appendix A.
in appendix A.
Note that both, the vector potential A(t) and the electric field 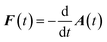 , affect the time-dependent Hamilton matrix
, affect the time-dependent Hamilton matrix ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) (q,t) in eqn (1) and influence the time evolution of the density matrix through
(q,t) in eqn (1) and influence the time evolution of the density matrix through
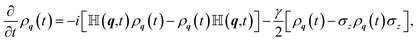 | (2) |
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) , and σx,z in eqn (2) are matrix–matrix multiplications.
, and σx,z in eqn (2) are matrix–matrix multiplications.
2.2 Compact visualization of differential excitation and valley polarization
Excitation in the triangular q-domains ∇K and ∇K′ around K and K′ of the initial conditions, representing together a unit cell of the Brillouin zone (see Fig. 1a), are defined as averaged local excitations c(q) in the respective domains of area ∇ in q-space,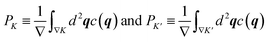 | (3) |
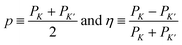 | (4) |
We obtain c(q) by numerically solving eqn (2) for a dense set of initial conditions q, sampling each of the two triangular domains with 512 × 222 = 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 initial conditions. Therefore we can define excitation p and valley polarization η locally in the initial conditions q with a resolution inversely proportional to the sampling. A natural graphical representation consists of color maps (scales are given in Fig. 1d) filling the area of the two triangles in Fig. 1a. Due to the underlying hexagonal symmetry, we can fold the triangles into a rectangle, cf. the transition from Fig. 1a and b.9
664 initial conditions. Therefore we can define excitation p and valley polarization η locally in the initial conditions q with a resolution inversely proportional to the sampling. A natural graphical representation consists of color maps (scales are given in Fig. 1d) filling the area of the two triangles in Fig. 1a. Due to the underlying hexagonal symmetry, we can fold the triangles into a rectangle, cf. the transition from Fig. 1a and b.9
Since in the end, p and η emerge from sums and differences over local conduction-band occupations c(q), one can perform part of this operation graphically by overlaying equivalent areas in the K and K′ triangles to arrive at Fig. 1c, which produces an even more compact representation.‡ This second step consists essentially of a π-rotation around the center of the line segment K–K′, which superimposes each point in ∇K with one point in ∇K′: q → q′ = f(q). By means of this mapping f we can define the local conduction-band occupations for p and η, respectively,
c±(q)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) c(q) ± c(f(q)) c(q) ± c(f(q)) | (5) |
They enable a detailed analysis, either in contour plots (Fig. 5, 7, 9) or distribution functions (Fig. 8). Of course, p and η, defined traditionally in eqn (4), follow equivalently from their local contributions eqn (5) as 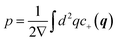 and
and 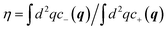 . For convenience, below we will use the terms “local excitation” and “local polarization” for c+ and c−, respectively.
. For convenience, below we will use the terms “local excitation” and “local polarization” for c+ and c−, respectively.
2.3 Asymmetric pulse shapes from multi-harmonic pulses
Large ionization probability all the way to damaging the sample is easy to achieve by increasing the field strength, in close analogy to atoms or molecules, where damaging corresponds to depletion of the ionized electron orbital. This, however, implies that excitation also occurs further away from the Dirac points at finite band gaps, and eventually, for large enough field strength throughout the unit cell with the consequence of a vanishing VP.The generation of significant VP hinges upon preserving the vicinity of the Dirac points as they are dominantly responsible for the excitation. This provides the means for selective excitation of the two valley domains upon breaking the equivalence in the excitation via the two Dirac points through suitable pulse forms. These requirements select combinations of appropriate field strength, vector potential and frequencies of the light pulse. An obvious choice fulfilling these requirements is a pulse close to a half-cycle, of suitable strength and linearly polarized along Δ, as demonstrated before.9 To make the interplay of laser parameters for excitation and VP more apparent and also, to assess the effect of dephasing, we will use multi-harmonic pulses. Asymmetric by construction, they look like pulse trains and provide a means to study the interplay of coherent multi-excitation electron dynamics and decoherence. We define these pulse trains as superpositions of harmonic overtones with an envelope determining the overall pulse length T,
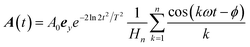 | (6a) |
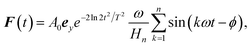 | (6b) |
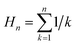 for normalization, i.e. A(0) = A0 for ϕ = 0. The relevant parameters in the pulse eqn (6) are the fundamental frequency ω (defined by the wavelength λ), the amplitude A0, the (full-width-at-half-maximum) pulse duration T, the number of harmonics n and the harmonic phase ϕ.
for normalization, i.e. A(0) = A0 for ϕ = 0. The relevant parameters in the pulse eqn (6) are the fundamental frequency ω (defined by the wavelength λ), the amplitude A0, the (full-width-at-half-maximum) pulse duration T, the number of harmonics n and the harmonic phase ϕ.
For n > 1 and ϕ = 0 the periodic part in eqn (6a), i.e. the term given by the sum 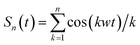 , is highly asymmetric. The contrast between maximum and minimum within one period Tω = 2π/ω is given by Cn = −Sn(tmax)/Sn(tmin) with tmax = Tω. For odd n, tmin = Tω/2, for even n there is no explicit analytical expression of tmin. Hence, for odd n
, is highly asymmetric. The contrast between maximum and minimum within one period Tω = 2π/ω is given by Cn = −Sn(tmax)/Sn(tmin) with tmax = Tω. For odd n, tmin = Tω/2, for even n there is no explicit analytical expression of tmin. Hence, for odd n
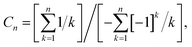 | (7) |
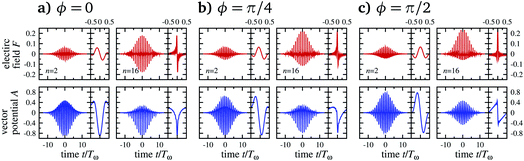 | ||
| Fig. 2 Field strength (upper row) and vector potential (lower) for multi-harmonic pulses eqn (6) as a function of time scaled by the fundamental period Tω of the harmonics. We show pulses for three harmonic phases ϕ and two different sizes n = 2 and n = 16. The right panels show the respective central periods. | ||
2.4 A paradigmatic example of excitation by a multi-harmonic pulse
Before we discuss excitation and VP resulting from different multi-harmonic pulses, we briefly illustrate with Fig. 3 how the strong field excitation mechanism proceeds through the Dirac points with the specific harmonic pulse shown in Fig. 3c. The time-dependent crystal momentum![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) = q + A(t), with the y-component ey·
(t) = q + A(t), with the y-component ey·![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) shown in Fig. 3b, is mapped into the unit cell in Fig. 3a with the green line and the initial condition q as a white-filled circle. Maximal and minimal excursion occur close to the maximum of the envelope as marked with arrows. During its evolution,
(t) shown in Fig. 3b, is mapped into the unit cell in Fig. 3a with the green line and the initial condition q as a white-filled circle. Maximal and minimal excursion occur close to the maximum of the envelope as marked with arrows. During its evolution, ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) oscillates back and forth on the green line with the amplitude shown in Fig. 3b. Once this amplitude is large enough,
(t) oscillates back and forth on the green line with the amplitude shown in Fig. 3b. Once this amplitude is large enough, ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) passes repeatedly by the Dirac point K′ (cross in the lower triangle and dashed line in Fig. 3b) as indicated by thin black lines in Fig. 3b–d. At these times, a sequence of transitions occurs between the valence and the conduction band as stated before and is clearly visible in Fig. 3d. Whether they lead to net excitation or de-excitation at a specific encounter of K′ depends on the relative phases of the electron excitation amplitudes.
(t) passes repeatedly by the Dirac point K′ (cross in the lower triangle and dashed line in Fig. 3b) as indicated by thin black lines in Fig. 3b–d. At these times, a sequence of transitions occurs between the valence and the conduction band as stated before and is clearly visible in Fig. 3d. Whether they lead to net excitation or de-excitation at a specific encounter of K′ depends on the relative phases of the electron excitation amplitudes.
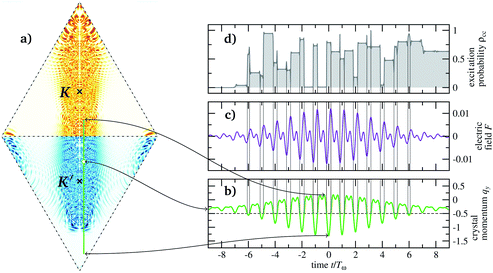 | ||
Fig. 3 (a) Local excitation c(q) as a function of the initial crystal momentum q for pulses eqn (6), with λ = 4 μm, A0 = Δ, n = 2, ϕ = 0. The Dirac points in the center of the triangular unit cells are marked by crosses. (b) Time-dependent crystal momenta ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) y(t) = qy + A(t) in the vertical direction. (c) Electric field Fy(t) in the vertical direction. (d) Corresponding local excitation ρq,cc(t) for y(t) = qy + A(t) in the vertical direction. (c) Electric field Fy(t) in the vertical direction. (d) Corresponding local excitation ρq,cc(t) for 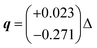 , marked with a white-filled circle in (a). , marked with a white-filled circle in (a). | ||
The final excitation c(q) for each initial condition is quantitatively indicated by the heat map in Fig. 3a revealing a quite complicated pattern across the unit cell but clearly confined laterally (in the qx-direction) around the straight line passing through the Dirac points. Overall, the asymmetric pulse affects the ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) with initial condition in the K′ triangle not equivalently to those starting in the K triangle regarding excitation. This holds true despite the fact that the Dirac points, responsible for the transitions, are visited by equal areas of initial conditions from both triangles of the unit cell, irrespective of the pulse shape. Differences in the excitation—the prerequisite for VP—emerge from the intricate coherent dynamics of
(t) with initial condition in the K′ triangle not equivalently to those starting in the K triangle regarding excitation. This holds true despite the fact that the Dirac points, responsible for the transitions, are visited by equal areas of initial conditions from both triangles of the unit cell, irrespective of the pulse shape. Differences in the excitation—the prerequisite for VP—emerge from the intricate coherent dynamics of ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t), sensitively depending on the respective initial conditions (see Fig. 3d). How these VP generate differences and excitation in the first place, depends on global features of the pulse and will be elucidated below.
(t), sensitively depending on the respective initial conditions (see Fig. 3d). How these VP generate differences and excitation in the first place, depends on global features of the pulse and will be elucidated below.
3 Illumination with harmonic pulses
3.1 Graphene in two-color pulses
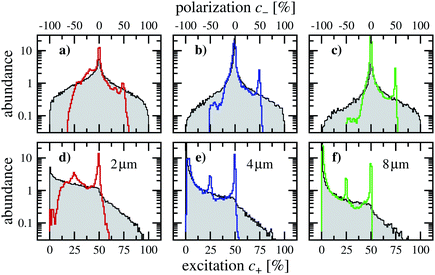
For a first impression, we investigate how the averaged excitation p and VP η depend on wavelength and dephasing, we present in Fig. 4 results for harmonic pulses eqn (6) with n = 2, containing the fundamental frequency corresponding to the wavelength, and the first overtone. One can see that p decreases while η increases almost linearly and changes sign. Moreover, dephasing reduces p by roughly 1/3, while it hardly affects η. Interestingly, the pulse with the highest η at λ = 8 μm is quite long with T = 160 fs. One can understand these trends better from the local excitation and polarization c±(q), shown in Fig. 5. Not surprisingly, dephasing blurs the interference pattern leaving less unexcited area (white) in the unit cell, cf. upper and lower row in Fig. 5. This is particularly obvious for the green color maps showing c+ in compact representation, as all the upper panels have more white space than the lower ones.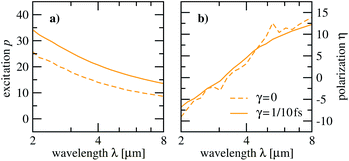 | ||
| Fig. 4 Excitation p (a) and valley polarization η (b) for a two-color pulse, i.e. n = 2 in eqn (6), as a function of the wavelength λ. The harmonic phase is ϕ = 0 and the pulse duration T = [λ/1 μm]20 fs. Results for a finite damping time γ = 1/10 fs are compared to those without any damping. | ||
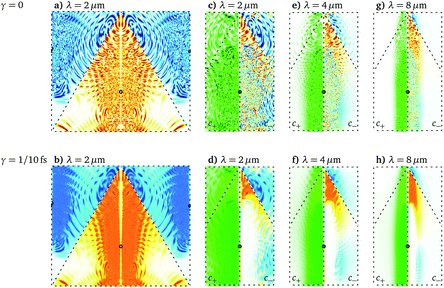 | ||
| Fig. 5 q -resolved conduction-band populations for selected wavelengths (λ = 2, 4, 8 μm). Shown is c(q), for λ = 2 μm only, and in compact form, cf. sketch in Fig. 1, the excitation c+(q) and the polarization c−(q). We show both results with (lower row) and without (upper row) damping. Color scales are given in Fig. 1d. | ||
One notes also, that c+ is more spread over the unit cell and is overall larger for smaller wavelengths (more green areas). For increasing wavelength, the excitation shrinks laterally towards the K′ point (black circle) and offers the selectivity which is necessary for large c−, and indeed, valley polarization increases towards larger wavelengths with the warm colors dominating the cold colors. Since we keep the vector potential fixed at the distance between the two Dirac points, A0 = Δ, decreasing the wavelength implies lowering the field strength. Therefore, transitions between the bands happen closer to the Dirac points. Next, we investigate what happens if n is increased systematically beyond 2 in multi-harmonic pulses.
3.2 Multi-harmonic pulses: dependence on number of harmonics
The arguments about the wavelength dependence of p and η given above for n = 2 do not explicitly depend on the number of harmonics in the pulse. Therefore, we expect the same qualitative behavior when increasing n. Fig. 6 reveals that this is only the case for the effect of dephasing, which remains generally larger for p than for η and hardly changes for p when n is increased. Surprisingly at first glance, neither p nor η depend monotonically on n. Rather p and η exhibit in most cases a maximum for a specific nmax(λ) ∈ [2, 32], which depends on the wavelength.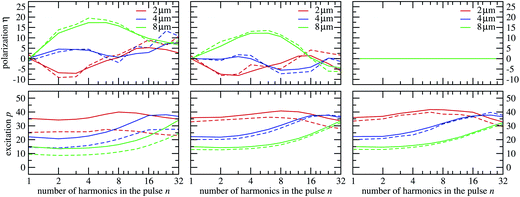 | ||
| Fig. 6 Excitation p and valley polarization η for multi-harmonic pulses eqn (6), as a function of the number of harmonics n in the pulse for ϕ = 0 (left), ϕ = π/4 (middle) and ϕ = π/2 (right). The laser wavelengths are λ = 2, 4, 8 μm and the corresponding pulse durations are T = 40, 80, 160 fs, respectively. | ||
Indeed, the VP approaches zero for small, and towards large, n. The limit n = 1 corresponds to an ordinary pulse which is symmetric in the vector potential and therefore cannot generate VP. The reason for vanishing VP towards large n is more subtle: large n implies that with large time derivatives of the vector potential’s harmonic components cos(kωt) there are large electric fields, cf. upper row in Fig. 2. These pulse parts impair the selectivity of the excitation and therefore the ability of the pulse to generate large η in the first place, despite the fact that increasing n produces increasingly asymmetric pulses in the vector potential, cf. lower row in Fig. 2. The even more complicated pattern, with two extrema of smaller absolute values of η for λ = 2 μm in Fig. 6, can be also attributed to lower selectivity, since for smaller wavelength, excitation is in general less confined in the unit cell of initial conditions.
The spread of the excitation over the unit cell with increasing n and for small λ can be directly read off the compact color maps for c+ in Fig. 7, where one sees that the panels for λ = 2 μm contain more green than those for λ = 8 μm and that n = 32 has in general the most dark green areas. Of course, this dependence on n is only pronounced if the wavelength is long enough to not cover the unit cell already for n = 2 in the excitation, which is the case for λ = 2 μm: the corresponding p is only weakly dependent on n (see Fig. 6).
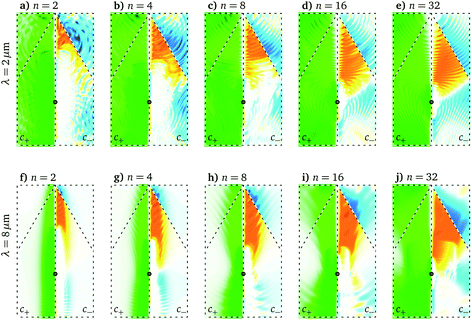 | ||
| Fig. 7 q -resolved excitation for selected numbers of harmonics (n = 2, 4, 8, 16, 32) for ϕ = 0, which corresponds to Fig. 6a. Again, we show c+ (left panels) and c− (right panels). The laser wavelengths are λ = 2, 8 μm and the pulse duration T = 40, 160 fs, respectively. It is γ = 1/10 fs. Color scales are given in Fig. 1d. | ||
3.3 Multi-harmonic pulses: dependence on the harmonic phase
For completeness we also show in Fig. 6 different harmonic phases ϕ whose effect is obvious: they hardly influence p, but with increasing ϕ the vector potential within a single period becomes more symmetric (see lower row in Fig. 2) decreasing VP and for ϕ = π/2 with fully symmetric A(t), it is impossible to generate VP. Interestingly, dephasing has less influence for more symmetric vector potentials (the difference between p with and without dephasing is much less for ϕ = π/2 than for ϕ = 0). Regarding VP, there is in general very little influence of dephasing regardless of the harmonic phase ϕ. Note that the pulse length T varies with the wavelengths between 40 and 160 fs, i.e., ultrashort pulses are not required for VP.4 The effects of dephasing and excitation distributions
Averaged over local excitation in the valley domains, p and η do not reveal details about dephasing in contrast to the excitation distributions (ED) for c± shown in Fig. 8 for n = 2. Most striking is the qualitative difference of coherent dynamics with smooth distributions (grey areas) and dephased dynamics exhibiting pronounced peaks (colored lines); note, however, the logarithmic scale. Not surprisingly, c− = 0% dominates as VP is difficult to achieve. How is this central peak and the (smaller) peaks at c− = ±50% related to the dominant peaks in the distributions of c+? This can be answered by looking at the differential probabilities in Fig. 9. Trivially, all initial conditions which do not lead to excitation (not shown) contribute to the peak at c− = 0% in Fig. 8, as can be seen from Fig. 9g and also from the fact that all ED have their maximum at c+ = 0. Note, however, that also the highest abundance of excitation (peak at c+ = 50% in Fig. 8d–f) does not contribute to c−, which becomes clear when looking at Fig. 9a, b and g.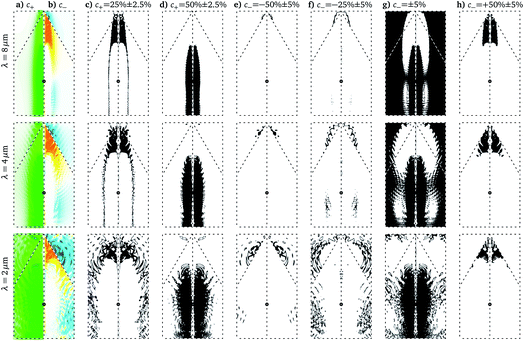 | ||
| Fig. 9 Local excitation maps corresponding to the peaks in Fig. 8. Initial conditions which contribute to the ranges of c+ (c and d) and c− (e–h) given on top are marked in black in the reduced q-space. For convenience we also show c+ (a) and c− (b). | ||
The peak at c+ = 25%, on the other hand, is the reason for the peak at c− = 50%. This becomes apparent, when comparing Fig. 9c with Fig. 9h. Although this peak constitutes the main contribution to VP, it does not come from the initial conditions with the highest excitation, which correspond to the green area in Fig. 9a. Rather, the strongest VP comes from excitation at the tip of the triangle in Fig. 9h and the red area in Fig. 9b. The principles that the systematics for c− > 0 follows are confirmed for c− < 0 in Fig. 9, where the corresponding differential probabilities are shown for consistency. Since negative c− is only dominant for λ = 2 μm, we do not discuss it here further.
5 Conclusions
We have given a detailed picture of how intense laser pulses affect excitation and valley polarization in graphene, as a representative gapless 2D material. Guided by insight from our previous work,9 we have focused on pulse trains with asymmetric shapes in each optical period generated by multi-harmonic components, linearly polarized along Δ = K − K′, the line connecting the Dirac points. We have constructed a compact representation of conduction-band occupations in terms of initial conditions in the unit cell, which has given us means to understand the electron dynamics from the local excitation and valley polarization.The guiding principles to achieve large valley polarization are two-fold: firstly, a pulse, linearly polarized along Δ, and with a maximal vector potential of A0 = Δ. Secondly, (for fixed A0) a moderate field strength to avoid uncontrolled excitation throughout the unit cell. The latter can be achieved by long wavelengths, and a finite number of overtones n in the harmonic pulse, where n is limited by the requirement of moderate field strength, which—the derivative of the vector potential—becomes large for large n. Although interferences from different excitation amplitudes are omnipresent, they do not influence excitation and valley polarization strongly for the scenarios investigated. This has become clear from the qualitative agreement of results with and without dephasing. It also means, that here dephasing does not pose an obstacle to achieve large valley polarization in gapless 2D materials.
6 Appendix: Hamilton matrix and density matrix equation
For completeness we derive here briefly the Hamilton matrix eqn (1) in the density matrix eqn (2). The starting point is the usual tight-binding two-band Hamilton matrix16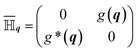 | (8a) |
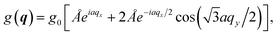 | (8b) |
In a laser pulse the crystal momentum becomes q → ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) (t) = q + A(t). We can write both density matrix and Hamilton matrix by means of the transformation
(t) = q + A(t). We can write both density matrix and Hamilton matrix by means of the transformation  , that makes eqn (8) at instance t diagonal,
, that makes eqn (8) at instance t diagonal,
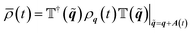 | (9a) |
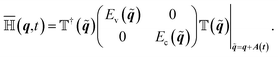 | (9b) |
The unitary matrix 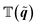 , with
, with  , is often referred to as the Houston basis.17 The equation of motion for the Houston basis density matrix ρq follows from the tight-binding version by means of eqn (10)
, is often referred to as the Houston basis.17 The equation of motion for the Houston basis density matrix ρq follows from the tight-binding version by means of eqn (10)
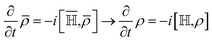 | (10) |
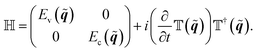 | (11) |
The time the derivative of eqn (11) can be rewritten 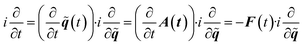 . In order to arrive at eqn (1) we note that E
. In order to arrive at eqn (1) we note that E![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) = Ec(
= Ec(![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) ) − Ev(
) − Ev(![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) ) and that the Houston basis
) and that the Houston basis 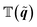 consists of two eigenvectors V
consists of two eigenvectors V![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) and W
and W![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) , for valence and conduction band, respectively. Whereas these vectors are complex, all matrix elements of the 2nd term in eqn (11) are real. The diagonal elements are identical and can thus be omitted. There we have the expression given in eqn (1).
, for valence and conduction band, respectively. Whereas these vectors are complex, all matrix elements of the 2nd term in eqn (11) are real. The diagonal elements are identical and can thus be omitted. There we have the expression given in eqn (1).
We introduce a dephasing term with a dephasing rate γ in order to allow for long driving pulses. It will dampen exclusively coherences in the Houston basis density matrix
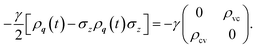 | (12) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Hamed Koochaki Kelardeh for discussions in the initial phase of this work We acknowledge financial support by the Deutsche Forschungsgemeinschaft through the Priority Program 1840.References
- S. Ghimire and D. A. Reis, Nat. Phys., 2019, 15, 10 Search PubMed.
- S. Ghimire, A. D. DiChiara, E. Sistrunk, P. Agostini, L. F. DiMauro and D. A. Reis, Nat. Phys., 2011, 7, 138 Search PubMed.
- G. Vampa, C. R. McDonald, G. Orlando, D. D. Klug, P. B. Corkum and T. Brabec, Phys. Rev. Lett., 2014, 113, 73901 CrossRef CAS PubMed.
- G. Vampa and T. Brabec, J. Phys., B, 2017, 50, 083001 CrossRef.
- J. Cayssol, C. R. Phys., 2013, 14, 760 CrossRef CAS.
- L. E. Golub and S. A. Tarasenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 201402 CrossRef.
- J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 16055 CrossRef CAS.
- S. A. Vitale, D. Nezich, J. O. Varghese, P. Kim, N. Gedik, P. Jarillo-Herrero, D. Xiao and M. Rothschild, Small, 2018, 14, 1870172 CrossRef.
- H. K. Kelardeh, U. Saalmann and J. M. Rost, 2021, arXiv2109.04249.
- A. Wirth, M. T. Hassan, I. Grguras, J. Gagnon, A. Moulet, T. T. Luu, S. Pabst, R. Santra, Z. A. Alahmed, A. M. Azzeer, V. S. Yakovlev, V. Pervak, F. Krausz and E. Goulielmakis, Science, 2011, 334, 195 CrossRef CAS PubMed.
- P. Krogen, H. Suchowski, H. Liang, N. Flemens, K.-H. Hong, F. X. Kärtner and J. Moses, Nat. Photonics, 2017, 11, 222 CrossRef CAS.
- M. S. Mrudul, Á. Jiménez-Galán, M. Ivanov and G. Dixit, Optica, 2021, 8, 422 CrossRef.
- C. Heide, T. Boolakee, T. Higuchi and P. Hommelhoff, JPhys Photonics, 2020, 2, 024004 CrossRef.
- Q. Z. Li, P. Elliott, J. K. Dewhurst, S. Sharma and S. Shallcross, Phys. Rev. B, 2021, 103, L081102 CrossRef CAS.
- S. A. Oliaei Motlagh, F. Nematollahi, V. Apalkov and M. I. Stockman, Phys. Rev. B, 2019, 100, 115431 CrossRef CAS.
- A. J. Leggett, Graphene: Electronic Band Structure and Dirac Fermions, University of Waterloo technical report, 2010 Search PubMed.
- W. V. Houston, Phys. Rev., 1940, 57, 184 CrossRef CAS.
Footnotes |
| † Asymmetry is here defined through |max{AΔ(t)}| ≫ |min{AΔ(t)}|. |
| ‡ Note, that this compactification requires pulses that are mirror-symmetric with respect to Δ. |
| This journal is © The Royal Society of Chemistry 2022 |