Photoelectron spectra of water and simple aqueous solutions at extreme conditions

Abstract

Determining the electronic structure of aqueous solutions at extreme conditions is an important step towards understanding chemical bonding and reactions in water under pressure (P) and at high temperature (T). We present calculations of the photoelectron spectra of water and a simple solution of NaCl under pressure at conditions relevant to the Earth’s interior (11 GPa and 1000 K). We combine first-principles and deep-potential molecular dynamics with electronic structure calculations with dielectric-dependent hybrid functionals. These functionals are defined with a fraction of exact exchange determined from the dielectric constant of the liquid computed in extreme conditions. We find a broadening of the spectra relative to ambient conditions, particularly prominent in the merging of the two main peaks below the onset of the spectra. Furthermore we find an overall red shift at high pressure and temperature, which is however not constant over the whole energy range and varies between 1.1 and 2.4 eV. Our results also show that the anion energy levels are closer to the valence band maximum of the liquid than at ambient conditions, indicating that as P and T are increased, the defect levels of Cl⁻ and OH⁻ in water may eventually lie below the valence band maximum of water. Finally, we characterize the ionization potential of hydrated species deriving from rapid water dissociation, e.g. hydrated hydroxide and hydronium, and we elucidate the electronic states associated with proton transfer events at high pressure. Our results represent a first, important step in predicting the electronic properties of solutions in super-critical conditions.

---

I. Introduction

Water-rich fluids are important constituents of the Earth’s crust and mantle^1–3 and they play a central role in many fundamental processes, including metasomatism,⁴ transport of oxidized carbon^5,6 and ultimately in the evolution of the continental crust.³ The presence of so called deep-earth aqueous fluids has been reported in aqueous pockets in diamond,⁷ metamorphic minerals^8,9 and stable hydrous silicate minerals under pressure (P),¹⁰ and inferred from seismic data¹¹ and conductivity measurements.^12,13

While most of the current knowledge of deep-earth aqueous fluids comes from geophysical models^14–23 and from vibrational spectroscopic measurements, progress has been made in recent years in understanding the properties of these fluids at the microscopic level, using first principles simulations. The latter have been used to investigate fundamental properties at high P and T (HPT) including the dielectric constant of water,^24,25 ionic speciation,^5,6 ion solvation^26,27 and ionic conductivity of simple solutions.^28–31 However, relatively little is known about the electronic structure³² of aqueous fluids under extreme conditions, which is important to understand, for instance, electron and proton transfer processes in redox reactions occurring^33,34 in water and solutions in contact with rocks in the Earth’s interior.

Many electronic structure probes used at ambient conditions are difficult to employ at high temperature and pressure. For example, photoelectron (PE) spectroscopy has been widely used to probe the electronic properties of hydrogen bonded liquids, providing information on their occupied energy levels,^35–37 including the ionization potentials (IP) of solvated ions,^38–41e.g. hydrated OH⁻, H₃O⁺, Cl⁻, Na⁺, thus elucidating their structural and chemical environment. However, obtaining PE spectra for HPT water and solutions is a challenging task not only because of the reactivity of water at high P and T, but also for the difficulty in preparing super-critical liquids in contact with vacuum and detecting PE signals with high time-resolution in the presence of rapid thermal expansion.^42–44

First principles theoretical methods based on quantum mechanical calculations have been applied to predict the PE spectra of several aqueous solutions at ambient P and T (APT),^{40,41,45–47} providing results in excellent agreement with experiments. In particular, recent investigations have shown that a combination of first-principles molecular dynamics (FPMD) and density functional theory calculations with dielectric-dependent hybrid (DDH) functionals⁴⁸ is a robust, predictive approach to study photoelectron spectra of aqueous fluids.^40,41 It is hence interesting to explore how to predict PE under extreme conditions and gain insight into the electronic properties of aqueous fluids at high P and T.

Here, we generalize the approach recently used to compute PE spectra at ambient conditions to the study of aqueous fluids under pressure, at high temperature. We carry out first principles simulations with semilocal and hybrid functionals, and we consider two specific systems at conditions (11 GPa and 1000 K) relevant to the Earth upper mantle, where pressure can reach ∼13 GPa and temperature ∼1700 K;^49,50 in particular we investigate pure water and a 0.68 M NaCl solution, whose structural and bonding properties have been previously studied.^27,31 We report PE spectra on an absolute scale, by using a technique to refer energy levels to vacuum which is appropriate for hot compressed fluids; we discuss results obtained with dielectric-dependent hybrid functionals, and with a fraction of exact exchange determined for the specific conditions studied here.³² We also analyze the contribution of dissociated species to the PE spectra, in particular hydroxide (OH⁻), hydronium (H₃O⁺) ions and H₄O₂, which play an important role in proton transfer processes and acid–base chemistry,^51–53 and contribute to the increased ionic conductivity³¹ of water under extreme conditions.

The rest of the paper is organized as follows: the methods used here are described in the next section, followed by a discussion of our results in Section 3. Our conclusions are presented in Section 4.

II. Methods

A. First-principles simulations and electronic structure calculations

We consider the FPMD trajectories generated at 11 GPa and 1000 K by Rozsa et al. and Zhang et al.^27,31 to model pure water and a 0.68 M NaCl solution, respectively. These trajectories were obtained with the Qbox⁵⁴ code, employing the Perdew–Burke–Ernzerhof (PBE)⁵⁵ functional, with 64 water molecules to model pure water and 126 water molecules and 1 NaCl formula to model the solution. The length of the trajectory is ∼240 (300) ps for pure water (NaCl solution). We note that in the case of the solution, the Na–Cl distance was constrained to be <6 Å in ref. 27 to sample ion-pair configurations. From the FPMD trajectories we extracted 500 (285) snapshots by every ∼0.5 (∼1) ps for pure water (NaCl solution), which we then used to compute the electronic density of state (EDOS), as well as the projected EDOS, with the Quantum ESPRESSO^56,57 code, using both the PBE semi-local and dielectric dependent hybrid (DDH) functionals.⁴⁸ The DDH functional was previously shown to provide an excellent description of PE spectra at ambient conditions, in good agreement with experimental measurements.^40,41 In order to model HPT conditions, we used a DDH functional with a fraction of exact exchange (42%) equal to the inverse of the macroscopic dielectric constant of water at 11 GPa and 1000 K, which was determined to be 2.37 in a recent study.³² In our electronic structure calculations, we used norm-conserving pseudopotentials⁵⁸ to describe the interactions between core and valence electrons, a plane-wave basis set with a kinetic energy cutoff of 60 Ry and only the Γ-point to sample the Brillouin zone.

To predict PE spectra comparable to experiments, the calculation of absolute energies referenced to vacuum is required, and the strategy chosen to do so in our work is described in detail in the next section.

B. Evaluation of absolute orbital energies

While eigenvalue and total energy differences are well defined, absolute energies obtained with the plane-wave pseudopotential method for periodic systems are not.^40,45,59 In order to obtain absolute energies [small epsilon, Greek, tilde]_i, i.e. to refer the electronic energies to vacuum, we evaluate:

[small epsilon, Greek, tilde]_i = ε_i − ΔV − V_bulk (1)

where ε_i denotes Kohn–Sham eigenvalues computed for either bulk water or a NaCl solution in periodic plane-wave calculations. The term V_bulk is the average electrostatic potential for bulk water samples, which can be easily computed following the procedure outlined in ref. 60. Consistent with the results reported in ref. 40, we found that the value of V_bulk, 0.81 eV, is insensitive to the choice of the energy functional. The term ΔV is the difference between the electrostatic potential in the bulk region of a water sample interfaced with vacuum, and the vacuum region. In previous calculations of PE spectra at ambient conditions, the term ΔV was obtained by carrying out MD simulations of water in contact with vacuum using empirical potentials and then carrying out electronic structure calculations on the trajectories generated for the water/vacuum slab. However, this scheme is not applicable at HPT, where hot, compressed water in contact with a vacuum region would immediately expand. Hence, here we adopt a different approach to compute ΔV that we call Slice and that we compare in Fig. 1 with other approaches adopted in the literature.

Fig. 1 Strategies to generate water samples in contact with vacuum: Vacuum (a), Wall (b) and Slice (c) (see text). The three rectangles schematically represent a slab used and periodically repeated in our pseudopotential-plane-wave calculations, and the white and blue regions denote vacuum and a water sample, respectively.

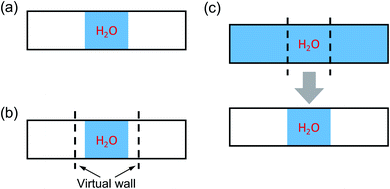
Fig. 1 illustrates three possible strategies to obtain ΔV, which are summarized below.

• Vacuum: a water sample at a chosen, initial density is in contact with vacuum within a periodically repeated slab that is equilibrated using MD at a given temperature. This scheme was used for calculations of PE spectra at APT and is applicable if the density of water is such that immediate evaporation is not observed, over the time scale of the simulations. Hence it is not applicable to simulate water at high P and T, where the sample would tend to expand into vacuum over short time scales.

• Wall: similar to the previous approach, a water sample is in contact with vacuum within a periodically repeated slab that is equilibrated using MD at given temperature. However in this case a repulsive potential is added to the Hamiltonian so as to maintain the water sample at a density corresponding to the desired pressure. Such a repulsive potential prevents water from evaporating into the vacuum portion of the slab. This method can in principle be used at any P–T conditions, however the results may be affected by the choice of the specific form of the repulsive potential and the approach requires the use of relatively large systems to obtain a converged electrostatic potential.

• Slice: a relatively large bulk water model is equilibrated in a periodically repeated supercell at desired P and T conditions. A slice of the sample is then extracted after equilibration and placed in contact with vacuum, with no further MD simulations of the whole slab. To avoid dangling bonds at the interface, when taking the slice, we retain the H–O covalent bonds. This scheme is applicable to any P–T conditions, provided a slice of sufficient thickness is chosen.

To reduce the computational cost in preparing the samples required to obtain ΔV, we carried out simulations with empirical potentials first, for benchmarking purposes, and then we used the deep-MD potential^61,62 implemented in the DeePMD-kit package.⁶³ The deep-MD potential (DP)⁶⁴ is trained on first principle data obtained with the SCAN functional⁶⁵ at HPT and allows for the proper description of dissociated species at extreme conditions, unlike empirical potentials. In addition, using the DP potential, simulations with cells larger than those affordable with FPMD can be carried out and longer time scales can be sampled with first-principle accuracy, as described below.

In order to assess the robustness of our methodology, we first carried out simulations with the TIP3P⁶⁶ potential and we compared results obtained with the Vacuum and Slice procedures at ambient conditions; we also compared our results with those previously reported in the literature. We then further compared the results obtained with the Wall and Slice methods at HPT. MD simulations were carried out in the NVT ensemble with the LAMMPS package.^67,68 A timestep of 2 (1) fs was used for TIP3P simulations at APT (11 GPa & 1000 K). When using the Vacuum method, our samples consisted of 108 water molecules interfaced with vacuum in a cell of dimensions 12.77 × 12.77 × 80 Å. When using the Slice method, we equilibrated water samples with 435 and 683 molecules at APT and 11 GPa & 1000 K, respectively, corresponding to the densities of 1.0 and 1.57 g cm⁻³ in a cell of dimensions 12.77 × 12.77 × 80 Å. The thickness of a slice was chosen to be 20 (18) Å at APT (11 GPa & 1000 K). When adopting the Wall method, we considered 300 water molecules at 11 GPa & 1000 K, and the wall/lj126 scheme implemented in the LAMMPS code. The distance between two virtual walls simulating a repulsive potential in the Hamiltonian was set to be 39 Å. The repulsive part of Lennard-Jones interactions between the wall and water was described by using carbon–oxygen Lennard-Jones parameters⁶⁹ to mimic the interaction with water oxygen atoms only. For all the procedures adopted here, the MD simulations with the TIP3P potential were performed for 4 ns following a 2 ns equilibration, with 200 equally-spaced snapshots extracted every 20 ps.

The results for the average potential obtained with the PBE functional on the configurations extracted from our MD simulations are presented in Fig. 2. Our results with the Vacuum method are nearly identical with those reported using the same scheme in the literature: 3.53 eV versus 3.54 eV.⁴⁰ When using the Slice method we obtain a value of 3.36 eV and we consider the difference relative to the result with the Vacuum method (0.17 eV) to be negligible, given that the position of the valence band maximum (VBM) of water is at approximately 10 eV (ref. 39–41 and 46) relative to vacuum. The difference of 0.17 eV may be ascribed to the specific surface of the chosen slice (the statistical error in our evaluation of ΔV is smaller than 0.1 eV).

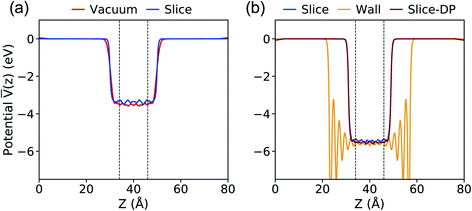Fig. 2 Plane-average electrostatic potential V̄ along the z direction perpendicular to the interface between water and vacuum, calculated with the PBE functional at ambient conditions (a) and 11 GPa & 1000 K (b). The vacuum level is set to zero. The equilibrium configurations were generated using molecular dynamics simulations and the TIP3P potential except for the case denoted as Slice-DP, for which we used the deep-MD potential.⁶¹ See Fig. 1 for the definition of different procedures. The dashed lines define the region used for averaging the electrostatic potential.

At 11 GPa and 1000 K, as reported in Fig. 2(b), ΔV is computed to be 5.43 (Slice) and 5.58 (Wall) eV. Again, we consider the difference of 0.15 eV to be small for the purpose of our study.

Next we compared the results obtained with the Slice method and the TIP3P potential with those obtained with the DP potential. When using the DP potential, we performed 210 independent MD simulations (with a time step of 0.25 fs) each of 13 ps long, at the end of which we extracted configurations for our electronic structure calculations. We obtained ΔV = 5.53 eV, in good agreement with the value computed with TIP3P, indicating that the value of ΔV depends rather weakly on subtle structural differences in the liquid samples. These comparisons between different approaches gave us confidence that the Slice method is a reliable technique to use both at APT and HPT.

Therefore, in the following we compute ΔV with the Slice method and the DP potential to obtain the spectra at HPT and to discuss the physical properties of water and the NaCl solution. We note that when using the DDH functional, we could only carry out calculations of ΔV for a small number of configurations (5), much smaller than with the PBE functional. Hence we estimated the difference between ΔV computed with PBE and DDH for those limited number of configurations, and we applied the same difference between the DDH and PBE result (5.31 vs. 5.53 eV) to all eigenvalues obtained at the DDH level of theory for the bulk samples.

III. Results and discussion

A. Photoelectron spectra of water and NaCl solution at high pressure and temperature

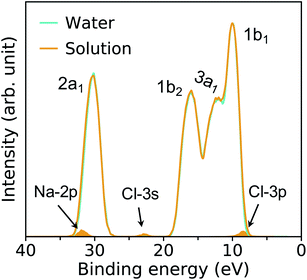
The PE spectra are evaluated as the EDOS of single-particle eigenvalues referred to vacuum, as an approximation to the electronic binding energies (BE). In Fig. 3, we compare low and high pressure spectra of the NaCl solution computed at the PBE (left hand side) and DDH (right hand side) level of theory. The positions in energy of peaks’ maxima are summarized in Table 1.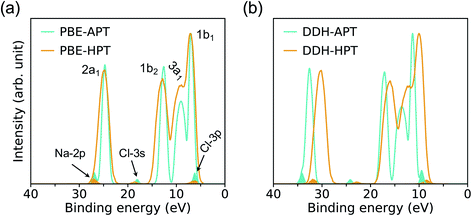

Fig. 3 Photoelectron spectra of a 1 M NaCl solution at ambient conditions (APT)⁴⁰ and a 0.68 M NaCl solution at high pressure conditions (HPT) (11 GPa & 1000 K) obtained with the PBE (a) and DDH (b) functionals. The intensities are rescaled to those of the water 1b₁ peak; the shaded areas show the distribution of ionization potentials of solvated Cl⁻ and Na⁺ ions.

Table 1 Electron binding energy (eV) of NaCl solution at ambient conditions (APT) and high pressure and temperature (HPT) (11 GPa & 1000 K) obtained with the PBE and DDH functionals. See Fig. 3 for the labeling of the electronic states

Method	2p (Na^+)	2a1	3s (Cl^−)	1b2	3a1	1b1	3p (Cl^−)
a Results at APT of a 1 M NaCl solution from ref. 40. b Results at 11 GPa & 1000 K of a 0.68 M NaCl solution.
PBE-APT^a	26.90	24.71	18.06	12.63	9.03	6.99	6.20
DDH-APT^a	34.04	32.57	24.15	17.14	13.56	11.34	9.46
PBE-HPT^b	27.02	24.81	18.62	12.84	8.98	7.12	6.28
DDH-HPT^b	31.92	30.18	22.93	15.98	12.01	10.02	8.41

---

The four major peaks (labeled, in order of increasing BE as: 2a₁, 1b₂, 3a₁, and 1b₁) are notably broadened at HPT, with the 3a₁ and 1b₁ features strongly overlapping with each other, consistent with larger structural fluctuations in the HPT samples. The DDH results show that the relative spacing of the water 2a₁ band with respect to the 1b₁ peak is decreased by ∼1.1 eV at high P, while that of 1b₂ and 3a₁ bands are less affected at extreme conditions. Interestingly, calculations with the DDH functional predict a reduction of the BE by roughly 1.1–2.4 eV at high pressure, depending on the character of electronic states; however calculation with the PBE or standard hybrid functionals such as PBE0 (ref. 70 and 71) yield negligible differences between the band positions in the PE spectra at high and low pressure. This finding is important and highlights the need to correctly take into account screening effects at HPT and correspondingly adjust the amount of exact exchange used to define hybrid functionals (∼60% in DDH at APT;^40,41 ∼42% in DDH at the HPT conditions of this study, corresponding to the dielectric constants ε_∞ = 1.78 and 2.37, respectively).

The ionization potentials (IPs) of hydrated Cl⁻ and Na⁺ at APT and HPT are indicated in Fig. 3 as shaded areas. Similar to the BE of water electronic states, the IPs of ions are underestimated by PBE, relative to DDH, and DDH results show a red shift with increasing P and T which is not reproduced by the PBE functional. In addition, when using the DDH functional, the relative positions of IPs referenced to water is slightly different at low and high P. In particular, the separation between the 3p-level of Cl⁻ and the 1b₁ peak of water is decreased by 0.27 eV, suggesting a modified electronic structure near the band edges of water at high P, which in turn may affect the chemical reactivity of solutions under extreme conditions. Our results hint at a possible tendency of anion levels to move below the valence band of water as a function of increasing pressure, at high T. We note that the BE of water and IP of ions are not sensitive to the Cl⁻–Na⁺ distance, hence the results reported here should be representative of weakly concentrated solutions.

B. Water dissociation

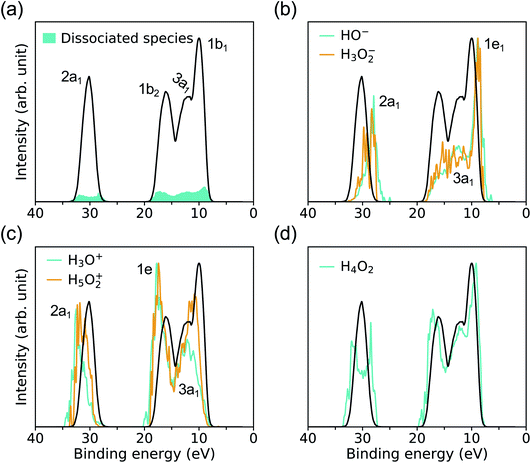
Fig. 4 compares the spectra obtained at HPT for water and the solution. We find that the effects of ions on the electronic properties of water are minor at the concentrations considered here (0.68–1 M);⁴¹ for example, the centers of the 1b₁ and 1b₂ peaks obtained in HPT water and in the solutions with the DDH functional differ by only 0.03 and 0.13 eV, respectively.

Fig. 4 Photoelectron spectra of water and a 0.68 M NaCl solution obtained with the DDH functional at 11 GPa & 1000 K. The intensities of the spectra are rescaled to the water 1b₁ peak; the shaded areas indicate the ionization potential of solvated Cl⁻ and Na⁺ ions.

In our FPMD simulations, we directly observe frequent dissociation events at HPT, indicating that water itself becomes an electrolyte. The short-lived dissociated products^27,31 are characterized using a cutoff distance for O–H bonds of 1.25 Å. A detailed analysis reveals that about 2% of water molecules are dissociated, into species including solvated HO⁻, H₃O⁺ and H₄O₂. These species play a critical role in proton transfer events and acid–base reactions in water.

As shown in Fig. 5(a), the signal coming from ionic species resulting from water dissociation spans the entire spectrum range. The signal is weak and expected to become more prominent at higher pressure and temperature, where the concentration of dissociated species will increase. The contributions to the overall PE signal of hydrated HO⁻ and H₃O⁺ are presented in Fig. 5(b) and (c), and it has been identified by carrying out projected EDOS calculations. Similar to ambient conditions, the solvated HO⁻ level is just above the VBM of water, and it originates from two degenerate lone-pair orbitals (1e₁) localized on the oxygen atom. The solvated H₃O⁺ levels lie instead close to the high-energy edge of the 1b₂ feature of bulk water and originates from the ionization from two degenerate covalent orbitals with mainly p-character (1e). However the IPs of hydrated HO⁻ and H₃O⁺ at HPT, peaking at 8.9 and 17.75 eV, are red-shifted relative to ambient conditions, where they are centered at ∼9.2 and ∼20 eV (∼9.99 and ∼19.01 eV) in the experiments of ref. 39 (calculated by many-body perturbation approach⁴⁶). In addition, the separation between the 1e₁ level of HO⁻ and 1b₁ peak of water is ∼1.91 eV at APT based on experiment,³⁹ while we find that at HPT it is 1.12 eV, when using DDH. Hence our simulations show that similar to the case of the Cl⁻, the level of HO⁻ gets closer to the VBM of water as pressure is increased.

Fig. 5 Signals of dissociated water species contributing to the photoelectron spectra (PE) of water under pressure, at high temperature, calculated with the DDH functional at 11 GPa & 1000 K. The full spectrum of bulkwater is represented by the black line. (a) The shaded areas (cyan) represent the total PE spectrum from all dissociated species (magnified five times for clarity). The intensities in (b) HO⁻ and H₃O₂⁻, (c) H₃O⁺ and H₅O₂⁺, (d) H₄O₂ are magnified between ∼100 (e.g. HO⁻ and H₄O₂) and ∼1000 (e.g. H₃O₂⁻) times.

To understand the electronic states involved in proton transfer events at high pressure, we plot the IP distributions for three hydrated intermediate complexes H₃O₂⁻, H₅O₂⁺ and H₄O₂ in Fig. 5(b–d). With respect to HO⁻, the IP of H₃O₂⁻ is blueshifted with a slightly enhanced signal near the 1b₂ region of bulk water, similar to what is found in proton transfer events at APT.⁴⁶ Compared to H₃O⁺, we observe a red shift in the IP of H₅O₂⁺ with increased spectral weights near the 1b₁ region of bulk water, again similar to what is observed in proton transfer events at APT.⁴⁶ For solvated H₄O₂ cluster referenced to bulk water, the major change at high pressure is the double-peak near the 2a₁ region of bulk water, giving rise to the 2a₁ peaks with lower or higher IP in the resulting species HO⁻ and H₃O⁺. The results reported here for ionization potentials of dissociated species in water may help, at least qualitatively, to understand proton transfer reactions at high pressure.

IV. Conclusions

In summary, we proposed a new computational scheme to evaluate photoelectron spectra of water and simple aqueous solutions at high P and T (HPT). By combining deep-MD and first-principles simulations, and electronic structure calculations with hybrid functionals, we computed the absolute orbital energies of water and a 0.68 M NaCl solution at 11 GPa and 1000 K, which are conditions relevant to the earth mantle. We found a broadening of the spectra relative to ambient conditions, particularly prominent for the merging of the 3a₁ and 1b₁ peaks of water. In addition we found an overall red shift of the HPT spectra relative to ambient conditions, which is however not constant over the whole energy range and varies between 1.1 and 2.4 eV. Our results also show that the anion energy levels are closer to the VBM of water at high pressure and temperature and we speculate that as P and T are increased, the “defect levels” of Cl⁻ and OH⁻ in water may eventually lie below the valence band maximum. We also characterized the IP of hydrated species deriving from rapid water dissociation, e.g. hydrated hydroxide and hydronium, and elucidated the electronic states associated with proton transfer events at high pressure. Our results represent a first step in predicting the electronic properties of solutions in super-critical conditions. Finally we note that the prediction of hybrid and PBE functionals for the electronic properties of the APT and HPT fluids are markedly different; in addition PBE predicts no notable changes between high and low pressure spectra, at variance with dielectric dependent hybrid functionals, when used with a screening fraction computed for the specific HPT conditions investigated here.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was completed with resources provided by the University of Chicago’s Research Computing Center. Z. Y. acknowledges support from the Advanced Materials for Energy-Water Systems Center, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences. C. Z. acknowledges support from Midwest Integrated Center for Computational Materials as part of the Computational Materials Sciences Program funded by the US Department of Energy, Office of Science, Basic Energy Sciences. We thank Marcello Puligheddu for useful discussions and Linfeng Zhang and Roberto Car for providing the deep-MD potential.

References

1. K. Bucher and I. Stober, Geofluids, 2010, 10, 241.
2. A. Liebscher, Geofluids, 2010, 10, 3.
3. C. E. Manning, Annu. Rev. Earth Planet. Sci., 2018, 46, 67.
4. A. Putnis and H. Austrheim, Geofluids, 2010, 10, 254.
5. D. Pan and G. Galli, Sci. Adv., 2016, 2, e1601278.
6. D. Pan and G. Galli, Nat. Commun., 2020, 11(1), 421.
7. O. Tschauner, S. Huang, E. Greenberg, V. Prakapenka, C. Ma, G. Rossman, A. Shen, D. Zhang, M. Newville and A. Lanzirotti, et al. , Science, 2018, 359, 1136.
8. J. Touret, Lithos, 2001, 55, 1.
9. B. W. Yardley and R. J. Bodnar, Geochem. Perspect., 2014, 3, 1.
10. M. Nishi, T. Irifune, J. Tsuchiya, Y. Tange, Y. Nishihara, K. Fujino and Y. Higo, Nat. Geosci., 2014, 7, 224.
11. G. C. Beroza and S. Ide, Annu. Rev. Earth Planet. Sci., 2011, 39, 271.
12. T. J. Shankland and M. E. Ander, J. Geophys. Res. Solid Earth, 1983, 88, 9475.
13. R. Hyndman and P. Shearer, Geophys. J. Int., 1989, 98, 343.
14. H. C. Helgeson and D. H. Kirkham, Am. J. Sci., 1976, 276.
15. J. C. Tanger and H. C. Helgeson, Am. J. Sci., 1988, 288, 19.
16. D. A. Sverjensky, B. Harrison and D. Azzolini, Geochim. Cosmochim. Acta, 2014, 129, 125.
17. D. Dolejš and C. Manning, Geofluids, 2010, 10, 20.
18. C. E. Manning, Rev. Mineral. Geochem., 2013, 76, 135.
19. J. W. Johnson, E. H. Oelkers and H. C. Helgeson, Comput. Geosci., 1992, 18, 899.
20. D. Fernandez, A. Goodwin, E. W. Lemmon, J. Levelt Sengers and R. Williams, J. Phys. Chem. Ref. Data, 1997, 26, 1125.
21. J.-M. Huizenga, Lithos, 2001, 55, 101.
22. D. Dolejš, Rev. Mineral. Geochem., 2013, 76, 35.
23. D. I. Foustoukos, Chem. Geol., 2016, 447, 183.
24. R. Hou, Y. Quan and D. Pan, J. Chem. Phys., 2020, 153, 101103.
25. D. Pan, L. Spanu, B. Harrison, D. A. Sverjensky and G. Galli, Proc. Natl. Acad. Sci., 2013, 110, 6646.
26. V. Rozsa and G. Galli, J. Chem. Phys., 2021, 154, 144501.
27. C. Zhang, F. Giberti, E. Sevgen, J. J. de Pablo, F. Gygi and G. Galli, Nat. Commun., 2020, 11(1), 3037.
28. A. F. Goncharov, N. Goldman, L. E. Fried, J. C. Crowhurst, I.-F. W. Kuo, C. J. Mundy and J. M. Zaug, Phys. Rev. Lett., 2005, 94, 125508.
29. M. French, T. R. Mattsson and R. Redmer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 174108.
30. M. French, S. Hamel and R. Redmer, Phys. Rev. Lett., 2011, 107, 185901.
31. V. Rozsa, D. Pan, F. Giberti and G. Galli, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6952.
32. D. Pan, Q. Wan and G. Galli, Nat. Commun., 2014, 5(1), 3919.
33. R. A. Marcus, J. Chem. Phys., 1956, 24, 966.
34. R. A. Marcus and N. Sutin, Biochim. Biophys. Acta Rev. Bioenerg., 1985, 811, 265.
35. B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176.
36. B. Winter, Nucl. Instrum. Methods Phys. Res. A, 2009, 601, 139.
37. R. Seidel, S. Thurmer and B. Winter, J. Phys. Chem. Lett., 2011, 2, 633.
38. B. Winter, R. Weber, I. V. Hertel, M. Faubel, P. Jungwirth, E. C. Brown and S. E. Bradforth, J. Am. Chem. Soc., 2005, 127, 7203.
39. B. Winter, M. Faubel, I. V. Hertel, C. Pettenkofer, S. E. Bradforth, B. Jagoda-Cwiklik, L. Cwiklik and P. Jungwirth, J. Am. Chem. Soc., 2006, 128, 3864.
40. A. P. Gaiduk, M. Govoni, R. Seidel, J. H. Skone, B. Winter and G. Galli, J. Am. Chem. Soc., 2016, 138, 6912.
41. T. A. Pham, M. Govoni, R. Seidel, S. E. Bradforth, E. Schwegler and G. Galli, Sci. Adv., 2017, 3, e1603210.
42. O. Link, E. Vöhringer-Martinez, E. Lugovoj, Y. Liu, K. Siefermann, M. Faubel, H. Grubmüller, R. B. Gerber, Y. Miller and B. Abel, Faraday Discuss., 2009, 141, 67.
43. E. Vöhringer-Martinez, O. Link, E. Lugovoy, K. Siefermann, F. Wiederschein, H. Grubmüller and B. Abel, Phys. Chem. Chem. Phys., 2014, 16, 19365.
44. T. Gladytz, B. Abel and K. R. Siefermann, Phys. Chem. Chem. Phys., 2015, 17, 4926.
45. T. A. Pham, C. Zhang, E. Schwegler and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060202.
46. C. W. Swartz and X. Wu, Phys. Rev. Lett., 2013, 111, 087801.
47. D. Opalka, T. A. Pham, M. Sprik and G. Galli, J. Chem. Phys., 2014, 141, 034501.
48. J. H. Skone, M. Govoni and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195112.
49. D. J. Frost, Elements, 2008, 4, 171.
50. A. B. Thompson, Nature, 1992, 358, 295.
51. M. Chen, L. Zheng, B. Santra, H.-Y. Ko, R. A. DiStasio Jr, M. L. Klein, R. Car and X. Wu, Nat. Chem., 2018, 10, 413.
52. M. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Chem. Phys., 1995, 103, 150.
53. D. Marx, A. Chandra and M. E. Tuckerman, Chem. Rev., 2010, 110, 2174.
54. F. Gygi, IBM J. Res. Dev., 2008, 52, 137.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
56. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
57. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901.
58. D. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494.
59. R. Sundararaman and Y. Ping, J. Chem. Phys., 2017, 146, 104109.
60. C. G. Van de Walle and R. M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5621.
61. L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001.
62. L. Zhang, J. Han, H. Wang, W. A. Saidi, R. Car and E. Weinan, Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS18, Curran Associates Inc., Red Hook, NY, USA, 2018, pp. 4441–4451.
63. H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178.
64. L. Zhang, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2021, 126, 236001.
65. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
66. D. J. Price and C. L. Brooks III, J. Chem. Phys., 2004, 121, 10096.
67. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2021, 108171.
68. S. Plimpton, J. Comput. Phys., 1995, 117, 1.
69. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188.
70. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982.
71. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.

---

Footnote

† These two authors contributed equally, listed in alphabetical order.

---