Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thallium adsorption onto phyllosilicate minerals†
Andreas
Voegelin
 *a,
Silvan
Wick
a,
Numa
Pfenninger
a,
Stefan
Mangold
b,
Bart
Baeyens
c and
Maria Marques
Fernandes
c
*a,
Silvan
Wick
a,
Numa
Pfenninger
a,
Stefan
Mangold
b,
Bart
Baeyens
c and
Maria Marques
Fernandes
c
aEawag, Swiss Federal Institute of Aquatic Science and Technology, Ueberlandstrasse 133, CH-8600 Duebendorf, Switzerland. E-mail: andreas.voegelin@eawag.ch
bKarlsruhe Institute of Technology, Hermann-von-Helmholtz Platz 1, D-76344 Eggenstein-Leopoldshafen, Germany
cPaul Scherrer Institute, Forschungsstrasse 111, CH-5232 Villigen PSI, Switzerland
First published on 24th May 2022
Abstract
The adsorption of thallium (Tl) onto phyllosilicate minerals plays a critical role in the retention of Tl in soils and sediments and the potential transfer of Tl into plants and groundwater. Especially micaceous minerals are thought to strongly bind monovalent Tl(I), in analogy to their strong binding of Cs. To advance the understanding of Tl(I) adsorption onto phyllosilicate minerals, we studied the adsorption of Tl(I) onto Na- and K-saturated illite and Na-saturated smectite, two muscovites, two vermiculites and a naturally Tl-enriched soil clay mineral fraction. Macroscopic adsorption isotherms were combined with the characterization of the adsorbed Tl by X-ray absorption spectroscopy (XAS). In combination, the results suggest that the adsorption of Tl(I) onto phyllosilicate minerals can be interpreted in terms of three major uptake paths: (i) highest-affinity inner-sphere adsorption of dehydrated Tl+ on a very low number of adsorption sites at the wedge of frayed particle edges of illite and around collapsed zones in vermiculite interlayers through complexation between two siloxane cavities, (ii) intermediate-affinity inner-sphere adsorption of partially dehydrated Tl+ on the planar surfaces of illite and muscovite through complexation onto siloxane cavities, (iii) low-affinity adsorption of hydrated Tl+, especially in the hydrated interlayers of smectite and expanded vermiculite. At the frayed edges of illite particles and in the vermiculite interlayer, Tl uptake can lead to the formation of new wedge sites that enable further adsorption of dehydrated Tl+. On the soil clay fraction, a shift in Tl(I) uptake from frayed edge sites (on illite) to planar sites (on illite and muscovite) was observed with increasing Tl(I) loading. The results from this study show that the adsorption of Tl(I) onto phyllosilicate minerals follows the same trends as reported for Cs and Rb and thus suggests that concepts to describe the retention of (radio)cesium by different types of phyllosilicate minerals in soils, sediments and rocks are also applicable to Tl(I).
Environmental significanceThe adsorption of thallium onto phyllosilicate minerals critically impacts on the retention and solubility of this potentially toxic element in soils and sediments. In this work, we studied thallium adsorption onto a range of environmentally relevant phyllosilicate minerals through a combination of macroscopic and synchrotron spectroscopic experiments. The results demonstrate the link between the mode and affinity of thallium uptake and confirm the notion that thallium is strongly retained by micaceous phyllosilicate minerals, in analogy to cesium. Model concepts regarding the retention of radiocesium by phyllosilicate minerals in soils and sediments are thus transferable to thallium and the assessment of its fate and impact in pristine and contaminated environments. |
1. Introduction
Thallium (Tl) is a potentially toxic trace metal that can pose a serious threat to human and environmental health.1 In the environment, Tl dominantly occurs as monovalent Tl(I), more rarely as trivalent Tl(III) in poorly soluble Tl2O3 (avicennite) or adsorbed onto hexagonal birnessite.3–5 In natural waters over the common pH and Eh range, the Tl+ cation is the prevalent and thermodynamically most stable Tl species.2,3 Monovalent Tl(I) exhibits chalcophilic and lithophilic character. Its lithophilic properties are due to the fact that the Tl+ cation has a similar ionic radius and a similarly low hydration enthalpy as K+, Rb+ and Cs+ cations. Accordingly, monovalent Tl(I) often shows a reactivity similar to K, Rb and Cs6–8 and can substitute K in a wide range of minerals, including mica and micaceous clay minerals.2,9,10From contaminated soils or sediments, Tl may be released into groundwater11,12 or be taken up by plants,13–15 and may thereby also enter the human food chain.16,17 The mobility and bioavailability of Tl in soils and sediments are dependent on its solubility, which is controlled by adsorption processes. Because of the geochemical properties of Tl, illite and related clay minerals have long been assumed to be key adsorbents of Tl in soils and sediments.18–20 In a study on a naturally Tl-rich soil developed on mineralized parent rock, we used X-ray absorption spectroscopy (XAS) to characterize the speciation of Tl and found that most Tl in topsoils was associated with illite (or other micaceous minerals).4 More recently, we concluded that most geogenic Tl in this soil was retained by fixation in the interlayers of illite, a minor fraction by adsorption as exchangeable Tl.21 A laboratory study on the adsorption of Tl onto purified natural illite8 showed that the adsorption of Tl in the presence of competing cations can be described by a 3-site cation exchange model that has originally been developed to model the highly selective adsorption of Cs+ and Rb+ onto illite.22 In this model, a limited number of high-affinity sites (“frayed edge sites”, FES) is assumed to represent the adsorption of dehydrated Tl+ (or Cs+, Rb+, K+) in the wedge a the frayed edges of illite platelets.23 A high number of low-affinity sites on the other hand is assumed to account for the adsorption of Tl+ on planar surfaces (planar sites, “PS”). The third type of site required to reproduce macroscopic adsorption isotherms is characterized by intermediate affinity and abundance, but its mechanistic interpretation is uncertain (“type-2 sites”). Cation exchange selectivity coefficients derived for Tl+ adsorption onto illite using the 3-site cation exchange model fell between reported selectivity coefficients of Cs+ and Rb+.8 XAS data supported the interpretation that Tl+ strongly adsorbed as dehydrated cation at frayed edge sites. Based on these results, and on the known geochemical analogy of Tl with Cs and Rb, it is plausible that other micaceous minerals that are known to strongly bind Cs+ and Rb+, such as muscovite,24–26 weathered biotite,27 vermiculite,28,29 illite-interlayered smectite,30 or glauconite31 are also important adsorbents for Tl. To date, however, only limited data exists on the uptake of Tl by muscovite or vermiculite.20,32,33
The aim of the present study was to contribute to a better understanding of the adsorption of Tl(I) onto mica and (micaceous) clay minerals. To this end, adsorption isotherms for Tl(I) were measured on Na- and K-exchanged illite, two muscovites and two vermiculites as well as on smectite. Adsorbed Tl was analyzed by Tl LIII-edge XAS to monitor variations in the mode of Tl uptake between minerals and as a function of Tl loading. Furthermore, we also studied the adsorption of Tl onto a purified clay mineral assemblage from a naturally Tl-rich topsoil.
2. Materials and methods
2.1. Phyllosilicate minerals used for Tl adsorption experiments
Illite du Puy (IdP) was purified and prepared as homoionic Na-exchanged IdP (Na–IdP; 19.8 g L−1; 100 mM NaCl) or K-exchanged IdP (K–IdP; 28.0 g L−1; 10 mM KCl) suspensions as described previously.8 Wyoming smectite (SWy-2) was purchased from the Source Clays Repository of the Clay Minerals Society (Chantilly, VA, USA) and was prepared as homoionic Na-exchanged SWy-2 suspension (Na–SWy; 20.1 g L−1; 100 mM NaCl) as described in previous work.34 The Na–IdP, K–IdP and Na–SWy suspensions were stored at 4 °C in the dark for further use.Adsorption experiments with muscovite and vermiculite were performed two times with different samples and slightly different laboratory protocols (A and B). Natural muscovite A (Musc-A; unknown origin) and thermally exfoliated vermiculite A (Verm-A; Vermex M, 2–4 mm particle size; Isola Vermiculite AG, Switzerland) were provided by Kurt Barmettler from the Soil Chemistry Group at ETH Zurich (Switzerland). Natural muscovite B (Musc-B; Aspanger Bergbau und Mineralwerke GmbH & Co KG, Austria) and thermally exfoliated vermiculite B (Verm-B; Thermax®, Austria) were kindly provided by Michael Plötze from ETH Zurich (Switzerland). The vermiculite Verm-B has previously been used to study Cs adsorption35 and the effect of sample pre-treatment on its cation exchange capacity (CEC).36
For the adsorption experiments, about 1 g of Musc-A, Verm-A and Verm-B were ground in a ball mill using a tungsten carbide jar (Retsch MM200; 17 hertz; 30 seconds). Musc-B was used as received. The minerals were repeatedly Na-exchanged in 1 M NaNO3, washed several times with doubly deionized (DDI) water, and freeze dried for further use.
A soil clay mineral fraction (SCF) was extracted from a naturally Tl-rich soil and treated to remove organic matter and oxides as described previously.21 The Na-exchanged SCF was stored as suspension in the dark at 4 °C for further use.
2.2. Mineral characterization
The illite used in this work has been used in an earlier Tl adsorption study,8 and has also been used to study the protonation and metal uptake of illite.37,38 Details on the purification procedure and the composition of Na–IdP can be found in these earlier studies. Another batch of illite from the same locality (Le Puy-en-Velay, France) has previously been used to study the adsorption of Cs.39 The muscovite and vermiculite samples were analyzed by X-ray diffraction (XRD) and scanning electron microscopy coupled with energy dispersive X-ray detection (SEM-EDX). The combined results confirmed that the samples consisted of muscovite or vermiculite (ESI Sections 1.1 and 1.2†). The soil clay mineral fraction (SCF) was extracted from a topsoil sample (PI 00–20) examined in an earlier study on the speciation of geogenic Tl in soils from Erzmatt (Switzerland).4 This soil sample had a pH of 6.5 (10 mM CaCl2) and contained 54% clay, 2.6% organic carbon, and 120 mg kg−1 geogenic Tl. The clay mineral fraction of this soil sample consists primarily of illite/muscovite, hydroxy-interlayered vermiculite/chlorite and interstratified illite-smectite.4 XRD data collected on the oriented Mg- and K-exchanged SCF and SEM-EDX data collected on the SCF qualitatively confirmed this analysis (ESI Sections 1.1 and 1.2†). Semiquantitative laboratory micro-XRF analysis of the SCF indicated a geogenic Tl content of 260 mg kg−1. The cation exchange capacities (CEC) of all samples are listed in Table 1 (see ESI Section 1.3† for details on source and method of determination).| Mineral | CEC (mmol kg−1) | Linear regression equations | Log(Kd/(L kg−1)) | Log(Kc,Tl–Na) | ||
|---|---|---|---|---|---|---|
| Log(KF) | n F | r 2 | ||||
| Na–IdP | 260 | 0.52 (0.20) | 0.48 (0.04) | 0.98 | 3.4 | 3.0 |
| K–IdP | 260 | 1.49 (0.08) | 0.85 (0.02) | 1.00 | 2.3 | — |
| Na–SWy | 860 | 0.91 (0.13) | 0.79 (0.03) | 1.00 | 2.0 | 1.1 |
| Musc-A | 121 | 0.88 (0.12) | 0.61 (0.02) | 1.00 | 3.0 | 3.0 |
| Musc-B | 144 | 1.10 (0.20) | 0.61 (0.04) | 1.00 | 3.3 | 3.1 |
| Verm-A | 1320 | 5.45 (0.45) | 1.53 (0.09) | 0.99 | 2.6 | 1.4 |
| Verm-B | 1590 | 13.5 (3.1) | 3.09 (0.63) | 0.89 | 2.0 | 0.8 |
| SCF | 290 | 0.71 (0.08) | 0.57 (0.02) | 1.00 | 3.1 | 2.6 |
2.3. Adsorption experiments
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 30
000 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 Tl(I) (in case of 100% Tl adsorption). Subsequently, the concentration of the background electrolyte was readjusted to the desired value by addition of a 10-fold concentrated electrolyte solution. After shaking by hand, the pH was measured and, if lower than 6.4, adjusted to 7.0 using NaOH. Subsequently, the suspensions were placed on an overhead shaker and reacted for about 14 days at room temperature. After phase separation by ultra-centrifugation (108
000 mg kg−1 Tl(I) (in case of 100% Tl adsorption). Subsequently, the concentration of the background electrolyte was readjusted to the desired value by addition of a 10-fold concentrated electrolyte solution. After shaking by hand, the pH was measured and, if lower than 6.4, adjusted to 7.0 using NaOH. Subsequently, the suspensions were placed on an overhead shaker and reacted for about 14 days at room temperature. After phase separation by ultra-centrifugation (108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g (max), 30
000g (max), 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, 1 h, Beckman Coulter Avanti J30i High-Performance Centrifuge), the pH was recorded in all supernatants before two 7 mL aliquots were sampled and acidified with 100 μL 65% HNO3 (Suprapur) for analysis by inductively coupled plasma mass spectrometry (ICP-MS).
000 rpm, 1 h, Beckman Coulter Avanti J30i High-Performance Centrifuge), the pH was recorded in all supernatants before two 7 mL aliquots were sampled and acidified with 100 μL 65% HNO3 (Suprapur) for analysis by inductively coupled plasma mass spectrometry (ICP-MS).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 Tl. The suspensions were reacted for 7 days at room temperature on an overhead shaker. After centrifugation (2700g, 4000 rpm, 5 min, Rotofix 32 Hettich), 20 mL aliquots of the supernatant were filtered, acidified and diluted for ICP-MS analysis, and pH was recorded in the residual solution.
000 mg kg−1 Tl. The suspensions were reacted for 7 days at room temperature on an overhead shaker. After centrifugation (2700g, 4000 rpm, 5 min, Rotofix 32 Hettich), 20 mL aliquots of the supernatant were filtered, acidified and diluted for ICP-MS analysis, and pH was recorded in the residual solution.
For adsorption experiments with Musc-B and Verm-B, the 50 mL PE tubes were filled with 26 mL of 0.1 M NaNO3, followed by the addition of 150 mg of the dried solids. If the pH of the suspensions was >8, it was set to ∼7 by addition of 1 M HCl. Subsequently, Tl(I) was spiked using a 10 mM TlNO3 stock solution to achieve nominal Tl(I) loadings of 300 to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1. After reaction for 7 days on an overhead shaker, the suspensions were centrifuged (400 rpm, 5 min), a 10 mL aliquot was filtered (0.2 μm nylon membrane) and acidified for analysis by ICP-MS, and pH was recorded in the remaining supernatant. The adsorption experiments with Musc-B were conducted in duplicates. After adsorption, the second sample for each loading was extracted with 0.1 M Ca(NO3)2. For this purpose, the supernatant after adsorption was decanted, and 50 mL of 0.1 M Ca(NO3)2 were added to the PE tubes. After reaction for 2 h on a table shaker and subsequent centrifugation, aliquots of the supernatant were filtered and acidified for analysis by ICP-MS, and the solids collected for XAS analysis.
000 mg kg−1. After reaction for 7 days on an overhead shaker, the suspensions were centrifuged (400 rpm, 5 min), a 10 mL aliquot was filtered (0.2 μm nylon membrane) and acidified for analysis by ICP-MS, and pH was recorded in the remaining supernatant. The adsorption experiments with Musc-B were conducted in duplicates. After adsorption, the second sample for each loading was extracted with 0.1 M Ca(NO3)2. For this purpose, the supernatant after adsorption was decanted, and 50 mL of 0.1 M Ca(NO3)2 were added to the PE tubes. After reaction for 2 h on a table shaker and subsequent centrifugation, aliquots of the supernatant were filtered and acidified for analysis by ICP-MS, and the solids collected for XAS analysis.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 Tl. The suspensions were reacted for 7 days. After centrifugation, a filtered aliquot (0.2 μm nylon membrane) of the supernatant was sampled for ICP-MS analysis, and the final pH was recorded in the remaining supernatant.
000 mg kg−1 Tl. The suspensions were reacted for 7 days. After centrifugation, a filtered aliquot (0.2 μm nylon membrane) of the supernatant was sampled for ICP-MS analysis, and the final pH was recorded in the remaining supernatant.
2.4. X-ray absorption spectroscopy
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 Tl were in general recorded in fluorescence mode, samples with Tl loadings of 10
000 mg kg−1 Tl were in general recorded in fluorescence mode, samples with Tl loadings of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and higher in transmission mode. The X-ray photon energy was aligned by measuring the X-ray near-edge structure (XANES) spectrum of Tl2O3 (maximum of whiteline at 12
000 and higher in transmission mode. The X-ray photon energy was aligned by measuring the X-ray near-edge structure (XANES) spectrum of Tl2O3 (maximum of whiteline at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 eV) and/or elemental Se(0) (K-edge; first maximum of first derivative at 12
688 eV) and/or elemental Se(0) (K-edge; first maximum of first derivative at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658 eV). All samples were measured at room temperature, few selected samples also at 20 K. An overview over all XAS measurements is given in Table S4.†
658 eV). All samples were measured at room temperature, few selected samples also at 20 K. An overview over all XAS measurements is given in Table S4.†
3. Results and discussion
3.1. Adsorption data
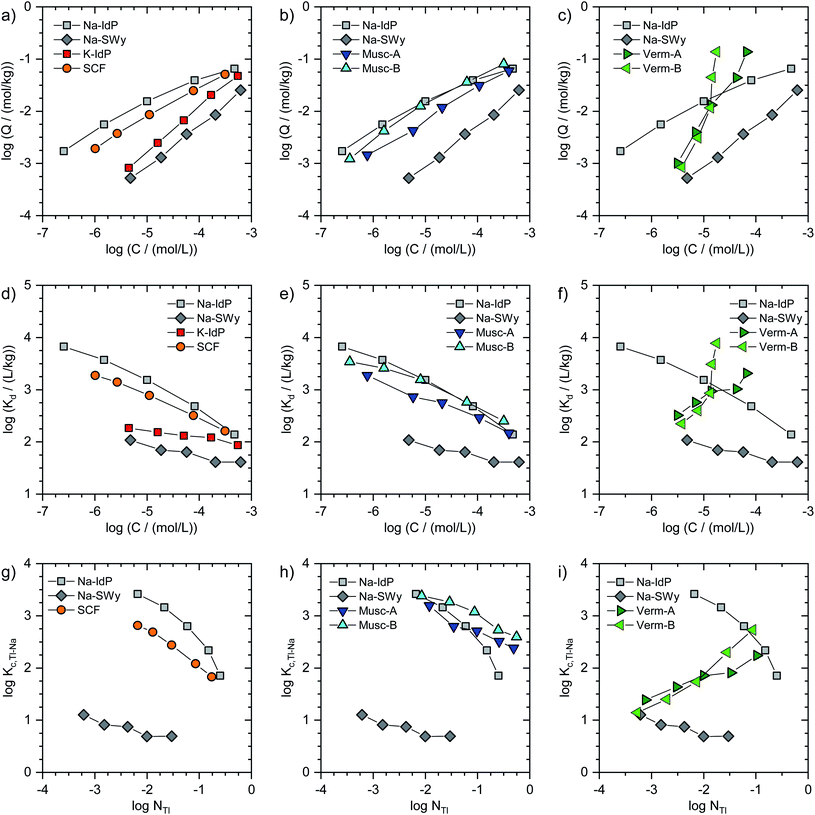
In Fig. 1, the Tl adsorption data for all phyllosilicate minerals are shown on the log-scale in three formats: (i) adsorbed amounts (Q) versus dissolved concentrations (C) (Fig. 1a–c), (ii) distribution coefficients (Kd) versus dissolved concentrations (C) (Fig. 1d–f), and (iii) cation exchange selectivity coefficients (Kc,Tl–Na) versus equivalent fractions of adsorbed Tl (NTl) (Fig. 1g–i). The tabulated results are given in the ESI (Table S3).† The adsorption data for Na–IdP and Na–SWy are shown in all panels for comparison with the other adsorbents. Final pH values in the suspensions ranged between pH 6.5 and pH 7.1 for Na–IdP, K–IdP, Na–SWy (one sample pH 7.9), Musc-A and SCF, and between pH 7.8 and pH 8.6 for Musc-B, Verm-A and Verm-B (Table S3†).The log-scale adsorption isotherms (Fig. 1a–c) were described by linear regression equations that correspond to the logarithmic form of the Freundlich isotherm equation:
Log(Q/(mol kg−1)) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KF + nF × log(C/(mol L−1)) KF + nF × log(C/(mol L−1)) | (1) |
Log(Kd/(L kg−1)) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KF + (nF − 1) × log(C/(mol L−1)) KF + (nF − 1) × log(C/(mol L−1)) | (2) |
For brevity, we in the following refer to log(Q/(mol kg−1)) as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q, to log(C/(mol L−1)) as log
Q, to log(C/(mol L−1)) as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, and to log(Kd/(L kg−1)) as log
C, and to log(Kd/(L kg−1)) as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd. Interpolated log
Kd. Interpolated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd values for a Tl concentration of 3.2 μM (log
Kd values for a Tl concentration of 3.2 μM (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = −5.5) are listed in Table 1.
C = −5.5) are listed in Table 1.
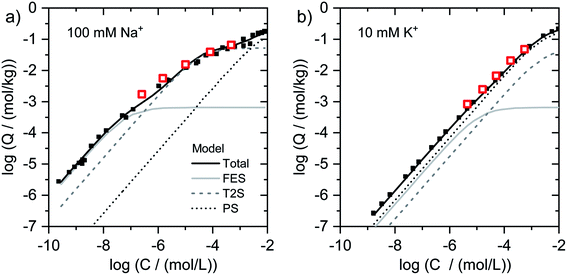 | ||
| Fig. 2 Isotherms for Tl adsorption onto (a) Na–IdP and (b) K–IdP as a function of dissolved Tl. Data from the present work (open red squares) are shown together with published adsorption data over larger concentrations ranges from Wick et al. (2018)8 (black squares) and corresponding model calculations based on the 3-site cation exchange model for illite (FES = frayed edge sites, T2S = type-2 sites; PS = planar sites). | ||
For the other adsorbents studied in this work, the available adsorption data did not allow to derive parameters for detailed (multisite) adsorption models. Nevertheless, conditional cation exchange selectivity coefficients that treat the entire CEC of the adsorbents as a single type of cation exchange site could be derived and interpreted in terms of their dependence on the equivalent fraction of adsorbed Tl. The exchange of adsorbed Na by Tl can be described by the cation exchange reaction
| NaX + Tl+ ↔ TlX + Na+ | (3) |
| Kc,Tl–Na = (NTl × CNa)/(NNa × CTl) | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = −5.5), using eqn (1) to derive the respective log
C = −5.5), using eqn (1) to derive the respective log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q. In Fig. 1g–i, the adsorption data for all adsorbents (except K–IdP where adsorption was measured in 10 mM K+ electrolyte) are shown as log(Kc,Tl–Na) versus log(NTl) (in the following referred to as log
Q. In Fig. 1g–i, the adsorption data for all adsorbents (except K–IdP where adsorption was measured in 10 mM K+ electrolyte) are shown as log(Kc,Tl–Na) versus log(NTl) (in the following referred to as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na and log
Kc,Tl–Na and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NTl, respectively). The data for Na–IdP and Na–SWy are shown in all panels for comparison. In the case of Na–IdP (Fig. 1g), log
NTl, respectively). The data for Na–IdP and Na–SWy are shown in all panels for comparison. In the case of Na–IdP (Fig. 1g), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na decreased by about 1.6
Kc,Tl–Na decreased by about 1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units from lowest to highest log
log units from lowest to highest log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NTl (Fig. 1g). This marked decrease reflects the stepwise saturation of an increasing number of adsorption sites with decreasing cation exchange selectivity, as represented by the progressive saturation of FES, T2S and PS in the 3-site cation exchange model calculations (Fig. 2).
NTl (Fig. 1g). This marked decrease reflects the stepwise saturation of an increasing number of adsorption sites with decreasing cation exchange selectivity, as represented by the progressive saturation of FES, T2S and PS in the 3-site cation exchange model calculations (Fig. 2).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NTl, the log
NTl, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na decreased by about 0.5
Kc,Tl–Na decreased by about 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units, with an average log
log units, with an average log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na of 0.85 ± 0.17 (Fig. 1g). The relatively low log
Kc,Tl–Na of 0.85 ± 0.17 (Fig. 1g). The relatively low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na at even the lowest log
Kc,Tl–Na at even the lowest log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NTl suggests that high affinity adsorption sites were not relevant over the probed concentration range. Indeed, a study on Cs adsorption onto another smectite indicated that high affinity adsorption sites similar to FES only contributed to Cs adsorption at Cs loadings far below the lowest Tl loadings in the present work.30 For Cs–Na exchange on the dominant cation exchange sites that represent most of the CEC, on the other hand, a log
NTl suggests that high affinity adsorption sites were not relevant over the probed concentration range. Indeed, a study on Cs adsorption onto another smectite indicated that high affinity adsorption sites similar to FES only contributed to Cs adsorption at Cs loadings far below the lowest Tl loadings in the present work.30 For Cs–Na exchange on the dominant cation exchange sites that represent most of the CEC, on the other hand, a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Cs–Na of 1.7 ± 0.7 had been derived,30 about 0.8
Kc,Cs–Na of 1.7 ± 0.7 had been derived,30 about 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units larger than the log
log units larger than the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na for Na–SWy reported above. For Cs–Na and Rb–Na exchange on Wyoming bentonite (similar to Na–SWy used in the present work), log
Kc,Tl–Na for Na–SWy reported above. For Cs–Na and Rb–Na exchange on Wyoming bentonite (similar to Na–SWy used in the present work), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Cs–Na and log
Kc,Cs–Na and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Rb–Na values of ∼1.2 and ∼0.5 have been reported for NCs or NRb of ∼0.05,45,46 compared to a log
Kc,Rb–Na values of ∼1.2 and ∼0.5 have been reported for NCs or NRb of ∼0.05,45,46 compared to a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na of 0.7 observed in the current study for NTl = 0.03 (Fig. 1g). Another study derived a log
Kc,Tl–Na of 0.7 observed in the current study for NTl = 0.03 (Fig. 1g). Another study derived a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Cs–Na of 0.8 for Na-saturated Wyoming smectite at a low Na background electrolyte concentration of 5 mM that allowed for a larger contribution of low-affinity Cs adsorption.47 Overall, the comparison of reported cation exchange selectivity coefficients for Cs–Na and Rb–Na exchange on Na-saturated smectite with the log
Kc,Cs–Na of 0.8 for Na-saturated Wyoming smectite at a low Na background electrolyte concentration of 5 mM that allowed for a larger contribution of low-affinity Cs adsorption.47 Overall, the comparison of reported cation exchange selectivity coefficients for Cs–Na and Rb–Na exchange on Na-saturated smectite with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na derived in the current work indicated that the adsorption affinity of Tl on smectite falls between the affinities of Cs and Rb, as previously reported for cation exchange on illite.8
Kc,Tl–Na derived in the current work indicated that the adsorption affinity of Tl on smectite falls between the affinities of Cs and Rb, as previously reported for cation exchange on illite.8
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units in terms of Tl loading at a given dissolved Tl concentration. At low dissolved Tl concentrations, the Tl loadings were slightly lower than for Na–IdP, but markedly higher than for Na–SWy, showing that the muscovites can bind Tl with very high affinity; as reflected by log
log units in terms of Tl loading at a given dissolved Tl concentration. At low dissolved Tl concentrations, the Tl loadings were slightly lower than for Na–IdP, but markedly higher than for Na–SWy, showing that the muscovites can bind Tl with very high affinity; as reflected by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd values of 3.0 (Musc-A) and 3.3 (Musc-B) for C = 3.2 μM (Table 1). At the highest dissolved Tl concentrations, the muscovites adsorbed similar amounts of Tl as Na–IdP (Fig. 1b and e). In combination with their lower CEC values, this suggested that the muscovites can strongly bind Tl even at high equivalent fractions (Fig. 1h). The extraction of one set of Tl-loaded Musc-B samples with 0.1 M Ca(NO3)2 (at a high solution-to-solid ratio of 333 mL g−1) released only between 1.4% of the adsorbed Tl at the lowest loading and 19% at the highest loading, confirming that Tl was strongly adsorbed.
Kd values of 3.0 (Musc-A) and 3.3 (Musc-B) for C = 3.2 μM (Table 1). At the highest dissolved Tl concentrations, the muscovites adsorbed similar amounts of Tl as Na–IdP (Fig. 1b and e). In combination with their lower CEC values, this suggested that the muscovites can strongly bind Tl even at high equivalent fractions (Fig. 1h). The extraction of one set of Tl-loaded Musc-B samples with 0.1 M Ca(NO3)2 (at a high solution-to-solid ratio of 333 mL g−1) released only between 1.4% of the adsorbed Tl at the lowest loading and 19% at the highest loading, confirming that Tl was strongly adsorbed.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na (Fig. 1i). At the lowest Tl loadings, the adsorption of Tl onto the Na-exchanged vermiculites resembled the adsorption of Tl onto Na–SWy. Towards the highest Tl loadings, the adsorption affinity of Tl for the vermiculites even exceeded the one for Na–IdP (Fig. 1f and i). Considering earlier results on the binding of Cs and Tl by vermiculite,28,33,48,49 this trend was attributed to Tl-induced interlayer collapse and the generation of an increasing number of high-affinity sorption sites in fresh wedge zones.
Kc,Tl–Na (Fig. 1i). At the lowest Tl loadings, the adsorption of Tl onto the Na-exchanged vermiculites resembled the adsorption of Tl onto Na–SWy. Towards the highest Tl loadings, the adsorption affinity of Tl for the vermiculites even exceeded the one for Na–IdP (Fig. 1f and i). Considering earlier results on the binding of Cs and Tl by vermiculite,28,33,48,49 this trend was attributed to Tl-induced interlayer collapse and the generation of an increasing number of high-affinity sorption sites in fresh wedge zones.
3.2. X-ray absorption spectroscopy
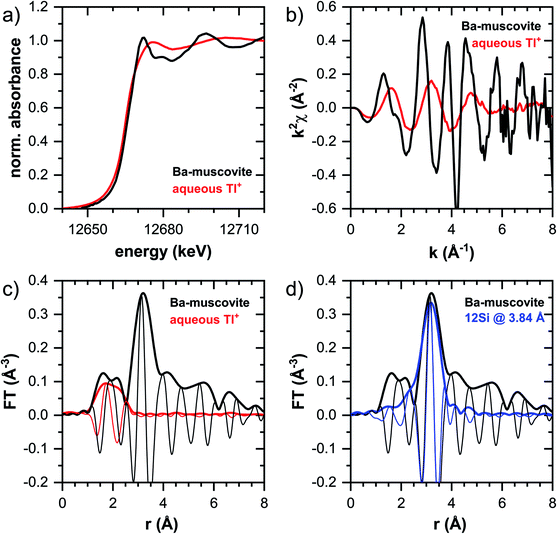
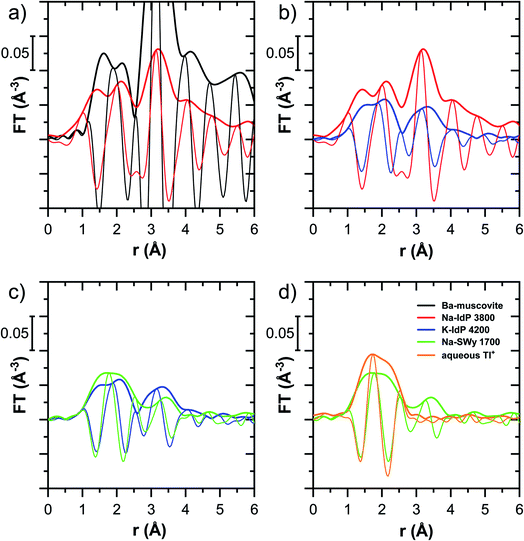
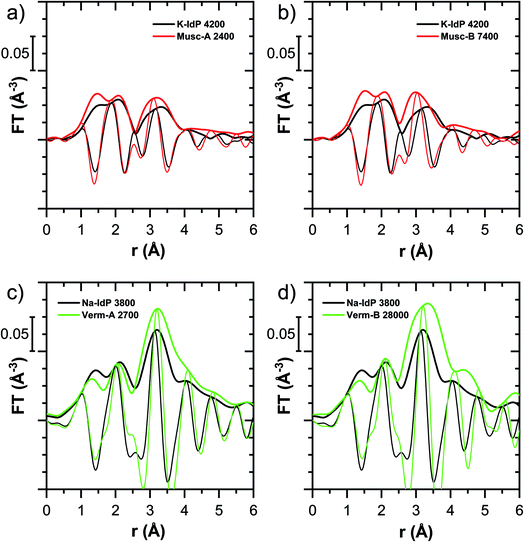
In this section, the Tl LIII-edge XANES and EXAFS reference spectra of Tl-containing Ba–muscovite and aqueous Tl+ are first discussed. Subsequently, an overview over spectral trends in the sample spectra is given, followed by a step-wise comparison and interpretation of spectral trends among the different minerals and as a function of Tl loading, and in relation to the macroscopic adsorption data. An overview over all analyzed spectra is given in Table S4.†The EXAFS spectrum of Tl(I) in Ba–muscovite features much higher amplitudes than the spectrum of hydrated aqueous Tl+ (Fig. 3). In the Fourier-transform, the magnitude of the first peak is very low for both compounds. This can be explained by substantial disorder in first-shell Tl–O coordination due to the lone electron pair of the Tl+ cation50 and the destructive interferences arising from a wide spread in Tl–O interatomic distances. The EXAFS spectrum of aqueous Tl+ has previously been described by 2 short and 2 long Tl–O paths with an average Tl–O distance of 2.875 Å.50 The shift of the imaginary part of the first-shell of Tl in Ba–muscovite to higher r-values points to a larger average first-shell Tl–O distance than in aqueous Tl+. This difference could be expected based on the K–O distance of 12-fold coordinated K+ in illite of 3.109 Å51 and the larger ionic radius of 12-fold coordinated Tl+ (1.70 Å) than K+ (1.64 Å).52
The analysis of the EXAFS of Tl-containing Ba–muscovite shown in Fig. 3 and of second spectrum recorded at 20 K by shell fitting indicated that the second FT peak can be modelled with 12 Si atoms at an average distance of 3.84 Å from the absorbing Tl atom, based on a Tl–Si single-scattering path derived from the structure of illite (ESI Section 3, Table S6 and Fig. S17†). The fitted distance was in good agreement with an average second-shell K–Si distance of 3.774 Å in illite51 and an EXAFS-derived Cs–Si distance of Cs incorporated into illite of 3.99 Å,53 considering that the ionic radius of 12-fold coordinated Tl+ (1.70 Å) falls in between the ionic radii of K+ (1.64 Å) and Cs+ (1.88 Å).52 We thus interpreted the peak around ∼3.2 Å in the Fourier-transformed EXAFS spectrum of Ba-rich muscovite as arising from 12-fold Si-coordinated Tl(I) between two adjacent siloxane cavities in the interlayer.
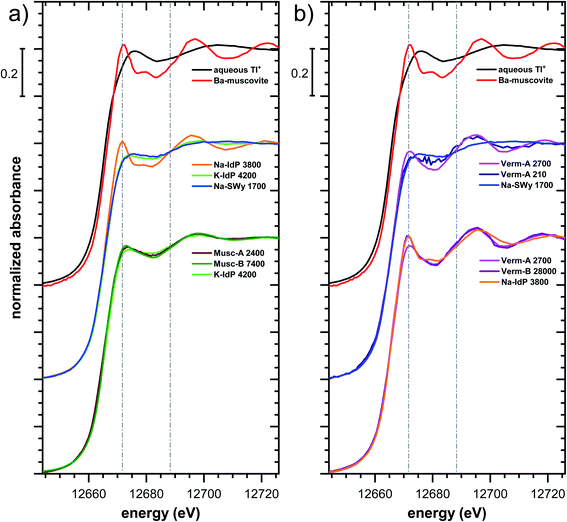 | ||
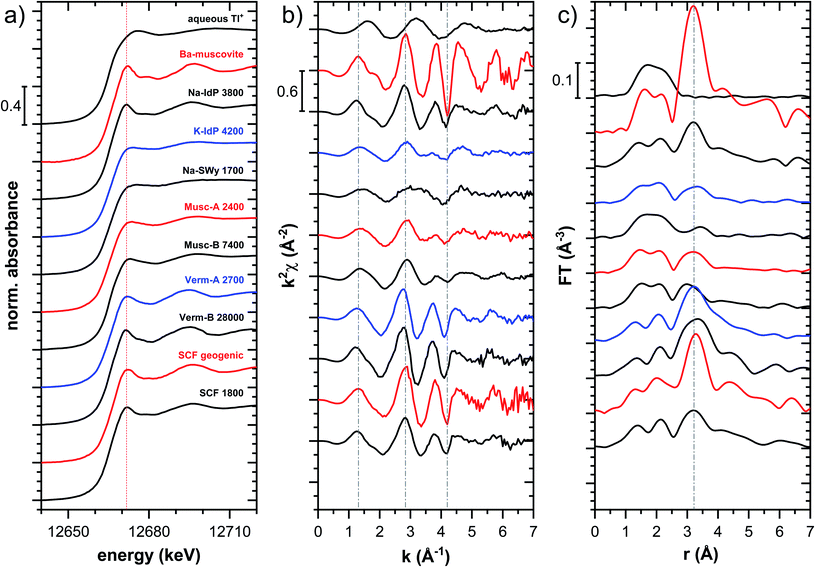
| Fig. 5 Comparison of the Tl LIII-edge XANES spectra of selected Tl-loaded phyllosilicate samples. Numbers in spectra labels indicate the Tl loading of the respective phyllosilicate in mg kg−1. Vertical lines serve to guide the eye. An enlarged version of figure focusing on post-edge oscillations is provided in Fig. S16.† | ||
The XANES and EXAFS spectra of the Tl-loaded phyllosilicate samples (Fig. 4–7, S6–S15 and S18–S20†) lacked detectable spectral contributions of Tl(III). Considering that the XANES and EXAFS spectra of Tl(III)-compounds are very distinct (Fig. S5†), this supported the expectation that oxidative uptake of Tl (as on vacancy-containing hexagonal birnessite5,54) was not relevant for the studied phyllosilicate minerals.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 (Fig. S6†), and matched closely to spectra of low amounts of Tl adsorbed onto Na–IdP from our earlier study8 (apart from beamline-related differences in X-ray energy resolution). In this earlier study, spectral changes at Tl loadings above ∼3800 mg kg−1 pointed to the increasing binding of hydrated Tl+ onto Na–IdP. Such a shift was not observed in the present study for two reasons: first, in our earlier study, the background Na concentration significantly decreased at Tl loadings above ∼3800 mg kg−1 due to dilution of the background electrolyte by the added Tl stock (which contained no Na), allowing for increasing low-affinity adsorption of hydrated Tl+ on planar surfaces. In contrast, in the present study, the background electrolyte concentration was kept constant at 100 mM Na at all Tl loadings, which limited the low-affinity adsorption of hydrated Tl+. Second, the highest Tl loading in the present study was about 4 times lower than in the earlier work, also limiting the extent of low-affinity uptake of hydrated Tl+.
000 mg kg−1 (Fig. S6†), and matched closely to spectra of low amounts of Tl adsorbed onto Na–IdP from our earlier study8 (apart from beamline-related differences in X-ray energy resolution). In this earlier study, spectral changes at Tl loadings above ∼3800 mg kg−1 pointed to the increasing binding of hydrated Tl+ onto Na–IdP. Such a shift was not observed in the present study for two reasons: first, in our earlier study, the background Na concentration significantly decreased at Tl loadings above ∼3800 mg kg−1 due to dilution of the background electrolyte by the added Tl stock (which contained no Na), allowing for increasing low-affinity adsorption of hydrated Tl+ on planar surfaces. In contrast, in the present study, the background electrolyte concentration was kept constant at 100 mM Na at all Tl loadings, which limited the low-affinity adsorption of hydrated Tl+. Second, the highest Tl loading in the present study was about 4 times lower than in the earlier work, also limiting the extent of low-affinity uptake of hydrated Tl+.
The EXAFS spectrum Na–IdP 3800 shown in Fig. 4 and 6 was recorded on a sample from our earlier study.8 This EXAFS spectrum rather than the one recorded on the analogous sample Na–IdP 3200 from the current study was used for further evaluation because of higher spectral quality. Comparison of the FT EXAFS spectrum of Na–IdP 3800 to the spectrum of Ba–muscovite (Fig. 6a) showed that the peak position and imaginary part of the second FT peak match closely. We therefore attribute the peak at ∼3.2 Å in the Na–IdP 3800 spectrum to contributions of second-shell Si around dehydrated Tl+ adsorbed at the frayed edges of illite platelets. Also above and below the second-shell Tl–Si peak, the oscillations in the imaginary part of the FT EXAFS of Na–IdP 3800 matched the oscillations of the spectrum of Tl-containing Ba–muscovite, supporting the interpretation that Tl in Na–IdP is similarly coordinated as in Ba–muscovite. In the case of dehydrated Tl+ adsorbed between two siloxane cavities, a Tl–Si coordination number of 12 as for Tl in the interlayer of Ba–muscovite would be expected. The much lower second-shell peak amplitude of Na–IdP 3800 may indicate that the disorder in Tl–Si coordination of Tl adsorbed at frayed edges of illite is much higher than in Ba–muscovite. A shell-fit analysis of the EXAFS spectra of Tl adsorbed onto Na–IdP recorded at room temperature and 20 K showed that the second-shell FT peak could be reasonably reproduced with 12 Si atoms at a distance of 3.95 Å, somewhat longer than in Ba–muscovite, and with higher Debye–Waller factors (ESI Section 3, Fig. S19 and Table S6†). Because this shell-fit was poorly constrained and based on a fixed coordination number, however, we cannot exclude that spectral contributions of Tl with lower degree of Tl–Si coordination limit the second-shell Tl–Si peak amplitude. Such contributions could arise from partially hydrated Tl+ that is adsorbed onto single siloxane cavities (with an ideal Tl–Si coordination number of 6) on planar surfaces or in the hydrated interlayer at frayed particle edges. However, we note that spectra of Na–IdP loaded with 300 mg kg−1 (1.5 mmol kg−1) and 50 mg kg−1 (0.25 mmol kg−1) Tl did not markedly deviate from the spectrum Na–IdP 3800 (19 mmol kg−1 Tl) (Fig. S18†), which suggests that local Tl coordination did not change over a wide range of Tl loadings. Taking further into account that the lowest loading of 0.25 mmol kg−1 was below the concentration of highest-affinity cation exchange sites in the 3-site cation exchange model for illite (0.65 mmol kg−1),8 it is therefore probable that the spectrum Na–IdP 3800 is representative for the coordination of Tl adsorbed at frayed edge sites between two siloxane cavities.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 additionally adsorbed Tl are shown in Fig. 8. Both the XANES and EXAFS of the spectrum of geogenic Tl exhibited weaker spectral features than the spectrum of Tl-containing Ba-muscovite (Fig. 3), but more pronounced signal amplitudes than the spectrum of Tl adsorbed at frayed edge sites of illite (Na–IdP 3800). Using LCF, both the XANES and EXAFS signal could be described by a major contribution from the spectrum Na–IdP 3800 and a minor contribution of the spectrum of Ba–muscovite (Fig. 8; Table 2). The XANES and EXAFS spectra of the sample SCF 1800 (with about 85% freshly adsorbed and 15% geogenic Tl) could be reasonably reproduced by a combination of a major contribution of the spectrum Na–IdP 3800 and a minor contribution of the spectrum Musc-A 2400 (Fig. 8). This result in combination with the adsorption data (Fig. 1) showed that the SCF has the capacity to bind freshly added Tl with high-affinity at frayed edge sites. The minor fraction of muscovite in the LCF, on the other hand, suggested that the capacity for high-affinity Tl uptake started to get saturated at a Tl loading of 1800 mg kg−1. This became apparent in the spectrum SCF 10000 with lowest signal amplitudes, for which LCF returned a similar or even larger fraction for the Musc-A 2400 than the Na–IdP 3800 reference spectrum. That the sum of fractions in the EXAFS LCF of the sample SCF 10000 was considerably lower than unity (Table 2) could indicate that the Musc-A 2400 reference spectrum did not adequately reproduce the spectral contribution of the least specifically adsorbed Tl. Importantly, reference spectra of Tl adsorbed onto vermiculite (Verm-A 2700, Verm-B 28000) were not required to reproduce the spectra of geogenic and adsorbed SCF.
000 mg kg−1 additionally adsorbed Tl are shown in Fig. 8. Both the XANES and EXAFS of the spectrum of geogenic Tl exhibited weaker spectral features than the spectrum of Tl-containing Ba-muscovite (Fig. 3), but more pronounced signal amplitudes than the spectrum of Tl adsorbed at frayed edge sites of illite (Na–IdP 3800). Using LCF, both the XANES and EXAFS signal could be described by a major contribution from the spectrum Na–IdP 3800 and a minor contribution of the spectrum of Ba–muscovite (Fig. 8; Table 2). The XANES and EXAFS spectra of the sample SCF 1800 (with about 85% freshly adsorbed and 15% geogenic Tl) could be reasonably reproduced by a combination of a major contribution of the spectrum Na–IdP 3800 and a minor contribution of the spectrum Musc-A 2400 (Fig. 8). This result in combination with the adsorption data (Fig. 1) showed that the SCF has the capacity to bind freshly added Tl with high-affinity at frayed edge sites. The minor fraction of muscovite in the LCF, on the other hand, suggested that the capacity for high-affinity Tl uptake started to get saturated at a Tl loading of 1800 mg kg−1. This became apparent in the spectrum SCF 10000 with lowest signal amplitudes, for which LCF returned a similar or even larger fraction for the Musc-A 2400 than the Na–IdP 3800 reference spectrum. That the sum of fractions in the EXAFS LCF of the sample SCF 10000 was considerably lower than unity (Table 2) could indicate that the Musc-A 2400 reference spectrum did not adequately reproduce the spectral contribution of the least specifically adsorbed Tl. Importantly, reference spectra of Tl adsorbed onto vermiculite (Verm-A 2700, Verm-B 28000) were not required to reproduce the spectra of geogenic and adsorbed SCF.
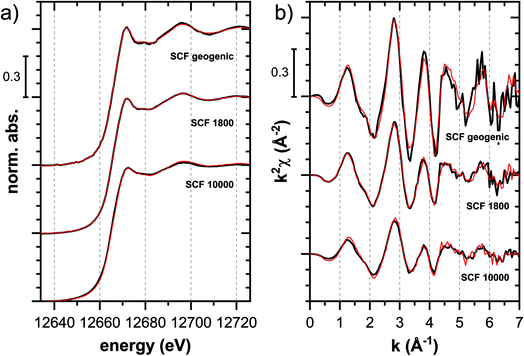 | ||
Fig. 8 Tl LIII-edge (a) XANES and (b) EXAFS spectra of a soil clay fraction (SCF) with ∼260 mg kg−1 geogenic Tl (SCF geogenic) and with an additional 1800 mg kg−1 (SCF 1800) or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 freshly adsorbed Tl (SCF 10000) (black lines) and linear fit reconstructions (red lines). LCF results are listed in Table 2. 000 mg kg−1 freshly adsorbed Tl (SCF 10000) (black lines) and linear fit reconstructions (red lines). LCF results are listed in Table 2. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646–12
646–12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 726 eV, fits of the EXAFS spectra over the k-range 3–7 Å−1. Fitted fractions were constrained to values between 0 and 1. The LCF reconstructions are shown in Fig. 8. NSSR = normalized sum of squared residuals
726 eV, fits of the EXAFS spectra over the k-range 3–7 Å−1. Fitted fractions were constrained to values between 0 and 1. The LCF reconstructions are shown in Fig. 8. NSSR = normalized sum of squared residuals
| Ba–musc | Na–IdP 3800 | Musc-A 2400 | Sum | NSSR | |
|---|---|---|---|---|---|
| XANES | |||||
| SCF geogenic | 0.26 | 0.74 | — | 1.00 | 0.00023 |
| SCF 1800 | — | 0.73 | 0.27 | 1.00 | 0.00004 |
| SCF 10000 | — | 0.35 | 0.66 | 1.01 | 0.00050 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| EXAFS | |||||
| SCF geogenic | 0.33 | 0.83 | — | 1.16 | 0.19 |
| SCF 1800 | — | 0.78 | 0.13 | 0.91 | 0.12 |
| SCF 10000 | — | 0.39 | 0.31 | 0.69 | 0.22 |
3.3. Relation between Tl adsorption affinity and uptake mechanisms
Decades of research offer evidence for several distinct modes of Cs adsorption onto clay minerals:57 (i) complexation of dehydrated Cs+ between two siloxane cavities at the wedge of the frayed edges of illite or weathered mica and at transitions between collapsed and expanded interlayer zones in vermiculite, (ii) complexation of partially hydrated Cs+ on a single siloxane cavity on the planar surfaces of muscovite or illite or in the expanded interlayer at frayed edges of illite, (iii) outer- or inner-sphere complexation of Cs+ in the hydrated interlayers of swelling clay minerals, and (iv) fixation of Cs+ in the interlayer of illite or muscovite over longer times. The combined macroscopic and spectroscopic results of this study show that the adsorption of Tl onto clay minerals occurs in analogy to Cs uptake and reveal a close link between the affinity and mode of Tl adsorption.For Na-exchanged illite, muscovite and smectite, the macroscopic Tl adsorption data at low dissolved Tl concentrations indicated a decrease in Tl adsorption affinity in the order Na–IdP ∼(≥) Musc-A ∼ Musc-B ≫ Na–SWy (Fig. 1; Table 1). In the XANES spectra, this trend was accompanied by a shift from spectra more closely resembling the spectrum of Tl in the interlayer of Ba–muscovite to spectra more closely resembling the spectrum of aqueous Tl+ (Fig. 4 and 5). In analogy, changes in k-space EXAFS amplitudes (Fig. 4) reflected a shift of the first-shell Tl–O peak from the distance of Ba–muscovite to the distance of aqueous Tl+ and a concomitant decrease of the second-shell Tl–Si peak amplitude (Fig. 4, 6 and 7). These spectral trends are in agreement with predominant adsorption of Tl onto Na–IdP via complexation of dehydrated Tl+ between two siloxane cavities at frayed edge sites, onto the muscovites via the binding of partly hydrated Tl+ onto single siloxane cavities on planar surfaces, and onto Na–SWy by mostly outer-sphere binding of hydrated Tl+ in hydrated interlayers. The combined results thus point to a decrease in adsorption affinity that is linked to the mode of Tl adsorption.
An analogous relation between adsorption affinity and adsorption mode was also observed for the two vermiculites: low levels of Tl were weakly adsorbed as hydrated Tl+ in the hydrated vermiculite interlayers, whereas high levels of Tl led to partial interlayer collapse and strong adsorption of dehydrated Tl+ at newly created wedge sites around collapsed interlayer zones (Fig. 1h, 5 and 7).
3.4. Cation exchange model sites and their relation to adsorption mechanisms
To describe the adsorption of Cs+, Rb+ and Tl+ onto illite in competition with NH4+, K+, Na+ and Ca2+, a 3-site cation exchange model has previously been successfully parameterized8,22,23,39 The three sites of this model account for: (i) a very small fraction of high-affinity adsorption sites, (ii) an intermediate fraction of medium-affinity adsorption sites, and (iii) a major fraction of adsorption sites with lowest affinity. The same model has also been used to describe Cs adsorption onto biotite, glauconite or micaceous sediments.24,31,63 In general, the low-abundance high-affinity sites are assumed to correspond to adsorption sites at the wedge of frayed particle edges (frayed edge sites, “FES”), the high-abundance low-affinity sites to cation exchange sites on planar surfaces (planar sites, “PS”). Since two cation exchange sites were found to be insufficient to adequately describe Cs+ and Rb+ adsorption isotherms over large concentration ranges, a third type of site with medium-affinity and medium-abundance has been invoked to improve data fits, referred to as “type-2 sites” (“T2S”).22,23,39 In the following, we discuss our spectroscopic and macroscopic results with respect to potential relations between adsorption model sites and the mechanisms of Tl uptake.In the case of Tl adsorbed onto homoionic Na–IdP, we interpreted the XAS of the sample Na–IdP 3800 with 19 mmol kg−1 adsorbed Tl as indicative for Tl complexation between two siloxane cavities at frayed particle edges. This interpretation was supported by the observation that no spectral changes were observed in samples with lower Tl loadings of 1.5 and 0.25 mmol kg−1 (Fig. S18†), the latter falling below the concentration of FES in the 3-site cation exchange model for illite of 0.65 mmol kg−1.8 The Tl loading of 19 mmol kg−1, however, was much higher than the concentration of FES on illite (derived from adsorption experiments with Na- or Ca-exchanged illite). This suggests that Tl adsorption at particle edges leads to the generation of fresh FES-like wedge sites and to increasing collapse of the frayed edge zone (similar to Tl+ induced collapse of vermiculite interlayers). Considering that the interlayers of Na-saturated illite platelets may become hydrated over several nanometers away from the particle edges,29,53 the amounts of Tl adsorbed via this process can be expected to largely exceed the FES concentration of the 3-site model. In the model calculations, Tl adsorption onto the sample Na–IdP 3800 (19 mmol kg−1) was mainly allocated to T2S (site concentration 52 mmol kg−1), adsorption onto the sample Na–IdP 50 (0.25 mmol kg−1 Tl) mainly to FES (site concentration 0.65 mmol kg−1) (Fig. 2). For Na–IdP, the T2S of the 3-site model may therefore account for intermediate-affinity Tl adsorption onto wedge sites that are freshly formed as a consequence of increasing Tl loading and frayed edge collapse.
In the case of K–IdP, the saturation of the illite with K prior to Tl adsorption induced the collapse of the expanded interlayer at particle edges. Accordingly, the adsorption of Tl onto K–IdP in 10 mM K+ electrolyte solution was mostly limited to planar surfaces. The XAS data suggested that Tl was predominantly adsorbed by complexation onto siloxane cavities, in analogy to Tl adsorption onto the muscovites. In the 3-site model, the Tl binding onto K–IdP was nearly exclusively described by the PS (Fig. 2). The PS, which represent the largest share of the CEC of illite, and the corresponding cation exchange selectivity coefficients, thus account for both inner- and outer-sphere binding of Tl+ on planar surfaces.
For the muscovites Musc-A and Musc-B, the XAS data pointed to predominant Tl adsorption via inner-sphere complexation onto siloxane cavities (Fig. 7). In line with this spectroscopic observation, the limited extraction of Tl adsorbed onto muscovite by CaCl2 and the high log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd and log
Kd and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na values (Fig. 1b, e and h) reflected that Tl was strongly retained. The log
Kc,Tl–Na values (Fig. 1b, e and h) reflected that Tl was strongly retained. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc,Tl–Na of Musc-A and Musc-B (3.0 and 3.1 at 3.2 μM dissolved Tl) were much larger than the Tl–Na exchange selectivity coefficient for the PS (1.2) in the 3-site model of illite.8 Therefore, we speculate that in the 3-site cation exchange model for illite, the T2S in combination with the PS also serve to account for variations in the adsorption affinity of Tl on planar surfaces as a function of surface loading, as different types of siloxane cavities62 get successively saturated.
Kc,Tl–Na of Musc-A and Musc-B (3.0 and 3.1 at 3.2 μM dissolved Tl) were much larger than the Tl–Na exchange selectivity coefficient for the PS (1.2) in the 3-site model of illite.8 Therefore, we speculate that in the 3-site cation exchange model for illite, the T2S in combination with the PS also serve to account for variations in the adsorption affinity of Tl on planar surfaces as a function of surface loading, as different types of siloxane cavities62 get successively saturated.
In order to more rigorously test the ability of the 3-site cation exchange model to describe competitive cation adsorption onto structurally distinct types of sites on illite or other micaceous minerals, competitive adsorption experiments with two strongly adsorbing cations (e.g., Tl and Cs or Rb) in mixed background electrolytes (e.g., Ca and K) in combination with the spectroscopic characterization of the adsorbed ions could prove useful.
3.5. Thallium uptake by a soil clay mineral assemblage
4. Conclusions
This study confirmed that micaceous clay minerals adsorb Tl through strong complexation at wedge sites in interlayers and through selective binding on planar surfaces. Variations in the extent and mode of Tl adsorption onto the different phyllosilicate minerals closely agree with trends reported for Cs and Rb. Accordingly, concepts for the assessment of the binding and solubility of radiocesium in soils and sediments such as the determination of the radiocesium interception potential (RIP) and considerations on adsorption competition with K and NH4, on adsorption reversibility,66,70 and on Cs availability for plant uptake71 should be transferable to Tl. Conversely, mechanistic insights into the adsorption of Tl(I) onto phyllosilicate minerals should equally be transferable to Cs and Rb.In this study, the adsorption of Tl onto phyllosilicate minerals was examined over periods of 7 to 14 days. The kinetics of adsorption or the extent to which Tl exchangeability decreases over time through slow diffusion into collapsed interlayers or through trapping at collapsed particle edges was not addressed. Further work on these processes and their consequences for Tl retention and solubility can be based on available knowledge on Cs. Another factor that warrants further study is the pH-dependence of Tl adsorption onto the different clay minerals, including the potential adsorption of Tl at amphoteric edge sites at particle edges. Finally, relatively high Tl loadings (>200 mg kg−1) were employed in this work to obtain samples that could be probed by XAS. Very small fractions of highest affinity adsorption sites that could exist on all studied minerals and be relevant at lower Tl loadings may therefore have been overlooked. Considering that natural soils often contain <1 mg kg−1 Tl,72 and that even Tl contents in heavily contaminated soils and sediments rarely exceed 100 mg kg−1, the adsorption of Tl onto phyllosilicate minerals at trace levels, and in the presence of competing trace (Cs, Rb) and major cations (K, NH4) warrants further study.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Marco Fleischmann is acknowledged for his assistance with laboratory experiments at Eawag, Brian Sinnet and Ralf Kägi (Eawag) for SEM-EDX sample preparation and sample analysis. Astrid Schaible, and Elmotaz Eltayeb (PSI) are thanked for their support with laboratory experiments and analyses at PSI. Kurt Barmettler and Michael Plötze (ETH Zurich) are thanked for providing muscovite and vermiculite sample materials, and Beda Hofmann (Natural History Museum, Bern, Switzerland) for providing a Tl-containing Ba-rich muscovite (“oellacherite”) from Lengenbach. The Swiss Light Source (Paul Scherer Institute (PSI), Villigen, Switzerland), the Dutch Belgian Beamline (DUBBLE; European Synchrotron Radiation Facility (ESRF), Grenoble, France), and the French National Synchrotron Soleil (Gif-sur-Yvette, France) are kindly acknowledged for the allocation of beam time, and Olga Safonova and Maarten Nachtegaal (SuperXAS, PSI), Dipanjan Banerjee (DUBBLE, ESRF), and Gautier Landrot (SAMBA, Soleil) for support during XAS data collection. This work was financially supported by the Swiss National Science Foundation under contract no. 200021_162364.References
- A. L. John Peter and T. Viraraghavan, Thallium: a review of public health and environmental concerns, Environ. Int., 2005, 31, 493–501 CrossRef PubMed.
- D. I. Kaplan and S. V. Mattigod, in Thallium in the Environment, ed. J. Nriagu, John Wiley & Sons, New York, 1998, pp. 15–29 Search PubMed.
- B. W. Vink, The behaviour of thallium in the (sub)surface environment in terms of Eh and pH, Chem. Geol., 1993, 109, 119–123 CrossRef CAS.
- A. Voegelin, N. Pfenninger, J. Petrikis, J. Majzlan, M. Plötze, A.-C. Senn, S. Mangold, R. Steininger and J. Göttlicher, Thallium speciation and extractability in a thallium- and arsenic-rich soil developed from mineralized carbonate rock, Environ. Sci. Technol., 2015, 49, 5390–5398 CrossRef CAS PubMed.
- C. L. Peacock and E. M. Moon, Oxidative scavenging of thallium by birnessite: explanation for thallium enrichment and stable isotope fractionation in marine ferromanganese precipitates, Geochim. Cosmochim. Acta, 2012, 84, 297–313 CrossRef CAS.
- K. M. Coup and P. J. Swedlund, Demystifying the interfacial aquatic geochemistry of thallium(I): new and old data reveal just a regular cation, Chem. Geol., 2015, 398, 97–103 CrossRef CAS.
- L. A. Martin, C. Simonucci, S. Rad and M. F. Benedetti, Effect of natural organic matter on thallium and silver speciation, J. Environ. Sci., 2020, 93, 185–192 CrossRef PubMed.
- S. Wick, B. Baeyens, M. Marques Fernandes and A. Voegelin, Thallium adsorption onto illite, Environ. Sci. Technol., 2018, 52, 571–580 CrossRef CAS PubMed.
- H. Heinrichs, B. Schulz-Dobrick and K. H. Wedepohl, Terrestrial geochemistry of Cd, Bi, Tl, Zn and Rb, Geochim. Cosmochim. Acta, 1980, 44, 1519–1533 CrossRef CAS.
- S. T. Rader, F. K. Mazdab and M. D. Barton, Mineralogical thallium geochemistry and isotope variations from igneous, metamorphic, and metasomatic systems, Geochim. Cosmochim. Acta, 2018, 243, 42–65 CrossRef CAS.
- T. Xiao, D. Boyle, J. Guha, A. Rouleau, Y. Hong and B. Zheng, Groundwater-related thallium transfer processes and their impacts on the ecosystem: southwest Guizhou Province, China, Appl. Geochem., 2003, 18, 675–691 CrossRef CAS.
- M. Manzano, C. Ayora, C. Domenech, P. Navarrete, A. Garralon and M.-J. Turrero, The impact of the Aznalcóllar mine tailing spill on groundwater, Sci. Total Environ., 1999, 242, 189–209 CrossRef CAS.
- A. Tremel, P. Masson, H. Garraud, O. F. X. Donard, D. Baize and M. Mench, Thallium in French agrosystems - II. Concentration of thallium in field-grown rape and some other plant species, Environ. Pollut., 1997, 97, 161–168 CrossRef CAS.
- A. Vaněk, M. Komárek, P. Vokurková, M. Mihaljevic, O. Šebek, G. Panušková, V. Chrastný and O. Drábek, Effect of illite and birnessite on thallium retention and bioavailability in contaminated soils, J. Hazard. Mater., 2011, 191, 170–176 CrossRef PubMed.
- H. Lehn and J. Schoer, Thallium-transfer from soils to plants: correlation between chemical form and plant uptake, Plant Soil, 1987, 97, 253–265 CrossRef CAS.
- M. D'Orazio, B. Campanella, E. Bramanti, L. Ghezzi, M. Onor, G. Vianello, L. Vittori-Antisari and R. Petrini, Thallium pollution in water, soils and plants from a past-mining site of Tuscany: sources, transfer processes and toxicity, J. Geochem. Explor., 2020, 209, 106434 CrossRef.
- T. Xiao, J. Guha, D. Boyle, C.-Q. Liu, B. Zheng, G. C. Wilson, A. Rouleau and J. Chen, Naturally occurring thallium: a hidden geoenvironmental health hazard?, Environ. Int., 2004, 30, 501–507 CrossRef CAS PubMed.
- A. Tremel, P. Masson, T. Sterckeman, D. Baize and M. Mench, Thallium in French agrosystems – I. Thallium contents in arable soils, Environ. Pollut., 1997, 95, 293–302 CrossRef CAS PubMed.
- A. R. Jacobsen, M. B. McBride, P. Baveye and T. S. Steenhuis, Environmental factors determining the trace-level sorption of silver and thallium to soils, Sci. Total Environ., 2005, 345, 191–205 CrossRef PubMed.
- A. D. Matthews and J. P. Riley, The occurrence of thallium in sea water and marine sediments, Chem. Geol., 1970, 6, 149–152 CrossRef CAS.
- S. Wick, B. Baeyens, M. Marques Fernandes, J. Göttlicher, M. Fischer, N. Pfenninger, M. Plötze and A. Voegelin, Thallium sorption and speciation in soils: role of micaceous clay minerals and manganese oxides, Geochim. Cosmochim. Acta, 2020, 288, 83–100 CrossRef CAS.
- E. Brouwer, B. Baeyens, A. Maes and A. Cremers, Cesium and rubidium ion equilibria in illite clay, J. Phys. Chem., 1983, 87, 1213–1219 CrossRef CAS.
- M. H. Bradbury and B. Baeyens, A generalised model for the concentration dependent uptake of caesium by argillaceous rocks, J. Contam. Hydrol., 2000, 42, 141–163 CrossRef CAS.
- J. M. Zachara, S. C. Smith, C. Liu, J. P. McKinley, R. J. Serne and P. L. Gassmann, Sorption of Cs+ to micaceous subsurface sediments from the Hanford site, USA, Geochim. Cosmochim. Acta, 2002, 66, 193–211 CrossRef CAS.
- J. P. McKinley, J. M. Zachara, S. M. Heald, A. Dohnalkova, M. Newville and S. R. Sutton, Microscale distribution of cesium sorbed to biotite and muscovite, Environ. Sci. Technol., 2004, 38, 1017–1023 CrossRef CAS PubMed.
- D. S. Kwong-Moses, W. Crawford Elliott, J. M. Wampler, B. A. Powell and D. M. Avant Jr, Sorption and desorption of radiocesium by muscovite separated from the Georgia kaolin, J. Environ. Radioact., 2020, 211, 106074 CrossRef CAS PubMed.
- H. Mukai, A. Hirose, S. Motai, R. Kikuchi, K. Tanoi, T. M. Nakanishi, T. Yaita and T. Kogure, Cesium adsorption/desorption behavior of clay minerals considering actual contamination conditions in Fukushima, Sci. Rep., 2016, 6, 21543 CrossRef CAS PubMed , 1–7..
- T. Kogure, K. Morimoto, K. TAmura, H. Sato and A. Yamagishi, XRD and HRTEM evidence for fixation of cesium ions in vermiculite clay, Chem. Lett., 2012, 41, 380–382 CrossRef CAS.
- A. Nakao, Y. Thiry, S. Funakawa and T. Kosako, Characterization of the frayed edge site of micaceous minerals in soil clays influenced by different pedogenetic conditions in Japan and northern Thailand, Soil Sci. Plant Nutr., 2008, 54, 479–489 CrossRef CAS.
- T. Missana, A. Benedicto, M. García-Gutiérrez and U. Alonso, Modeling cesium retention onto Na-, K- and Ca-smectite: effects of ionic strength, exchange and competing cations on the determination of selectivity coefficients, Geochim. Cosmochim. Acta, 2014, 128, 266–277 CrossRef CAS.
- Y. Bruneel, L. Van Laer, S. Brassinnes and E. Smolders, Characterisation of the highly selective caesium sorption on glauconite rich sands of contrasting geological formations, Appl. Geochem., 2021, 128, 104926 CrossRef CAS.
- M. Chen, P. Wu, S. Li, S. Yang, Z. Lin and Z. Dang, The effects of interaction between vermiculite and manganese dioxide on the environmental geochemical process of thallium, Sci. Total Environ., 2019, 669, 903–910 CrossRef CAS PubMed.
- G. Frantz and R. M. Carlson, Effects of rubidium, cesium, and thallium on interlayer potassium release from Transvaal vermiculite, Soil Sci. Soc. Am. J., 1987, 51, 305–308 CrossRef CAS.
- B. Baeyens and M. H. Bradbury, A mechanistic description of Ni and Zn sorption on Na-montmorillonite Part I: titration and sorption measurements, J. Contam. Hydrol., 1997, 27, 199–222 CrossRef CAS.
- J. Bors, A. Gorny and S. Dultz, Iodide, caesium and strontium adsorption by organophilic vermiculite, Clay Miner., 1997, 32, 21–28 CrossRef CAS.
- A. Steudel, P. G. Weidler, R. Schuhmann and K. Emmerich, Cation exchange reactions of vermiculite with Cu-triethylenetetramine as affected by mechanical and chemical pretreatment, Clays Clay Miner., 2009, 57, 486–493 CrossRef CAS.
- M. H. Bradbury and B. Baeyens, Sorption modelling on illite. Part II: actinide sorption and linear free energy relationships, Geochim. Cosmochim. Acta, 2009, 73, 1004–1013 CrossRef CAS.
- M. H. Bradbury and B. Baeyens, Sorption modelling on illite. Part I: titration measurements and the sorption of Ni, Co, Eu and Sn, Geochim. Cosmochim. Acta, 2009, 73, 990–1003 CrossRef CAS.
- C. Poinssot, B. Baeyens and M. H. Bradbury, Experimental and modelling studies of caesium sorption on illite, Geochim. Cosmochim. Acta, 1999, 63, 3217–3227 CrossRef CAS.
- K. Hettmann, K. Kreissig, M. Rehkämper, T. Wenzel, R. Mertz-Kraus and G. Markl, Thallium geochemistry in the metamorphic Lengenbach sulfide depost, Switzerland: Thallium-isotope fractionation in a sulfide melt, Am. Mineral., 2014, 99, 793–803 CrossRef CAS.
- B. A. Hofmann and M. D. Knill, Geochemistry and genesis of the Lengenbach Pb-Zn-As-Tl-Ba-mineralisation, Binn Valley, Switzerland, Miner. Deposita, 1996, 31, 319–339 CrossRef CAS.
- R. Dähn, A. M. Scheidegger, A. Manceau, M. L. Schlegel, B. Baeyens, M. H. Bradbury and D. Chateignier, Structural evidence for the sorption of Ni(II) atoms on the edges of montmorillonite clay minerals: a polarized X-ray absorption fine structure study, Geochim. Cosmochim. Acta, 2003, 67, 1–15 CrossRef.
- B. Ravel and M. Newville, ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- L. A. Martin, A. Wissocq, M. F. Benedetti and C. Latrille, Thallium (Tl) sorption onto illite and smectite: implications for Tl mobility in the environment, Geochim. Cosmochim. Acta, 2018, 230, 1–16 CrossRef CAS.
- R. G. Gast, Standard free energies of exchange for alkali metal cations on Wyoming bentonite, Soil Sci. Soc. Am. Proc., 1969, 33, 37–41 CrossRef CAS.
- M. G. M. Bruggenwert and A. Kamphorst, in Soil Chemistry: B. Physico-Chemical Models, ed. G. H. Bolt, Elsevier, Amsterdam, 1979, pp. 141–203 Search PubMed.
- C. B. Durrant, J. D. Begg, A. B. Kersting and M. Zavarin, Cesium sorption reversibility and kinetics on illite, montmorillonite, and kaolinite, Sci. Total Environ., 2018, 610–611, 511–520 CrossRef CAS PubMed.
- L. Dzene, E. Tertre, F. Hubert and E. Ferrage, Nature of the sites involved in the process of cesium desorption from vermiculite, J. Colloid Interface Sci., 2015, 455, 254–260 CrossRef CAS PubMed.
- X. Yin, X. Wang, H. Wu, T. Ohnuki and K. Takeshita, Enhanced desorption of cesium from collapsed interlayer regions invermiculite by hydrothermal treatment with divalent cations, J. Hazard. Mater., 2017, 326, 47–53 CrossRef CAS PubMed.
- I. Persson, F. Jalilehvand and M. Sandström, Structure of the solvated thallium(I) ion in aqueous, dimethyl sulfoxide, N,N-dimethylpropyleneurea, and N,N-dimethylthioformamide solution, Inorg. Chem., 2002, 41, 192–197 CrossRef CAS PubMed.
- V. A. Drits, B. B. Zviagina, D. K. McCarthy and A. L. Salyn, Factors responsible for crystal-chemical variations in the solid solutions from illite to aluminoceladonite and from glauconite to celadonite, Am. Mineral., 2010, 95, 348–361 CrossRef CAS.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- A. J. Fuller, S. Shaw, M. B. Ward, S. J. Haigh, J. F. W. Mosselmans, C. L. Peacock, S. Stackhouse, A. J. Dent, D. Trivedi and I. T. Burke, Caesium incorporation and retention in illite interlayers, Appl. Clay Sci., 2015, 108, 128–134 CrossRef CAS.
- S. Wick, J. Peña and A. Voegelin, Thallium sorption onto manganese oxides, Environ. Sci. Technol., 2019, 53, 13168–13178 CrossRef CAS PubMed.
- L. N. Lammers, I. C. Bourg, M. Okumura, K. Kolluri, G. Sposito and M. Machida, Molecular dynamics simulations of cesium adsorption on illite nanoparticles, J. Colloid Interface Sci., 2017, 490, 608–620 CrossRef CAS PubMed.
- T. Ikeda, S. Suzuki and T. Yaita, Characterization of adsorbed alkali metal ions in 2:1 type clay minerals from first-principles metadynamics, J. Phys. Chem. A, 2015, 119, 8369–8375 CrossRef CAS PubMed.
- M. Okumura, S. Kerisit, I. C. Bourg, L. N. Lammers, T. Ikeda, M. Sassi, K. M. Rosso and M. Machida, Radiocesium interaction with clay minerals: theory and simulation advances Post–Fukushima, J. Environ. Radioact., 2019, 210, 105809 CrossRef CAS PubMed.
- S. Kerisit, M. Okumura, K. M. Rosso and M. Machida, Molecular simulation of cesium adsorption at the basal surface of phyllosilicate minerals, Clays Clay Miner., 2016, 64, 389–400 CrossRef CAS.
- M. L. Schlegel, K. L. Nagy, P. Fenter, L. Cheng, N. C. Sturchio and S. D. Jacobsen, Cation sorption on the muscovite (001) surface in chloride solutions using high-resolution X-ray reflectivity, Geochim. Cosmochim. Acta, 2006, 70, 3549–3565 CrossRef CAS.
- S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Monovalent ion adsorption at the muscovite (001)−solution interface: relationships among ion coverage and speciation, interfacial water structure, and substrate relaxation, Langmuir, 2012, 28, 8637–8650 CrossRef CAS.
- I. C. Bourg, S. S. Lee, P. Fenter and C. Tournassat, Stern layer structure and energetics at mica−water interfaces, J. Phys. Chem. C, 2017, 121, 9402–9412 CrossRef CAS.
- N. Loganathan and A. G. Kalinichev, Quantifying the mechanisms of site-specific ion exchange at an inhomogeneously charged surface: case of Cs+/K+ on hydrated muscovite mica, J. Phys. Chem. C, 2017, 121, 7829–7836 CrossRef.
- J. Kyllönen, M. Hakanen, A. Lindberg, R. Harjula, M. Vehkamäki and J. Lehto, Modeling of cesium sorption on biotite using cation exchange selectivity coefficients, Radiochim. Acta, 2014, 102, 919–929 CrossRef.
- A. de Koning and R. N. J. Comans, Reversibility of radiocesium sorption on illite, Geochim. Cosmochim. Acta, 2004, 68, 2815–2823 CrossRef CAS.
- R. N. J. Comans, M. Haller and P. de Peter, Sorption of cesium on illite: non-equilibrium behaviour and reversibility, Geochim. Cosmochim. Acta, 1991, 55, 433–440 CrossRef CAS.
- R. N. J. Comans, Kinetics and reversibility of radiocesium sorption on illite and sediments containing illite, In: Mineral-Water Interfacial Reactions: Kinetics and Mechanisms, ed. D. L. Sparks and T. J. Grundl, ACS Symposium Series, 1999, vol. 715, pp. 179–201 Search PubMed.
- M. Goto, R. Rosson, W. C. Elliott, J. M. Wampler, S. Serkiz and B. Kahn, Interactions of radioactive and stable cesium with hydroxy-interlayered vermiculite grains in soils of the Savannah river site, South Carolina, USA, Clays Clay Miner., 2014, 62, 161–173 CrossRef CAS.
- L. K. Zaunbrecher, W. C. Elliott, J. M. Wampler, N. Perdrial and D. I. Kaplan, Enrichment of cesium and rubidium in weathered micaceous materials at the Savannah river site, South Carolina, Environ. Sci. Technol, 2015, 49, 4226–4234 CrossRef CAS PubMed.
- K. Fujii, N. Yamaguchi, N. Imamura, M. Kobayashi, S. Kaneko and M. Takahashi, Effects of radiocesium fixation potentials on 137Cs retention in volcanic soil profiles of Fukushima forests, J. Environ. Radioact., 2019, 198, 126–134 CrossRef CAS PubMed.
- B. Delvaux, N. Kruyts, E. Maes and E. Smolders, in Trace Elements in the Rhizosphere, ed. G. E. Gobran, W. W. Wenzel and E. Lombi, CRC Press, Boca Raton, 2001 Search PubMed.
- Y.-G. Zhu and E. Smolders, Plant uptake of radiocesium: a review of mechanisms, regulation and applications, J. Exp. Bot., 2000, 51, 1635–1645 CrossRef CAS PubMed.
- Geochemical Atlas of Europe. Part 1: Background Information, Methodology and Maps, ed. R. Salminen, Geological Survey of Finland, Espoo, 2005 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2em00028h |
| This journal is © The Royal Society of Chemistry 2022 |