Open Access Article
Open Access ArticleComparability of semivolatile organic compound concentrations from co-located active and passive air monitoring networks in Europe†
Jiří
Kalina
a,
Kevin B.
White
 a,
Martin
Scheringer
a,
Martin
Scheringer
 *ab,
Petra
Přibylová
a,
Petr
Kukučka
a,
Ondřej
Audy
a,
Jakub
Martiník
a and
Jana
Klánová
*a
*ab,
Petra
Přibylová
a,
Petr
Kukučka
a,
Ondřej
Audy
a,
Jakub
Martiník
a and
Jana
Klánová
*a
aRECETOX, Faculty of Science, Masaryk University, Kotlarska 2, 611 37 Brno, Czech Republic. E-mail: martin.scheringer@recetox.muni.cz; jana.klanova@recetox.muni.cz
bInstitute of Biogeochemistry and Pollutant Dynamics, ETH Zürich, 8092 Zürich, Switzerland. E-mail: scheringer@usys.ethz.ch
First published on 25th April 2022
Abstract
Passive air sampling (PAS) has been used to monitor semivolatile organic compounds (SVOCs) for the past 20 years, but limitations and uncertainties persist in the derivation of effective sampling volumes, sampling rates, and concentrations. As a result, the comparability of atmospheric levels measured by PAS and concentrations measured by active air sampling (AAS) remains unclear. Long-term PAS data, without conversion into concentrations, provide temporal trends that are similar to, and consistent with, trends from AAS data. However, for more comprehensive environmental and human health assessments of SVOCs, it is also essential to harmonize and pool air concentration data from the major AAS and PAS monitoring networks in Europe. To address this need, we calculated and compared concentration data for 28 SVOCs (including organochlorine pesticides (OCPs), polychlorinated biphenyls (PCBs), polybrominated diphenyl ethers (PBDEs), and polycyclic aromatic hydrocarbons (PAHs)) at the six monitoring sites in Europe with 10 years of co-located AAS (EMEP) and PAS (MONET) data: Birkenes, Košetice, Pallas, Råö, Stórhöfði, and Zeppelin. Atmospheric SVOC concentrations were derived from PAS data using the two most common computation models. Long-term agreement between the AAS and PAS data was strong for most SVOCs and sites, with 79% of the median PAS-derived concentrations falling within a factor of 3 of their corresponding AAS concentrations. However, in both models it is necessary to set a sampler-dependent correction factor to prevent underestimation of concentrations for primarily particle-associated SVOCs. In contrast, the models overestimate concentrations at sites with wind speeds that consistently exceed 4 m s−1. We present two recommendations that, if followed, allow MONET PAS to provide sufficiently accurate estimates of SVOC concentrations in air so that they can be deployed together with AAS in regional and global monitoring networks.
Environmental significanceActive air sampling (AAS) has historically been used to measure atmospheric concentrations of semivolatile organic compounds (SVOCs) but is impractical for long-term monitoring in most regions of the world. Passive air sampling (PAS) is a more feasible alternative, but after 20 years of combined global air monitoring, the comparability of concentration data between AAS and PAS is still unclear. However, data harmonization and pooling between major AAS and PAS monitoring networks is essential for evaluating the effectiveness of global regulations and the impacts of SVOCs on environmental and human health. Our study identifies strong agreement between 10 years of co-located AAS and PAS concentrations in most cases and confirms the potential for harmonization and pooling of SVOC air monitoring data. |
Introduction
Semivolatile organic compounds (SVOCs) are a broad class of atmospheric pollutants that include polycyclic aromatic hydrocarbons (PAHs) and persistent organic pollutants (POPs), such as polychlorinated biphenyls (PCBs), organochlorine pesticides (OCPs), and polybrominated diphenyl ethers (PBDEs). Within Europe, SVOCs have been monitored since the 1990s at active air sampling (AAS) sites under the European Monitoring and Evaluation Programme (EMEP) (Norwegian Institute for Air Research, NILU).1 Baseline concentrations were established across the continent, but continuous long-term monitoring of SVOCs is primarily performed at sites in Northern and Western Europe. In 2003, the MONET passive air sampling (PAS) network was established by RECETOX (Masaryk University, Czech Republic) to address SVOC monitoring gaps in Central and Eastern Europe.2 The network has since expanded, with MONET PAS now deployed in 27 countries across Europe, as well as 9 countries across Africa,3 and generating valuable information on the atmospheric behavior of SVOCs.4–6 However, the comparability between atmospheric levels measured by PAS and atmospheric concentrations measured by AAS remains the subject of ongoing investigation and discussion.7–11There are several methods for converting atmospheric levels of SVOCs measured by the most common kinetic PAS (mass per sampler) into atmospheric concentrations as those measured by AAS (mass per volume of sampled air), all of which are based on the concept of sampling rate (RS). The RS quantitatively describes the uptake of SVOCs by PAS and is dependent on compound-specific chemical properties, as well as local meteorological conditions such as wind speed, pressure, humidity, and temperature.12 Methods for the determination of RS range from site-specific field calibrations based on parallel AAS and PAS deployment or the use of sampler depuration compounds,13 to physicochemical models aiming for broad applicability.7 While the role of temperature in SVOC uptake has generally been well understood since the advent of PAS,14 many studies have attempted to elucidate the influence of other meteorological parameters, particularly wind speed.15–21 Models based on these uptake relationships – such as the original GAPS template by Harner22 and the newer GAPS model by Herkert et al.23 – provide acceptable air concentration estimates for the majority of sampling sites under typical meteorological conditions, but larger differences between modelled and field-based RS may be observed at sites that experience extreme temperatures and/or wind speeds.8,23 This indicates that the relationship between meteorological factors and SVOC uptake is still not satisfactorily described. For example, wind speeds above a certain threshold may cause a transition from laminar to turbulent flow inside passive samplers, which significantly increases RS and is not reflected in current models.12,15,18
We have previously shown that SVOC concentrations from co-located EMEP AAS and MONET PAS monitoring sites provide similar long-term temporal trends despite differences in individual sample values and units between the networks.4,9 However, there is also a need to harmonize AAS and PAS monitoring results with respect to absolute SVOC air concentrations in order to generate consistent data across Europe for more robust environmental and human exposure assessments. We have also previously described sources of uncertainty and challenges for the harmonization of AAS and PAS SVOC air sampling, such as differences in sampler design,11,24,25 including potentially problematic artifacts,4,26 as well as differences in analytical performance between laboratories generating global SVOC air monitoring data.27 This study focuses on the final source of uncertainty for harmonization of AAS and PAS data – the determination of RS – using ten years (2009–2018) of continuous air monitoring data for PAHs, PCBs, OCPs, and PBDEs from the six sites in Europe with co-located EMEP AAS and MONET PAS to derive field-based RS and compare them with results from the most commonly used models22,23 for RS determination. This comparison enables us to address the challenge of reducing the uncertainties of PAS data7 to improve the potential for harmonization of SVOC air monitoring data across Europe.
Methods
Air sampling and chemical analysis
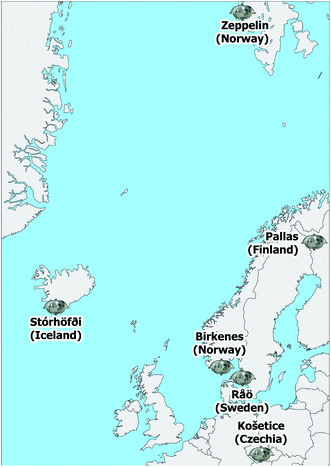
The six air monitoring stations across Europe with long-term co-located EMEP AAS and MONET PAS are Birkenes (Norway), Košetice (Czech Republic), Pallas (Finland), Råö (Sweden), Stórhöfði (Iceland), and Zeppelin (Svalbard, Norway). For the purposes of this study, we investigated a decade of concurrent monitoring data from both networks at these sites (1-January-2009 to 31-December-2018) obtained from the publicly available EMEP (EBAS, NILU) and MONET (Genasis, RECETOX) databases. Compound selection was constrained to the 24 SVOCs monitored by both networks at all (or most) of the six sites over the selected period: alpha- and gamma-hexachlorocyclohexane (α-HCH, γ-HCH), hexachlorobenzene (HCB), and p,p′-dichlorodiphenyldichloroethylene (p,p′-DDE); PCBs 28, 52, 101, 118, 138, 153, and 180; fluoranthene (FLA), fluorene (FLU), phenanthrene (PHE), pyrene (PYR), benzo-a-pyrene (BAP), anthracene (ANT), benzo-ghi-perylene (BGP), benzo-a-anthracene (BAA); and PBDEs 47, 99, 100, 153, and 154.Detailed information on sampling site locations and EMEP sampling and analytical procedures is provided in Table S1 in the ESI.† A map of the sites is provided in Fig. 1. MONET PAS is performed using polyurethane foam (PUF) disk samplers (PUF-PAS); see White et al.3,5 for standard MONET sampling and analytical procedures. Since EMEP sites are operated by different national research laboratories, the sampling, analytical, and data reporting procedures for AAS varied significantly between the six sites (Table S1†). While the sampling and reporting differences can be resolved by further data treatment, a recent global intercomparison suggests that differences in analytical performance between the laboratories may introduce an additional source of uncertainty that limits data comparability.27 Compared to EMEP, the MONET PAS data and procedures were more consistent between sites since they are all operated by RECETOX. However, there was a change in the MONET sampling procedure at all sites from a 28-d exposure period (2009–2011) to an 84-d exposure period (2011–2018). The temporal sampling regimes of all EMEP AAS and MONET PAS data at all sites are depicted in Fig. S1 in the ESI.†
Data aggregation
Prior to aggregation, all values below the limit of quantification (LOQ) were substituted by 0.5 × LOQ. These substitutions were performed for 5% of OCP, 16% of PCB, 12% of PAH, and 33% of PBDE data from EMEP AAS; and for 3% of OCP, 27% of PCB, 23% of PAH, and 26% of PBDE data from MONET PAS. The LOQs varied depending on the laboratory and monitoring period, ranging from 1 × 10−5 ng m−3 for PBDEs to 0.74 ng m−3 for PAHs in the AAS measurements and from 3.6 × 10−8 ng d−1 for PBDEs to 2.9 ng d−1 for PCB 118 in the PAS measurements.To account for the differences in sampling periods between the sites/networks and to decrease random variability in the data, a quarterly aggregation (91 days) was applied to all EMEP AAS data and all MONET PAS data, separately, within each year (2009–2018). The four quarters of each year were defined as Q1 (January–March), Q2 (April–June), Q3 (July–September), and Q4 (October–December), resulting in 40 concentration values per compound for both the AAS and PAS data over the ten-year monitoring period. The aggregation was carried out as a weighted average of concentrations of the primary samples with different sampling period lengths. The weight of each sample was derived from the number of days in each quarter covered by that sample. For example, if the sample covered only a few days of a specific quarter, its weight was substantially lower compared with a sample spanning over two months within the quarter. The selected 91-d period of the quarters was long enough to cover the 84-d PAS sampling period and several corresponding weekly or monthly AAS sampling periods, while still preserving some measure of seasonal variability in the data (vs. annual aggregation).
As previously discussed, some gaps occurred in the AAS and PAS data over the ten-year monitoring period (Fig. S1†). In cases where a gap between two subsequent samples at a site was longer than half of the quarter (>45 days), no data aggregation was performed, and an empty value was assigned to that quarter at that site. Since gaps in sampling varied between networks and sites, only quarters with overlapping aggregated values for both the AAS and PAS data were used for further analysis of field-based RS (3127 values in total: 655 for OCPs, 1116 for PCBs, 1058 for PAHs, and 298 for PBDEs). Quarterly aggregates for both networks at all sites and all compound groups across the ten-year monitoring period are depicted in Fig. S2.†
Sampling rate computation and analysis
To convert atmospheric SVOC levels measured by MONET PAS (ng d−1) to atmospheric concentrations as measured by EMEP AAS (ng m−3), site- and time-specific RS values (m3 d−1) were computed using the two most frequently used models: ‘Harner’ RS and ‘Herkert’ RS.The ‘Harner’ RS values were computed quarterly with the original GAPS template model22 using the average temperature over each quarter at each site (eqn (1)):
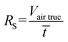 | (1) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) , corrected for the particle sampling efficiency of the sampler (eqn (2)):
, corrected for the particle sampling efficiency of the sampler (eqn (2)):| Vair true = Vair (1 − Φ + Φepart) | (2) |
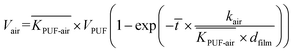 | (3) |
 is the corrected partition coefficient between the air and the PUF disk (eqn (4)):
is the corrected partition coefficient between the air and the PUF disk (eqn (4)):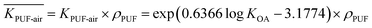 | (4) |
The ‘Herkert’ RS were computed quarterly with the updated GAPS model23 using hourly temperatures and wind speeds over each quarter at each site (eqn (5)):
| RS = AS × kV | (5) |
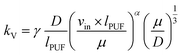 | (6) |
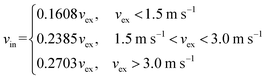 | (7) |
Detailed information on the derivation of these equations and the use of these two models is provided elsewhere;8,12,14,21,23,28 see Table S2† for a list of model input parameters used for MONET PAS. Since consistent meteorological measurements over the monitoring period were not available at every site, all meteorological parameters necessary for sampling rate computations were generated hourly over the entire monitoring period (2009–2018) using the NASA MERRA-2 model,29 as previously described.3,8,23 To assess differences between RS values generated by these models and real monitored data, a third set of RS values was calculated (‘field’ RS) based on the ratios of PAS:AAS aggregated values corresponding to the same sampling quarter.
It is important to note that PAS concentrations were calculated twice using both models. The initial calculations were based on the default epart value of 100% typically used for GAPS PAS. It has previously been observed that the epart value for MONET PAS is substantially lower than 100% due to differences in sampler design between MONET and GAPS,24,30 but the range of values reported is large with no consensus. However, the unrealistically high RS values modelled in the initial run made it possible to calibrate a MONET PAS-specific epart value so that adjusted PAS concentrations could be calculated a second time with both models.
The statistical significance of differences between the three RS sets for all individual compounds, sites, and quarters was evaluated with the Mann–Whitney U test31 and the Kruskal–Wallis test.32 Compared to the modelled RS, the field RS spanned several orders of magnitude, including some extremely high and low values that may have been caused by contamination during sample handling and transport, or errors in compound analysis and data treatment. To prevent the results of this study from being affected by such extreme values, lower and upper thresholds (L, U) were set for each site/compound subset of RS as 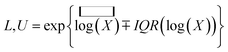 where X is the RS subset,
where X is the RS subset, 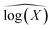 is the median over the log-transformed RS values in the subset, and IQR(log(X)) is the interquartile range of the log-transformed RS values in the subset. In total, 3% of the field RS values exceeded these thresholds and were removed from the dataset as outliers. This correction assumes that the RS are approximately log-normally distributed, as confirmed in Fig. S3.†
is the median over the log-transformed RS values in the subset, and IQR(log(X)) is the interquartile range of the log-transformed RS values in the subset. In total, 3% of the field RS values exceeded these thresholds and were removed from the dataset as outliers. This correction assumes that the RS are approximately log-normally distributed, as confirmed in Fig. S3.†
Results & discussion
Concentrations and sampling rates
Atmospheric MONET PAS concentrations initially calculated from both models with an epart value of 100% were generally higher than the corresponding EMEP AAS concentrations. The magnitude of this difference varied greatly depending on model-, site-, and compound-specific factors. AAS and PAS (Harner- and Herkert-modelled) concentrations over the 10-year monitoring period are presented for eight selected SVOCs (two from each compound class) in Fig. 2; see Fig. S4† for all remaining SVOCs. Of the 127 site/compound comparisons included in this study, only 22% of the Harner-modelled PAS concentrations, and 11% of the Herkert-modelled PAS concentrations, were not significantly different from their corresponding AAS concentrations (p > 0.05). However, it is well established that PAS provides long-term integrations rather than concentrations identical to those from AAS; the agreement is generally deemed to be strong if PAS concentrations are within a factor of 2–3 of AAS concentrations.10,33 According to this more lenient criterion, 79% of the Harner-modelled median PAS concentrations are within a factor of 3 of the corresponding AAS concentrations (Table S3†). In comparison, only 60% of the Herkert-modelled median PAS concentrations are within a factor of 3 of the corresponding AAS concentrations due to significantly higher concentrations for the majority of SVOCs at both Birkenes and Pallas when compared to the Harner-modelled concentrations. This discrepancy was unexpected, as previous studies have found negligible differences in the output concentrations between the two models for most sites/compounds,8,34 despite their different input parameters. Similar negligible differences were observed in this study at the other four sites, with median PAS concentrations from the two models falling within a factor of 1.5 of each other for all SVOCs at Košetice, Råö, Stórhöfði, and Zeppelin. However, as mentioned above, Herkert-modelled concentrations are 2.8–4.8 times higher than the corresponding Harner-modelled concentrations for all SVOCs at Birkenes, and 2.0–4.8 times higher at Pallas, suggesting some site-specific influences at these two sites on input parameters for the Herkert model that are not incorporated in the Harner model, such as wind speed. The other major site-specific result was at Stórhöfði, where both models yielded significantly higher PAS concentrations for all SVOCs except the lowest-molecular-weight PCBs (28, 52, 101) and PBDEs (47, 99, 100); for the remaining SVOCs, Harner-modelled median PAS concentrations are 9–44 times higher than the corresponding AAS concentrations, and Herkert-modelled concentrations are 8–37 times higher.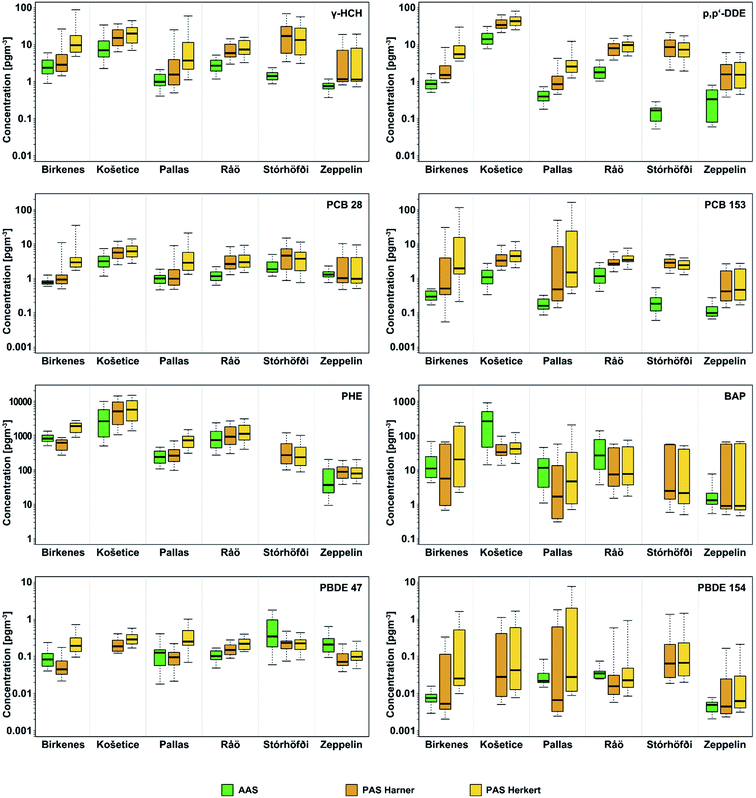 | ||
| Fig. 2 Boxplots of SVOC concentrations in air (two selected representatives in each compound class) from EMEP active air sampling (AAS) and MONET passive air sampling (PAS) calculated by the ‘Harner’ and ‘Herkert’ models (epart = 100%). Boxplots represent ten years of overlapping monitoring data (2009–2018). Thick black lines represent medians, boxes span from 25th to 75th percentiles, and whiskers represent the 5th and 95th percentiles. See Fig. S4† for all other SVOCs included in this study. | ||
The Harner RS values are relatively constant across all site/compound combinations, with median values spanning 3.3–4.4 m3 d−1. The Herkert RS values are similar to these values at Košetice, Råö, Stórhöfði, and Zeppelin, but with slightly more variability in the median values, ranging from 2.3 to 5.7 m3 d−1 (Table S4†). In contrast, the Herkert RS values are substantially lower at Birkenes and Pallas compared to the other sites, with median values ranging 1.0–1.7 m3 d−1 (Table S4†), resulting in the significant difference between the Harner- and Herkert-modelled concentrations observed at these two sites (Fig. 2). Conversely, the high modelled concentrations by both models at Stórhöfði correspond to extremely high field RS values at this site, with median values ranging 12–66 m3 d−1 for PCBs and 45–280 m3 d−1 for OCPs (Table S4†). Aside from Stórhöfði, the field RS still varied to a significantly greater extent across all other site/compound combinations compared to the Harner and Herkert RS, with median field RS ranging two orders of magnitude from 0.3–33 m3 d−1 (Fig. 3; see Fig. S5† for all SVOCs).
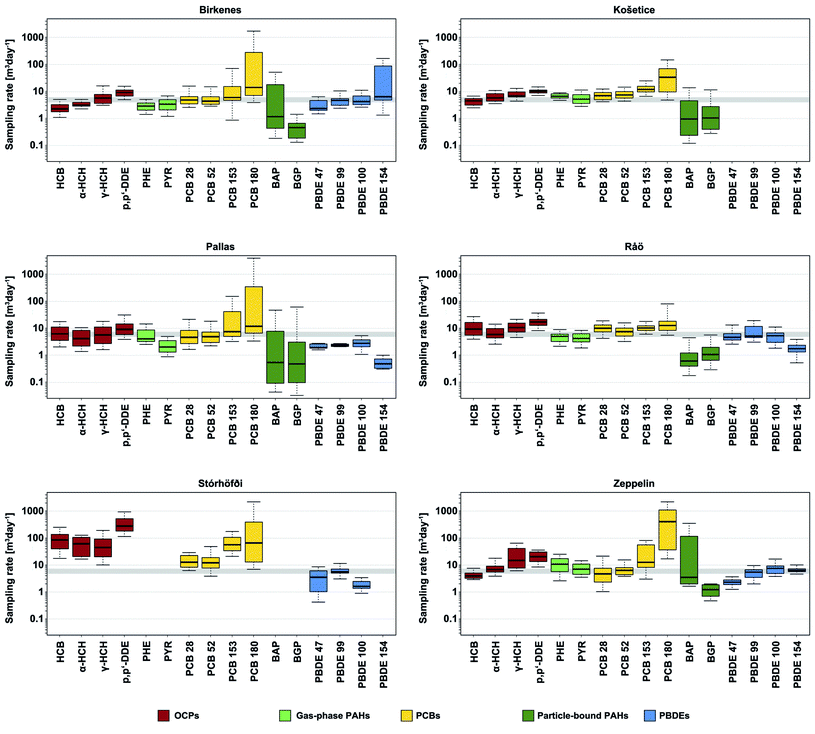 | ||
| Fig. 3 Boxplots of field sampling rates derived from quarterly-aggregated EMEP AAS and MONET PAS SVOC data measured at six stations during the period 2009–2018 (n = 8–39; Fig. S2†). Four selected representatives within each SVOC group are presented and distinguished by colour: OCPs (red), PAHs (light and dark green representing predominantly gas-phase and particle-bound PAHs, respectively), PCBs (yellow), and PBDEs (blue). SVOC groups and individual compounds are ordered by increasing KOA from left to right. Thick black lines represent medians, boxes range from 25th to 75th percentiles, and whiskers represent the 5th and 95th percentiles. Narrow grey shaded areas represent the range of RS often used for PAS (4–6 m3 d−1). | ||
These differences in field RS between sites are affected by variations in meteorological conditions, frequency and duration of AAS and PAS sampling, analytical procedures and performance (AAS data are from four different laboratories; Table S1†),27 and random variation associated with individual values.35 Differences caused by meteorological factors are partially accounted for in the mathematical models for kinetic sampling22,23 and random variation in both AAS and PAS data may be reduced by repeated sampling over longer periods of time.4,9 In addition, the inherent chemical properties of individual SVOCs also affect their RS. In particular, the octanol-air partition coefficient (KOA) of SVOCs plays a key role in their uptake by passive samplers,10,14 and accurately describes many of the compound-specific differences in field RS observed in this study. For example, field RS increased with increasing log KOA for the SVOCs predominantly (>95%) in the gas phase (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 8.8),4e.g., α-HCH, γ-HCH, HCB, PCB 28, PCB 52, FLU, PHE, ANT, with PAS uptake of these compounds primarily controlled by absorption dynamics.22,28 In contrast, field RS decreased for the transition group of SVOCs (8.8 < log
KOA < 8.8),4e.g., α-HCH, γ-HCH, HCB, PCB 28, PCB 52, FLU, PHE, ANT, with PAS uptake of these compounds primarily controlled by absorption dynamics.22,28 In contrast, field RS decreased for the transition group of SVOCs (8.8 < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 11.3) due to a shift from predominantly in the gas-phase to the particle-bound phase. Finally, for the SVOCs predominantly (>95%) in the particle phase (log
KOA < 11.3) due to a shift from predominantly in the gas-phase to the particle-bound phase. Finally, for the SVOCs predominantly (>95%) in the particle phase (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA > 11.3), e.g., BAP, BGP, PBDE 153, PBDE 154, the field RS were approximately one order of magnitude lower than for the gas-phase SVOCs, as previously observed for MONET PAS8,10 due to low particle sampling efficiency.4,30
KOA > 11.3), e.g., BAP, BGP, PBDE 153, PBDE 154, the field RS were approximately one order of magnitude lower than for the gas-phase SVOCs, as previously observed for MONET PAS8,10 due to low particle sampling efficiency.4,30
Influence of particle sampling efficiency
It is important to note that the Harner and Herkert models were both calibrated and developed based on GAPS passive samplers and initially run here on the default assumption that they have an atmospheric particle sampling efficiency (epart) of 100%.22,23 Previous studies of gas-particle partitioning have observed that MONET passive samplers have a much lower epart, but the values range considerably, from the frequently used estimate of 10% (ref. 16) to as high as 54%,30 so it was deemed necessary to derive a MONET-specific epart value to accurately model PAS-derived concentrations. Previous MONET studies have reported RS values of primarily particle-bound SVOCs such as higher-molecular-weight PAHs and PBDEs approximately one order of magnitude lower than those of predominantly gas-phase SVOCs.4,8,10,16 The same effect is apparent in the present study for more than 70% of the particle-bound SVOC (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA > 11.3), with a median ratio of field-to-modelled RS values of 0.32 for the Harner RS and 0.52 for the Herkert RS values. This indicates that the modelled RS values for these compounds are overestimated if not adjusted for the lower epart (see Table 1 for individual sites). In contrast, the median ratio between field- and modelled-RS values of the gas-phase SVOCs (log
KOA > 11.3), with a median ratio of field-to-modelled RS values of 0.32 for the Harner RS and 0.52 for the Herkert RS values. This indicates that the modelled RS values for these compounds are overestimated if not adjusted for the lower epart (see Table 1 for individual sites). In contrast, the median ratio between field- and modelled-RS values of the gas-phase SVOCs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 8.8) is 1.53 for the Harner RS and 2.33 for the Herkert RS.
KOA < 8.8) is 1.53 for the Harner RS and 2.33 for the Herkert RS.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 8.8) and particle-phase SVOCs (log
KOA < 8.8) and particle-phase SVOCs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA > 11.3) with MONET PAS particle sampling efficiencies of both 100% and 18%
KOA > 11.3) with MONET PAS particle sampling efficiencies of both 100% and 18%
| Birkenes | Košetice | Pallas | Råö | Stórhöfði | Zeppelin | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Particle sampling efficiency (e part ) | 100% | 18% | 100% | 18% | 100% | 18% | 100% | 18% | 100% | 18% | 100% | 18% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
Gas phase SVOCs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA< 8.8) KOA< 8.8) |
||||||||||||
| Field RS/Harner RS | 0.9 | 0.9 | 1.6 | 1.6 | 1.0 | 1.1 | 1.8 | 1.8 | 11.3 | 11.4 | 1.7 | 1.7 |
| Field RS/Herkert RS | 2.8 | 2.8 | 1.9 | 1.9 | 2.6 | 2.8 | 2.0 | 2.0 | 9.1 | 9.2 | 1.7 | 1.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
Particle phase SVOCs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA> 11.3) KOA> 11.3) |
||||||||||||
| Field RS/Harner RS | 0.6 | 2.7 | 0.2 | 0.7 | 0.2 | 0.8 | 0.3 | 1.1 | — | — | 0.8 | 2.7 |
| Field RS/Herkert RS | 2.6 | 9.7 | 0.2 | 0.8 | 0.5 | 2.4 | 0.3 | 1.5 | — | — | 0.8 | 2.8 |
Over all sites, the ratios of field-to-modelled RS values for the particle-phase SVOCs are lower by a factor of 0.18 than the ratios for the gas-phase SVOCs (16% for Harner RS and 19% for Herkert RS). This suggests that, for the particle-bound SVOCs, the modelled RS values are overestimated by a factor of approximately five (1/0.18). This value of 18% was therefore used as an empirical estimate of the MONET-specific PAS particle sampling efficiency; it is significantly lower than the default 100% value, but consistent with the 10% estimate16 typically used for MONET PAS. All Harner- and Herkert-modelled concentrations and RS values were therefore adjusted and recalculated with epart = 18% rather than the default of 100%, following the same method as Bohlin-Nizzetto et al.,8 and these adjusted RS values were used for further analysis. This adjustment had negligible effects on the modelled concentrations of the gas-phase SVOCs but led to an increase in the modelled concentrations of the particle-phase SVOCs (Table 1). As a result, the differences between PAS and AAS concentrations became more similar for gas-phase and particle-bound SVOCs at most sites (Fig. 4), but some site-specific discrepancies persisted and were attributed to local meteorological differences, particularly wind speed.
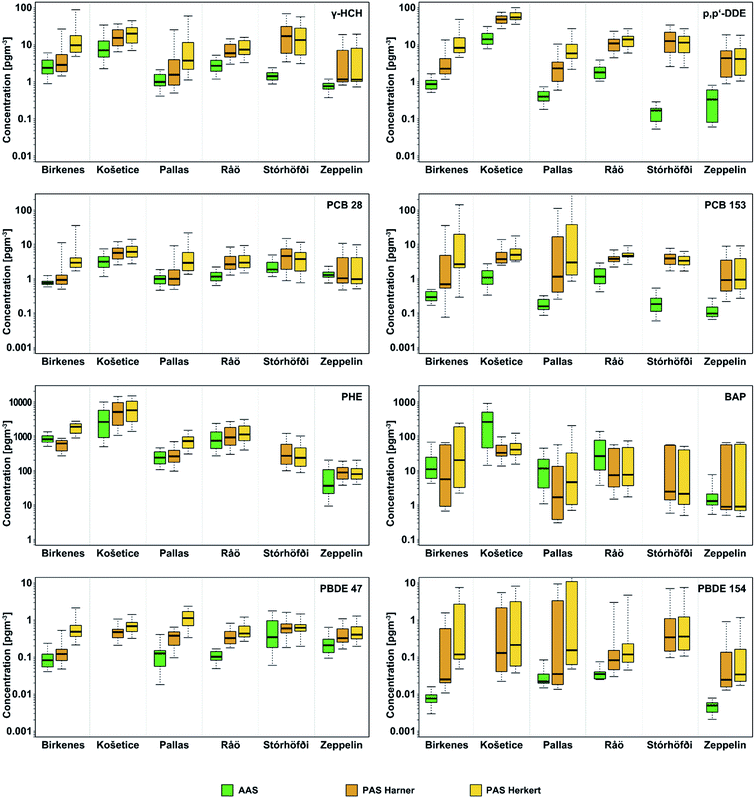 | ||
| Fig. 4 Boxplots of SVOC concentrations in air from EMEP active air sampling (AAS) and MONET passive air sampling (PAS) calculated by the adjusted ‘Harner’ and ‘Herkert’ models (epart = 18%). Boxplots represent ten years of overlapping monitoring data (2009–2018). Thick black lines represent medians, boxes span from 25th to 75th percentiles, and whiskers represent the 5th and 95th percentiles. See Fig. S6† for all other SVOCs included in this study. | ||
Influence of wind speed
The major difference between the Harner and Herkert models is how the RS values are affected by local meteorology. The Harner model simply incorporates average site temperatures over the deployment period;22 the Herkert model incorporates more detailed meteorological parameters at a much greater time resolution, including hourly wind speeds.23 While the Harner model has proven to be reliable for calculating concentrations of SVOCs from PAS at most GAPS sampling sites around the world, elevated RS values have been observed at some extremely windy sites.36,37 The influence of wind speed on RS has been thoroughly explored by Tuduri et al.,15 who found that an external wind speed of approximately 4 m s−1 represents the threshold corresponding to a change in internal airflow within the sampler from laminar to turbulent for the PAS used by both MONET and GAPS.18 For wind speeds from 0–4 m s−1, RS (for PCBs) gradually increases from approximately 4.5 to 15 m3 d−1; however, RS sharply increases with increasing wind speeds above 4 m s−1, up to ∼40 m3 d−1 at 7.5 m s−1.15 This effect provides a likely explanation for the significantly elevated field-RS values, and lower values of the modelled RS, observed here primarily at Stórhöfði. Not only is Stórhöfði the windiest meteorological station in Europe,38 but it was also the only site included in this study with a median wind speed over the entire monitoring period greater than 4 m s−1 (5.2 m s−1), with 66% of the hourly wind speeds exceeding this threshold (Table 2) and some even exceeding 20 m s−1 (Fig. S7†). Conversely, median wind speeds at Košetice, Råö, and Zeppelin were 2.7–3.5 m s−1 (with only 20–42% of hourly wind speeds above 4 m s−1), corresponding to good agreement between field and modelled RS, as previously discussed.| Birkenes | Košetice | Pallas | Råö | Stórhöfði | Zeppelin | |
|---|---|---|---|---|---|---|
| Ratios of median sampling rates | ||||||
| Field RS/Harner RS | 0.9 | 1.6 | 1.0 | 1.5 | 7.6 | 1.7 |
| Field RS/Herkert RS | 3.2 | 2.0 | 2.6 | 1.8 | 7.0 | 1.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Hourly wind speed data | ||||||
| Median wind speed (m s−1) | 0.5 | 2.7 | 0.6 | 2.8 | 5.2 | 3.5 |
| Wind speeds >4 m s−1 (%) | 0 | 23 | 0 | 20 | 66 | 42 |
The Herkert model was designed as an improvement to the original Harner model by incorporating the results of Tuduri et al.15 to account for the influence of wind speed on RS at particularly windy sites. However, the RS values from the Herkert model are still significantly lower than the field RS (Table 2). The dependency of RS on external wind speed (vex) within the Herkert model (i.e., RS ∼ f(vex)) is not continuous but rather defined for three wind speed ranges (<1.5 m s−1, 1.5–3.0 m s−1, >3.0 m s−1) as shown in eqn (7). While the magnitude of this dependency varies between the three ranges, the underlying relationship remains linear in the square root of vex (RS ∼ f(vexα); where α = 0.5 for laminar flow under all conditions).21 Yet studies have shown that when turbulent airflow conditions exist within the sampler (e.g., when the external wind speed exceeds 4.0 m s−1), the dependency of RS on vex is stronger, ranging from sub-linear (α = 0.63),34 to linear (α = 1),16,19 or greater than linear (α > 1).15,20,39,40 As a result, the constant square-root shape of the dependency, regardless of extremely high wind speeds, leads to an underestimation of modelled RS over periods of strong wind.
The discrepancy between the modelled Harner RS and Herkert RS at Birkenes and Pallas is the other major site-specific result identified in this study. As previously discussed, Herkert RS values at these two sites were significantly lower than both the field RS and the Harner RS, suggesting a site- and model-specific effect such as wind speed as observed at Stórhöfði. However, the hourly wind speeds at these two sites were substantially lower than at the other four sites, with medians of 0.5–0.6 m s−1 and 0% exceeding the 4 m s−1 threshold (Table 2 and Fig. S7†). This indicates that the Herkert model also underestimates RS at sites with very low wind speeds. Schuster et al.34 suggest this may be an artifact of the MERRA meteorological model underestimating wind speeds at sites where presence of a forest cover may have been incorrectly assumed.
By applying the square-root dependency between the mass transfer coefficient (kV) and the internal wind speed (vin) within the Herkert model (α = 0.5, eqn (6)), we derived a set of theoretical vin values back-calculated from all of the field RS derived in this study (blue dots in Fig. 5). A substantial number of these back-calculated vin values are extremely high (Fig. 5), providing further evidence that the square-root dependency of α = 0.5 is unrealistic for high external wind speeds (vex). We then compared the back-calculated vin values with modelled values of vin derived from the external wind speeds within the model by eqn (7) (black line in Fig. 5). The discrepancy between these two sets of data is presented in Fig. 5 and indicates an underestimation of RS by the Herkert model by approximately a factor of 2 at Råö, Košetice and Pallas, and increasing in magnitude with both decreasing wind speed (factor of 3 at Birkenes) and increasing wind speed (up to several orders of magnitude at Stórhöfði).
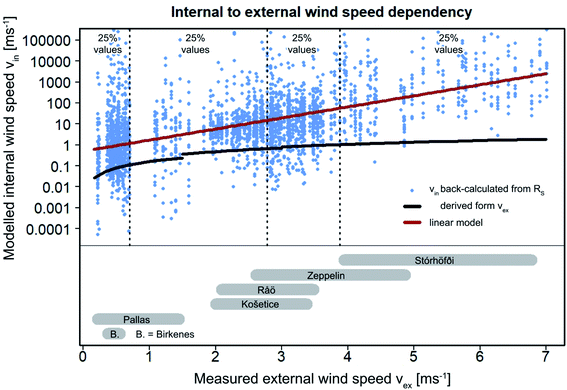 | ||
| Fig. 5 Relationship between internal wind speed, vin, and external wind speed, vex, for theoretical values of vin back-calculated from field RS (blue dots) and the stepwise linear dependency (eqn (7)) of vin on vex used within the Herkert model (black line). The red line was estimated by a linear model on log-transformed vin values and represents the relationship between vin and vex as the best fit of the field data. Wind speed ranges (5th to 95th percentile of median wind speeds over the sampling period) for the six sites are depicted as horizontal grey bars. | ||
Overall, the Harner model works well for the majority of sites, with some well-established uncertainties due to the exclusion of meteorological parameters other than temperature, but substantially underestimates RS if wind speed exceeds 4 m s−1. Conversely, the Herkert model is well designed for incorporating the influence of wind speed, but the brief calibration conducted in this study on a ten-year-long data series from sites with different meteorological conditions indicates that the dependency of the mass transfer coefficient, kV, on external wind speed, vex may be too shallow, leading to an underestimation of RS at sites with particularly low or high wind speeds.
Conclusions
Long-term atmospheric data from the major global semivolatile organic compound monitoring networks using active or passive air sampling have been shown to be internally consistent and to provide similar temporal trends, even when concentration units are not directly comparable. However, data harmonization between active EMEP air sampling and passive MONET air sampling – the two largest atmospheric SVOC monitoring networks in Europe – is still essential for more comprehensive evaluations of the effectiveness of both regional and global regulatory measures on these chemicals, as well as assessments of their impacts on environmental and human health across the continent. After 10 years of continuous parallel monitoring, results of this study indicate that there is good agreement between the long-term atmospheric SVOC concentrations measured by the two networks and methods, with nearly 80% of the median MONET PAS concentrations falling within a factor of 3 of their corresponding EMEP AAS concentrations. However, we have identified several cases where the agreement was poor, so any potential pooling of data must consider these cases and their conditions. For compound-specific considerations, the sampler-specific particle sampling efficiency of any passive sampler design should be well understood and accounted for in models for calculating RS. For site-specific considerations, modelled PAS concentrations are substantially overestimated compared to AAS at sites where the wind speed consistently exceeds 4 m s−1. We have provided a potential adjustment to the Herkert model to address this issue by increasing the power of the dependency (α) between the mass-transfer coefficient (kV) and the site wind speed (vex) to account for a possible transition from laminar to turbulent airflow within passive samplers. However, such an adjustment will require more in-depth model calibration and development beyond the scope of this study. Until the Herkert model can more accurately estimate atmospheric concentrations at high wind speeds, PAS concentrations from windy sites (above 4 m s−1) should be excluded from any comparisons to AAS concentrations. It should also be noted that even in cases where the long-term agreement was strong, substantial variability can be observed in comparisons of individual samples or shorter time periods, which may limit the potential for pooling short-term AAS and PAS data. Nonetheless, the strong agreement observed between the majority of AAS and PAS concentrations for most SVOCs and sites provides support for the harmonization and pooling of long-term EMEP and MONET concentration data as long as the compound- and site-specific recommendations are followed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support of the Research Infrastructures RECETOX RI (No. LM2018121) and ACTRIS RI (LM2015037) financed by the Ministry of Education, Youth and Sports of the Czech Republic (MEYS), and MEYS (Operational Programme Research, Development and Education (OP RDE) of the European Structural and Investment Funds: No. CZ.02.1.01/0.0/0.0/17_043/0009632). This study was supported from the European Union's Horizon 2020 research and innovation programme under grant agreements No. 857560, No. 820852, No. 689443. This work was also supported by the CETOCOEN PLUS project (CZ.02.1.01/0.0/0.0/15_003/0000469). This publication reflects only the authors' view and the European Commission is not responsible for any use that may be made of the information it contains. We thank our sampling technicians, laboratory staff and on-site monitoring partners without whom the MONET network would not be possible. We also acknowledge the Norwegian Institute of Air Research for their continued maintenance of the open access EBAS database used in this study, as well as Pernilla Bohlin Nizzetto, Roland Kallenborn, and Eva Brorstöm-Lundén for providing additional information about EMEP sampling sites. Access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum provided under the programme “Projects of Large Research, Development, and Innovations Infrastructures” (CESNET LM2015042), is greatly appreciated.References
- K. Tørseth, W. Aas, K. Breivik, a. M. Fjeraa, M. Fiebig, A.-G. Hjellbrekke, C. Lund Myhre, S. Solberg and K. E. Yttri, Introduction to the European Monitoring and Evaluation Programme (EMEP) and Observed Atmospheric Composition Change during 1972–2009, Atmos. Chem. Phys., 2012, 12(12), 5447–5481, DOI:10.5194/acp-12-5447-2012.
- P. Pribylova, R. Kares, J. Boruvkova, P. Cupr, R. Prokes, J. Kohoutek, I. Holoubek and J. Klanova, Levels of Persistent Organic Pollutants and Polycyclic Aromatic Hydrocarbons in Ambient Air of Central and Eastern Europe, Atmos. Pollut. Res., 2012, 3(4), 494–505, DOI:10.5094/apr.2012.057.
- K. B. White, J. Kalina, M. Scheringer, P. Přibylová, P. Kukučka, J. Kohoutek, R. Prokeš and J. Klánová, Temporal Trends of Persistent Organic Pollutants across Africa after a Decade of MONET Passive Air Sampling, Environ. Sci. Technol., 2021, 55, 9413–9424, DOI:10.1021/acs.est.0c03575.
- J. Kalina, M. Scheringer, J. Borůvková, P. Kukučka, P. Přibylová, P. Bohlin-Nizzetto and J. Klánová, Passive Air Samplers As a Tool for Assessing Long-Term Trends in Atmospheric Concentrations of Semivolatile Organic Compounds, Environ. Sci. Technol., 2017, 51(12), 7047–7054, DOI:10.1021/acs.est.7b02319.
- K. B. White, O. Sáňka, L. Melymuk, P. Přibylová and J. Klánová, Application of Land Use Regression Modelling to Describe Atmospheric Levels of Semivolatile Organic Compounds on a National Scale, Sci. Total Environ., 2021, 793, 148520, DOI:10.1016/j.scitotenv.2021.148520.
- J. Kalina, M. Scheringer, J. Borůvková, P. Kukučka, P. Přibylová, O. Sáňka, L. Melymuk, M. Váňa and J. Klánová, Characterizing Spatial Diversity of Passive Sampling Sites for Measuring Levels and Trends of Semivolatile Organic Chemicals, Environ. Sci. Technol., 2018, 52, 10599–10608, DOI:10.1021/acs.est.8b03414.
- F. Wania and C. Shunthirasingham, Passive Air Sampling for Semi-Volatile Organic Chemicals, Environ. Sci.: Processes Impacts, 2020, 22(10), 1925–2002, 10.1039/D0EM00194E.
- P. Bohlin-Nizzetto, L. Melymuk, K. B. White, J. Kalina, V. O. Madadi, S. Adu-Kumi, R. Prokeš, P. Přibylová and J. Klánová, Field- and Model-Based Calibration of Polyurethane Foam Passive Air Samplers in Different Climate Regions Highlights Differences in Sampler Uptake Performance, Atmos. Environ., 2020, 238, 117742, DOI:10.1016/j.atmosenv.2020.117742.
- J. Kalina, K. B. White, M. Scheringer, P. Přibylová, P. Kukučka, O. Audy and J. Klánová, Comparability of Long-Term Temporal Trends of POPs from Co-Located Active and Passive Air Monitoring Networks in Europe, Environ. Sci.: Processes Impacts, 2019, 21(7), 1132–1142, 10.1039/c9em00136k.
- E. Holt, P. Bohlin-Nizzetto, J. Borůvková, T. Harner, J. Kalina, L. Melymuk and J. Klánová, Using Long-Term Air Monitoring of Semi-Volatile Organic Compounds to Evaluate the Uncertainty in Polyurethane-Disk Passive Sampler-Derived Air Concentrations, Environ. Pollut., 2017, 220, 1100–1111, DOI:10.1016/j.envpol.2016.11.030.
- L. Melymuk, P. Bohlin, O. Sáňka, K. Pozo and J. Klánová, Current Challenges in Air Sampling of Semivolatile Organic Contaminants: Sampling Artifacts and Their Influence on Data Comparability, Environ. Sci. Technol., 2014, 48(24), 14077–14091, DOI:10.1021/es502164r.
- N. T. Petrich, S. N. Spak, G. R. Carmichael, D. Hu, A. Martinez and K. C. Hornbuckle, Simulating and Explaining Passive Air Sampling Rates for Semivolatile Compounds on Polyurethane Foam Passive Samplers, Environ. Sci. Technol., 2013, 47(15), 8591–8598, DOI:10.1021/es401532q.
- C. Moeckel, T. Harner, L. Nizzetto, B. Strandberg, A. Lindroth and K. C. Jones, Use of Depuration Compounds in Passive Air Samplers: Results from Active Sampling-Supported Field Deployment, Potential Uses, and Recommendations, Environ. Sci. Technol., 2009, 43(9), 3227–3232, DOI:10.1021/es802897x.
- M. Shoeib and T. Harner, Using Measured Octanol-Air Partition Coefficients to Explain Environmental Partitioning of Organochlorine Pesticides, Environ. Toxicol. Chem., 2002, 21(5), 984–990, DOI:10.1002/etc.5620210513.
- L. Tuduri, T. Harner and H. Hung, Polyurethane Foam (PUF) Disks Passive Air Samplers: Wind Effect on Sampling Rates, Environ. Pollut., 2006, 144(2), 377–383, DOI:10.1016/J.ENVPOL.2005.12.047.
- J. Klánová, P. Čupr, J. Kohoutek and T. Harner, Assessing the Influence of Meteorological Parameters on the Performance of Polyurethane Foam-Based Passive Air Samplers, Environ. Sci. Technol., 2008, 42(2), 550–555, DOI:10.1021/es072098o.
- C. Chaemfa, E. Wild, B. Davison, J. L. Barber and K. C. Jones, A Study of Aerosol Entrapment and the Influence of Wind Speed, Chamber Design and Foam Density on Polyurethane Foam Passive Air Samplers Used for Persistent Organic Pollutants, J. Environ. Monit., 2009, 11(6), 1135–1139, 10.1039/b823016a.
- J. Thomas, T. M. Holsen and S. Dhaniyala, Computational Fluid Dynamic Modeling of Two Passive Samplers, Environ. Pollut., 2006, 144(2), 384–392, DOI:10.1016/j.envpol.2005.12.042.
- A. A. May, P. Ashman, J. Huang, S. Dhaniyala and T. M. Holsen, Evaluation of the Polyurethane Foam (PUF) Disk Passive Air Sampler: Computational Modeling and Experimental Measurements, Atmos. Environ., 2011, 45(26), 4354–4359, DOI:10.1016/j.atmosenv.2011.05.052.
- P. C. Tromp, H. Beeltje, J. O. Okeme, R. Vermeulen, A. Pronk and M. L. Diamond, Calibration of Polydimethylsiloxane and Polyurethane Foam Passive Air Samplers for Measuring Semi Volatile Organic Compounds Using a Novel Exposure Chamber Design, Chemosphere, 2019, 227, 435–443, DOI:10.1016/j.chemosphere.2019.04.043.
- N. J. Herkert, A. Martinez and K. C. Hornbuckle, A Model Using Local Weather Data to Determine the Effective Sampling Volume for PCB Congeners Collected on Passive Air Samplers, Environ. Sci. Technol., 2016, 50(13), 6690–6697, DOI:10.1021/acs.est.6b00319.
- T. Harner, 2017_v1_5_Template for Calculating Effective Air Sample Volumes for PUF and SIP Disk Samplers_Sept_15, 2017 Search PubMed.
- N. J. Herkert, S. N. Spak, A. Smith, J. K. Schuster, T. Harner, A. Martinez and K. C. Hornbuckle, Calibration and Evaluation of PUF-PAS Sampling Rates across the Global Atmospheric Passive Sampling (GAPS) Network, Environ. Sci.: Processes Impacts, 2018, 20(1), 210–219, 10.1039/c7em00360a.
- J. Klánová, J. Kohoutek, L. Hamplová, P. Urbanová and I. Holoubek, Passive Air Sampler as a Tool for Long-Term Air Pollution Monitoring: Part 1. Performance Assessment for Seasonal and Spatial Variations, Environ. Pollut., 2006, 144(2), 393–405, DOI:10.1016/j.envpol.2005.12.048.
- P. Čupr, J. Klánová, T. Bartoš, Z. Flegrová, J. Kohoutek and I. Holoubek, Passive Air Sampler as a Tool for Long-Term Air Pollution Monitoring: Part 2. Air Genotoxic Potency Screening Assessment, Environ. Pollut., 2006, 144(2), 406–413, DOI:10.1016/j.envpol.2005.12.045.
- L. Melymuk, P. Bohlin-Nizzetto, R. Prokeš, P. Kukučka and J. Klánová, Sampling Artifacts in Active Air Sampling of Semivolatile Organic Contaminants: Comparing Theoretical and Measured Artifacts and Evaluating Implications for Monitoring Networks, Environ. Pollut., 2016, 217, 97–106, DOI:10.1016/j.envpol.2015.12.015.
- L. Melymuk, P. B. Nizzetto, T. Harner, K. B. White, X. Wang, M. Y. Tominaga, J. He, J. Li, J. Ma, W.-L. Ma, B. H. Aristizábal, A. Dryer, B. Jimenéz, J. Muñoz-Arnanz, M. Odabasi, Y. Dumanoglu, B. Yaman, C. Graf, A. Sweetman and J. Klánová, Global Intercomparison of Polyurethane Foam Passive Air Samplers Evaluating Sources of Variability in SVOC Measurements, Environ. Sci. Policy, 2021, 125, 1–9, DOI:10.1016/j.envsci.2021.08.003.
- M. Shoeib and T. Harner, Characterization and Comparison of Three Passive Air Samplers for Persistent Organic Pollutants, Environ. Sci. Technol., 2002, 36(19), 4142–4151, DOI:10.1021/es020635t.
- R. Gelaro, W. McCarty, M. J. Suárez, R. Todling, A. Molod, L. Takacs, C. A. Randles, A. Darmenov, M. G. Bosilovich, R. Reichle, K. Wargan, L. Coy, R. Cullather, C. Draper, S. Akella, V. Buchard, A. Conaty, A. M. da Silva, W. Gu, G.-K. Kim, R. Koster, R. Lucchesi, D. Merkova, J. E. Nielsen, G. Partyka, S. Pawson, W. Putman, M. Rienecker, S. D. Schubert, M. Sienkiewicz and B. Zhao, The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Clim., 2017, 30(14), 5419–5454, DOI:10.1175/JCLI-D-16-0758.1.
- M. Z. Markovic, S. Prokop, R. M. Staebler, J. Liggio and T. Harner, Evaluation of the Particle Infiltration Efficiency of Three Passive Samplers and the PS-1 Active Air Sampler, Atmos. Environ., 2015, 112, 289–293, DOI:10.1016/j.atmosenv.2015.04.051.
- H. B. Mann and D. R. Whitney, On a Test of Whether One of Two Random Variables Is Stochastically Larger than the Other, Ann. Math. Stat., 1947, 18(1), 50–60, DOI:10.1214/aoms/1177730491.
- W. H. Kruskal and W. A. Wallis, Use of Ranks in One-Criterion Variance Analysis, J. Am. Stat. Assoc., 1952, 47(260), 583, DOI:10.2307/2280779.
- T. Harner, M. Bartkow, I. Holoubek, J. Klanova, F. Wania, R. Gioia, C. Moeckel, A. J. Sweetman and K. C. Jones, Passive Air Sampling for Persistent Organic Pollutants: Introductory Remarks to the Special Issue, Environ. Pollut., 2006, 144(2), 361–364, DOI:10.1016/j.envpol.2005.12.044.
- J. K. Schuster, T. Harner, A. Eng, C. Rauert, K. Su, K. C. Hornbuckle and C. W. Johnson, Tracking POPs in Global Air from the First 10 Years of the GAPS Network (2005 to 2014), Environ. Sci. Technol., 2021, 55, 9479–9488, DOI:10.1021/acs.est.1c01705.
- Y. Li and F. Wania, Partitioning between Polyurethane Foam and the Gas Phase: Data Compilation, Uncertainty Estimation and Implications for Air Sampling, Environ. Sci.: Processes Impacts, 2021, 23(5), 723–734, 10.1039/d1em00036e.
- K. Pozo, T. Harner, F. Wania, D. C. G. Muir, K. C. Jones and L. A. Barrie, Toward a Global Network for Persistent Organic Pollutants in Air: Results from the GAPS Study, Environ. Sci. Technol., 2006, 40(16), 4867–4873, DOI:10.1021/es060447t.
- K. Pozo, T. Harner, S. C. Lee, F. Wania, D. C. G. Muir and K. C. Jones, Seasonally Resolved Concentrations of Persistent Organic Pollutants in the Global Atmosphere from the First Year of the GAPS Study, Environ. Sci. Technol., 2009, 43(3), 796–803, DOI:10.1021/es802106a.
- P. Dagsson-Waldhauserova, O. Arnalds and H. Olafsson, Long-Term Variability of Dust Events in Iceland (1949–2011), Atmos. Chem. Phys., 2014, 14(24), 13411–13422, DOI:10.5194/acp-14-13411-2014.
- L. Melymuk, M. Robson, P. A. Helm and M. L. Diamond, Evaluation of Passive Air Sampler Calibrations: Selection of Sampling Rates and Implications for the Measurement of Persistent Organic Pollutants in Air, Atmos. Environ., 2011, 45(10), 1867–1875, DOI:10.1016/j.atmosenv.2011.01.011.
- C. Moeckel, T. Harner, L. Nizzetto, B. Strandberg, A. Lindroth and K. C. Jones, Use of Depuration Compounds in Passive Air Samplers: Results from Active Sampling-Supported Field Deployment, Potential Uses, and Recommendations, Environ. Sci. Technol., 2009, 43(9), 3227–3232, DOI:10.1021/es802897x.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2em00007e |
| This journal is © The Royal Society of Chemistry 2022 |