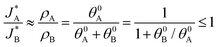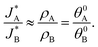Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Parallel water photo-oxidation reaction pathways in hematite photoanodes: implications for solar fuel production†
Anton
Tsyganok
 a,
Paulino
Monroy-Castillero‡
a,
Paulino
Monroy-Castillero‡
 b,
Yifat
Piekner
b,
Yifat
Piekner
 c,
Arik
Yochelis
c,
Arik
Yochelis
 *bc and
Avner
Rothschild
*bc and
Avner
Rothschild
 *ad
*ad
aDepartment of Materials Science and Engineering, Technion – Israel Institute of Technology, Haifa 3200002, Israel. E-mail: avnerrot@technion.ac.il
bDepartment of Solar Energy and Environmental Physics, Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Sede Boqer Campus, Midreshet Ben-Gurion 8499000, Israel. E-mail: yochelis@bgu.ac.il
cDepartment of Physics, Ben-Gurion University of the Negev, Be’er Sheva 8410501, Israel
dThe Nancy & Stephen Grand Technion Energy Program (GTEP), Technion – Israel Institute of Technology, Haifa 3200002, Israel
First published on 29th April 2022
Abstract
Water photo-oxidation on stable metal-oxide photoanodes presents a critical challenge for solar fuel production. This reaction is widely considered to proceed in a sequential pathway with four stepwise hydroxide-coupled hole transfer steps, resulting in oxidized surface intermediates that trap holes while their adsorbates change forms (e.g., from –OH to ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O to –OOH and back to –OH) so as to maintain charge neutrality. Here we study the potentiodynamic discharge characteristics of hematite photoanodes following polarization under water photo-oxidation conditions. Upon turning the light off, some of the oxidized intermediates discharge spontaneously whereas others remain oxidized for a while. The metastable intermediates discharge in a double-peak wave during cathodic potential sweep (in the dark). The relative peak heights were found to reverse after long time delays since turning the light off. This unexpected observation indicates that the discharge proceeds in parallel pathways, suggesting the same for the reverse reaction that leads to water photo-oxidation. Complementary photoelectrochemical impedance spectroscopy measurements display distinct charge transfer features, supporting the prevalence of parallel pathways in the water photo-oxidation reaction. Through a micro-kinetic model, we derive a criterion that explains why peak reversal, as observed in our measurements, can emerge only from parallel pathways. The prevalence of parallel pathways fundamentally broadens the current paradigm of the water photo-oxidation reaction mechanism, and it may inspire new strategies to reduce the high overpotential of this reaction so as to enhance the efficiency of solar fuel production.
O to –OOH and back to –OH) so as to maintain charge neutrality. Here we study the potentiodynamic discharge characteristics of hematite photoanodes following polarization under water photo-oxidation conditions. Upon turning the light off, some of the oxidized intermediates discharge spontaneously whereas others remain oxidized for a while. The metastable intermediates discharge in a double-peak wave during cathodic potential sweep (in the dark). The relative peak heights were found to reverse after long time delays since turning the light off. This unexpected observation indicates that the discharge proceeds in parallel pathways, suggesting the same for the reverse reaction that leads to water photo-oxidation. Complementary photoelectrochemical impedance spectroscopy measurements display distinct charge transfer features, supporting the prevalence of parallel pathways in the water photo-oxidation reaction. Through a micro-kinetic model, we derive a criterion that explains why peak reversal, as observed in our measurements, can emerge only from parallel pathways. The prevalence of parallel pathways fundamentally broadens the current paradigm of the water photo-oxidation reaction mechanism, and it may inspire new strategies to reduce the high overpotential of this reaction so as to enhance the efficiency of solar fuel production.
Broader contextWater photo-oxidation on metal-oxide photocatalysts presents a challenge for solar fuel production. This reaction involves four photo-generated holes that oxidize two water molecules to produce an oxygen molecule and four protons. The multihole reaction gives rise to different oxidized intermediates at the surface of the photocatalyst that may lead to electron–hole recombination which degrades the photoconversion efficiency. Understanding the reaction mechanism presents experimental and theoretical challenges. This work addresses these challenges by studying the discharge characteristics of oxidized intermediates, formed under water photo-oxidation conditions, as a function of time and potential following light turn-off and returning to equilibrium conditions. Double-peak cathodic discharge waves are observed, indicating the presence of two metastable intermediates with different redox potentials. Surprisingly, the relative peak heights were found to reverse after long time delays (>2 min) since light turn-off, suggesting that the respective intermediates represent different reaction pathways occurring in parallel rather than sequential steps of the same reaction. This conclusion is confirmed by theoretical analysis of the potentiodynamic discharge kinetics for sequential and parallel reactions. The prevalence of parallel reactions fundamentally broadens the paradigm of the water photo-oxidation reaction mechanism, suggesting that interactions between coexisting pathways may lead to complex self-organized kinetic effects. |
Introduction
The water photo-oxidation reaction on stable metal–oxide photoanodes is one of the bottlenecks for high-efficiency photoelectrochemical (PEC) devices for solar fuel production.1 Overcoming this bottleneck involves judicious selection and optimization of the photoanode composition and microstructure, and requires comprehensive understanding of the reaction mechanism to guide these efforts. The current understanding of the reaction mechanism2 relies on a sequential pathway of four proton-coupled electron transfer (PCET) steps proceeding in a stepwise manner at the reaction site, following Rossmeisl and Norskov's celebrated model of the oxygen evolution reaction (OER) on metal–oxide surfaces.3,4 In the case of alkaline water photo-oxidation on n-type metal–oxide photoanodes, a common scenario in PEC water splitting, the PCET steps are replaced by hydroxide-coupled hole transfer steps,2 where the salient difference between the water photo-oxidation reaction under light and the OER in dark emerges from the photo-generation and recombination of holes and electrons with excess free energy that give rise to a photovoltage. Each step results in a surface intermediate that traps a hole while its adsorbate changes form, e.g. from –OH to![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O to –OOH and back to –OH, so as to maintain charge neutrality. This model has been widely applied to study TiO2, WO3, α-Fe2O3 (hematite) and other photoanodes,2,5,6 to the extent that it is taken for granted by many researchers, whereas alternative pathways and different reaction mechanisms are usually overlooked. This work provides another angle into this paradigm, presenting experimental results supported by theoretical analysis that reveal the prevalence of parallel reaction pathways with distinct metastable intermediates in the case of water photo-oxidation on hematite photoanodes that serves here as a case study for stable metal-oxide photoanodes.
O to –OOH and back to –OH, so as to maintain charge neutrality. This model has been widely applied to study TiO2, WO3, α-Fe2O3 (hematite) and other photoanodes,2,5,6 to the extent that it is taken for granted by many researchers, whereas alternative pathways and different reaction mechanisms are usually overlooked. This work provides another angle into this paradigm, presenting experimental results supported by theoretical analysis that reveal the prevalence of parallel reaction pathways with distinct metastable intermediates in the case of water photo-oxidation on hematite photoanodes that serves here as a case study for stable metal-oxide photoanodes.
Different models of the OER mechanism have been proposed over the years since the pioneering studies of Bockris7 and Conway8 in the 1950's, see review articles on this topic.9,10 Some of these models involve O–O bond formation between neighboring metal–oxo species, known as the bi-nuclear OER mechanism.11 In contrast, the popular model mentioned in the previous paragraph follows Kobussen's OER pathway12 and assumes a sequence of four PCET steps on a single reaction site, known as the mono-nuclear OER mechanism.11 The main argument in favor of the mono-nuclear mechanism is that it excludes the high activation barrier for the recombination of oxygen atoms from neighboring metal-oxo species.3,4 The counter argument is that this consideration relies on the equilibrium free energies of the reaction intermediates, whereas non-equilibrium thermodynamics are controlled by kinetics rather than energetics (although the two are linked by the Sabattier principle).13 Another argument that challenges the mono-nuclear mechanism argues that it does not account for the effect of the applied overpotential on the intermediates’ free energies.14 Notably, there are strategies to reduce the barrier for O–O bond formation between neighboring metal-oxo species that facilitate the bi-nuclear mechanism in certain OER catalysts.15 The bi-nuclear mechanism and its descendant bi-functional mechanism that involves a hydrogen acceptor species next to the reaction site11 are of much interest as they provide promising routes to break the universal scaling relationships between different adsorbates that give rise to the high (360 ± 60 mV) thermodynamic overpotential in the mono-nuclear mechanism16 by spreading the four-electron reaction over two sites.17 In recent years, a growing number of studies report theoretical and experimental evidences supporting these mechanisms in champion OER catalysts such as MnO2, NiOOH and FeOOH.18,19 Inspired by our previous work on bi-functional H2O2 photo-oxidation on hematite photoanodes,20 we hypothesize that a bi-nuclear mechanism may be at play in water photo-oxidation (without sacrificial reagents) on metal-oxide photoanodes, perhaps in addition to the mono-nuclear mechanism. Should this be the case, where distinct reaction pathways may occur in parallel to each other, this can lead to unexpected consequences that emerge from mutual interactions between different pathways. For example, the competition for photo-generated holes and reaction sites between H2O2 and water photo-oxidation reactions leads to unusual features such as photocurrent hysteresis and negative differential resistance under certain conditions that facilitate critical competition.20 Notably, mutual interactions between different pathways are known in other electrochemical reactions where they give rise to rich nonlinear behaviors such as spatiotemporal oscillations, Turing and spiral patterns, and domain walls separating different surface adsorbates.21–24
To explore this intriguing hypothesis, we use hematite (α-Fe2O3) photoanodes as a model system to investigate the fate of oxidized intermediates following applying high potential under illumination, conditions that lead to water photo-oxidation and oxygen evolution. Water photo-oxidation on hematite photoanodes (usually doped ones) has been the subject of intense investigation, with many studies addressing the role of surface states (aka intermediates) in this reaction. While some studies highlight the deleterious effect of surface states that induce ‘back electron–hole recombination’ that shifts the photocurrent onset potential to high potentials,25 and propose ways to eradicate it by using suitable co-catalysts and overlayers,26 other studies highlight the beneficial role they play as a vessel for the elementary hole transfer steps in the water photo-oxidation reaction.27 The difference between contributing and non-contributing surface states was discussed by Bieberle-Hütter et al.28 Bisquert et al. discussed the difference between direct and indirect hole transfer from the valence band or through surface states, respectively,29 and, together with Hamann et al., argued that water photo-oxidation on hematite occurs by the latter process whereby the surface states are oxidized by trapping photogenerated holes.27 Using terminology from earlier studies on TiO2 photoanodes,30 Durrant et al. coined the term ‘long-lived holes’ to describe holes that manage to survive long enough (sub-seconds to seconds) to participate in the water photo-oxidation reaction on hematite photoanodes (as well as other metal-oxides).31 Peter et al. used the term ‘surface trapped holes’ to describe these species,32 and postulated that they might correspond to metastable oxidized intermediates in the form of Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O.33 The density of the long-lived surface trapped holes was reported by Durrant et al. to reach up to 4 × 1014 cm−2 under sunlight-equivalent illumination, which is much higher than typical densities of extrinsic surface states that do not contribute to water photo-oxidation.34,35
O.33 The density of the long-lived surface trapped holes was reported by Durrant et al. to reach up to 4 × 1014 cm−2 under sunlight-equivalent illumination, which is much higher than typical densities of extrinsic surface states that do not contribute to water photo-oxidation.34,35
The long-lived surface trapped holes have distinct optical signatures that enable to monitor their photogeneration and fate when the light turns on and off, respectively, using spectro-electrochemistry and transient optical measurements. Durrant et al. observed a narrow absorption band at 580 nm that was found to increase with increasing bias above the photocurrent onset potential where water photo-oxidation begins, and to decay slowly after turning the light off, suggesting that it corresponds to a metastable oxidized intermediate of the water photo-oxidation reaction.36 Using in silico density functional theory (DFT) calculations based on the mono-nuclear OER model, Caspary Toroker et al. assigned this 580 nm absorption band to Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediates of the water photo-oxidation reaction,37 providing theoretical support to earlier experimental studies regarding the chemical identity of the long-lived surface trapped holes. Using operando infrared spectroscopy measurements combined with isotopically labeled water, Hamann et al. provided direct evidence for an oxygen-containing surface species generated during water photo-oxidation on hematite in alkaline electrolyte, and assigned it to Fe(IV)
O intermediates of the water photo-oxidation reaction,37 providing theoretical support to earlier experimental studies regarding the chemical identity of the long-lived surface trapped holes. Using operando infrared spectroscopy measurements combined with isotopically labeled water, Hamann et al. provided direct evidence for an oxygen-containing surface species generated during water photo-oxidation on hematite in alkaline electrolyte, and assigned it to Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediates,6 reconciling previous discussions on the nature of the long-lived surface trapped holes in hematite photoanodes. However, the identification of Fe(IV)
O intermediates,6 reconciling previous discussions on the nature of the long-lived surface trapped holes in hematite photoanodes. However, the identification of Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediates does not exclude alternative reaction pathways that may occur in parallel. Indeed, alternative reaction pathways were proposed occasionally. Based on rate law analysis, Durrant et al. suggested mono- and bi-nuclear reaction pathways to account for the transition from a first order reaction at low light intensities to a third order reaction at high light intensities, respectively.35 This analysis was applied also to other metal-oxides (TiO2, BiVO4), and supported by DFT calculations.34 Li et al. proposed an interplay between two distinct surface intermediates taking part in the reaction mechanism.38 Another optional bi-molecular reaction pathway was proposed by Hamann et al. based on surface state population measurements.39
O intermediates does not exclude alternative reaction pathways that may occur in parallel. Indeed, alternative reaction pathways were proposed occasionally. Based on rate law analysis, Durrant et al. suggested mono- and bi-nuclear reaction pathways to account for the transition from a first order reaction at low light intensities to a third order reaction at high light intensities, respectively.35 This analysis was applied also to other metal-oxides (TiO2, BiVO4), and supported by DFT calculations.34 Li et al. proposed an interplay between two distinct surface intermediates taking part in the reaction mechanism.38 Another optional bi-molecular reaction pathway was proposed by Hamann et al. based on surface state population measurements.39
In addition to spectro-electrochemical and transient optical measurements, the surface trapped holes can also be investigated by analyzing capacitive features in electrochemical impedance spectroscopy (EIS), photoelectrochemical impedance spectroscopy (PEIS), chopped-light voltammetry (CLV)40,41 and cathodic discharge measurements (CDM) following polarization under potential and illumination conditions that give rise to water photo-oxidation.39,40 In CDM, the sample is first pre-oxidized by applying sufficient anodic bias under illumination so as to give rise to oxygen evolution. Then, the light is turned off to stop the photogeneration of electrons and holes. Some of the oxidized intermediates that were formed during the pre-oxidation step decay spontaneously when the light is turned off, resulting in a cathodic spike that resembles the cathodic spikes in CLV measurements,42 whereas others remain oxidized for a while. These metastable oxidized intermediates are then forced to discharge (reduce) by sweeping the potential to lower values, giving rise to a cathodic discharge wave that is associated with the charge of the photoholes stored in them. CDM provides a powerful tool to measure the charge that was stored in the metastable oxidized intermediates and their potentiodynamic discharge characteristics such as the dependence on the initial bias potential, the discharge rate and the effect of surface treatments.39,43
In this study, we address the puzzling questions regarding the role of metastable oxidized intermediates in the water photo-oxidation reaction mechanism on doped hematite photoanodes. Through time-dependent CDM, we monitor their potentiodynamic discharge characteristics and show the existence of parallel pathways that involve metastable intermediates with different decay rates that give rise to distinct peaks in the cathodic discharge wave. Surprisingly, the relative heights of these peaks were found to reverse at long time delays (before sweeping the potential to lower values), an observation that cannot be reasoned by a sequential pathway where the charge transfers in a stepwise manner from one intermediate state to another. This was observed for hematite films of different thicknesses (ca. 20, 80 and 120 nm), doped with different dopants (Zn, Ti and Sn), deposited on different substrates (sapphire, silicon and glass) coated with different current collectors (NTO, FTO, ITO and Pt), and deposited at different temperatures (300, 500 and 700 °C), suggesting a general phenomenon rather than sample specific characteristics. Using a micro-kinetic model, we show why peak reversal, as observed in our measurements, indicates parallel pathways rather than a sequential pathway. Our results shed new light on the controversy regarding the nature of the oxidized intermediates and their role in the photo-oxidation reaction mechanism, revealing the prevalence of distinct metastable intermediates and parallel reaction pathways. We speculate that the coexisting pathways may interact with each other to provide complex reaction mechanisms that are yet to be explored.
Experimental procedures
Sample preparation and material characterizations
Thin film (∼100 nm) hematite photoanodes were deposited by pulsed laser deposition (PLD) using a turn-key PLD workstation (PLD/MBE 2100, PVD Products, USA) equipped with a KrF pulsed excimer laser beam (λ = 248 nm, COMPex PRO 102 Excimer Laser, Lambda Physik/Coherent). The main photoanode reported in the article was deposited at a set-point temperature of 700 °C from a Zn-doped (1 cat%) Fe2O3 target on a lattice-matched Nb-doped (1 cat%) SnO2 (abbreviated NTO) coated (0001) sapphire substrate to obtain heteroepitaxial growth. The sample preparation method is described in details in ref. 44, and material characterizations including XRD, TEM, SEM and AFM of a nearly identical sample to this photoanode (the two samples were deposited in the same batch) are reported in ref. 45, demonstrating a heteroepitaxial hematite film with atomically smooth flat surface. Another photoanodes include polycrystalline hematite layers of different thicknesses (ranging from ca. 20 to 120 nm) that were deposited at 300 °C (and subsequently annealed at 500 °C) from a Sn-doped (1 cat%) Fe2O3 target on tin-doped indium oxide (abbreviated ITO) coated eagle glass substrate (EAGLE XG, Corning) as reported in ref. 46; or at 500 °C from the same Sn-doped Fe2O3 target on a platinum coated Si substrate; or at 500 °C from a Ti-doped (1 cat%) Fe2O3 target on a commercial fluorine-doped tin oxide (abbreviated FTO) coated glass substrate (TEC 15). Photoelectrochemical and electrochemical measurements of these specimens are reported in Section S4 (ESI†), displaying qualitatively similar results to the main photoanode (Zn-doped hematite) reported in the article, indicating that the behavior discussed herein is generic to hematite photoanodes with different dopants, impurities and microstructures. It is noted that interdiffusion from the transparent current collector to the hematite layer is expected to be effective at temperatures above 600 °C.47 The photoanodes examined in this work include samples processed below and above this critical temperature.Photoelectrochemical measurements
Photoelectrochemical measurements were performed in a standard three-electrode setup using the previously reported “cappuccino cell”,48 with a round aperture of 0.11 cm2. The measurements were carried out in 1 M NaOH in deionized (DI) water. An Hg/HgO electrode (RE-61AP, ALS-Japan) filled with 1 M NaOH aqueous solution was used as a reference electrode, and a platinum wire coil as a counter electrode. The potential values are reported in the reversible hydrogen electrode (RHE) scale. The measurements were carried out using a CompactStat potentiostat (Ivium). Linear sweep voltammetry (LSV) measurements were carried out in a sweep rate of 10 mV s−1. A broad-band white LED (Mightex GCS-6500-15-A0510, glacier white 6500 K) was used as a light source. The illumination source was calibrated to 100 mW cm−2 using a calibrated Si photodiode (AK-300 dye-sensitized reference PV cell, Konica Minolta, Singapore). Typical LSV voltammograms of the main photoanode (comprising a heteroepitaxial Zn-doped hematite film) measured under dark and light conditions are presented in Fig. 1a. In addition to LSV, chopped-light voltammetry (CLV) measurements were carried out under similar conditions while chopping the light on and off every 1 s, see Fig. 1a.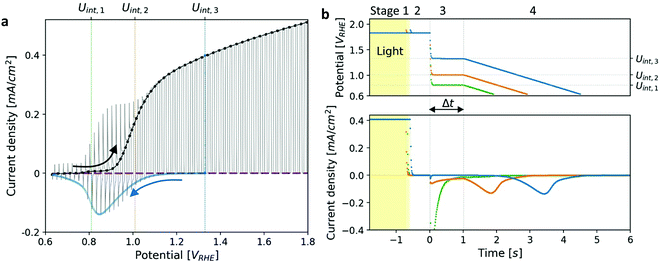 | ||
| Fig. 1 Photocurrent voltammetry and cathodic discharge measurements of a heteroepitaxial Zn-doped hematite photoanode. (a) Linear sweep voltammetry (LSV) measurements under dark (purple), light (black) and chopped-light (grey) conditions. The cathodic discharge wave obtained for Uint,3 = 1.33 VRHE (Fig. 1b) is overlaid in blue. (b) Cathodic discharge measurements (CDM) for three intermediate potentials (Uint) in the third stage, as indicated in the top panel. The respective potentials are also marked in (a). The top panel shows the potential applied during different stages of the measurement, and the bottom panel shows the current response to changes in the illumination and applied potential. | ||
Cathodic discharge measurements
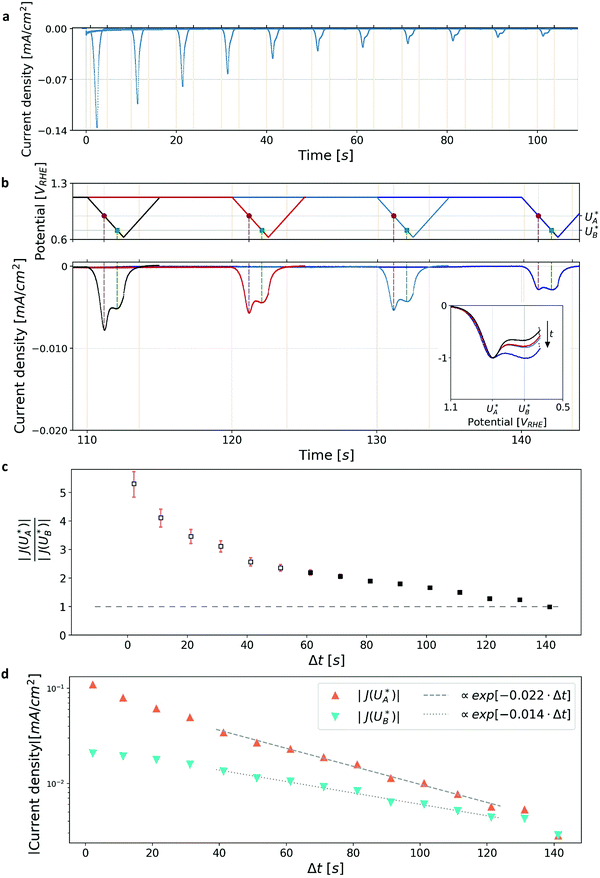
Cathodic discharge measurements (CDM) after anodic polarization under potential and illumination conditions sufficient to drive water photo-oxidation and oxygen evolution were carried out to measure the amount of charge stored as surface trapped holes in oxidized intermediates, and their potentiodynamic discharge characteristics upon turning the light off and subsequently sweeping the potential cathodically after various time delays ranging from seconds to minutes. CDM were introduced by Wilson to measure the population of surface states in TiO2 photoanodes,49 and were later applied to study the potentiodynamic discharge characteristics of oxidized intermediates in hematite photoanodes.39,44 The classical CDM sequence comprises three stages: (1) anodic polarization at a specified high potential (Uhigh) within the water photo-oxidation range until stabilization of the photocurrent; (2) turning the light off while holding the potential at the same level (Uhigh) as in the first stage for a short duration (thold); and (3) fast cathodic sweep (at a rate of 200 mV s−1) to a specified low potential (Ulow), followed by cyclic voltammetry between Ulow and Uhigh for several cycles.39 This sequence is illustrated in the Section S3 (ESI†). In this work we introduce a modified sequence with another stage between the second and third stages of the classical sequence, in which the potential is reduced to an intermediate value (Uint) between the low and high potentials (Ulow < Uint < Uhigh) for a set delay time (Δt) before the potential sweep (from Uint to Ulow) commences. This allows discharging the oxidized intermediates from different starting potentials, Uint, without altering the initial conditions in the first stage in which they were created by capturing photogenerated holes at a high potential, Uhigh, sufficient to oxidize the intermediates and derive water photo-oxidation. Furthermore, it also allows monitoring the spontaneous decay of the metastable oxidized intermediates in the absence of photo-generation of holes (and electrons) as a function of the delay time (Δt) and applied potential (Uint) before they are forced to discharge by the cathodic potential sweep that follows this stage. The modified CDM sequence and the current response to the changes in illumination and potential conditions are shown in Fig. 1b top and bottom panels, respectively.Results and discussion
Linear sweep voltammograms for a heteroepitaxial Zn-doped hematite photoanode measured in dark, light and chopped-light conditions are shown in Fig. 1a (purple, black and grey curves, respectively). The chopped-light voltammogram traces the dark and light voltammograms and the steady-state dark current is zero throughout the measurement (see Fig. S1, ESI†), except for anodic and cathodic capacitive spikes at the moments when the light was turned on and off, respectively. The spikes disappear at potentials larger than 1.05 VRHE, where the photocurrent “plateau” region begins (the plateau region is where the photocurrent rises modestly with increasing potentials, with a nearly constant slope). Similarly to previous reports,39,41 the largest spikes appear at the photocurrent onset potential, Uonset = 0.9 VRHE. These spikes arise from charging (oxidizing) of surface intermediates by trapping photogenerated holes upon turning the light on, and discharging (reducing) them through electron–hole recombination upon turning it off. When the light is turned on, the photogenerated holes are captured in acceptor surface states occupied by electrons that correspond to the ground state of the water photo-oxidation reaction intermediates (often marked as Fe–OH),20,28,39 giving rise to a positive (anodic) current spike. When the light is turned off, a negative (cathodic) current spike is observed due to discharging (reducing) the oxidized (charged) intermediates by recombination of the surface trapped holes with electrons. In other words, electrons re-occupy the oxidized intermediates in the absence of photogenerated holes. The discharge process proceeds until the electron occupation reaches steady state in dark conditions, as dictated by the Fermi level that is controlled by the applied potential.To demonstrate the correlation between the chopped-light and cathodic discharge measurements, Fig. 1b presents the results of CDM with different intermediate potentials Uint which are also marked in the chopped-light voltammogram presented in Fig. 1a. In the first stage, the photoanode was held under illumination and a potential of 1.83 VRHE (Uhigh), displaying a steady photocurrent density of 0.41 mA cm−2, as shown in Fig. 1b (bottom panel). Then, in the next stage, the light was turned off at t = −0.5 s without changing the applied potential, leading to immediate current drop to zero value (see Fig. 1b, bottom panel), in agreement with the dark current voltammogram presented in Fig. 1a (purple curve). No spike is observed at the transition between the first and second stages, in agreement with the lack of capacitive cathodic spikes at high potentials in the chopped-light voltammogram presented in Fig. 1a (grey curve). In the next stage, at t = 0 s the potential was dropped to an intermediate value (Uint) of 1.33, 1.01 or 0.8 VRHE (blue, orange, and green curves, respectively). For the highest value, Uint,3 = 1.33 VRHE (blue curve), the abrupt potential drop resulted in nothing but a tiny capacitive spike. The cathodic spike grew for Uint,2 = 1.01 VRHE (orange curve), and extended throughout the 1 s duration of this stage. For the lowest value, Uint,1 = 0.8 VRHE (green curve), it grew even further into a very prominent spike that discharged the oxidized intermediates nearly completely. These results are in agreement with the cathodic spikes observed in the chopped-light voltammograms at the respective potentials (Fig. 1a, grey curve).
The cathodic spikes are attributed to recombination between electrons (majority charge carriers) and surface-trapped holes in metastable oxidized intermediates that were formed in the first stage of the CDM. The lower the intermediate potential (Uint) that was applied in the third stage, the lower was the energy band bending towards the surface (a.k.a. surface band bending), thereby enhancing the recombination between electrons and surface-trapped holes, as explained below. Finally, in the last stage, the potential was swept down to 0.63 VRHE, forcing the remaining surface-trapped holes to recombine with electrons, giving rise to the cathodic discharge waves observed in the second and third measurements (orange and blue curves, respectively). Note the salient difference between the cathodic discharge spike and wave observed in the third and fourth stages, respective. The spike results from a sudden drop in the applied potential from Uhigh to Uint, whereas the wave results from a linear sweep from Uint to Ulow. As shown in Fig. 1b (bottom panel), the cathodic discharge wave is delayed for CDM starting from higher Uint values. This delay results from the fact that it takes longer time to reach the potentials were recombination prevails, while starting from higher Uint values and keeping the same sweep rate (200 mV s−1) for all measurements. The cathodic discharge wave is also smaller for measurements from lower Uint values because more oxidized intermediates (surface-trapped holes) were reduced (discharged) in the previous stage. But otherwise the cathodic discharge waves observed for the CDM with Uint = 1.33 and 1.01 VRHE (blue and orange curves, respectively) have similar shapes, with a peak at 0.87 VRHE, which is commensurate with the photocurrent onset potential (Fig. 1a), in agreement with previous studies.40,41,44 The CDM with = 0.8 VRHE (green curve) had a prominent cathodic discharge spike in the third stage, in which the potential dropped to 0.8 VRHE where the oxidized intermediates are no longer (meta)stable, with a tail extending into the fourth stage. No cathodic discharge wave is observed for this measurement because the intermediates had already been discharged (for the most part) by the time the cathodic potential sweep began. The cathodic discharge wave for the CDM with Uint,3 = 1.33 VRHE is overlaid, after converting the time scale to a potential scale (according to the top panel of Fig. 1b), on the photocurrent voltammograms presented in Fig. 1a (blue curve). The observation that it traces the envelope of the cathodic current spikes in the CLV (grey curve) corroborates that both measurements probe the same physico-chemical process, i.e., charge carrier recombination between electrons and surface-trapped holes.41
The total charge obtained by integrating the cathodic discharge current over the second, third and fourth stages yields the amount of surface-trapped holes that were captured in surface intermediates in the first stage. The integrated charge depends on the illumination and potential conditions in the first stage and is independent on the potential Uint from which the potential sweep begins (see Fig. S2, ESI†). Here our modified CDM with the additional intermediate stage differs from the classical DCM where the potential sweep begins from the highest potential (Uhigh) applied in the entire measurement (see Fig. S3, ESI†), which affects the integrated charge in a certain range of potential values (Fig. S2, ESI†). For Uhigh above 1.2 VRHE the integrated charge reaches ca. one hole per Fe site at the surface. Such a high surface charge density cannot be reasoned by defect surface states whose concentration is typically much lower than that, indicating that it originates from oxidized intermediates of the water photo-oxidation reaction.34,35 We note that although the cathodic discharge currents are measured in dark, where no photogeneration of holes and electrons takes place, they hold valuable information on the preexisting oxidized intermediates that gave rise to the water photo-oxidation reaction in the first stage. To confirm that this is the case, subsequent cyclic voltammetry measurements between Uhigh and Ulow performed in dark display negligible cathodic discharge currents (see Section S4, ESI†). In the absence of light the (thermal) generation of holes is negligible (for n-type hematite), therefore no significant concertation of oxidized intermediates can be formed, except for high anodic bias beyond the range examined in our measurments.39,50 This proves that the cathodic discharge current observed in the first potential sweep corresponds to the reduction of preexisting oxidized intermediates that had been formed previously in the first stage where water photo-oxidation prevailed.
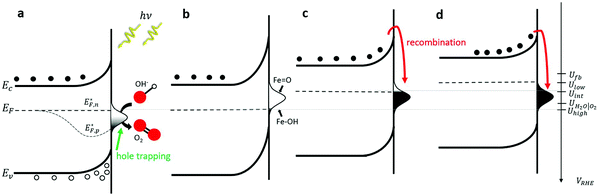
To put these observations into the broader context of semiconductor surface states51 and provide deeper insight into the underlying physics, Fig. 2 depicts schematic energy band diagrams representing the four stages in our CDM. In these illustrations, the reaction intermediates are represented by a Gaussian distribution of mid-gap surface states. The upwards band bending from the bulk (left) to the surface (right) implies that the surface states are negatively charged, which correspond to acceptor surface states occupied by electrons in the jargon of semiconductor surfaces.51 In terms of the reaction coordinate, the occupied surface states correspond to the ground state of the reaction intermediates, Fe–OH. In thermal equilibrium, i.e., without illumination and when the steady-state net current is zero, the surface state occupation probability is determined, according to Fermi–Dirac statistics, by their energy position with respect to the Fermi energy (EF), such that states below EF are mostly occupied by electrons whereas those above EF are mostly empty. Thus, the occupation probability increases with decreasing bias potentials, as shown in Fig. 2b–d by the increasing ratio between occupied and empty states, presented by black and white shading, respectively. This general description is in agreement with the specific characteristics of our system. Considering the point of zero charge (PZC) of hematite is much lower (∼8.5)52 than the high pH (13.6) of the alkaline electrolyte in our measurements, the surface is negatively-charged at rest (i.e., in open circuit conditions). The negative surface charge arises, presumably, from chemisorbed OH− ions on Fe surface sites (marked Fe–OH), which are widely considered as forming the ground state of the intermediates of the water (photo)oxidation reaction in alkaline electrolyte.6,36 Under anodic polarization, the applied bias draws the Fermi level below the flat-band potential (Ufb, reported to be 0.3 VRHE for 1% Zn-doped hematite),53 resulting in higher chemisorption of OH− ions and deeper band bending than in rest (open circuit) conditions. At sufficiently high potentials the surface states are aligned with the conduction band such that direct injection of electrons from the surface states to the conduction band becomes possible. This gives rise to an anodic current and oxygen evolution, i.e., water oxidation (without illumination). Our voltammetry and CDM measurements have not reached such conditions, as can be seen by the zero steady-state dark current in Fig. 1a and b, respectively.
The situation is different under illumination, i.e., in the first stage of the CDM, where the electron occupation probability is not dictated by a single Fermi level which is controlled by the applied potential. Under illumination there are two distinct quasi-Fermi levels, one for the electrons 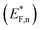 and another one for the holes
and another one for the holes 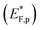 , and the surface state occupation is governed by kinetics, such that preferential capture of photogenerated holes, aka surface trapped holes, reduces the electron population in the surface states with respect to the dark state (at the same bias potential), as depicted in Fig. 2a (compared with Fig. 2b). Consequently, the surface band bending decreases (compare Fig. 2a with Fig. 2b). This photo-induced change in the surface potential gives rise to surface photovoltage,54 which adds up to the external potential applied by the power source to drive the water photo-oxidation reaction and generate an anodic photocurrent. In the second stage, the light is turned off, thereby turning off the photocurrent and the photovoltage. As a result, the steady-state current drops to zero, in accordance with the dark voltammogram presented in Fig. 1a (purple dashed line curve). In addition, no transient capacitive current is observed upon turning the light off, as can be seen in the CDM results presented in Fig. 1b (bottom panel), and also in agreement with the chopped-light voltammogram that shows no current spikes at high potentials (Fig. 1a, grey curve). This is due to the high potential (Uhigh = 1.83 VRHE) that gives rise to low electron occupation probability in the surface states, and the high energy barrier (due to the large surface band bending, see Fig. 2b) for bulk electrons to cross the electron-depleted space charge region in order to reach the surface states. In the third stage, the potential drops abruptly from Uhigh to, thereby increasing the electron occupation probability in the surface states and decreasing the energy barrier for electron transport from the bulk to the surface. As a result, more electrons populate the surface states than in the previous stage, as illustrated in Fig. 2c (compared with Fig. 2b). This leads to temporary (capacitive) electron flow to the surface until the surface states reach the new occupation probability imposed by the applied potential (Uint), resulting in the transient cathodic discharge spikes observed in this stage (see Fig. 1b, bottom panel). The lower the intermediate potential (Uint) is, the larger the cathodic discharge spike is. In the fourth stage, the potential is swept to even lower potentials (down to Ulow), further decreasing the surface band bending and increasing the electron population in the surface states (Fig. 2d), giving rise to the cathodic discharge wave observed in Fig. 1b (bottom panel). The filling of the surface states by electron in stages 2 to 4 of the CDM sequence is often called electron back-injection in the photoelectrochemical water splitting jargon.25 Herein, we refer to this process as discharging (reducing) of the pre-oxidized (charged) intermediates that were formed in the first stage under illumination and high anodic bias, conditions in which water photo-oxidation prevailed. In accordance with the mono-nuclear model of the water photo-oxidation reaction pathway,6 the ground state (reduced) and metastable (oxidized) intermediates may be referred to as Fe–OH and Fe
, and the surface state occupation is governed by kinetics, such that preferential capture of photogenerated holes, aka surface trapped holes, reduces the electron population in the surface states with respect to the dark state (at the same bias potential), as depicted in Fig. 2a (compared with Fig. 2b). Consequently, the surface band bending decreases (compare Fig. 2a with Fig. 2b). This photo-induced change in the surface potential gives rise to surface photovoltage,54 which adds up to the external potential applied by the power source to drive the water photo-oxidation reaction and generate an anodic photocurrent. In the second stage, the light is turned off, thereby turning off the photocurrent and the photovoltage. As a result, the steady-state current drops to zero, in accordance with the dark voltammogram presented in Fig. 1a (purple dashed line curve). In addition, no transient capacitive current is observed upon turning the light off, as can be seen in the CDM results presented in Fig. 1b (bottom panel), and also in agreement with the chopped-light voltammogram that shows no current spikes at high potentials (Fig. 1a, grey curve). This is due to the high potential (Uhigh = 1.83 VRHE) that gives rise to low electron occupation probability in the surface states, and the high energy barrier (due to the large surface band bending, see Fig. 2b) for bulk electrons to cross the electron-depleted space charge region in order to reach the surface states. In the third stage, the potential drops abruptly from Uhigh to, thereby increasing the electron occupation probability in the surface states and decreasing the energy barrier for electron transport from the bulk to the surface. As a result, more electrons populate the surface states than in the previous stage, as illustrated in Fig. 2c (compared with Fig. 2b). This leads to temporary (capacitive) electron flow to the surface until the surface states reach the new occupation probability imposed by the applied potential (Uint), resulting in the transient cathodic discharge spikes observed in this stage (see Fig. 1b, bottom panel). The lower the intermediate potential (Uint) is, the larger the cathodic discharge spike is. In the fourth stage, the potential is swept to even lower potentials (down to Ulow), further decreasing the surface band bending and increasing the electron population in the surface states (Fig. 2d), giving rise to the cathodic discharge wave observed in Fig. 1b (bottom panel). The filling of the surface states by electron in stages 2 to 4 of the CDM sequence is often called electron back-injection in the photoelectrochemical water splitting jargon.25 Herein, we refer to this process as discharging (reducing) of the pre-oxidized (charged) intermediates that were formed in the first stage under illumination and high anodic bias, conditions in which water photo-oxidation prevailed. In accordance with the mono-nuclear model of the water photo-oxidation reaction pathway,6 the ground state (reduced) and metastable (oxidized) intermediates may be referred to as Fe–OH and Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, respectively, as depicted in Fig. 2b. We note that this study does not pretend to make any claims about the chemical identity of the intermediates, where we rely on previous studies that were discussed in the introduction. Therefore, this assignment is not binding.
O, respectively, as depicted in Fig. 2b. We note that this study does not pretend to make any claims about the chemical identity of the intermediates, where we rely on previous studies that were discussed in the introduction. Therefore, this assignment is not binding.
Turning back to the CDM results, we note that the cathodic discharge waves in Fig. 1c are asymmetric in shape, indicating they comprise of more than one peak. To examine their characteristics more closely, Fig. 3 presents the cathodic discharge waves alone, for CDM with different delay times in the third stage. In these measurements, the photoanode was biased under illumination at Uhigh = 1.53 VRHE in the first stage, then the light was turned off in the second stage, and after 0.5 s the potential was dropped abruptly to Uint = 1.13 VRHE and held constant for different delay times Δt, until finally it was swept to Ulow = 0.63 VRHE in the fourth stage (at a sweep rate of 200 mV s−1). Unlike previous CDM studies of hematite photoanodes in which the cathodic discharge sweep was performed shortly after the light was turned off,39,43,44 this work deliberately introduces a variable time delay (Δt) before the cathodic discharge sweep in order to examine the (meta)stability of the oxidized intermediates. The Δt-dependent cathodic discharge plots presented in Fig. 3 show that the cathodic discharge waves change drastically in both amplitude and shape as a function of Δt, indicating that the oxidized intermediates are not stable at Uint =1.13 VRHE, where they spontaneously decay in minutes. With increasing delay times the cathodic discharge wave becomes more asymmetric and eventually splits into two distinct peaks after Δt = 50 s. The potential values that correspond to the crusts (current minima) of the first and second peaks are 0.89 and 0.73 VRHE (marked 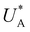 and
and 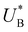 , respectively), as can be seen in the bottom panel of Fig. 3b. The ratio between the peak heights decreases as Δt increases, reaching a unity value at Δt = 140 s, as shown in Fig. 3c. In another measurements peak height reversal was observed after long Δt, such that the second peak turned higher than the first peak, see Fig. S8 (ESI†). The two peaks in the cathodic discharge waves reflects the reduction of two different intermediate states to which we refer as A and B with peak crusts at
, respectively), as can be seen in the bottom panel of Fig. 3b. The ratio between the peak heights decreases as Δt increases, reaching a unity value at Δt = 140 s, as shown in Fig. 3c. In another measurements peak height reversal was observed after long Δt, such that the second peak turned higher than the first peak, see Fig. S8 (ESI†). The two peaks in the cathodic discharge waves reflects the reduction of two different intermediate states to which we refer as A and B with peak crusts at 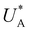 and
and 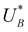 , respectively (see Fig. 3b). The Δt-dependent decay of the discharge current at the respective peak crusts is presented in Fig. 3d. Both peaks decay exponentially with Δt, but the decay rate of state A is higher than that of state B. This observation implies that the kinetic rate constants associated with the charge transfer reactions by the respective intermediates obey kA > kB.
, respectively (see Fig. 3b). The Δt-dependent decay of the discharge current at the respective peak crusts is presented in Fig. 3d. Both peaks decay exponentially with Δt, but the decay rate of state A is higher than that of state B. This observation implies that the kinetic rate constants associated with the charge transfer reactions by the respective intermediates obey kA > kB.
Double-peak cathodic discharge waves were reported in previous studies,40,44 where the lower potential peak that was observed below the photocurrent onset potential was attributed by Zandi and Hamann to defect states that do not contribute to the water photo-oxidation reaction.40 In our case, the lower potential peak appears close to the photocurrent onset potential, suggesting it is linked to oxidized intermediates of the water photo-oxidation reaction. We note that double-peak cathodic discharge waves were also observed in our earlier study44 for Sn-doped hematite photoanodes that were deposited at 800 °C, conditions that are reported to remove the aforementioned defect states,40 further supporting that the additional peak is related to water photo-oxidation rather than spurious defects. The results presented in Fig. 3 and Section S4 (ESI†) show that double-peak cathodic discharge waves are prevalent in hematite photoanodes with different dopants, impurities and microstructures. They were observed in photoanodes deposited at 500 °C (see Fig. S5 and S6, ESI†), below the critical temperature (600 °C) for interdiffusion from the transparent current collector,47 as well as photoanodes deposited at 700 °C (Fig. 3) and 800 °C (Ref. 44), well above the critical temperature for interdiffusion. Therefore, the observed behavior seems to be intrinsic for hematite doped with different dopants (Zn and Sn), regardless of unintentional impurities. In some cases, however, double-peak waves were difficult to resolve (see Fig. S7, ESI† for example), particularly in the presence of a steady-state dark current that intermingles with the capacitive current of the cathodic discharge wave.
The observation of distinct cathodic discharge peaks with different decay rates indicates the presence of distinct metastable oxidized intermediates that were produced under water photo-oxidation conditions in the first stage of the CDM. The specific characteristics of these peaks, i.e., their magnitude, the potentials at which they appear and the fact that they did not regenerate upon anodic potential sweep without light (see the cyclic voltammograms that follow the fourth stage, presented in Section S4, ESI†), suggest that both peaks are linked to the water photo-oxidation reaction. The observation that the peak height ratio changes as a function of the delay time and, at some point, flips over (see Fig. S8, ESI†) suggests that they arise from different reaction pathways that proceed in parallel to each other, rather than two stepwise charge transfer steps of a multi-step sequential pathway (with state A being the first one to discharge during the cathodic potential sweep since 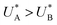 , see Fig. 3b). We note that in the sequential reaction pathway, the charge that is discharged first from state A must transfer through state B before reaching the ground state. Peak reversal as observed in Fig. 3b and Fig. S8 (ESI†) cannot be reasoned by this scenario, as detailed in the theoretical section (below), suggesting that the two discharge peaks represent distinct metastable intermediates that discharge in different pathways, i.e., two coexisting reaction pathways rather than a single one.
, see Fig. 3b). We note that in the sequential reaction pathway, the charge that is discharged first from state A must transfer through state B before reaching the ground state. Peak reversal as observed in Fig. 3b and Fig. S8 (ESI†) cannot be reasoned by this scenario, as detailed in the theoretical section (below), suggesting that the two discharge peaks represent distinct metastable intermediates that discharge in different pathways, i.e., two coexisting reaction pathways rather than a single one.
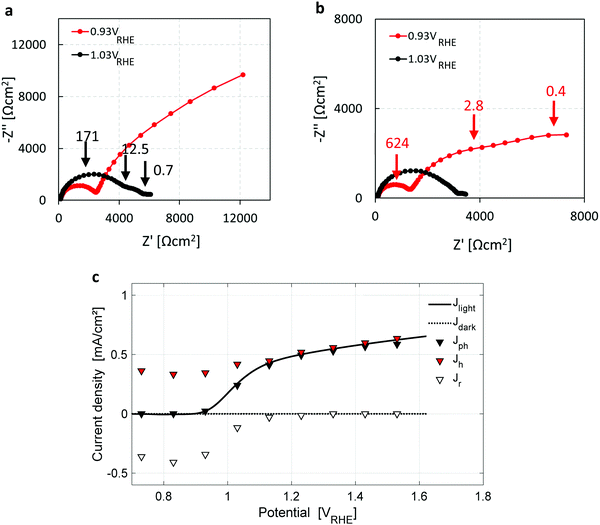
Seeking further support for this disruptive conclusion, photoelectrochemical impedance spectroscopy (PEIS) and intensity modulated photovoltage spectroscopy (IMVS) measurements were carried out to shed more light on the water photo-oxidation reaction mechanism. PEIS measurements near the photocurrent onset potential, Uonset, support the coexistence of parallel charge transfer processes represented by two low-frequency semicircles (in addition to the high-frequency semicircle that corresponds to the hole current from the bulk to the surface) in the Nyquist plots presented in Fig. 4a and b for two light intensities of 50 and 100 mW cm−2, respectively. Charge transport gives rise to a high-frequency semicircle, typically in the 100–1000 Hz range, whereas charge transfer processes give rise to low-frequency semicircles, typically in the 1–10 Hz range.33 It is noted that the low-frequency semicircles are well-separated when the applied potential is close to Uonset, which changes at different light intensities (Fig. 4a and b) due to the light intensity dependent photovoltage, as reported elsewhere.55 The PEIS results were combined with IMVS measurements (presented in Section S6, esi) to extract the forward current of photogenerated holes arriving at the surface, and the backward current due to surface recombination of electrons and holes, using the analysis method reported by Klotz et al.56 The results are presented in Fig. 4c, overlaid with the dark and light voltammograms from Fig. 1a. The surface recombination current (open triangles) diminishes above 1.2 VRHE, explaining the lack of a cathodic discharge spike in case of an abrupt potential drop in the third stage of the CDM for Uint > 1.2 VRHE, as demonstrated by the blue curve (Uint = 1.33 VRHE) in Fig. 1b. The PEIS and IMVS results corroborate that the cathodic discharge spike and wave observed in the third and fourth stages of our CDM (Fig. 1b) arise from recombination of electrons with surface-trapped holes stored in oxidized intermediates of the water photo-oxidation reaction, and that there are two distinct intermediates with different relaxation times. They also explain the lack of prominent spikes in the third stage for Uint above 1.2 VRHE. The absence of prominent recombination at these potentials results in metastability of the surface-trapped holes that last up to several minutes in the absence of light.
In contrast to previous CDM measurements in which the cathodic potential sweep commenced shortly after light turn off,39,44 here we introduce an intermediate stage with a time delay before the potential sweep that enables investigating the metastability of the oxidized intermediates and provides new insight into their potentiodynamic discharge characteristics, leading to the observation of two discharge peaks that show up clearly only after long delay times. In the following, we employ a micro-kinetic approach to examine the inherent difference between a multi-step sequential reaction and parallel reaction pathways. We show that the potentiodynamic characteristics of our system, as observed in Fig. 3, can occur only when parallel pathways are in play. Our theoretical analysis supports the empirical observations and provides deeper insight into the effect of parallel pathways on the water photo-oxidation mechanism.
Theoretical analysis
Model equations for sequential and parallel pathways
To elucidate the experimental results and shed light on their implication, we construct a micro-kinetic model for the cathodic discharge current, assuming that the latter results from the reduction of metastable oxidized intermediates to their ground state through recombination of electron with surface-trapped holes. In light of the double peak features observed in the CDM and PEIS measurements (Fig. 3 and 4, respectively), we consider two distinct intermediate states, such that the time-dependent cathodic discharge current density J(t), comprises the sum of their partial contributions Ji=A,B(t) at the same moment: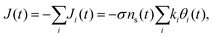 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βU(t)] in our model, where γ and β are constants. We note that the qualitative behavior does not alter for different γ and β values. For simplicity, the partial Ji=A,B contributions are expressed in absolute values, where the minus sign in eqn (1) signifies that the total current is cathodic, in accordance with the CDM results.
exp[−βU(t)] in our model, where γ and β are constants. We note that the qualitative behavior does not alter for different γ and β values. For simplicity, the partial Ji=A,B contributions are expressed in absolute values, where the minus sign in eqn (1) signifies that the total current is cathodic, in accordance with the CDM results.
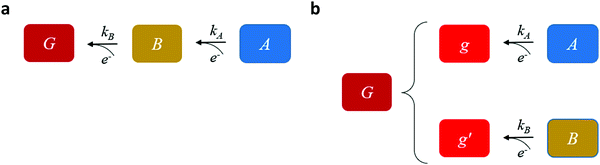
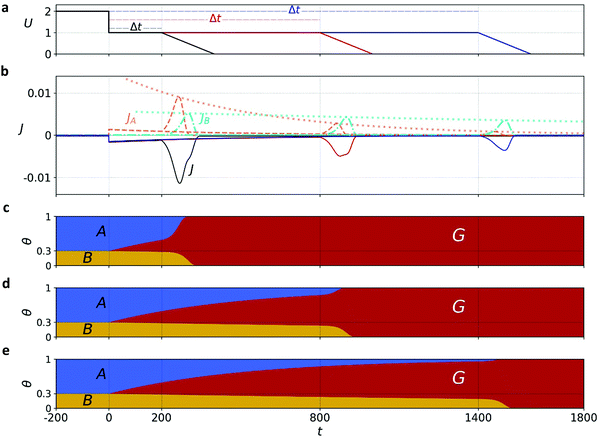
Our goal is to provide fundamental insight on the potentiodynamic behavior of our system, as reflected in the CDM results presented in Fig. 3, and specifically into the mechanism underlying the peak reversal observed in Fig. 3b and Fig. S8 (ESI†), rather than prescribe a quantitative description of the results (data fitting). Therefore, to keep fidelity to the measurements and preserve analytical simplicity, we seek a clear distinction between the most basic possibilities that are schematically illustrated in Fig. 5: (I) A sequential pathway that follows stepwise charge transfer steps between two metastable oxidized intermediates (A and B) before reaching the fully reduced ground state (G), A → B → G, as illustrated in Fig. 5a; or (II) Two parallel pathways, where each one of the metastable oxidized states decays directly to its ground state, A → g and B → g′, where g and g′ are the fully reduced ground states of the respective intermediates, as illustrated in Fig. 5b. Although the two scenarios may appear as simplifications, in the following we show that they actually provide a fundamental insight into the observation of peak reversal, as demonstrated in Fig. S8 (ESI†). Moreover, their general validity holds upon extension to more complicated scenarios, although in such cases the analysis is typically not amenable to analytical solutions as in the simplified model presented here.
Mathematically, both the sequential and parallel pathways are modeled by systems of three first order ordinary differential equations (ODE) that account for the basic properties of the CDM: (I) a linear time-dependent sweep of the applied potential, U(t); (II) coexistence of two charge transfer reactions occurring sequentially or in parallel to each other (as presented in Fig. 5a and b, respectively); and (III) conservation of surface sites such that the total surface coverage of different intermediate states remains constant, θT ≡ θA + θB + θG, where for the parallel pathway θG ≡ θg + θg′. The model equations for the sequential pathway (A → B → G) read:
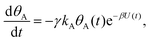 | (2a) |
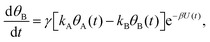 | (2b) |
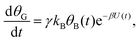 | (2c) |
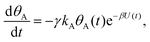 | (3a) |
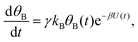 | (3b) |
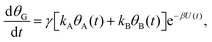 | (3c) |
Both systems can be analytically solved for applied potential of the form U(t) = U0 − v(t − t0), where v is a constant sweep rate of the potential, and U0 is the potential value at the initial time t0. For eqn (2a) and (3a) the charge transfer from species A is decoupled from the rest of the processes and as such can be thought as the driving term, yielding
| θA(t) = θ0Ae−kAΦ(t), | (4) |
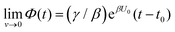 . Solutions for θB(t), however, are different for each pathway. For the sequential pathway (eqn (2b)), we obtain
. Solutions for θB(t), however, are different for each pathway. For the sequential pathway (eqn (2b)), we obtain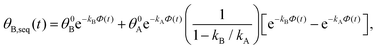 | (5) |
| θB,par(t) = θ0Be−kBΦ(t), | (6) |
From eqn (1) we obtain the total current density:
| J(t) = −JA(t) − JB(t) = −σγe−βU(t)(kAθA(t) + kBθB(t)). | (7) |
Comparison with the CDM results
Comparison of the micro-kinetic model with the CDM results (Fig. 3) is conducted via J(t) according to eqn (7), while keeping fidelity to the experimental results for which state A is the first to discharge since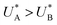 and therefore
and therefore 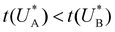 , kA ≥ kB and θ0A> θ0B. The kA ≥ kB condition is not only qualitatively consistent with the current decays observed in Fig. 3d, but it also agrees with the absence of any observation of oscillatory kinetics or a persistent single peak dominance at all times, which would be a signature for kA < kB in the sequential reaction. Generally speaking, sequential reactions with kA < kB may give rise to a dominant second peak via the second charge transfer reaction (B → G), provided that θ0A < θ0B. However, under such conditions, peak reversal would occur in the reverse order such that the second peak (at
, kA ≥ kB and θ0A> θ0B. The kA ≥ kB condition is not only qualitatively consistent with the current decays observed in Fig. 3d, but it also agrees with the absence of any observation of oscillatory kinetics or a persistent single peak dominance at all times, which would be a signature for kA < kB in the sequential reaction. Generally speaking, sequential reactions with kA < kB may give rise to a dominant second peak via the second charge transfer reaction (B → G), provided that θ0A < θ0B. However, under such conditions, peak reversal would occur in the reverse order such that the second peak (at 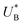 ) dominates first (i.e., at short delay times), and the first peak (at
) dominates first (i.e., at short delay times), and the first peak (at 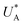 ) dominates later (at long delay times), in contrast to the results in Fig. 3b and Fig. S8 (ESI†).
) dominates later (at long delay times), in contrast to the results in Fig. 3b and Fig. S8 (ESI†).
Through the time-dependent solutions obtained for the evolution of θA(t), θB(t) and θG(t), we reconstruct JA(t) and JB(t) via the potential sweep U(t) (for details see Section S7, ESI†). Solutions for both pathways indicate that for a wide range of examined parameters and initial conditions (including their partition), see typical cathodic discharge waves presented in Sections S7 and S8 (ESI†), only the parallel pathway demonstrates peak reversal that qualitatively agrees with our CDM. While for parallel reactions A, B are interchangeable, we note for mathematical completeness that sequential reactions with kA < kB may demonstrate peak reversal if θ0B > θ0A, but since these conditions are inconsistent with the CDM results we rule them out. In the following we focus on the parallel pathway model with kA ≥ kB and θ0A > θ0B.
Exemplary results of the parallel pathway calculations are presented in Fig. 6a and b, where the top panel shows the input potential profiles for three delay times Δt; the middle panel shows the output (calculated) cathodic discharge current (black solid line) and its partial components JA(t) and JB(t) (red and green dashed lines, respectively, expressed in absolute values); Fig. 6c, d and e show the time-dependent evolution of θA(t), θB(t) and θG(t) in response to the potential changes presented in Fig. 6a. We note that all our calculations cover stages 2 to 4 of the CDM measurements, whereas stage 1 is excluded. To account for the exclusion of this stage, where water photo-oxidation prevails, the model assumes that all the surface intermediates (both A and B) are oxidized at the beginning of the timeline covered by the model (i.e., at t = −200 s in Fig. 6), which corresponds to the moment in which the light was turned off. Note that after the abrupt step in the applied potential at t = 0 s, the oxidized intermediates decay slowly to the ground state due to slow recombination, and the decay is accelerated upon further sweep of the applied potential to lower values that reinforces fast recombination.
The calculated discharge waves presented in Fig. 6b are consistent with the CDM results presented in Fig. 3b and Fig. S8 (ESI†) in all the salient qualitative observations: metastable decay during the time delay stage, double-peak cathodic discharge waves, and peak reversal at extended delay times. We verified that the results are robust with respect to different potential sweep rates and thus, in qualitative agreement with our CDM as well as other reports.39 Next, we provide a rigor analysis of the qualitative difference between the sequential and parallel pathways.
Distinguishing between sequential and parallel pathways
Let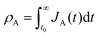 and
and 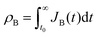 be the electronic charge densities transferred by the cathodic discharge reactions to the metastable oxidized intermediates A and B, respectively, where t0 is moment when the light turns off and the cathodic discharge begins. At t → ∞ all the oxidized intermediates decay to their ground state G, i.e., θ∞A, θ∞B → 0 and θ∞G → 1, as shown in Fig. 6c-e. In the parallel pathways mechanism, the charge transfer rates of intermediatesA and B depend on their initial coverages, such that ρA ∝ θ0A and ρB ∝ θ0B. In the sequential pathway mechanism, ρB is proportional to θ0A + θ0B since the A intermediates discharge first to the B intermediates before reaching the ground state G (see Fig. 5). This fundamental difference between the two mechanisms leads to different ratios between ρA and ρB, as summarized in Table 1.
be the electronic charge densities transferred by the cathodic discharge reactions to the metastable oxidized intermediates A and B, respectively, where t0 is moment when the light turns off and the cathodic discharge begins. At t → ∞ all the oxidized intermediates decay to their ground state G, i.e., θ∞A, θ∞B → 0 and θ∞G → 1, as shown in Fig. 6c-e. In the parallel pathways mechanism, the charge transfer rates of intermediatesA and B depend on their initial coverages, such that ρA ∝ θ0A and ρB ∝ θ0B. In the sequential pathway mechanism, ρB is proportional to θ0A + θ0B since the A intermediates discharge first to the B intermediates before reaching the ground state G (see Fig. 5). This fundamental difference between the two mechanisms leads to different ratios between ρA and ρB, as summarized in Table 1.
| Mechanism | ρ A | ρ B | ρ A/ρB |
|---|---|---|---|
| Sequential pathway | θ 0A | θ 0A + θ0B | θ 0A/(θ0A + θ0B) |
| Parallel pathways | θ 0A | θ 0B | θ 0A/θ0B |
Based on the relations in Table 1, we formulate a definitive distinction between the sequential and parallel pathways and explain why peak reversal can be expected only for the latter mechanism. Consistent with the CDM results presented in Fig. 3b, and for the sake of argument, let us assume that the discharge peaks of the oxidized intermediates A and B are well separated, and their widths are similar and constant, so that their area (i.e., the integrated charge transferred from them to their ground states) scales with the peak heights (for details see Section S8, ESI†). Consequently, the peak height ratio approximates the integrated charge ratio ρA/ρB, which indicates that for the sequential pathway it cannot exceed 1. In contrast, in the parallel pathway mechanism the peak height ratio scales with the ratio between the initial coverages of the respective intermediate states, which may be larger or smaller than 1:
Consequently, the above analysis provides the required insight into the origin why peak reversal can only occur under parallel pathways.
Although in the above calculations, we assumed for the sake of the analytical derivation of the sequential pathway limit that the peaks are well separated, we have verified numerically that the limit is indeed a generic property, independent of the similar and constant width assumption of adjacent peaks (see Section S8, ESI†). Moreover, the qualitative applicability of the results can be broadened, for example, to multiple short-lived intermediate species whose reduction reactions are fast resulting in significant overlap of the two peaks. In this case, the main differences between the two pathways will be deduced (albeit again only numerically) from the differences in the total density current: J(t) = −(n + 1)JA(t) − (m + 1)JB(t), where n and m are integers corresponding to extra intermediate steps (with fast reactions) that may occur after each one of the slow reduction reactions of species A or B, respectively. Under the conventional assumption that the water (photo)oxidation reaction involves four adsorbate species and four charge transfer steps, as discussed in the introduction, the sequential pathway is limited to three oxidized intermediates that can be reduced, thus, (m + n) can be only 1 or 0. The resulting current ratio limit changes to 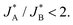 We avoid, however, showing here all the details and/or speculating about other possible charge transfer models while focusing on the qualitative distinction between the sequential and parallel pathways that can be uncovered with a good agreement already from two charge transfer reactions.
We avoid, however, showing here all the details and/or speculating about other possible charge transfer models while focusing on the qualitative distinction between the sequential and parallel pathways that can be uncovered with a good agreement already from two charge transfer reactions.
Conclusions and outlook
Studies on the mechanism of water photo-oxidation on metal oxide photoanodes for photoelectrochemical water splitting typically rely on one reaction pathway or another. The most established pathway follows Kobussen's mono-nuclear OER mechanism,12 modified to account for the OH−-coupled hole transfer steps that take place in water photo-oxidation in alkaline electrolytes,2 as in the case of hematite photoanodes.6 Nevertheless, recent studies on electrolytic water oxidation (without photogeneration of electrons and holes) propose alternative pathways, such as bi-nuclear and bi-functional pathways11 or lattice oxygen taking place as an active site in the reaction (LOER),59 suggesting that alternative pathways may exist, perhaps even co-exist, also in the case of water photo-oxidation. This work presents strong evidence for the co-existence of two distinct pathways proceeding in parallel to each other, instead of a sequential pathway with multiple steps occurring one after the other. We speculate that the two co-existing pathways may interact with each other, leading to spatiotemporal phenomena with unexpected complex dynamics similarly to other electrochemical reactions21–24,60 and catalytic surface reactions.61 For instance, competition for sites and photogenerated holes between different pathways may lead to unexpected features such as hysteresis and negative differential resistance, as reported recently for water photo-oxidation in the presence of low concentration of H2O2.20 This implies that realistic understanding of the reaction mechanism should consider plural pathways and the possibility of interactions between co-existing pathways which may lead to complex self-organized kinetic effects, ranging from domain wall dynamics through spiral- and standing-waves, and to spatiotemporal chaos. Collective effects such as these may influence performance parameters such as overpotential and rate in ways that have never been considered before. Further research in this direction may benefit the design of photocatalytic materials and tuning their operation conditions for optimal performance. For example, by tailoring the interaction between different pathways so as to avoid the high energy barriers that lead to high overpotentials, one may envision new strategies to bypass the universal scaling law62 that limits the efficiency of most of the known water oxidation catalysts,17 possibly leading the way to high-efficiency water splitting for green hydrogen and solar fuel production.Author contributions
A. T. and P. M. C. developed the methodology. A. T. fabricated most of the samples, performed the photo-electrochemical measurements and the impedance data analysis. P. M. C. performed the theoretical analysis. Y. P. fabricated the Sn doped hematite sample on ITO substrate. P. M. C and A. T. wrote the first draft of the manuscript. A. Y. and A. R. supervised the project and finalized editing of the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
We thank the anonymous reviewers for their insightful comments. The research was supported by Israel's Ministry of Science and Technology grant #3-14423. A. R. acknowledges the support of the L. Shirley Tark Chair in Science and the Grand Technion Energy Program (GTEP). A. T. acknowledges the generous financial support by the Israel Ministry of Energy as a part of the scholarship program in the field of energy (219-01-044).References
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- A. Valdés, J. Brillet, M. Grätzel, H. Gudmundsdóttir, H. A. Hansen, H. Jónsson, P. Klüpfel, G. J. Kroes, F. Le Formal, I. C. Man, R. S. Martins, J. K. Nørskov, J. Rossmeisl, K. Sivula, A. Vojvodic and M. Zäch, Phys. Chem. Chem. Phys., 2012, 14, 49–70 RSC.
- J. Rossmeisl, Z.-W. W. Qu, H. Zhu, G.-J. J. Kroes and J. K. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- A. Govind Rajan, J. M. P. Martirez and E. A. Carter, ACS Catal., 2020, 10, 11177–11234 CrossRef CAS.
- O. Zandi and T. W. Hamann, Nat. Chem., 2016, 8, 778–783 CrossRef CAS PubMed.
- J. O. M. Bockris, J. Chem. Phys., 1956, 24, 817–827 CrossRef CAS.
- B. E. Conway and P. L. Bourgault, Can. J. Chem., 1959, 37, 292–307 CrossRef CAS.
- X. Zhang and A. Bieberle-hütter, ChemSusChem, 2016, 9, 1223–1242 CrossRef CAS PubMed.
- R. L. Doyle, I. J. Godwin, M. P. Brandon and M. E. G. Lyons, Phys. Chem. Chem. Phys., 2013, 15, 13737–13783 RSC.
- M. Busch, Curr. Opin. Electrochem., 2018, 9, 278–284 CrossRef CAS.
- A. G. C. Kobussen and G. H. J. Broers, J. Electroanal. Chem., 1981, 126, 221–240 CrossRef CAS.
- H. Ooka, J. Huang and K. S. Exner, Front. Energy Res., 2021, 9, 155 Search PubMed.
- K. S. Exner, Electrochim. Acta, 2021, 375, 137975 CrossRef CAS.
- T. A. Betley, Q. Wu, T. Van Voorhis and D. G. Nocera, Inorg. Chem., 2008, 47, 1849–1861 CrossRef CAS PubMed.
- S. Divanis, T. Kutlusoy, I. M. Ingmer Boye, I. C. Man and J. Rossmeisl, Chem. Sci., 2020, 11, 2943–2950 RSC.
- Z. F. Huang, J. Song, S. Dou, X. Li, J. Wang and X. Wang, Matter, 2019, 1, 1494–1518 CrossRef.
- A. J. Tkalych, H. L. Zhuang and E. A. Carter, ACS Catal., 2017, 7, 5329–5339 CrossRef CAS.
- L. Bai, S. Lee and X. Hu, Angew. Chem., 2021, 133, 3132–3140 CrossRef.
- Y. Y. Avital, H. Dotan, D. Klotz, D. A. Grave, A. Tsyganok, B. Gupta, S. Kolusheva, I. Visoly-Fisher, A. Rothschild and A. Yochelis, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- D. Li, Y. Sun, Z. Yang, L. Gu, Y. Chen and H. Zhou, Joule, 2018, 2, 1265–1277 CrossRef CAS.
- M. T. M. Koper, J. Chem. Soc., Faraday Trans., 1998, 94, 1369–1378 RSC.
- M. Orlik, J. Solid State Electrochem., 2008, 13, 245–261 CrossRef.
- K. Krischer, N. Mazouz and P. Grauel, Angew. Chem., Int. Ed., 2001, 40, 850–869 CrossRef CAS PubMed.
- F. Le Formal, S. R. Pendlebury, M. Cornuz, S. D. Tilley, M. Grätzel and J. R. Durrant, J. Am. Chem. Soc., 2014, 136, 2564–2574 CrossRef CAS PubMed.
- F. Le Formal, N. Tétreault, M. Cornuz, T. Moehl, M. Grätzel and K. Sivula, Chem. Sci., 2011, 2, 737–743 RSC.
- B. Klahr, S. Gimenez, F. Fabregat-Santiago, T. Hamann and J. Bisquert, J. Am. Chem. Soc., 2012, 134, 4294–4302 CrossRef CAS PubMed.
- K. George, T. Khachatrjan, M. van Berkel, V. Sinha and A. Bieberle-Hütter, ACS Catal., 2020, 10, 14649–14660 CrossRef CAS.
- L. Bertoluzzi, P. Lopez-Varo, J. A. Jiménez Tejada and J. Bisquert, J. Mater. Chem. A, 2016, 4, 2873–2879 RSC.
- J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891 CrossRef CAS PubMed.
- A. J. Cowan and J. R. Durrant, Chem. Soc. Rev., 2013, 42, 2281–2293 RSC.
- L. M. Peter, K. G. U. Wijayantha and A. A. Tahir, Faraday Discuss., 2012, 155, 309–322 RSC.
- L. M. Peter, J. Solid State Electrochem., 2013, 17, 315–326 CrossRef CAS.
- C. A. Mesa, L. Francàs, K. R. Yang, P. Garrido-Barros, E. Pastor, Y. Ma, A. Kafizas, T. E. Rosser, M. T. Mayer, E. Reisner, M. Grätzel, V. S. Batista and J. R. Durrant, Nat. Chem., 2020, 12, 82–89 CrossRef CAS PubMed.
- F. Le Formal, E. Pastor, S. D. Tilley, C. A. Mesa, S. R. Pendlebury, M. Grätzel and J. R. Durrant, J. Am. Chem. Soc., 2015, 137, 6629–6637 CrossRef CAS PubMed.
- M. Barroso, C. A. Mesa, S. R. Pendlebury, A. J. Cowan, T. Hisatomi, K. Sivula, M. Grätzel, D. R. Klug and J. R. Durrant, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15640–15645 CrossRef CAS PubMed.
- N. Yatom, O. Neufeld and M. Caspary Toroker, J. Phys. Chem. C, 2015, 119, 24789–24795 CrossRef CAS.
- J. Li, W. Wan, C. A. Triana, H. Chen, Y. Zhao, C. K. Mavrokefalos and G. R. Patzke, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed.
- B. Klahr, S. Gimenez, F. Fabregat-Santiago, J. Bisquert and T. W. Hamann, Energy Environ. Sci., 2012, 5, 7626 RSC.
- O. Zandi and T. W. Hamann, J. Phys. Chem. Lett., 2014, 5, 1522–1526 CrossRef CAS PubMed.
- F. Le Formal, K. Sivula and M. Grätzel, J. Phys. Chem. C, 2012, 116, 26707–26720 CrossRef CAS.
- L. M. Abrantes and L. M. Peter, J. Electroanal. Chem., 1983, 150, 593–601 CrossRef CAS.
- B. Klahr and T. Hamann, J. Phys. Chem. C, 2014, 118, 10393–10399 CrossRef CAS.
- D. A. Grave, D. Klotz, A. Kay, H. Dotan, B. Gupta, I. Visoly-Fisher and A. Rothschild, J. Phys. Chem. C, 2016, 120, 28961–28970 CrossRef CAS.
- A. Tsyganok, D. Klotz, K. D. Malviya, A. Rothschild and D. A. Grave, ACS Catal., 2018, 8, 2754–2759 CrossRef CAS.
- Y. Piekner, H. Dotan, A. Tsyganok, K. D. Malviya, D. A. Grave, O. Kfir and A. Rothschild, ACS Photonics, 2018, 5, 5068–5078 CrossRef CAS.
- K. C. Bedin, A. L. M. Freitas, A. Tofanello, I. Rodríguez-Gutiérrez and F. L. Souza, Int. J. Ceram. Eng. Sci., 2020, 2, 204–227 CrossRef CAS.
- T. Lopes, L. Andrade, H. A. Ribeiro and A. Mendes, Int. J. Hydrogen Energy, 2010, 35, 11601–11608 CrossRef CAS.
- R. H. Wilson, J. Electrochem. Soc., 1980, 127, 228 CrossRef CAS.
- C. Y. Cummings, F. Marken, L. M. Peter, A. A. Tahir and K. G. U. Wijayantha, Chem. Commun., 2012, 48, 2027–2029 RSC.
- W. Mönch, Semiconductor Surfaces and Interfaces, Springer, 2001, vol. 26 Search PubMed.
- S. Chatman, P. Zarzycki and K. M. Rosso, Phys. Chem. Chem. Phys., 2013, 15, 13911–13921 RSC.
- S. Kumari, C. Tripathi, A. P. Singh, D. Chauhan, R. Shrivastav, S. Dass and V. R. Satsangi, Curr. Sci., 2006, 91, 1062–1064 CAS.
- L. Kronik and Y. Shapira, Surf. Sci. Rep., 1999, 37, 1–206 CrossRef CAS.
- G. Segev, H. Dotan, K. D. Malviya, A. Kay, M. T. Mayer, M. Grätzel and A. Rothschild, Adv. Energy Mater., 2016, 6, 1500817 CrossRef.
- D. Klotz, D. S. Ellis, H. Dotan and A. Rothschild, Phys. Chem. Chem. Phys., 2016, 18, 23438–23457 RSC.
- R. B. Darling, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 4071–4083 CrossRef PubMed.
- K. George, M. Van Berkel, X. Zhang, R. Sinha and A. Bieberle-Hütter, J. Phys. Chem. C, 2019, 123, 9981–9992 CrossRef CAS.
- E. Fabbri and T. J. Schmidt, ACS Catal., 2018, 8, 9765–9774 CrossRef CAS.
- B. Bozzini, C. Mele, L. P. Bicelli and L. D. Urzo, Int. J. Electrochem. Sci., 2008, 3, 356–408 Search PubMed.
- R. Imbihl and G. Ertl, Oscillatory Kinetics in Heterogeneous Catalysis, 1995, vol. 95 Search PubMed.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee03953a |
| ‡ Current address: General Coordination of Government Innovation, Government of Jalisco, Ciudad Creativa Digital, Guadalajara 44100, Mexico. |
| This journal is © The Royal Society of Chemistry 2022 |