Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
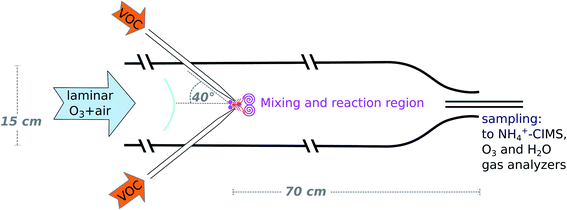
The INNpinJeR: a new wall-free reactor for studying gas-phase reactions†
Wiebke
Scholz
 *a,
Bernhard
Mentler
*a,
Bernhard
Mentler
 a,
Lukas
Fischer
a,
Torsten
Berndt
a,
Lukas
Fischer
a,
Torsten
Berndt
 b and
Armin
Hansel
b and
Armin
Hansel
 *a
*a
aUniversity of Innsbruck, Technikerstraße 25, Innsbruck, Austria. E-mail: Wiebke.Scholz@student.uibk.ac.at; Armin.Hansel@uibk.ac.at
bLeibniz-Institut für Troposphärenforschung e.V., Permoserstraße 15, 04318 Leipzig, Germany
First published on 20th December 2021
Abstract
Here we characterize the new Innsbruck wall free impinging jets reactor (INNpinJeR) and compare its performance with the TROPOS free jet flow system by quantifying oxidation products of the well-understood ozonolysis reactions of tetramethyl ethylene (TME) and cyclohexene with an ammonium chemical ionization mass spectrometer. We support the results with flow and chemical simulations on the k-ε RANS steady-state flow field. Flow simulations show a mixing region in the center of the reactor that does not disturb the surrounding laminar main flow. Quantitative detection of several peroxy radicals strongly suggests negligible wall contacts. Direct comparison with the TROPOS flow system using cyclohexene ozonolysis with the same analytical technique shows very good reproducibility. The total effective reaction time amounts to 9.0–9.3 seconds found from the flow and chemistry simulations and 9.4 ± 1.1 seconds according to the analysis of TME ozonolysis products. These features allow for characterizing the sensitivity of analytical instruments towards different oxidation products, including RO2 radicals, but most importantly we can conclude, that the Innsbruck wall-free INNpinJeR can be used to study gas-phase chemistry under atmospherically relevant conditions without significant influence of interface chemistry.
Environmental significanceOrganic peroxy radicals (RO2) are short-lived intermediates in the oxidation of volatile organic compounds (VOC) and belong together with alkoxy (RO) radicals, OH and HO2 to the ROx radicals. Rapid cycling among ROx and NOx (NOx = NO + NO2) lies at the core of photochemical mechanisms that regulate the atmospheric composition and its associated impacts on air quality and climate. We designed a flow reactor (INNpinJeR) specifically to study the formation and the fate of RO2 radicals without having to deal with disturbing wall reactions. Observations of individual RO2 radicals with highly sensitive instruments at the INNpinJeR will challenge current chemistry models and improve our mechanistic understanding. |
1 Introduction
Natural and anthropogenic volatile organic compounds (VOC) are emitted into our atmosphere in large amounts. OH, O3, NO3 or Cl radicals initially start the degradation of VOC producing almost exclusively peroxy radicals (RO2) as short-lived intermediates. Recently, RO2 radical isomerization, followed by the addition of O2, referred to as autoxidation, has been discovered to play an important role in the atmosphere,1,2 leading to higher-functionalized RO2 radicals. The rates of the intramolecular hydrogen-shifts are highly structure dependent with theoretical rate coefficients covering orders of magnitude (10−6 to 102 s−1).3,4 They start to compete with bimolecular reactions with NO, HO2 or other peroxy radicals (R′O2) in the atmosphere, when the rate coefficient of isomerization is larger than ∼0.01 s−1 and can lead to the formation of highly oxidized organic molecules even in polluted environments, when the isomerization rates are in the order of 1 s−1 or higher.5,6 This is for example the case for some peroxy radicals from different alkenes like isoprene,6 some monoterpenes7 or also cyclohexene.8 Therefore the reactivity of the different reactants plays a decisive role in the volatility distribution of the longer-lived oxidized products (oVOC).9 The volatility of oVOCs, in turn, affects to what extent they contribute to the formation or growth of secondary organic aerosols.10 By enhancing the conversion of NO to NO2, RO2 and HO2 radicals play a catalytic role in the formation of ground-level ozone, thereby increasing the oxidation capacity and worsening air pollution.11 While the first oxidation steps are characterized well for small VOC, for more complex VOC they are not yet fully elucidated. To summarize, reaction rates and product yields of RO2 radicals affect pollutant concentrations under different environmental conditions but are still not fully understood. Therefore, we aim to quantitatively and holistically investigate the degradation of VOC during the first seconds of such reactions at atmospherically relevant conditions. This requires the combination of highly sensitive analytical instruments such as chemical ionization mass spectrometers12–14 coupled to wall-free flow reactors at best.Wall loss rates should best be significantly smaller than the other loss rates of peroxy radicals to have a minor influence on the product distribution. In contrast to research groups that use oxidation flow reactors (OFRs) for investigating SOA yields, our focus is on the basic understanding of the first steps of gas-phase reactions. Therefore our setup differs significantly from OFRs, which have typically long reaction times so that secondary organic aerosols can be formed but non-negligible wall contacts. For a detailed chemical understanding non-negligible wall-contacts can be problematic: For example, Bernhammer et al.15 showed for the isoprene oxidation system that hydroperoxides convert on metal surfaces to the more volatile compounds. Lambe et al.16 found for two oxidation flow reactors to study SOA formation (with reaction times in the order of minutes) that the SOA yield depends on the reactor design. They attributed the lower transmission efficiency of SO2 compared to CO2 in their Toronto photooxidation tube to not fully passivated walls. This highlights, why negligible wall-contacts are really important to study atmospheric chemistry: wall losses (or chemical conversion at interfaces) depend on the wall material as well as on the chemical structure of the molecules. In general, radicals, which are highly reactive are quickly lost at surfaces and could form unwanted volatile products in surface-assisted reactions with adsorbed low volatile compounds.17
A laminar flow can help to reduce wall contacts, but even with a laminar flow, negligible wall contacts are only achievable for short reaction times.
Berndt et al.8 have successfully implemented an (almost) wall-free flow reactor with the TROPOS free-jet flow system, based on a previous experimental setup from Presto and Donahue,18 and was able to quantify production rates of accretion products from peroxy radicals for the first time.19,20
In this study we present the new Innsbruck impinging jets flow reactor (INNpinJeR) and compare its performance with the TROPOS flow system. The reactors are similar in that both use only a short reaction time in favor of negligible wall contacts. Therefore, particles have no time to form under atmospherically relevant reactant concentrations and the reactors are not suited to study gas-to-particle conversion. However, the details of the two reactors and the internal flow fields are different: The TROPOS flow system uses one movable free jet carrying ozone that quickly mixes into the surrounding flow (air + VOC) due to its fast velocity and a carefully designed nozzle shape. Its inner metal inlet line is therefore rather long. In our reactor, on the other hand, a fast micromixing followed by a slower mesomixing of the reactants in the center flow is achieved by four freely impinging jets of air carrying the organics of interest. The other reactant (here: ozone) enters the reactor at the very beginning, diluted in the main flow. Thereby the inlet for the radicals is substantially shorter and is made out of glass. Therefore also HO2 can easily enter the INNpinJeR, which is mostly destroyed in the long metal inlet line of the TROPOS reactor. Additionally, by using four freely impinging jets, the shape of the nozzles is not so critical in our case, making the setup easier to rebuild. The TROPOS reactor requires 100 slpm total flow to produce a stable and efficient mixing. The four impinging jets help us to reduce the overall flow down to 33 slpm. The comparison here will be a critical test of the effects that a different flow system has on the product formation and whether using an “effective reaction time”, is in general possible for this type of reactors.
In confined impinging jet reactors, mixing times of only 10 ms due to high turbulent energy dissipation rates have been shown experimentally by Johnson and Prud'homme,21 using competing reactions with different rates. The high energy dissipation in impinging jets occurs, because the kinetic energy of each jet stream converts into a turbulent-like motion through the redirection of the flow, nicely shown in CFD simulations.22 Our approach is new in that sense, that we use four impinging jets oriented at an angle of 40° in relation to the main flow direction in an unconfined space, since we want to avoid wall contacts.
For characterizing the reactor, we are using the well-understood ozonolysis reaction of tetramethyl ethylene (TME) and compare the results regarding cyclohexene ozonolysis with those obtained at the TROPOS reactor.14 For these two systems, the ozonolysis rate coefficients,23 as well as OH yields,24 are well-known. In the last years, Rissanen et al.25 and Berndt et al.8 studied ozonolysis-derived cyclohexene radical reaction and autoxidation pathways computationally and experimentally. To directly compare the two reactors, we apply the same chemical ionization mass spectrometric (CIMS) technique at the INNpinJeR as described by Hansel et al.14 at the TROPOS reactor, which is the ammonium-CIMS based on the ion source developed by Breitenlechner et al. Precursor ions are (H2O)0–2(NH3)0,1NH4+-clusters that softly ionize the oVOC products and peroxy radicals at thermal collision energies. Hansel et al.14 showed the ability of this ionization technique to detect radicals and achieved carbon closure of the reacted cyclohexene by ozonolysis under constantly dry experimental conditions at the TROPOS reactor. Carbon closure could be reached because the ammonium CIMS is detecting even lightly oxidized molecules and the soft cluster ionization technique reduces fragmentation. Therefore it is well suited to investigate the first-generation products, radical reactions, and their products.
After characterizing the reactor and comparing it with the TROPOS flow system, we will discuss, whether the reactor can be treated using a 0D box model and quantify possible error sources when calculating rate coefficients of RO2 accretion reactions. We also discuss the influence of bimolecular reactivity towards peroxy radicals by further reactants like HO2 and RO2 on derived accretion rate coefficients.
2 Methods
The design of the wall-free Innsbruck impinging jets reactor (INNpinJeR) combines fast micro-mixing of impinging jets with a wall contact-free reactor design. Please find a schematic drawing in Fig. 1. It consists of a glass tube with a total length of 170 cm and an inner diameter of 15 cm. The reaction region is 70 cm long. The 100 cm before the reaction region are required to laminarize the main flow, which consists of dried and purified air and carries an adjustable ozone concentration. Four nozzles with an inner diameter of 2 mm are injecting the VOC-flow jet-like into the reactor's center flow at an angle of 40° in relation to the main flow direction. These inlets are removable and out of glass, so that they are easy to clean, and also semivolatile compounds can be studied. The impinging jets create localized turbulence at the center axis, while the main flow remains laminar – acting as a sheath flow at the outer parts of the tube. Downstream from the nozzles, the VOC reacts with the reactant (ozone) in the main flow. At the open outflow, the tube diameter is reduced to 6 cm to inhibit the mixing of lab air into the sample air by an enhanced outflow velocity. We used a flow of 33 slpm for the main flow and 2.4 slpm for the total VOC flow for the data presented in the results section. The VOC flow corresponds to a flow velocity through the nozzles of about 2.2 m s−1. These settings correspond to the minimum main flow rates that give repeatable results. In experiments with changing VOC concentration, the concentration within the VOC flow was changed, while the flow rate remains the same.The temperature of the reaction gas was measured at the outflow of the reactor. The whole setup, the compressed-air tank, the adsorbers, and the whole tubing is at laboratory temperature so that we expect the gas stream to have the same temperature. We estimate a temperature uncertainty of ±2 K. We performed several degradation experiments with tetramethyl ethylene (C6H12, TME) and cyclohexene (C6H10), respectively. The different parameters are listed in Table 1.
| Experiment VOC | [O3] (1011 cm−3) | [VOC] (1011 cm−3) | [NO] (1010 cm−3) | T (K) |
|---|---|---|---|---|
| TME (a) | 39 | 0.12–1.2 | — | 300 |
| TME (b) | 7–35 | 1.2 | — | 300 |
| C6H10@TROPOS | 23 | 0.1–140 | — | 295 |
| C6H10 (a) | 39 | 0.2–120 | — | 303 |
| C6H10 (b) | 0.15–14 | 38 | — | 302 |
| C6H10 (c) | 17 | 6 | 0.15–1.9 | 293 |
2.1 Gas preparation and trace gas analysis
We produced purified air as carrier gas by compressing, drying, and cleaning outdoor air. The scroll compressor (Spiral-Air SPR3, RIKA Kompressoren GmbH) pressurizes air to 5–8 bar. The air is precleaned by a pressure swing adsorption stage containing activated charcoal (KA-MT4, Parker Hannifin), which dries the air to a dewpoint of −50 °C and removes part of the volatile organic compounds (VOC). Afterward, the air passes a second cleaning stage containing activated charcoal, two molecular sieves with pore sizes of 4 Å and 3 Å, and a HEPA filter. We adapted this adsorption process from Berndt et al.8 The summed VOC concentration in the resulting purified air does not exceed a few ppt, measured by the PTR3, designed by Breitenlechner et al.13 33 slpm of the purified air enter the flow reactor as the main flow. Bypassing a small fraction of the main flow, typically (1.00 ± 0.05) slpm, through a UVP ozone generator (Analytik Jena) produces an adjustable ozone concentration, that is followed by an ozone monitor (Thermo Environmental Instruments 49C). For the NO experiment (C6H10 (c)), an adjustable flow of 4–100 sccm, carrying an NO concentration of approximately 300 ppb was mixed into the total flow. In Table 1 the measured concentration at the center outflow of the reactor is stated as measured by a NOx-monitor (Thermo Environmental Instruments 42 iQ).2.4 slpm of purified air carrying an adjustable concentration of a VOC that serves as the second reactant are introduced through the four impinging jets. This part of the flow consists of purified air carrying an adjustable concentration of a VOC that serves as the second reactant. Here this is either TME or cyclohexene. The respective VOC, as well as NO, were prepared in advance in clean and ozone-free SilcoCans (from Restek) with inert coating and a volume of 6 liters. Please find details on the preparation of the SilcoCans in Section S1.2.†
2.2 Product analysis with the ammonium-CIMS
The ammonium chemical-ionization-mass-spectrometer (NH4+-CIMS) samples 7.5 standard liters per minute from the center of the reactor's outflow through a 70 cm long PTFE tubing with an inner diameter of 1.0 cm, corresponding to a residence time within the inlet of 0.44 seconds. Finally, a core sampling of the sample-gas directly in front of the ion-molecule reaction region (IMR) guarantees, that only the center flow of 1.5 slpm is analyzed. The core sampling reduces inlet line losses of radicals to about 33% in the sampled air when assuming a diffusivity of 0.1 cm2 s−1, so that the inlet loss correction for radicals is a factor of 1.5. The NH4+-CIMS can detect oVOCs as well as peroxy radicals with high sensitivity and has been successfully deployed in flow reactor studies before.19,26 Described in detail by Hansel et al.,14 our NH4+-CIMS is based on the design of the PTR3.13 Inside the IMR, (NH3)0,1(H2O)0–2NH4+ reagent ions softly ionize oxidized organic compounds in the sample air at thermal collision energies and a pressure of 75 mbar. The soft ionization by ligand switching and the low field gradients between the ion source and the time of flight mass spectrometer ensure minimal if any fragmentation of the ionized analyte.Direct calibration of the majority of the oxidation products is not possible, because reference standards do not exist. Zaytsev et al.27 demonstrated, that decanone, containing only one carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) moiety, is ionized by the ammonium clusters at the kinetic limit. High-level quantum chemical calculations have revealed that cluster bond energies between ammonium reagent ions and a single C
O) moiety, is ionized by the ammonium clusters at the kinetic limit. High-level quantum chemical calculations have revealed that cluster bond energies between ammonium reagent ions and a single C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety in small carbonyls are 27 kcal mol−1.28 Products having more oxygen-containing moieties can form additional hydrogen bonds with ammonium reagent ions increasing the bond energy as was shown recently for aminium reagent ions.29 Such large cluster bond energies make ligand switching reactions between ammonium reagent ions and oVOC products exothermic thus fast and these product cluster ions survive the different stages in the mass spectrometer without collision-induced fragmentation.14
O moiety in small carbonyls are 27 kcal mol−1.28 Products having more oxygen-containing moieties can form additional hydrogen bonds with ammonium reagent ions increasing the bond energy as was shown recently for aminium reagent ions.29 Such large cluster bond energies make ligand switching reactions between ammonium reagent ions and oVOC products exothermic thus fast and these product cluster ions survive the different stages in the mass spectrometer without collision-induced fragmentation.14
During the presented experiments, we performed calibrations with hexanone, heptanone as well as acetone, using a gas standard. Because Zaytsev et al.27 recently showed that the sensitivity of hexanone is only at 80% of the kinetic limit in ammonium mode, we correct the obtained calibration factor from hexanone of the different experiments by a factor of 1.25. Please find more details and a summary of all calibration and correction factors in Section S1.4.† For acetone and the structurally similar CH3C(O)CH2O2 peroxy radical we used the measured acetone calibration factor. More functional groups typically increase the bonding strength between the ammonium and the analyte, so that we can use the kinetic limit sensitivity to calibrate them. For all oxidation products of cyclohexene, including the peroxy radicals we used the hexanone calibration factor, which was corrected by a factor of 1.25 to represent the kinetic limit and therefore the maximum sensitivity of our instrument. Concentrations calculated in this way represent lower limits.
We used the same settings for the cyclohexene ozonolysis experiments at both reactors. As voltage and flow settings affect the observed primary ion distribution, we prove this by showing the primary ion distributions in Fig. S1.† We acquired the data with the TOFDAQ Recorder from TOFWERK (https://www.tofwerk.com/software/tofdaq/) and analyzed them using the TOF-Tracer2 software (https://github.com/lukasfischer83/TOF-Tracer2).30
2.3 Simulation of flow and chemistry
We modeled the flow in the Innsbruck impinging jets flow reactor (INNpinJeR) with the open-source tool OpenFOAM 4.1 from HELYX OS using the OpenFOAM k-ω-shear stress transport model31 with a Reynolds averaged Navier–Stokes (RANS) steady-state approach (simpleFOAM). Details about the mesh can be found in Section S1.5.†Because we are interested in reactions of very diluted compounds, which do not impact the temperature of the carrier gas, we can simplify our case and reduce computational costs to a minimum: we chose to simulate the transport of the reactants as passive tracers until reaching a steady-state of the concentration profile. This approach is reasonable as long as the conversion of the reactants is negligible. Therefore we applied a Newtonian transport model, that uses a turbulent effective diffusion coefficient,
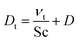 | (1) |
| O3 + VOC → ∑products | (2) |
Peroxy radicals (RO2) are formed in reaction (2) with different yields (yRO2) as indicated in reaction (3).
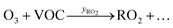 | (3) |
Under low-NO conditions, RO2 radicals react prevailingly with HO2 forming ROOH (eqn (4)) and with other peroxy radicals R′O2 (eqn (5a)–(5c)).
| RO2 + HO2 → ROOH + O2 | (4) |
 | (5a) |
 | (5b) |
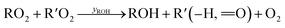 | (5c) |
For our simplified simulations, we ignore further reactions of the products of pathways (5b) and (5c). For both reaction systems we discuss, the OH produced is reacting nearly completely with the precursor VOC, producing just another peroxy radical. In the case of the peroxy radicals from cyclohexene oxidation, the accretion pathway appears to be very important as high concentrations of the accretion products were observed in the previous experiment.14 We do not go into the details of secondary product formation here, but only investigate, to what extent our reactor's features influence RO2 losses and secondary product formation as a whole. A numerical approach is necessary due to inhomogeneities in the concentration, flow fields and (turbulent) diffusion, that need to be taken into account.
3 Results
3.1 Simulation results of the flow and simplified reaction
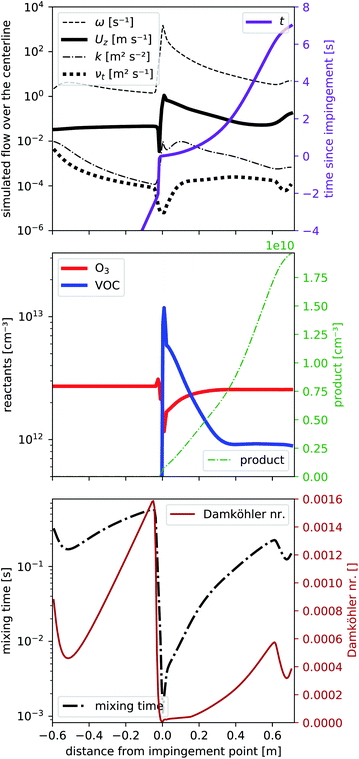
To determine the flow characteristics of the reactor, we performed steady-state simulations (residuals <1 × 10−5) based on the Reynolds-averaged Navier–Stokes equation that includes the transport of a passive tracer. In a first step, we excluded chemical reactions to reduce the required computation time, which allowed us to optimize our reactor design and volumetric flows by running the simulation multiple times. We used TME ozonolysis to find the best flow settings.In Fig. 2 we present different parameters along the centerline of the reactor from −0.6 m to the exit at +0.7 m. At 0.0 m the impingement point is located. The simulated volumetric flow rates were 33 slpm as the main flow and 2.4 slpm as the VOC flow, divided into four VOC inlets. These settings showed the least wall contacts at a minimized main flow according to the simulations discussed in detail in Sections 3.2 and 3.3. In Fig. 2a we see from −0.6 m to 0.0 m a slight enhancement of the center velocity in flow direction Uz (black, bold, solid line) as well as a decay of the kinematic eddy viscosity νt (black, bold, dotted line) and the turbulent kinetic energy k (black, dash-dotted line) while a laminar flow field evolves. These simulation results are expected because our initialization at the entrance assumes velocity boundary conditions that are independent of the radius. The first part of the reactor is solely simulated to create a laminar flow field just before the impingement point at 0.0 m. Directly before the impingement point, there is a small stagnant area: the flow velocity slows down first before being strongly enhanced to its maximum located right after the impingement point. Alongside the velocity, Uz also the turbulent kinetic energy k and the specific turbulence dissipation rate ω peak, before all parameters slowly decay as a function of reaction time shown as solid violet line. The pronounced dissipation and the reduced turbulent viscosity νt close to the impingement point reflect the strong micromixing in that region.
At the end of the reactor (from 0.6 to 0.7 m) we reduce the reactor radius in a funnel shape to increase the flow velocity which also slightly increases the turbulence in order to avoid room air being mixed into the sampling line.
As concentrations of the reactants are low (far below 1 ppm), we can assume, that the effect of reactants and products on the flow pattern will be negligible and are therefore simulating the reaction on the precalculated steady-state flow field. Fig. 2b shows the concentrations of the reactants O3 (solid red line) and one VOC (solid blue line) together with one product (dotted green line) according to the simplified reaction (2) with a rate coefficient of k2 = 1.0 × 10−15 cm3 s−1. The rate coefficient is comparable to literature reaction rate coefficients of TME ozonolysis32,33 so that the product would correspond e.g. to acetone, formed with a yield of unity from TME ozonolysis.
At the impingement point, the VOC concentration is strongly enhanced, while ozone decreased due to a displacement effect by the fast VOC-containing air streams. Due to the fast mixing at the impingement point, the immediate decrease of the VOC (and the increase of ozone) is fast, then slows down. Ozone is uniformly distributed over the entire volume of the flow tube and its deviation from the final steady-state concentration is therefore smaller than that of the VOC. This imbalance close to the impingement point leads to enhanced product formation rates (see Fig. S2a†) in the first centimeters. Furthermore, directly upstream the impingement point back-mixing occurs due to the vortices formed there. Consequently, the product concentration is non-zero at the impingement point. We will give this a closer look in Section 3.2. Further downstream, the product concentration seems to increase more than right after the impingement point. While it may seem contradictory at first, it can be explained by a smaller flow velocity further downstream and becomes fully evident when considering the product concentration as a function of the reaction time (in Fig. 2a). Compared to the reaction time, the product increases faster right after impingement. When analyzing the effect of this inhomogeneity on product formation, we will therefore use the “effective reaction time”, described in Section 3.2.
Finally in Fig. 2c the mixing timescale
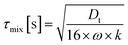 | (6) |
| τchem,min [s] = (k2·max([VOC],[O3]))−1 | (7) |
We get the Damköhler number
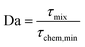 | (8) |
3.2 Effective reaction time
Now we evaluate to what extent the inhomogeneity of the reactants close to the impingement point affects the product concentrations at the outflow. Therefore we compare the experimentally obtained “effective reaction time” of the TME ozonolysis reaction with the simulated effective reaction time along the centerline.By using an effective reaction time teffective, we take into account the non-ideality of the flow field in our reactor: the concentration of a product p along the centerline from the reaction of two precursor reactants with position-dependent concentrations due to the non-ideality of the reactor (e.g. because of outward advection and diffusion of the compounds, see Fig. 5) r1 and r2 would be
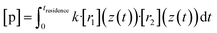 | (9) |
Now, when the reaction conditions are chosen such, that the chemical losses of the reactants remain negligible, the concentrations of the reactants can be split into two parts: one, that is the concentration after perfect mixing of the flows (without chemical conversion), which can be changed experimentally by adjusting the input concentration of the reactant ([r1,2]0), and another part that contains the position dependence that is only determined by the flow fields in the reactor, that are kept the same for every experiment. The concentrations of the reactants are always remaining in a range, where they do not affect the flows. Different molecular diffusivities of different compounds do not play a role either, as the turbulent diffusivity is a lot larger in the full reaction region. Therefore:
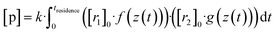 | (10a) |
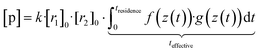 | (10b) |
| [p] = k·[r1]0·[r2]0·teffective | (10c) |
Eqn (10c) is in that form only valid when chemical losses of the reactants remain negligible, which we used for experimentally determining the effective reaction time in the INNpinJeR using TME ozonolysis. Nonetheless, the effective reaction time can also be used for cases, where the reactant concentrations get depleted. In that case, instead of [r1]0,[r2]0 = constant, one can still solve the chemical system with coupled differential equations, but using the time frame of the effective reaction time instead of coupling the chemical system to the flow dynamics, if we can show, that it captures the radial advection/diffusion effects well for different compounds. Summarizing, teffective corresponds to the integral over all non-ideal features that are solely determined by radial advection and diffusion of the compounds.
The reaction kinetics and product formation of TME ozonolysis are well understood so that this system is suitable to characterize the INNpinJeR experimentally. The main products of the ozonolysis reaction, depicted in Fig. 3, are acetone and the CH3C(O)CH2O2 peroxy radical. Under conditions of negligible radical wall losses and negligible secondary reactions we expect to detect both products with a yield of unity.
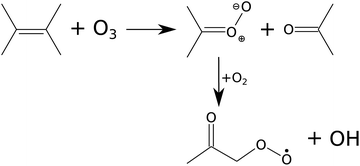 | ||
| Fig. 3 Scheme of TME ozonolysis. Acetone and a Criegee intermediate – decaying to the peroxy radical (CH3C(O)CH2O2) and OH – are formed with unity yields. | ||
In Fig. 4a we plot measured concentrations of the two ozonolysis products (determined using the acetone calibration factor for both compounds and correcting for background signals and radical wall losses in the short inlet line) against the TME reaction rate. The slope of the fit to the data points (with zero intercept) corresponds to the effective reaction time. We find that the effective reaction time is 9.4 ± 1.1 seconds and thereby significantly longer than the center flow residence time in the reactor of seven seconds according to the simulation (Fig. 2). In Fig. 4b the effective reaction time, determined from simulated product concentrations (see Section S1.6†), is plotted against the residence time in the reactor. The determined effective reaction times are very similar for both products (see Table 2). The ROOR from the RO2 + RO2 accretion reaction gives a slightly smaller effective reaction time. We chose these very different products as extreme examples because they are formed from precursors with different concentration distributions over the reactor. The effective reaction times for both compounds are nonetheless very similar (and within the experimental uncertainties), which demonstrates that the effective reaction time is a useful parameter to summarize the flow and mixing effects in this type of reactors. The nonlinearity of the effective reaction time (in Fig. 4b) can be attributed to the enhanced reactant concentrations close to the impingement point and varying diffusional losses along the flow direction coordinate z. Please find more details in Section S1.6.† The experiment and the simulation were performed under the condition,
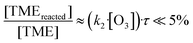 | (11) |
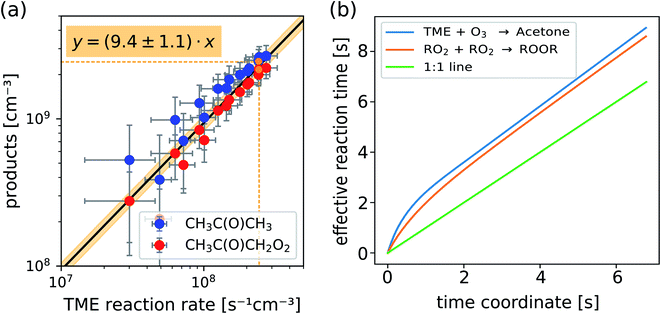 | ||
| Fig. 4 Measured concentrations of acetone and the main radical CH3C(O)CH2O2 (a) and calculated effective reaction times vs. residence time in the reactor (b) as determined from 2D chemistry simulations (see Section S1.6, eqn (S15) and (S16)†). | ||
| Experiment | Total | TME + O3 → acetone + RO2 | 9.4 ± 1.1 s |
|---|---|---|---|
| Simulation | Total | TME + O3 → acetone + RO2 | 9.3 s |
| Total | RO2 + RO2 → ROOR | 9.0 s | |
| Thereof in… | Reactor | TME + O3 → acetone + RO2 | 8.9 s |
| RO2 + RO2 → ROOR | 8.6 s | ||
| Inlet | 0.4 s | ||
To truly compare the simulation with the measurement of the reaction time by TME ozonolysis, we also need to consider that the reaction is ongoing in the inlet line. With an inlet flow of 10 slpm through a 1/2 inch tube, the residence time in the inlet corresponds to 0.44 seconds in addition. Adding these, we get a theoretical effective reaction time of 9.0–9.3 seconds in very good agreement with the measured value. This comparison shows, that using the effective reaction time as a parameter for the 0D box model calculations for the reactor, will not infer a large error. We summarized the effective reaction times in Table 2.
3.3 Negligible wall contacts
It is quite remarkable, that the concentrations of the CH3C(O)CH2O2 peroxy radical, which is quickly lost upon wall collisions, and that of acetone are nearly equal in Fig. 4a, applying loss corrections only for the inlet line. This is expected from theory. Nonetheless, it is not easily shown experimentally as it requires negligible radical losses in the reactor where the compounds spend most of the time and a short and well-characterized inlet as well as an instrument that can detect radicals with high sensitivity.The flow and passive tracer simulations also suggest negligible effects. In Fig. 5a we show simulations of the local Reynolds number as defined by Tao et al.36 and in Fig. 5b the concentrations of a passive tracer (VOC), presented as cross-sections. Stream tracers (grey), initialized at the sample point (white cross, 65 cm below the impingement point), initialized with different initial radii, show the separation of the center and the outer flow. The stream tracers start in a circular area with a radius of 2 cm in Fig. 5a and 1 cm in Fig. 5b around the sampling point. Further downstream than 40 cm from the impingement point, the VOC distribution changes only slightly since concentration gradients have flattened. The VOC concentration close to the walls is less than 20% of the center concentration in that region. Any product created at the walls needs to diffuse back into the sampled center flow; thus the impact is even far lower: as seen in Fig. 5b, the local Reynolds number
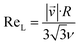 | (12) |
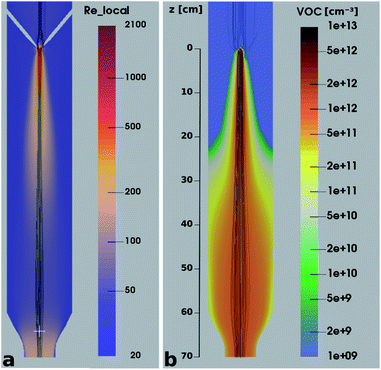 | ||
| Fig. 5 Local Reynolds number (a) and VOC concentration (b) in a cross section of the reactor overlaid with streamtracers (grey), initialized with different radii at the sampling position. | ||
3.4 Production of second generation products
We performed gas-phase reactions utilizing the same NH4+-CIMS and identical settings at the TROPOS free jet flow system and at the new INNpinJeR. We first investigated the ozonolysis of cyclohexene (kCyHex+O3 ≈ 8.0 × 10−17 cm3 s−1,37,38 OH-yield 0.54 ± 0.11,24kCyHex+OH = 6.7 × 10−11 cm3 s−1)39 to compare the results obtained in Innsbruck (INNpinJeR) with results from TROPOS that are published in Hansel et al.14 The reaction conditions are such that the produced OH is mainly reacting with cyclohexene to form the peroxy radical HO–C6H10O3.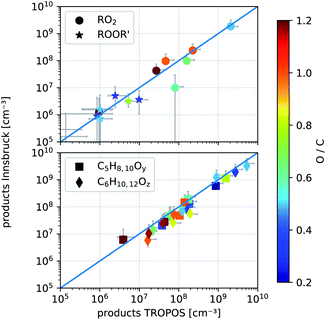 | ||
| Fig. 6 Comparison of detected product concentrations from cyclohexene ozonolysis in the IBK (August 2017, T = 304 ± 2 °C) and TROPOS flow reactor (May 2017, T = 295 ± 2 K). In the upper panel we compare RO2 radicals and their accretion products ROOR′ between the two setups. The lower panel shows all other detected closed shell products with given formulas and y, z ∈ 1, 2,…, 5. The O-to-C ratio determines the color of the markers. The error bars are calculated according to eqn (S4) and (S5).† | ||
| TROPOS | Innsbruck | Factor | |
|---|---|---|---|
| Effective reaction time [s] | 7.9 | 9.4 | 1.19 |
| O3 [cm−3] | 2.34 × 1012 | 3.9 × 1012 | 1.67 |
| C6H10 [cm−3] | 4.0 × 1012 | 2.5 × 1012 | 0.625 |
| Combined factor | 1.24 |
The measured product concentrations in the two experiments agree within the stated uncertainties, both for the radicals and the closed-shell products. Only one compound, marked as a ring in the upper panel of Fig. 6, with the formula C5H9O3, deviates significantly from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. A product with this sum formula has not been observed before. During NO addition performed at the INNpinJeR, we further observed a product with the exact mass of C5H9O2NO2, suggesting that a new peroxy radical with the formula C5H9O3 probably exists. Furthermore, we observed accretion products formed by RO2 + R′O2 → ROOR′ + O2 reactions involving a C5H9O3 peroxy radical. The data are shown in Section S2.1.† A collision-induced dissociation ramp in our NH4+-CIMS shows, that the peroxy radicals and their clusters with ammonium are stable enough to survive ionization and transfer into the TOF without fragmentation. Therefore we can exclude, that the compound with the formula C5H9O3 is a fragment of another peroxy radical. So far this is the first time this peroxy radical has been observed in cyclohexene ozonolysis. To elucidate the detailed formation mechanism further experimental studies are needed.
1 line. A product with this sum formula has not been observed before. During NO addition performed at the INNpinJeR, we further observed a product with the exact mass of C5H9O2NO2, suggesting that a new peroxy radical with the formula C5H9O3 probably exists. Furthermore, we observed accretion products formed by RO2 + R′O2 → ROOR′ + O2 reactions involving a C5H9O3 peroxy radical. The data are shown in Section S2.1.† A collision-induced dissociation ramp in our NH4+-CIMS shows, that the peroxy radicals and their clusters with ammonium are stable enough to survive ionization and transfer into the TOF without fragmentation. Therefore we can exclude, that the compound with the formula C5H9O3 is a fragment of another peroxy radical. So far this is the first time this peroxy radical has been observed in cyclohexene ozonolysis. To elucidate the detailed formation mechanism further experimental studies are needed.
In both reactors, we were able to measure accretion rate coefficients kacc as shown for C6H11O3 + C6H9O8 as an example in Fig. 7, based upon eqn (13), which is valid, when the peroxy radicals increase linearly with reaction time.26
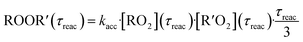 | (13) |
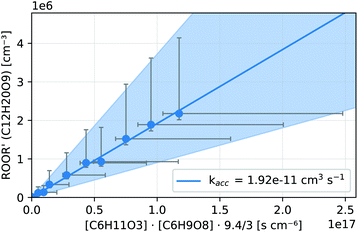 | ||
| Fig. 7 Kinetic analysis of the accretion product formation of C6H11O3 + C6H9O8 in the INNpinJeR during the ozone ramp in experiment C6H10 (b). The data are fitted with a function f(x) = kacc·x. The fitted paramater kacc is given in the legend. The shaded area depicts the uncertainty of kacc due to the possible systematic errors of the peroxy radicals and their accretion product (see Section S1.4†). | ||
In Table 4 we present measured rate coefficients for a number of peroxy radical pairs from the experiments C6H10 (b) and C6H10@TROPOS. The corresponding plots, similar to Fig. 7 can be found in Section S2.4.†
| RO2 | R′O2 | ROOR′ | @INNpinJeR | @TROPOS |
|---|---|---|---|---|
| T = 302 K | T = 295 K | |||
| C6H11O3 | C6H11O3 | C12H22O4 | 1.2 × 10−12 | 0.5 × 10−12 |
| C6H11O3 | C6H9O6 | C12H20O7 | 9.8 × 10−12 | 6.9 × 10−12 |
| C6H11O3 | C6H9O8 | C12H20O9 | 1.9 × 10−11 | 1.9 × 10−11 |
| C5H9O5 | C6H9O8 | C11H18O11 | 7.3 × 10−11 | 4.3 × 10−11 |
We present only formation rate coefficients of those accretion products for which only one combination of peroxy radicals exist (e.g. C12H18O10 could be formed via C6H9O6 + C6H9O6 and via C6H9O8 + C6H9O4 and is therefore excluded).
The accretion rate coefficients obtained at the two reactors agree typically within a factor 2, which agrees with uncertainties stated in previous publications.26 There is also a clear trend showing higher rate coefficients for accretion of more oxidized peroxy radicals as discussed by Berndt et al.26 Uncertainties from the NH4+-CIMS calibration and the background correction might affect the rate coefficients. The overall very good agreement between the two reactors commends the “wall-free” reactor design.
• enhanced production of the RO2 radicals close to the impingement point and
• additional losses of the RO2 radicals by
– high (approximately linearly increasing) RO2 concentrations and
– high (constant) background HO2 concentrations
could affect accretion rate coefficients obtained from the RO2 and ROOR concentrations in the outflow. A detailed explanation as well as analytical solutions for the two special cases
• high but constant HO2 concentrations and low RO2 concentrations
• or high RO2 concentrations and negligible HO2 concentrations
can be found in Section S2.2.1.†
The numerical simulation takes into account the full reaction system (eqn (2)–(5c)), the inhomogeneous precursor concentration as well as the partly turbulent, partly diffusive dispersion of the compounds within the reactor. For simplicity, we assume negligible NOx concentrations.
We conducted simplified simulations of the reaction system with different bimolecular reactivities r2m of the peroxy radicals:
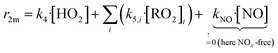 | (14) |
For our simulations we assume fast RO2 isomerization rates (risom > 1 s−1, τisom ≪ τreac = 9.4 ± 1.1 s) in accordance with results from Berndt et al.8 for peroxy radicals from cyclohexene ozonolysis. They observed that the peroxy radicals increase linearly in time and nearly parallel within the reactor as their ratio is determined within the first second. Therefore, the effect of isomerization on accretion product formation rates is small for the cyclohexene system. In Section S2.5† we shortly discuss uncertainties in case of unknown isomerization rates.
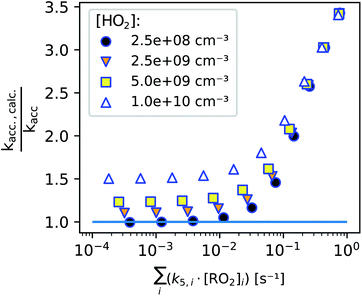
In Fig. 8, we summarize our model findings by evaluating, how large the systematic error would be, calculating kacc,calc according to eqn (13) although a perfect linear increase of the peroxy radicals with time is not given. All data points shown include the enhanced production of RO2 radicals in the first seconds, while the two loss terms are varied by varying either the background HO2 concentration (legend, symbols) or the total bimolecular reactivity of the peroxy radicals with each other (x-axis).
We find that as long as the bimolecular reactivity of the peroxy radicals with each other is below 0.01 s−1 and the HO2 concentration is small, the calculated accretion rate coefficient would exactly match the actual one (as set in the simulation). This shows, that the enhanced peroxy radical production in the first seconds of the reaction does not influence our result.
The additional losses on the other hand do affect the determined accretion rate coefficient: high HO2 concentrations and a fast bimolecular reactivity of the peroxy radicals with each other both enhance the calculated accretion rate coefficient, because the peroxy radicals start approaching a steady state within the reaction time when these additional losses become non-negligible. Therefore it is important to perform experiments under low radical conditions. As shown in previous publications, accretion rate coefficients range from 10−13 cm3 s−1 for less functionalized to about 10−10 cm3 s−1 for highly oxidized peroxy radical pairs.2,26 For the highest reaction rate coefficients, a maximum concentration of summed peroxy radicals of some 108 cm−3 should not be clearly exceeded to determine the accretion rate coefficients according to eqn (13). In the case of peroxy radicals that react significantly slower, this limit concentration could be accordingly somewhat higher.
While we are able to quantitatively detect most peroxy radicals, we, unfortunately, can not yet pinpoint the actual HO2 concentration in the reactor. Assuming that the HO2 concentration is not higher than 2 × 109 cm−3, such an HO2 background concentration would not have a significant effect on accretion rate coefficients as seen in Fig. 8 (details can be found in the ESI, Section S2.3†). The main difficulty here is to run experiments with reasonably low reactant concentrations while avoiding additional uncertainties due to background removal when product concentrations become too small, highlighting the importance of using as clean carrier gas as possible.
4 Conclusions and outlook
We introduced the new Innsbruck impinging jets reactor (INNpinJeR). OpenFOAM simulations showed that the impinging jets create a mixing environment in the center flow that does not affect the surrounding laminar sheath flow. Enhanced reactant concentrations close to the impingement point initially lead to faster product formation. We can account for this by using an “effective reaction time” of 9.4 ± 1.1 seconds, which is longer than the actual residence time. We have demonstrated that we can use the effective reaction time to investigate accretion product formation, assuming linear increasing RO2 radical concentrations with time, as long as the bimolecular reactivity of the peroxy radicals remains small.We were able to reproduce results from the TROPOS reactor14 with the INNpinJeR within the stated uncertainty range of a factor 2. Detected peroxy radical concentrations compare well with literature and previous results. This very good agreement between the two setups points towards a well-characterized system in which wall contacts can be assumed negligible. This is the first time, the detailed results of the cyclohexene ozonolysis system could be reproduced in two different setups.
Overall, the reactor gave promising results, using the two simple reaction systems of cyclohexene and tetramethyl ethylene ozonolysis. Due to negligible wall contacts by only requiring a total clean gas flow of 33 slpm, the reactor design simplifies the analysis of gas-phase chemical reaction systems. Being able to use 0D box model calculations using the effective reaction time will additionally simplify future more complex chemical analyses at our INNpinJeR, which holds great potential to study for example RO2 + HO2 reactions in the future due to its short inlets at the beginning of the reactor.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank K. Pielok for her support with the experiments at the TROPOS flow system. This work was supported by the Innovative Training Networks – ITN (CLOUD-Motion H2020-MSCA-ITN-2017 no. 764991) and by a doctoral scholarship (2021/1) of the University of Innsbruck.Notes and references
- J. D. Crounse, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. Lett., 2013, 4, 3513–3520 CrossRef CAS.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I.-H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurten, L. B. Nielsen, S. Jorgensen, H. G. Kjaergaard, M. Canagaratna, M. D. Maso, T. Berndt, T. Petaja, A. Wahner, V.-M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479 CrossRef CAS PubMed.
- K. H. Møller, T. Berndt and H. G. Kjaergaard, Environ. Sci. Technol., 2020, 54, 11087–11099 CrossRef PubMed.
- K. H. Møller, K. H. Bates and H. G. Kjaergaard, J. Phys. Chem. A, 2019, 123, 920–932 CrossRef PubMed.
- F. Bianchi, T. Kurte, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, R. Wildt, H. Junninen, T. Jokinen, M. Kulmala, D. R. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehn, Chem. Rev., 2019, 119(6), 3472–3509 CrossRef CAS PubMed.
- P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes, M. D. Smarte, J. M. St Clair, A. P. Teng, X. Zhang and J. H. Seinfeld, Chem. Rev., 2018, 118, 3337–3390 CrossRef CAS PubMed.
- K. H. Møller, R. V. Otkjær, J. Chen and H. G. Kjaergaard, J. Phys. Chem. A, 2020, 124, 2885–2896 CrossRef PubMed.
- T. Berndt, S. Richters, R. Kaethner, J. Voigtländer, F. Stratmann, M. Sipilä, M. Kulmala and H. Herrmann, J. Phys. Chem. A, 2015, 119, 10336–10348 CrossRef CAS PubMed.
- M. Schervish and N. M. Donahue, Atmos. Chem. Phys., 2020, 20, 1183–1199 CrossRef CAS.
- D. Stolzenburg, L. Fischer, A. L. Vogel, M. Heinritzi, M. Schervish, M. Simon, A. C. Wagner, L. Dada, L. R. Ahonen, A. Amorim, A. Baccarini, P. S. Bauer, B. Baumgartner, A. Bergen, F. Bianchi, M. Breitenlechner, S. Brilke, S. Buenrostro Mazon, D. Chen, A. Dias, D. C. Draper, J. Duplissy, I. El Haddad, H. Finkenzeller, C. Frege, C. Fuchs, O. Garmash, H. Gordon, X. He, J. Helm, V. Hofbauer, C. R. Hoyle, C. Kim, J. Kirkby, J. Kontkanen, A. Kürten, J. Lampilahti, M. Lawler, K. Lehtipalo, M. Leiminger, H. Mai, S. Mathot, B. Mentler, U. Molteni, W. Nie, T. Nieminen, J. B. Nowak, A. Ojdanic, A. Onnela, M. Passananti, T. Petäjä, L. L. J. Quéléver, M. P. Rissanen, N. Sarnela, S. Schallhart, C. Tauber, A. Tomé, R. Wagner, M. Wang, L. Weitz, D. Wimmer, M. Xiao, C. Yan, P. Ye, Q. Zha, U. Baltensperger, J. Curtius, J. Dommen, R. C. Flagan, M. Kulmala, J. N. Smith, D. R. Worsnop, A. Hansel, N. M. Donahue and P. M. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9122–9127 CrossRef CAS PubMed.
- J. H. Seinfeld, Science New Series, 1989, 243, 745–752 CAS.
- A. Kürten, L. Rondo, S. Ehrhart and J. Curtius, Atmos. Meas. Tech., 2011, 4, 437–443 CrossRef.
- M. Breitenlechner, L. Fischer, M. Hainer, M. Heinritzi, J. Curtius and A. Hansel, Anal. Chem., 2017, 89, 5824–5831 CrossRef CAS PubMed.
- A. Hansel, W. Scholz, B. Mentler, L. Fischer and T. Berndt, Atmos. Environ., 2018, 186, 248–255 CrossRef CAS.
- A.-K. Bernhammer, M. Breitenlechner, F. N. Keutsch and A. Hansel, Atmos. Chem. Phys., 2017, 17, 4053–4062 CrossRef CAS.
- A. T. Lambe, A. T. Ahern, L. R. Williams, J. G. Slowik, J. P. S. Wong, J. P. D. Abbatt, W. H. Brune, N. L. Ng, J. P. Wright, D. R. Croasdale, D. R. Worsnop, P. Davidovits and T. B. Onasch, Atmos. Meas. Tech., 2011, 4, 445–461 CrossRef CAS.
- W. Jud, L. Fischer, E. Canaval, G. Wohlfahrt, A. Tissier and A. Hansel, Atmos. Chem. Phys., 2016, 16, 277–292 CrossRef CAS.
- A. A. Presto and N. M. Donahue, J. Phys. Chem. A, 2004, 108, 9096–9104 CrossRef CAS.
- T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Supporting Information Accretion Product Formation from Self-And Cross-Reactions of RO2 Radicals in the Atmosphere, 2018 Search PubMed.
- T. Berndt, B. Mentler, W. Scholz, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Environ. Sci. Technol., 2018, 52, 11069–11077 CrossRef CAS PubMed.
- B. K. Johnson and R. K. Prud’homme, AIChE J., 2003, 49, 2264–2282 CrossRef CAS.
- Y. Liu, M. G. Olsen and R. O. Fox, Lab Chip, 2009, 9, 1110–1118 RSC.
- R. Atkinson, S. M. Aschmann, J. Arey and B. Shorees, J. Geophys. Res.: Atmos., 1992, 97, 6065–6073 CrossRef CAS.
- S. M. Aschmann, E. C. Tuazon, J. Arey and R. Atkinson, J. Phys. Chem. A, 2003, 107, 2247–2255 CrossRef CAS.
- M. P. Rissanen, T. Kurtén, M. Sipilä, J. A. Thornton, J. Kangasluoma, N. Sarnela, H. Junninen, S. Jørgensen, S. Schallhart, M. K. Kajos, R. Taipale, M. Springer, T. F. Mentel, T. Ruuskanen, T. Petäjä, D. R. Worsnop, H. G. Kjaergaard and M. Ehn, J. Am. Chem. Soc., 2014, 136, 15596–15606 CrossRef CAS PubMed.
- T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Angew. Chem., Int. Ed., 2018, 57, 3820–3824 CrossRef CAS PubMed.
- A. Zaytsev, M. Breitenlechner, A. R. Koss, C. Y. Lim, J. C. Rowe, J. H. Kroll and F. N. Keutsch, Atmos. Meas. Tech., 2019, 12, 1861–1870 CrossRef CAS PubMed.
- E. Canaval, N. Hyttinen, B. Schmidbauer, L. Fischer and A. Hansel, Front. Chem., 2019, 7, 191 CrossRef PubMed.
- T. Berndt, N. Hyttinen, H. Herrmann and A. Hansel, Commun. Chem., 2019, 2, 21 CrossRef.
- L. Fischer, M. Breitenlechner, E. Canaval, W. Scholz, M. Striednig, M. Graus, T. G. Karl, T. Petäjä, M. Kulmala and A. Hansel, Atmos. Meas. Tech., 2021, 14, 8019–8039 CrossRef.
- F. Menter and T. Esch, Proc. COBEM 2001, Invited Lectures, 2001, vol. 20, pp. 117–127 Search PubMed.
- R. E. Huie and J. T. Herron, Int. J. Chem. Kinet., 1975, 7(1), 165–181 Search PubMed.
- M. Witter, T. Berndt, O. Böge, F. Stratmann and J. Heintzenberg, Int. J. Chem. Kinet., 2002, 34, 394–403 CrossRef CAS.
- H. G. Ouwersloot, J. Vilà-Guerau de Arellano, C. C. van Heerwaarden, L. N. Ganzeveld, M. C. Krol and J. Lelieveld, Atmos. Chem. Phys., 2011, 11, 10681–10704 CrossRef CAS.
- L. Kaser, T. Karl, B. Yuan, R. L. Mauldin, C. A. Cantrell, A. B. Guenther, E. G. Patton, A. J. Weinheimer, C. Knote, J. Orlando, L. Emmons, E. Apel, R. Hornbrook, S. Shertz, K. Ullmann, S. Hall, M. Graus, J. De Gouw, X. Zhou and C. Ye, Geophys. Res. Lett., 2015, 42, 10894–10903 CrossRef CAS.
- J. Tao, S. Chen and W. Su, Sci. China: Phys., Mech. Astron., 2013, 56, 263–269 CAS.
- C. R. Greene and R. Atkinson, Int. J. Chem. Kinet., 1992, 24, 803–811 CrossRef CAS.
- D. J. Stewart, S. H. Almabrok, J. P. Lockhart, O. M. Mohamed, D. R. Nutt, C. Pfrang and G. Marston, Atmos. Environ., 2013, 70, 227–235 CrossRef CAS.
- R. Atkinson, Chem. Rev., 1986, 86, 69–201 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ea00072a |
| This journal is © The Royal Society of Chemistry 2022 |