Short- vs. long-range elastic distortion: structural dynamics of a [2 × 2] tetrairon(II) spin crossover grid complex observed by time-resolved X-Ray crystallography

Abstract

Spin crossover complexes (SCO) are among the most studied molecular switches due to their potential use in displays, sensors, actuators and memory components. A prerequisite to using these materials is the understanding of the structural changes following the spin transition at out-of-equilibrium conditions. So far, out-of-equilibrium studies in SCO solids have been focused on mononuclear complexes, though a growing number of oligonuclear SCO complexes showing cooperative effects are being reported. Here, we use time-resolved pink Laue crystallography to study the out-of-equilibrium dynamics of a [2 × 2] tetranuclear metallogrid of the form [Fe^II₄L^Me₄](BF₄)₄·2MeCN ([L^Me]⁻ = 4-methyl-3,5-bis{6-(2,2′-bipyridyl)}pyrazolate). The out-of-equilibrium spin state switching induced by a ps laser pulse demonstrates that the metallogrid exhibits a multi-step response similar to that reported for mononuclear complexes. Contrary to the mononuclear complexes, the metallogrid shows two types of elastic distortions at different time scales. The first is a short-range distortion that propagates over the entire Fe₄ grid complex during the ps time scale, and it is caused by the rearrangement of the coordination sphere of the photo-switching ion and the constant feedback between strongly linked metal ions. The second is a long-range distortion caused by the anisotropic expansion of the lattice during the ns time scale, observed in mononuclear materials. The structural analysis demonstrates that the long-range prevails over the short-range distortion, inducing the largest deformation of both the entire grid and the coordination sphere of each metal ion. The present study sheds light on the out-of -equilibrium dynamics of a non-cooperative oligonuclear complex.

---

Introduction

Spin crossover (SCO) solids of 3d⁴–3d⁷ transition metal complexes are an archetype of switchable molecule-based materials, able to switch between two states termed high spin (HS) and low spin (LS) through the application of external stimuli such as temperature, pressure or light irradiation.^1–5 This spin switch leads to a change in magnetic, mechanical, electrical and optical properties accompanied by a structural reorganisation from the coordination polyhedron to the macroscopic scale.^6,7 This structure–property relationship is infallible at the heart of the SCO research field, and therefore, much effort has been devoted to its study at equilibrium and out-of-equilibrium conditions.

The out-of-equilibrium dynamics in solids of mononuclear SCO complexes have been studied by a combination of time-resolved pump–probe optical spectroscopy and X-ray diffraction measurements. These studies have demonstrated a multi-step response to an fs laser pulse at particular time scales, namely photoinduced, elastic and thermal switching, occurring in the ps, ns and μs regime, respectively.^8–12 The initial step corresponds to a local photo-switching from LS to HS via intersystem crossing through metal-to-ligand charge transfer excitation, which is accompanied by a structural reorganisation at the molecular scale. Here, the photo-switched fraction of molecules is proportional to the laser excitation density: one photon switches one metal centre from the LS to the HS state. The second step, known as the ‘elastic step’, is associated with an additional conversion to the HS state and the volume expansion of the lattice at the material scale, which is not instantaneous and requires propagation of strain waves¹³ at the speed of sound (∼2000 ms⁻¹). Finally, a third increase in the HS fraction is triggered on the μs time scale by an increase of the average temperature of the crystal due to heat diffusion in what is known as the ‘thermal step’.¹⁴

In spite of the progress made to understand the fundamental mechanisms that drive the switching dynamics of SCO solids, most of these studies have been limited to mononuclear complexes. The time scales and the structural reorganisation for oligomeric complexes in solid state are still unknown. This type of complexes is appealing because the strong linking between metal centres by rigid ligands can produce an elastic communication between them, which can lead to intramolecular cooperativity between connected metal centres.^15–18 [2 × 2] metallogrids are examples of oligonuclear complexes, where metal ions and four ditopic ligand strands give a matrix-like structure with up to four potentially addressable sites arranged in a square.^19–25 This type of complexes is appealing because they have the potential to exhibit intramolecular cooperativity through the strong linking of metal centres. For example, [2 × 2] metallogrids based on the R-3,5-bis{6-(2,2′-bipyridyl)}pyrazolate ligand family (R = H, Me, Br denotes the substituent at the pyrazolate-C⁴ position) have demonstrated an elastic communication between the four metal sites since the geometric and electronic changes associated with each spin transition have a knock-on effect on the electronic states of the neighbouring metal centres.^26–29 Other SCO grids in mixed-spin state showing other features such as multistability have been reported by Ruben et al.³⁰ and Oshio et al.,¹⁹ among others.^20,22,23

In a previous work, we reported the structural changes accompanying the thermal and light-induced spin crossover (SCO) of the [2 × 2] tetranuclear metallogrid of the form [Fe^II₄L^Me₄](BF₄)₄·2MeCN (L^Me = 4-methyl-3,5-bis{6-(2,2′-bipyridyl)}pyrazolate), here called FE4 (Fig. 1).³¹ In solid state, FE4 crystallises in the C2/c space group, and the asymmetric unit cell at 100 K contains only half of the molecule, with two crystallographic-symmetry-independent metal ions, one in LS state, Fe(A), and one in HS state, Fe(B). The other vertices necessary to form the grid are generated by symmetry. The material exhibits a gradual thermal phase transition from a 2HS–2LS configuration below 250 K to a 3HS–1LS configuration above this temperature (Fig. 1c). Our previous multi-temperature crystallographic analysis revealed the elastic communication between metal centres since the LS → HS transition, which occurs at only one metal ion, has a strong effect on the distortion of the coordination environment of adjacent metal ions and over the entire grid. We also postulated that this elastic communication was responsible for the continuous rearrangement of the metallogrid upon light excitation. The latter result contrasts with what has been observed in time-resolved studies of mononuclear SCO complexes, which present a single reorganisation upon excitation.^8,10 However, our previous study focused only on the photo-induced step. The structural modification during the wave propagation (elastic step) and thermal homogenisation (thermal step) remains unknown. Therefore, the aim of this contribution is to discuss the structural dynamics of FE4 from the photo-induced step to the thermal step. We show how mononuclear and oligonuclear complexes follow the same multi-step process after light irradiation with a ps laser pulse. However, the metallogrid shows two types of elastic distortions at different steps of the out-equilibrium process: a short-range distortion taking place during the photoinduced step and a long-range distortion that prevails during the elastic step.

Fig. 1 (a) Molecular representation of the [Fe₄L^Me₄]⁴⁺ grid. Fe(A) ions are in LS state and Fe(B) ions are in HS states. Counter ions, solvent molecules and hydrogen atoms are omitted for clarity. (b) Pyrazole-bridged compartmental ligand HL^Me. (c) Schematic representation of the 2HS–2LS to 3HS–1LS transition in the FE4 grid. LS and HS ions are shown in green and red, respectively.

Methods

Synthesis and steady state spectroscopy

The complex grid FE4 and its ligand HL^Me were synthesised following the procedures reported in the literature.²⁷ UV-vis and FTIR spectra at room temperature have been reported in a previous publication and they will not be discussed here.³¹

Time-resolved pink Laue crystallography

Time-resolved intensity data were collected at the BioCARS station at the Advanced Photon Source, Argonne National Laboratory, IL, USA. TRXRD data were collected at an undulator setting of 15 keV with a Rayonix MX340-HS detector. Pulses from a Ti:sapphire laser tuned to 390 nm wavelength were used as a pump source and set perpendicular to φ-rotation axis. The time delay between the laser pump and the X-ray probe was set by varying the arrival times of the picosecond laser pulses with respect to the synchrotron X-ray pulses. Delay times (dt) between the laser pump and the probe were varied from 100 ps to 100 μs. Two additional reference measurements were taken, one at the negative delay time (dt < 0) of −200 ps and the other without any laser excitation, the so called ‘static’ data set. Laser power was set at 2.0 (mJ mm⁻²) per pulse. Below fluences of 1 (mJ mm⁻²) per pulse no light-induced changes were observable. Since, in some compounds, the thermal step is only observable when the laser-induced heat increases the temperature beyond the SCO transition temperature,¹¹ crystallographic data were acquired at 220 K to ensure the thermal transition at μs time scale. This is 30 K below the thermal phase transition temperature, which prevents transition due to any accumulated heat during the laser-OFF/ON cycle.

The recorded data sets for all time delays covered a 180° scan with 1° step. Laser-OFF and laser-ON frames were collected in immediate succession to minimise the effect of long-range fluctuations in the beam's position or intensity. The OFF/ON cycle pump–probe cycle was repeated five times for each frame to allow for subsequent statistical background estimation and filtering of the intensities. A new crystal was used for each time delay to prevent effects of degradation. Crystals used in this study had approximate dimensions of 90 × 120 × 50 μm³.

The pink Laue diffraction images were processed with the software package Precognition/Epinorm,³² using variable elliptical integration for all time delays. After integration, two methods were used during the wavelength normalisation and data reduction. In the first, the laser-OFF and laser-ON data sets were scaled together, but the repetitive and symmetry-related reflections from both data sets were merged separately. These data sets were used to obtain the photodifference maps for the elastic and thermal steps. In the second method, the same procedure was followed except for replacing the laser-OFF with the ‘static’ data set. The procured reduced data sets were used to obtain the structural models at each delay time. For all data sets, initial models of the crystal structures were first obtained with the SHELXT-2014 ³³ program and then refined using the SHELXL-2014 ³⁴ program within the Olex2 ³⁵ software package. Thermal ellipsoid plots (50% of probability) for all time-resolved data sets are provided in ESI (Fig. S1–S21†).

In our previous work, photodifference maps for the photoinduced step were rather noisy. To avoid this, the LaueUtil tool kit^36,37 was used to obtain the photodifference maps for delay times between 100 ps and 700 ps. A more detailed procedure for data treatment with Precognition/Epinorm and LaueUtil is given by Velazquez-Garcia et al.³⁸

Modification of the coordination environment

The Octadist³⁹ program was used to determine the 〈Fe–N〉 bond length and the trigonal distortion parameter, describing the octahedral coordination environment of the metal centres in each compound. The trigonal distortion parameter, Θ, is the sum of the deviations from 60° of the twenty-four N–Fe–N angles, six per pseudo three-fold axis, measured on a projection of opposite triangular faces of the {FeN₆} octahedron, orientated by superimposing the face centroids (see Fig. S22†).

Estimation of the high spin fraction (X_HS)

It is very well known that the SCO is accompanied by structural modification on the {FeN₆} coordination sphere,^6,40–43 for instance, the deformation of the polyhedron and changes of the average metal–ligand distance. From LS to HS, the {FeN₆} octahedron becomes less regular, while the 〈Fe–N〉 bond length expands by approximately 0.2 Å; the latter varies depending on the concerned ligands. In the case of FE4, the asymmetric unit contains only half of a molecule, and the 〈Fe–N〉 of the transiting atom Fe(A) encompasses information of the atom that undergoes SCO and the atom that remains in the LS state. Consequently, the maximum bond length expansion is expected to reach ∼0.1 Å.

In the time domain, the increase of 〈Fe(A)–N〉 is due to an increase in population of the HS molecules. Therefore, the variation of the HS fraction was estimated from the time variation of the 〈Fe(A)–N〉 according to:¹⁰

where Δ〈Fe(A)–N〉 is the variation of the average metal–ligand bond length of atom Fe(A) at delay times dt > 0 with respect to the refence measurement dt < 0. 〈Fe(A)–N〉_HS and 〈Fe(A)–N〉_LS are the average metal–ligand bond lengths of Fe(A) at the 3HS–1LS and 2HS–2LS configurations, respectively. Since the value of 〈Fe(A)–N〉_HS is unknown, the value of the denominator was replaced by the maximum bond length expansion expected for the Fe(A) ion.

An alternative way to estimate the variation of the HS fraction is to use the X-ray structure factors as performed in our previous work.³¹ However, the accuracy of that method is largely limited by the approximation resulting from structure factor corrections through the Debye–Waller factor.¹⁰ Moreover, our previous method included a rough estimation of the structure factor of the pure HS state, since it was not possible to obtain from the multi-temperature study. Though inaccurate, this method provides an estimation of the variation of the HS fraction. Since the average bond lengths show a clear and steady change, the variation of the HS fraction was obtained from the temporal evolution of 〈Fe(A)–N〉.

Analysis of temperature differences due to laser exposure

An estimate of the temperature difference between the laser-ON and laser-OFF data sets was obtained from the photo-Wilson plot.^44,45 The plots for all data collected are shown in Fig. S23–S26.† The slope of the plot corresponds to twice the average Debye–Waller factor (2ΔB^ON–OFF), associated with the isotropic atomic motion (for more information see the temperature difference section in ESI†). Therefore, measuring ΔB between laser-ON and laser-OFF data sets provides an estimate of the temperature increase due to laser exposure through the associated increase in thermal motion. Values of ΔB^ON–OFF ≈ 0 indicate a non-detectable global heating of the sample, while values greater than zero suggest an increase in temperature of the crystal.

Results

Photoinduced, elastic and thermal steps

The time evolution of X_HS after laser irradiation (Fig. 2a) demonstrates a three steps response similar to that reported for mononuclear complexes.^8–12 At first, the local photoinduced switching of Fe(A) ions from LS to HS state is shown from 100 ps to 700 ps through the temporal evolution of X_HS (Fig. 2a). At this stage, the LS → HS transition is performed without energy exchange with the environment as observed in the time-delay dependance of the isotropic thermal factor, ΔB^ON–OFF, in Fig. 2b. The observed rise of ΔX_HS to ∼7% indicates an instantaneous increase of the HS fraction in the first 100 ps (time resolution of the experiment) and an almost complete relaxation to its original state around 700 ps. As the material has mostly returned to its ground state configuration, the second increase of ∼15% in the HS fraction, between 800 ps and 800 ns, is then mainly related to the expansion of the crystal volume due to lattice heat. The temperature increase due to laser exposure can be easily detected by the increase of ΔB^ON–OFF, while the volume expansion can be observed by the deformation of the Bragg peaks in the reciprocal lattice from 800 ps (Fig. 2c). Finally, the laser induced heat gives rise to the thermal step and an additional ∼10% increase of the HS fraction observed on the μs time scale. A comparison of the isotropic thermal factor obtained in the time domain, ΔB^ON–OFF = 0.22, with that previously obtained at thermal equilibrium, ΔB^{250 K–220 K} = 0.21, allows for estimating the corresponding temperature increase after μs delays to ∼30 K.

Fig. 2 (a) Time-delay dependence of Δ〈Fe(A)–N〉 associated with the variation of the HS fraction, ΔX_HS. (b) Time dependance of the isotropic thermal factor, ΔB^ON–OFF. Photoinduced (PI), elastic (ES) and thermal (TS) steps are shown in blue, green and red, respectively. (c) Crystallographic images of the 800 ps data set, showing a deformation of the Bragg peaks between the laser-OFF and laser-ON.

Photodifference maps

The structural reorganisation upon excitation is illustrated in the photodifference maps^46–49 of the form F^ON_obs–F^OFF_obs based on all independent reflections with I/σ(I) > 3 (Fig. 3). To highlight the displacement of the Fe ions, isosurfaces are drawn between ±0.028 and 0.33 e ų. The molecular response on excitation at any time is observed by the shift of electron density of the Fe(A) and Fe(B) ions. A thermal difference map⁵⁰ of the form F^{260 K}_obs–F^{250 K}_obs obtained in our previous work³¹ is placed in Fig. 3a as a reference of the structural reorganisation at equilibrium conditions. The photodifference maps show the different structural responses of the FE4 grid at each step of the out-of-equilibrium process. During the photoinduced step (Fig. 3b and c), the maps illustrate the continuous reorganisation of the grid caused by rearrangement of the coordination sphere of the transiting ion and the constant feedback between strongly linked metal ions, as reported previously.³¹ It is worth noting that the smallest shift in electron density during this step occurs at 600 ps, since most of the photo-switched metal centres have relaxed to their original state at that delay time. After that, the elastic step takes place and strain waves propagate through the crystals, which induces a shift in the electron density toward the direction of the propagating wave. Since the crystals used have anisotropic shapes, the propagation of the strain waves takes different times along different crystallographic axes. Fig. 3f and g illustrate the propagation of waves along the c and a axes at 800 ps and 100 ns, respectively. Finally, the temperature homogenisation over the crystal in μs regime results in the thermal population of the HS state and a structural change comparable with that obtained at equilibrium conditions. Consequently, the electron density shift of the photodifference map (Fig. 3g) resembles that observed in the reference thermal difference map of the thermal spin transition.

Fig. 3 (a) Thermal difference Fourier maps of FE4 between 260 and 250 K. (b–h) Photodifference maps of FE4 along the b axis. Isosurfaces (green positive, red negative) and delay times are shown on each figure. Arrows give approximate directions of the electron density shift. The symbol ⊙ indicates an outside and inside of the plane electron density shift, while O symbols indicate only out-of-the-plane electron density shifts.

Structural reorganisation at the atom site

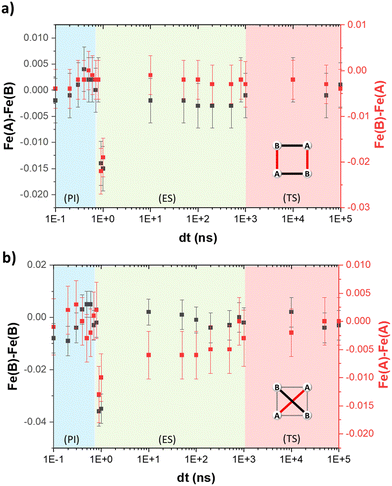
The temporal evolution of the average Fe–N bond length of the transiting metal ion Fe(A) follows the same trend as the change of the HS fraction, since the latter was estimated from the former. Therefore, upon excitation, the 〈Fe(A)–N〉 expands three times due to the increase in the HS population at photoinduced, elastic and thermal steps (Fig. 2a). Fig. 4a shows that a similar trend is observed in the temporal evolution of 〈Fe–N〉 of the non-transiting metal ion Fe(B). However, the change is smaller than that seen for the Fe(A) ion. Since the Fe(B) ion remains in the HS state throughout, the changes in the bond lengths are considered as a knock-on effect from the structural reorganisation of the grid after the spin transition in the Fe(A) ion.

Fig. 4 Time-delay dependence of (a) 〈Fe(B)–N〉 and (b) the variation of the trigonal distortion parameter, ΔΘ, of both the Fe(A) and Fe(B) ions. Photoinduced (PI), elastic (ES) and thermal (TS) steps are shown in blue, green and red, respectively.

The variation of the trigonal distortion parameter in the time domain for both Fe(A) and Fe(B) is shown in Fig. 4b. The figure shows a significant fluctuation of ΔΘ, in particular for the Fe(B) ion, during the photoinduced step, while a sharp distortion at 1 ns with slow relaxation up to 1 μs is observed during the elastic step. The first is attributed to the continuous rearrangement of the grid upon excitation and the second to the propagation of strain waves and the anisotropic expansion of the unit cell. Finally, the coordination environment of both metal ions slightly rearranges during the thermal step, showing smaller changes in the value of ΔΘ.

Molecular rearrangement

An important aspect to consider during the out-of-equilibrium dynamics of oligonuclear complexes is the geometrical rearrangement of the metal centres. The FE4 grid forms a parallelogram, defined by the four iron ions. As seen in Fig. 5, the shape of the quadrilateral changes constantly during the photoinduced step. In particular, the Fe(A)–Fe(A) and Fe(B)–Fe(B) distances continuously fluctuate during the first 700 ps after light irradiation. This suggests a constant rearrangement of the grid upon excitation as noted previously. During the elastic step, a sharp contraction of all the Fe–Fe distances by 0.01 Å or more at 1 ns delay time is attributed to the propagation of strain waves and the anisotropic expansion of the lattice. After this distortion, the grid slowly recovers its original dimensions between 100 ns and 100 μs after light excitation.

Fig. 5 Time dependence of the Fe–Fe distances in FE4 grid: (a) Fe(A)-Fe(B) and Fe(B)-Fe(A), and (b) Fe(B)-Fe(B) and Fe(A)-Fe(A). Photoinduced (PI), elastic (ES) and thermal (TS) steps are shown in blue, green and red, respectively.

Discussion

As it happens in the mononuclear Fe^II and Fe^III complexes, the out-of-equilibrium dynamics in the [2 × 2] metallogrid FE4 feature different consecutive steps at particular time scales, namely the photoinduced, elastic and thermal steps, occurring in the ps, ns and μs regimes, respectively (Fig. 6a).^8–12 In the first step, the absorption of light at molecular level locally switches a fraction of the molecules, changing one of the Fe^II ions from a LS to HS state. Here, the initial reorganisation of the molecule takes place as it is discussed below. Then, the related molecular swelling and the lattice heating induces an internal pressure and generate a nonlinear wave, resulting in lattice expansion and crystal deformation at the material scale. Such pressure front induces an over-compressed region followed by a depression, which favours the LS → HS switching and leads to a second increase in the ΔX_HS in the ns time domain.⁸ In the third step, a third increase in the ΔX_HS in the μs time scale is triggered by the average temperature increase of the sample due to heat diffusion. Here, the temperature is homogeneous within the sample and the reciprocal lattice recovers its initial shape. Finally, an additional step comes from the recovery to thermal equilibrium with the sample environment (cryostat). This step is typically achieved in ms regime.

Fig. 6 Schematic representation of (a) the out-of-equilibrium process in SCO complexes, (b) the short-range distortion in FE4 and (c) long-range distortion in FE4. Green and red spheres represent LS and HS Fe^II ions, respectively. Half-red half-green spheres represents the transiting metal centre in two crystallographically identical sites.

The main difference between the out-of-equilibrium dynamics of mononuclear and oligonuclear SCO complexes is the appearance of a short-range elastic deformation during the photoinduced step in the latter material. Similar to the mononuclear complexes, the LS → HS photo-switching in metallogrids also occurs in less than 15 ps, as shown by the studies in solution.⁵¹ Nevertheless, in FE4, the iron ions are strongly linked and the reorganisation of the {FeN₆} coordination sphere of the transiting ion, concomitant to the spin flip, triggers a short-range elastic distortion that propagates through the whole grid as reported in our previous work³¹ (Fig. 6b). Here, such distortion is not only observed in the constant shift of electron density in the photodifference maps but also in the abrupt variation of the trigonal distortion of the Fe(B) ion and the continuous fluctuation of the Fe(A)–Fe(A) and Fe(B)–Fe(B) distances during the photoinduced step. However, since FE4 shows only bi-stability between the 2HS–2LS and the 3HS–1LS configuration,^27,31 it remains unknown if the short-range distortion can trigger intramolecular cooperativity in other oligonuclear complexes with multi-stability.

One of the questions left open in our previous study was the possible coupling during the elastic step between the short-range molecular distortion, created by the molecular rearrangement of strongly-linked metal ions, and the long-range lattice distortion, caused by the propagation of strain waves. In this work, we do not observe any coupling between both types of distortions. Once the lattice starts its anisotropic expansion, the long-range distortion prevails over the short-range one, causing all metallic ions to move in the direction of the propagating strain waves (Fig. 6c). Therefore, we conclude that the long-range elastic distortion is dominant during the elastic step and this persists until the thermal step takes place in the μs regime. However, the strong linking of metal ions has an important effect during the elastic step. The distortion of the lattice induces a significant change in the coordination environment of all metal ions, which is amplified by the large size of the molecule and the strong linking between metal ions, as observed by the largest variation of the trigonal distortion parameter of Fe(A) and Fe(B) and the significant change in the Fe–Fe distances at dt = 1 ns. This effect could be beneficial for other types of grids with multi-stability. Since the distortion of the coordination environment of the metal ion favours the HS state, the large distortion during the elastic step could trigger the transformation of more than one metal ion within the grid, i.e. intramolecular cooperativity. However, further studies are necessary to understand the effects of the elastic distortions in different types of oligonuclear SCO complexes.

Finally, the heating of the lattice by the laser flash, associated with an increase of the Debye–Waller factor, is accompanied by the thermal population of the HS state, which occurs on the μs time scale. Although a variation of ΔB^ON–OFF has been detected since the beginning of the elastic step, the photodifference maps and the variation of 〈Fe(A)–N〉 suggest that the long-range elastic deformation prevails over any temperature change. Therefore, it is only in the μs time scale when the temperature increase predominates over the distortion, leading to a molecular arrangement comparable to that obtained at equilibrium conditions.

It is useful to note that in our previous work,³¹ we observed the structural changes in the FE4 grid during the first 5 ns after light irradiation. The structural response was observed mostly through photodifference maps with some support of a rough estimation of the structural changes and the variation of the HS fraction. The low temperature, 100 K, slowed down the thermal effects (elastic and thermal step) and helped to preserve the photo-switched molecules for up to 2 ns after light irradiation, compared with the approximately 700 ps of this work. However, the low number of time points taken and the low repetition per time point during the data collection didn't allow to determine with precision the beginning of the elastic and/or thermal steps. Therefore, the method during data collection of the current work was set to one crystal per dt with high repetition (5 laser-ON/OFF). This allows to calculate with greater precision the structural changes after laser irradiation and determine the three main steps of the out-of-equilibrium process.

It is also worth noting that the present study has been limited to a bi-stable [2 × 2] metallogrid, whose thermal transition from a 2HS–2LS to a 3HS–1LS configuration shows no cooperativity. Further investigations are necessary to determine the structural dynamics of other oligonuclear complexes with different geometries and that show multi-stability and cooperativity. A detailed analysis of the out-of-equilibrium dynamics of more complex SCO compounds, especially during the first two steps, would provide the key factors to design new SCO materials with tailored properties.

Conclusions

A prerequisite to successfully use materials with bi- or multi-stability is our understanding of the physical mechanism involved in the transformation induced by a short laser pulse. Therefore, out-of-equilibrium studies on solids have been performed for different Fe^II and Fe^III SCO complexes.^8–12 However, such studies have been limited to mononuclear complexes, despite the recent progress in the synthesis of several polymetallic and oligomeric SCO complexes. In this paper, we present the out-of-equilibrium dynamics of a [2 × 2] metallogrid triggered by a ps laser flash. The dynamics of the FE4 grid follow the same sequence observed for the mononuclear complexes, described by three consecutive steps (i.e. photoinduced, elastic and thermal steps) at characteristic time-scales (ps, ns, and μs, respectively). Contrary to the mononuclear materials, two types of elastic distortions take place at different steps of the process. During the photoinduced step, a short-range distortion appears from the continuous molecular rearrangement of the grid triggered by the LS → HS photo-switching of only one metal ion. The second is a long-range distortion, which corresponds to the anisotropic deformation of the lattice taking place during the elastic step. This distortion prevails over the first one, and it induces the largest change in the coordination environment of all metal ions. Although the results of this work reveal the structural dynamics of an oligonuclear Fe^II SCO complex, further research is needed to understand the effects of strongly linked metal ions in out-of-equilibrium processes, in particular, during the first two steps. The understanding of these effects is a key feature to establish the foundation of how to control the properties of SCO materials with bi- and multi-stability.

Author contributions

JJVG drafted the manuscript. JJVG, KB and DS performed the time-resolved crystallographic experiment with assistance from RH in beamline operation at APS. ST and FM conceived the study. FM and SD designed the molecules. JW synthesised the material. ST contributed to analysing and writing the manuscript. All authors provided input and agreed on the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research used resources of the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357. Use of BioCARS was also supported by the National Institute of General Medical Sciences of the National Institutes of Health under grant number P41 GM118217. Time-resolved set-up at Sector 14 was funded in part through a collaboration with Philip Anfinrud (NIH/NIDDK). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The current work has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 217133147/SFB 1073, projects B06, C02. HG-recruitment, HG-Innovation “ECRAPS”, HG-Innovation DSF/DASHH and CMWS. We are grateful for the support and suggestion of Vukica Šrajer on the use of PRECOGNITION and Bertrand Fournier on the use of LaueUtil.

References

1. P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054.
2. P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds I-III, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004.
3. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313.
4. A. Bousseksou, C. R. Chim, 2018, 21, 1055.
5. K. S. Murray, in Spin–Crossover Materials, John Wiley & Sons, Ltd, 2013, pp. 1–54.
6. P. Guionneau, Dalton Trans., 2014, 43, 382–393.
7. E. Collet and P. Guionneau, C. R. Chim., 2018, 21, 1133–1151.
8. E. Collet, N. Moisan, C. Baldé, R. Bertoni, E. Trzop, C. Laulhé, M. Lorenc, M. Servol, H. Cailleau, A. Tissot, M.-L. Boillot, T. Graber, R. Henning, P. Coppens and M. B.-L. Cointe, Phys. Chem. Chem. Phys., 2012, 14, 6192.
9. M. Lorenc, J. Hébert, N. Moisan, E. Trzop, M. Servol, M. Buron-Le Cointe, H. Cailleau, M. L. Boillot, E. Pontecorvo, M. Wulff, S. Koshihara and E. Collet, Phys. Rev. Lett., 2009, 103, 028301.
10. H. Cailleau, M. Lorenc, L. Guérin, M. Servol, E. Collet and M. Buron-Le Cointe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66, 189–197.
11. M. Lorenc, C. Balde, W. Kaszub, A. Tissot, N. Moisan, M. Servol, M. Buron-Le Cointe, H. Cailleau, P. Chasle, P. Czarnecki, M. L. Boillot and E. Collet, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054302.
12. R. Bertoni, M. Lorenc, H. Cailleau, A. Tissot, J. Laisney, M.-L. Boillot, L. Stoleriu, A. Stancu, C. Enachescu and E. Collet, Nat. Mater., 2016, 15, 606–610.
13. S. Techert, J. Appl. Crystallogr., 2004, 37, 445–450.
14. C. Enachescu, A. Hauser, J.-J. Girerd and M.-L. Boillot, ChemPhysChem, 2006, 7, 1127–1135.
15. O. Kahn and C. J. Martinez, Science, 1998, 279, 44–48.
16. P. J. van Koningsbruggen, Y. Garcia, O. Kahn, L. Fournès, H. Kooijman, A. L. Spek, J. G. Haasnoot, J. Moscovici, K. Provost, A. Michalowicz, F. Renz and P. Gütlich, Inorg. Chem., 2000, 39, 1891–1900.
17. J. Schweifer, P. Weinberger, K. Mereiter, M. Boca, C. Reichl, H. Kooijman, M. Grunert and W. Linert, Inorg. Chim. Acta, 2002, 10.
18. E. M. Zueva, E. R. Ryabikh and S. A. Borshch, Inorg. Chem., 2011, 50, 11143–11151.
19. T. Matsumoto, G. N. Newton, T. Shiga, S. Hayami, Y. Matsui, H. Okamoto, R. Kumai, Y. Murakami and H. Oshio, Nat. Commun., 2014, 5, 3865.
20. Y.-T. Wang, S.-T. Li, S.-Q. Wu, A.-L. Cui, D.-Z. Shen and H.-Z. Kou, J. Am. Chem. Soc., 2013, 135, 5942–5945.
21. B. Schäfer, J.-F. Greisch, I. Faus, T. Bodenstein, I. Šalitroš, O. Fuhr, K. Fink, V. Schünemann, M. M. Kappes and M. Ruben, Angew. Chem., Int. Ed., 2016, 55, 10881–10885.
22. E. Breuning, M. Ruben, J.-M. Lehn, F. Renz, Y. Garcia, V. Ksenofontov, P. Gütlich, E. Wegelius and K. Rissanen, Angew. Chem., Int. Ed., 2000, 39, 2504–2507.
23. D. Wu, O. Sato, Y. Einaga and C. Duan, Angew. Chem., 2009, 121, 1503–1506.
24. M. Ruben, J. Rojo, F. J. Romero-Salguero, L. H. Uppadine and J.-M. Lehn, Angew. Chem., Int. Ed., 2004, 43, 3644–3662.
25. M. Ruben, E. Breuning, J.-M. Lehn, V. Ksenofontov, F. Renz, P. Gütlich and G. B. M. Vaughan, Chem. – Eur. J., 2003, 9, 4422–4429.
26. B. Schneider, S. Demeshko, S. Dechert and F. Meyer, Angew. Chem., Int. Ed., 2010, 49, 9274–9277.
27. B. Schneider, S. Demeshko, S. Neudeck, S. Dechert and F. Meyer, Inorg. Chem., 2013, 52, 13230–13237.
28. M. Steinert, B. Schneider, S. Dechert, S. Demeshko and F. Meyer, Inorg. Chem., 2016, 55, 2363–2373.
29. S. A. Borshch and E. M. Zueva, Eur. J. Inorg. Chem., 2013, 2013, 1009–1014.
30. I. Šalitroš, R. Herchel, O. Fuhr, R. González-Prieto and M. Ruben, Inorg. Chem., 2019, 58, 4310–4319.
31. J. de J. Velazquez-Garcia, K. Basuroy, D. Storozhuk, J. Wong, S. Demeshko, F. Meyer, R. Henning and S. Techert, Dalton Trans., 2022, 51, 6036–6045.
32. J. Z. Ren, Precognition User Guide with Reference and Tutorials, Renz Research, Inc., Westmont, IL, U.S.A., 2006.
33. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
34. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
35. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
36. J. A. Kalinowski, A. Makal and P. Coppens, J. Appl. Crystallogr., 2011, 44, 1182–1189.
37. J. A. Kalinowski, B. Fournier, A. Makal and P. Coppens, J. Synchrotron Radiat., 2012, 19, 637–646.
38. J. J. Velazquez-Garcia, J. Wong, K. Basuroy, D. Storozhuk, S. Saouane, R. Henning and S. Techert, arXiv, 2020,  DOI:10.48550/arXiv.2010.05781.
39. R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. Harding, Dalton Trans., 2021, 50, 1086–1096.
40. M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119.
41. S. Alvarez, J. Am. Chem. Soc., 2003, 125, 6795–6802.
42. R. T. Acha and M. Pilkington, CrystEngComm, 2015, 17, 8897–8905.
43. C. Boilleau, N. Suaud and N. Guihéry, J. Chem. Phys., 2012, 137, 224304.
44. M. S. Schmøkel, R. Kamiński, J. B. Benedict and P. Coppens, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66, 632–636.
45. I. I. Vorontsov and P. Coppens, J. Synchrotron Radiat., 2005, 12, 488–493.
46. M. D. Carducci, M. R. Pressprich and P. Coppens, J. Am. Chem. Soc., 1997, 119, 2669–2678.
47. S. Techert, F. Schotte and M. Wulff, Phys. Rev. Lett., 2001, 86, 2030–2033.
48. J. Hallmann, W. Morgenroth, C. Paulmann, J. Davaasambuu, Q. Kong, M. Wulff and S. Techert, J. Am. Chem. Soc., 2009, 131, 15018–15025.
49. C. D. Kim, S. Pillet, G. Wu, W. K. Fullagar and P. Coppens, Acta Crystallogr., Sect. A: Found. Crystallogr., 2002, 58, 133–137.
50. M. Messerschmidt, T. Tschentscher, M. Cammarata, A. Meents, C. Sager, J. Davaasambuu, G. Busse and S. Techert, J. Phys. Chem. A, 2010, 114, 7677–7681.
51. M. A. Naumova, A. Kalinko, J. W. L. Wong, S. Alvarez Gutierrez, J. Meng, M. Liang, M. Abdellah, H. Geng, W. Lin, K. Kubicek, M. Biednov, F. Lima, A. Galler, P. Zalden, S. Checchia, P.-A. Mante, J. Zimara, D. Schwarzer, S. Demeshko, V. Murzin, D. Gosztola, M. Jarenmark, J. Zhang, M. Bauer, M. L. Lawson Daku, D. Khakhulin, W. Gawelda, C. Bressler, F. Meyer, K. Zheng and S. E. Canton, J. Chem. Phys., 2020, 152, 214301.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2195543–2195550, 2195552–2195555 and 2195574–2195582. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt02638d

---