Synthesis and reactivity of dinuclear copper(I) pyridine diimine complexes

Abstract

The reaction of a tethered pyridine diimine (PDI) ligand with copper(I) chloride yielded a μ-chlorido bridged cationic dicopper(I) PDI complex, which is a rare structural motif. The geometric constraint of the ligand is fostering attractive van der Waals interactions between the coplanar pyridine units. This is supported by an Atoms in Molecules (AIM) and NCI (non-covalent interaction) analysis. Reaction with carbon monoxide yields the corresponding mono- and dicarbonyl complexes, which display reversible binding of carbon monoxide. This equilibrium was studied by ¹³C-NMR exchange spectroscopy and complemented by DFT and LNO-CCSD(T) calculations.

---

Introduction

Copper carbonyl complexes were first observed and characterized in the middle of the 18^th century. One of the first reports describes the carbon monoxide (CO) uptake of an aqueous solution containing a strong protic acid and copper(I) chloride.¹ Nevertheless, isolation of copper(I) carbonyl compounds as pure solids without a CO atmosphere was achieved around 100 years later, due to the weak bonding of CO to copper(I).²

The classical binding of CO to transition metal compromises of three contributions: σ donation from CO by its HOMO, π acceptance (π back-bonding) and the often-neglected π donation. For copper(I), a closed shell d¹⁰ system, the 3d-shell is full and the 4p-orbitals are energetically too high for a strong σ or π donation from the ligand. Lastly, π acceptance of CO could be possible, but the 3d orbital energies are too low for strong π back-bonding. Therefore, carbon monoxide is often weakly and reversibly bonded to the copper(I) center.³ Despite these energetic drawbacks, ligand systems and the analogous copper(I) carbonyl complexes were synthesized and isolated as stable products since the 1980s. One of the first complexes were Cu(CF₃CO₂)CO and [HB(Pz)₃]CuCO, which were stable in the absence of a CO atmosphere.^2,4,5

Since these first advances, the number of investigated copper carbonyl species has grown significantly, featuring a wide range of ligands, which are suitable for the stabilization of copper carbonyl units.^3,6,7 Besides tris(pyrazolyl)borate and pyridylalkylamine ligands, pyridine diimine ligands are suitable to form copper(I) carbonyl complexes.^6,8,9 Pyridine diimine ligands feature a good modularity with regard to the electronic structure and the steric hinderance around the metal center. Another feature of PDI ligands is their non-innocence due to low lying π* orbitals.^10–13 In fact, a structure of a copper(I) carbonyl PDI complex was reported in 2016 by Gilbertson et al. featuring a rare square-planar coordination sphere for a copper(I) center. In the latter complex the ligand substitution of acetonitrile and CO is immediate and reversible.⁶ Another approach to achieve stabilization of the Cu(I)–CO bond in a PDI manifold was realized with a dinuclear concept in a Cu₂(μ²-C,C CO) binding motif.^14–16

In the literature a wide range of dicopper(I) complexes with short copper-copper distances and similar coordination spheres are reported.^17–20 Often, these dicopper(I) compounds exhibit cuprophilic interactions, which are strongly dependent on the coordination sphere of the single copper centers and the copper-copper distance.²¹ Cuprophilic interactions were long discussed and often considered negligible compared to the heavier elements like silver or gold.^22–24 The occurrence of cuprophilic interactions were suggested by short copper-copper distances between 2.4 and 2.8 Å, but were later observed by spectroscopic studies.^25,26 A few dicopper(I) bridging CO complexes are reported and show Cu–Cu distances between 2.417(2) Å and 2.422(1) Å.^14–16 Here, it should be emphasized that the sum of the van der Waals radii (2.80 Å) and even the Cu–Cu distance in bulk copper (2.556 Å) are longer than the reported distances in the dicopper(I) μ-C,C carbonyls.²¹ These short distances indicate a cuprophilic interaction between the copper(I) centers.

Herein, we report the synthesis of a new PDI ligand with two binding manifolds based on a previously established ligand synthesis route by us.²⁷ Additionally, the synthesis of a cationic dicopper(I) complex with a small dichloridocuprate(I) and a large anion tetrakis(3,5-bis-(trifluoromethyl)-phenyl)borate ([BAr^F₄]⁻) is described. Furthermore, the reactivity of the cationic dicopper(I) complex towards CO is investigated.

Results and discussion

Preparation and properties

The naphthyl bridged pyridine diimine ligand 2 was synthesized by the condensation of neo-pentylamine with the ketone precursor 1 in 74% yield (Scheme 1).²⁷ Due to the neo-pentyl substituents ligand 2 displays a good solubility in aliphatic solvents, e.g. n-pentane and n-hexane. The ¹H-NMR spectrum of 2 at room temperature (RT) reveals a time averaged C_2v-symmetrical spectrum with the expected A₂B₂-spin system for the diastereotopic methylene protons of the neo-pentyl substituent, resulting in a pseudo-quartett. Crystallization from n-hexane afforded pale yellow crystals suitable for single crystal X-ray diffraction. In the solid state a C₂-symmetrical structure of 2 is observed with an E, E′, E′′ and E′′′ arrangement regarding the largest substituents (see ESI†).

Scheme 1 Synthetic route to complex 4. (a) para-toluenesulfonic acid, neo-pentylamine, 15 h, reflux, benzene, 74%; (b) CuCl, 15 h, RT, DCM, 71%; (c) Na[BAr^F₄], 15 h, RT, benzene, 86%.

From the reaction of the PDI ligand 2 with 3 equivalents of copper(I)-chloride in dichloromethane (DCM) the analytically pure cationic dicopper(I) complex 3 was obtained in 71% yield. It should be noted that complex 3 is also exclusively formed, despite in lower yield, when only 2 equivalents CuCl were employed. The solubility of 3 in polar solvents (nitromethane, dimethylformamide, acetone) is very good and reduced in less polar solvents, e.g. DCM, tetrahydrofuran (THF). To increase the solubility of this complex further for intended low temperature studies and to remove ambiguities due to competing reactions of the [CuCl₂]⁻ cuprate counterion, we performed an anion exchange with the [BAr^F₄]⁻ anion. Classical salt metathesis reaction of complex 3 with one equivalent of Na[BAr^F₄] in benzene allowed complete exchange of the dichloridocuprate(I) counter ion to yield compound 4 with the bulkier [BAr^F₄]⁻ anion. As expected, complex 4 displays a significantly higher solubility in apolar solvents, e.g. benzene or toluene.

The ¹H-NMR spectra of 3 and 4 at RT display sharp resonances indicating diamagnetic complexes. For both 3 and 4, singlets were observed for the methyl substituents of the ketimine groups, the tert-butyl group and the pyridine protons (see ESI†). Together with the A₂B₂M₂ pattern for the protons of the naphthalene backbone and an A₂B₂ spin system for the diastereotopic methylene protons of the neo-pentyl group this suggested a C_2v-symmetrical structure at RT (cf. below for variable temperature (vT) behaviour).

For complex 3 reddish crystals suitable for single crystal diffraction were obtained by layering a saturated tetrahydrofuran solution with n-hexane at room temperature and for compound 4 by recrystallization from benzene. Both complex 3 and 4 crystallize in the triclinic space group P1̄. The unit cell of compound 3 contains two independent cationic complexes and two dichloridocuprate(I) counterions as well as two co-crystallized tetrahydrofuran molecules, while 4 crystallizes with one cationic complex fragment, one anionic [BAr^F₄]⁻ and 4 co-crystallized benzene molecules.

The cationic complexes display μ-chlorido-bridged copper(I) ions chelated by the corresponding PDI ligand manifolds with essentially identical bonding parameters for the latter (Fig. 1, Table 1 and ESI†). The cationic complexes display idealized C₂-symmetry deviating from the suggested C_2v-symmetrical structure based on the NMR data in solution and will be discussed below. It should be noted that the observed [Cu₂Cl]⁺ fragment stabilized by six nitrogen donor ligands is a rare structural motif.^28–30

Fig. 1 Molecular structure of the cationic complex 3 with anisotropic displacement parameters shown at the 50% probability level. Hydrogen atoms, the anion dichloridocuprate(I) and solvent molecules are omitted for clarity. The neo-pentyl moieties are displayed as sticks for a better overview.

Table 1 Important averaged bond lengths (Å) and angle (deg) with esd's in parentheses for the PDI ligand 2 and the copper complexes 3, 4

	2	3	4
Cu–Cu	—	2.705(7)	2.8347(7)
Cu–Cl	—	2.224(5)	2.223(7)
Cu–Npy	—	2.006(1)	1.995(8)
Cu–Nim	—	2.238(21)	2.268(69)
Nim–Cim	1.270(4)	1.279(3)	1.279(3)
Cim–Cpy	1.498(4)	1.502(4)	1.500(2)
Cpy–Npy	1.341(3)	1.335(4)	1.341(1)
∠Cu–Cl–Cu	—	74.9(3)	79.20(3)
Δ	0.192	0.194	0.189

---

The (potential) non-innocence of PDI ligands is well-established in the literature and the C_imine–N_imine and C_imine–C_pyridine bond distances are indicators for its oxidation state. These bond lengths can be combined into a single parameter Δ, which gives a numeric expression for the electron density being held by the ligand.¹³ The averaged values Δ = 0.194 and 0.189 Å (Δ = 0.192 Å in the free ligand 2) for complex 3 and 4, respectively, reflects the innocence of the PDI ligands (Table 1) and hence Cu(I) oxidation states for this diamagnetic complex.

The chlorido ligand is located on an idealized C₂-axis and thus bridges the two Cu centers symmetrically. The Cu–Cl bond distances 2.224 Å are in the expected range for a μ-chlorido copper(I) unit.^28,29,31 Neglecting Cu–Cu interactions, the copper centers are four-coordinate, displaying a disphenoidal structure with N_pyridine–Cu–Cl angles in the range of 147–158°. The averaged distances between the two copper centers in complex 3 of 2.705(7) Å are rather short and lie slightly below the sum of the van der Waals radii of 2.80 Å.³² Such short distances between copper centers are an indicator for possible cuprophilic interactions.²¹ For compound 4 with the [BAr^F₄]⁻ anion, the Cu–Cu distance is notably longer (0.13 Å), which is accompanied by an increase of the angle of the μ-chlorido Cu–Cl–Cu unit by 4.3°. Both anions display no direct bonding to the Cu centers based on inspection of the crystal packing (distances). In order to address whether this lengthening effect can be attributed to the (i) anion, (ii) packing effects or (iii) the co-crystallized solvent molecules, complex 3 was additionally crystallized by layering a saturated DCM solution with n-hexane. In dichloromethane 3 crystallizes in the monoclinic space group P2₁/n with two cationic independent complex fragments, two dichloridocuprate(I) anions and two DCM molecules. Remarkably, the Cu–Cu distance remains essentially unchanged and displays only negligible shortening by 0.01 Å to 2.6918(9) Å. While this observation does not allow to rule out items (ii) and (iii) it implies that the anion might have an influence on the Cu–Cu distance.

In the course of our investigations, we noted the temperature dependence of the ¹H-NMR spectra of 3, indicated by the splitting of the homo- and enantiotopic tert-butyl, ketimine and the aromatic pyridine ¹H-NMR signals upon lowering of the temperature. This behaviour was consistent with lowering of the time-averaged C_2v-symmetry at RT to a C₂-symmetrical structure in the slow exchange regime at −80 °C as observed in the solid state. For this dynamic process a barrier of 9 kcal mol⁻¹ was estimated from the coalescence temperature at −70 °C for the ketimine protons. From a line shape analysis of the ¹H-NMR spectra in CD₂Cl₂ between −40 °C and −80 °C the temperature dependent rate constants were derived (see ESI†). From the linear Eyring plot, the activation parameters ΔH^‡ = 9.6 ± 1 kcal mol⁻¹ and ΔS^‡ = 3.2 ± 0.3 cal mol⁻¹ K⁻¹ were obtained. In agreement with this analysis a low barrier of E_A = 4 kcal mol⁻¹ was derived for this process in density functional theory (DFT) calculations. The C_2v-symmetrical transition state is shown in Fig. 2. In contrast to these results temperature independent ¹H-NMR spectra were observed for the dicopper complex 4 with the [BAr^F₄]⁻ anion; even at −80 °C these signals were consistent with a time-averaged C_2v-symmetrical structure (see ESI†).

Fig. 2 Calculated C_2v-symmetrical transition state with displacement vectors of the cationic copper(I) model complex with methyl rather than neo-pentyl substituents.

We suspected that the apparent differences in the NMR spectra of 3 and 4 were due to the type of ion pairing, i.e. solvent separated ion pairing with the weakly coordinating [BAr^F₄]⁻ anion in 4 and contact or tight ion pairing in 3. We have therefore turned to conductivity measurements of a dilution series of complex 3 and 4 between 10⁻³ and 10⁻⁶ mol L⁻¹ in dichloromethane (Fig. 3).

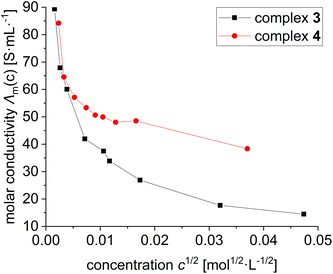Fig. 3 Conductivity measurements in DCM at RT with different concentrations of complex 3 und 4. The molar conductivity was plotted against the square root of the concentration.

Inspection of Fig. 3 reveals that the molar conductivities for both complex 3 and 4 do not display a linear dependence on the square root of the concentrations, which would be expected for 1 : 1 electrolytes. They can be rather described as weak electrolytes, with complex 4 displaying a substantially higher molar conductivity than 3. This difference is caused by stronger dissociation to solvent separated ion pairs in 4 with the larger weekly coordinating [BAr^F₄]⁻ anions. For complex 3 the molar conductivity is interpreted in terms of tight respectively contact ion pairs. At low temperatures this ion pair may lock in the cationic complex 3 into its C₂-symmetrical structure.

To get more insight into a possible interaction of the copper(I) centers, DFT calculations were performed. The derived Wiberg and Fuzzy Cu–Cu bond orders are sizable (0.31 and 0.36), while the Mayer bond order is small (0.11). Consistent with a weak interaction, the local force analysis for the two Cu centers derived with the LMODEA^33–35 program package revealed a local force constant close to zero (0.224 mDyn Å⁻¹). DFT relaxed potential energy scans were performed for the dependence on the Cu–Cu distance. The results display a very flat potential along the Cu–Cu axis (Fig. 4). Within an energy difference from about 1 kcal mol⁻¹ the Cu–Cu distance varies between 0.35 Å and 0.40 Å depending on the density functional.

Fig. 4 Calculated relaxed potential energy scan for the cationic complex fragment with different DFT functionals. Grimme's D3 dispersion correction with Becke–Johnson damping (D3-BJ) was employed for the PBE, PBE0 and CAM-B3LYP functionals.

An AIM analysis revealed no bond critical point (BCP) between the copper(I) centers. We observed 3 BCPs between carbon atoms of the two adjacent pyridine units (Fig. 5), however. The small corresponding electron densities (ρ: 0.0066–0.012 au) and small positive values for the Laplacian of electron density, ∇²ρ (0.023–0.043 au) are indicative of weak attractive van der Waals interactions. This is readily explained by the short distance between the nearly coplanar pyridine rings of 3.25 Å, which is in the range of the interlayer value of 3.35 Å in graphite. As detailed above, the rings in the C₂-symmetrical structure are slightly parallel displaced, while they ought to be eclipsed in C_2v-symmetry.³⁶

Fig. 5 Bond critical points between carbon atoms of the adjacent pyridine units. C_para: ρ = 0.0127 eA⁻³, ∇²ρ = 0.0427 eA⁻⁵; C_ortho: ρ = 0.0067 eA⁻³, ∇²ρ = 0.0217 eA⁻⁵.

Further support for an attractive interaction between the two PDI units was provided by a NCI plot of complex 3. These plots show regions of weak dispersive and attractive interactions. The color code ranges from blue (most stabilizing) through green (weakly stabilizing) to red (most destabilizing). For simplicity, we replaced the neo-pentyl groups by methyl substituents, which seems to be granted since all four tert-butyl groups point to the outside of the molecule. Inspection of the NCI plot shown in Fig. 6 reveals weakly attractive forces between the PDI manifolds (green isosurface). The cyan colored isosurface between the two copper centers indicates a more stabilizing attractive interaction, which was not revealed in the aforementioned AIM analysis. These results point towards an attractive van der Waals interaction between the two molecule halves.

Fig. 6 NCI plot for the cationic methyl substituted model complex viewed along the Cu1b–Cu1a axis.

Reaction with carbon monoxide

Exposing the dark green DCM solution of 3 with an excess of carbon monoxide leads to a reddish solution. The UV/vis spectrum displayed a hypsochromic shift from 482 nm to 455 nm with concomitant sharpening and decrease of the absorption band (see ESI†). In situ IR reaction observation revealed a CO stretching band at 2098 cm⁻¹ indicating an end-on copper(I) carbon monoxide complex with a small amount of π back-bonding.^3,6 Upon purging with dinitrogen the color changed back to dark green; the carbon monoxide IR band disappeared (Fig. 7) and the μ-chlorido complex 3 was reinstalled.

Fig. 7 In situ IR absorption spectra for the reversible reaction of the dicopper(I) complex 3 with CO.

To rule that the [Cu₂Cl]⁻ counter ion is involved in this process, the reaction was also carried with complex 4. In this experiment the same stretching band at 2098 cm⁻¹ and reversibility for CO binding was observed (see ESI†). In the course of these investigations, we discovered that the color of the CO adduct slightly changes and reversibly upon lowering of the temperature. Thus, under a CO atmosphere the dark reddish solution at RT changes to pale-yellow at −95 °C, which is confirmed by an UV/vis dip probe measurement revealing a hypsochromic shift from 455 to 411 nm.

To gain further insight into this behaviour, we investigated the vT dependence of the IR- and NMR-spectroscopic properties of the copper(I) carbon monoxide system. Interestingly, no change was observed in the IR spectra upon lowering the temperature to −95 °C (see ESI†). As will be discussed later, this can be explained by DFT calculations, which evidenced negligible differences of the ν(CO) IR bands (<4 cm⁻¹) for the anticipated mono- and dicarbonyl species shown in Scheme 2. By contrast, the ¹³C-NMR spectra of the reaction mixture of 3 with excess ¹³C labeled carbon monoxide revealed a temperature dependence. At RT, the ¹³C-NMR spectrum of a mixture of complex 3 with ca. 22 equivalents ¹³CO in CD₂Cl₂ displayed a broad resonance at 174.8 ppm suggesting CO coordination to the copper center. It should be noted that no signal was observed at the anticipated chemical shift at δ = 184.1 ppm for free ¹³CO. The resonance at 174.8 ppm is in good agreement with values for d¹⁰-configured end-on copper carbonyl complexes, which fall in the range of 168.4 to 171.1 ppm.^37,38 It deserves a special notion that the vT ¹H-NMR spectrum remained essentially unchanged consistent with a time averaged C_2v-symmetrical structure (see ESI†). Lowering the temperature of the sample to −80 °C results in a high-field shift with intermittent broadening and eventual splitting into two signals at 171.0 and 169.1 ppm (Fig. 8).

Scheme 2 Reversible CO binding in complex 3 (left, blue) with an analogous colour code to Fig. 10.

Fig. 8 vT ¹³C-NMR spectra of complex 3 with 22 equivalents of ¹³CO at temperatures between 20 °C and −80 °C.

The signal pattern together with an apparent coalescence at ca. −50 °C suggested an exchange process. We have therefore recorded a ¹³C exchange spectroscopy (EXSY) spectrum and a ¹³C spin saturations transfer NMR experiment at −80 °C, which clearly supported exchange of the CO signals on the NMR time scale (see ESI†). We considered dissociation of the bridging μ-chlorido ligand upon coordination of the CO ligand to yield a dicationic complex with two square-planar PDI copper(I) carbonyl units. This would lead to a change from a 1 : 1 to a 1 : 2 electrolyte, causing a significant increase of the molar conductivity. However, the molar conductivity remained essentially unchanged, when the reaction of 3 with excess of CO was monitored at RT, thus ruling out dissociation of the chlorido ligand. We therefore propose that the dynamic process is based on the exchange equilibrium between the monocarbonyl and dicarbonyl complex (Scheme 2).

Support for this proposal was provided through the DFT calculated ¹³C-NMR chemical shifts for the monocarbonyl species at δ = 167.2 ppm and the C₂-symmetrical dicarbonyl complex (δ = 168.2 ppm.) A vibrational analysis revealed only a neglible differrence of 4 cm⁻¹ for the δ(CO) bands of the mono- (2098 cm⁻¹) and dicarbonyl complexes (2091 and 2095 cm⁻¹) thus providing an explanation for the temperature independence of the IR-spectra. Furthermore, LNO-CCSD(T) calculations for model complexes with methyl rather than neopentyl substituents revealed low binding energies of 15.3 and 17.2 kcal mol⁻¹ for the first and second carbonyl ligand, which is fully consistent with reversible CO binding.

According to DFT calculations the distance between the two Cu centers increases and the angle at the bridging chlorido ligand opens up, upon coordination of CO (Fig. 9).

Fig. 9 Geometry changes upon CO coordination (values in Å and °), without (left) one (middle) and two carbonyl (right) ligands.

The observed shifts of the transitions in the UV/vis spectra could be reproduced in MRCI-DFT calculations, which are visualized in Fig. 10. Thus, the lowest energy transition of the dicarbonyl complex is both hypso- and hypochromic explaining the observed color change from red to colorless in going from the mono- to the dicarbonyl complex. The calculated UV/vis spectrum is also in agreement with the chlorido complex 3. Since several transitions contribute to the calculated spectra in these complexes, we refrain from a discussion of the individual transitions (cf. ESI†).

Fig. 10 Simulated UV/vis spectra with Gaussian broadening (0.16 eV) based of the MRCI-DFT calculated transitions.

Conclusions

The readily available dinucleating PDI ligand 2 provides access to cationic dinuclear copper complex, which are symetrically bridged by a μ-chlorido ligand. The complexes display short Cu(I) centers contacts below the van der Waals distances, which are dependent on the counterion. AIM and NCI analysis reveal attractive van der Waals interactions between the two molecule halves; the PDI ligands are nearly coplanar with a distance of 3.25 Å, which is fostered by the naphthyl linker between the two PDI units. Upon reaction with CO an exchange equilibrium between the mono- and dicarbonyl complexes with intact μ-chlorido bridge is established with a concomitant temperature dependence of the color.

Experimental section

General considerations

Unless otherwise specified all preparations of the complexes were performed under an inert atmosphere of nitrogen in a MBraun glovebox. THF and benzene were distilled before use from sodium/benzophenone ketyl. Absolute dichloromethane, hexane and toluene were taken from a MBraun solvent purification system. Deuterated THF was dried over sodium benzophenone ketyl and deuterated dichloromethane was dried over calcium hydride and stored under nitrogen. The ligand precursor 1 ²⁷ and Na[BAr^F₄]³⁹ were synthesized following published procedures. All other chemicals were purchased from commercial sources and used as received.

Instrumentation

The NMR spectra were recorded using Bruker Fourier 300 MHz, Bruker AVANCE 400 MHz, Bruker AVANCE I 400 MHz, Bruker DRX 500 or Bruker AVANCE III 600 MHz NMR spectrometers. ¹H- and ¹³C-NMR chemical shifts are reported in parts per million (ppm). Abbreviations used in the description of the NMR data are as follows: br, broad; p, pseudo; s, singlet; d, doublet; t, triplet; q, quartet; and m, multiplet. UV/Vis spectra were measured with an Avantes AvaSpec-ULS2048L StarLine, an Avantes AvaLight Hal-S as light source and a StellarNet DP400 dip probe with 4 mm path length. In situ IR spectra were recorded with a Mettler Toledo reactIR 15 and a DST Series 6.3 mm AgX Fiber Conduit. MALDI mass spectra were recorded on a MALDI TOF/TOF Bruker UltrafleXtreme SmartBeam II Laser system using an anthracene matrix. Elemental analyses were performed using Elementar Vario ELIII or EuroVector/Hecatech EuroEA elemental analysers. X-ray data were collected radiation at 100 K on a Bruker AXS SMART APEX II diffractometer with Mo Kα and a SuperNova Oxford diffractometer with Mo Kα or Cu Kα radiation.

Computations

DFT calculations were carried out with versions 7.5 and 7.6 of the parallelized Turbomole program package.⁴⁰ All-electron def2-TZVPP basis sets were employed for all atoms, the RI-DFT method was used with the corresponding RIJ-auxiliary basis. Where applicable Grimme's D3 van der Waals corrections with Becke–Johnson (BJ) damping was employed, for Head-Gordon's WB97X-V DFT functional this is contained in density based dispersion corrections by Voorhis VV10 non-local van der Waals functional. Solvation effects were included within the COSMO formalism using a dielectric constant of ε = 9.0. The geometries were fully optimized without geometry or symmetry constraints; for the chlorido and dicarbonyl complexes the C₂-symmetrical structures corresponded nevertheless to the energetic minima. Minima were confirmed by the absence of imaginary frequencies in the calculations of the analytic second derivatives, for the transition state only one imaginary frequency was observed. The coordinates of the optimized geometries are tabulated in the ESI.† For the energetic dependence on the Cu–Cu distances relaxed PES were carried out.

Local natural orbital LNO-CCSD(T) calculations were carried out with the freely available MRCC (2020) program package (https://www.mrcc.hu/) using the default thresholds (lcorthr = normal).⁴¹ Geometries optimized at the PBE-D3BJ/def2-TZVPP/Cosmo(ε = 9.0) level were employed with def2-TZVPP basis sets in combination with complementary def2-QZVPP/C auxiliary correlation basis sets. The solvation correction was obtained from the energy differences of two single point calculations at the PBE-D3BJ(COSMO(ε = 9.0)/def2-TZVPP) and PBE-D3BJ/def2-TZVPP (gas phase) level. Back corrections for the LNO-CCSD(T) energies to free enthalpies (ΔG₂₉₈) were carried out with thermochemical data obtained from the DFT calculations at the PBE-D3BJ/def2-TZVPP level. ¹³C-NMR chemical shifts, δ(¹³CO), were calculated with the PBE-D3BJ DFT functional and def2-TZVP basis sets for all atoms and were referenced to the values derived for SiMe₄ obtained at the same level according to δ(¹³CO) = σ(Si(¹³CH₃)₄)_calc − σ(¹³CO)_calc.

The QTAIM calculations were performed with the MultiWfn (ver. 3.8) program package (https://sobereva.com/multiwfn/),⁴² plots were generated with the Chimera program package (https://www.cgl.ucsf.edu/chimera/). The NCI calculations were carried out with IGMPLOT ver. 2.6.9 (https://igmplot.univ-reims.fr/index.php using the wavefunction based method (QM mode).⁴³ The required wfx file was obtained from a Turbomole generated Molden file and subsequent conversion by Molden2aim (https://github.com/zorkzou/Molden2AIM). NCIPlots were obtained with VMD (https://www.ks.uiuc.edu/Research/vmd/) with input files generated by IGMPLOT's vmdpath script.

MRCI-DFT calculcations were performed with the parallelized DFT/MRCI program package, which was gratefully provided by the Marian group.⁴⁴ The Becke half-and-half Kohn–Sham references were calculated with the Orca 5.03 program package.^45,46 For the MRCI-DFT calculations the latest Hamiltonian (R2018) was employed. For the initial referecence space all singlet and doublet excitations of 10 electron of the highest lying 5 occupied orbitals into the lowest lying 7 empty orbitals were calculated. From this calculation an improved reference space was obtained, which was employed for a successive MRCI-DFT run.

Synthesis and characterization

Ligand 2. Neo-pentylamine (5.50 mL, 4.10 g, 47.0 mmol), the ligand precursor 1 (2.30 g, 5.11 mmol) and catalytic amounts of para-toluenesulfonic acid were suspended in 125 mL benzene. In a Dean-Stark apparatus the mixture was heated to reflux for 15 h. The solvent was removed and the residue was dissolved in 100 mL dichloromethane. The organic layer was washed three times with a 0.5 molar potassium carbonate solution and two times with demineralized water. The organic layer was dried over magnesium sulphate and the solvent was removed. Recrystallisation from n-hexane afforded pale yellow crystals (2.73 g, 3.76 mmol, 74%) after 7 days at −35 °C. ¹H-NMR: (300 MHz, CDCl₃): δ [ppm] = 8.04 (dd, ³J = 8.3 Hz, ⁴J = 1.4 Hz, 2H), 7.68 (s, 4H), 7.63 (dd, ³J = 8.3 Hz, ³J = 7.1 Hz, 2H), 7.51 (dd, ³J = 7.1 Hz, ⁴J = 1.4 Hz, 2H), 3.11 (pq, 8H), 2.22 (s, 12H), 0.95 (s, 36H). ¹³C-NMR: (75 MHz, CDCl₃): δ [ppm] = 165.1 (4C), 155.5 (4C), 150.9 (2C), 138.3 (2C), 135.4 (1C), 131.2 (2C), 129.8 (2C), 128.8 (1C), 125.6 (2C), 122.0 (4C), 64.3 (4C), 32.6 (4C), 28.2 (12C), 12.8 (4C). MALDI-MS: m/z = 727.5 [C₄₈H₆₆N₆ − H]⁺. Elemental analysis: calcd (found) for C₄₈H₆₆N₆: C 79.29 (79.10), H 9.15 (9.35), N 11.56 (11.43).

Complex 3. Ligand 2 (313 mg, 413 μmol) and copper(I) chloride (138 mg, 1.39 mmol) were suspended in 10 mL dichloromethane. The suspension was stirred for 15 h at room temperature. The dark green reaction mixture was filtered and the solvent was evaporated. The residue was dissolved in 5 mL dichloromethane and was layered with 15 mL n-hexane. After 3 days at room temperature, dark needles (300 mg, 293 μmol, 71%) were obtained. ¹H-NMR: (600 MHz, CD₂Cl₂): δ [ppm] = 8.22 (d, ³J = 7.9 Hz, 2H), 7.78 (m, 4H), 7.70 (s, 4H), 3.62 (pq, 8H), 2.33 (s, 12H), 1.07 (s, 36H). ¹³C-NMR: (151 MHz, CD₂Cl₂): δ [ppm] = 166.5 (4C), 153.6 (2C), 152.9 (4C), 136.2 (1C), 135.4 (2C), 133.4 (2C), 131.9 (2C), 128.2 (1C), 126.9 (2C), 125.5 (4C), 65.3 (4C), 34.2 (4C), 28.9 (12C), 16.6 (4C). MALDI-MS: m/z = 889.3 [C₄₈H₆₆N₆ClCu₂]⁺. Elemental analysis: calcd (found) C₄₈H₆₆Cl₃Cu₃N₆: C 56.30 (55.85), H 6.50 (6.41), N 8.21 (8.12).

Complex 4. Complex 3 (151 mg, 147 μmol) and sodium (tetrakis(3,5-bis(trifluoromethyl)-phenyl)borate (136 mg, 153 μmol) were suspended in toluene. The suspension was stirred for 15 h at room temperature. The reaction mixture was filtered and the solvent was evaporated. The residue was dissolved in benzene and cooled to 0 °C to afford dark crystals (222 mg, 127 μmol, 86%) after 15 h. ¹H-NMR: (300 MHz, THF-d₈): δ [ppm] = 8.25 (dd, ³J = 8.1 Hz, ⁴J = 1.7 Hz, 2H), 7.81 (s, 4H), 7.75 (m, 12H), 7.53 (bs, 4H), 3.62 (pq, 8H), 2.33 (s, 12H), 1.01 (s, 36H). ¹³C-NMR: (75 MHz, THF-d₈): δ [ppm] = 165.1 (4C), 163.0 (4C), 155.4 (2C), 151.7 (2C), 136.9 (1C), 136.7 (2C), 135.8 (8C), 132.3 (2C), 131.9 (2C), 130.2 (8C), 127.5 (1C), 126.6 (4C), 123.9 (8C), 118.3 (4C), 64.5 (4C), 34.8 (4C), 28.9 (12C), 15.1 (4C). MALDI-MS: m/z = 887.3 [C₄₈H₆₆N₆ClCu₂]⁺, 863.1 [BAr^F₄]⁻. Elemental analysis: calcd (found) C₈₀H₇₈BClCu₂F₂₄N₆: C 54.82 (55.10), H 4.49 (4.66), N 4.79 (4.61).

Author contributions

The ligand synthesis was developed by W. Dammann, the remaining experiments were performed by M. Stephan, calculations by P. Burger.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Martin Kleinschmidt for assistance with the MRCI/DFT program.

References

1. M. I. Bruce, J. Organomet. Chem., 1972, 44, 209–226.
2. A. F. Scott, L. L. Wilkening and B. Rubin, Inorg. Chem., 1969, 8, 2533–2534.
3. R. D. Pike, Organometallics, 2012, 31, 7647–7660.
4. M. R. Churchill, B. G. DeBoer, F. J. Rotella, O. M. Abu Salah and M. I. Bruce, Inorg. Chem., 2002, 14, 2051–2056.
5. M. I. Bruce and A. P. P. Ostazewski, J. Chem. Soc., Chem. Commun., 1972, 20, 1124–1125.
6. P. M. Cheung, R. F. Berger, L. N. Zakharov and J. D. Gilbertson, Chem. Commun., 2016, 52, 4156–4159.
7. S. Kealey, A. J. P. White, A. D. Gee and N. J. Long, Eur. J. Inorg. Chem., 2014, 11, 1896–1905.
8. B. de Bruin, E. Bill, E. Bothe, T. Weyhermuller and K. Wieghardt, Inorg. Chem., 2000, 39, 2936–2947.
9. J. M. Holland, X. Liu, J. P. Zhao, F. E. Mabbs, C. A. Kilner, M. Thornton-Pett and M. A. Halcrow, J. Chem. Soc., Dalton Trans., 2000, 19, 3316–3324.
10. E. P. Beaumier, A. J. Pearce, X. Y. See and I. A. Tonks, Nat. Rev. Chem., 2019, 3, 15–34.
11. S. C. Bart, K. Chlopek, E. Bill, M. W. Bouwkamp, E. Lobkovsky, F. Neese, K. Wieghardt and P. J. Chirik, J. Am. Chem. Soc., 2006, 128, 13901–13912.
12. Q. Knijnenburg, S. Gambarotta and P. H. Budzelaar, Dalton Trans., 2006, 46, 5442–5448.
13. C. Römelt, T. Weyhermüller and K. Wieghardt, Coord. Chem. Rev., 2019, 380, 287–317.
14. G. Doyle, K. A. Eriksen, M. Modrick and G. Ansell, Organometallics, 1982, 1, 1613–1618.
15. M. Pasquali, C. Floriani, G. Venturi, A. Gaetani-Manfredotti and A. Chiesi-Villa, J. Am. Chem. Soc., 1982, 104, 4092–4099.
16. M. Pasquali, C. Floriani, A. Gaetani-Manfredotti and C. Guastini, J. Am. Chem. Soc., 1981, 103, 185–186.
17. I. Dutta, S. De, S. Yadav, R. Mondol and J. K. Bera, J. Organomet. Chem., 2017, 849–850, 117–124.
18. M. Sarkar, P. Pandey and J. K. Bera, Inorg. Chim. Acta, 2019, 486, 518–528.
19. B. Liu, C. Chen, Y. Zhang, X. Liu and W. Chen, Organometallics, 2013, 32, 5451–5460.
20. S. Ogawa, H. Katsuragi, T. Ikeda, K. Oshima, S. Satokawa, Y. Yamazaki and T. Tsubomura, Dalton Trans., 2021, 50, 8845–8850.
21. N. V. S. Harisomayajula, S. Makovetskyi and Y. C. Tsai, Chem. – Eur. J., 2019, 25, 8936–8954.
22. H. Schmidbaur and A. Schier, Angew. Chem., Int. Ed., 2015, 54, 746–784.
23. M. A. Carvajal, S. Alvarez and J. J. Novoa, Chemistry, 2004, 10, 2117–2132.
24. S. Dinda and A. G. Samuelson, Chemistry, 2012, 18, 3032–3042.
25. C.-M. Che, Z. Mao, V. M. Miskowski, M.-C. Tse, C.-K. Chan, K.-K. Cheung, D. L. Phillips and K.-H. Leung, Angew. Chem., 2000, 112, 4250–4254.
26. D. L. Phillips, C.-M. Che, K. H. Leung, Z. Mao and M.-C. Tse, Coord. Chem. Rev., 2005, 249, 1476–1490.
27. W. Dammann, T. Buban, C. Schiller and P. Burger, Dalton Trans., 2018, 47, 12105–12117.
28. M. S. Ziegler, N. A. Torquato, D. S. Levine, A. Nicolay, H. Celik and T. D. Tilley, Organometallics, 2018, 37, 2807–2823.
29. K. Tsuchida, Y. Senda, K. Nakajima and Y. Nishibayashi, Angew. Chem., Int. Ed., 2016, 55, 9728–9732.
30. E. P. McMoran, D. R. Powell, F. Perez, G. T. Rowe and L. Yang, Inorg. Chem., 2016, 55, 11462–11472.
31. M. Panera, J. Diez, I. Merino, E. Rubio and M. P. Gamasa, Inorg. Chem., 2009, 48, 11147–11160.
32. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
33. Y. Tao, W. Zou, M. Freindorf, M. Makos, N. Verma and E. Kraka, Local Vibrational Mode Analysis, Program LMODEA(F90), Ver. 2.0.0, Computational and Theoretical Chemistry Group (CATCO), SMU, Dallas, Texas 75275 USA, 2020.
34. E. Kraka, W. Zou and Y. Tao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1480.
35. W. Zou, Y. Tao, M. Freindorf, D. Cremer and E. Kraka, Chem. Phys. Lett., 2020, 748, 137337.
36. R. E. Franklin, Acta Crystallogr., 1951, 4, 253–261.
37. H. Willner, J. Schaebs, G. Hwang, F. Mistry, R. Jones, J. Trotter and F. Aubke, J. Am. Chem. Soc., 1992, 114, 8972–8980.
38. Y. Souma, J. Iyoda and H. Sano, Inorg. Chem., 1976, 15, 968–970.
39. M. Brookhart, B. Grant and A. F. Volpe, Organometallics, 1992, 11, 3920–3922.
40. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
41. P. R. Nagy and M. Kallay, J. Chem. Theory Comput., 2019, 15, 5275–5298.
42. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
43. C. Lefebvre, H. Khartabil, J. C. Boisson, J. Contreras-Garcia, J. P. Piquemal and E. Henon, ChemPhysChem, 2018, 19, 724–735.
44. C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 9, 1394.
45. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, 1327.
46. F. Neese, ORCA – an Ab Initio, Density Functional and Semiempirical Program Package, V. 4.2.1, MPI für Chemische Energiekonversion, Mülheim a.d. Ruhr, Germany, 2019.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2182451, 2182438, 2182437 and 2182427. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt02307e

---