Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Guest-induced magnetic exchange in paramagnetic [M2L4]4+ coordination cages†
Mukesh K.
Singh
 *,
Alvaro
Etcheverry-Berríos
*,
Alvaro
Etcheverry-Berríos
 ,
Julia
Vallejo
,
Sergio
Sanz
,
Julia
Vallejo
,
Sergio
Sanz
 ,
José
Martínez-Lillo‡
,
José
Martínez-Lillo‡
 ,
Gary S.
Nichol
,
Gary S.
Nichol
 ,
Paul J.
Lusby
,
Paul J.
Lusby
 * and
Euan K.
Brechin
* and
Euan K.
Brechin
 *
*
EaStCHEM School of Chemistry, The University of Edinburgh, David Brewster Road, Edinburgh, EH9 3FJ, Scotland, UK. E-mail: msingh2@exseed.ed.ac.uk; Paul.Lusby@ed.ac.uk; ebrechin@ed.ac.uk
First published on 10th May 2022
Abstract
Paramagnetic complexes that possess magnetically switchable properties show promise in a number of applications. A significantly underdeveloped approach is the use of metallocages, whose magnetic properties can be modulated through host–guest chemistry. Here we show such an example that utilises a simple [CuII2L4]4+ lantern complex. Magnetic susceptibility and magnetisation data shows an absence of exchange in the presence of the diamagnetic guest triflate. However, replacement of the bound triflate by ReBr62− switches on antiferomagnetic exchange between the Cu and Re ions, leading to an S = 1/2 ground state for the non-covalent complex [ReBr62−⊂CuII2L4]2+. Comparison of this complex to a “control” palladium-cage host–guest complex, [ReBr62−⊂PdII2L4]2+, shows that the encapsulated ReBr62− anions retain the same magnetic anisotropy as in the free salt. Theoretically calculated spin-Hamiltonian parameters are in close agreement with experiment. Spin density analysis shows the mode of interaction between the CuII and ReIV centres is through the Re-Br⋯Cu pathway, primarily mediated through the Cu(dx2−y2)|Brsp|Re(dyz) interaction. This is further supported by overlap integral calculations between singly occupied molecular orbitals (SOMOs) of the paramagnetic ions and natural bonding orbitals analysis where considerable donor-to-acceptor interactions are observed between hybrid 4s4p orbitals of the Br ions and the empty 4s and 4p orbitals of the Cu ions.
Introduction
Amongst the many hundreds of coordination cages to appear in the past 30 years, the Pd2L4 topology, first described by Steel,1 is the simplest, arguably the most versatile and one of the most well-studied.2–7 It has been investigated in multiple contexts, as it's host–guest chemistry can be tuned to bind anions,8 as well as neutral species.9,10 This versatility has allowed it to be exploited for a number of applications that involve the binding of drug5 and imaging molecules,11 as well as substrates for catalysis.12,13 Paramagnetic M2L4 lantern cages are much less well explored,14 indeed investigations of the magnetic behaviour of any supramolecular cages remains virtually unexplored.15 However, the host–guest chemistry of these systems offers a range of potential advantages for the exploitation of magnetic materials properties. These include, for example, the reversible inducement of magnetic exchange interactions, the encapsulation of unstable/reactive molecules or those with unusual geometries/coordination numbers, solid-state dilution, and the tuning of magnetic anisotropy. Such properties are sought-after for the construction of single-ion16 and single-molecule magnets,17 electron–spin based qubits,18 and may find application in magnetic sensing, switching and molecular recognition.19 Functionalisation of the organic framework would also aid surface deposition and the transformation of 0D molecular cages to 2D sheets and/or 3D MOFs imbued with the same physical properties.Successful ingress of a magnetic guest into a magnetic host may have little effect on magnetic properties if there are no significant interactions between the two, nor any geometrical change in either component. However, this is unlikely if size/symmetry/electrostatic matching is efficient. Encapsulation may solely induce structural changes to the host/guest and this has previously been shown to have significant impact upon, for example, the magnetic anisotropy of 3d transition metal ions in magnetic MOFs,20 and the high spin–low spin transition temperature in spin crossover materials.21 Indeed, recent studies of single-ion magnets have shown how crucial geometry is in determining magnetisation relaxation dynamics,22 and thus metallosupramolecular cages could play a key role here if their internal cavity can be designed to suit a specific d/f metal ion geometry. Covalent bonding through an intervening organic/inorganic ligand or a short dipolar interaction between the metal ions in the host and guest will mediate a magnetic exchange interaction, the sign and strength of which can be controlled by the nature of the linker and the identity of the metal ions. This then allows for control over the magnetic ground/excited states of the cage, the manipulation of which underpins application in a breadth of technologies.23
Interesting potential guest molecules include the rhenium(IV) hexahalides, [ReX6]2−, that possess very large spin–orbit coupling constants (λ ∼ 1000 cm−1 in the free ion) that results in significant magnetic anisotropy. In addition, spin delocalisation of the electron density from the metal to the halide imparts significant Re–X⋯X–Re intermolecular exchange interactions which can be strong enough to induce magnetic order in the salts of these anions at relatively high temperatures.24,25 For example, K2[ReBr6] shows antiferromagnetic order below 14 K.26 Here we show that the [ReBr6]2− anion can be encapsulated inside a paramagnetic [CuII2L4]4+ (L = 1,3-bis(3-ethynylpyridyl)benzene) cage by reporting the synthesis and characterisation of three related species, [CuII2L4(H2O)(OTf)3](OTf)·MeCN (1), ReBr6⊂ [PdII2L4](BF4)2 (2) and ReBr6⊂ [CuII2L4(OTf)2] (3).
Results and discussion
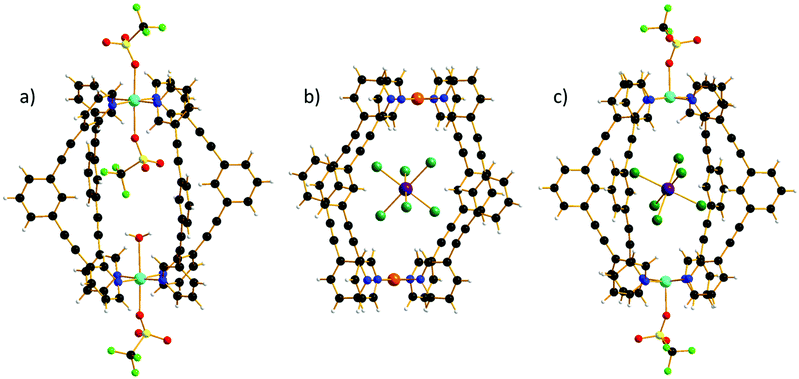
All three cages, 1–3, are made from the self-assembly of four molar equivalents of ligand molecule L with two molar equivalents of the corresponding metal salt (1), followed by one molar equivalent of guest (2–3) (see the ESI for full details†). Complex formation was confirmed by electrospray ionization mass spectrometry (ESI–MS), the spectra showing 1–3 remain intact in solution (Fig. S1–S3†). The 1H spectra of [PdII2L4](BF4)4 shows the expected seven signals,3,27 while the 1H spectra of the host–guest complex 2 show only five signals (Fig. S4–S6†). The missing signals correspond to the cavity protons (Ha and He) that strongly interact with the paramagnetic guest (H⋯Br–Re, distances in the range Ha⋯Br 2.46–3.03 Å and He⋯Br 2.99–3.25 Å). The hydrodynamic radii determined by 1H NMR DOSY experiments for both [PdII2L4](BF4)4 and the host–guest complex (2) are ∼10 Å, confirming that the guest has been encapsulated in the host cavity (Fig. S7†).Single crystal X-ray crystallography (see the ESI for full details†) reveals that 1–3 crystallise in triclinic (1, 2) and monoclinic (3) crystal systems and structure solution was performed in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (1, 2) and P21/c (3) space groups (Table S1†). All three cages possess the same general structure (Fig. 1, Tables S2–S4†), with the host framework conforming to the well-known lantern-like [M2L4]4+ cage. The CuII ions in 1 are six coordinate and in Jahn–Teller (JT) distorted octahedral geometries (Cu–NL = 1.99–2.06 Å; Cu–O = 2.32–2.62 Å; cis, 87–94°; trans, 176–177°), with triflate ions bonded in the outward facing apical sites and a combination of a single triflate and a water molecule bound in the inward facing apical positions, presumably because two internally bound anions would be prohibited due to space constraints. Charge balance is maintained through the presence of an additional triflate anion that lies outwith the cage, but with close contacts to both the Ph groups of the ditopic ligand, L (C(H)⋯O/F, 3.2–3.6 Å) and to the apical OTf molecule (O/F⋯O/F, 2.6–2.9 Å). The sole MeCN of crystallisation is H-bonded to the H2O molecule (O(H)⋯N, 2.97 Å) and therefore partially occupies the cavity of cage, protruding out between two L ligands. The L ligands of neighbouring cages interdigitate with C(Ph)⋯C(Ph) distances >3.5 Å which, alongside the distorted/flexible Cu geometry and the presence of anions/solvents, may account for the severe twisting of the L ligand geometry (Fig. S8†) enforcing a reduction from the pseudo tetragonal symmetry of the [Pd2L4]4+ cage. From analysis of the extended structures in 2–3, it is clear that both the guest anion and the crystallographic symmetry also play a key role in dictating molecular symmetry (Fig. S9†). For example, there are two orientations of the cage in 3 compared to one orientation in all the other cages and no uncoordinated anions, leading to a distinctly different packing arrangement in the crystal.
(1, 2) and P21/c (3) space groups (Table S1†). All three cages possess the same general structure (Fig. 1, Tables S2–S4†), with the host framework conforming to the well-known lantern-like [M2L4]4+ cage. The CuII ions in 1 are six coordinate and in Jahn–Teller (JT) distorted octahedral geometries (Cu–NL = 1.99–2.06 Å; Cu–O = 2.32–2.62 Å; cis, 87–94°; trans, 176–177°), with triflate ions bonded in the outward facing apical sites and a combination of a single triflate and a water molecule bound in the inward facing apical positions, presumably because two internally bound anions would be prohibited due to space constraints. Charge balance is maintained through the presence of an additional triflate anion that lies outwith the cage, but with close contacts to both the Ph groups of the ditopic ligand, L (C(H)⋯O/F, 3.2–3.6 Å) and to the apical OTf molecule (O/F⋯O/F, 2.6–2.9 Å). The sole MeCN of crystallisation is H-bonded to the H2O molecule (O(H)⋯N, 2.97 Å) and therefore partially occupies the cavity of cage, protruding out between two L ligands. The L ligands of neighbouring cages interdigitate with C(Ph)⋯C(Ph) distances >3.5 Å which, alongside the distorted/flexible Cu geometry and the presence of anions/solvents, may account for the severe twisting of the L ligand geometry (Fig. S8†) enforcing a reduction from the pseudo tetragonal symmetry of the [Pd2L4]4+ cage. From analysis of the extended structures in 2–3, it is clear that both the guest anion and the crystallographic symmetry also play a key role in dictating molecular symmetry (Fig. S9†). For example, there are two orientations of the cage in 3 compared to one orientation in all the other cages and no uncoordinated anions, leading to a distinctly different packing arrangement in the crystal.
There are multiple close contacts between the ortho protons of both the pyridine and phenyl moieties of L and the Br ions of the guest (C–H⋯Br–Re, ∼2.5–3.7 Å), in agreement with the NMR data. The CuII ions in 3 are 5-coordinate and square pyramidal in geometry (Cu–NL = 2.01 Å; Cu–O = 2.24 Å; cis, 88–98°; trans, 168–174°), with the triflate ions bonded in the outward facing apical sites and the Br ions of the guest occupying the positions sitting below the square plane of the CuII ion (Cu⋯Br, ∼4.3 Å). The Cu⋯Cu distance is now ∼12.2 Å compared to ∼11.5 Å in 1, again reflecting the increased interactions between host–guest when the ReBr62− anion is introduced.
Magnetic properties
Direct current magnetic susceptibility (χ) and magnetisation (M) data for 1–3 were measured in the T = 270–2 K, B = 0.1 T and T = 2–7 K, B = 0.5–5.0 T temperature and field ranges, respectively. These are plotted as the χT product versus T and M versus B in Fig. 2. For the quantitative interpretation of the magnetic properties of 1–3 we used spin-Hamiltonian (1):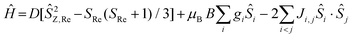 | (1) |
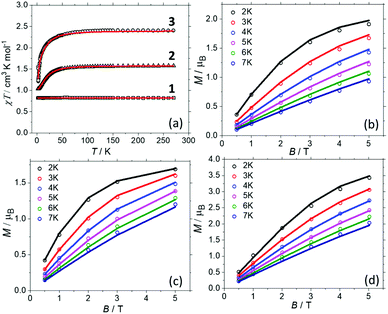 | ||
| Fig. 2 (a) Magnetic susceptibility data for 1–3 measured in an applied field, B = 0.1 T. (b–d) Magnetisation data for 1–3, respectively, in the T = 2–7 K range in fields up to, B = 5 T. The solid lines represent the simultaneous fits of the susceptibility and magnetisation data to spin-Hamiltonian (1). See the main text and Table 1 for the best fit parameters. | ||
| 1 | 2 | 3 | ||
|---|---|---|---|---|
| Expt | Expt | Expt | Calc | |
| J CuRe/cm−−1 | — | — | −0.45(1) | −0.15 |
| J CuCu/cm−−1 | 0.0 | — | 0.0 | 0.0 |
| D Re/cm−−1 | — | +21.9(1) | +21.9(1) | +23.0 |
| g Cu | 2.095 | — | 2.095(1) | 2.162 |
| g Re | — | 1.832(1) | 1.832(1) | 1.749 |
In complex 1, the two CuII ions sit at a distance of ∼11.5 Å and even though they are connected by a conjugated organic ligand (L) one would not expect to see any significant magnetic interaction between them. This is reflected in the χT data which is invariant with temperature, and both the susceptibility and magnetisation data can be simultaneously fitted with JCu–Cu = 0.0 cm−1 with gCu = 2.095. The susceptibility and magnetisation data for 2 are near identical to those reported in the literature for [ReBr6]2− salts.24 This is to be expected since there has been little distortion to its geometry upon encapsulation, as shown in the overlay plots in Fig. S10† and shape analysis (Table S5†).28 Thus a simultaneous fit of the susceptibility and magnetisation data affords gRe = 1.832, DRe = +21.9 cm−1, in agreement with both previously published experimental24 and theoretical values.29 In order to the fit the data for 3, the gCu, gRe and DRe from the fits of compounds 1 and 2 were fixed, and only the JCu–Re interaction allowed to vary. A simultaneous fit of the susceptibility and magnetisation data to spin-Hamiltonian (1) afforded JCu–Re = −0.45 cm−1. The data cannot be fitted without including exchange between the Cu and Re metal ions. Thus, the experimental magnetic data suggests: (a) there is no magnetic interaction between the CuII centres (at least for the sensitivity of a SQUID magnetometer). (b) There is a small but finite antiferromagnetic interaction between the CuII–ReIV ions. (c) Analogous DRe values to previously published ReIV metal salts are observed for the encapsulated ReBr62− ions, due to retention of analogous/non-distorted structures. In order to probe these details further, we now turn to theory.
Theoretical calculations
CASSCF/NEVPT2 calculations performed on the ReBr62− guest in 3 suggests that the major contribution to DRe comes from the spin–flip transition |dyz/xz → dxy|. Due to the relatively weak π-donor nature of the Br ion, the splitting between the dyz/xz and dxy orbitals is found to be rather small, facilitating strong in-plane anisotropy (Table S6 and Fig. S11, S12†).30 In order to estimate the JCu–Cu and JCu–Re exchange interactions DFT calculations have been performed on complexes 1 and 3. Calculations suggest no interaction between the two CuII ions in 1 and 3, but a non-negligible antiferromagnetic JCu–Re = −0.15 cm−1 in 3 leading to an S = ½ ground state (Table 1, see ESI for computational details†). Spin density analysis shows the exchange is primarily mediated via the ReIV–Br⋯CuII pathway (Fig. S13†). Overlap integral calculations31–35 between singly occupied molecular orbitals (SOMOs) of the paramagnetic ions, which helps in analysing the sign and magnitude of magnetic exchange interactions, reveal one moderately strong orbital interaction between the ReIV–Br⋯CuII centres (Cu(dx2−y2)|Br3|Re(dyz); Fig. 3, S14, Table S7†) leading to an antiferromagnetic interaction. In the other two possible interactions (Cu(dx2−y2)||Re(dxz) and Cu(dx2−y2)||Re(dxy)), the ReIV magnetic orbitals (dxz/xy) are not directly interacting with the CuII(dx2−y2) orbital, rather they interact through the long, extended π/π* orbitals of L (Fig. S14 and Table S7†). The contribution from these two interactions to the magnetic exchange interaction is thus expected to be minimal. To further confirm the significance of the Br3 atoms in mediating the exchange interaction, we have replaced Br1 and Br2 with point charges (Fig. S15†) and observe a minimal decrease in the magnitude of antiferromagnetic magnetic exchange interaction (−0.15 cm−1 to −0.12 cm−1). This is also supported by natural bonding orbitals (NBOs) analysis,36 where considerable donor → acceptor interactions are observed between hybrid |4s0.374px0.63| orbitals of Br3 and the empty 4s and 4p orbitals on Cu (Table S8†).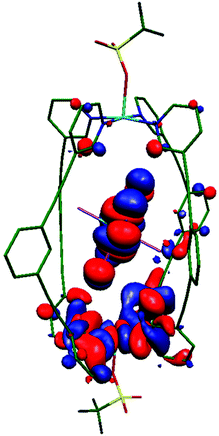 | ||
| Fig. 3 Computed overlap integral showing the Cu(dx2−y2)||Re(dyz) interaction in 3 mediating the strongest contribution to the antiferromagnetic exchange in the Re–Br⋯Cu moiety. | ||
Conclusions
Lantern-like guest⊂[M2L4]4+ coordination cages, normally associated with diamagnetic metals ions such as PdII, can also be made with paramagnetic MII ions, here CuII, through simple self-assembly of four molar equivalents of the ligand molecule (L = 1,3-bis(3-ethynylpyridyl)benzene) with two molar equivalents of the corresponding metal salt, followed by one molar equivalent of guest, forming [CuII2L4(H2O)(OTf)3](OTf)·MeCN (1), ReBr6⊂[PdII2L4](BF4)2 (2) and ReBr6⊂[CuII2L4(OTf)2] (3), respectively. Complex formation was confirmed by ESI-MS and 1H NMR, both revealing solution stability. Magnetic measurements combined with theoretical calculations show that: (a) there is no magnetic interaction between the CuII ions in the “empty” [Cu2L4]4+ cage, 1. (b) The geometry of the encapsulated [ReBr6]2− ion remains essentially unchanged with respect to its metal salt and thus the axial zero-field splitting parameter, DRe, also remains the same. (c) The ingress of the ReBr62− ion induces a magnetic exchange interaction between the ReIV guest and the CuII host, mediated primarily by the Cu(dx2−y2)||Re(dyz) orbitals in the Re–Br⋯Cu pathway leading to dominant antiferromagnetic exchange and an S = ½ ground state for the complex. This was confirmed by overlap integral calculations and NBOs analysis where significant donor-to-acceptor interactions are observed between hybrid |4s0.374px0.63| orbitals of the Br ions and the empty 4s, 4p orbitals of the Cu ions. The ability of paramagnetic host complexes to encapsulate paramagnetic guest complexes highlights some interesting possibilities for future work. These include: (1) the ability to switch on/off magnetic interactions through simple solution-based/redox chemistry, or through external perturbation, e.g. light, pressure, magnetic/electric fields. (2) To specifically design host frameworks able to isolate/stabilise unstable/reactive magnetic molecules or those with unusual geometries/coordination numbers. The structural and physical characterisation of such species will have potential application across a breadth of electron–spin based quantum technologies.Author contributions
M. K. S., A. E. B., J. V., S. S. and J. M. L. performed the synthesis and characterisation. G. S. N. performed the XRD. P. J. L. and E. K. B. conceived the idea. All authors contributed to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
EKB/PJL thank the EPSRC for funding (grants EP/M008398/1 & EP/P025986/1). This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 882686 (MaSCHiP) and agreement No 832488 (MMQIP).References
- D. A. McMorran and P. J. Steel, Angew Chem., Int. Ed., 1998, 37, 3295–3297 CrossRef CAS PubMed
.
- G. H. Clever, S. Tashiro and M. Shionoya, Angew. Chem., Int. Ed., 2009, 48, 7010–7012 CrossRef CAS PubMed
.
- P. Liao, B. W. Langloss, A. M. Johnson, E. R. Knudsen, F. S. Tham, R. R. Julian and R. J. Hooley, Chem. Commun., 2010, 46, 4932–4934 RSC
.
- N. Kishi, Z. Li, K. Yoza, M. Akita and M. Yoshizawa, J. Am. Chem. Soc., 2011, 133, 11438–11441 CrossRef CAS PubMed
.
- J. E. M. Lewis, E. L. Gavey, S. A. Cameron and J. D. Crowley, Chem. Sci., 2012, 3, 778–784 RSC
.
- W. M. Bloch, J. J. Holstein, W. Hiller and G. H. Clever, Angew. Chem., Int. Ed., 2017, 56, 8285–8289 CrossRef CAS PubMed
.
- J. E. M. Lewis, A. Tarzia, A. J. P. White and K. E. Jelfs, Chem. Sci., 2020, 11, 677–683 RSC
.
- H. Lee, J. Tessarolo, D. Langbehn, A. Baksi, R. Herges and G. H. Clever, J. Am. Chem. Soc., 2022, 144, 3099–3105 CrossRef CAS PubMed
.
- D. P. August, G. S. Nichol and P. J. Lusby, Angew. Chem., Int. Ed., 2016, 55, 15022–15026 CrossRef CAS PubMed
.
- M. Yamashina, M. Akita, T. Hasegawa, S. Hayashi and M. Yoshizawa, Sci. Adv., 2017, 3, e1701126/1–e1701126/6 CAS
.
- B. Woods, R. D. M. Silva, C. Schmidt, D. Wragg, M. Cavaco, V. Neves, V. F. C. Ferreira, L. Gano, T. S. Morais, F. Mendes, J. D. G. Correia and A. Casini, Bioconjugate Chem., 2021, 32, 1399–1408 CrossRef CAS PubMed
.
- V. Martí-Centelles, A. L. Lawrence and P. J. Lusby, J. Am. Chem. Soc., 2018, 140, 2862–2868 CrossRef PubMed
.
- J. Wang, T. A. Young, F. Duarte and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 41, 17743–17750 CrossRef PubMed
.
- Z. Li, N. Kishi, K. Yoza, M. Akita and M. Yoshizawa, Chem. – Eur. J., 2012, 18, 8358–8365 CrossRef CAS PubMed
.
- A. J. Scott, J. Vallejo, A. Sarkar, L. Smythe, E. R. Marti, G. S. Nichol, W. T. Klooster, S. J. Coles, M. Murrie, G. Rajaraman, S. Piligkos, P. J. Lusby and E. K. Brechin, Chem. Sci., 2021, 12, 5134–5142 RSC
.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC
.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS
.
- R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS PubMed
.
- M. Ohba, K. Yoneda, G. Agusti, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4767–4771 CrossRef CAS PubMed
.
- J. Vallejo, F. R. Fortea-Pérez, E. Pardo, S. Benmansour, I. Castro, J. Krzystek, D. Armentano and J. Cano, Chem. Sci., 2016, 7, 2286–2293 RSC
.
- G. J. Halder, C. J. Kepert, B. Moubaraki, K. S. Murray and J. D. Cashion, Science, 2002, 298, 1762–1765 CrossRef CAS PubMed
.
- M. Feng and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574–7594 CrossRef CAS PubMed
.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed
.
- J. Martínez-Lillo, J. Faus, F. Lloret and M. Julve, Coord. Chem. Rev., 2015, 289–290, 215–237 CrossRef
.
- C. H. Woodall, G. A. Craig, A. Prescimone, M. Misek, J. Cano, J. Faus, M. R. Probert, S. Parsons, S. Moggach, J. Martinez-Lillo, M. Murrie, K. V. Kamenev and E. K. Brechin, Nat. Commun., 2016, 7, 13870 CrossRef CAS PubMed
.
- V. Minkiewicz, G. Shirane, B. Frazer, R. Wheeler and P. Dorain, J. Phys. Chem. Solids, 1968, 29, 881–884 CrossRef CAS
.
- D. P. August, G. S. Nichol and P. J. Lusby, Angew. Chem., Int. Ed., 2016, 55, 15022–15026 CrossRef CAS PubMed
.
- SHAPE, version 2.0, continuous shape measures calculation; Electronic Structure Group, Universiat de Barcelona: Barcelona, Spain, 2010.
- S. K. Singh and G. Rajaraman, Nat. Commun., 2016, 7, 10669 CrossRef CAS PubMed
.
- D. J. Cutler, M. K. Singh, G. S. Nichol, M. Evangelisti, J. Schnack, L. Cronin and E. K. Brechin, Chem. Commun., 2021, 57, 8925–8928 RSC
.
- A. E. Dearle, D. J. Cutler, H. W. L. Fraser, S. Sanz, E. Lee, S. Dey, I. F. Diaz-Ortega, G. S. Nichol, H. Nojiri, M. Evangelisti, G. Rajaraman, J. Schnack, L. Cronin and E. K. Brechin, Angew. Chem., Int. Ed., 2019, 58, 16903–16906 CrossRef CAS PubMed
.
- M. K. Singh and G. Rajaraman, Inorg. Chem., 2019, 58, 3175–3188 CrossRef CAS PubMed
.
- M. K. Singh, T. Rajeshkumar, R. Kumar, S. K. Singh and G. Rajaraman, Inorg. Chem., 2018, 57, 1846–1858 CrossRef CAS PubMed
.
- S. Hazra, S. Bhattacharya, M. K. Singh, L. Carrella, E. Rentschler, T. Weyhermueller, G. Rajaraman and S. Mohanta, Inorg. Chem., 2013, 52, 12881–12892 CrossRef CAS PubMed
.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS
.
- M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732–17735 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of materials and methods, additional figures. CCDC 1570738, 1570741 and 1570740. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt01385a |
| ‡ Current address: Instituto de Ciencia Molecular (ICMol), Universitat de València, c/Catedrático José Beltrán 2, 46980, Paterna, València, Spain. |
| This journal is © The Royal Society of Chemistry 2022 |