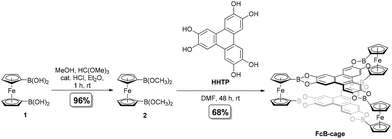
Open Access Article
Open Access ArticleDesign of a D3h-symmetry prismatic tris-(ferrocene-1,1′-diyl) molecular cage bearing boronate ester linkages†
Maurycy
Krzyżanowski
 a,
Anna M.
Nowicka
a,
Anna M.
Nowicka
 b,
Krzysztof
Kazimierczuk
b,
Krzysztof
Kazimierczuk
 c,
Krzysztof
Durka
c,
Krzysztof
Durka
 a,
Sergiusz
Luliński
a,
Sergiusz
Luliński
 a and
Artur
Kasprzak
a and
Artur
Kasprzak
 *a
*a
aFaculty of Chemistry, Warsaw University of Technology, Noakowskiego Str. 3, 00-664 Warsaw, Poland. E-mail: artur.kasprzak@pw.edu.pl; akasprzak@ch.pw.edu.pl
bFaculty of Chemistry, University of Warsaw, Pasteura Str. 1, 02-093 Warsaw, Poland
cCentre of New Technologies, University of Warsaw, Banacha 2C, 02-097 Warsaw, Poland
First published on 22nd June 2022
Abstract
This paper presents a simple, highly selective, and efficient (isolated yield of 68%) synthesis of a novel D3h-symmetry prismatic tris-(ferrocene-1,1′-diyl) organic cage (FcB-cage) by incorporating a boronate ester as a linkage motif. 1,1′-Diboronated derivatives of ferrocene and 2,3,6,7,10,11-hexahydroxytriphenylene (HHTP) were used as the starting materials. The synthesized cage was comprehensively characterized by spectroscopic and microscopic methods, powder X-ray diffraction, thermogravimetry and voltammetry. Cyclic voltammetry analysis revealed the electronic communication between the ferrocene units of the FcB-cage. In addition, to better understand the mechanism behind the synthesis of such a cage, as well as its geometric properties, we performed DFT calculations.
Introduction
Boronic esters are among the most widely used linkage motifs in the synthesis of highly organized structures, e.g., covalent organic frameworks (COFs).1–5 In fact, some of the first COFs were synthesized by polycondensation of diboronic acids and 2,3,6,7,10,11-hexahydroxytriphenylene (HHTP).6 The usefulness of boronic ester linkages stems from their D2h symmetry and the thermodynamically favoured esterification reaction.7 In the synthesis of COFs, one starting material is a knot component, whilst the other is the linker. The starting materials are often rigid, planar, and aromatic organic building blocks commonly featuring the D2h, D3d, D4h, or D6h symmetry.8 In recent years, COFs have gathered much attention because of their interesting features, such as designable crystalline structure.9–11 For example, a hexagonal, honey-comb-like 2D COF can be constructed via the condensation reaction of two molecules, one having the D3d symmetry and the other having the D2h symmetry.12 COFs are not, however, limited to only 2D sheets. For example, when one of the building blocks has a Td symmetry, 3D COFs can be obtained.13Alternatively, it was demonstrated that discrete organic cages could be synthesized instead of COFs using different starting materials that induce the 3D geometry.14–17 Such cages are commonly porous organic materials. Their synthesis usually employs imine bond formations, based on the reaction between amine and aldehyde components. In fact, imine motifs are also frequently used in COF synthesis. Interestingly, it was demonstrated that the COF material could be obtained instead of a respective organic cage molecule upon changing the aldehyde component, e.g., the planar and aromatic dialdehyde featuring the D2h symmetry.18 This is just another example of the close relationship between COFs and organic cages, as simply changing the symmetry of building blocks can lead to a COF or a cage. The utility of boronate esters in such chemistry has been demonstrated and toughly reviewed in recent years.19,20 For example, the [2 + 2] type condensation of 1,1′-ferrocenediboronic acid (1) with pentaerythritol was used by Aldridge to generate a dimeric macrocycle,21 whilst Kobayashi and co-workers reported the usage of bis(catechol) linkages toward the synthesis of boronate containing capsules22 (see Fig. 1). In addition, regarding the different types of organic cages, it is important to differentiate between organic and metal–organic cages. The latter ones utilize the metal-ligand coordination bonds, which induces the desired geometry.23 There are various examples of utilizing boronate ester groups for the construction of organic24–26 and metal–organic boronate ester cages.27
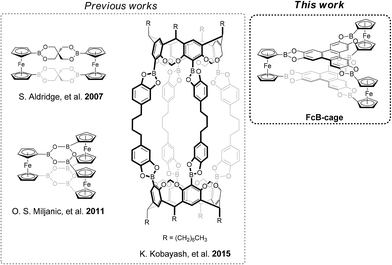 | ||
| Fig. 1 Examples of previous organized molecules bearing a boronated ester linkage21,22,33 and the aim of this work. | ||
Ferrocene is one of the more interesting building blocks of organic cages. Recently, it has been demonstrated that organic cages derived from 1,1′-diformylferrocene can be easily and effectively synthesized by means of the imine bond formation reaction with C3-symmetric aromatic amines.28,29 Such an organic cage can be viewed as two parallel 2D sheets connected via a linkage that is perpendicular to those sheets. More specifically, the two parallel 2D sheets are rigid aromatic frameworks, while the three linkages are the ferrocene units. Taking into account that ferrocene itself is composed of two planar cyclopentadienyl (Cp) units linked together via an iron cation perpendicular to them, it is a highly geometry-inducing starting material that enables the synthesis of organic cages. Such ferrocene-containing organic cages are of interest not only because they are redox-active30,31 but also because they may share some properties with their COF counterparts such as sensing ability32 or gas storage.17
Planar and highly symmetrical organic cages comprising boronate ester linkages have not been reported yet, with the boroxine-containing organic cage (see Fig. 1)33 being the most similar reported molecule of that type. Taking into account the recently reported usefulness of 1,1′-disubstituted ferrocene derivatives, which strongly induce the formation of organic cages, this work aimed at selective synthesizing an organic cage (FcB-cage; Scheme 1) derived from HHTP and 1 by means of a boronate ester formation. Density functional theory (DFT) calculations were performed to better understand the structure of a cage and rationalize the thermodynamic advantages of its formation over the oligomeric structures.
Results and discussion
Synthesis of FcB-cage
The synthesis of FcB-cage under optimized conditions is presented in Scheme 1. At first, the trials were performed with 1 (3 equivalents) and HHTP (2 equivalents). Inspired by the reports of the synthesis of HHTP derived COFs,3,5,34 1,4-dioxane/mesitylene (1/1 v/v) was used as a solvent system (for the optimization experiments, see section 1, ESI†). We expected that the product shall precipitate from the reaction mixture. No formation of the product was, however, observed after stirring the reagents at room temperature for several days. Changing the temperature to 85 °C also did not result in the formation of the FcB-cage and once again only starting materials were recovered. Attempts to synthesize the FcB-cage by applying the reported procedures for the synthesis of other ferrocene containing organic cages, which employed methanol or ethanol as the solvent,28,29 were also unsuccessful (in the recovery of starting materials). We suspected that the difficulties in dissolving 1 or HHTP could be the culprit behind those above-discussed unsatisfactory results. Therefore, the subsequent trials were performed in the solvent that had been earlier proved to dissolve both the starting materials, namely N,N-dimethylformamide (DMF). To our delight, in this case, a precipitate was formed. However, there appeared to be a significant concentration threshold equal to 10 mM (with the respect to compound 1). In other words, when the concentration of compound 1 was 1, 2, 4, or 8 mM, the formation of a precipitate was not observed. While DMF enabled the partial formation of the cage, the reaction yield was relatively low (ca. 40%), and the presence of oligomers in the sample was observed (see section 1, ESI†). We suspected that it resulted from the poor solubility of the intermediate products in DMF. In fact, the formation of organized organic cages requires the good solubility of the starting materials and the intermediate products in the reaction solvent. In order to omit those limitations, 1,1′-bis(dimethoxyboryl)ferrocene (2), a methanol ester derivative of 1, was used in the next trials, which is far more soluble than 1.The reported synthesis of 2 involved the metathesis of 1,1′-bis(dibromoboryl)ferrocene with methoxytrimethylsilane.35 To avoid the use of hazardous boron tribromide we developed a more convenient route which uses the easily accessible and air-stable 133 as the starting material (Scheme 1). We were pleased to find that the esterification of B(OH)2 groups with methanol proceeded readily in Et2O at room temperature upon the addition of trimethyl orthoformate and a catalytic amount of HCl (a few drops of a 2 M ethereal solution). The addition of HC(OMe)3 was essential for shifting the equilibrium towards the product as it reacts with water formed during esterification. Overall, the process resembles the formation of dimethyl acetals or ketals from respective carbonyl derivatives. It could also be potentially valuable for the synthesis of other boronic esters. It should be noted that product 2 was obtained as a viscous red oil which is prone to rapid hydrolysis in contact with water and moist air resulting in the recovery of 1.
The solubility of 2 in common organic solvents was incredibly better than 1. The synthesis of the target FcB-cage from 2 and HHTP was carried out in DMF at room temperature. The molar concentrations of the starting materials were 11.5 mM (3 equiv.) and 7.7 mM (2 equiv.) for 2 and HHTP, respectively. Under optimized conditions, we were able to obtain the FcB-cage in good yield (68%). It is worth noting that the protocol is easy-to-perform; the reaction set-up was simple, as the reactants were placed in a flask, and then the solvent was added. In addition, the target FcB-cage precipitated from the reaction mixture and was then washed with DMF and acetone to remove the unreacted starting materials and impurities. In addition, we tested a mechanochemical synthesis of the FcB-cage from 1 and HHTP in a ball mill using the liquid-assisted grinding technique (a drop of DMF was added). However, PXRD analysis revealed that 1 did not undergo reaction under such conditions.
Characterization of FcB-cage
The FcB-cage was found to be practically insoluble in any solvent. The 1H NMR spectrum of the FcB-cage in DMSO-d6 measured immediately after sample preparation comprised peaks coming from the building blocks of the FcB-cage, namely 1,1′-ferrocenediboronic acid (1) and HHTP. We suspected that it resulted from the boronate esters being sensitive to the presence of water, which causes their hydrolysis to the parent boronic acid and alcohol (diol). When the spectrum was measured after stirring the FcB-cage in DMSO-d6 for 24 hours at room temperature in air (see the Experimental section), the intensity of those peaks increased (Fig. S1, ESI†), which supported our hypothesis of the hydrolysis of boronate ester linkages forming the FcB-cage (no products of partial hydrolysis of the cage were observed). Interestingly, the peak integrals suggested that the molar ratio of the building blocks is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (1
2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HHTP). This molar ratio is in good agreement with the proposed structure of the FcB-cage. High-resolution mass spectrometry (HRMS) further supported the successful synthesis of the FcB-cage (Fig. S3, ESI†). Importantly, HRMS analysis suggested that the sample did not contain any high- or low-mass oligomeric side-products.
HHTP). This molar ratio is in good agreement with the proposed structure of the FcB-cage. High-resolution mass spectrometry (HRMS) further supported the successful synthesis of the FcB-cage (Fig. S3, ESI†). Importantly, HRMS analysis suggested that the sample did not contain any high- or low-mass oligomeric side-products.
We performed solid-state NMR experiments to gain deeper insights into the structural features of the FcB-cage. The 13C MAS NMR spectrum of the FcB-cage generally agrees with the expectations (Fig. 2). Due to signal broadening and the relatively small difference in the chemical shifts of non-equivalent carbon of Cp rings, it is impossible to distinguish their separate resonances. Thus, the spectrum shows one intense resonance of ferrocenyl carbon atoms centred at 77.5 ppm. In contrast, one can easily assign the signal at 108.6 ppm to the carbon atoms of the HHTP linker located at the ortho positions with respect to the O-bound carbons.36 In addition, the spectrum shows the resonances at 128.2 and 150.4 ppm, which can be unambiguously assigned to the quaternary carbon atoms of the central ring of HHTP and the peripheral O-bound carbon atoms of this linker, respectively. The 11B MAS NMR spectrum of the FcB-cage shows a single symmetrical resonance centred at 24.9 ppm (Fig. 2). It confirms the presence of boronate groups as it essentially resembles signals typically observed for arylboronic acids and esters under isotropic conditions (ca. 25–30 ppm).37 A closer inspection reveals shoulders at both sides of the signal which may point to slight differences in boron shielding; this effect may be attributed to a different environment of the boron atoms at the periphery of the crystallites.
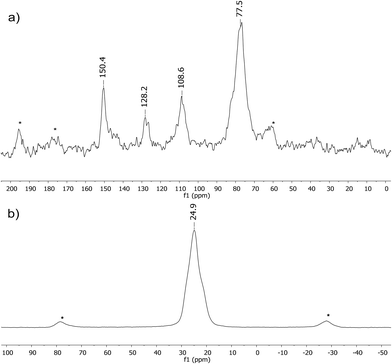 | ||
| Fig. 2 13C (a) and 11B MAS NMR (b) spectra of the FcB-cage (spinning frequency 12 kHz, spinning sidebands are marked with asterisks). | ||
Attenuated total reflectance Fourier-transform infrared (ATR-FT-IR) spectroscopy provided further insights into the FcB-cage structure. The ATR-FT-IR spectrum of the FcB-cage (Fig. S4, ESI†) shows a strong broadband of B–O stretching vibrations at 1360 cm−1. Although there are some literature examples in which the authors were able to define a particular shift in this region and distinguish between boronic esters, boronic acids or boroxines,38 in the FcB-cage the interpretation is rather ambiguous. The band splits into several components, which may be attributed to the overlap with the B–C stretching vibrations or the results from the deviation of the FcB-cage from the D3h symmetry. The latter hypothesis is also supported by the observation of the ATR-FT-IR pattern in the 1000–1070 cm−1 region. The appearance of moderately strong sharp bands is expected for boronic esters, whereas in the case of FcB-cage the bands are broad and split into several signals. The more diagnostic vibrational mode, that has been conserved in the 640–680 cm−1 range for most boronic esters, involves the out-of-plane movements of the boron and oxygen atoms. This characteristic band is indeed observed at 670 cm−1 and its assignment was unambiguously confirmed by DFT calculations. Nonetheless, this band typically splits into several sharp peaks for boronic esters, while in the case of the FcB-cage it is slightly broadened and jagged.
The above-discussed absorption bands in the ATR-FT-IR spectrum of the FcB-cage suggest that a boronate ester structure was indeed formed. However, because the direct interpretation is ambiguous at some points, a machine learning technique was applied.39–41 For this purpose, the SVM (support vector machines) model with rbf (radial basis function) kernels was used (Fig. S5, ESI†).42 The details of the machine learning technique and the crucial parameters dealing with this analysis are presented in section 3, ESI.† The dataset consisted of 28 different molecules, all of them being boronate ester or boroxine derivatives.38 Hyperparameters present in the SVM model with rbf kernels are: regularization constant (C) and kernel hyperparameter (γ). In order to find the most optimal values of those hyperparameters, a grid search was performed. The best parameters were found to be 0.001 for the γ parameter and 1 for C. Even when disregarding the characteristic band in the range of 1015–1069 cm−1, 100% accuracy was achieved. Despite the fact that the differences between the IR spectra of boroxines and boronic esters are quite subtle, the respective signals can be grouped into clusters, thus easily differentiating both types of compounds. After the classifying algorithm had been successfully established, we could move on to classify the IR signal of the product. Because exactly four values of frequencies need to be extracted from the spectrum, the values were determined by firstly extracting all values of the signal in the area of interest, and then averaging those values, which resulted in mean frequencies that have values of 1387, 1321, 1246 and 680 cm−1. The applied classifying algorithm predicted that the product is an ester with a 67% probability. When incorporating the characteristic signal, the probability grew to 88%.
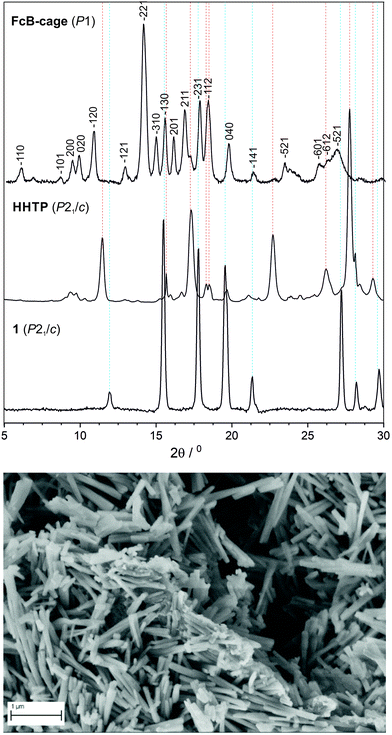
Powder X-ray diffraction (PXRD) pattern (Fig. 3) points to an ordered, micro- or nanocrystalline character of the FcB-cage due to the presence of several relatively sharp peaks in the 2θ range of 4–20°. Pawley refinement allowed to index all of the observed peaks (Fig. S18, ESI†), i.e., there were no additional peaks left, indicating that the sample is homogeneous and is not contaminated by unreacted substrates. This is in accordance with the SEM analysis showing uniform nanocrystallites which strongly point to phase homogeneity. The volume of the proposed monoclinic cell is 3522 Å3 which roughly corresponds to the volume of two molecules of the FcB-cage (V = 1715 Å3). In addition, the size of those nanocrystallites estimated using the Scherrer equation is ca. 30–40 nm which is roughly in agreement with their width range measured based on the scanning electron microscopy (SEM) images (Fig. 3). Thus, it can be claimed that the outcomes of the PXRD and SEM analyses are highly consistent and thus the presence of oligomeric species in the FcB-cage sample is unlikely. Lastly, it is worth noting that the energy-dispersive X-ray spectroscopy analysis confirmed the presence of expected atoms in the molecular formula of the FcB-cage (for data see Table S2, ESI†).
The thermal stability of the FcB-cage was investigated under a N2 atmosphere by thermogravimetric analysis (TGA) (Fig. S9, ESI†). A slow continuous mass loss (ca. 7%) is observed below 300 °C. It is presumably due to the removal of traces of moisture and solvents. Overall, the material exhibits a relatively high thermal resistance in agreement with its compact structure composed of aromatic building blocks. In addition, the material exhibits long-term stability under ambient conditions as the PXRD pattern of a sample remained essentially unchanged after several months. A more significant (ca. 20%) mass loss of the molecular structure occurs in the temperature range of 400–600 °C. It is accompanied by the exothermic peak of the DSC curve with the maximum at ca. 550 °C indicating that the degradation of the material presumably resulted from the thermolysis of B–C bonds.
The results of the elemental analysis of the FcB-cage were consistent with the expected elemental composition of the sample. Small differences between the calculated and found values originate from the hygroscopic nature of the FcB-cage resulting in the presence of water in the sample. The presence of water in the FcB-cage sample can be clearly observed in the TGA thermogram (Fig. S9, ESI†). It is worth noting that commercially available HHTP, used as the reactant in the synthesis of FcB-cage, also contains some amount of water. The results of the elemental analysis suggested the presence of 5 molecules of water in the formula (for the FcB-cage: calcd for C66H36B6Fe3O12: C, 63.25; H, 2.90; for FcB-cage + 5H2O: calcd for C66H46B6Fe3O17: C, 59.00; H, 3.45, found: C, 58.86; H, 3.35). The estimated content of water from TGA is 6.97 wt%. The content of water in the sample calculated from the above-listed formula is ca. 7.18 wt%. Thus, the content of water estimated by elemental analysis and TGA are in good agreement. Slight differences result from the different methods of sample preparation for the analysis.
To study the electrochemical properties of the FcB-cage, electrochemical analyzes were performed in anhydrous dimethylsulfoxide (DMSO) with the addition of 0.10 M of tetrabutylammonium hexafluorophosphate (TBAPF6) as a supporting electrolyte. Before the experiment, the electrode surface was modified with the FcB-cage. The electrochemical characteristics of the modified electrode (GC/FcB-cage-TBABF4-Nafion®) were obtained using cyclic voltammetry at various electrode scan rates ranging from 0.002 to 0.4 V s−1. The obtained voltammograms are presented in Fig. 4. The obtained voltammetric curves are characterized by the three pairs of current peaks (EOx/ERed: 0.67 V/0.18 V; 0.96 V/0.53 V and 1.20 V/0.82 V) that correspond to the three ferrocene units present in the FcB-cage structure. It should be stressed that the poor current signal separation (especially in the anodic region, see inset in Fig. 4) is a consequence of the strong coordinating properties of PF6− anions,43–45 and the separation of those peaks declined with increasing scan rate. The HOMO energy level calculated on the basis of the first oxidation potential is −5.71 eV, which is in agreement with the DFT-calculated value of −5.78 eV. For comparison, the anodic and cathodic peaks for the one electron redox process for native ferrocene are centred at 0.42 V (EOx) and 0.33 V (ERed),46 for 1,1′-ferrocenediboronic acid (1) at ca. 0.2 V (EOx) and ca. 0.17 V (ERed),47 whilst for 1,1′-ferrocenediboronic acid bis-pinacol ester at. 0.31 V (EOx) and ca. 0.28 V (ERed).48 In addition, the existence of several current peaks for 1,1′-ferrocenediboronic acid derived dimeric structures has been previously observed, such as in the case of dimers comprising indacene based tetrol units (EOx/ERed: 0.23 V/ca.0.20 V and 0.39 V/ca.0.35 V).48 For the FcB-cage, the cathodic signals are better defined than the anodic signals. Moreover, the presence of three pairs of current signals indicates the electronic communication between ferrocene units in the FcB-cage. We consider that electronic communication is transferred through bonding by triphenylene core as the electronic effect of redox processes for each boronated ferrocene unit. This is also reflected by the much higher first oxidative potential of the FcB-cage with respect to ferrocene and its 1,1′-diboronic derivatives. In general, the introduction of the boron atom to the ferrocene unit decreases the Eox value. In contrast the removal of one electron in the FcB-cage requires higher energy. At the same time the reverse electrochemical processes, i.e. reduction of respective cationic states, are kinetically hampered leading to the large hysteresis effect. These observations can be explained in terms of the resonance effect between the ferrocene units induced by their close distance, parallel orientation, flat geometry of the boron coordination sphere and the π-electron conducting properties of the HHTP linker. This effect was not observed for the dimeric structures comprising 1,1′-diboronated ferrocene and indacene-based tetraol units due to the aliphatic nature of the latter component.
Finally, due to the fact that the FcB-cage was immobilized on the electrode surface, its electrode process should be a surface process. In order to confirm this hypothesis, the dependence of the oxidation signal intensity as a function of the electrode scan rate was plotted and the obtained dependencies are presented in the inset graph of Fig. 4 (bottom). The linear dependence I = f(v) indicates the surface electrode process.
Theoretical insights into the formation of the FcB-cage
The molecular structure of the FcB-cage was established on the basis of DFT calculations. The B97D functional with the 6-311++G(d,p) basis set was selected as it can accurately describe the π–π interactions between the HHTP aromatic units. Although the B3LYP functional is more frequently used than B97D, it falsely predicts the dispersion interactions between HHTP units. The single-molecule optimization of the FcB-cage shows that the molecule deviates from its initial D3h symmetry (Fig. 5). This is manifested by the slight puckering of the HHTP moieties, twisting of the ferrocene units with respect to the HHTP planes and the deflection of the C–B bonds from the Cp rings. Such molecular deformations enable the in-plane shifting of the HHTP units by 0.117 Å ensuring more advantageous π-stacking interactions. For comparison, the in-plane shifting of two independent π-stacking HHTP molecules optimized at the same level of theory is 0.387 Å. The intramolecular distance between the root-mean-square HHTP planes in the FcB-cage is 3.311 Å, which is close to the value obtained for the HHTP dimer (3.184 Å). The Cp rings in the ferrocene moieties adopt nearly eclipsed conformation. The slight twist of the Cp rings enhances the formation of the complementary pairs of B⋯O interactions between parallel boronic units, although further calculations indicate that they provide a marginal contribution to the total stabilization energy of the cage. In a subsequent step, the intramolecular interaction energy between HHTP units was calculated by extracting the ferrocene moieties from the structure. In such a discrete dimeric pair, the boron atoms were terminated with hydrogen atoms, while the positions of the remaining atoms were preserved from the optimized molecule FcB-cage. The BSSE-corrected interaction energy is 87.0 kJ mol−1. Thus the π-stacking interactions provide a very important contribution to the total stabilization of the FcB-cage structure.It can be expected that the formation of the FcB-cage proceeds in several successive steps (see Scheme 2). At first, the molecule of HHTP reacts with molecule 2 to produce the 2-HHTP adduct with ΔG = −20.4 kJ mol−1. The rotation of the Cp rings is not hampered as the energy difference between the two extreme conformers, namely syn-2-HHTP and anti-2-HHTP, is only 1.9 kJ mol−1. The reaction of 2-HHTP with another HHTP molecule to give 2-HHTP2 is thermodynamically highly favoured due to the dispersive interactions between the HHTP moieties (ΔG = −69.0 kJ mol−1). Consequently, the syn-2-HHTP2 conformer is more stable than anti-2-HHTP2 by 57.5 kJ mol−1 and the ferrocene rotation ceases. Further reaction of 2-HHTP2 with another molecule of 2 can lead to either the cage or oligomeric structure. The selectivity of this process strongly depends on molecular conformation. Specifically, the parallel orientation of the HHTP molecules in syn-2-HHTP2 enables the fine incorporation of the second ferrocene units to give 22-HHTP2 (Scheme 2) with a Gibbs free enthalpy of −50.5 kJ mol−1, although the calculations suggest that the reaction proceeds through several elemental steps as depicted in Scheme S1 (ESI†). As the rotation of ferrocene Cp rings in 2-HHTP2 is hampered, the appearance of oligomeric products, in which HHTP units are not stacked, can be excluded. Thus, it can be concluded that the main driving force for the formation of the discrete cage structure is the presence of strong dispersive forces, exemplified by the relatively large energy differences between syn-2-HHTP2 and anti-2-HHTP2. The final reaction of 22-HHTP2 with the third molecule 2 to give the FcB-cage structure is also energetically favoured with ΔG = −76.9 kJ mol−1. The total Gibbs free enthalpy for the generation of the FcB-cage from the starting materials is −216.8 kJ mol−1 indicating that the process is thermodynamically highly beneficial.
 | ||
| Scheme 2 Proposed mechanism for the formation of the FcB-cage together with the energy diagram (presented in the frame). | ||
The FcB-cage readily precipitates from the solution and the obtained product is sparingly soluble in common organic solvents. This is related to the size of the molecule and its compact character. In addition, it can be expected that cages likely stack on top of each other. According to our calculations, the interaction energy between two molecules FcB-cage is equal to 107.6 kJ mol−1, i.e., it is higher by 20.6 kJ mol−1 than the intramolecular interaction within the cage. In such a dimeric structure, the intermolecular distance between the neighboured HHTP planes is 3.217 Å, which is approximately equal to the distance of two independently π-stacked HHTP molecules. At the same time, the molecules are in-plane shifted by 0.382 Å. It is expected that the further propagation of this motif would produce the π-stacking molecular chains.
Conclusions
In conclusion, a novel D3h-symmetric ferrocenylated organic cage bearing boronate ester linkages (FcB-cage) has been selectively and effectively synthesized under mild conditions by employing an easy-to-perform reaction. The MAS NMR, ATR-FT-IR, and HRMS analyses supported the structure formulation of the target product as a pure material without traces of oligomeric side-products. The presence of peaks in the low 2θ range in the PXRD pattern implies that the cage crystallizes in large unit cells. In the SEM image, nanocrystallites can be seen whose size coincides with the observed PXRD peak broadenings. It is worth noting that SEM and PXRD analyses were highly consistent and enabled the exclusion of the presence of oligomeric species in the FcB-cage sample. The TGA analysis confirmed the high thermal stability of the cage. Lastly, voltammetric analyses revealed that there is electronic communication between the ferrocene units through bonding with a triphenylene core, and since the cage is immobilized on the electrode surface, its electrode processes occur on the surface of the electrode. On the basis of DFT calculations, the molecular structure of the cage was established. Further analysis of the intermediate products enabled us to decipher the reaction mechanism, which explains the selective formation of the cage. By the synthesis of the new ferrocenylated cage bearing boronate ester linkages, this work contributes to the further progress in the synthesis of organized compounds bearing metallocene as a building block.Experimental
Materials and methods
Chemical reagents and solvents for the synthesis were commercially purchased and purified according to the standard methods, if necessary. Sonication was performed using a Bandelin Sonorex RK 100 H ultrasonic probe with temperature control (ultrasonic peak output/HF power: 320 W/80 W; 35 kHz).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 666 Hz, recycle delay 5 s, number of scans 128, and acquisition time 100 ms. The 13C spectra were measured using the CP-MAS sequence with 1H decoupling and the following parameters: 13C: π/2 pulse width 3.2 μs, 1H: π/2 pulse width 2.5 μs, spectral width 50
666 Hz, recycle delay 5 s, number of scans 128, and acquisition time 100 ms. The 13C spectra were measured using the CP-MAS sequence with 1H decoupling and the following parameters: 13C: π/2 pulse width 3.2 μs, 1H: π/2 pulse width 2.5 μs, spectral width 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz, recycle delay 2 s, number of scans 1024, acquisition time 40 ms. All datasets were processed using the Mestrenova 12.0 software, using exponential apodization (100 Hz), zero-filling to 16k points and baseline correction using a polynomial fit of the 3rd order.
000 Hz, recycle delay 2 s, number of scans 1024, acquisition time 40 ms. All datasets were processed using the Mestrenova 12.0 software, using exponential apodization (100 Hz), zero-filling to 16k points and baseline correction using a polynomial fit of the 3rd order.
Synthesis
13C MAS NMR (176.05 MHz, ppm) δ 150.4, 128.2, 108.6, 77.5; 11B MAS NMR (224.62 MHz, ppm) δ 24.9; ATR-FT-IR, v 1387, 1321, 1292, 1245, 1162, 1117, 1059, 1027 cm−1; TOF-HRMS (ESI): calcd for C66H37B6Fe3O12 [M + H]+ = 1254.0922, found: m/z 1254.0922; EDS: B, 6.22; C, 61.46; O, 20.9; Fe, 11.3 wt%; Elem. anal. calcd for C66H36B6Fe3O12: C, 63.25; H, 2.90, found: C, 58.86; H, 3.35.
1H NMR (DMSO-d6, 400 MHz, ppm), δ 9.77 (s, 12H; O–H, HHTP), 7.60 (s, 12H; Ar–H, HHTP), 7.46 (s, 12H; B(OH)2, 1), 4.34 (t, J = 1.8 Hz, 12H; Cp–H, 1), 4.17 (t, J = 1.8 Hz, 12H; Cp–H, 1). The calculated molar ratio of1:HHTPis 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 2.
2.
Theoretical calculations
Theoretical calculations were performed using the Gaussian16 program.50 Molecules were optimized using the B97D functional51 (DFT) with 6-311++G(d,p) basis set.52 As the crystal data was not available for the FcB-cage, the initial structure was generated manually in the GaussView program.53 The initial structure of 2 was built based on the crystal structure of 1 by the substitution of hydrogen atoms with methyl groups. There are two polymorphic forms of 1; in one form, the boronic groups are in the syn conformation with respect to each other,54 while in the second they are in the anti position due to the rotation of the Cp rings.55 Thus, the initial structures of syn-2 and anti-2 conformers were constructed based on the molecular geometries derived from the corresponding crystal structures of 1. According to our computations, the syn and anti rotamers of 2 are equally stabilized in solution (ΔE = 0.1 kJ mol−1) and the interconversion energy barrier is below 4 kJ mol−1, which is in line with a very small energy barrier for Cp rotation in ferrocene and its derivatives. The introduction of the boronic group has a marginal effect on Cp ring rotation unless it is hampered by the strong intramolecular interactions as is observed for the 2-HHTP2 intermediate. In the next step, several different conformations of boronic groups namely, syn–syn, syn–anti, and anti–anti were considered (Fig. S10, ESI†). According to our results, the syn–anti conformation of the boronic ester group is the most favoured, which is the common feature for the number of boronic acids and their derivatives.56,57 The rotation of the boronic ester group around the B–C bond was calculated using the scan procedure in Gaussian (other parameters were optimised during the scan procedure). The calculated energy barrier is 33 kJ mol−1. The most stable conformation of 2 was taken for the subsequent calculation of the reaction mechanism. The intermediate structures en route to the final product FcB-cage were initially built using the GaussView programme and then subjected to the optimisation procedure. Following geometry optimization, the vibrational frequencies were calculated and the results showed that the optimized structures are stable geometric structures (no imaginary frequencies, Table S3, ESI†). In the optimization processes, no symmetry constraints were applied. The molecular volume of the FcB-cage was calculated with Gaussian using the keyword ‘volume’, which defines the volume inside the electron density isosurface of 0.001 e bohr−1.3 Gibbs free energies were obtained from the frequency calculations with the temperature set to 298 K. To take into account the experimental conditions all calculations were performed in the presence of the solvent field with the polarizable continuum model (PCM) using the CPCM polarizable conductor calculation model and DMF was used as the solvent.58 The geometries of the optimized structures are provided in the ESI (Fig. S8–S10†) as well as the supplementary .xyz format file. The dimer interaction energies were calculated using the supermolecular method including Basis Set Superposition Error (BSSE). The intramolecular interaction energy between the HHTP units in the FcB-cage was calculated after extracting ferrocene moieties from the structure of the B–C bonds. The boron atoms were terminated with the hydrogen atoms. The FcB-cage dimer was freely optimized prior to the intermolecular energy calculations (Fig. S14, ESI†).Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Warsaw University of Technology is acknowledged. The publication and M. K.'s contribution are a part of the “Szkoła Orłów” project, co-financed by the European Social Fund under the Knowledge-Education-Development Operational Programme, Axis III, Higher Education for the Economy and Development, Measure 3.1, Competences In Higher Education. This work was supported by the National Science Centre (Poland) within the framework of the project DEC-UMO-2016/21/B/ST5/00118 (K. D., S. L.). The authors thank Wroclaw Centre for Networking and Supercomputing (http://www.wcss.pl), grant No. 285, for providing computer facilities (Gaussian16).References
- S. Wan, J. Guo, J. Kim, H. Ihee and D. Jiang, Angew. Chem., Int. Ed., 2008, 47, 8826–8830 CrossRef CAS PubMed.
- E. L. Spitler and W. R. Dichtel, Nat. Chem., 2010, 2, 672–677 CrossRef CAS PubMed.
- K. Gontarczyk, W. Bury, J. Serwatowski, P. Wieciński, K. Woźniak, K. Durka and S. Luliński, ACS Appl. Mater. Interfaces, 2017, 9, 31129–31141 CrossRef CAS PubMed.
- P. Pacholak, K. Gontarczyk, R. Kamiński, K. Durka and S. Luliński, Chem. – Eur. J., 2020, 26, 12688–12688 CrossRef CAS PubMed.
- E. L. Spitler, B. T. Koo, J. L. Novotney, J. W. Colson, F. J. Uribe-Romo, G. D. Gutierrez, P. Clancy and W. R. Dichtel, J. Am. Chem. Soc., 2011, 133, 19416–19421 CrossRef CAS PubMed.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed.
- B. J. Smith, N. Hwang, A. D. Chavez, J. L. Novotney and W. R. Dichtel, Chem. Commun., 2015, 51, 7532–7535 RSC.
- K. Geng, T. He, R. Liu, S. Dalapati, K. T. Tan, Z. Li, S. Tao, Y. Gong, Q. Jiang and D. Jiang, Chem. Rev., 2020, 120, 8814–8933 CrossRef CAS PubMed.
- J. W. Colson and W. R. Dichtel, Nat. Chem., 2013, 5, 453–465 CrossRef CAS PubMed.
- S. Bi, C. Yang, W. Zhang, J. Xu, L. Liu, D. Wu, X. Wang, Y. Han, Q. Liang and F. Zhang, Nat. Commun., 2019, 10, 2467 CrossRef PubMed.
- E. Jin, J. Li, K. Geng, Q. Jiang, H. Xu, Q. Xu and D. Jiang, Nat. Commun., 2018, 9, 4143 CrossRef PubMed.
- N. Huang, L. Zhai, D. E. Coupry, M. A. Addicoat, K. Okushita, K. Nishimura, T. Heine and D. Jiang, Nat. Commun., 2016, 7, 12325 CrossRef PubMed.
- H. Ding, J. Li, G. Xie, G. Lin, R. Chen, Z. Peng, C. Yang, B. Wang, J. Sun and C. Wang, Nat. Commun., 2018, 9, 5234 CrossRef CAS PubMed.
- A. I. Cooper, ACS Cent. Sci., 2017, 3, 544–553 CrossRef CAS PubMed.
- T. Kunde, T. Pausch and B. M. Schmidt, Chem. – Eur. J., 2021, 27, 8457–8460 CrossRef CAS PubMed.
- T. Tozawa, J. T. A. Jones, S. I. Swamy, S. Jiang, D. J. Adams, S. Shakespeare, R. Clowes, D. Bradshaw, T. Hasell, S. Y. Chong, C. Tang, S. Thompson, J. Parker, A. Trewin, J. Bacsa, A. M. Z. Slawin, A. Steiner and A. I. Cooper, Nat. Mater., 2009, 8, 973–978 CrossRef CAS PubMed.
- T. Kunde, E. Nieland, H. V. Schröder, C. A. Schalley and B. M. Schmidt, Chem. Commun., 2020, 56, 4761–4764 RSC.
- X. Li, C. Yang, B. Sun, S. Cai, Z. Chen, Y. Lv, J. Zhang and Y. Liu, J. Mater. Chem. A, 2020, 8, 16045–16060 RSC.
- K. Severin, Dalton Trans., 2009, 5254 RSC.
- R. Nishiyabu, Y. Kubo, T. D. James and J. S. Fossey, Chem. Commun., 2011, 47, 1124–1150 RSC.
- J. K. Day, C. Bresner, I. A. Fallis, L.-L. Ooi, D. J. Watkin, S. J. Coles, L. Male, M. B. Hursthouse and S. Aldridge, Dalton Trans., 2007, 3486 RSC.
- K. Tamaki, A. Ishigami, Y. Tanaka, M. Yamanaka and K. Kobayashi, Chem. – Eur. J., 2015, 21, 13714–13722 CrossRef CAS PubMed.
- T. K. Ronson, J. P. Carpenter and J. R. Nitschke, Chem, 2022, 8, 557–568 CAS.
- N. Schäfer, M. Bühler, L. Heyer, M. Röhr and F. Beuerle, Chem. – Eur. J., 2020, 27, 6077–6085 CrossRef PubMed.
- K. Kataoka, T. D. James and Y. Kubo, J. Am. Chem. Soc., 2007, 129, 15126–15127 CrossRef CAS PubMed.
- Z. Shan, X. Wu, B. Xu, Y. Hong, M. Wu, Y. Wang, Y. Nishiyama, J. Zhu, S. Horike, S. Kitagawa and G. Zhang, J. Am. Chem. Soc., 2020, 142, 21279–21284 CrossRef CAS PubMed.
- E. Giraldi, R. Scopelliti, F. Fadaei-Tirani and K. Severin, Inorg. Chem., 2021, 60, 10873–10879 CrossRef CAS PubMed.
- A. Kasprzak and P. A. Guńka, Dalton Trans., 2020, 49, 6974–6979 RSC.
- A. I. Kosińska, M. K. Nisiewicz, A. M. Nowicka and A. Kasprzak, ChemPlusChem, 2021, 86, 820–826 CrossRef PubMed.
- D. Astruc, Eur. J. Inorg. Chem., 2017, 2017, 6–29 CrossRef CAS.
- B. Gélinas, T. Bibienne, M. Dollé and D. Rochefort, Can. J. Chem., 2020, 98, 554–563 CrossRef.
- C. Bravin, A. Guidetti, G. Licini and C. Zonta, Chem. Sci., 2019, 10, 3523–3528 RSC.
- T.-H. Chen, W. Kaveevivitchai, N. Bui and O. Š. Miljanić, Chem. Commun., 2012, 48, 2855 RSC.
- R. L. Li, N. C. Flanders, A. M. Evans, W. Ji, I. Castano, L. X. Chen, N. C. Gianneschi and W. R. Dichtel, Chem. Sci., 2019, 10, 3796–3801 RSC.
- M. Scheibitz, M. Bolte, J. W. Bats, H.-W. Lerner, I. Nowik, R. H. Herber, A. Krapp, M. Lein, M. C. Holthausen and M. Wagner, Chem. – Eur. J., 2005, 11, 584–603 CrossRef CAS PubMed.
- L. M. Salonen, D. D. Medina, E. Carbó-Argibay, M. G. Goesten, L. Mafra, N. Guldris, J. M. Rotter, D. G. Stroppa and C. Rodríguez-Abreu, Chem. Commun., 2016, 52, 7986–7989 RSC.
- H. Nöth and B. Wrackmeyer, Nuclear Magnetic Resonance Spectroscopy of Boron Compounds, Springer Berlin Heidelberg, Berlin, Heidelberg, 1978 Search PubMed.
- M. K. Smith and B. H. Northrop, Chem. Mater., 2014, 26, 3781–3795 CrossRef CAS.
- I. H. Sarker, SN Comput. Sci., 2021, 2, 160 CrossRef PubMed.
- X. F. Cadet, O. Lo-Thong, S. Bureau, R. Dehak and M. Bessafi, Sci. Rep., 2019, 9, 19197 CrossRef CAS PubMed.
- N. Artrith, K. T. Butler, F.-X. Coudert, S. Han, O. Isayev, A. Jain and A. Walsh, Nat. Chem., 2021, 13, 505–508 CrossRef CAS PubMed.
- J. Cervantes, F. Garcia-Lamont, L. Rodríguez-Mazahua and A. Lopez, Neurocomputing, 2020, 408, 189–215 CrossRef.
- R. J. LeSuer and W. E. Geiger, Angew. Chem., Int. Ed., 2000, 39, 248–250 CrossRef CAS PubMed.
- A. Simonova, I. Magriñá, V. Sýkorová, R. Pohl, M. Ortiz, L. Havran, M. Fojta, C. K. O'Sullivan and M. Hocek, Chem. – Eur. J., 2020, 26, 1286–1291 CrossRef CAS PubMed.
- H. Fink, N. J. Long, A. J. Martin, G. Opromolla, A. J. P. White, D. J. Williams and P. Zanello, Organometallics, 1997, 16, 2646–2650 CrossRef CAS.
- B. Wang and J. Anzai, Int. J. Electrochem. Sci., 2015, 10, 3260–3268 CAS.
- K. Lehmann, O. Yurchenko and G. Urban, J. Phys.: Conf. Ser., 2014, 557, 012008 CrossRef.
- K. Ono, Y. Tohyama, T. Uchikura, Y. Kikuchi, K. Fujii, H. Uekusa and N. Iwasawa, Dalton Trans., 2017, 46, 2370–2376 RSC.
- R. Knapp and M. Rehahn, J. Organomet. Chem., 1993, 452, 235–240 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- R. Dennington, T. Keith and J. Milla, GaussView, Version 6.1.1, Semichem Inc., Shawnee Mission, KS, 2019.
- M. Bolte , CSD Communication(Private Communication), 2011, Refcode: OBEBUU.
- G. J. Palenik, Inorg. Chem., 1969, 8, 2744–2749 CrossRef CAS.
- I. D. Madura, K. Czerwińska and D. Sołdańska, Cryst. Growth Des., 2014, 14, 5912–5921 CrossRef CAS.
- K. Durka, K. N. Jarzembska, R. Kamiński, S. Luliński, J. Serwatowski and K. Woźniak, Cryst. Growth Des., 2012, 12, 3720–3734 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Optimalization experiments, spectral characterization, additional discussion on machine learning, thermal properties, SEM data, and theoretical calculations. See DOI: https://doi.org/10.1039/d2dt01306a |
| This journal is © The Royal Society of Chemistry 2022 |