Anionic ordering in Pb₂Ti₄O₉F₂ revisited by nuclear magnetic resonance and density functional theory

Abstract

A combination of ¹⁹F magic angle spinning (MAS) nuclear magnetic resonance (NMR) and density functional theory (DFT) were used to study the ordering of F atoms in Pb₂Ti₄O₉F₂. This analysis revealed that F atoms predominantly occupy two of the six available inequivalent sites in a ratio of 73 : 27. DFT-based calculations explained the preference of F occupation on these sites and quantitatively reproduced the experimental occupation ratio, independent of the choice of functional. We concluded that the Pb atom's 6s² lone pair may play a role (∼0.1 eV per f.u.) in determining the majority and minority F occupation sites with partial density of states and crystal orbital Hamiltonian population analyses applied to the DFT wave functions.

---

1 Introduction

Understanding the mechanisms that produce ionic ordering in materials may lead to control of the self-assembly of ordered super lattices on an underlying crystal structure. Because ordered and disordered structures have remarkably different electronic and transport properties, controlling ordering is a key step in material design. For example, the properties of mixed-anion compounds strongly depend on the degree of order or disorder of the anions.^1,2 Anionic ordering can cause heteroleptic coordinations or low-dimensional structures, which in turn modify electronic properties.^1,2 This intriguing possibility to modify a material has attracted significant attention.^3–6 Some ABX₃ perovskites are typical examples. SrTaO₂N and BaTaO₂N have a high dielectric constant because of their O/N anionic ordering.^7–9 In addition, an oxyhydride SrVO₂H shows two-dimensional electron conduction and compression anisotropy because of the O/H anionic ordering.¹⁰

In complex composite materials, multiple anions and cations are heteroleptically coordinated, and their concentrations typically obey valence charge neutrality conditions. When differences in ionic radii, electronegativity, or polarizability are large, some materials tend to exhibit ionic ordering.^11,12 However, although O²⁻ and F⁻ are neighboring anions in the periodic table, the oxyfluorides nevertheless exhibit anionic ordering, depending on the structure. Whereas simple cubic perovskites (SrFeO₂F,¹³ BaFeO₂F,¹⁴ PbScO₂F,¹⁵ BaScO₂F,¹⁶ AgFeOF₂,¹⁷ BaInO₂F,¹⁸ and AgTiO₂F ¹⁹) adopt disordered configurations, a variety of Ruddlesden–Popper-type layered perovskites (Sr₂CuO₂F₂,²⁰ Sr₂FeO₃F,^21,22 Ba₂InO₃F,²³ Ba₂ScO₃F,²⁴ Sr₂MnO₃F,²⁵ Sr₃Fe₂O_5−xF_y ^21,26) exhibit ordered configurations of F⁻.²⁷ For an ordered structure to be formed, migration energy barriers must be small enough to allow the minimum free energy configuration to be achieved via practical annealing temperatures and times. The lowest energy structure frequently can be found by considering Pauling's second rule,²⁸ which explains that an ionic structure will be stable when the sum of the strength of the electrostatic bonds around an ion are equal to its charge. Thus, according to Pauling's second rule, F⁻ should prefer a more open site compared with O²⁻, leading to O/F anionic ordering. Some nonlayered oxyfluorides with or akin to perovskite structure showing a complete or partial anionic ordering have been reported, such as Pb₂Ti₂O_5.4F_1.2 ²⁹ Pb₂OF₂,³⁰ and Pb₂Ti₄O₉F₂.³¹ The anionic ordering of some nonlayered oxyfluorides is considered to be due to the Jahn–Teller distortion by the 6s² lone pair.^29,31

Among the nonlayered oxyfluorides with anionic ordering, Pb₂Ti₄O₉F₂ is especially attractive to study because this material uniquely has an isostructural oxide Bi₂Ti₄O₁₁.^31,32 Both Pb²⁺ and Bi³⁺ have the same electronic configuration and 6s² lone pairs. Bi₂Ti₄O₁₁ undergoes antiferroelectric-paraelectric transitions from C2/c to C2/m, whereas Pb₂Ti₄O₉F₂ does not.^31,32 The high-temperature paraelectric phase of Bi₂Ti₄O₁₁ (C2/m) adopts the same space group symmetry as Pb₂Ti₄O₉F₂.³² Because the Bi₂Ti₄O₁₁-type structure is significantly low symmetric, an anionic ordering can exist in Pb₂Ti₄O₉F₂. Structural analyses based on the synchrotron X-ray diffraction (SXRD) patterns revealed the presence of anionic ordering.³¹ However, this conclusion is debatable because heavier Pb atoms in the system could hamper the identification of F occupation sites.

In this work, the anionic ordering in Pb₂Ti₄O₉F₂ was reexamined via a combination of ¹⁹F magic angle spinning (MAS) nuclear magnetic resonance (NMR) experiments and density functional theory (DFT) simulations. The ¹⁹F MAS NMR analysis revealed that F atoms randomly occupy two of the six sites in a ratio of 73 : 27, overturning the previous conclusion that F atoms selectively occupy a single site.³¹ DFT calculations identified the majority and minority F occupation sites and quantitatively reproduced the experimental occupation ratio, independent of the choice of functional. Partial density of states (PDOS) and crystal orbital Hamiltonian population (COHP) analyses were performed on the DFT results, showing that the 6s² lone pairs may play a role (∼0.1 eV per f.u.) in determining the majority and minority F occupation sites. On the other hand, DFT calculations revealed that the low-symmetric anionic coordinates around the cations may barely be due to the steric effects of 6s² lone pairs. This result goes against the current discussion in this class of materials and implies that the influence of 6s² lone pairs on the structural distortion might be similarly not significant in some of the other Pb-based oxyfluorides such as Pb₂Ti₂O_5.4F_1.2 ²⁹ and Pb₂OF₂.³⁰

2 Experimental details

The powder samples of Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁ were prepared by solid-state reaction, as previously reported.^31,32 The Pb₂Ti₄O₉F₂ was synthesized from a mixture of PbO (99.9%, Rare Metallic Co.), PbO₂ (99.9%, Rare Metallic Co.), PbF₂ (99.9%, Rare Metallic Co.), and TiO₂ (rutile, 99.9%, Rare Metallic Co.) powders that were weighed to be 10 mol% F-rich to compensate for the loss of F during the reaction.³³ The pelletized mixture was sealed in an evacuated Pyrex tube and treated at 823 K for 12 h in an electric furnace, followed by natural cooling to room temperature. The Bi₂Ti₄O₁₁ was synthesized from a stoichiometric mixture of Bi₂O₃ (99.9%, Rare Metallic Co.) and TiO₂ (99.9%, Rare Metallic Co.) powders. The pelletized mixture was treated at 1273 K for 12 h in air in an electric furnace, followed by natural cooling to room temperature.

Production of a single phase for both Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁ samples were confirmed via SXRD. SXRD patterns were collected with a large Debye-Scherrer camera installed at beamline BL02B2 of the SPring-8 synchrotron radiation facility using a glass capillary and a solid-state detector.³⁴ The crystallographic parameters were refined by the Rietveld method using the RIETAN-FP program.³⁵ The electron density distributions were estimated by the maximum entropy method (MEM) using the Dysnomia program.³⁶

Solid-state NMR experiments were conducted on a homemade spectrometer with a 4 mm T3 probe (Varian) in a magnetic field of 4.7 T. All ¹⁹F NMR transients under MAS were accumulated using a background suppression method. The radio frequency field strength was 100 kHz, corresponding to 2.5 μs of π/2 pulse length. The longitudinal relaxation time (T₁) was obtained by analyzing a build-up curve measured with a saturation recovery method. Rotational resonance experiments, which allow for solving whether the chemical-shift filter was set to half of the inverse of the difference between two signals and the MAS rate, was set to the inverse of the difference between two signals in rotational resonance experiments (further details given in ESI‡).

3 Calculation details

The DFT calculations were performed with Quantum Espresso.³⁷ Perdew–Burke–Ernzerhof (PBE),³⁸ Becke–Lee–Yang–Parr (BLYP),^39,40 and Perdew–Wang 1991 (PW91)^41,42 semi-local exchange–correlation functionals were employed. The valence orbitals were expanded with plane waves. The cutoff energy was 100 Ry, and the k-point mesh was 7 × 7 × 5 for a unit cell. With this choice of parameters, the energy difference between the first and second most stable anionic ordering patterns of Pb₂Ti₄O₉F₂ converged below 2 meV per f.u. These two ordering patterns are denoted as F-in-site6 and F-in-site5 in section 4.1. The core orbitals were described by the projector augmented wave (PAW) method.⁴³ PAW pseudopotentials were taken from the pslibrary.⁴⁴ Comparing the results of PAW and ultrasoft pseudopotentials in the pslibrary⁴⁴ revealed that the relative total energies among the different anionic orderings are identical within 1 meV per f.u. Therefore, the errors from pseudopotential approximation would be negligible for this system. Ultrasoft pseudopotentials were used to calculate the electrostatic energies because PAW pseudopotentials cannot separately provide the electrostatic energies because the one-center term includes both electrostatic and exchange–correlation energies.⁴⁵ The PDOS of Pb₂Ti₄O₉F₂ was obtained with the PBE functional. The LOBSTER code⁴⁶ was used to perform the COHP analyses based on the PBE-DFT results with the pbeVaspFit2015 basis set.^47,48 Every DFT calculation was performed for the energetically optimized structure.

4 Results and discussion

4.1 Determination of anionic configurations

As shown in Fig. 1, Pb₂Ti₄O₉F₂ has six different anion sites, which are denoted by site 1–6. Previous structural analysis based on SXRD patterns has indicated that F atoms selectively occupy site 6, which is the closest site to the Pb atom.³¹ Here, that earlier conclusion is reexamined using NMR experiments and DFT simulations.

Fig. 1 The crystal structure of Pb₂Ti₄O₉F₂ at 300 K. The numbers indicate the numbers of anion sites.

A ¹⁹F MAS NMR spectrum of Pb₂Ti₄O₉F₂ is shown together with a peak fitting result in Fig. 2. By fitting the spectrum with three Gaussians, the peak positions were obtained as −45 ppm, −58 ppm, and −63 ppm, with an area ratio of 26.1 : 1.8 : 72.1. The peak positions correspond to the ¹⁹F atoms in different distinct sites, and the area ratio indicates their occupancy ratio. Through-space correlation NMR experiments were conducted to confirm whether the ¹⁹F atoms showing in the two main peaks exist in the same crystal phase. When the MAS rate was matched to the resonant frequency difference of the two main peaks, both peak intensities varied periodically with mixing time. However, when the MAS rate was faster than the resonant frequency difference, neither peak intensity changed (details in ESI‡). This means that the dipole interaction that disappeared because of MAS was reintroduced by rotational resonance, and the magnetization was exchanged during the mixing time. Thus, the F sites showing the two main signals are nearby in the same crystalline phase, Pb₂Ti₄O₉F₂.

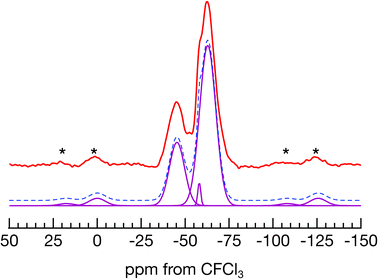Fig. 2 A ¹⁹F MAS NMR spectrum of Pb₂Ti₄O₉F₂ (top) and peak fitting result (bottom). The asterisks indicate spinning sidebands.

The position of the F occupation sites corresponding to the two main peaks in the ¹⁹F MAS NMR experiment must be determined using another method. Therefore, the energies of different F occupation patterns were evaluated with DFT to find the majority and minority F occupation sites corresponding to the two main peaks. In reality, numerous F occupation patterns are possible, and we cannot study all of them. Therefore, targets were restricted to be the cases in which F atoms selectively occupy each of the sites, and the F atom's stability in each site was evaluated. Table 1 lists the relative total energies given by PBE,³⁸ BLYP,^39,40 and PW91^41,42 functionals. In the table, for example, F-in-site2 indicates the case in which F atoms selectively occupy site 2. The F stability at site 3 was evaluated as E (F-in-site3) ≡2E (one F atom in site 3 and the other in site 6 in the unit cell) – E (F-in-site6) because the multiplicity of site 3 is one (multiplicity of the other sites is two). The three functionals qualitatively and quantitatively agree with each other. F-in-site6 and F-in-site5 give the first and second lowest energies, so the majority and minority F occupation sites are sites 6 and 5, respectively. The experimental third tiny peak at −58 ppm corresponds to the F occupancy in site 4. The percentages in the parentheses in Table 1 indicate the ratios of Boltzmann factors of the relative energies under the synthesis temperature, 823 K. These percentages correspond to the F occupation ratio of the anion sites. The ratio between the percentages of F-in-site6 and F-in-site5, approximately 70 : 30, closely agrees with that between the experimental F occupation ratios of the majority and minority sites, 73 : 27.

Table 1 Comparisons of the energy differences (eV per f.u.) between alternative anionic ordering patterns in Pb₂Ti₄O₉F₂. All energies are differences with the energy of F-in-site6. The percentages indicate the ratios of the corresponding Boltzmann factors at the synthesis temperature, 823 K. F-in-site3 does not indicate an anionic ordering pattern different from the others, as described in the main text

	ΔE (PBE)	ΔE (BLYP)	ΔE (PW91)
F-in-site1	1.019 (0.0%)	0.965 (0.0%)	1.018 (0.0%)
F-in-site2	0.935 (0.0%)	0.889 (0.0%)	0.937 (0.0%)
F-in-site3	0.513 (0.1%)	0.514 (0.1%)	0.543 (0.0%)
F-in-site4	0.321 (0.8%)	0.308 (0.9%)	0.322 (0.7%)
F-in-site5	0.061 (29.5%)	0.066 (28.0%)	0.058 (30.3%)
F-in-site6	0.000 (69.7%)	0.000 (71.1%)	0.000 (69.0%)

---

4.2 Reason why sites 5 and 6 have a preference for F atoms

To understand the origin of the F-in-site6 and F-in-site5 stabilization, PBE,³⁸ BLYP,^39,40 and PW91^41,42 functionals were used to compare the electrostatic energies with the total energies, as shown in Fig. 3. The results of the three functionals are qualitatively consistent with each other. The total energies in Fig. 3 are identical to those listed in Table 1. The total energies are roughly proportional to the electrostatic energies, consistent with a previous systematic study on NdNiO₂F by simulations.⁴⁹ However, F-in-site6, which had the lowest total energy, is an exception to Pauling's second rule²⁸ because the lowest electrostatic energy was predicted for the F-in-site5.

Fig. 3 Comparison of electrostatic energies and total energies calculated by DFT, using PBE (blue circles), BLYP (orange squares), and PW91 (green triangles) functionals. The minimum electrostatic energy (i.e., F-in-site5) and total energy (i.e., F-in-site6) are set to be zero, and the others are relative to this for every functional.

The reason of the small deviation (∼0.1 eV per f.u.) from Pauling's second rule²⁸ is unclear. However, the steric effects introduced by the 6s² lone pairs may explain this deviation. Fig. 4 shows the PDOS of each F ordering pattern in Pb₂Ti₄O₉F₂ given by the PBE functional. A peak of Pb-6s (indicated by an arrow) hybridized with O-2p exists at the valence band maximum (VBM). This peak is considered to be a signal of the orbital hybridization described by the revised lone-pair (RLP) model.⁵⁰ This model proposes that the antibonding hybridized orbital of Pb-6s and O-2p_z is further stabilized by hybridizing with the Pb-6p orbital. This antibonding orbital distributes opposite to the O⁵⁰ and interrupts bonding with the other anions. The PDOS figures show that F-in-site6 has the smallest Pb-6s peak (i.e., the weakest RLP hybridization), presumably owing to the absence of O6 (i.e., an O ion in site 6) that is the closest to Pb and has the largest 2p density of states (DOS) at the VBM. Furthermore, the magnitudes of the hybridization between Pb-6s and O/F6-2p were evaluated for F-in-site5 and F-in-site6 in terms of integrated COHP (ICOHP) by the COHP analysis applied to the PBE–DFT results. Here, ICOHP indicates how much the hybridization contributes to the stabilization by the binding. The ICOHPs of Pb-O6 in F-in-site5 and Pb-F6 in F-in-site6 are −2.81 and −0.90 eV, so the contribution of the 6s² lone pair is certainly smaller when F atoms occupy site 6. This explanation for the F-in-site6 stabilization is an exception to Pauling's second rule.²⁸

Fig. 4 PDOS of different F occupation patterns obtained by DFT. The arrows indicate the peaks accompanied by the antibonding hybrid orbitals explained by the lone-pair model. For the F-in-site6 case, the O(site6)-2p distribution is not shown because site 6 is occupied by F atoms.

4.3 Comparison between Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁

Fig. 5 compares the experimental structures of Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁, which were obtained by the Rietveld analysis of SXRD patterns. The SXRD patterns are provided in the ESI.‡ Comparing the isostructural Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁, the anionic configurations around the cations are more symmetric in Pb₂Ti₄O₉F₂ than in Bi₂Ti₄O₁₁. For example, the difference of the smallest (blue) and largest (red) interatomic distances are smaller in Pb₂Ti₄O₉F₂ than in Bi₂Ti₄O₁₁. It is worth noting that this trend is the exact opposite of some Ruddlesden–Popper-type layered perovskites. The (B site metal)–O₆ octahedra in layered perovskite oxides are often distorted by the Jahn–Teller effect.^21,51 The F atoms selectively occupy the apical sites and lead to significantly longer (B site metal)–F^apical distance than (B site metal)–O^apical and O^equatorial distances.^20–25 However, the oxyfluoride Pb₂Ti₄O₉F₂ is less distorted than the isostructural oxide Bi₂Ti₄O₁₁, as shown in Fig. 5.

Fig. 5 Experimental geometries of Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁ obtained via Rietveld refinement of SXRD patterns. The smallest and largest interatomic distances are shown with blue and red colors, respectively.

Table 2 compares the experimental structure and theoretical F-in-site6 and F-in-site5 structures of Pb₂Ti₄O₉F₂. The theoretical values are given as the mean values of the three functionals. The errors indicate the unbiased deviations of the means. The F-in-site5 is slightly less symmetric than F-in-site6, but their differences are not significant, which indicates that the low-symmetric anionic configurations around the cations in Pb₂Ti₄O₉F₂ are barely due to the steric effects of 6s² lone pairs: the structure is naively low-symmetric. The less symmetric structure of Bi₂Ti₄O₁₁ than Pb₂Ti₄O₉F₂ can be simply explained by that Bi³⁺ cations are more positive than Pb²⁺ cations and prefer to be closer to anions. In the case of Bi₂Ti₄O₁₁, the steric effects of 6s² lone pairs may also contribute to the low-symmetric anionic configurations as discussed based on the MEM analyses in the ESI.‡ The finding from Table 2 demonstrates that the influence of 6s² lone pairs on the structural distortion might be similarly not significant in some of the other Pb-based oxyfluorides such as Pb₂Ti₂O_5.4F_1.2 ²⁹ and Pb₂OF₂.³⁰

Table 2 Parameters of the experimental structure and DFT structures (F-in-site5 and F-in-site6) obtained for Pb₂Ti₄O₉F₂. The values for the DFT structures are given as the mean values of the three functionals. The errors indicate the unbiased deviations of the means. The second rows for the F-in-site6 and F-in-site5 indicate the differences from experimental values in percentages

		a	b	c	β (°)	Pb-O/F4	Pb-O/F5	Pb-O/F6^shorter	Pb-O/F6^longer
Expt.	Å	14.63	3.83	10.75	135.58	2.56	2.95	2.42	2.56
F-in-site6	Å	15.07(8)	3.84(1)	10.54(7)	133.44(6)	2.54(1)	2.93(2)	2.44(1)	2.58(1)
	%	+3.0(6)	+0.3(3)	−2.0(7)	−1.6(1)	−0.1(3)	−0.8(5)	+1.0(2)	+0.9(2)
F-in-site5	Å	14.83(7)	3.84(1)	10.60(6)	132.30(2)	2.58(1)	3.03(1)	2.37(1)	2.58(2)
	%	+1.4(5)	+0.2(3)	−1.4(6)	−2.4(1)	+1.6(3)	+2.7(4)	−2.0(4)	+0.9 (6)

---

5 Conclusion

A combination of ¹⁹F MAS NMR experiments and DFT simulations were used to investigate the anionic ordering in Pb₂Ti₄O₉F₂. The ¹⁹F MAS NMR experiments showed that F atoms predominantly occupy two of the six distinct available sites in Pb₂Ti₄O₉F₂ in a ratio of 73 : 27. DFT calculations identified the majority and minority F occupation sites to be sites 6 and 5, respectively. The occupation ratios between sites 6 and 5 were quantitatively reproduced by theory, independent of the choice of functional. PDOS and COHP analyses revealed that the 6s² lone pairs of Pb atom may play a role (∼0.1 eV per f.u.) in determining the site 6 (5) the majority (minority) site, against what is predicted by Pauling's second rule.²⁸

The low-symmetric anionic coordinates around the cations in Pb₂Ti₄O₉F₂ have been considered to be the consequence of the steric effect by the 6s² lone pairs, as well as Bi₂Ti₄O₁₁,³² Pb₂Ti₂O_5.4F_1.2,²⁹ and some Aurivillius oxides ABi₂Nb(Ta)₂O₉.⁵² However, our DFT results indicate that the 6s² lone pairs may barely induce a structural distortion in Pb₂Ti₄O₉F₂. This finding demonstrates that the influence of 6s² lone pairs on the structural distortion might be similarly not significant in some of the other Pb-based oxyfluorides such as Pb₂Ti₂O_5.4F_1.2 ²⁹ and Pb₂OF₂.³⁰

Author contributions

K.O., T.I., and D.K. conceived the ideas of this work. All the authors contributed to the discussion and writing of the paper. K.O. and K.Y. synthesized the Pb₂Ti₄O₉F₂ and Bi₂Ti₄O₁₁ samples, analyzed the crystal structures, and performed MEM analyses. Y.N., Y.T., and N.N. performed the ¹⁹F MAS NMR measurements. T.I., D.K., and K.H. performed the ab initio calculations. M.I., R.M., and F.A.R. supervised the work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Erica Heinrich for valuable help with manuscript preparation. The VESTA program⁵³ was used to visualize the experimental and DFT crystal structures and electronic densities. The authors thank Prof. Sudo and Mr. Kitao of Kindai University for their help in the solid state NMR measurement. This work was partially supported by a Grant-in-Aid for Scientific Research on Innovative Area “Mixed Anion (Project JP17H05489, JP19H04706)” (JSPS). The synchrotron radiation experiments were performed at the BL02B2 of SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2016A1157 and 2018A1227). The ab initio calculations were performed with the computational resources of the Research Center for Advanced Computing Infrastructure (RCACI) at JAIST. The authors gratefully thank Division of Joint Research Center, Kindai University, for the solid-state NMR measurements. T. I. and F. A. R. acknowledge support from US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. K. O. is grateful for financial support from Kansai Research Foundation for technology promotion and a Grant-in-Aids for Scientific Research (C) (Project JP16K05731 and 21K04659). K. H. is grateful for financial support from MEXT-KAKENHI (JP19K05029, JP21K03400, JP21H01998, and JP22H02170), and the Air Force Office of Scientific Research (Award Numbers: FA2386-20-1-4036). R. M. is grateful for financial supports from MEXT-KAKENHI (22H05146, 21K03400 and 19H04692), from the Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049;FA2386-19-1-4015), and from JSPS Bilateral Joint Projects (JPJSBP120197714).

References

1. H. Kageyama, T. Yajima, Y. Tsujimoto, T. Yamamoto, C. Tassel and Y. Kobayashi, Exploring Structures and Properties through Anion Chemistry, Bull. Chem. Soc. Jpn., 2019, 92, 1349–1357.
2. K. Maeda, F. Takeiri, G. Kobayashi, S. Matsuishi, H. Ogino, S. Ida, T. Mori, Y. Uchimoto, S. Tanabe, T. Hasegawa, N. Imanaka and H. Kageyama, Recent Progress on Mixed-Anion Materials for Energy Applications, Bull. Chem. Soc. Jpn., 2022, 95, 26–37.
3. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Expanding frontiers in materials chemistry and physics with multiple anions, Nat. Commun., 2018, 9, 772.
4. R. Kuriki, T. Ichibha, K. Hongo, D. Lu, R. Maezono, H. Kageyama, O. Ishitani, K. Oka and K. Maeda, A Stable, Narrow-Gap Oxyfluoride Photocatalyst for Visible-Light Hydrogen Evolution and Carbon Dioxide Reduction, J. Am. Chem. Soc., 2018, 140, 6648–6655.
5. T. Oshima, T. Ichibha, K. S. Qin, K. Muraoka, J. J. M. Vequizo, K. Hibino, R. Kuriki, S. Yamashita, K. Hongo, T. Uchiyama, K. Fujii, D. Lu, R. Maezono, A. Yamakata, H. Kato, K. Kimoto, M. Yashima, Y. Uchimoto, M. Kakihana, O. Ishitani, H. Kageyama and K. Maeda, Undoped Layered Perovskite Oxynitride Li₂LaTa₂O₆N for Photocatalytic CO₂ Reduction with Visible Light, Angew. Chem., Int. Ed., 2018, 57, 8154–8158.
6. T. Oshima, T. Ichibha, K. Oqmhula, K. Hibino, H. Mogi, S. Yamashita, K. Fujii, Y. Miseki, K. Hongo, D. Lu, R. Maezono, K. Sayama, M. Yashima, K. Kimoto, H. Kato, M. Kakihana, H. Kageyama and K. Maeda, Two-Dimensional Perovskite Oxynitride K₂LaTa₂O₆N with an H⁺/K⁺ Exchangeability in Aqueous Solution Forming a Stable Photocatalyst for Visible-Light H₂ Evolution, Angew. Chem., Int. Ed., 2020, 59, 9736–9743.
7. Y.-I. Kim, P. M. Woodward, K. Z. Baba-Kishi and C. W. Tai, Characterization of the Structural, Optical, and Dielectric Properties of Oxynitride Perovskites AMO₂N (A = Ba, Sr, Ca; M = Ta, Nb), Chem. Mater., 2004, 16, 1267–1276.
8. K. Page, M. W. Stoltzfus, Y.-I. Kim, T. Proffen, P. M. Woodward, A. K. Cheetham and R. Seshadri, Local Atomic Ordering in BaTaO₂N Studied by Neutron Pair Distribution Function Analysis and Density Functional Theory, Chem. Mater., 2007, 19, 4037–4042.
9. M. Yang, J. Oró-Solé, J. A. Rodgers, A. B. Jorge, A. Fuertes and J. P. Attfield, Anion order in perovskite oxynitrides, Nat. Chem., 2010, 3, 47–52.
10. T. Yamamoto, D. Zeng, T. Kawakami, V. Arcisauskaite, K. Yata, M. A. Patino, N. Izumo, J. E. McGrady, H. Kageyama and M. A. Hayward, The role of π-blocking hydride ligands in a pressure-induced insulator-to-metal phase transition in SrVO₂H, Nat. Commun., 2017, 8, 1217.
11. J. P. Attfield, Principles and Applications of Anion Order in Solid Oxynitrides, Cryst. Growth Des., 2013, 13, 4623–4629.
12. A. Fuertes, Prediction of Anion Distributions Using Pauling's Second Rule, Inorg. Chem., 2006, 45, 9640–9642.
13. C. M. Thompson, C. K. Blakely, R. Flacau, J. E. Greedan and V. V. Poltavets, Structural and magnetic behavior of the cubic oxyfluoride SrFeO₂F studied by neutron diffraction, J. Solid State Chem., 2014, 219, 173–178.
14. F. J. Berry, F. C. Coomer, C. Hancock, O. Helgason, E. A. Moore, P. R. Slater, A. J. Wright and M. F. Thomas, Structure and magnetic properties of the cubic oxide fluoride BaFeO₂F, J. Solid State Chem., 2011, 184, 1361–1366.
15. T. Katsumata, M. Nakashima, H. Umemoto and Y. Inaguma, Synthesis of the novel perovskite-type oxyfluoride PbScO₂F under high pressure and high temperature, J. Solid State Chem., 2008, 181, 2737–2740.
16. R. L. Needs and M. T. Weller, A New 2+/3+ Perovskite: The Synthesis and Structure of BaScO₂F, J. Solid State Chem., 1998, 139, 422–423.
17. F. Takeiri, T. Yamamoto, N. Hayashi, S. Hosokawa, K. Arai, J. Kikkawa, K. Ikeda, T. Honda, T. Otomo, C. Tassel, K. Kimoto and H. Kageyama, AgFeOF₂: A Fluorine-Rich Perovskite Oxyfluoride, Inorg. Chem., 2018, 57, 6686–6691.
18. T. Katsumata, R. Suzuki, N. Satoh, S. Suzuki, M. Nakashima, Y. Inaguma, D. Mori, A. Aimi and Y. Yoneda, Synthesis of new perovskite-type oxyfluorides, BaInO₂F and comparison of the structure among perovskite-type oxyfluorides, J. Solid State Chem., 2019, 279, 120919.
19. Y. Inaguma, K. Sugimoto and K. Ueda, Synthesis of the perovskite-type oxyfluoride AgTiO₂F: an approach adopting the HSAB principle, Dalton Trans., 2020, 49, 6957–6963.
20. M. Ai-Mamouri, P. P. Edwards, C. Greaves and M. Slaski, Synthesis and superconducting properties of the strontium copper oxy-fluoride Sr₂CuO₂F_2+δ, Nature, 1994, 369, 382–384.
21. G. Simon Case, A. L. Hector, W. Levason, R. L. Needs, M. F. Thomas and M. T. Weller, Syntheses, powder neutron diffraction structures and Mössbauer studies of some complex iron oxyfluorides: Sr₃Fe₂O₆F_0.87, Sr₂FeO₃F and Ba₂InFeO₅F_0.68, J. Mater. Chem., 1999, 9, 2821–2827.
22. A. L. Hector, J. A. Hutchings, R. L. Needs, M. F. Thomas and M. T. Weller, Structural and Mössbauer study of Sr₂FeO₃X (X = F, Cl, Br) and the magnetic structure of Sr₂FeO₃F, J. Mater. Chem., 2001, 11, 527–532.
23. R. L. Needs and M. T. Weller, Synthesis and structure of Ba₂InO₃F: oxide/fluoride ordering in a new K₂NiF₄ superstructure, J. Chem. Soc., Chem. Commun., 1995, 353–354.
24. R. L. Needs, M. T. Weller, U. Scheler and R. K. Harris, Synthesis and structure of Ba₂InO₃X (X = F, Cl, Br) and Ba₂ScO₃F; oxide/halide ordering in K₂NiF₄-type structures, J. Mater. Chem., 1996, 6, 1219–1224.
25. Y. Su, Y. Tsujimoto, Y. Matsushita, Y. Yuan, J. He and K. Yamaura, High-Pressure Synthesis, Crystal Structure, and Magnetic Properties of Sr₂MnO₃F: A New Member of Layered Perovskite Oxyfluorides, Inorg. Chem., 2016, 55, 2627–2633.
26. Y. Tsujimoto, K. Yamaura, N. Hayashi, K. Kodama, N. Igawa, Y. Matsushita, Y. Katsuya, Y. Shirako, M. Akaogi and E. Takayama-Muromachi, Topotactic Synthesis and Crystal Structure of a Highly Fluorinated Ruddlesden–Popper-Type Iron Oxide, Sr₃Fe₂O_5+xF_2−x(x∼0.44), Chem. Mater., 2011, 23, 3652–3658.
27. L.-S. Du, F. Wang and C. P. Grey, High-Resolution ¹⁹F MAS and ¹⁹F–¹¹³Cd REDOR NMR Study of Oxygen/Fluorine Ordering in Oxyfluorides, J. Solid State Chem., 1998, 140, 285–294.
28. L. Pauling, The nature of the chemical bond and the structure of molecules and crystals: an introduction to modern structural chemistry, Cornell University Press, Ithaca, N.Y., 1960, pp. 543–562.
29. K. Oka, H. Hojo, M. Azuma and K. Oh-ishi, Temperature-Independent, Large Dielectric Constant Induced by Vacancy and Partial Anion Order in the Oxyfluoride Pyrochlore Pb₂Ti₂O_6−δF_2δ, Chem. Mater., 2016, 28, 5554–5559.
30. Y. Inaguma, K. Ueda, T. Katsumata and Y. Noda, Low-temperature formation of Pb₂OF₂ with O/F anion ordering by solid state reaction, J. Solid State Chem., 2019, 277, 363–367.
31. K. Oka and K. Oh-ishi, Observation of Anion Order in Pb₂Ti₄O₉F₂, Inorg. Chem., 2015, 54, 10239–10242.
32. V. Kahlenberg and H. Böhm, The structures of α- and β-Bi₂Ti₄O₁₁, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 11–18.
33. T. Katsumata, M. Nakashima, Y. Inaguma and T. Tsurui, Synthesis of New Perovskite-Type Oxyfluoride, PbMnO₂F, Bull. Chem. Soc. Jpn., 2012, 85, 397–399.
34. S. Kawaguchi, M. Takemoto, K. Osaka, E. Nishibori, C. Moriyoshi, Y. Kubota, Y. Kuroiwa and K. Sugimoto, High-throughput powder diffraction measurement system consisting of multiple MYTHEN detectors at beamline BL02B2 of SPring-8, Rev. Sci. Instrum., 2017, 88, 085111.
35. F. Izumi and K. Momma, Three-Dimensional Visualization in Powder Diffraction, Solid State Phenomena, 2007, 130, 15–20.
36. K. Momma, T. Ikeda, A. A. Belik and F. Izumi, Dysnomia, a computer program for maximum-entropy method (MEM) analysis and its performance in the MEM-based pattern fitting, Powder Diffr., 2013, 28, 184–193.
37. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100.
40. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
41. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
42. J. P. Perdew and Y. Wang, Erratum: Accurate and simple analytic representation of the electron-gas correlation energy [Phys. Rev. B 45, 13244 (1992)], Phys. Rev. B, 2018, 98, 079904.
43. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
44. A. Dal Corso, Pseudopotentials periodic table: From H to Pu, Comput. Mater. Sci., 2014, 95, 337–350.
45. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
46. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory, J. Comput. Chem., 2020, 41, 1931–1940.
47. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids, J. Comput. Chem., 2013, 34, 2557–2567.
48. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035.
49. Y. Kurauchi, T. Katayama, A. Chikamatsu and T. Hasegawa, Two-Dimensional Fluorine Distribution in a Heavily Distorted Perovskite Nickel Oxyfluoride Revealed by First-Principles Calculation, J. Phys. Chem. C, 2019, 123, 31190–31195.
50. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Stereochemistry of post-transition metal oxides: revision of the classical lone pair model, Chem. Soc. Rev., 2011, 40, 4455–4463.
51. D. Lee and H. N. Lee, Controlling Oxygen Mobility in Ruddlesden–Popper Oxides, Materials, 2017, 10, 368.
52. Ismunandar and B. J. Kennedy, Gunawan and Marsongkohadi, Structure ofABi₂Nb₂O₉ (A = Sr, Ba): Refinement of Powder Neutron Diffraction Data, J. Solid State Chem., 1996, 126, 135–141.
53. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnotes

† This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).

‡ Electronic supplementary information (ESI) available. CCDC 2159898, 2159899 and 2191023. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt00839d

§ These two authors contributed equally.

---