Molecular ruby: exploring the excited state landscape

Abstract

The discovery of the highly NIR-luminescent molecular ruby [Cr(ddpd)₂]³⁺ (ddpd = N,N′-dimethyl-N,N′-dipyridin-2-ylpyridine-2,6-diamine) has been a milestone in the development of earth-abundant luminophors and has led to important new impulses in the field of spin–flip emitters. Its favourable optical properties such as a high photoluminescence quantum yield and long excited state lifetime are traced back to a remarkable excited state landscape which has been investigated in great detail. This article summarises the results of these studies with the aim to create a coherent picture of the excited state ordering and the ultrafast as well as long-timescale dynamics. Additional experimental data is provided to fill in gaps left by previous reports.

---

Introduction

In metal-to-ligand charge transfer (MLCT) emitters such as [Ru(bpy)₃]²⁺ an excited state ordering of ¹GS, ³MLCT, ¹MLCT and ³MC is commonly found and exploited for different applications like photocatalysis (GS = ground state, MC = metal-centered state, bpy = 2,2′-bipyridine).¹

In contrast, spin–flip emitters with the prototype ruby (Al₂O₃: Cr³⁺) possess a richer excited state landscape in the relevant energy region.^2,3 For a d³ electron configuration in O_h symmetry as found in octahedral Cr^III compounds, the metal-centered ⁴A₂, ²E/²T₁, ²T₂ and ⁴T₂ states are important (Fig. 1). Additionally, charge transfer states can play a role in excitation and decay processes.^4,5

Fig. 1 Tanabe–Sugano (TS) diagram of the d³ electron configuration in an octahedral ligand field with C/B = 4 and exemplary microstates.^4,14 The two important excited state quartet/doublet crossing points are highlighted with a circle and a square, respectively. Dotted lines in the microstates indicate strong electronic mixing.

In d³ spin–flip emitters, excitation to the ⁴T₂ state is followed by intersystem crossing (ISC) to the doublet states ²E/²T₁, from which phosphorescence to the quartet GS ⁴A₂ occurs.⁶ As the term “spin–flip emitter” suggests, this transition merely involves the flipping of a single electron spin. The ²E state features only unpaired electrons, while two electrons are paired in ²T₁ and ²T₂ states (Fig. 1).⁴ For spin–flip emission, the ²E/²T₁ states need to be the lowest excited states. Additionally, a large energy gap to the ⁴T₂ state is necessary to prevent ²E/²T₁ → ⁴T₂ back-ISC (bISC) and fast relaxation via⁴T₂ → ⁴A₂ fluorescence, internal conversion (IC) or ligand dissociation.⁷ This is achieved via a large ligand field splitting Δ₀, since the energy of the interconfigurational ⁴T₂ state is linearly dependent on Δ₀, while the energies of the intraconfigurational states ²E, ²T₁ and ²T₂ are essentially independent of Δ₀ and instead vary with interelectronic repulsion quantified by the Racah parameters B and C (Fig. 1).⁸ In general, Cr^III ions possess a small instrinsic ligand field splitting due to the primogenic effect.⁹

In ruby, the six oxido ligands exert a strong ligand field on the Cr³⁺ ions because of the short Cr–O distance imposed by the corundum host lattice. This results in a ⁴T₂ absorption band at 551 nm and strong phosphorescence at 694.3 (R₁ line) as well as 692.9 nm (R₂ line) via the slightly split ²E → ⁴A₂ transitions.^2,10 This emission with a lifetime of 4268 ± 6 μs and a photoluminescence quantum yield of 90 ± 5% was the cornerstone of the first laser in 1960.^2,3,11 In contrast, molecular Cr^III complexes like [Cr(bpy)₃]³⁺ (Φ = 0.089%)¹² or [Cr(tpy)₂]³⁺ (Φ < 0.001%)¹³ suffer from poor quantum yields due to the small Δ₀ facilitating bISC and other deactivation pathways (tpy = 2,2′:6′,2′′-terpyridine).⁴

Ground and excited states of the molecular ruby

In 2015, a breakthrough was achieved with the discovery of the strongly near infrared (NIR) luminescent complex [Cr(ddpd)₂]³⁺ (Fig. 2, ddpd = N,N′-dimethyl-N,N′-dipyridin-2-ylpyridine-2,6-diamine). Irradiation in the ⁴A₂ → ⁴T₂ and ligand-to-metal charge transfer (LMCT) absorption band at 435 nm yields a very intense dual phosphorescence at 738 and 775 nm (²T₁/²E → ⁴A₂, purple area in Fig. 3) with a lifetime of 1122 μs and quantum yields of 11% in aqueous and 13.7% in acetonitrile solution at room temperature.^7,15 The excitation spectra observed at 775 nm closely follow the absorption spectra in the region 300–500 nm demonstrating that all states efficiently evolve to the emissive states. Indeed, only a weak fluorescence (⁴T₂ → ⁴A₂, blue area in Fig. 3) at 500 nm was found with a lifetime⁷ of 3 ns and a quantum yield of approximately 0.01% (see ESI†). Overall, [Cr(ddpd)₂]³⁺ vastly outperforms classical chromium(III) complexes and hence was called molecular ruby.¹⁶ Detailed follow-up studies revealed several aspects underlying the reasons for its success.

Fig. 2 Molecular structure of [Cr(ddpd)₂]³⁺.

Fig. 3 Absorption spectra (H₂O: black line, CD₃CN: red line, see ESI†), MCD spectrum (H₂O/glycerol, 7 K, 7 T) and separately normalized fluorescence (blue area) and phosphorescence spectra (purple area, aerated H₂O) of [Cr(ddpd)₂]³⁺ and TD-DFT (B3LYP/Def2-TZVPP) calculated difference densities of the ⁴A₂ → ⁴T₂ transitions with an isosurface value of 0.005 a.u.^7,17

The ⁴A₂ GS of [Cr(ddpd)₂]³⁺ exhibits an almost spherical spin distribution as expected for a d³ configuration (Fig. 4). A small zero-field splitting of D = +0.18 cm⁻¹ and E = −0.06 cm⁻¹ was found through Q-band electron paramagnetic resonance (EPR) spectroscopy at 5 K.¹⁷ The [CrN₆] σ-skeleton is close to octahedral, but the π-bonding lowers the actual symmetry (point group D₂). Thus, all E and T terms found in the TS diagram (Fig. 1) should be split in [Cr(ddpd)₂]³⁺.

Fig. 4 CASSCF(7,12)-NEVPT2 derived state diagram at the GS geometry of [Cr(ddpd)₂]³⁺ with dominating electron configurations in the microstates and calculated spin-densities at an isosurface value of 0.05 a.u.²⁰

How large is the ligand field splitting Δ₀ in [Cr(ddpd)₂]³⁺, in other words, where is [Cr(ddpd)₂]³⁺ located in the TS diagram (Fig. 1)? Investigation of the absorption bands including the ⁴A₂ → ⁴T₂ transition at 435 nm with magnetic circular dichroism (MCD) spectroscopy at 7 K and 7 T in frozen solution and DFT calculations revealed Δ₀ ≫ 20 B (Fig. 3).¹⁷ Thus, the large ⁴T₂–²T₁/²E energy gap effectively suppresses bISC to the ⁴T₂ states as relaxation pathway. The large Δ₀ was rationalized with the strongly σ-donating nature of the electron-rich ligand ddpd and its six-membered chelate rings leading to an almost perfectly octahedral [CrN₆] coordination geometry and a large metal–ligand σ-orbital overlap.⁷

Multireference calculations with perturbation correction and ab initio ligand field analysis (CASSCF(3,5)-NEVPT2-AILFT) yielded Δ₀ = 23 000 cm⁻¹, B = 964 cm⁻¹ and C/B = 3.08 as ligand field parameters (B(free Cr³⁺ ion) = 918 cm⁻¹)¹⁸ and split E and T states.¹⁹ A larger active space in a CASSCF(7,12)-NEVPT2 calculation was used to generate the state diagram in Fig. 4.²⁰ According to this calculation, Δ₀ of [Cr(ddpd)₂]³⁺ is located close to the second quartet-doublet crossing point ⁴T₂–²T₂ in the TS diagram (black square in Fig. 1). Although the absolute calculated values are too high, trends can be well reproduced.¹⁹ In contrast to perfectly octahedral complexes such as [Cr(CN)₆]³⁻, CASSCF(7,12)-NEVPT2 calculations of [Cr(ddpd)₂]³⁺ place a spin-paired ²T₁-derived microstate below a ²E-derived true spin–flip microstate (²T₁(1) and ²E(1) in Fig. 4).^19,20 Thus the energy level ordering calculated for [Cr(ddpd)₂]³⁺ (Fig. 4) differs from the TS diagram (Fig. 1).

The sharp phosphorescence bands (purple area in Fig. 3) suggest that the emissive excited doublet states ²T₁(1) and ²E(1) are essentially nested, i.e. only weakly distorted relative to the ⁴A₂ GS, as expected for the unchanged (t_2g)³ electron configuration in the doublet states compared to the GS (Fig. 4).

The CASSCF calculated energy difference between the lowest doublet states ΔE amounts to 580 cm⁻¹.²⁰ Experimentally, values of 650 cm⁻¹ and 700 cm⁻¹ were derived from the emission band energy difference and the slopes of Boltzmann plots obtained from temperature dependent emission spectra in various solvents (Fig. 5), respectively.²¹

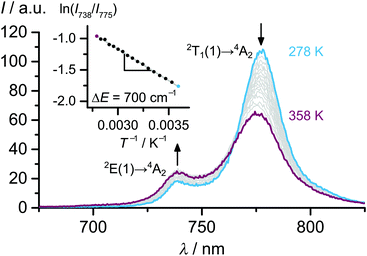Fig. 5 Phosphorescence spectra of [Cr(ddpd)₂][BF₄]₃ in H₂O at variable temperature. The inset shows the Boltzmann plot ln(I₇₃₈/I₇₇₅) vs. T⁻¹/K⁻¹. The slope corresponds to −ΔE/k_B with the energy difference of the emissive states ΔE and the Boltzmann constant k_B.²¹

The ²E(1) and ²T₁(1) states share the same lifetime as well as a similar geometry as the ⁴A₂ ground state suggesting only a very small barrier for internal conversion (IC) between the two lowest doublet states. The two lowest emissive states are in thermal equilibrium (Fig. 5).²¹ Using ΔE = 700 cm⁻¹ a Boltzmann factor N₇₃₈/N₇₇₅ of 0.032 is calculated at 293 K.

The area ratio A₇₄₀/A₇₇₆ of the emission bands in MeCN fitted with two Voigt functions amounts to 0.091 (see ESI, Fig. S2 and Table S2†) indicating that the radiative transition ²E(1) → ⁴A₂ at 738 nm is approximately 0.091/0.032 = 2.8 times more allowed than the ²T₁(1) → ⁴A₂ radiative transition at 775 nm. The spin-forbidden ⁴A₂ → ²T₁/²E absorption bands (red line in Fig. 3) with extinction coefficients of <0.3 M⁻¹ cm⁻¹ in a concentrated acetonitrile solution were fitted with three Voigt functions and give a similar area ratio of A₇₃₆/A₇₇₀ = 2.96 (see ESI, Fig. S1 and Table S1†). This also indicates that the ⁴A₂ → ²E(1) transition is ca. 3 times more allowed than the ⁴A₂ → ²T₁(1) transition. Based on the calculations presented in Fig. 4 these bands were assigned to ⁴A₂ → ²T₁(1), ⁴A₂ → ²E(1) and ⁴A₂ → ²T₁(2) transitions, respectively (see ESI, Table S1† for details). The area ratio of the 736 and 770 nm absorption bands of 3.0 agrees with the value derived from the emission data (see above). The small Stokes shifts of 37 and 83 cm⁻¹ for the high-energy and low-energy emission bands, respectively, support the proposed nested nature of the doublet excited states. The data also suggest a slightly more pronounced geometric distortion of the ²T₁ state compared to the ²E state, which may facilitate the radiative transitions between the GS and ²E(1) state.

Below ca. 130 K (KBr pellet), the high-energy emission band vanishes and only the lowest ²T₁ derived microstate is populated (Fig. 6). Furthermore, the ²T₁(1) → ⁴A₂ emission band shows vibrational progression at 795 and 811 nm (Fig. 6).²² The doublet state population ²E(1)/²T₁(1) was modulated in Fourier-transform infrared (FTIR) pump–pump–probe(IR) and pump–dump–probe(IR) experiments at 290 and 20 K.²² Step-scan FTIR spectroscopy differentiated ²E and ²T₁ derived microstates and suggested that [Cr(ddpd)₂]³⁺ in the ²E(1) state nearly perfectly resembles the ⁴A₂ geometry, while the ²T₁(1) derived microstate is slightly distorted giving rise to an excited state IR spectrum which differs from the GS IR spectrum.²² These experiments show the effect of pairing two electrons in a t_2g-orbital. However, the exact (Jahn–Teller) distortional mode is not fully elucidated, yet.

Fig. 6 Phosphorescence spectra of [Cr(ddpd)₂][BF₄]₃ as KBr pellet between 290 and 10 K after excitation at 355 nm. The inset shows the region of the transition at about 739 nm, where the low-energy emission intensity at each temperature is normalized to 1 for better visibility of the decrease of the high-energy band at lower temperature.²²

Pressure shifts both emissive doublet states to lower energies similar to ruby (−0.8 cm⁻¹ kbar⁻¹)²³ but with a much stronger effect, i.e. 13–15 cm⁻¹ kbar⁻¹ for the low-energy ²T₁(1) and ca. 8 cm⁻¹ kbar⁻¹ for the high-energy ²E(1) emission (Fig. 7).²⁰ These energy shifts result from small geometric changes under pressure likely involving N–Cr–N angles which is much more pronounced in the molecular ruby than in the oxidic lattice of ruby.²⁰

Fig. 7 Normalized pressure-dependent phosphorescence spectra of [Cr(ddpd)₂][BF₄]₃ between 0.001 and 45.469 kbar in nujol together with a ruby crystal (right).^20,23

Ultrafast dynamics and dark excited states

According to CASSCF-NEVPT2 calculations, the ⁴T₂ states are approximately degenerate with the higher-energy ²T₂ states at the Franck Condon (FC) geometry (Fig. 4). This implies, that Δ₀ of [Cr(ddpd)₂]³⁺ is well-separated from the first excited state crossing point ²T₁/²E/⁴T₂ (black circle in Fig. 1) but very close to the second crossing point ²T₂/⁴T₂ in the TS diagram (in the FC state at GS geometry, black square in Fig. 1). Consequently, when exciting [Cr(ddpd)₂]³⁺ to the ⁴T₂ states, a high density of ²T₂ states with their vibrational levels is present in this FC region. Additionally, the CASSCF calculations yielded significant spin–orbit couplings (SOCs) of 42, 97 and 45 cm⁻¹ for the pathways from ⁴T₂(1) to ²T₂(2), ²E(1) and ²T₁(2), respectively.¹⁹ This is in agreement with El-Sayed's rule that states that SOC between two states is large when a change in multiplicity (here: quartet → doublet) is accompanied by a change in orbital angular momentum (here: e_g* → t_2g).²⁴ Overall, the high density of states, relatively large SOC and small ⁴T₂–²T₂ energy difference at FC geometry could facilitate ⁴T₂ → ²T₂ ISC in [Cr(ddpd)₂]³⁺.²⁵

In fact, the fully relaxed, emissive doublet states ²T₁/²E of [Cr(ddpd)₂]³⁺ are reached within τ = 3.5 ps after excitation to ⁴T₂ states.²⁶ Very likely, the ISC process is even faster (τ_ISC < 200 fs) and the picosecond time constant rather applies to vibrational cooling (VC) and IC between doublet states. The fluorescence quantum yield Φ_Fl ≈ 0.01% allows to derive an upper limit for the ISC quantum yield of Φ_ISC < 99.99%. In the structurally similar [Cr(bpmp)₂]³⁺ (bpmp = 2,6-bis(2-pyridylmethyl)pyridine) a lower limit for Φ_ISC of 92 ± 5% was determined via doublet–triplet energy transfer and laser flash photolysis experiments.¹⁹

Interestingly, in the classical organic sensitizer benzophenone Ph₂C=O the predicted relaxation cascade S₁ → T₂ → T₁ → S₀ with almost isoenergetic T₂ and S₁ states²⁷ is analogous to the one proposed for [Cr(ddpd)₂]³⁺ with ⁴T₂ → ²T₂ → ²T₁/²E → ⁴A₂.

Femtosecond transient absorption spectra covering the Vis-NIR range after excitation with 435 nm pulses show broad excited state absorptions (ESA) covering the 500–900 nm spectral range (ESA1: 14 000 cm⁻¹ and ESA2: 12 300 cm⁻¹, Fig. 8). These evolve with a common time constant of ca. 3.2 ps to ESAs at 534 nm (ESA3: 18 700 cm⁻¹) and 1389 nm (ESA4: 7200 cm⁻¹, see ESI, Fig. S4 and S5†).²⁶ ESA3 and ESA4 are assigned to ²T₁/²E → ²LMCT and ²T₁/²E → ²T₂ transitions, respectively. Addition of ESA3 to the ²T₁ energy yields an energy of 31 600 cm⁻¹ (316 nm) for the ²LMCT state, which corresponds to the respective ⁴LMCT absorptions found in the GS absorption spectra (Fig. 3). ESA4 in the NIR region helps to experimentally estimate the energy of the dark ²T₂ states by summation of the emission energy (775 nm, 12 900 cm⁻¹) and the ESA4 energy (1389 nm, 7200 cm⁻¹) giving 20 100 cm⁻¹ (498 nm). This energy is indeed slightly below the CASSCF calculated energy of ⁴T₂ states at the GS geometry.

Fig. 8 Fs-Transient absorption spectra of [Cr(ddpd)₂]³⁺ in CH₃CN after excitation at 435 nm and excited state diagram with CASSCF(7,12)-NEVPT2 calculated energies (see ESI† for details, ESA = excited state absorption).²⁶

The ⁴T₂ states should be Jahn–Teller distorted due to the singly occupied e_g* orbitals and the doubly occupied t_2g orbitals. Indeed DFT calculations reveal, that the optimised lowest ⁴T₂ microstate displays elongated Cr–N bond lengths of terminal pyridines in a single ddpd ligand (2.08 Å → 2.42 Å).⁷ As the energy of this quartet state drops dramatically with increasing Cr–N distances, it is essential for high stability and strong emission that the ISC is fast and preferably in the FC region before vibrational relaxation in the ⁴T₂ state takes place.

With this interpretation, [Cr(ddpd)₂]³⁺ hits a sweet spot in the TS diagram which enables a fast ISC pathway ⁴T₂(1) → ²T₂(2) to the doublet states at the FC geometry via the dark ²T₂ states in addition to the direct ⁴T₂(1) → ²E(1) and ⁴T₂(1) → ²T₁(2) pathways with a higher energy difference. The vibrational relaxation within the quartet states along the Cr–N Jahn–Teller modes (in x- and y-direction)²⁸ might be comparably slow due to a low potential energy gradient at the FC geometry. In any case, the fast ISC avoids vibrational relaxation within the quartet states and thus suppresses undesired fluorescence from the ⁴T₂ state, non-radiative decay by ⁴T₂ surface crossing with the GS, and even Cr–N bond dissociation. In fact, [Cr(ddpd)₂]³⁺ is particularly photostable, even at low pH in contrast to e.g. [Cr(bpy)₃]³⁺.^6,7

Long-lived spin–flip states

The dynamics of the long-lived excited states depend on the presence of high-energy oscillators²⁹ and quenchers,^26,30 the excited state distortion²² and the temperature.^21,22

The doublet states can relax non-radiatively via energy transfer (EnT) to vibrational overtones of nearby C–H oscillators (multiphonon relaxation).³¹ [Cr(ddpd)₂]³⁺ has a comparably small spectral overlap integral (SOI) with the ν⁴ and the ν⁵ C–H overtones associated with the pyridine rings (Fig. 9). This results in a small rate constant for non-radiative decay k_nr and thus a high quantum yield.²⁹

Fig. 9 C–H and C–D vibrational overtone spectra of model pyridine ligands and their overlap with the phosphorescence bands of [Cr(ddpd)₂]³⁺ (SOI = spectral overlap integral).²⁹

After deuteration of the ligand, there is only a significant SOI with a higher C–D overtone (ν⁶) with an extinction coefficient which is roughly two orders of magnitude smaller than ν⁵(C–H).²⁹ Thus, deuterated [Cr(ddpd)₂]³⁺ shows an even smaller k_nr and a record quantum yield of 30%. The limited increase from 13.7 to 30% might in part be associated with the near degeneracy of the fifth C–D overtone (ν⁶) and the ²T₁(1) → ⁴A₂ emission band (Fig. 9),²⁹ yet direct ²T₁ → ⁴A₂ ISC plays a role as well, irrespective of the deuteration level.

As stated above, at high enough thermal energy the ²E and ²T₁ states equilibrate leading to dual emission. Below ca. 130 K, the ²E(1) band vanishes, the ²T₁(1) emission band sharpens and shifts to lower energy (785 nm in KBr, Fig. 6) showing that the ²T₁(1) state is stabilized (vertical displacement of the ²T₁(1) potential energy well). The phosphorescence quantum yield increases dramatically between 70 and 10 K (Fig. 6).²²

The increase in phosphorescence quantum yield at very low temperatures might be associated with the sharpening of the ²T₁(1) emission band, which reduces the SOI with the third C–H vibrational overtone (ν⁴) of the ligand. Additional explanations for the higher phosphorescence quantum yield at low T might be a reduction of other thermally activated non-radiative decay pathways and the enhancement of the radiative decay via larger distortion of the ²T₁(1) state relative to the ground state lifting Laporte's rule.³² In fact, the radiative rate k_r decreases dramatically from pseudooctahedral [Cr(ddpd)₂]³⁺ (k_r = Φ/τ = 122 s⁻¹ in CH₃CN)¹⁵ to the electronically similar but perfectly centrosymmetric Cr^III complex [Cr(tpe)₂]³⁺ (k_r = 18.2 s⁻¹, tpe = 1,1,1-tris(pyrid-2-yl)ethane).³³

Triplet oxygen quenches the long-lived phosphorescence of [Cr(ddpd)₂]³⁺ induced by 435 nm excitation via Dexter energy transfer to form the ground state complex and ¹O₂ with a quantum yield of 61% in acetonitrile.²⁶ The typical ¹O₂ phosphorescence at 1274 nm appears even after direct spin-forbidden excitation of [Cr(ddpd)₂]³⁺ to its ²T₁/²E states at 771 and 735 nm, respectively (see ESI, Fig. S3†), confirming that the doublet states of [Cr(ddpd)₂]³⁺ sensitize ¹O₂.

The excited state landscape of [Cr(ddpd)₂]³⁺ is sketched in Fig. 10 along with experimentally determined energies, rate constants and quantum yields, summarising excitation, excited state dynamics to the emissive doublet states, excited state absorptions, non-radiative relaxation in particular multiphonon relaxation as well as radiative transitions.

Fig. 10 Experimentally^7,21,26,29 determined excited state energy landscape of the molecular ruby [Cr(ddpd)₂]³⁺ in CH₃CN and time constants determined so far with exemplary microstates for the MC states derived from CASSCF(7,12)-NEVPT calculations,²⁰ the rate constant of non-radiative decay k_nr and the rate constant for energy transfer to vibrational overtones k_EnT (which is included in k_nr). The Jahn–Teller coordinate refers to the ⁴T₂ state while the ^4/2LMCT states likely display other distortions from the GS geometry.

Future outlook

Following the report of [Cr(ddpd)₂]³⁺ the underlying design principles gave rise to a large number of highly luminescent Cr^III complexes.^{19,33–35,36} Current efforts are directed to shifting the emission energy of molecular ruby derivatives to lower or higher energy by ligand modifications^19,37 and by modification of the central metal and electron configuration from d³-Cr^III to d²-V^III.³⁸ Variation of the counter ions of [Cr(ddpd)₂]³⁺ and surrounding matrix as well as shielding of the metal center by sterically demanding groups proved to be fruitful strategies to enhance quantum yields and lower oxygen sensitivity.¹⁵ Applications of molecular ruby derivatives in upconversion,³⁹ circularly polarized emission,^34,35,40 sensing,^20,21,41 photosensitization for organic synthesis²⁶ or photodynamic therapy³⁰ and others had already been demonstrated or are currently explored.

Author contributions

W. R. K. provided the resources (synthesis of [Cr(ddpd)₂]³⁺), performed the investigation (measurement of Φ_Fl), visualized the data and wrote the original drafts. C. R. performed the fs-transient absorption spectroscopy. R. N. performed the investigation of the phosphorescence lifetimes, the spin-forbidden absorption and ¹O₂ sensitization experiments with NIR excitation. K. H. conceptualized the article, acquired the funding, supervised the project and wrote the original drafts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Johannes Hunger for his support in this project and Dr Christoph Förster for constructive criticism of the manuscript. Financial support from the Deutsche Forschungsgemeinschaft [DFG, Priority Program SPP 2102 “Light-controlled reactivity of metal complexes” (HE 2778/13-1)] is gratefully acknowledged. We thank the DFG for grant INST 247/1018-1 FUGG to K. H.; W. R. K. is grateful for a Kekulé scholarship of the Fonds der Chemischen Industrie.

Notes and references

1. (a) F. Teplý, Phys. Sci. Rev., 2020, 5, 20170171; (b) O. S. Wenger, Chem. – Eur. J., 2019, 25, 6043–6052.
2. T. H. Maiman, Nature, 1960, 187, 493–494.
3. C. Degli Esposti and L. Bizzocchi, J. Chem. Educ., 2007, 84, 1316.
4. W. R. Kitzmann, J. Moll and K. Heinze, Photochem. Photobiol. Sci., 2022 DOI:10.1007/s43630-022-00186-3 , in press.
5. R. D. Dill, R. I. Portillo, S. G. Shepard, M. P. Shores, A. K. Rappé and N. H. Damrauer, Inorg. Chem., 2020, 59, 14706–14715.
6. S. Otto, M. Dorn, C. Förster, M. Bauer, M. Seitz and K. Heinze, Coord. Chem. Rev., 2018, 359, 102–111.
7. S. Otto, M. Grabolle, C. Förster, C. Kreitner, U. Resch-Genger and K. Heinze, Angew. Chem., Int. Ed., 2015, 54, 11572–11576.
8. D. Zare, B. Doistau, H. Nozary, C. Besnard, L. Guénée, Y. Suffren, A.-L. Pelé, A. Hauser and C. Piguet, Dalton Trans., 2017, 46, 8992–9009.
9. (a) Y. Tang, S. Zhao, B. Long, J.-C. Liu and J. Li, J. Phys. Chem. C, 2016, 120, 17514–17526; (b) J. K. McCusker, Science, 2019, 363, 484–488.
10. D. D. Ragan, R. Gustavsen and D. Schiferl, J. Appl. Phys., 1992, 72, 5539–5544.
11. R. S. Quimby and W. M. Yen, J. Appl. Phys., 1980, 51, 1780–1782.
12. A. D. Kirk and G. B. Porter, J. Phys. Chem., 1980, 84, 887–891.
13. J.-R. Jiménez, B. Doistau, C. Besnard and C. Piguet, Chem. Commun., 2018, 54, 13228–13231.
14. (a) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 753–766; (b) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779; (c) J. Oppenheim and J. Miller, Tanabe-Sugano for Mathematica, 2019, available at: https://github.com/JulesOpp/Tanabe-Sugano, accessed 7 December 2021.
15. C. Wang, W. R. Kitzmann, F. Weigert, C. Förster, X. Wang, K. Heinze and U. Resch-Genger, ChemPhotoChem, 2022, e202100296.
16. (a) P. A. Scattergood, in Organometallic Chemistry, ed. N. J. Patmore and P. I. P. Elliott, Royal Society of Chemistry, Cambridge, 2020, vol. 43, pp. 1–34; (b) M. Dorn, N. R. East, C. Förster, W. R. Kitzmann, J. Moll, F. Reichenauer, T. Reuter, L. Stein and K. Heinze, in Comprehensive Inorganic Chemistry III, ed. J. Reedijk, Elsevier, San Diego, 2022.
17. S. Lenz, H. Bamberger, P. P. Hallmen, Y. Thiebes, S. Otto, K. Heinze and J. van Slageren, Phys. Chem. Chem. Phys., 2019, 21, 6976–6983.
18. A. B. P. Lever, Inorganic electronic spectroscopy, Elsevier, Amsterdam, 1st edn, 1968.
19. F. Reichenauer, C. Wang, C. Förster, P. Boden, N. Ugur, R. Báez-Cruz, J. Kalmbach, L. M. Carrella, E. Rentschler, C. Ramanan, G. Niedner-Schatteburg, M. Gerhards, M. Seitz, U. Resch-Genger and K. Heinze, J. Am. Chem. Soc., 2021, 143, 11843–11855.
20. S. Otto, J. P. Harris, K. Heinze and C. Reber, Angew. Chem., Int. Ed., 2018, 57, 11069–11073.
21. S. Otto, N. Scholz, T. Behnke, U. Resch-Genger and K. Heinze, Chem. – Eur. J., 2017, 23, 12131–12135.
22. P. Boden, P. Di Martino-Fumo, G. Niedner-Schatteburg, W. Seidel, K. Heinze and M. Gerhards, Phys. Chem. Chem. Phys., 2021, 23, 13808–13818.
23. R. A. Forman, G. J. Piermarini, J. D. Barnett and S. Block, Science, 1972, 176, 284–285.
24. M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838.
25. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025.
26. S. Otto, A. M. Nauth, E. Ermilov, N. Scholz, A. Friedrich, U. Resch-Genger, S. Lochbrunner, T. Opatz and K. Heinze, ChemPhotoChem, 2017, 1, 344–349.
27. (a) K. Shizu and H. Kaji, J. Phys. Chem. A, 2021, 125, 9000–9010; (b) S. Yabumoto, S. Sato and H. Hamaguchi, Chem. Phys. Lett., 2005, 416, 100–103.
28. K. Mack, A. Wünsche von Leupoldt, C. Förster, M. Ezhevskaya, D. Hinderberger, K. W. Klinkhammer and K. Heinze, Inorg. Chem., 2012, 51, 7851–7858.
29. C. Wang, S. Otto, M. Dorn, E. Kreidt, J. Lebon, L. Sršan, P. Di Martino-Fumo, M. Gerhards, U. Resch-Genger, M. Seitz and K. Heinze, Angew. Chem., Int. Ed., 2018, 57, 1112–1116.
30. U. Basu, S. Otto, K. Heinze and G. Gasser, Eur. J. Inorg. Chem., 2019, 37–41.
31. E. Kreidt, C. Kruck and M. Seitz, in Handbook on the physics and chemistry of rare earths. Including actinides, ed. J.-C. G. Bünzli, V. K. Pecharsky, G.-Y. Adachi, K. A. Gschneidner and E. LeRoy, North-Holland, Amsterdam, Oxford, 2018, vol. 53, pp. 35–79.
32. O. Laporte and W. F. Meggers, J. Opt. Soc. Am., 1925, 11, 459.
33. S. Treiling, C. Wang, C. Förster, F. Reichenauer, J. Kalmbach, P. Boden, J. P. Harris, L. M. Carrella, E. Rentschler, U. Resch-Genger, C. Reber, M. Seitz, M. Gerhards and K. Heinze, Angew. Chem., Int. Ed., 2019, 58, 18075–18085.
34. J.-R. Jiménez, B. Doistau, C. M. Cruz, C. Besnard, J. M. Cuerva, A. G. Campaña and C. Piguet, J. Am. Chem. Soc., 2019, 141, 13244–13252.
35. J.-R. Jiménez, M. Poncet, S. Míguez-Lago, S. Grass, J. Lacour, C. Besnard, J. M. Cuerva, A. G. Campaña and C. Piguet, Angew. Chem., Int. Ed., 2021, 60, 10095–10102.
36. (a) J.-R. Jiménez, M. Poncet, B. Doistau, C. Besnard and C. Piguet, Dalton Trans., 2020, 49, 13528–13532; (b) S. Otto, C. Förster, C. Wang, U. Resch-Genger and K. Heinze, Chem. – Eur. J., 2018, 24, 12555–12563.
37. (a) N. Sinha, J.-R. Jiménez, B. Pfund, A. Prescimone, C. Piguet and O. S. Wenger, Angew. Chem., Int. Ed., 2021, 60, 23722–23728; (b) L. Stein, P. Boden, R. Naumann, C. Förster, G. Niedner Schatteburg and K. Heinze, Chem. Commun., 2022, 58, 3701–3704.
38. (a) M. Dorn, J. Kalmbach, P. Boden, A. Kruse, C. Dab, C. Reber, G. Niedner-Schatteburg, S. Lochbrunner, M. Gerhards, M. Seitz and K. Heinze, Chem. Sci., 2021, 12, 10780–10790; (b) M. Dorn, K. Mack, L. M. Carrella, E. Rentschler, C. Förster and K. Heinze, Z. Anorg. Allg. Chem., 2018, 644, 706–712; (c) J. P. Zobel, T. Knoll and L. González, Chem. Sci., 2021, 12, 10791–10801; (d) M. S. Fataftah, S. L. Bayliss, D. W. Laorenza, X. Wang, B. T. Phelan, C. B. Wilson, P. J. Mintun, B. D. Kovos, M. R. Wasielewski, S. Han, M. S. Sherwin, D. D. Awschalom and D. E. Freedman, J. Am. Chem. Soc., 2020, 142, 20400–20408.
39. (a) J. Kalmbach, C. Wang, Y. You, C. Förster, H. Schubert, K. Heinze, U. Resch-Genger and M. Seitz, Angew. Chem., Int. Ed., 2020, 59, 18804–18808; (b) C. Wang, F. Reichenauer, W. R. Kitzmann, C. Kerzig, K. Heinze and U. Resch-Genger, Angew. Chem., Int. Ed., 2022, 61, e202202238.
40. (a) C. Dee, F. Zinna, W. R. Kitzmann, G. Pescitelli, K. Heinze, L. Di Bari and M. Seitz, Chem. Commun., 2019, 55, 13078–13081; (b) M. Poncet, A. Benchohra, J.-R. Jiménez and C. Piguet, ChemPhotoChem, 2021, 5, 880–892.
41. C. Wang, S. Otto, M. Dorn, K. Heinze and U. Resch-Genger, Anal. Chem., 2019, 91, 2337–2344.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt00569g

---