Covalency in AnCl₂ (An = Th–No)

Abstract

A potential connection has previously been proposed between the emergence of unexpected covalent behaviour in various transcurium complexes and the increasing stability of the +2 oxidation state in the later members of the actinide series. We recently used computational methods to study AnCl₃, finding evidence for energy degeneracy driven covalency in the later actinides, and here present a comparative study of AnCl₂. The An–Cl bond lengths of the latter divide into two data sets; Th–Np, Cm, Bk and Pu, Am, Cf–No. On average the An–Cl bond length decreases for both sets but, with significant increases between Np and Pu, and between Bk and Cf, unlike the former group (Pu, Am, Cf–No)Cl₂ have significantly larger lengths than the corresponding trichlorides. Using a range of Natural Bond Orbital (NBO), Natural Resonance Theory (NRT) and Quantum Theory of Atoms In Molecules (QTAIM) metrics, the covalency of the dichloride bonds is analysed. We find that the first group of dichlorides are similar to their trichloride counterparts and possess significantly more covalent bonds than (Pu, Am, Cf–No)Cl₂. We believe this change in covalent behaviour across the series for the dichlorides is due to a decreased involvement of the 6d orbital in the later elements (as a result of the f–d excitation energy exceeding the d-stabilisation energy of the actinide ions in question). Moreover, we find that unlike the trichlorides, where the QTAIM delocalisation index indicates that covalency plateaus/moderately increases, An–Cl covalency decreases across the second half of the series for AnCl₂. We attribute this difference in behaviour to a lack of significant energy degeneracy driven covalency for the dichlorides, with the energy difference between the dichlorides’ β 5f and 3p Natural Atomic Orbitals being larger than for the trichlorides. Hence we find it is not the presence of a stable +2 oxidation state, but instead the extent of energy matching between the actinide 5f orbitals and the ligand 3p, that drives covalency in the transcurium chlorides.

---

Introduction

Covalency in the actinide series remains a subject of intense ongoing interest. It has been invoked, for example, as a factor in actinide/lanthanide separation processes such as TALSPEAK (trivalent actinide lanthanide separations by phosphorus-reagent extraction from aqueous complexes), which uses a DTPA ligand to separate Am³⁺ and Cm³⁺ from nuclear waste.^1,2 While the early members of the actinide series have relatively diffuse f orbitals which can overlap spatially with the valence orbitals of ligating atoms, as the series is crossed, the actinide 5f orbitals stabilise and contract, reducing spatial overlap with the ligands. This stabilisation can bring the 5f orbitals into closer energy proximity with ligand orbitals, which can result in significant metal/ligand atomic orbital mixing in molecular orbitals, without there being significant spatial overlap. We previously highlighted this idea, referred to as energy degeneracy-driven covalency, in density functional theory (DFT) studies of AnCp₄ and AnCp₃ (An = Ac–Cm; Cp = η⁵-C₅H₅).^3,4 We employed the Quantum Theory of Atoms in Molecules (QTAIM) for the first time in the 5f series, and analysed bond critical point metrics, which indicated a decrease in covalency from U to Cm, by contrast to orbital mixing and spin density data, which suggested that Am forms the most covalent An–Cp bond. Energy degeneracy driven-covalency has also been established experimentally, for example in the combined use of K-edge XANES spectroscopy and DFT by Su et al. on AnCl₆ (An = Th–Pu). These authors concluded that there is an increased contribution of the spatially contracted, but lower energy, 5f orbital in the metal ligand bond from Th to Pu, and a decrease in the more diffuse, higher energy, 6d.⁵ This combination of DFT and spectroscopy has also been employed to study covalency in actinide ligand bonds by several other groups.^6–11 Furthermore, experiment has also validated the use of QTAIM parameters to measure covalency; for example, changes in chemical shifts in both ¹³C and ¹⁵N nuclear magnetic resonance (NMR) spectra show good correlation with bond order metrics, for a range of actinide ligand bonds.^12,13

In addition to the separation of specific radionuclides from nuclear waste, another important application of actinide covalency is the decorporation of actinides from the human body. In the event of radiological contamination, such as the Fukushima Daiichi Nuclear Power Plant incident in 2011, it is important to safely remove actinide fission products, as well as ¹³⁷Cs, ⁹⁰Sr and ¹³¹I, from biological systems.¹⁴ Currently, multidentate hydroxypyridinonate (HOPO) ligands have been successful in vitro and in vivo experiments and hence appear a promising option for medical use.^15–26 This work has focused on the removal of actinides in the first half of the series (U, Np–Cm), as these elements are generally found in the highest concentrations in nuclear reactors. Nevertheless, developing treatments to safely remove actinides from the second half of the series, such as californium and berkelium, is also important. That said, and despite heroic efforts by a number of researchers, our understanding of the latter half of the actinide series is still somewhat lacking. As one moves across the period, as well as the 5f orbitals contracting, the +3 oxidation state becomes increasingly favourable, and thus many have speculated that these later elements should act (chemically) like the lanthanides. However, despite these similarities, the transcurium elements differ from the lanthanides in one significant way – the actinides’ 3°/2° reduction potential becomes significantly higher than the lanthanides’ by Bk,^27,28i.e. the late actinides possess a more stable divalent state than both the earlier actinides and their lanthanide counterparts. In fact, by Cf, the E°(3/2) redox potential is −1.60 V, which is similar to that of Sm (−1.55 V), for which the divalent state is stable enough that it is widely used as a reducing agent in organic chemistry (SmI₂).^28,29 Furthermore, with a few known divalent californium compounds (e.g. solid state CfCl₂, CfBr₂ and CfI₂),^30–32 and experimental reports of the presence of thin layers on the surface of metallic californium that exist in a metastable divalent state, there is no doubt the divalent state is accessible for this element.^27,28,33 The divalent state is also achievable for the lanthanides and the earlier actinides, though bulky ligands such as substituted Cp rings, N(SiMe₃)₂, C(SiMe₃)₃ and N(SiⁱPr₃) are required to stabilise it.^34–42

The intense radioactivity of Cf limits its study. Indeed, up until 2014 only five single crystal structures containing this element had been determined: Cf(IO₃)₃, CfCl₃ (in the orthorhombic and hexagonal forms), Cf(Cp)₃ and [Cf(H₂O)₉][CF₃SO₃]_3; all of which have isotypic lanthanide analogues, thus supporting the view that the late actinides behave like the lanthanides.^43–46 However, in 2014 Polinski et al. reported the first synthesis of californium borate (Cf[B₆O₈(OH)₅]), which reignited the question – what is the true chemical behaviour of the second half of the actinide series?⁴⁷ This was because, not only was this structure different from previously synthesised actinide borate complexes (and the isoelectronic lanthanide, Dy), but the properties differed from those of the free ion, with unexpected covalent behaviour (reduced magnetic moment, broad f–f transitions due to vibronic coupling and significant charge transfer indicated from CASSCF as well as DFT-based ELF analysis and NBO charges). Thus, californium not only appears to act differently from the lanthanides, and has covalent interactions with the ligands in this complex, but also it differs from the behaviour of the earlier actinides. One reason suggested for the ‘alterations in californium's physical and chemical properties’ by Cary et al., was the ‘relative ease with which formally Cf(III) can be reduced to Cf(II)’.⁴⁸ It was suggested that the covalent behaviour of the later member of the series differs from both the lanthanides and the earlier members of series, with californium lying at this ‘break’/turning point between the two types of covalent behaviour, and with the later elements appearing to have increased participation of the 5f orbitals in their bonding.

Since the 2014 study, several berkelium complexes have also been synthesised: Bk[B₆O₈(OH)₅], Bk(HDPA)₃, Bk(HOPO)₃ and Bk(DOPO)₃.^11,49,50 In these examples Bk appears to behave similarly to the corresponding Cf complexes, not only leading to the question at what position in the series does this proposed ‘break’ in covalent behaviour lie? but, as Kelley et al. have previously highlighted, if this change in behaviour is in fact dependent on the accessibility of the +2 state, as Bk does not possess a stable divalent state.⁵¹

We have recently investigated covalency across the actinide series by studying AnCl₃ (An = Th–No).⁵² We employed DFT, Natural Bond Orbital (NBO), Natural Resonance Theory (NRT) and QTAIM analysis, and showed that whilst there is a decrease in covalency across the first half of the series, there is levelling off with a moderate increase for the second half. This supports the previous suggestion that the second half of the series acts differently from the first half, with the behaviour coinciding with the previously reported^27,28 increased stability of the +2 oxidation state. In the present paper, we apply the techniques used to analyse the trichlorides to the corresponding dichlorides, and examine the stability of the +2 oxidation state across the series and the effect of the lower oxidation state on An–Cl bond covalency, finding that the late dichlorides do not possess a more covalent An–Cl bond than their trichloride counterparts.

Computational and methodological details

Density functional theory was employed throughout this study using the Gaussian 16 software package, revision A.03,⁵³ in conjugation with the PBE0 hybrid functional.⁵⁴ For all geometry optimizations the actinide metals were treated with relativistic effective core potentials (ECPs) developed by the Stuttgart-Dresden group,⁵⁵ which restricts 60 electrons to the core region, in conjunction with the associated segmented contracted valence basis sets. Chlorine atoms were treated with the cc-pVDZ basis set.⁵⁶ The SCF = XQC keyword was applied for all molecules, along with the superfine integration grid and opt = verytight. Harmonic vibrational frequencies were calculated to ensure the optimised geometries were true energetic minima. Spin–orbit coupling has not been included.

Single point all-electron calculations were performed at the small-core ECP optimised geometries using the DKH2 Hamiltonian and SARC basis sets designed by Schuchardt et al.,⁵⁷ with the addition of extra g polarization functions designed by Pantazis and Neese.⁵⁸ As with the ECP calculations, the chlorine atoms were treated with the cc-pVDZ basis set and the keyword SCF = XQC was included.

The enthalpies of the following reactions: AnCl₃ → AnCl₂ + ½ Cl₂ (An = Th–No) were calculated, by the addition of the ECP calculated thermal corrections to enthalpy, to the single point DKH2/SARC calculated energies.

Quantum Theory of Atoms-in-Molecules calculations were performed using the AIMALL 17.11.14 software package,⁵⁹ with the standard integration method and basin quadrature, on .wfx files generated from the all-electron single point calculations. Natural Population Analysis, Natural Bond Orbital and Natural Resonance Theory calculations were also performed on the all-electron single point electronic structures, using the NBO7 package.⁶⁰ For NBO analysis the CHOOSE option was used to define all the metal–chlorine bonds as double bonds, as explained the main text.

As with the previous study of AnCl₃, all dichloride structures were calculated with the highest spin multiplicity for the expected electronic configuration of the system, i.e. the 7s and 6d orbitals are assumed to be unoccupied. For example, for UCl₂, a pure U²⁺ state should have the electronic configuration 5f⁴6d⁰7s⁰, and thus a multiplicity of 5 was used. However, when using a multiplicity of 7 and 6 (expected electronic configurations of 5f⁸6d⁰7s⁰ and 5f⁹6d⁰7s⁰) for CmCl₂ and BkCl₂ respectively, there was high spin contamination, with the ECP geometry optimised structure having a difference from the expected 〈S²〉 of 0.886 and 0.370, and the single point all electronic structures having differences of 0.920 and 0.373, for Cm and Bk respectively. Hence, the geometry optimisations were repeated with a range of multiplicities, with the higher multiplicities of 9 and 8 not only producing lower energy but also less spin contaminated structures for these two systems (as shown in Table SI1†, which also collects the 5f electronic configurations, electronic states and point groups). As discussed in more detail in the results and discussion section, the higher multiplicity calculations for CmCl₂ and BkCl₂ produced geometries with shorter bond lengths that are similar to the earlier actinides, and these structures also have decreased NPA 5f and increased 7s and 6d populations.

Results and discussion

Across the series the dichlorides are bent, possessing C_2v symmetry. Our An–Cl bond length data for the dichloride structures are presented in Table SI2† and are compared with the An–Cl bond lengths of the corresponding AnCl₃ geometries (produced from our previous work⁵²) in Fig. 1. From Th to Np the bond lengths for the dichlorides are very similar to the trichlorides (although they decrease at a slightly larger rate). However, at Pu there is a significant increase in bond length and, with the exception of Cm and Bk, the dichlorides from Pu–Md consistently have a significantly longer bond length than the corresponding trichlorides. In NoCl₃ the bond length is similar value to NoCl₂, supporting our previous suggestion that the bond lengthening in NoCl₃vs. the immediately preceding elements occurs due to the increased stability of the +2 oxidation state. Overall, there is a partitioning of the bond lengths into two sets; (Th–Np, Cm, Bk) and (Pu, Am, Cf–No).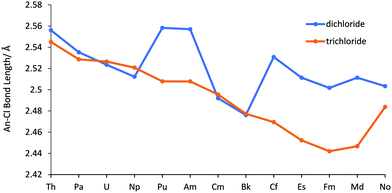

Fig. 1 An–Cl bond lengths in AnCl₂, and AnCl₃ from our previous work.⁵²

NPA data are given in Table SI3† and Fig. 2. For (Th–Np, Cm, Bk), the 5f population in AnCl₂ is similar to that found in a +3 oxidation state, with the excess 5f population (the difference between the expected 5f population of the actinide +2 ion and the NPA 5f population) being significantly negative. The decreased population of the 5f is accompanied by higher 7s and 6d population, as shown in Fig. 2b. By contrast, (Pu, Am, Cf–No) have 5f populations close to the expected population of the An(II) state. This separation of the NPA data into the two groups of elements parallels the bond lengths.

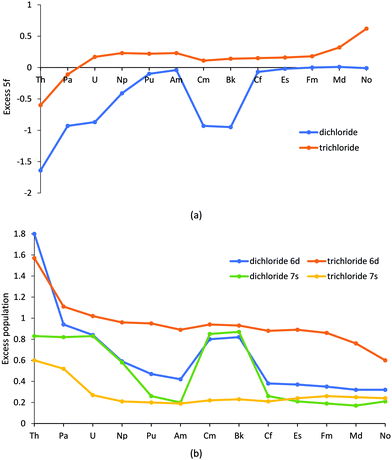Fig. 2 The (a) excess 5f population and (b) excess/total 6d and 7s population from Natural Population Analysis for AnCl₂, and AnCl₃ from our previous work.⁵²

To our knowledge there are no previously reported experimental or theoretical bond lengths for the gas-phase dichlorides, but the trends seen here are similar to other actinide data. First, the peak at Pu coincides with a sharp increase in atomic volume found in studies of metallic Pu and Am.^61,62 The proposed reason for this is the transition from bonding/itinerant to non-bonding/localized f electrons in the post neptunium elements. In our study, the NPA charges (Fig. SI2 and Table SI4†) also indicate an increase in ionic behaviour for (Pu, Am, Cf–No), with the higher charges for these elements suggesting a decrease in charge transfer from ligand to metal. However, as CmCl₂ and BkCl₂ behave more similarly to the earlier actinides we do not believe that the change in the behaviour of the 5f electrons accounts (or at least not fully) for the bond length trends in Fig. 1. Instead, as there is a close relationship between the 6d population (Fig. 2b) and NPA charge, we propose that the bond length trend is strongly influenced by the 6d population of the actinide. This suggestion is supported by the fact the earlier divalent actinides have previously been observed to not only possess a significant 6d population, but also to utilise 6d electrons in bonding, with Mikheev and Rumer noting (through the use of co-crystallization studies with a Gd₂Cl₃ matrix) that (Th–Np, Cm, Bk) have d electron occupation in their divalent state.⁶³ Mihkeev and Rumer suggested that the d orbital is populated in these elements because they have a lower f–d excitation energy than their d orbital stabilisation energy (in other words, the penalty of promoting a 5f electron into the virtual 6d orbital is compensated by a stabilising energy gain). However, as one moves across the series, the 5f orbitals stabilise, and it becomes energetically more costly to promote a 5f electron to the virtual d orbital; thus, as the later divalent actinides’ f–d excitation energy exceeds the d orbital stabilisation energy, the d orbitals are no longer (significantly) involved in bonding.

The cause of the increased stability that an increased d orbital population provides to a system is complex and still not fully understood, and could be due to a number of reasons, such as: crystal field splitting effects, possibility of dimerization, more favourable f-orbital occupancy (e.g. allowing 5f half-shell filling) or increased covalency in the actinide–ligand bond.⁶³ The latter may well account for the shorter-than-expected An–Cl bond in (Th–Np, Cm, Bk)Cl₂. The increased 6d population seen for CmCl₂ and BkCl₂ is revisited below.

The enthalpy change for the following reaction was calculated for An = Th–No with a range of density functionals, and the PBE0 and PBE data are plotted in Fig. 3.

AnCl₃ → AnCl₂ + ½ Cl₂

Fig. 3 The enthalpy of reaction of AnCl₃ → AnCl₂ + ½ Cl₂.

The positive values indicate that the trichlorides are more stable than the dichlorides across the entire series, although the dichlorides generally stabilise as the actinide becomes heavier. This trend is in general agreement with previous work, which also suggests the +2 oxidation state becomes more stable across the series.^27,28 The general trend is interrupted at two points at the PBE0 level. Firstly, at U, which is a small minimum in the first half of the series. Recalculation with other functionals (Fig. 3 and SI3†), however, shows that the small minimum at U is functional dependent, occurring for PBE0 and B3PW91, but not for B3LYP, BLYP or PBE. Secondly, the gradual decrease to Am and the subsequent increase at Cm, is also seen in other studies,^27,28 including computational work by Vasiliu et al. (shown in Fig. SI4†).⁶⁴ This can be explained by the stability of the half-filled 5f shell, achieved by Cm³⁺ and Am²⁺. The increase/plateau from Cm to Bk at the PBE0/PBE level is not so readily explained, however, though a potential cause is discussed in the ESI.†

The preference for 5f⁷ occupation accounts for the increased stability of the higher multiplicity of Cm (9), as this results in a 5f population of 7.07 (instead of c. 8, which would be expected with a multiplicity of 7 for Cm(II)) and increased population of the 7s and 6d orbitals (Fig. 2b). This in turn explains why Cm acts like the earlier actinides, whose properties seem to be driven by the increased population of the 6d orbital.

To explore the reason for the increasing stability of the +2 oxidation state across the series, we performed a QTAIM analysis. The An–Cl delocalisation index δ(An,Cl) is shown in Table SI4† and Fig. 4, and has a similar trend to the bond lengths in Fig. 1, with (Pu, Am, Cf–No) displaying smaller values than the other dichlorides, as well as their corresponding trichloride structures. These dichlorides are the ones with significantly longer bonds (Fig. 1). As δ(An,Cl) is a measure of bond order, the results support the suggestion that the members of the series which have a larger An–Cl bond length and lower 6d population, possess a less covalent An–Cl bond. Moreover, Fig. 4 reveals that unlike the trichlorides, for which δ(An,Cl) generally increases across the second half of the series, the dichlorides’ δ(An,Cl) values decrease from Cf to No. This not only suggests that increased covalent behaviour is not the reason for increased (relative) dichloride stability at the end of the series (Fig. 2), but also indicates a change in behaviour from the trichlorides. In our previous work, we suggested that the small increase in δ(An,Cl) from Cf to Md for the trichlorides was due to an energy match between the 5f metal and 3p ligand orbitals, i.e. energy degeneracy driven covalency. Thus, the opposite trend in δ(An,Cl) for the later AnCl₂ suggests either a lack of energy matching or that it occurs to a lesser extent. The Wiberg Bond Index (WBI), shown in Table SI4 and Fig. SI6,† supports these observations, as it has a very similar trend to the δ(An,Cl) (R² = 0.965), albeit with a consistently lower magnitude across the series (Mean Absolute Deviation between δ(An,Cl) and WBI = 0.198).

Fig. 4 The An–Cl delocalisation index δ(An,Cl) for AnCl₂ and AnCl₃.⁵²

The energies of metal and ligand orbitals, and hence energy degeneracy driven covalency, can be sensitive to the computational approach used. In our previous work on AnCl₃, we performed a functional comparison between PBE and PBE0, and found that the meta GGA (PBE) showed a marginally better energy matching than the hybrid (PBE0) between the metal 5f and chlorine 3p orbitals.⁵² It was clear, however, that despite differences in magnitude, the overall trends between the two functionals were similar, and hence that the trends presented here for AnCl₂ are representative of DFT approaches.

As the dichlorides do not become more covalent across the series, their increased relative stability indicated by the enthalpy calculations must arise due to increased ionic bond strength. This assumption is supported by Fig. 5 (and Table SI6†), which shows the average (α and β) ionic/covalent bond order obtained from NRT calculations. These data highlight that the dichlorides all possess a very ionic An–Cl bond across the series. Moreover, the NRT trend is somewhat similar to the bond lengths in Fig. 1, with a larger ionic vs. covalent bond order ratio associated with the late actinides, once more suggesting increased ionic behaviour from Pu–Md (excepting Cm and Bk). Furthermore, as with δ(An,Cl), the dichlorides’ ionicity increases from Cf–Md, again highlighting a difference in behaviour between the trichlorides and dichlorides in the latter half of the series. NRT also further supports the assumption that there is an absence/smaller degree of energy degeneracy driven covalency, or at least by the same mechanism seen for the trichlorides, as when splitting the ionic/covalent bond order into its α and β components (Fig. SI8†), the ratio for the two sets of orbitals both increase at the end of the series, by contrast to the trichlorides for which the α spin's ratio increases but the β spin's, where the energy matching and increased covalency occurs, decreases.

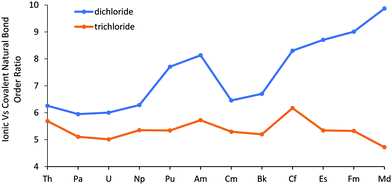Fig. 5 The ratio of the ionic to covalent contributions to the natural bond order in AnCl₂ and AnCl₃ (from previous work⁵²). No is excluded, as it did not converge on a resonance structure for the β orbitals.

We now turn to NBO analysis of the dichlorides. As with the trichlorides, the default NBO options produced a rather varied picture across the series, with ThCl₂ possessing double bonds, PaCl₂ triple bonds, UCl₂ and NpCl₂ triple bonds in the α manifold and single in the β, whilst (Pu–No)Cl₂ possessed single bonds. Therefore, to obtain a consistent comparison across the series, and with the trichlorides in the previous study,⁵² double bonds were imposed across the series via the CHOOSE option (thus resulting in all molecules having σ-type NBO and a π-type NBO for both the α and β orbitals). Similar to the trichlorides, the NBOs are dominated by the chlorine ligand; as shown in Table SI7,† the metal involvement to the NBOs (m%) are ≤11.76%. The average m% for the dichlorides (as shown in Fig. SI9 and Table SI7†) follows the same trend as the bond length, δ(An,Cl) and NRT, i.e. (Th–Np, Cm, Bk) have a m% value similar to the trichlorides, but as one progresses across the series and the 6d population decreases for elements Pu, Am, Cf–No, the m% decreases significantly. The breakdown of the σ and π NBOs is shown in Tables SI8–S11† and Fig. 6 for An = Th–Md, and Fig. SI10† for An = Th–No. As with the trichlorides, the d orbital dominates the metal orbital contribution, with the f contribution being smaller across the series for both σ (Fig. 6a) and π (Fig. 6b) type orbitals. Those compounds previously noted to have shorter bond lengths, larger excess d populations and δ(An,Cl) are also the ones with the largest d character in their σ and π NBOs.

Fig. 6 Actinide d and f natural atomic orbital contributions (%) to the (a) σ type and (b) π type NBOs for AnCl₂. (NoCl₂ is omitted as it is a full shell thus is not divided into α and β – see SI10† for the corresponding graph for the whole series where the α and β compositions are averaged for An = Th–Md).

Our previous study of AnCl₃ identified An 5f/Cl 3p energy degeneracy covalency in the later members of the series. The NBO composition data for AnCl₂, however, differ significantly from those of AnCl₃ (Fig. SI18†) post Bk; there is not a peak in β f% for the second half of the series for the σ-type and a much smaller peak from Cf to Md for π-type orbitals for the dichlorides. Fig. 7 (and Table SI12†), which shows the average 5f and 3p NAO energy difference, indicates that the dichlorides’ average metal 5f orbital and chlorine 3p β orbital energy difference is larger than the trichlorides’, and never reaches the energy match seen with FmCl₃. This supports reduced energy degeneracy covalency in the β orbitals of the later AnCl₂, and the lesser f% increase for the dichloride β spin orbitals. Furthermore, unlike in the analogous plot for the trichlorides, there is no peak in the α f% for the π-type orbitals at Am. This is supported by Fig. 7, as it shows significant average energy difference between the 5f and 3p α orbitals for AmCl₂, thereby emphasising the connection between peaks in f% contribution to NBOs and energy degeneracy driven covalency. There is an energy match at Cf for the 5f α spin orbitals, but as these metal orbitals are full at this point in the series, they are unable to accept electrons from the chloride orbitals and no energy degeneracy covalency is seen.

Fig. 7 The average energy difference (Hartrees) between the 5f and 3p NAOs on the An and Cl centres respectively for AnCl₂ and AnCl₃ ⁵² (An = Pu–Md).

By contrast to the trichlorides, the dichlorides do not have a strong correlation between the β metal and ligand NHO energy difference (Fig. 8 and Table SI12†) and the β f% contribution to the NBO (Fig. 6). For example, for the dichlorides’ π β orbital, despite a peak from Am to Bk in both the NBO contribution and NHO energy difference data, the f% in the NBO contribution decreases significantly at Cf, whereas the NHO energy difference gradually decreases to Es. The trend in β f% in the NBO appears to be related to the energy difference between the 5f and 3p NAOs in Fig. 7, with the f% and energy match between the ligand and metal orbitals decreasing from Bk to Cf and increasing at Es. However, unlike the trichlorides’ β π metal NHOs, which are composed almost exclusively of d or f character, the dichlorides’ β π NHOs have a significant s and p character. In fact, for almost all types of NBO that have small f%, there is a corresponding higher s% and/or p%. Thus, the NHO energy is not solely influenced by the 5f, but also by the energy of the other orbitals. This proposal that that dichlorides’ β NBO properties are influenced by more than the 6d and 5f orbitals is supported by the increase in NHO overlap integrals seen in Fig. SI17 and Table SI13† at Cf, where there is a decrease in f% and an increase in the spatially more diffuse p% in the NBO. In other words, there is less energy degeneracy driven covalency at the end of the series for the dichlorides, and hence maximising orbital overlap is a more important factor in stabilising a bonding interaction between the actinide metal and chloride ligand.

Fig. 8 The average energy difference (Hartrees) between the Cl and An localised NHOs involved in the β spin σ and π type NBOs for AnCl₂ (An = Am–Md).

Conclusions

The story of the actinide dichlorides is one of two groups. (Th–Np, Cm, Bk) possess bond lengths similar to the trichlorides, which are significantly shorter than those of the other AnCl₂. According to QTAIM, NBO and NRT analysis, the An–Cl bonds in (Th–Np, Cm, Bk)Cl₂ are more covalent than those of the dichlorides of the second group (Pu, Am, Cf–No). NPA shows a significant decrease in the expected 5f and increase in the 6d population of these compounds, and NBO composition data also highlight increased 6d character in their bonds. This increased involvement of the 6d orbital has been previously witnessed by Mikheev and Rumer, who suggested that these members of the series promote an electron from a 5f orbital to a higher energy virtual 6d orbital to stabilise the +2 state, as population of the d orbital provides a net stabilisation. Thus, we suggest that the increased covalency seen for these compounds is driven by the population of the spatially more diffuse 6d orbital.

As one moves across the series the 5f orbitals decrease in energy and the f–d excitation energy becomes larger than the d stabilisation energy. Thus, it is no longer energetically beneficial to promote a 5f electron to the 6d orbital. The reduced population of the spatially more diffuse 6d orbital, and the well-established contraction of the 5f orbitals, leads to overlap between the ligand and metal orbitals decreasing significantly towards the end of the series, and hence to more ionic bonding. In AnCl₃ the contraction and stabilisation of the An 5f β spin orbitals generates energy degeneracy driven covalency through energy matching with the Cl 3p orbitals for the later An, but even for the heavier AnCl₂ this energy difference is still relatively large, and there is no significant energy driven covalency.

We find that the +2 oxidation state becomes more stable vs. the +3 across the series. Mikeev and Rumer have previously suggested that this stability is related to the energy lowering of the 5f orbitals. We find that this energy lowering leads, in the case of the trichlorides, to energy degeneracy driven covalency in the later members of the series, but that this effect is much smaller for the dichlorides. Hence the divalent state may be more accessible in the latter half of the actinide series but, for chloride ligands at least, it is not more covalent.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to The University of Manchester for a PhD studentship to SC, and to its Computational Shared Facility and associated support services.

References

1. B. Weaver and F. A. Kappelmann, Report ORNL-3559, 1964.
2. B. Weaver and F. A. Kappelmann, J. Inorg. Nucl. Chem., 1968, 30, 263.
3. M. J. Tassell and N. Kaltsoyannis, Dalton Trans., 2010, 39, 6719.
4. I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131.
5. J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2018, 140, 17977–17984.
6. T. Glaser, B. Hedman, K. O. Hodgson and E. I. Solomon, Acc. Chem. Res., 2000, 33, 859–868.
7. M. C. Heaven, B. J. Baker and I. O. Antonov, J. Phys. Chem. A, 2014, 118, 10867–10881.
8. S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor, R. L. Martin, D. K. Shuh and T. Tyliszczak, Chem. Sci., 2014, 5, 351–359.
9. A. Formanuik, A. M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. McInnes and D. P. Mills, Nat. Chem., 2017, 9, 578–583.
10. Y. Zhang, W. Duan, Q. Wang, L. Zheng, J. Wang, J. Chen and T. Sun, J. Synchrotron Radiat., 2022, 29, 11–20.
11. M. P. Kelley, G. J. P. Deblonde, J. Su, C. H. Booth, R. J. Abergel, E. R. Batista and P. Yang, Inorg. Chem., 2018, 57, 5352–5363.
12. K. C. Mullane, P. Hrobarik, T. Cheisson, B. C. Manor, P. J. Carroll and E. J. Schelter, Inorg. Chem., 2019, 58, 4152–4163.
13. J. Du, J. A. Seed, V. E. J. Berryman, N. Kaltsoyannis, R. W. Adams, D. Lee and S. T. Liddle, Nat. Commun., 2021, 12, 1–11.
14. K. Anzai, N. Ban, T. Ozawa and S. Tokonami, J. Clin. Biochem. Nutr., 2012, 50, 2–8.
15. M. Sturzbecher-Hoehne, G. J. Deblonde and R. J. Abergel, Radiochim. Acta, 2013, 101, 359–366.
16. M. Sturzbecher-Hoehne, T. A. Choi and R. J. Abergel, Inorg. Chem., 2015, 54, 3462–3468.
17. M. Sturzbecher-Hoehne, B. Kullgren, E. E. Jarvis, D. D. An and R. J. Abergel, Chem. – Eur. J., 2014, 20, 9962–9968.
18. M. Sturzbecher-Hoehne, C. NgPakLeung, A. D'Aleó, B. Kullgren, A.-L. Prigent, D. K. Shuh, K. N. Raymond and R. J. Abergel, Dalton Trans., 2011, 40, 8340–8346.
19. P. W. Durbin, B. Kullgren, J. Xu and K. N. Raymond, Radiat. Prot. Dosim., 1994, 53, 305–309.
20. D. D. An, B. Kullgren, E. E. Jarvis and R. J. Abergel, Chem.-Biol. Interact., 2017, 267, 80–88.
21. J. Xu, B. Kullgren, P. W. Durbin and K. N. Raymond, J. Med. Chem., 1995, 38, 2606–2614.
22. J. Xu and K. N. Raymond, Inorg. Chem., 1999, 38, 308–315.
23. D. D. An, J. A. Villalobos, J. A. Morales-Rivera, C. J. Rosen, K. A. Bjornstad, S. S. Gauny, T. A. Choi, M. Sturzbecher-Hoehne and R. J. Abergel, Int. J. Radiat. Biol., 2014, 90, 1055–1061.
24. R. J. Abergel, P. W. Durbin, B. Kullgren, S. N. Ebbe, J. Xu, P. Y. Chang, D. I. Bunin, E. A. Blakely, K. A. Bjornstad, C. J. Rosen, D. K. Shuh and K. N. Raymond, Health Phys., 2010, 99, 401–407.
25. T. A. Choi, A. M. Furimsky, R. Swezey, D. I. Bunin, P. Byrge, L. V. Iyer, P. Y. Chang and R. J. Abergel, J. Pharm. Sci., 2015, 104, 1832–1838.
26. P. W. Durbin, B. Kullgren, J. Xu and K. N. Raymond, Radiat. Prot. Dosim., 1998, 79, 433–443.
27. F. H. David, Radiochim. Acta, 2008, 96, 135–144.
28. P. D. Dau, D. K. Shuh, M. Sturzbecher-Hoehne, R. J. Abergel and J. K. Gibson, Dalton Trans., 2016, 45, 12338–12345.
29. J. L. Namy, P. Girard and H. B. Kagan, Nouv. J. Chim., 1977, 1, 5.
30. J. R. Peterson, R. L. Fellows, J. P. Young and R. G. Haire, Radiochem. Radioanal. Lett., 1977, 31, 277–282.
31. J. R. Peterson and R. D. Baybarz, Inorg. Nucl. Chem. Lett., 1972, 8, 423–431.
32. J. F. Wild, E. K. Hulet, R. W. Lougheed, W. N. Hayes, J. R. Peterson, R. L. Fellows and J. P. Young, J. Inorg. Nucl. Chem., 1978, 40, 811–817.
33. S. Heathman, T. Le Bihan, S. Yagoubi, B. Johansson and R. Ahuja, Phys. Rev. B: Condens. Matter, 2013, 87, 214111.
34. T. D. Tilley, R. A. Andersen, B. Spencer and A. Zalkin, Inorg. Chem., 1982, 21, 2647–2649.
35. W. J. Evans, I. Bloom, W. E. Hunter and J. L. Atwood, J. Am. Chem. Soc., 1981, 103, 6507–6508.
36. D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Dalton Trans., 1973, 10, 1021–1023.
37. G. Qi, Y. Nitto, A. Saiki, T. Tomohiro, Y. Nakayama and H. Yasuda, Tetrahedron, 2003, 59, 10409–10418.
38. C. Eaborn, P. B. Hitchcock, K. Izod, Z.-R. Lu and J. D. Smith, Organometallics, 1996, 15, 4783–4790.
39. N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103.
40. R. R. Langeslay, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, Chem. Sci., 2015, 6, 517–521.
41. M. R. MacDonald, M. E. Fieser, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2013, 135, 13310–13313.
42. H. S. La Pierre, A. Scheurer, F. W. Heinemann, W. Hieringer and K. Meyer, Angew. Chem., Int. Ed., 2014, 53, 7158–7162.
43. R. E. Sykora, Z. Assefa, R. G. Haire and T. E. Albrecht-Schmitt, Inorg. Chem., 2006, 45, 475–477.
44. J. H. Burns, O. Ridge and O. Ridge, J. Inorg. Nucl. Chem., 1973, 35, 1171–1177.
45. P. G. Laubereau and J. H. Burns, Inorg. Chem., 1970, 9, 1091–1095.
46. E. Galbis, J. Hernández-Cobos, C. Den Auwer, C. Le Naour, D. Guillaumont, E. Simoni, R. R. Pappalardo and E. Sánchez Marcos, Angew. Chem., Int. Ed., 2010, 49, 3811–3815.
47. M. J. Polinski, E. B. Garner, R. Maurice, N. Planas, J. T. Stritzinger, T. G. Parker, J. N. Cross, T. D. Green, E. V. Alekseev, S. M. Van Cleve, W. Depmeier, L. Gagliardi, M. Shatruk, K. L. Knappenberger, G. Liu, S. Skanthakumar, L. Soderholm, D. A. Dixon and T. E. Albrecht-Schmitt, Nat. Chem., 2014, 6, 387–392.
48. S. K. Cary, M. Vasiliu, R. E. Baumbach, J. T. Stritzinger, T. D. Green, K. Diefenbach, J. N. Cross, K. L. Knappenberger, G. Liu, M. A. Silver, A. E. Deprince, M. J. Polinski, S. M. Van Cleve, J. H. House, N. Kikugawa, A. Gallagher, A. A. Arico, D. A. Dixon and T. E. Albrecht-Schmitt, Nat. Commun., 2015, 6, 1–8.
49. M. A. Silver, S. K. Cary, J. A. Johnson, R. E. Baumbach, A. A. Arico, M. Luckey, M. Urban, J. C. Wang, M. J. Polinski, A. Chemey, G. Liu, K. W. Chen, S. M. Van Cleve, M. L. Marsh, T. M. Eaton, L. J. Van De Burgt, A. L. Gray, D. E. Hobart, K. Hanson, L. Maron, F. Gendron, J. Autschbach, M. Speldrich, P. Kögerler, P. Yang, J. Braley and T. E. Albrecht-Schmitt, Science, 2016, 353, 888.
50. S. S. Galley, S. A. Pattenaude, C. A. Gaggioli, Y. Qiao, J. M. Sperling, M. Zeller, S. Pakhira, J. L. Mendoza-Cortes, E. J. Schelter, T. E. Albrecht-Schmitt, L. Gagliardi and S. C. Bart, J. Am. Chem. Soc., 2019, 141, 2356–2366.
51. M. P. Kelley, J. Su, M. Urban, M. Luckey, E. R. Batista, P. Yang and J. C. Shafer, J. Am. Chem. Soc., 2017, 139, 9901–9908.
52. S. Cooper and N. Kaltsoyannis, Dalton Trans., 2021, 50, 1478–1485.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Version A. 03), Gaussian, Inc., Wallingford, CT, 2016.
55. X. Cao, M. Dolg and H. Stoll, J. Chem. Phys., 2003, 118, 487–496.
56. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
57. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
58. D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684.
59. T. A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019.
60. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2018.
61. S. Y. Savrasov, G. Kotliar and E. Abrahams, Nature, 2001, 410, 793–795.
62. R. C. Albers, Nature, 2001, 410, 759–761.
63. N. B. Mikheev and I. A. Rumer, Radiochim. Acta, 1999, 85, 49–55.
64. M. Vasiliu, T. Jian, J. K. Gibson, K. A. Peterson and D. A. Dixon, Inorg. Chem., 2020, 59, 4554–4566.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt00315e

‡ Current address: National Nuclear Laboratory Limited, 5th Floor, Chadwick House, Birchwood Park, Warrington, WA3 6AE.

---