On the magnetic structure and magnetic behaviour of the most distorted member of the series of RNiO₃ perovskites (R = Lu)

Abstract

The crystal structure of LuNiO₃ perovskite has been examined below RT and across T_N = 125 K by neutron powder diffraction. In this temperature region (2–298 K), well below the metal–insulator transition this oxide exhibits at T_MI = 599 K, this material is insulating and characterized by a partial charge disproportionation of the Ni valence. In the perovskite structure, defined in the monoclinic P2₁/n space group, there are two inequivalent Ni sites located in alternating octahedra of different sizes. The structural analysis with high-resolution techniques (λ = 1.594 Å) unveils a subtle increase of the charge disproportionation as temperature decreases, reaching δ_eff = 0.34 at 2 K. The magnetic structure has been investigated from low-T NPD patterns collected with a larger wavelength (λ = 2.52 Å). Magnetic peaks are observed below T_N; they can be indexed with a propagation vector k = (½, 0, ½), as previously observed in other RNiO₃ perovskites for the Ni sublattice. Among the three possible solutions for the magnetic structure, the first one is discarded since it would correspond to a full charge ordering (Ni²⁺ + Ni⁴⁺), with magnetic moments only on Ni²⁺ ions, not compatible with the structural findings assessing a partial charge disproportionation. The best agreement is found for a non-collinear model with two different moments in Ni1 and Ni2 sites, 1.4(1) μ_B, and m 0.7(1) μ_B at 2 K, the ordered magnetic moments lying on the a–c plane. This is similar to that found for YNiO₃. In complement, the magnetic and thermal properties of LuNiO₃ have been investigated. AC susceptibility curves exhibit a clear peak centered at T_N = 125 K, corresponding to the establishment of the Ni antiferromagnetic structure. This is corroborated by DC susceptibility and specific heat measurements. Magnetization vs. field measurements confirm that the system is antiferromagnetic down to 2 K, without any further magnetic change. This linear behavior is also observed in the paramagnetic regime (T > T_N).

---

Introduction

Magnetic dynamics and ordering in electron correlated oxides show multiple physical phenomena that have attracted the attention of the scientific community for years, as they could contribute to new spintronics devices to surpass current electronics limitations.^1–3 In particular, electron correlations and magnetic interactions in RNiO₃ perovskites are both responsible for the paradigmatic metal to insulator (MI) transition these oxides undergo as a function of temperature and the rare-earth size, and the low-temperature antiferromagnetic phases due to Ni spin ordering below an antiferromagnetic Néel temperature (T_N)^4–8 and subsequent ordering of the magnetic rare-earths. This system displays several properties suitable for applications, as in optical switches,⁹ superlattices,^10,11 fuel cells¹² or memory devices.¹³ These fascinating perovskite oxides were first described by Demazeau in 1971,¹⁴ who prepared the whole series (R = La⋯Lu) under hydrostatic pressures of 6 GPa to stabilize trivalent Ni cations. The MI transitions were not described until 20 years later,^6,7 given the difficulties inherent to their synthesis. Later on, the associated structural transitions were thoroughly studied for different rare-earth derivatives, trying to clarify the structure–properties interplay.^15–18 The rare-earth cation R³⁺ radii determine the distortion of the ideal perovskite structure, which turns into a MI transition temperature (T_MI) and T_N evolution across the rare-earth series. As such, the less-distorted member LaNiO₃ shows a metallic behavior in all the stability temperature range, and no antiferromagnetic phase is observed at low temperatures. By contrast, for the subsequent members, the T_MI increases from PrNiO₃ (T_MI = 130 K) to LuNiO₃ (T_MI = 599 K) and the T_N shows a monotonic variation. The nature of the electronic transition has been systematically studied by spectroscopic and diffraction techniques.^19–23 Charge disproportionation^15,24–28 and charge ordering^29,30 are the main mechanisms proposed to explain charge localization in the insulating regime, as the smaller rare-earth derivatives (R = Y, Dy → Lu) display a concomitant transition from the more regular perovskite high-temperature orthorhombic (Pbnm) structure to the low-temperature insulating monoclinic (P2₁/n) structure, which shows an alternating breathing-like distortion of the NiO₆ octahedral arrangement. However, for larger rare-earths RNiO₃ (R = Pr → Gd) a non-periodic charge ordering has been observed.^24,31,32 This model, also called bond-disproportionation, has been linked to a small or negative charge transfer gap³³ and a strong electron–lattice coupling.^34,35

The AFM magnetic ordering has been ascribed to spin interactions of the Ni sublattice with an unusual propagation vector of k = (½, 0, ½), with alternating ferromagnetic interactions in the strong covalent bonding across Ni and O atoms. Another proposed magnetic structure would be described with k = (¼, ¼, ¼), in which contiguous Ni spins are arranged almost orthogonal to each other, depicting a 90° spin spiral magnetic order.^36–40 As well, the different structural distortion resulting from the R³⁺ cation radii alter the magnetic transition temperature due to the variation of the superexchange Ni–O–Ni angle. Even though T_N matches T_MI for the larger (R = Pr, Nd) members, for the smaller rare-earths (R = Sm, Lu) T_N < T_MI, which indicates that the magnetic transition is not directly coupled to the MI electronic transition. One particular example is HoNiO₃, which has shown long magnetic ordering of the rare-earth decoupled to the magnetic moment of Ni atoms.⁴¹ Meanwhile, magnetic studies of LaNiO₃ single crystals confirms that there is no intrinsic long-range magnetic ordering in this material⁴² and RMN experiments on TlNiO₃ displayed a new magnetic phase, still uncharted in other derivatives.⁴³ Recently, site-selective contributions of the two different Ni positions in NdNiO₃ were measured by resonant inelastic X-ray scattering (RIXS), yielding a model based on a strong competition between ferromagnetic double-exchange and antiferromagnetic superexchange interactions.²² Moreover, it was predicted that materials with simultaneous charge ordering and magnetism would show ferroelectricity with a large polarization, as in the AFM phase of RNiO₃.^43,44 However, the ferroelectric polarization is determined by the exact magnetic structure, and therefore, further investigation is required.

In the present contribution we describe a high-resolution NPD study for the smallest rare-earth cation, R = Lu, for which the magnetic structure and some magnetic significant details were still lacking. LuNiO₃ is an excellent system where to investigate the magnetic arrangement of Ni³⁺ spins, taking advantage of the non-magnetic character of the Lu partner, showing, in the other side, a considerably more distorted crystal structure with narrower super-exchange angles than YNiO₃. A specific heat study across T_N is essential to determine the temperature of establishment of the long-range ordering of the Ni sublattice, in complement to magnetic susceptibility and magnetization measurements.

Experimental section

LuNiO₃ perovskite oxide was prepared at high hydrostatic pressure, from stoichiometric mixtures of analytical grade Ni(OH)₂ (99%, Aldrich Chemical Company Inc.) and Lu₂O₃ (99.9%, Alfa Aesar, Karlsruhe, Germany). They were ground in an agate mortar with 30% KClO₄ (>99.5%, Fluka Chemika, Buchs, Switzerland), incorporated to provide an in situ high-oxygen pressure, in order to promote the oxidation of nickel to Ni³⁺. The precursor mixture was introduced into gold capsules of 5 mm diameter. These capsules were set in graphite cylinders acting as heaters, with Pyrex sleeves acting as pressure medium. The final pressure was applied in cold; the temperature was increased at 20 °C min⁻¹ up to 900 °C. Pressurization and depressurization rates were 2 GPa h⁻¹. After the heating period (20 min), the samples were rapidly cooled (100 °C s⁻¹) and then the pressure was slowly released. Therefore, the high-pressure products were quenched to a metastable state, where they were kinetically stable for long times. The KCl resulting from the decomposition of KClO₄ and traces of Lu₂O₃ and NiO was (partially) eliminated by washing the resulting powder in a diluted HNO₃ solution at 60 °C. The samples were then dried at 150 °C for 1 h in air.

The nature of the resulting powder was assessed by laboratory X-ray diffraction (XRD) in a Bruker-AXS D8 diffractometer (40 kV, 30 mA), with Cu Kα radiation (λ = 1.5418 Å). NPD patterns were collected at the high-resolution D2B neutron diffractometer of ILL-Grenoble. Although only a relatively small amount of sample was obtained from the high-pressure experiments (about 0.5 g), good quality patterns could be collected with the high-flux mode and a counting time of 4 h. A wavelength of 1.594 Å was selected from a Ge monochromator. A room temperature (RT, 298 K) pattern was collected, and then additional patterns at 175 K, 80 K and 2 K were recorded in the same diffractometer. For the investigation of the establishment of the Ni ordering, an additional sequential NPD patterns were acquired in the 2–150 K interval at the D1B multidetector diffractometer, with λ = 2.52 Å.

Magnetic susceptibility was measured in a SQUID Magnetometer from Quantum Design (QD, USA) model MPMS-5S in the range of 1.8 K till 400 K and magnetic fields up to 5 T. Complementary data on magnetization at high magnetic fields (14 T) and AC magnetic susceptibility were performed in a VSM and AC options of the PPMS system from QD. Heat capacity measurement in the range 1.8 K up to 300 K at different applied external magnetic fields (up to 9 T) was measured in the PPMS system with a heat pulse method.

Results & discussion

Low-temperature crystal structures

LuNiO₃ oxide was obtained as a well-crystallized polycrystalline powder. The XRD diffraction pattern is given in ref. 45. The MI transition was reported to take place at 599 K.⁴⁵ A previous NPD study established that its perovskite structure, at RT, can be defined in the monoclinic P2₁/n space group, since at this temperature the insulating state is well established, and characterized by a charge-disproportionation phenomenon. In P2₁/n, Ni atoms occupy two independent crystallographic sites with slightly different charge, 3 + δ and 3 − δ, in such a way that there are alternating small and large octahedra, respectively, along the 3 directions of the crystal (Fig. 1a).

Fig. 1 (a) View of the LuNiO₃ crystal structure, illustrating the alternation of Ni1O₆ (brown) and Ni2O₆ (grey) octahedra. (b) Rietveld plot of LuNiO₃ at 175 K, above the AFM regime. The second and third series of Bragg peaks correspond to minor NiO and Lu₂O₃ impurities, respectively.

A NPD pattern was collected at RT, to confirm previous findings, and the Rietveld plot is displayed in Fig. S1 (ESI†), illustrating the quality of the fit. The crystal structure was also refined from the NPD patterns collected at 175 K (Fig. 1b), just above the establishment of the antiferromagnetic structure, and at 80 K and 2 K, already in the antiferromagnetic phase (as described below, T_N = 125 K for LuNiO₃). The Rietveld plots from high-resolution NPD data at those temperatures are also included in the ESI† (Fig. S2 and S3). In all cases, the structures can be refined in the monoclinic P2₁/n space group; no structural phase transitions are detected in the 2–298 K temperature range. The structural parameters at 2, 80, 175 and 298 K are included in Table 1. The unit-cell parameters a and c decrease as expected from the thermal contraction (Fig. 2), whereas b exhibits a non-monotonic evolution, with a change of tendency at about the magnetic ordering temperature, perhaps driven by a magnetostriction phenomenon. The monoclinic β angle (inset of Fig. 2) increases upon cooling, defining a somewhat more distorted structure, and is stable below 80 K. The thermal evolution obtained in a sequential acquisition in the 2–140 K range in the D1B diffractometer is included in the ESI† (Fig. S4).

Fig. 2 Thermal variation of the unit-cell parameters and unit-cell volume of LuNiO₃, determined from NPD data (high-resolution D2B diffractometer, λ = 1.594 Å). The inset shows the evolution of the monoclinic β angle. The standard deviations are smaller than the size of the symbols.

Table 1 Structural parameters of the LuNiO₃ in the 2–298 K temperature range, determined from NPD data with λ = 1.594 Å

LuNiO3, P21/n
T (K)	2	80	175	298
a (Å)	5.10437(8)	5.10774(6)	5.10974(7)	5.11184(7)
b (Å)	5.49716(8)	5.50056(6)	5.50096(6)	5.49937(6)
c (Å)	7.3252(1)	7.33125(7)	7.33757(8)	7.34130(9)
V (Å^3)	205.540(5)	205.974(4)	206.247(4)	206.377(4)
β (°)	90.182(1)	90.1821(9)	90.1733(9)	90.158(1)
R 4e (x y z)
X	0.9797(5)	0.9766(5)	0.9774(5)	0.9778(4)
Y	0.0791(2)	0.0785(3)	0.0787(3)	0.0774(2)
Z	0.2513(6)	0.2502(5)	0.2499(5)	0.2509(5)
B iso (Å^2)	0.09(4)	0.25(5)	0.35(5)	0.30(4)
O1 4e (x y z)
X	0.1111(4)	0.1103(5)	0.1099(5)	0.1092(4)
Y	0.4618(4)	0.4627(4)	0.4622(4)	0.4624(4)
Z	0.2433(4)	0.2450(4)	0.2445(4)	0.2459(4)
B iso (Å^2)	0.06(4)	0.38(5)	0.42(6)	0.30(5)
O2 4e (x y z)
X	0.6943(6)	0.6944(5)	0.6949(6)	0.6967(5)
Y	0.3094(8)	0.3109(7)	0.3101(7)	0.3102(7)
Z	0.0520(4)	0.0536(4)	0.0539(4)	0.0541(4)
B iso (Å^2)	0.02(5)	0.39(6)	0.41(6)	0.24(5)
O3 4e (x y z)
X	0.1812(6)	0.1835(6)	0.1840(6)	0.1811(5)
Y	0.2005(7)	0.2029(6)	0.2019(7)	0.1991(7)
Z	0.9421(5)	0.9441(5)	0.9435(5)	0.9442(4)
B iso (Å^2)	0.14(6)	0.48(6)	0.37(7)	0.24(5)
Ni1 2d (½ 0 0)
B iso (Å^2)	0.10(5)	0.25(6)	0.17(6)	0.21(5)
Ni2 2c (½ 0 ½)
B iso (Å^2)	0.00(5)	0.34(6)	0.28(6)	0.13(5)
Agreement factors
R I (%)	4.34	3.39	3.31	7.63
R p (%)	8.85	13.4	13.9	12.3
R wp (%)	9.65	11.5	12.0	11.5
R exp (%)	4.31	10.36	10.46	7.62
χ ^2	5.01	1.24	1.31	2.29

---

It is interesting to unveil the evolution of the charge disproportionation effect upon cooling down the LuNiO₃ perovskite. This can be evaluated from the Ni–O distances of the two Ni1O₆ and Ni2O₆ octahedra. The phenomenological Brown's bond valence model estimates the formal valence of a bond from the measured bond lengths for each central atom, v_i = Σs_i, s_i = exp[(r₀ − r_i)/B]. For the pair Ni–O, r₀ = 1.686; B = 0.37. The calculated valences for Ni1 and Ni2 are listed in Table 2 for the different temperatures. The valences are significantly lower than 3+ for Ni1 and higher than 3+ for Ni2. Consequently, the appearance of two alternating Ni states with 3 − δ and 3 + δ′ valences give evidence of a charge disproportionation phenomenon associated with the insulating phase, as described before^{15,18,28,36,45} for pure RNiO₃ perovskites. The distortion of the NiO₆ octahedra (Δ_d) is comparable for both Ni1 and Ni2 sites (Table 2), and vary within the interval 0.5–1.6 × 10⁻⁴. In order to evaluate the evolution of the degree of disproportionation, we defined δ_eff = (δ + δ′)/2, which is also included in Table 2. As shown in Fig. 3a, the difference between 〈Ni1–O〉 and 〈Ni2–O〉 subtly increases upon cooling down, implying a progressive enhancement of the charge disproportionation δ_eff as temperature decreases (Fig. 3b). This effect had already been described above RT, in the temperature range RT < T < T_MI where the sample is still insulating, displaying a progressive fading of the charge disproportionation upon heating, with an abrupt collapse immediately below T_MI. The present results indicate that this observation also plays below RT, although in a softer way.

Fig. 3 (a) Temperature variation of the average 〈Ni1–O〉 and 〈Ni2–O〉 octahedral distances, from NPD data, and (b) thermal evolution of the charge disproportionation degree in LuNiO₃.

Table 2 Average Ni–O bond distances (〈Ni–O〉), calculated Ni valence, distortion factor and δ_eff defined as the average difference Ni valence from the nominal valence of 3+

T (K)	〈Ni1–O〉	〈Ni2–O〉	Ni1 valence	Ni2 valence	Δ d × 10^−4 (NiO6)1	Δ d × 10^−4 (NiO6)2	δ eff
2	1.997(1)	1.912(1)	2.59(1)	3.27(1)	0.519	1.488	0.34(1)
80	1.995(1)	1.913(1)	2.605(9)	3.25(1)	1.20	0.65	0.322(9)
175	1.995(1)	1.915(1)	2.605(9)	3.24(1)	0.88	0.99	0.318(9)
295	1.995(1)	1.917(1)	2.612(9)	3.22(1)	1.622	0.805	0.30(1)

---

Magnetic structures

The sequential NPD patterns collected at D1B multidetector diffractometer (λ = 2.52 Å) for LuNiO₃ show the appearance of magnetic reflections in the low-angle region, below a critical temperature of 130 K. In fact, this is slightly above the T_N of 125 K determined by magnetic and specific heat measurements, described below, which just signals some error in the temperature determination in the cryostat coupled to the neutron diffractometer.

To solve the magnetic structure we start by establishing the indexation of the extra reflections to determine the propagation vector of the magnetic ordering. We observe that all the small reflections of magnetic origin can be indexed considering a commensurate magnetic unit cell given by (2a, b, 2c) of the room temperature structural unit cell, implying a propagation vector k = (½, 0, ½). This is the same propagation vector found in all the previously studied nickelates besides the ordering of the rare earth in HoNiO₃, where Ho sublattice shows k = (0, 0, 0) as propagation vector.

To determine the possible magnetic structures compatible with the symmetry of the monoclinic space group P2₁/n and a propagation vector k = (½, 0, ½), we have followed the representation analysis based on group theory described by Bertaut⁴⁶ and detailed in ref. 39.

In the insulating phase (space group P2₁/n), Ni ions are split in two independent sites Ni1 and Ni2 occupying the positions (½, 0, 0) and (0, ½, 0), respectively. Their associated magnetic structure can be considered then as composed of two independent sublattices: one with m₁ in (½, 0, 0) and m₂ in (0, ½, ½); the other with m₃ in (0, ½, 0) and m₄ in (½, 0, ½). The basic functions for both sites are the following:

Site 1. IRrep(2): m_1x − m_2x, m_1y + m_2y, m_1z − m_2z

 IRrep(4): m_1x + m_2x, m_1y − m_2y, m_1z + m_2z

Site 2. IRrep(1): m_3x − m_4x, m_3y + m_4y, m_3z − m_4z

 IRrep(3): m_3x + m_4x, m_3y − m_4y, m_3z + m_4z

After checking all the possible combinations, we obtain the best refinement when considering the basis function m_1x + m_2x, m_1y − m_2y, m_1z + m_2z for the first sublattice and m_3x + m_4x, m_3y − m_4y, m_3z + m_4z for the second one. Like in the case of YNiO₃³⁶ and HoNiO₃ at 10 K,⁴¹ we observe that a collinear model with moments lying in the a–c plane is the most simple to fit satisfactorily the observed magnetic reflections, but it is by no means, unique. We observe a triple degeneracy; three models of magnetic arrangements can explain our diffraction data, in all cases with the magnetic moments in the a–c plane. The first one is that considering a complete charge ordering of the Ni ions with Ni1 sites hosting high spin Ni²⁺ ions and Ni2 sites occupied by Ni⁴⁺ and zero moment ions. This solution is nevertheless inconsistent with the structural data, which indicates a maximum charge disproportionation of δ_eff = 0.34 at 2 K. The second possible result is the mentioned collinear model, but with different moments for Ni1 and Ni2 sites, resulting from the charge disproportionation between the two Ni sites subsequent to the oxygen-breathing mode. The third ordering consists on a non-collinear magnetic structure that can be described as (m_1x + m_2x, 0, m_1z + m_2z) for Ni1 site and (m_3x + m_4x, 0, −m_3z − m_4z) for Ni2 site and which is represented in Fig. 4a. In spite of very subtle differences between the three models, we found a somewhat best agreement with the non-collinear ordering and the less suitable seems to be the one consisting of magnetic Ni²⁺, and non-magnetic Ni⁴⁺ ions. Unfortunately, these minor differences remain within the accuracy range.

Fig. 4 (a) Magnetic structure of LuNiO₃ at 2 K. (b) Rietveld refinement from NPD data at 2 K. The first tick marks correspond to the position of the structural reflections of LuNiO₃ and the second series corresponds to the magnetic reflections.

The refinement at the lowest measured temperature, 2 K, gives for the collinear magnetic structure

m (Ni1) = [1.3(1), 0, 0.9(0.2)]

m (Ni2) = [0.46(7), 0, 0.33(6)]

with resulting values of magnetic moments m (Ni1) = 1.6(1) μ_B, and m (Ni2) = 0.6(1) μ_B.

And for the non-collinear magnetic structure

m (Ni1) = [1.00(8), 0, 1.03(8)]

m (Ni2) = [0.48(4), 0, −0.49(4)]

and values of magnetic moments m (Ni1) = 1.4(1) μ_B, and m (Ni2) = 0.7(1) μ_B.

The agreement between the measured and calculated neutron powder-diffraction patterns at 2 K, for the non-collinear model, is displayed in Fig. 4b.

Fig. 5 displays the thermal evolution of the refined magnetic moments on both Ni1 and Ni2 positions. We do not identify any change in the position of the magnetic reflections or in their relative intensity up to the Néel temperature, as observed in Fig. 5, assessing the stability of the described magnetic ordering in all the temperature range.

Fig. 5 Temperature evolution of the ordered magnetic moments on the Ni1 and Ni2 sites. A regular evolution is observed in all the temperature range from 2 K up to the ordering temperature, T_N.

Magnetic and thermal properties

The AC magnetic susceptibility for LuNiO₃ is presented in Fig. 6. A clear peak in the χ′ susceptibility, almost independent of the excitation frequency, is observed at T_N = 125 K, indicating the ordering of the Ni sublattice. The DC magnetic susceptibility shows a similar peak around the same ordering temperature. The temperature dependence of the inverse susceptibility (inset Fig. 6) presents a linear behavior, corresponding to a paramagnetic moment of 4.2 μ_B per Ni atom, with strong antiferromagnetic interactions, as indicated by a Θ_W = −631 K. The paramagnetic moment is close to the one expected for Ni³⁺ spin only (3.9 μ_B).

Fig. 6 (a) AC magnetic susceptibility for LuNiO₃ at different frequencies. The inset shows the inverse DC magnetic susceptibility in the paramagnetic regime (above T_N). (b) Field dependence of magnetization at 1.8 K for LuNiO₃.

The field dependence of magnetization is presented in Fig. 6b for LuNiO₃ up to an external magnetic field of 7 T. In this particular case, only the nickel sublattice is ordered (T_N = 125 K), and the system is antiferromagnetic down to 2 K, without any further magnetic change. This mostly linear behavior is also observed in the paramagnetic regime (T > T_N); however the slight curvature observed at 2 K is probably related to the complex non-collinear magnetic structure, as discussed above.

The DC magnetic susceptibility for LuNiO₃ is displayed in Fig. 7. The measurement was performed under a magnetic field of 100 Oe in the whole temperature range. A cusp is observed at T_N = 125 K, corresponding to the onset for antiferromagnetic ordering of the Ni sublattice, in excellent agreement with the observation in AC susceptibility.

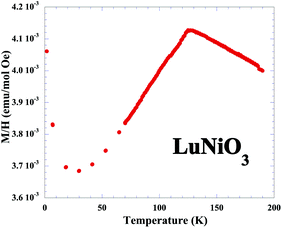Fig. 7 Temperature dependence of the dc magnetic susceptibility for LuNiO₃, under an applied field of 100 Oe.

Fig. 8 displays the temperature dependence of the specific heat for LuNiO₃ at different external magnetic fields. The data of specific heat shows a clear transition (lambda type) at T_N = 125 K, corresponding to the antiferromagnetic long-range order of the Ni sublattice, completely in agreement with the magnetic susceptibility and neutron diffraction data. In order to remove the contribution to the specific heat coming from the phonon vibrations in this temperature range, we simulated the lattice contribution to the C_p by three harmonic oscillators centered in frequencies equivalent to 200 K, 550 K and 910 K (Fig. 8b). After the subtraction of the calculation coming from the 3 harmonic oscillators, the obtained (ΔC/T)_Mag should be related only to the AF phase transition. The data are presented as an inset in Fig. 8a, with a clear lambda-type anomaly, which is rather independent on the applied external magnetic field (up to 9 T), as expected for AF ordering. The calculation presented in Fig. 8b is valid in the range of temperature higher than 60–80 K, where the electronic and Schottky-type contributions to the specific heat are negligible.

Fig. 8 (a) Temperature dependence of the specific heat for LuNiO₃ perovskite. The inset shows the magnetic part of the specific heat (ΔC/T_Mag) at different applied magnetic fields, around T_N = 125 K. (b) Calculation of the lattice contribution, simulated as 3 harmonic oscillators centered a frequencies equivalent to 200 K, 550 K and 910 K.

The integration of the C/T_Mag will give the change on the magnetic entropy associated with the AF ordering transition of the nickel sublattice. In principle, Ni³⁺ ions correspond to S = 3/2. The maximum magnetic entropy associated with the ordering of the Ni³⁺ ions will be ΔS = 2R ln(2S + 1). Under this simple estimation, ΔS = 2R ln 4 = 23.05 J mol⁻¹ K⁻¹. However, the experimental value obtained in Fig. 9 is only 1.2 J mol⁻¹ K⁻¹, which is far below the expected value for the complete ordering of the Ni³⁺ sub-lattice.

Fig. 9 Change in the magnetic entropy associated with the transition temperature in LuNiO₃.

Conclusions

High-resolution NPD data collected for LuNiO₃ in the 2–298 K temperature range, in the insulating regime, demonstrate that the crystal structure of this perovskite oxide stabilizes a charge disproportionation implying a separation of two kinds of (NiO₆) octahedra (large Ni1O₆ and small Ni2O₆) described in a pseudo-orthorhombic unit cell characterized by a subtle monoclinic distortion (β ∼ 90.182(1)° at 2 K) in the P2₁/n space group. The degree of charge disproportionation, estimated by the bond-valence model from the average 〈Ni1–O〉 and 〈Ni2–O〉 distances, slightly increases upon cooling down from RT to 2 K, ongoing with the trend already observed above RT, always in the insulating state (T < T_MI = 599 K). Magnetic susceptibility (AC, DC) together with specific heat measurements indicate the onset of antiferromagnetic ordering (T_N) to happen at 125 K. The strongly negative Weiss temperature Θ_W = −631 K already indicates the presence of strong antiferromagnetic interactions. Indeed, the low-T NPD patterns exhibit the appearance of magnetic peaks below T_N, yielding a fully developed magnetic structure at 2 K, involving the Ni spins. After evaluating the different solutions given by the group theory, the best fit corresponds to a non-collinear arrangement of Ni moments, lying on the a–c plane, with sizably larger moment values for Ni1 supporting a 3 − δ charge than for Ni2 (associated with 3 + δ charge), which is fully consistent with the structural determination of a partial charge disproportionation for this perovskite.

Author contributions

JAA prepared the sample and analysed the structural NPD data together with FSS; MTFD collected the neutron data and analysed the magnetic structure; JLM performed and analysed the magnetic measurements; all the authors participated in the discussion of results and redaction of the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Spanish Ministry of Science, Innovation and Universities through grant MAT2017-84496-R, cofinanced by FEDER. The authors wish to express their gratitude to ILL technical staff for making the facilities available for the neutron diffraction experiments.

Notes and references

1. E. Dagotto, Science, 2005, 309, 257–262.
2. H. Béa, M. Gajek, M. Bibes and A. Barthélémy, J. Phys.: Condens. Matter, 2008, 20, 434221.
3. H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa and Y. Tokura, Nat. Mater., 2012, 11, 103–113.
4. M. Medarde, C. Dallera, M. Grioni, B. Delley, F. Vernay, J. Mesot, M. Sikora, J. A. Alonso and M. J. Martínez-Lope, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245105.
5. J. B. Torrance, P. Lacorre, C. Asavaroengchai and R. M. Metzger, J. Solid State Chem., 1991, 90, 168–172.
6. P. Lacorre, J. B. Torrance, J. Pannetier, A. I. Nazzal, P. W. Wang and T. C. Huang, J. Solid State Chem., 1991, 91, 225–237.
7. J. Torrance, P. Lacorre, A. Nazzal, E. Ansaldo and C. Niedermayer, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 8209.
8. G. Catalan, Phase Transitions, 2008, 81, 729–749.
9. Z. Liao, N. Gauquelin, R. J. Green, K. Müller-Caspary, I. Lobato, L. Li, S. Van Aert, J. Verbeeck, M. Huijben, M. N. Grisolia, V. Rouco, R. El Hage, J. E. Villegas, A. Mercy, M. Bibes, P. Ghosez, G. A. Sawatzky, G. Rijnders and G. Koster, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9515–9520.
10. M. Wu, E. Benckiser, P. Audehm, E. Goering, P. Wochner, G. Christiani, G. Logvenov, H.-U. Habermeier and B. Keimer, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195130.
11. F. Y. Bruno, K. Z. Rushchanskii, S. Valencia, Y. Dumont, C. Carrétéro, E. Jacquet, R. Abrudan, S. Blügel, M. Ležaić, M. Bibes and A. Barthélémy, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 195108.
12. G. Amow and S. J. Skinner, J. Solid State Electrochem., 2006, 10, 538–546.
13. K. Ramadoss, F. Zuo, Y. Sun, Z. Zhang, J. Lin, U. Bhaskar, S. Shin, M. A. Alam, S. Guha and D. Weinstein, IEEE Electron Device Lett., 2018, 39, 1500–1503.
14. G. Demazeau, A. Marbeuf, M. Pouchard and P. Hagenmuller, J. Solid State Chem., 1971, 3, 582–589.
15. J. A. Alonso, M. J. Martínez-Lope, M. T. Casais, M. A. G. Aranda and M. T. Fernández-Díaz, J. Am. Chem. Soc., 1999, 121, 4754–4762.
16. M. L. Medarde, J. Phys.: Condens. Matter, 1997, 9, 1679.
17. J. A. Alonso, M. J. Martínez-Lope and I. Rasines, J. Solid State Chem., 1995, 120, 170–174.
18. J. A. Alonso, M. J. Martínez-Lope, M. T. Casais, J. L. Martínez, G. Demazeau, A. Largeteau, J. L. García-Muñoz, A. Muñoz and M. T. Fernández-Díaz, Chem. Mater., 1999, 11, 2463–2469.
19. J. Shamblin, M. Heres, H. Zhou, J. Sangoro, M. Lang, J. Neuefeind, J. A. Alonso and S. Johnston, Nat. Commun., 2018, 9, 86.
20. B. Torriss, A. Ibrahim, T. Ozaki and M. Chaker, Phys. Rev. B, 2018, 98, 165132.
21. W. Liang, H. Hou, Y. Lin and S.-N. Luo, J. Phys. D: Appl. Phys., 2018, 52, 75303.
22. Y. Lu, D. Betto, K. Fürsich, H. Suzuki, H.-H. Kim, G. Cristiani, G. Logvenov, N. B. Brookes, E. Benckiser and M. W. Haverkort, Phys. Rev. X, 2018, 8, 31014.
23. K. Fürsich, Y. Lu, D. Betto, M. Bluschke, J. Porras, E. Schierle, R. Ortiz, H. Suzuki, G. Cristiani and G. Logvenov, Phys. Rev. B, 2019, 99, 165124.
24. U. Staub, G. I. Meijer, F. Fauth, R. Allenspach, J. G. Bednorz, J. Karpinski, S. M. Kazakov, L. Paolasini and F. d'Acapito, Phys. Rev. Lett., 2002, 88, 126402.
25. M. Medarde, M. T. Fernández-Díaz and P. Lacorre, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 212101.
26. A. Mercy, J. Bieder, J. Íñiguez and P. Ghosez, Nat. Commun., 2017, 8, 1677.
27. D. J. Gawryluk, J. Rodríguez-Carvajal, P. Lacorre, M. T. Fernández-Díaz and M. Medarde, 2018, arXiv Prepr. arXiv1809.10914, 90.
28. J. A. Alonso, M. J. Martínez-Lope, I. A. Presniakov, A. V. Sobolev, V. S. Rusakov, A. M. Gapochka, G. Demazeau and M. T. Fernández-Díaz, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–12.
29. V. Bisogni, S. Catalano, R. J. Green, M. Gibert, R. Scherwitzl, Y. Huang, V. N. Strocov, P. Zubko, S. Balandeh, J. M. Triscone, G. Sawatzky and T. Schmitt, Nat. Commun., 2016, 7, 1–8.
30. J. Shamblin, M. Heres, H. Zhou, J. Sangoro, M. Lang, J. Neuefeind, J. A. Alonso and S. Johnston, Nat. Commun., 2018, 9, 1–7.
31. M. Zaghrioui, A. Bulou, P. Lacorre and P. Laffez, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 81102.
32. F. Serrano-Sánchez, J. L. Martínez, F. Fauth and J. A. Alonso, Dalton Trans., 2021, 50, 7085–7093.
33. S. Johnston, A. Mukherjee, I. Elfimov, M. Berciu and G. A. Sawatzky, Phys. Rev. Lett., 2014, 112, 106404.
34. J. Rodríguez-Carvajal, S. Rosenkranz, M. Medarde, P. Lacorre, M. T. Fernandez-Díaz, F. Fauth and V. Trounov, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 456–464.
35. R. Jaramillo, S. D. Ha, D. M. Silevitch and S. Ramanathan, Nat. Phys., 2014, 10, 304–307.
36. J. A. Alonso, J. L. García-Muñoz, M. T. Fernández-Díaz, M. A. G. Aranda, M. J. Martínez-Lope and M. T. Casais, Phys. Rev. Lett., 1999, 82, 3871–3874.
37. Y. Bodenthin, U. Staub, C. Piamonteze, M. García-Fernández, M. J. Martínez-Lope and J. A. Alonso, J. Phys.: Condens. Matter, 2011, 23, 36002.
38. I. R. Buitrago and C. I. Ventura, J. Magn. Magn. Mater., 2015, 394, 148–154.
39. A. Muñoz, J. A. Alonso, M. J. Martínez-Lope and M. T. Fernández-Díaz, J. Solid State Chem., 2009, 182, 1982–1989.
40. J. L. García-Muñoz, M. A. G. Aranda, J. A. Alonso and M. J. Martínez-Lope, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–5.
41. M. T. Fernández-Díaz, J. A. Alonso, M. J. Martínez-Lope, M. T. Casais and J. L. García-Muñoz, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 1444171–1444175.
42. K. Dey, W. Hergett, P. Telang, M. M. Abdel-Hafiez and R. Klingeler, J. Cryst. Growth, 2019, 524, 125157.
43. L. Korosec, M. Pikulski, T. Shiroka, M. Medarde, H. Luetkens, J. A. Alonso, H. R. Ott and J. Mesot, Phys. Rev. B, 2017, 95, 60411.
44. G. Giovannetti, S. Kumar, D. Khomskii, S. Picozzi and J. van den Brink, Phys. Rev. Lett., 2009, 103, 156401.
45. J. A. Alonso, M. J. Martinez-Lope, M. T. Casais, J. L. Garcia-Munoz and M. T. Fernandez-Dıaz, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 1756.
46. E. F. Bertaut, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 4, 217.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1dt03571a

---