Open Access Article
Open Access ArticleIn defence of oxidation states
Nicholas C.
Norman
* and
Paul G.
Pringle
 *
*
University of Bristol, School of Chemistry, Bristol, BS8 1TS, UK. E-mail: n.c.norman@bristol.ac.uk; paul.pringle@bristol.ac.uk
First published on 26th November 2021
Abstract
In this Perspective, some of the criticisms which have been made concerning the use of oxidation states are addressed, particularly in the context of the teaching of inorganic chemistry. The Oxidation State method and the Covalent Bond Classification method are compared and contrasted, and it is concluded that while each method has its strengths and weaknesses, both are important in teaching and it should be recognized that no single model or method is appropriate in all circumstances.
Introduction
The concept of an oxidation state or oxidation number for an element in a particular compound can be traced back to Lavoisier in the latter part of the 18th century. During the following hundred or so years, this concept was refined such that by the early 20th century, its definition and usage in modern chemical parlance had become well established.1 To this day, the assignment of an oxidation state is widely employed in describing the chemistry of elements from across the entire periodic table. Oxidation states have been, and continue to be, used to systematize large swathes of coordination chemistry, bioinorganic chemistry (particularly metalloenzymes and metal-mediated electron-transfer pathways), organometallic chemistry (which incorporates homogeneous catalysis), redox catalysis, inorganic solid-state chemistry (including battery technology2), and electrochemistry (consider tables of standard electrode potentials and Latimer or Frost diagrams). Moreover, oxidation state is central to a theme that permeates much of chemical reactivity, namely oxidation and reduction. Its use has endured because it is easily understood, generally simple to apply and acts as a unifying concept that is helpful in drawing parallels between apparently very different chemical entities. For example, there are commonalities in the properties of the Cu(II) site present in copper sulfate pentahydrate, Cu-containing ceramic superconductors, blue copper proteins, and the organocopper species recently identified to be reactive intermediates in Cu-catalysed oxidative aryl cross-coupling reactions.3From the brief encomium above, the usefulness of oxidation states might appear self-evident but their value has nevertheless been questioned, notably by some of the advocates of the Covalent Bond Classification (CBC) method.4–6 In this article, our principal objective will be to focus on the value and utility of the oxidation state (OS) method but we state from the outset our opinion that the CBC method (outlined in Chart 1) has made a significant contribution to the classification and systematisation of ligand types, especially in transition metal chemistry, and indeed compound types in general through the introduction of so-called MLX plots.4–6 It also has an internal rigour which has contributed to resolving some of the arguments and inconsistencies around electron-counting methods which persist to this day. However, having said that, claims have been made that the CBC method offers considerable advantages over more traditional approaches which employ oxidation states, particularly for the teaching of inorganic chemistry,5 and it is this claim that we principally wish to challenge. While it is certainly true that there are cases where the assignment of an oxidation state is ambiguous or where its value is questionable, we assert that the CBC method is not quite the panacea that some of its advocates have claimed. Moreover, the CBC method has some inconsistencies and ambiguities of its own, but before moving on to examine these matters in more detail, we will summarise some of the foundations on which we will build.
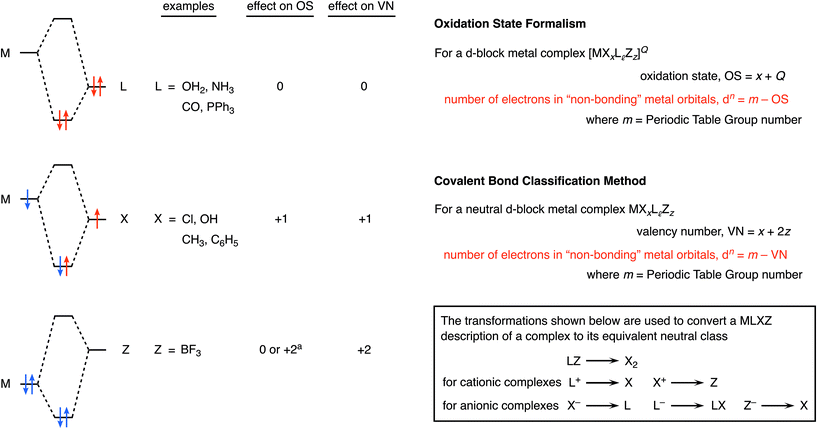
The most definitive text on oxidation states is probably the 2014 IUPAC Technical Report entitled Toward a Comprehensive Definition of Oxidation State7a in which the authors provide the following definition: the oxidation state of a bonded atom equals its charge after ionic approximation.7a–c A comprehensive description of the CBC method is provided in ref. 4–6 but, in brief, it categorises ligands as L, X or Z according to whether they are two-electron, one-electron or zero-electron donors respectively (see Chart 1 for an outline), and highlights, amongst other quantities, VN, the valency number (or valence) of the central atom to which the ligands are bonded. Much has been written more widely about the concept of valence8,9 which, since at least the time of Sidgwick,10 may be defined as: the number of electrons that an atom uses in bonding. Importantly, oxidation state and valence are not the same although they too often continue to be conflated and confused.9
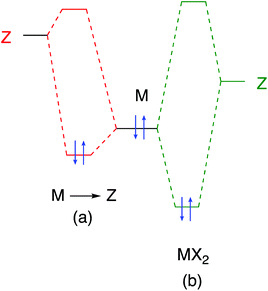
Besides oxidation state (and valence), another important feature of complexes of the d-block metals is the number of non-bonding electrons (the dn number) which is widely employed in the teaching of transition metal chemistry since it can often be used to rationalize the magnetism of complexes together with the coordination geometries they adopt. Chart 1 illustrates the formulas used for determining the dn number from both the OS and CBC methods from which it is clear that the two methods can only give the same value for dn if the valence number (VN) is equal to the oxidation state (OS).4 However there are important classes of compounds where VN and OS differ, in particular, for binuclear compounds that contain a metal–metal bond, e.g. [Mn2(CO)10], and for complexes in which the d-block metal is in a negative oxidation state, e.g. Na[Co(CO)4] and Na2[Fe(CO)4]. Each of these cases will be addressed below.
In ref. 5, the following statement is made: ‘In large part, the problems encountered in the use of oxidation states to classify covalent compounds result from the fact that it is an approach that forces ionic character on a compound that may have little such nature’. We contend that the assignment of an oxidation state does not ‘force’ anything, and the definition of oxidation state offered in the IUPAC Technical Report noted above7a refers to an ionic approximation. What this means when assigning an oxidation state to an element is that the groups to which it is bonded are removed according to electronegativity differences and (usually) in their closed-shell configurations so that atoms such as chlorine, for example, are removed as chloride, i.e. Cl−. In other words, the bonding electrons are assigned to the more electronegative atom. There is no suggestion or implication that the compound in question is necessarily ionic; it is a formalism which partitions atoms or groups according to their respective electronegativity differences. Hence, the oft-encountered term, formal oxidation state, and OS is often represented using Roman numerals (I, II, III etc.) to distinguish it from a real charge for which Arabic numerals (1, 2, 3 etc.) are employed.
Further criticisms of OS focus on two main issues: (i) ambiguities in assigning oxidations states and (ii) a lack of chemical insight that OS offers.5,11 It is true that there can sometimes be ambiguities in the assignment of an oxidation state but for most compounds, this is not the case and ambiguities are also present within the CBC method (see below). Moreover, with regard to chemical insight, both methodologies can be misleading in some circumstances. Examples of each issue are discussed below mostly involving transition metal compounds, since this is where the concept of oxidation state finds its widest application, but first, some examples from organic chemistry are considered.
Organic chemistry
Methane derivatives
The point has been made that the formal oxidation state of the carbon in a series of tetravalent compounds can vary from –IV in CH4 to IV in CCl4 with an oxidation state of 0 being represented by species such as CH2Cl2 and CMe4.5 This arises for CH2Cl2 because Cl is more electronegative than C and so is removed (formally) as Cl− whereas H is less electronegative than C and so is removed as H+ which then leads to an OS of 0. In CMe4, the methyl carbons attached to the central carbon are considered to have the same electronegativity such that there is no case for partitioning the C–C bonds heterolytically (this is the case generally where the bonded elements are the same).7 According to the CBC method (Chart 1), all of these species would be described as MX4 (i.e. tetravalent carbon). In general, for organic chemistry, the use of an oxidation state is unnecessarily complicated compared with the CBC approach because for much of organic chemistry, carbon is intermediate in electronegativity between H and the other atoms or groups to which it is commonly bonded. For these reasons, oxidation state is rarely employed although the closely related oxidation level (see below) is more widely used and for a good reason.Alcohols
Alcohols comprise another set of examples which is considered problematic for OS.9 Thus, the formal oxidation state of the carbon to which the OH group is bonded in the compounds CH3OH, MeCH2OH, Me2CHOH and Me3COH is –II, –I, 0 and I respectively. However, it has been proposed that hydrogens in organic molecules be removed with no charge.12 Although this runs counter to partitioning either by electronegativity or in terms of removing a species in a closed-shell configuration, adopting this proposal would result in the oxidation state for the carbon carrying the OH group in the species noted above being C(I) in each case.12 On the face of it, this might seem a little perverse (although C and H do have similar electronegativities) but there is a demonstrable value in using this approach. Thus, organic chemistry does make use of the fact that an oxidation level can be assigned to a carbon atom that depends solely on the number of bonds to heteroatoms, for example: 0 in alkanes, 1 in alcohols; 2 in aldehydes and ketones, 3 in carboxylic acids and their derivatives, and 4 in carbon dioxide (see Chart 2 for a fuller list of functional groups which can be categorised in this way). This approach has considerable merit since it indicates for any particular transformation whether an oxidising or reducing agent (or neither) will be needed; converting an alcohol into a ketone will require an oxidising agent, for example. To rely only on valence and to question the value of an oxidation level is therefore to remove a useful heuristic for teaching synthetic organic chemistry.Transition metal chemistry
Classical coordination complexes
Consider the following three coordination compounds of cobalt: [Co(NH3)6]3+, [CoCl3(NH3)3] and [CoCl6]3−. The recognition that in assigning an oxidation state, NH3 is removed as a neutral ligand and Cl as chloride (Cl−) leads directly and straightforwardly to the conclusion that all three compounds contain Co(III) and therefore have a d6 configuration. However, it has been stated that the relationship between these molecules is obfuscated by the fact that the molecules possess different charges.5 Furthermore, it is suggested that by converting each of these complexes into the ‘equivalent neutral class’ of ML3X3, their relationship to each other is revealed (Fig. 1). The assertion that the designation of ML3X3 for the two homoleptic species [Co(NH3)6]3+ and [CoCl6]3− simplifies matters or makes the teaching of this chemistry easier to understand is a moot point. Moreover, with regard to the teaching of transition metal coordination chemistry in general, the assignment of an oxidation state is useful because, for mononuclear complexes, it can be employed to quickly determine the dn configuration and therefore predict or rationalise the coordination geometry; for example, four-coordinate Pd(0) has a d10 configuration and such complexes are exclusively tetrahedral whereas four-coordinate Pd(II) has a d8 configuration and complexes are, with very few exceptions, square planar. A case can be made that for the examples given above, the CBC method for calculating the dn number is also straightforward but we will return to this point later when considering complexes in which the metal centre has a negative oxidation state.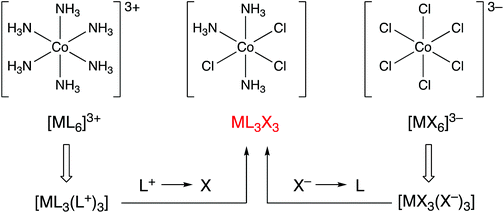 | ||
| Fig. 1 The CBC approach to showing that three Co(III) complexes with different charges are members of the same equivalent neutral class by using transformations shown in Chart 1. Whether [CoCl3(NH3)3] adopts the fac- or mer-geometry makes no difference. This figure is an abbreviated version of Fig. 10 in ref. 5. | ||
Organometallic complexes
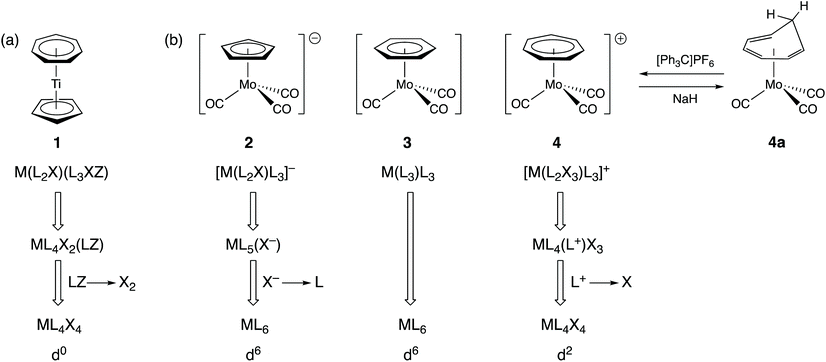
In organotransition metal chemistry, the ligand C7H7 is often cited as an exemplar of why the assignment of oxidation states is confusing. Thus, for the complex [Ti(η5-C5H5)(η7-C7H7)] (1), there is little ambiguity when it comes to the cyclopentadienyl ligand since, in assigning an oxidation state, we would expect to remove this as C5H5− both on the grounds of electronegativity (carbon is more electronegative than titanium) and on the basis of C5H5− being a closed-shell species since it has six π-electrons and conforms to the Hückel 4n + 2 rule for aromatic stability. The ambiguity arises with the C7H7 ligand. It could be treated as the antiaromatic C7H7− based on electronegativity but if it is to be removed as a closed-shell species, then it could be either C7H7+ with six π-electrons or C7H73− with ten π-electrons, both of which satisfy the Hückel 4n + 2 rule (where n = 1 or 2 respectively). Accordingly, the titanium centre in compound 1 can be assigned an oxidation state of 0, II or IV. We would maintain that the closed-shell argument and the highly electropositive nature of Ti leads fairly directly to considering the best representation of this ligand to be C7H73− in this instance and hence the assignment of an oxidation state of Ti(IV) and a d0 configuration to compound 1.The CBC method classifies C7H7 as a L2X3 ligand and this arises from an initial classification as L3XZ (the reason for the Z component is elaborated upon below) and then recognising that an LZ combination is equivalent to X2 (see Chart 1);13 C7H7 is therefore categorised as a seven-electron donor. This is certainly acceptable in terms of one method of counting electrons (treat all the ligands as neutral) but since it is almost invariably the case in transition metal complexes that X ligands are X− according to electronegativity arguments, C7H7 as L2X3 is akin to C7H73−. Indeed, the CBC designation for 1 is ML4X4, resulting in the Ti having a valency (VN) of 4 and a d0 configuration [Fig. 2(a)] which is the same as that derived from the OS approach outlined above.
It is conceded that there is some ambiguity with C7H7 as a ligand when it comes to assigning metal oxidation states. However, consider the three isoelectronic compounds [Mo(CO)3(η-C5H5)]− (2), [Mo(CO)3(η-C6H6)] (3) and [Mo(CO)3(η-C7H7)]+ (4) [Fig. 2(b)]. Clearly compound 3 with all neutral ligands is Mo(0) but so is compound 2 if we treat the C5H5 ligand as C5H5−. The same oxidation state of Mo(0) is then obtained for compound 4 if the C7H7 ligand is removed as C7H7+ which is consistent not only with it being a closed-shell 6π-electron species but also with its method of synthesis which is by abstraction of H− from the neutral cycloheptatriene complex 4a [Fig. 2(b)]. Were the C7H7 ligand in 4 to be counted as C7H73−, it would then contain Mo(IV). The homologous series represented by compounds 2–4 does highlight the care which needs to be taken with C7H7 and shows that it can be treated either as C7H7+ or as C7H73− according to the compound in which it is present. A judgement therefore needs to be made with respect to the compound being considered and its chemistry; for instance, compound 4 is susceptible to nucleophilic attack at the C7H7 ring, for example by hydride, to regenerate 4a [Fig. 2(b)], i.e. it is behaving like a complex of tropylium. Thus, there is a level of complexity here albeit one which is not resolved by always considering C7H7 to be a L2X3 ligand. Furthermore, application of the CBC rules would categorise compounds 2 and 3 as ML6 species whilst compound 4 would be classed as ML4X4 (each according to the definition of equivalent neutral class noted above). This difference in the classification of 2 and 3vs.4 seems neither warranted nor helpful, particularly for teaching purposes.13
Other complexes which have been used as exemplars in demonstrating the advantages of the CBC method over the OS approach are the metallocene complexes [ZrR(η5-C5H5)2]+ (5), [ZrR2(η5-C5H5)2] (6), [ZrR3(η5-C5H5)2]− (7) and [WH3(η5-C5H5)2]+ (8).5 These are respectively classified initially as ML4X3+, ML4X4, ML4X5− and ML4X5+ which are then, in terms of their equivalent neutral class, represented as ML3X4, ML4X4, ML5X4 and ML3X6 (Fig. 3). Assuming all the ligands C5H5, R and H to carry a formal negative charge, the zirconium compounds 5–7 all contain Zr(IV) and compound 8 contains W(VI). The CBC approach offers no discernible advantage when it comes to understanding the chemistry of compounds 5–7 other than that the equivalent neutral class designation provides an alternative method of assigning the oxidation state (simply the number of X ligands, as noted earlier). However, compounds such as 8, and indeed many polyhydrides in high formal oxidation states, are reducing rather than oxidising and care must therefore be exercised in automatically assuming that high oxidation state compounds are always oxidising agents especially in the case of polyhydrides. This is, therefore, an example of where the OS is not consistent with the observed chemistry but as will be discussed below, in other cases, this is a criticism which can also be levelled at the CBC method.
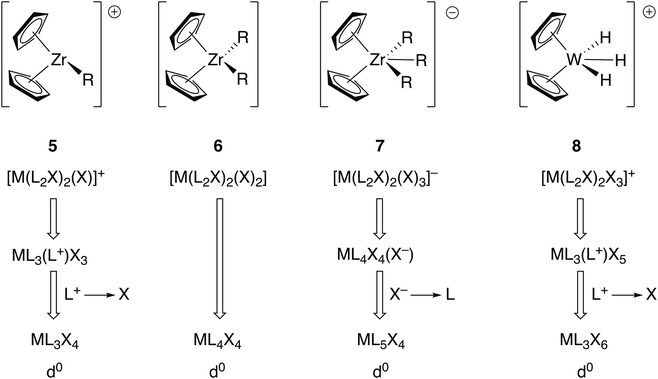 | ||
| Fig. 3 CBC analysis of the metallocenes 5–8 gives the equivalent neutral class shown. The OS assignments are Ti(IV) and W(VI). This figure is derived from Fig. 12 in ref. 5. | ||
Nitrosyl complexes
The nitrosyl ligand, NO, presents some difficulties in oxidation state assignment which few would dispute but it will be argued that NO causes rather more difficulties for the CBC method. As is well known, NO can coordinate to a metal centre in either a bent or a linear fashion which, in terms of assigning an oxidation state, are generally treated as NO− and NO+.14 In the CBC approach, bent and linear forms are represented as X and X3 respectively,5 although linear NO was originally classified as LX.4,15 The reason offered for linear NO being X3 is that linear NO should initially be classified as LXZ since the HOMO/LUMO (the N–O π* orbitals) are partially occupied such that the X and Z components have essentially the same energy (this is also the reason for the initial classification of C7H7 as L3XZ noted above).6 Since LZ is equivalent to X2, the LXZ for NO becomes X3. However, if this X3 classification for linear NO is adopted, the series of tetrahedral complexes [Cr(NO)4], [Mn(CO)(NO)3], [Fe(CO)2(NO)2] and [Co(NO)(CO)3] (which are all isoelectronic with Ni(CO)4 and all contain linear NO ligands16) would be classified as MX12, MLX9, ML2X6, and ML3X3 respectively (see Chart 3). Any insight into the chemistry of these species which would follow from these CBC assignments (including the dn numbers in the Cr and Mn examples) is at best, opaque and the situation is little improved if the linear NO ligands are treated as LX.17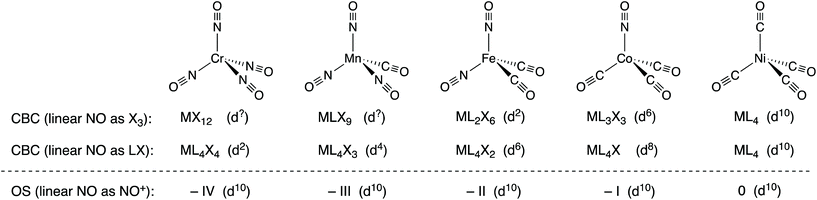 | ||
| Chart 3 The isoelectronic series of complexes [M(NO)x(CO)4−x] and their classification according to the CBC method, where linear NO is designated as either X3 or LX, and the OS method where linear NO is treated as NO+. The oxidation states and dn values for each method are also shown. Note that while the coordination number for all these species is clearly four, the Ligand Bond Number (LBN), as defined within the CBC method,4–6,13 is different for each of them. | ||
Alternatively, the same compounds could all be described as examples of d10 complexes with formal oxidation states –IV, –III, –II, and –I (despite some prior objections to doing so18) all with the expected tetrahedral geometry and analogous to the known isoelectronic carbonyl species [Cr(CO)4]4−, [Mn(CO)4]3−, [Fe(CO)4]2−, [Co(CO)4]− each with the metal centre in the same formal oxidation state of –IV, –III, –II, and –I respectively. We would argue that this is a situation where the OS method offers clear advantages over the alternative CBC approach.
Negative oxidation state complexes
Complexes, such as those discussed in the previous section, in which the metal is in a formal negative oxidation state are not uncommon and these can be divided into two categories: (i) complexes containing non-innocent ligands (e.g. bipy, dithiolates) where the coordinated ligand is the site of the added electrons that produce the formal negative oxidation state; (ii) complexes containing ligands that are considered innocent (e.g. CO) where the metal is the site of the added electrons.19 In reality, this division is somewhat blurred because the electron density will be delocalised to a greater or lesser extent over the metal and ligands in both categories, but the focus here is on the second category.Collman's reagent, Na2[Fe(CO)4] (9), is made by the reduction of [Fe(CO)5] with Na metal; it is a widely used, commercially available reagent whose chemistry is dominated by the high reactivity of the anion [Fe(CO)4]2− with electrophiles. It is generally considered to be an Fe(–II) complex which therefore has a d10 configuration, consistent with its tetrahedral shape and diamagnetism. As shown in Fig. 4 however, and as explicitly set out in ref. 6, the CBC treatment of [Fe(CO)4]2− leads to its classification as ML4X2 (in terms of its equivalent neutral class since L− corresponds to LX) which places it, rather incongruously, in the same equivalent neutral class as [FeCl2(OH2)4] (10). However, according to how dn configurations are calculated within the CBC method (m – VN; see Chart 1), both 9 and 10 would be assigned a d6 configuration and therefore tetrahedral [Fe(CO)4]2− would be predicted, erroneously, to be paramagnetic.20
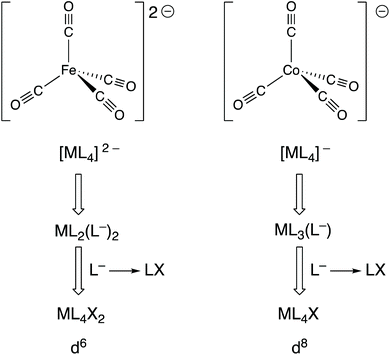 | ||
| Fig. 4 A CBC analysis for two examples, [Fe(CO)4]2− and [Co(CO)4]−, of metal carbonylates [M(CO)n]Q− which are known for M in groups 4–9 and where Q can be 1–4. | ||
Moreover, a similar CBC analysis of any complex of a metal in a formal negative oxidation state, –x, will always lead to a valency number of x if the complex is represented as its equivalent neutral class, and hence a difference between the dn configurations assigned by the OS and CBC methods of 2x. This is a serious discrepancy in the value of dn which stems from the incompatibility of the valence number (which can only be positive) with negative oxidation states.21 This discrepancy matters because, as illustrated for [Fe(CO)4]2− above, the dn configuration can be used to predict and rationalise the structure and properties of a complex.
Indeed, one of the most useful applications of the dn configuration in the teaching of transition metal chemistry is the prediction of the geometry of four-coordinate metal complexes and especially in the distinction between the expected geometries for d10 (invariably tetrahedral) and d8 (square planar with strong-field ligands). Consider the anion [Co(CO)4]− which is prepared by the reduction of [Co2(CO)8] with Na metal and has been widely studied, in part due to its role in homogeneous catalysis. It is diamagnetic and the geometry around the Co centre is tetrahedral, both of which are expected from the oxidation state of the Co being –I and it therefore having a d10 configuration. The CBC method applied to [Co(CO)4]− leads to an equivalent neutral class of ML4X (see Fig. 4) corresponding to a valency number of 1 from which a d8 configuration is derived. The problem with this assignment is that four-coordinate d8 complexes are either square planar and diamagnetic or, if tetrahedral, paramagnetic. The CBC method thus fails to account for the tetrahedral, diamagnetic nature of [Co(CO)4]−.20,22
Compounds containing metal–metal bonds
Consider the two mercury compounds HgCl2 and Hg2Cl2. In the latter (whose redox properties are the basis of the calomel electrode), the presence of a Hg–Hg bond leads to both compounds being classified as MX2 species under CBC rules. Both certainly contain divalent mercury but the oxidation state in each is different; in the former, the mercury is in oxidation state II whilst in the latter it is I. The obvious difference in the chemistry of these two compounds is that HgCl2 does not react with chlorine whereas Hg2Cl2 does, being oxidised to HgCl2 [see Scheme 1(a)]. Likewise, treatment of HgCl2 with a reducing agent gives Hg2Cl2. This redox chemistry is entirely to be expected based on the oxidation states involved whereas no such insight is gained from the recognition that both species are classified as MX2.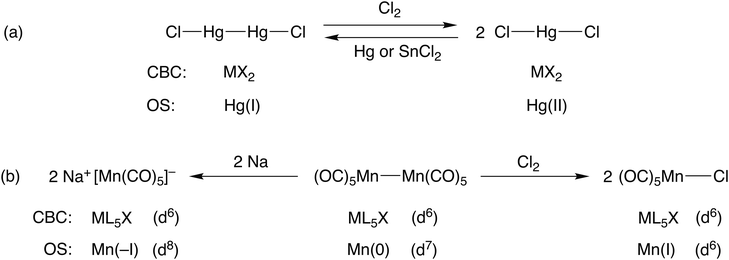 | ||
| Scheme 1 An illustration of how the OS method is useful for rationalising the redox chemistry associated with compounds containing metal–metal bonds. | ||
Furthermore, this is a general problem within the CBC approach when considering compounds that contain element-element bonds. Consider the three manganese compounds shown in Scheme 1(b): Na[Mn(CO)5], a Mn nucleophile; [MnCl(CO)5], a Mn electrophile; [Mn2(CO)10], a source of Mn(CO)5 radicals and which can be oxidised by Cl2 or reduced by Na metal. The CBC method classifies each of them as ML5X with a d6 configuration (wrongly, we maintain, for Na[Mn(CO)5]) whereas the oxidation state of the Mn would be assigned as –I, I and 0 respectively. The different oxidation states in these three compounds leads to an expectation of them having the different chemistries they exhibit, in contrast to the CBC approach which obscures their differences. This is one of the reasons why we disagree with the following statement made in comparing CBC with OS:5 ‘Specifically, because the oxidation state approach reduces the description of a covalent molecule to the value of the charge on an isolated atom, with no ligands attached, it is evident that the oxidation state assignment can provide only very limited insight into the nature of the molecule itself’ [original emphasis].
Having made the points outlined above, it should be recognised that oxidation states can only be assigned to individual atoms in molecules. For mononuclear metal complexes, the utility of the OS method and the derived dn configuration for rationalising and predicting structural, physical and chemical properties lies at the core of much of the teaching of transition metal chemistry. For binuclear compounds, however, the situation regarding the assignment of dn configurations requires some discussion. For example, in [Mn2(CO)10] the oxidation state of the Mn centres is 0 with a derived d7 configuration for each Mn, according to the OS method for calculating dn set out in Chart 1 and shown in Scheme 1(b). However, if the value of n in dn is the number of essentially non-bonding d electrons associated with the metal centre (albeit recognising that they will be involved to some degree in both σ- and π-bonding interactions), then the presence of the Mn–Mn σ-bond in [Mn2(CO)10], which clearly involves the use of one d electron from each Mn centre, means that a d6 assignment for each Mn in [Mn2(CO)10] would be more appropriate.23 The CBC method, which classifies each Mn in [Mn2(CO)10] as ML5X, means that a value of d6 is arrived at directly and this is clearly an advantage of the CBC approach over that of the OS method (this point is made explicitly in ref. 5). Nevertheless, this must be set against the CBC assigning the same equivalent neutral class to all three manganese species in Scheme 1(b) which thereby obscures the conspicuous differences in their chemistry.
Homogeneous catalysis
One of the great success stories of organometallic chemistry over the last half century or more has been its application in homogeneous catalysis. Oxidation states are of such widespread use in understanding the mechanisms of organometallic catalysis that they are embedded in all textbook discussions of the topic. In many catalytic cycles, the metal interchanges between two oxidation states, often separated by two units, via oxidative addition and reductive elimination steps. Some notable examples: are Rh(I)/Rh(III) or Ir(I)/Ir(III) in alkene hydrogenation, methanol carbonylation, hydroformylation and hydroborylation; Ni(0)/Ni(II) in hydrocyanation; Pd(0)/Pd(II) in a plethora of C–C, C–N and C–O coupling reactions (Scheme 2); Pt(0)/Pt(II) in alkene and alkyne diboration, hydrosilylation and hydrophosphination. The oxidation state changes are unambiguous, and the geometries of the intermediates can be understood in terms of the derived dn configurations. Using the CBC method to reclassify the various species in the catalytic cycle with a MLXZ designation does offer an alternative approach. However, although (as noted earlier for polyhydrides) some care should always be exercised in interpreting chemical behaviour in terms of oxidation states, it is frequently intuitively clear why strongly electron-donating ligands and strongly electron-accepting ligands might preferentially stabilise higher and lower oxidation state species respectively and thereby modulate the rates of particular steps or even arrest them completely (see caption to Scheme 2 for an example). Again, such insight does not so easily follow from a CBC classification of the species present in the cycle.24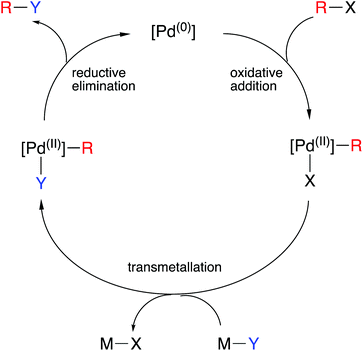 | ||
| Scheme 2 An outline generic mechanism for Pd-catalysed cross-coupling reactions (Y can be a C-, N- or O-nucleophile) showing the critical role of the oxidative addition and reductive elimination steps. Electron-rich phosphines are often the ligands of choice for these reactions which can be rationalised by recognising that the oxidative addition is the turnover-limiting step.25 | ||
Z ligands
As noted in Chart 1 and described in detail in ref. 4–6, the CBC method classifies Z ligands as electron-pair acceptors (i.e. as a Lewis acid) with the metal centre acting as an electron-pair donor (i.e. as a Lewis base). Although not a common class of ligand, many complexes have now been characterised which incorporate a multidentate boratrane ligand which comprises a Z-type boron centre along with usually two or three S- or P-donor sites, each one of which can be labelled as an L ligand.26 There has been much discussion and some disagreement about how to treat boratranes (and indeed Z ligands generally) in terms of assigning an oxidation state to the metal to which they are bound. One approach27 favours treating the boron as neutral, both in the sense of formal charge and its effect on determining an oxidation state, whereas the other approach,28 based on the rules of the CBC method, effectively assigns a 2− charge to the boron centre. This, of course, has implications for the dn configuration assigned to the metal centre: dn in the former and dn−2 in the latter (see Fig. 5). Here is not the place to reprise the arguments set out in ref. 27 and 28 in detail and it is accepted that ligands of this type are problematic when it comes to assigning an oxidation state. Electronegativity is of little help since boron's electronegativity is within the range seen for many transition metals. In terms of partitioning according to a closed-shell approach, then BX3 does not have a closed shell whereas BX32− does; however, [BX3]2− dianions are very rare boron(I) species outside of this context and it appears to be equally valid to consider a metal–BX3 complex to be a conventional Lewis acid–base adduct. It is worth noting that there is a parallel between BX3 and H+ (the other common Z ligand); once coordinated, H+ can be treated as H− (hydride being a well-known chemical species) making protonation of a metal centre an example of oxidative addition.It should be pointed out that, in addition to the issues with σ-acceptor Z ligands discussed above, complexities arise where the Z formalism is applied to π-acceptor ligands. Consider carbenes, for example. These are classified within the CBC framework as X2 in the case of Schrock alkylidenes or as L in the case of Fischer carbenes.5 Schrock alkylidenes (which are nucleophilic carbenes) can be considered as complexes of CR22− whereas Fischer carbenes (which are electrophilic carbenes) are neutral, i.e. CR2. However, in Table 6 in ref. 6, Fischer carbenes are classified as LZ′ for which the following explanation of Z′ is provided (for CR2 as well as for CO, bent NO, C6H6, C4H6 and C2H4 which are also classified with a Z′ component): ‘The Z′ backbonding component is undetermined. As such, it is neglected for the purpose of determining the [MLlXxZz] classification…’. Further on in the same article,6 it is proposed that the Z′ component can be neglected for CO but not for NO which requires extensive backbonding to coordinate to a metal centre; this relates in part to the discussion noted earlier about NO being classified as a LXZ ligand and the reason for the Z component being explicitly included. However, are CO and NO that different? CO is universally considered to be an excellent π-acceptor when coordinated to electron-rich metals and could quite reasonably be denoted as an LZ ligand in such cases. However, LZ is equivalent to X2 (Chart 1) and so a terminal CO could be considered to be an X2 ligand and species such as [W(CO)6] would then be classified as MX12! The point here is that if the Z′ component is significant then LZ′ effectively becomes LZ and LZ is equivalent to X2. At some stage, therefore, a judgement has to be made about how to treat a ligand such as CR2 (or for that matter C2H4vs. C2F4) according to the substituents the ligand carries. Moreover, this is no idle judgement since the choice of LZ or X2 affects the metal d-electron count in much the same way as does the argument over the σ–Z ligands outlined above. A nuanced and considered discussion about Z interactions (and particularly π–Z interactions) is set out in some detail in ref. 6. However, the point remains that if it is accepted that judgements have to be made in the designation of common ligands within the CBC method (i.e. L vs. X2 according to how much Z component there is), it is not unreasonable to make a judgement in terms of boratranes and that it might be the case that one or other of the descriptions is more appropriate in different cases. Indeed, computational studies for two particular boratranes are considered in ref. 27 for which it seems that precisely such a judgement should be made in terms of the nature of the M–B bond and the resulting d-electron count.
Concluding remarks
Arguments about the usefulness or otherwise of oxidation states are nothing new7 and we can highlight a robust and relatively recent exchange of views concerning oxidation states and calculated charges on metals in a range of solid-state transition metal compounds.29 Chemistry is a complicated subject and like all complicated subjects, whilst we strive for and value simple models to help us rationalise what we observe, we must accept that there will sometimes be exceptions to even the most useful of them. Consider for example, Crystal Field Theory and VSEPR Theory in inorganic chemistry, or the use of curly arrows in organic chemistry. These are tremendously valuable heuristics, but there are limitations to their application, and we should not judge them too harshly as a result when those limitations are exposed. In the context of this article, we contend that there will never be a simple and easily taught model that will work in every case when it comes to counting electrons and assigning their distribution within a molecule because any such model will always be an approximation for MO theory. We are minded to quote Frenking, Schwerdtfeger and co-workers who, in a recent review article, offer the following aphorism: ‘Chemical bonding models are not right or wrong, they are more or less useful’.30 This is sometimes stated even more succinctly as, ‘All models are wrong but some are useful’.31There is no doubt that the CBC approach has considerable merit in the teaching of chemistry, and of organometallic chemistry in particular, but the same can also be said for oxidation states. Neither is without its difficulties in certain cases, but both should be part of the toolbox of any chemist intent on understanding the endless variety of chemical compounds and the reactions they undergo. We argue that the two approaches should be seen as complementary. In many cases, either will suffice whilst in other situations one or other may offer some advantage. Inasmuch as a plurality of models offers a challenge to us as educators, then that is a challenge we must embrace rather than seek to avoid.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We would like to thank the following people who have made helpful comments on earlier versions of this article: Manfred Bochmann (University of East Anglia, UK), Vernon Gibson (Imperial College, UK), Anthony Hill (ANU, Australia), and Mark Winter (University of Sheffield, UK).References
- W. B. Jensen, The Origin of the Oxidation State Concept, J. Chem. Educ., 2007, 84, 1418–1419 CrossRef CAS.
- See for example, A. Manthiram, A Reflection on Lithium-Ion Battery Cathode Chemistry, Nat. Commun., 2020, 11, 1550 CrossRef CAS PubMed.
- (a) Q. Zhang, Y. Liu, T. Wang, X. Zhang, C. Long, Y.-D. Wu and M.-X. Wang, Mechanistic Study on Cu(II)-Catalyzed Oxidative Cross-Coupling Reaction between Arenes and Boronic Acids under Aerobic Conditions, J. Am. Chem. Soc., 2018, 140, 5579–5587 CrossRef CAS PubMed; (b) Q. Zhang, T. Wang, X. Zhang, S. Tong, Y.-D. Wu and M.-X. Wang, Radical Reactivity, Catalysis, and Reaction Mechanism of Arylcopper(II) Compounds: The Missing Link in Organocopper Chemistry, J. Am. Chem. Soc., 2019, 141, 18341–18348 CrossRef CAS PubMed.
- M. L. H. Green, A New Approach to the Formal Classification of Covalent Compounds and Elements, J. Organomet. Chem., 1995, 500, 127–148 CrossRef CAS.
- M. L. H. Green and G. Parkin, Application of the Covalent Bond Classification Method for the Teaching of Inorganic Chemistry, J. Chem. Educ., 2014, 91, 807–816 CrossRef CAS.
- G. Parkin, Classification of Organometallic Compounds, in Comprehensive Organometallic Chemistry III, Elsevier, 2007, vol. 1, 1–57 Search PubMed.
- (a) P. Karen, P. McArdle and J. Takats, Toward a Comprehensive Definition of Oxidation State (IUPAC Technical Report), Pure Appl. Chem., 2014, 86, 1017–1081 CAS; (b) For an abbreviated summary, see P. Karen, P. McArdle and J. Takats, Comprehensive Definition of Oxidation State (IUPAC Recommendations 2016), Pure Appl. Chem., 2016, 88, 831–839 CAS; (c) P. Karen, Oxidation State, A Long-Standing Issue, Angew. Chem., Int. Ed., 2015, 54, 4716–4726 CrossRef CAS PubMed.
- D. W. Smith, Valence, Covalence, Hypervalence, Oxidation State and Coordination Number, J. Chem. Educ., 2005, 82, 1202–1204 CrossRef CAS.
- G. Parkin, Valence, Oxidation Number, and Formal Charge: Three Related but Fundamentally Different Concepts, J. Chem. Educ., 2006, 83, 791–799 CrossRef CAS.
- N. V. Sidgwick, The Electronic Theory of Valence, Oxford, London, 1927 Search PubMed.
- The Chemistry of Ruthenium, ed. E. A. Seddon and K. R. Seddon, Elsevier, New York, 1984, ch. 2 Search PubMed.
- G. Calzaferri, Oxidation Numbers, J. Chem. Educ., 1999, 776, 362–363 CrossRef.
- In the CBC model, the parameter LBN (ligand bond number) is defined as the total number of L, X and Z functions surrounding the metal. For complexes having only simple L and X ligands, the LBN corresponds to the coordination number (CN). For η5-C5H5 (L2X) and η6-C6H6 (L3) the LBN is 3 whereas for η7-C7H7 (L2X3) the LBN is 5. Alternatively, the isoelectronic 6π systems [C5H5]−, C6H6 and [C7H7]+ can all be considered to donate three electron pairs and thereby occupy three coordination sites. Thus, for many organometallic complexes, the LBN and CN are not the same and this point is explicit within the CBC method.
- We accept that the issue of the NO ligand is more complicated than a simple bent vs. linear description might imply. Thus, examples are known for M–N–O units with a whole range of angles at N, a topic addressed many years ago by Enemark and Feltham: (a) J. H. Enemark and R. D. Feltham, Stereochemical Control of Valence. III. The {CoNO}8 Group in Ligand Fields of C4v, C2v and Cs Symmetry, J. Am. Chem. Soc., 1974, 96, 5004–5005 CrossRef CAS; (b) J. H. Enemark and R. D. Feltham, Principles of Structure, Bonding, and Reactivity for Metal Nitrosyl Complexes, Coord. Chem. Rev., 1974, 13, 339–406 CrossRef CAS.
- The X3 designation for linear NO is taken from Table 1 in ref. 5. However, in Table 6 in ref. 6, linear NO is listed as X3 with a bar above the X whereas in ref. 4 linear NO is classified as LX bar by analogy with a three-electron donor amido ligand (the bar indicating that the ligating atom is polyfunctional4).
- L. Hedberg, K. Hedberg, S. K. Satija and B. I. Swanson, Structure and Bonding in Transition-Metal Carbonyls and Nitrosyls. 1. Gas-Phase Electron-Diffraction Investigations of Tetranitrosylchromium [Cr(NO)4], Carbonyltrinitrosylmanganese [MnCO(NO)3], and Dicarbonyldinitrosyliron [Fe(CO)2(NO)2], Inorg. Chem., 1985, 24, 2766–2771 CrossRef CAS.
- That the bonding of NO to metals remains contentious, is amply demonstrated by the following articles on the anion [Fe(CO)3(NO)]−. In ref. 7c, Karen draws attention to the fact that, although [Fe(CO)3(NO)]− contains a linear NO ligand, MO calculations suggest the NO should be treated as NO− rather than as NO+ and hence an oxidation state of Fe(0) with a d8 configuration should be assigned to the complex. ( J. E. M. N. Klein, B. Miehlich, M. S. Holzwarth, M. Bauer, M. Milek, M. M. Khusniyarov, G. Knizia, H-J. Werner and B. Plietker, The Electronic Ground State of [Fe(CO)3(NO)]−: A Spectroscopic and Theoretical Study, Angew. Chem., Int. Ed. Engl., 2014, 53,1790–1794 Search PubMed). More recently, precisely the opposite conclusion has been drawn based on X-ray spectroscopy and computational methods, in which it is suggested that the NO ligand in [Fe(CO)3(NO)]− should be treated as NO+ and hence an oxidation state of Fe(–II) and a d10 configuration be assigned in which case [Fe(CO)3(NO)]− is isoelectronic with [Fe(CO)4]2−. ( L. Burkhardt, Y. Vukadinovic, M. Nowakowski, A. Kalinko, J. Rudolph, P-A. Carlsson, C. R. Jacob and M. Bauer, Electronic Structure of the Hieber Anion [Fe(CO)3(NO)]− Revisited by X-ray Emission and Absorption Spectroscopy, Inorg. Chem., 2020, 59, 3551–3561 Search PubMed).
- G. B. Richter-Addo and G. B. Legzdins, Metal Nitrosyls, Oxford University Press, New York, 1992 Search PubMed.
- (a) J. E. Ellis, Adventures with Substances Containing Metals in Negative Oxidation States, Inorg. Chem., 2006, 45, 3167–3186 CrossRef CAS PubMed; (b) J. E. Ellis, Metal Carbonyl Anions: from [Fe(CO)4]2− to [Hf(CO)6]2− and Beyond, Organometallics, 2003, 22, 3322–3338 CrossRef CAS.
- J. Cirera, E. Ruiz and S. Alvarez, Stereochemistry and Spin State in Four-Coordinate Transition Metal Compounds, Inorg. Chem., 2008, 47, 2871–2889 CrossRef CAS PubMed.
- The problem would disappear if the equivalent neutral class formalism were abandoned for complexes in negative oxidation states whereby [Fe(CO)4]2− would be considered simply as [FeL4]2−. Thus, the two additional electrons would convert d8-FeL4 to d10-[FeL4]2−; we thank M. J. Winter for pointing this out. This suggestion has, to the best of our knowledge, not previously been made, although the fact that VN cannot be negative was explicitly stated in ref. 4. We also recognise that different dn numbers for metal carbonylate anions according to whether they are calculated using OS or CBC methods is noted in ref. 4 [Table 10].
- If this species is represented as [ML4]−, then the correct dn configuration is obtained for the reasons given in ref. 21. We would argue, therefore, that the term equivalent neutral class is misleading in situations like this since, in terms of their dn number, the species [ML4]− and ML4X are not equivalent.
- To the best of our knowledge, this adjustment of the dn configuration specifically in binuclear, metal-metal bonded complexes has not previously been suggested.
- The terms oxidative addition and reductive elimination do feature in MLX plots which highlight the sort of reactivity present in homogeneous catalytic cycles (see ref. 4 and 6).
- J. G. de Vries, Palladium-Catalysed Coupling Reactions in Organometallics as Catalysts in the Fine Chemical Industry, in Topics in Organometallic Chemistry, ed. M. Beller and H. U. Blaser, Springer, Berlin, Heidelberg, 2012, vol. 42 Search PubMed.
- For a recent review, see: G. Bouhadirab and D. Bourissou, Complexes of Ambiphilic Ligands: Reactivity and Catalytic Applications, Chem. Soc. Rev., 2016, 45, 1065–1079 RSC.
- A. F. Hill, An Unambiguous Electron-Counting Notation for Metallaboratranes, Organometallics, 2006, 25, 4741–4743 CrossRef CAS.
- G. Parkin, A Simple Description of the Bonding in Transition Metal Borane Complexes, Organometallics, 2006, 25, 4744–4747 CrossRef CAS.
- (a) R. Resta, Charge States in Transition, Nature, 2008, 453, 735 CrossRef CAS PubMed; (b) H. Raebiger, S. Lany and A. Zunger, Charge Self-Regulation upon Changing the Oxidation State of Transition Metals in Insulators, Nature, 2008, 453, 763–766 CrossRef CAS PubMed; (c) H. Raebiger, S. Lany, A. Zunger and R. Resta, Oxidation Numbers as Social Security Numbers: Are they Predictive or Postdictive?, Nat. Preced., 2009 DOI:10.1038/npre.2009.4012.1; (d) M. Jansen and U. Wedig, A Piece of the Picture – Misunderstanding of Chemical Concepts, Angew. Chem., Int. Ed., 2008, 47, 10026–10029 CrossRef CAS PubMed; (e) G. Aullon and S. Alvarez, Oxidation States, Atomic Charges and Orbital Populations in Transition Metal Complexes, Theor. Chem. Acc., 2009, 123, 67–73 Search PubMed.
- L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chemical Bonding and Bonding Models in Main-Group Chemistry, Chem. Rev., 2019, 119, 8781–8845 CrossRef CAS PubMed.
- G. E. P. Box, Robustness in the strategy of scientific model building. Robustness in Statistics, ed. R. L. Launer and G. N. Wilkinson, Academic Press, New York, San Francisco, London, 1979, pp. 201–236 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Whether the value is 0 or +2 is debatable, depending on the strength of the Lewis acidity of Z and the availability of the lone pair on M (see later).
Whether the value is 0 or +2 is debatable, depending on the strength of the Lewis acidity of Z and the availability of the lone pair on M (see later).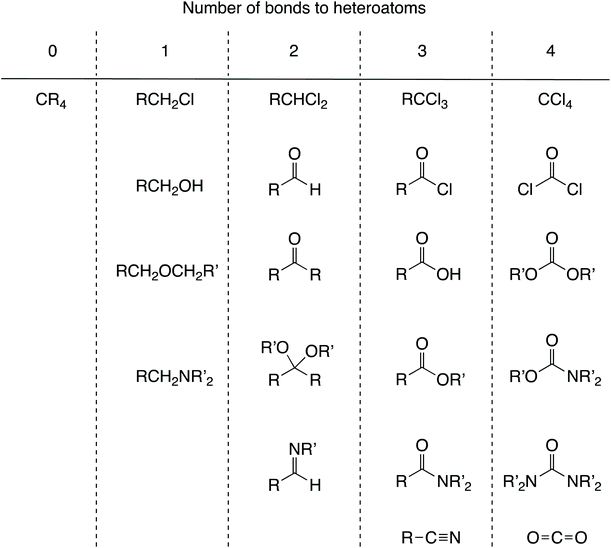
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, for example. Converting a functional group A to a functional group B will require an oxidising agent if B is in a column to the right of A, a reducing agent if B is in a column to the left of A, and neither an oxidising agent nor reducing agent if A and B are in the same column.
O, for example. Converting a functional group A to a functional group B will require an oxidising agent if B is in a column to the right of A, a reducing agent if B is in a column to the left of A, and neither an oxidising agent nor reducing agent if A and B are in the same column.