Local and nanoscale methanol mobility in different H-FER catalysts

Abstract

The dynamical behaviour of methanol confined in zeolite H-FER has been studied using quasielastic neutron scattering (QENS) and classical molecular dynamics (MD) simulations to investigate the effects of the Si/Al ratio on methanol dynamics in different Brønsted acidic FER catalysts. QENS probed methanol mobility at 273–333 K in a commercial FER sample (Si/Al = 10) at methanol saturation, and in a FER sample synthesised from naturally sourced Ghanaian kaolin (FER-GHA, Si/Al = 35–48), also at saturation. Limited mobility was observed in both samples and an isotropic rotation model could be fit to the observed methanol motions, with average mobile fractions of ∼20% in the commercial sample and ∼15% in the FER-GHA, with rotational diffusion coefficients measured in the range of 0.82–2.01 × 10¹¹ s⁻¹. Complementary molecular dynamics simulations were employed to investigate methanol mobility in H-FER over the same temperature range, at a loading of ∼6 wt% (close to experimental saturation) in both a fully siliceous H-FER system and one with Si/Al = 35 to understand the effect of the presence of Brønsted acid sites on local and nanoscale mobility. The simulations showed that methanol diffusivity was significantly reduced upon introduction of Brønsted acid sites into the system by up to a factor of ∼3 at 300 K, due to strong interactions with these sites, with residence times on the order of 2–3 ps. The MD-calculated translational diffusivities took place over a timescale outside the observable range of the employed QENS spectrometer, varying from 0.34–3.06 × 10⁻¹¹ m² s⁻¹. QENS observables were reproduced from the simulations to give the same isotropic rotational motions with rotational diffusion coefficients falling in a similar range to those observed via experiment, ranging from 2.92–6.62 × 10¹¹ s⁻¹ between 300 and 400 K.

---

1. Introduction

The behaviour of methanol in zeolites is of interest owing to its relevance across a range of catalytic applications. The zeolite-catalysed conversion of methanol to hydrocarbons (MTH), for example, is a widely studied process, which was first commercialised in New Zealand in 1985 (ref. 1) with the use of zeolite ZSM-5. The analysis of the behaviour of the MTH species in ZSM-5 has been critical in many experimental and theoretical studies aiming to elucidate the mechanisms behind this reaction in zeolites.^2–6 Several key reactions fall under the MTH umbrella, including the methanol-to-gasoline reaction (MTG)⁷ and the methanol-to-olefins (MTO)⁸ reaction, which have been studied widely in zeolites such as chabazite (specifically SAPO-34 (ref. 9 and 10) for MTO), as well as the aforementioned ZSM-5.^7,11 Despite the wide variety of MTH reactions, and the collection of proposed mechanisms and pathways,¹² the exact effect of the zeolite structure and topology on the catalytic properties is not yet fully understood.¹³ The interaction between the adsorbate and the structural features of the zeolite, including but not limited to the active sites,¹⁴ along with the mobility of each species through the micropores, are the main driving forces behind the catalytic properties of such microporous materials. Therefore, modifications to the composition and the pore structure of the zeolite have a direct impact on its catalytic performance. However, a range of techniques are required to fully understand such effects on the behaviour of active species.

Recent studies have suggested that ferrierite-type (FER) zeolites may be an effective catalyst for use in methanol conversion, facilitating the formation of dimethyl ether (DME) by methanol dehydration. They could possibly outclass MFI and BEA framework types in this process, due to reduced coke generation, as its small (10 and 8 membered ring) pores block the formation of larger molecules.^15–17 DME has received significant attention due to its potential application as an alternative fuel source,¹⁸ importantly providing reduced exhaust emissions in diesel vehicles – as well as being present in the initial stages of both the MTO and MTG transformations.¹⁹ One additional advantage to employing FER is that it can be synthesized from naturally sourced materials, such as kaolinite.^20–23 The synthesis of FER zeolites from kaolinite could allow for the cheaper production of catalysts for sustainable fuel synthesis. However, the larger-scale application of zeolites produced this way is hindered by issues such as the inclusion of a wider range of cations²¹ or changes in the zeolite macrostructure.²⁰ Despite previous studies on the catalytic applications of FER zeolites, an in-depth understanding of the methanol interactions with the active sites and the resulting effects on macroscale observations such as catalytic activity/selectivity, or even the nanoscale mobility within these FER systems is yet to be achieved.

In terms of methanol/acidic site interactions in zeolites, the adsorption of methanol in zeolites HY and H-ZSM-5 has been probed using QM/MM calculations,²⁴ showing a range of adsorption energies, from −70 to −106 kJ mol⁻¹ in HY and −78 to −126 kJ mol⁻¹ in H-ZSM-5, depending on not only the zeolite topology but also the methodology applied and the siting/orientation of the molecule itself. Methanol adsorption within FER zeolites has also been studied using periodic DFT,²⁵ showing that a single methanol molecule will form coordinated hydrogen-bonds with Brønsted acid sites (BASs) and the framework oxygen in FER – giving an adsorption energy of −77 kJ mol⁻¹. Other ab initio studies also showed that the adsorption energy between methanol and acid sites across TON, FER and MFI zeolite topologies can vary on the order of ∼20 kJ mol⁻¹.²⁶ More recent studies have shown how ab initio methods are required to fully capture the interactions of adsorbates with acid sites. Cnudde et al. investigated the diffusion of ethene and propene through 8-ring windows in CHA-type zeolite H-SAPO-34 finding that the presence of Brønsted acid sites in the 8-ring enhances the diffusion process due to the formation of a favourable π-complex host–guest interaction.²⁷ Ferri et al. also showed that the stability of key intermediates involved in the MTO process is influenced by preferential stabilisation upon confinement, dependent on the zeolite framework and composition, within the 8-ring window – controlling the final olefin product distribution.²⁸ It is clear from the range of studies cited that a number of factors play a role in the interactions between methanol, the catalyst active sites and framework, which are of significant relevance to both catalytic properties but also, crucially, the diffusivity of methanol throughout the zeolite catalyst.

The effect of BASs on methanol diffusion and other dynamics has also been explored experimentally in other zeolite systems such as zeolite Y (ref. 29) and H-ZSM-5 (ref. 3 and 30–32) via quasielastic neutron scattering (QENS) experiments. In both systems, significant decreases in mobility were observed as the Si/Al ratio was decreased, attributed to H-bonding between the methanol and BASs. In fact, complete immobilisation of the methanol has been observed in H-ZSM-5,⁶ where further spectroscopic measurements suggested that room temperature methoxylation can occur. This has been proposed as a key step in the initial stages of multiple important catalytic reactions, such as the direct synthesis of ethene^33,34 and as a starting point for C–C bond formation.³⁵

While QENS experiments and other neutron-based techniques³⁶ can provide valuable insights into the behaviour of molecules confined in porous catalysts, combining these techniques with classical molecular dynamics simulations (MD) is particularly powerful, as both methods probe the same time (10 ps–100 ns) and length scales (0.1–100 nm). This combination offers detailed insight into both the translational and rotational motion of molecules, as well as the adsorbate-framework and adsorbate–adsorbate interactions of species confined within zeolites.^37,38 This complementarity is particularly clear when MD is used to reproduce QENS observables, such as the intermediate scattering function (ISF) or elastic incoherent structure factor (EISF), allowing for direct comparison between the two techniques. Classical MD was recently employed by Botchway et al.³⁹ to probe the dynamics of methanol in zeolites beta and MFI as a function of Si/Al ratio. The study showed that the zeolite topology had a significant effect on the methanol dynamics, with diffusion coefficients in ZSM-5 not exceeding 10 × 10⁻¹⁰ m² s⁻¹, compared to diffusion rates two orders of magnitude higher in zeolite beta, owing to the larger pore dimensions. Further analysis of the radial distribution functions and residence times revealed that strong H-bonds between methanol and the acid sites in H-ZSM-5 are formed, offering further insight into the differences in performance of these two catalytic materials.

In the current study, QENS and MD simulations are used to investigate the dynamics of methanol confined within FER-type zeolites. Experimentally, the dynamics of methanol in a commercially produced FER sample were compared to that in FER synthesised from naturally sourced kaolin, to investigate the effects of the aforementioned structural imperfections in the more cheaply sourced material. The kaolin source was chosen due to the alumina content which was at least 60% lower than the silica content – required for the synthesis of high silica type zeolites. The MD simulations investigated the effect of the inclusion of BASs on the nanoscale diffusion of methanol, but were also employed to reproduce QENS observables and thus probe differences in local motions as a function of H-FER composition.

2. Methodology

2.1 Quasielastic neutron scattering experiments

The QENS experiments employed two zeolite FER samples; a commercial sample and a sample synthesised from naturally sourced Ghanaian kaolin (herein referred to as FER-GHA). The commercial sample, obtained from Zeolyst International (CP914C), had Si/Al ratio = 10 and was received originally in its NH₄ form, subsequently converted to its H-FER form by heating from room temperature to 798 K for 4 hours, at a heating rate of 5 K min⁻¹. The FER-GHA sample was synthesised from kaolin, (see ESI† section 1.0 for procedure), resulting in a sample with a Si/Al ratio in the range of 35 to 48 as deduced by energy dispersive X-ray (EDX) – see ESI† 1.4 for characterisation details. Both samples were dried for 4 hours, ramping up the temperature at 1 K min⁻¹ to 120 °C under vacuum to avoid dealumination of the framework before loading. Methanol was subsequently loaded into each system using He as a carrier gas. The saturation point in the commercial sample was found to be at 7.34 wt% loading – almost 5 molecules per unit cell (MPUC). A slightly lower loading of 6.26 wt% (∼4 MPUC) was also used for comparison. The FER-GHA sample was loaded to saturation at 10.18 wt% methanol (∼7 MPUC) by the same procedure. MPUC calculations included in ESI† 1.4. This slightly higher loading is likely achieved due to the inclusion of strongly adsorbing cations within the sample – see EDX for more details in ESI† 1.4. The methanol-dosed and non-dosed zeolite samples were then transferred, in an inert atmosphere, to thin-walled aluminium cans of annular geometry where a 1 mm annulus was used to avoid multiple scattering from the sample.

The QENS experiments were carried out using the OSIRIS spectrometer⁴⁰ at the ISIS pulsed neutron and muon source. Measurements were conducted at approximately 6 K, to obtain the resolution function, and the sample was subsequently heated to 273, 303 and 333 K for further data collection. The 002 reflection from the pyrolytic graphic analyser was used, giving an energy resolution of 24.5 μeV at FWHM, with energy transfers measured in a window of ±0.55 meV. The detectors covered measurements over a Q range of 0.2–1.8 Å⁻¹. The neutron scattering signal from the empty zeolite samples was measured (which contain a very low quantity of hydrogen) and the signal was subtracted from the methanol-loaded samples, leaving only the signal from the methanol itself. This procedure also removes any minor scattering from the Al sample vessel. All QENS data were fitted using the neutron scattering analysis packages DAVE⁴¹ and Mantid.⁴²

2.2 Molecular dynamics simulations

In this section, we shall describe the construction of the model FER systems, the forcefields used to describe the zeolite, methanol and methanol–zeolite interactions, and the procedure used for the molecular dynamics simulations. Further details may be found in section ESI† 1.1.

2.2.1 FER framework construction. Ferrierite is a medium pore zeolite with two perpendicular intersecting channels of 4.8 Å and 5.4 Å diameters. The 108 atom siliceous FER, which has an orthorhombic unit cell (UC)⁴³ with l mmm symmetry, was extended to a 1 × 1 × 2 cell and substituted with two aluminium atoms – Fig. 1 shows the 2 × 2 × 4 cell – giving a Si/Al ratio of 35 that falls between the two experimental samples. See section ESI† 1.1 for full details of the framework construction and aluminium siting. The Brønsted acidic FER UC and its siliceous counterpart were then replicated to create 4 × 4 × 8 (75.2 Å × 56.2 Å × 59.5 Å) supercells of ca. 14 000 framework atoms – Fig. S1.1† – and periodic boundary conditions were employed. Although simulation cells of a smaller size can be used, a larger cell allows full utilisation of DLPOLY's parallelisation capabilities, maintaining the same level of statistics, more efficiently, compared to running a smaller simulation cell for a longer time period.

Fig. 1 H-FER type zeolite 2 × 2 × 4 supercell upon BAS substitution, pre-expansion to the production supercell, viewed from the 010 and 001 directions. Silicon (yellow), oxygen (red) and aluminium (blue). ‘A’ shows a magnified snapshot of a Brønsted acidic site in the Si/Al = 35 cell.

A flexible zeolite model was employed with non-bonded interactions described using the potentials of Schröder et al.,⁴⁴ which were developed mainly from empirical fitting to structural and physical properties of α-quartz, by Sanders et al.,⁴⁵ and Al₂O₃. Atoms are assigned full ionic charges, apart from the oxygen of the BAS (O_b) which is assigned a charge of −1.426 and its associated proton (H_b) a charge of +0.426. The three-body potential (used for mediating the O–Si–O and O–Al–O angles) was replaced by that of Ramsahye and Bell⁴⁶ – based on those from Kramer et al.,⁴⁷ derived from ab initio methods and fitting to experimental values of α-quartz and zeolites MAP and Na–Y – which maintain framework stability to low Si/Al ratios. A full list of the parameters used to model the zeolite framework is compiled in Table S1.† Before methanol insertion, the framework was equilibrated to 300 K via MD simulation using the DLPOLY 4 code⁴⁸ in the canonical (NVT) ensemble, using a Berendsen⁴⁹ thermostat and a timestep of 0.5 fs until thermal and energetic fluctuations had stabilised, after at least 80 ps.

2.2.2 Methanol loading. After framework equilibration, methanol molecules were placed into the framework at ∼6 wt% loading, similar to the QENS measurements and equivalent to 4 molecules per UC – a section is shown in Fig. 2 – and the entire loaded cell can be seen in Fig. S1.1.† While methanol loadings can have significant effects on diffusivity, as demonstrated by Plant et al.,⁵⁰ we are working at catalytically relevant loadings i.e. saturation, thus matching our QENS experiments.

Fig. 2 Initial placement of methanol molecules within the Brønsted acid site containing FER zeolite cell.

The methanol molecules were described by a flexible model, using the intramolecular potentials and charges of Plant et al.⁵¹ – Table S2† – whose potentials are modified from those of Blanco and Auerbach⁵² following Mulliken analysis of DFT calculations.

The intermolecular methanol–methanol interactions are also described by the potentials of Plant et al.⁵¹ – Table S3† – which were obtained by a slight modification of those given by the CVFF forcefield.⁵³ Again, the potentials of Plant et al. were used to describe the interaction between methanol and the zeolite framework.⁵² Potentials for the interaction of methanol with Brønsted acid sites were still required and these were taken from the work of Shubin et al.,⁵⁴ derived from the study of the adsorption of butanol isomers in H-ZSM-5 by Monte Carlo and MD simulation. This combination of forcefields has previously given activation energies of diffusion within the experimental error of QENS measurements of methanol in zeolite Y systems,²⁹ and we are thus confident of their suitability to model the systems presented here, and for direct comparison with our QENS experiments. The parameters themselves are listed in Table S3.† The methanol-containing cells were finally subjected to an energy minimisation to stabilise the initial configuration of methanol molecules loaded into the zeolite framework.

2.2.3 Molecular dynamics simulation procedure. DLPOLY 4 (ref. 48) was employed for all MD simulations, with a timestep of 0.5 fs and using a van der Waals cutoff of 10 Å, with the Coulombic interactions treated by the Ewald method. Each system was equilibrated in the NVT ensemble at 300 K, 350 K and 400 K for 80 ps to ensure that the system reached minimal thermal and energetic fluctuations, followed by production runs in the microcanonical (NVE) ensemble. In the canonical ensemble, during the equilibration runs, a Berendsen⁴⁹ thermostat was used to control the temperature. The production runs in the microcanonical ensemble lasted for a total of 2.1 nanoseconds, with the initial 100 ps omitted to allow the system to stabilise. The positions of the atoms were recorded once every picosecond, resulting in 2000 records of the atomic positions. The self-diffusion coefficient (D_s) of methanol was then calculated. The position of the carbon atom of the methanol molecule was tracked and the mean squared displacement (MSD) was calculated at each timestep across all molecules. Although calculating diffusivity from the centre of mass of the molecule may seem a more accurate measure, the difference is insignificant in the ballistic region, with the diffusion coefficients lying well within error of each other – see ESI† 1.2 – and would incur an additional computational expense. We employed the Einstein relation to calculate the D_s as shown in eqn (1), provided the log(MSD)-log(t) relationship was linear.The statistics of each individual run were improved using the method of multiple time origins, detailed in ESI† 1.2. The diffusion coefficient was then extracted from the linear portion of this MSD plot, in each case from 200 ps to the end of the MSD at 1 ns. In order to understand the adsorbate–adsorbate and adsorbate–zeolite interactions, several different radial distribution functions (RDFs) were calculated using the atomic trajectories from the MD simulations. This was carried out using the integrated module for RDFs within the Visual Molecular Dynamics⁵⁵ package.

To understand the methanol-BAS interactions further, the contact correlation function between the methanol molecules and the Brønsted acid sites in the Si/Al ratio = 35 was also calculated, detailed in ESI† 1.3, to obtain an average residence time of a methanol molecule at a BAS.

The rotational motions of methanol in FER were also probed, including reproduction of QENS observables such as the intermediate scattering function (ISF) and the elastic incoherent structure factor (EISF), allowing for direct comparison with our experiments. A 100 ps production run was performed which recorded the atomic positions every 0.1 ps The atomic positions were used to calculate the ISF (shown as the powder average expression):

where N is the total number of atoms and d_i the vector from the molecule's centre of mass to one of the hydrogen atoms at time t. The ISF is directly measured in QENS experiments and thus its calculation allows for direct comparison across experiment and simulation. The method of multiple time origins was also used in the calculation of the ISF, where ten 50 ps trajectories were generated, each offset by 5 ps to cover the entire 100 ps simulation. The resulting ISF may be fitted with an exponential function of the form:where i is the number of exponentials required for satisfactory fitting and . The baseline value – B(Q) – corresponds to the (EISF) as it relates to the atomic arrangement as t → ∞, thus providing the molecular rotation symmetry. Therefore, the baseline can be plotted as a function of Q in an analogous procedure to the QENS experiments and Γ₁ is equivalent to the half-width half-maximum (HWHM) of the quasielastic scattering function (or dynamical structure factor) and as such may be used to calculate the rotational diffusion coefficient.

3. Results and discussion

3.1 Zeolite characterisation

Both the commercial FER and FER-GHA samples underwent characterisation using SEM, EDX, nitrogen sorption, X-ray diffraction (XRD), and neutron diffraction which took place simultaneously with the QENS experiments. For the full characterisation data and comprehensive discussion see ESI† 1.4 and 1.5. XRD confirmed the FER zeolite topology – although the FER-GHA has more non-crystalline domains. The commercial FER has a significantly higher surface area as determined by the Brunauer–Emmett–Teller (BET) method with a total surface area of 293 m² g⁻¹ compared to 41 m² g⁻¹ in the FER-GHA sample. SEM imaging revealed that, unlike the commercial sample, the FER-GHA contains two different crystallite morphologies – making calculation of the average particle size problematic. The commercial sample was measured to have an average particle diameter of ∼0.1 μm. EDX analysis further revealed that, in contrast to the commercial sample, the FER-GHA sample contained large amounts of Fe as well as Na, Mg, K & Ca concurrent with the use of a natural mineral source material.

3.2 QENS experiments

In this section we shall detail the QENS derived dynamics of methanol confined in the commercial FER and FER-GHA zeolite samples. Before beginning the analysis, the bulk crystallinity of both FER samples was confirmed using both X-ray and neutron diffraction (carried out using the OSIRIS diffraction detectors which cover a narrow d-spacing⁴⁰). A less ordered structure was found for the FER-GHA sample which may be attributed to the presence of impurities and a range of different counterions as observed using EDX. More information and characterisation may be found in ESI† 1.4 and 1.5.

3.2.1 Analysis of QENS experiments. The QENS spectra at 273 K for the 6.26 wt% loaded commercial sample and 10.18 wt% loaded FER-GHA sample are shown in Fig. 3. The corresponding spectra for the 7.34 wt% loaded commercial sample are found in the ESI† 1.7. The data were fitted to a delta function convoluted with the resolution measurement at 6 K, which gives the resolution function accounting for elastic scattering and thus static protons in the fitting process, a single Lorentzian function to fit the quasielastic broadening and a flat background to account for the Debye–Waller factor and other motions outside of the instrumental window. The Lorentzian was omitted in either the first two or three Q values of all datasets as the resolution function and background gave satisfactory fitting. This dominance of the elastic component suggests that motions over the longer distances sampled at low Q values (such as translational motion) are not taking place frequently enough to be observed over the timescale probed by the OSIRIS spectrometer.

Fig. 3 Subtracted QENS spectra of (a) 6.26 wt% methanol loaded commercial FER and (b) 10.18 wt% methanol loaded FER-GHA at 273K at Q = 0.74, 0.91, 1.16, 1.33, and 1.49 Å⁻¹. Left hand plot shows raw intensity, right hand shows log intensity. Alternate spectra are shown for clarity.

We note that all three samples show extremely small contributions from the Lorentzian component at all Q values, suggesting that very limited dynamics take place over the ∼1–100 ps timescale probed by the OSIRIS spectrometer. Thus the elastic component of the spectrum is dominant at all Q values (length scales). However, the QENS spectra are also plotted as a function of log intensity (right-hand figure), where the presence of the Lorentzian component is clear, indicating that the dynamic population, while small, is quantifiable. The presence of a dominant elastic peak at all Q values, and therefore a significant proportion of ‘static’ protons in the system, has been observed in a number of similar studies^6,51 and may be attributed to a range of phenomena, such as hydrogen-bonding to BASs,⁶ strong sorbate–sorbate interactions⁵¹ or potentially steric hindrance due to the small pore size of FER. These will be discussed in more detail in the subsequent QENS and MD simulation analyses.

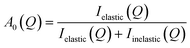
As mentioned, the presence of a small Lorentzian component (which is not present at low Q values) and a dominant elastic peak could suggest that localised motions are present. These may be probed by calculating the EISF, which is given by:

and is the proportion of total scattered intensity which is elastic. Fig. 4 shows the experimental EISF of methanol in the 6.26 wt% loaded commercial FER sample at 273 K.

Fig. 4 Experimental EISF plot for methanol in the 6.26 wt% methanol loaded commercial FER sample at 273 K. (a) Shows raw models (where the 3-site and uniaxial rotational models are overlapping) whilst (b) shows the models with an incorporated mobile fraction in brackets.

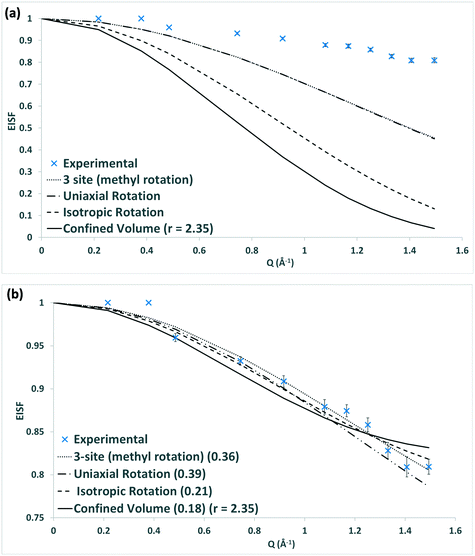
The Q dependence of the EISF gives information about the nature and geometry of the localised motion which is taking place. This may be characterised by a number of models – illustrated in Fig. 5 – each of which describes a different behaviour of the methanol, such as isotropic rotation (random rotation of the whole methanol molecule), 3-site rotation, or uniaxial rotation (describing jumping between three energy minima or continuous rotor-like rotation of the methyl group respectively), and diffusion confined to a sphere (the Volino–Dianoux model of a molecule translating inside a sphere – or cage – of a specific radius).⁵⁶ A full explanation of each model and the associated parameters can be found in the ESI† 1.6, and information on their derivation may be found in other resources.^57,58

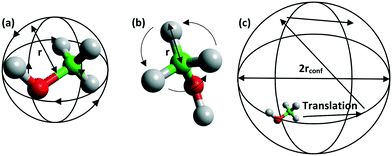Fig. 5 Schematic of a methanol molecule (a) rotating isotropically, (b) its methyl protons rotating uniaxially or in a jump manner, and (c) diffusion confined to a sphere.

The raw models shown in Fig. 4a are not able to give fits to the experimental EISF, falling well below the points at all Q values. The scattering is more elastic than the model predicts and as such a higher proportion of the confined methanol must only be scattering elastically and must therefore be immobile over the instrumental timescale. This may be accounted for by employing a mobile fraction (p_x) into the EISF fitting, which varies across each system and temperature, whereby the EISF (A_o(Q)) is scaled to compensate for the immobile molecules to give an effective EISF (A^eff₀(Q)):

A^eff₀(Q) = p_x[A_o(Q)] + (1 − p_x) (5)

At 273 K, the best fit for each model is indicated in the legend of Fig. 4b. The small mobile fractions demonstrate the extremely hindered mobility of the methanol in both samples, potentially for the reasons mentioned, i.e. sterics, H-bonding to acid sites and sorbate–sorbate interactions.

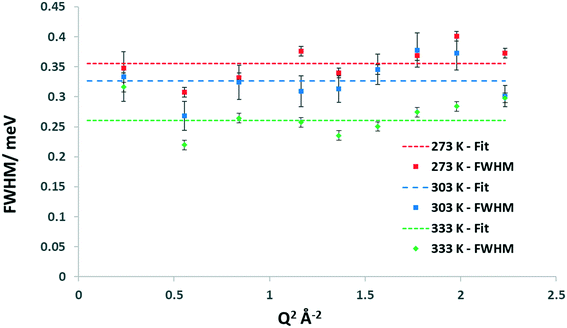
In order to determine the rate of the localised motion, the full-width at half-maximum (FWHM) of the quasielastic Lorentzian component of the fit is analysed, which is plotted in Fig. 6 for the 6.26 wt% loaded commercial FER at 273 K.

Fig. 6 Experimental FWHM plots for methanol in the 6.26 wt% methanol loaded commercial FER sample at 273 K as well as the line of best fit.

Fig. 6 shows that the FWHM is independent of Q², suggesting that the methanol is undergoing rotational motion. In the case of diffusion confined to a sphere, one would observe such independence below the Q² value radius of the sphere above which Q² dependence is observed – within the distance that diffusive behaviour may be observed, followed by conformance to a model of translational motion.⁵⁹ Based on analysis of both the EISF and the FWHM we can conclude that one of the three rotational models is most likely. Given the associated energy transfers which are of a similar magnitude to those reported by Matam et al.³² for an isotropic methanol rotation, we therefore tentatively suggest that we are observing isotropic rotational dynamics, particularly as the methyl rotations would be taking place over a faster timescale. We note that the rotational diffusion coefficient derived for methanol in commercial H-FER at 273 K with a value of 1.35 × 10¹¹ s⁻¹, is higher by a factor of 2.8 than that obtained by Matam et al. for methanol in ZSM-5, at 298 K. This may potentially be explained by differences in the zeolite topologies, the Si/Al ratios and the methanol loading.

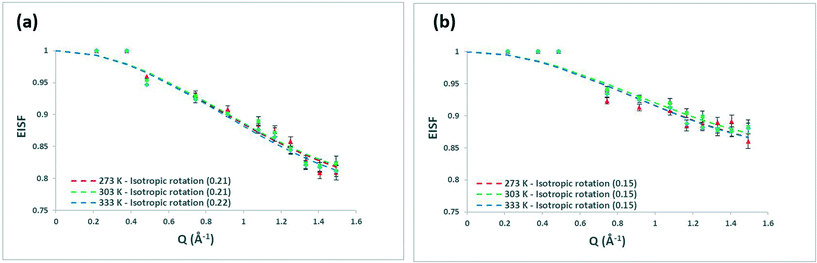
We shall now discuss the methanol behaviour as a function of temperature. Fig. 7 shows the EISF plots of the 6.26 wt% methanol-loaded commercial H-FER and 10.18 wt% loaded FER-GHA samples, with the 7.34 wt% loaded commercial FER in Fig. S1.8,† which are all fit to the isotropic rotation model. Their related mobile fractions are listed in Table 1.

Fig. 7 Experimental EISF plots for methanol in the (a) 6.26 wt% methanol loaded commercial FER and (b) 10.18 wt% loaded FER-GHA samples at 273 K, 303 K and 333 K as well as the fit of the isotropic rotation model with their commensurate mobile fractions.

Table 1 Mobile fractions of methanol from EISF fitting in commercial and GHA FER samples at 273 K, 303 K and 333 K

Temperature (K)	Mobile fraction (%)
	Commercial FER (6.26 wt%)	Commercial FER (7.34 wt%)	FER-GHA (10.18 wt%)
273	20.9	21.0	15.4
303	20.7	18.3	14.6
333	21.5	21.0	15.4

---

In all systems, we note that the mobile fraction never surpasses 22%, illustrating the limited dynamics of methanol in all systems over the timescale probed. Upon observing the EISF plots in Fig. 7a and b, we note the significant overlap in error across systems at the different temperatures – showing the lack of significant temperature effects on the mobile population of methanol in these samples in the measured temperature range. Mobile fractions of ∼20% in the commercial sample and ∼15% in the FER-GHA sample are observed, and the marginally lower mobile fraction, despite the higher Si/Al ratio, in the FER-GHA may be due to a combination of the larger, strongly adsorbing counterions present in the sample (as shown by EDX – further details in ESI† 1.4) and the presence of amorphous silica as discussed in ESI† 1.5 – containing many silanol groups available for hydrogen-bonding with the methanol.

We now use the Q dependence of the FWHM of the Lorentzian component to calculate the rate of rotation. The plots for the 6.26 wt% loaded commercial sample are shown in Fig. 8, with the 7.34 wt% loaded commercial FER and 10.18 wt% loaded FER-GHA shown in section 1.9 of the ESI.†

Fig. 8 Q ²-Dependence of the FWHM of the Lorentzian component for the 6.26 wt% methanol loaded commercial FER sample at 273 K, 303 K and 333 K. The dotted lines indicate a line of best fit.

The average width of the FWHM was used to calculate the rotational diffusion coefficients, listed in Table 2.

Table 2 Rotational diffusion coefficients of methanol in commercial and FER-GHA samples at 273 K, 303 K and 333 K

Temperature (K)	D rot (1 × 10^11 s^−1)
	Commercial FER (6.26 wt%)	Commercial FER (7.34 wt%)	FER-GHA (10.18 wt%)
273	1.35 ± 0.10	2.03 ± 0.23	1.64 ± 0.16
303	1.24 ± 0.09	1.48 ± 0.15	1.16 ± 0.11
333	0.90 ± 0.07	1.17 ± 0.10	0.83 ± 0.07

---

The D_rot values vary from ∼0.8–2 × 10¹¹ s⁻¹ across all systems, with the highest values obtained in the commercial FER system at the higher loading, and the lowest values obtained in the FER-GHA sample. This may, again, be due to the inclusion of additional cations in the FER-GHA sample as shown in the EDX in ESI† 1.4. These D_rot values are of a similar magnitude to those previously observed in H-ZSM-5 at 325 K with a D_rot of 0.3–0.5 × 10¹¹ s⁻¹,^3,30 although consistently higher by a factor of 3–4. The values are also of a similar magnitude to those obtained from the MD simulations discussed in the next section. We note there appears to be a decrease in D_rot with temperature, which may appear counter-intuitive. However, we must treat this observation with caution, as it is important to consider the aforementioned very large elastic component of the QENS spectra and the very small total quasielastic signal. Such a small component may present issues with the fitting procedure, as illustrated by the error values associated with each D_rot, which, when considered in terms of the absolute values, show very little difference between D_rot values as a function of temperature. Another possible fitting issue may arise from increasing rates of rotation with temperature, causing the width of the quasielastic broadening to approach the maximum energy transfer measured by the instrument. As such, the broadening associated with such a fast rotation may be accounted for by the linear background function, which may lead to artificially reduced widths of the Lorentzian component as the broader intensity is transferred to the background. However, additional studies of zeolite systems dosed to full methanol saturation are necessary before we can conclude that the observed trend is anything more than a result of the fitting difficulties due to the small quasielastic component present in the experimental data.

3.3 Molecular dynamics simulation analysis

In the following section, we will provide a detailed analysis of the molecular dynamics simulations. The first part will be focussed on nanoscale translational diffusion and the second part will concentrate on the direct comparison of the localised motions between the simulation and experiment.

3.3.1 Translational diffusion. We now discuss the effect of the presence of Brønsted acid sites on the diffusivity of methanol in siliceous and acidic FER type zeolites in our classical MD simulations. The MSD plots for both the siliceous and Si/Al = 35 (BAS-containing) systems at all temperatures are shown in Fig. 9. All systems show reasonable linearity, after 200 ps, maintaining agreement with the Einstein relation.

Fig. 9 Mean squared displacement plots of methanol in siliceous (solid lines) and Si/Al = 35 FER cells (dotted lines) at 300 K, 350 K and 400 K.

Table 3 lists the self-diffusion coefficients of methanol in the different FER systems, ranging from 0.86 to 2.72 × 10⁻¹¹ m² s⁻¹ in the siliceous system and from 0.26 to 1.65 × 10⁻¹¹ m² s⁻¹ in the Si/Al = 35 system. Increasing the temperature from 300 K to 400 K results in an increase in diffusivity by a factor of ∼3 in the siliceous system and ∼6 in the Si/Al = 35 system. These self-diffusivities are an order of magnitude lower than those reported for methanol simulated at loadings of ∼1.1 and ∼2.2 wt% in MFI, which reach up to 10 × 10⁻¹⁰ m² s⁻¹, and ∼3 orders of magnitude smaller than zeolite beta at loadings of 1.7 and 3.4 wt%.³⁹ They are also ∼2 orders of magnitude lower than simulated values in zeolite HY at loadings of ∼1.7 wt%.²⁹ The observed differences in diffusivity can be rationalised by considering both the loading, which is significantly higher in our FER systems – increasing the number of adsorbate–adsorbate interactions – as well as the topology of the zeolite, where FER has the smallest pore size across these systems. The reported diffusion coefficients suggest that translational diffusion takes place over a timescale that is too long to be observed by the OSIRIS spectrometer, which would explain why our QENS experiments are observing localised motions such as isotropic rotation, rather than translational diffusion.

Table 3 Diffusion coefficients of methanol in siliceous and Brønsted acid site containing (Si/Al = 35) FER cells at 300 K, 350 K and 400 K

Temperature (K)	D s ± error (10^−11 m^2 s^−1)
	Siliceous	Si/Al = 35
400	2.72 ± 0.43	1.65 ± 0.36
350	1.33 ± 0.01	0.72 ± 0.01
300	0.89 ± 0.04	0.26 ± 0.00
E a (kJ mol^−1)	11.0	18.2

---

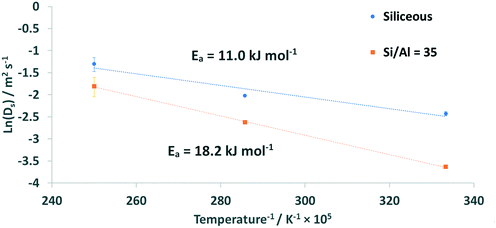
Using the determined diffusion coefficients, the activation energy (E_a) for the diffusion process can be calculated using the Arrhenius plot in Fig. 10.

Fig. 10 Arrhenius plot of MD modelled methanol diffusion in siliceous and Si/Al = 35 FER zeolites.

The calculated E_a is significantly higher when acidic sites are present in the zeolite framework, as the E_a for the siliceous system is 11.0 (+2.1/−2.0) kJ mol⁻¹ whereas for the Si/Al = 35 system E_a = 18.2 (+2.1/−2.4) kJ mol⁻¹.

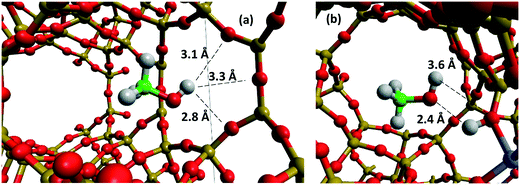
To investigate the significant effect of the BAS on methanol mobility in more detail, RDF plots illustrating the interactions between the BAS and the confined methanol are shown in Fig. 11 and S1.10.† Fig. S1.10† illustrates the hydrogen-bonding between the hydroxyl oxygen of the methanol and the proton of the BAS and indicates that strong coordination occurs, with an intense peak at ∼2.75 Å followed by a secondary coordination shell at ∼4.5 Å. Fig. 11 illustrates the interaction between the hydroxyl hydrogen of the methanol (H_OMe) and either the oxygen of the framework, in the siliceous case, or the oxygen of the bridging hydroxyl of the Brønsted acid site. We note that the oxygen atoms in the FER framework are not all equivalent and thus the average RDF may not be directly comparable between the BAS oxygens and all other oxygens. It is clear, however, that strong interaction occurs with the BAS, indicated by the sharp peak at ∼3.5 Å for the BAS-containing systems beginning at 2 Å. In contrast, the interaction with the nearby framework oxygens of the siliceous system – Fig. 12 – shows almost equal coordination distance with a methanol hydroxyl hydrogen at any distance above a minimum of 2.75 Å from the zeolite oxygen. This first interaction is closer than the BAS interaction because the Brønsted hydrogen is causing steric hindrance and the molecule is orientated in the opposite direction to maximise hydrogen-bonding (Fig. 12b). However, it is clear that there is a significant increase in zeolite–methanol interaction caused by the BAS, which is the main driving force for the reduction in diffusivity.

Fig. 11 RDF between the methanol hydroxyl hydrogen (H_OMe) and zeolitic oxygens, either from the framework in the siliceous cells or of the Brønsted acid site oxygen in the Si/Al = 35 cells, at 300 K and 400 K.

Fig. 12 (a) Interaction between the methanol hydroxyl hydrogen and zeolitic oxygens of the siliceous framework at 300 K. (b) The interaction between the methanol hydroxyl oxygen and Brønsted acid site at 300 K.

The coordination between the BAS and the methanol molecules was further probed using the contact correlation function, as outlined in ESI† section 1.3 to derive the residence time of the methanol molecules at the site. The residence times at 300 K, 350 K and 400 K were calculated at 3.00, 2.50 and 1.96 ps respectively. These values fall in a very similar range to that observed in zeolite beta and slightly below that of ZSM-5,³⁹ which suggests that regardless of the different pore dimensions, the length of time spent at a BAS for methanol is relatively consistent.

As expected, temperature increases result in a decrease in the residence time. This is reflected in the changes in the RDFs between the oxygen of the methanol and the proton of the BAS (Fig. S1.10†) which show the decreasing probability of the strong interaction at 2.75 Å, which is very strongly related to the increase in the diffusivity observed.

3.3.2 Rotational dynamics. Analysis of the rotational motion of methanol was carried out to compare directly with the analysis of the QENS data in the previous section. The intermediate scattering function (ISF) was calculated from the obtained atomic trajectories – using eqn (2) – and fit to the exponential function in eqn (3). Fig. 13 shows a sample of the ISFs calculated from our MD simulations at 300 K, at low, mid and higher Q values in the siliceous and Si/Al = 35 systems. Two exponentials were needed to fit the obtained function. A faster decay in the ISF is seen in the siliceous system than in the Si/Al = 35 system, suggesting that more rotational freedom is present in the system without acidic sites present.

Fig. 13 Calculated intermediate scattering functions from MD simulations of siliceous FER, and Si/Al = 35 FER, cells at 300 K.

The baseline of this function can be considered as an exponential where t = ∞ and thus represents the final atomic arrangement in Q space; the dependence of the baseline with Q provides the rotational symmetry of the molecule and hence is equivalent to the EISF obtained by our QENS experiments.⁶⁰ The EISF obtained from these baselines can then be plotted as a function of Q and fitted to the models described in ESI† section 1.6. An example of this fitting for the siliceous system at 300 K is shown in Fig. 14a and plots of the calculated EISFs at 300 K and 400 K in the siliceous and Si/Al = 35 systems are seen in Fig. 14b.

Fig. 14 (a) Elastic incoherent structure factor plots obtained from MD simulations for methanol rotating in the siliceous system at 300 K. (b) Calculated elastic incoherent structure factor from MD simulations of FER siliceous cells or Si/Al = 35 cells, at 300 K and 400 K. Both with their mobile fractions included in brackets.

A single isotropic rotation gives a satisfactory fit for the 300 K system and this was thus applied across all simulations. A single isotropic rotation would likely mask any type of more localised rotation (such as 3-site or uniaxial rotation of methyl groups) which may be observed over a shorter timescale, and hence would be the dominant motion to which the EISF could be fit. The very similar shape of the EISFs across all systems suggest that the rotational behaviour of the molecule, in terms of the geometry of rotation, is similar across temperatures. The observed decay is slightly faster in the siliceous system compared to the BAS containing systems, due to the higher mobile fractions employed in the fitting. This suggests that the BASs, in the Si/Al = 35 systems, are also reducing the rotational freedom of the methanol molecules compared to the siliceous systems, similar to that observed for translational motion due to the coordination between methanol and the acidic sites illustrated in Fig. 13 and 14.

The fitted mobile fractions for each system are listed in Table 4. The interactions between the methanol and BASs in the Si/Al = 35 systems result in slightly decreased mobile fractions compared to the siliceous analogues, ranging from 0.95 to 0.98 in the siliceous system and 0.89–0.95 in the Si/Al = 35 systems, as the temperature is increased. These mobile fractions are of course significantly higher than those observed via experiment and these discrepancies may well stem from imperfections in our model. In particular, differences in structure between the model cell and the real system, such as a lack of defects, surface silanols which are strongly adsorbing⁶¹ (often associated with mesopores) and intergrowths, which are not captured by our perfect, infinitely crystalline model. Additionally, the choice of forcefield, which has not been developed and fitted for this specific combination of adsorbate and zeolite, may be partially responsible. It is important to acknowledge that any non-specific forcefield will have inherent approximations which can only be properly addressed through the detailed empirical (or quantum mechanical) fitting of guest–host interactions.

Table 4 Mobile fractions and rotational diffusion coefficients (D_rot) of methanol fromintermediate scattering function fitting in simulated siliceous and Si/Al = 35 FER zeolites

Temperature (K)	Siliceous		Si/Al = 35
	Mobile fraction	D rot (1 × 10^11 s^−1)	Mobile fraction	D rot (1 × 10^11 s^−1)
300	0.96	2.92	0.89	3.57
350	0.97	4.40	0.93	5.02
400	0.98	5.73	0.95	6.63

---

In order to calculate a rotational diffusion coefficient (D_r), the isotropic model of rotation characterised from MD simulations may be fit to an intermediate scattering function, as in eqn (6), where R is the radius of rotation for a methanol molecule:

The average D_r from the first 5 Q values is used and the first 6 terms of the summation over l are retained, the decay constant of the intermediate scattering function exponents (Γ₁) and (Γ₂) of eqn (3) can be treated in the same way as the half-width at half-maximum of a Lorentzian used to fit the quasielastic part of an experimental QENS signal. The D_r values obtained are plotted in Fig. 15. More detail about the calculation of the rotational diffusion coefficients resulting from the ISF fitting can be found in ESI† 1.11.

Fig. 15 Rotational diffusion coefficients (D_rot) of methanol from elastic incoherent structure factor fitting in simulated siliceous and Si/Al = 35 FER zeolites and experimental 6 wt% loaded commercial sample and FER-GHA.

The rotational diffusion coefficients range from ∼2.9–6.6 × 10¹¹ s⁻¹ over the measured temperature range. Very similar trends are observed in both the siliceous and Si/Al = 35 systems with the latter showing a slightly higher D_rot. We consider that the slightly higher D_rot calculated in the system with Brønsted acid sites may be related to the lower mobile fraction of methanol in the Si/Al = 35 system, leaving fewer molecules in the pore system to interact with others, and thus have their rotation hindered through sorbate-sorbate interactions. Matam et al.³ reported a D_rot of 3 × 10¹⁰ s⁻¹ for the isotropic rotation of methanol in ZSM-5 at 325 K, whereas Omojola et al.³⁰ reported a D_rot of 2.6 × 10¹⁰ s⁻¹ at 325 K, falling below our calculated values for the isotropic rotation at similar temperatures. Thus, the MD-calculated rotational diffusion coefficients are 3–5 times higher than equivalent systems in experiment. The simulation would be expected to predict values at the upper limit of experiment, potentially due to the inconsistencies with the experimental system and possible forcefield related issues considered earlier.

4. Conclusions

Quasielastic neutron scattering experiments and classical molecular dynamics simulations have been employed to investigate the dynamical behaviour of methanol within FER type zeolites. The QENS experiments were performed between 273 K and 333 K on samples of commercial FER (Si/Al = 10), with methanol loadings of 6.26 wt% and 7.34 wt%, and FER synthesised from natural Ghanaian kaolin (FER-GHA) (Si/Al = 35–48), with a loading of 10.18 wt%. MD simulations were run with loadings of 4 molecules per unit cell (6 wt%) and the effect of the presence of Brønsted acid sites (Si/Al = 35 vs. a fully siliceous cell) on methanol diffusion was probed.

The QENS experiments show that methanol has very limited mobility in both the commercial and FER-GHA samples on the 1–100 ps timescales probed by the OSIRIS spectrometer. No translational diffusion was measurable, with isotropic rotation being observed as in previous studies of different zeolite systems. Fitting of the experimental EISF to an isotropic rotation model necessitated the incorporation of mobile fractions of ∼20% in the commercial FER samples at 6.26 wt% and 7.34 wt% loadings and ∼15% in the FER-GHA sample at 10.18 wt% loading, suggesting mobility is more hindered in the FER-GHA sample. The D_rot values varied from ∼0.8–2 × 10¹¹ s⁻¹ across all systems, where the commercial FER system at 7.34 wt% loading gave the highest values, and the lowest values were obtained in the FER-GHA sample. These D_rot values are of a similar magnitude to those previously observed in H-ZSM-5 at 325 K, although consistently higher by a factor of 3–4.

The classical MD simulations show very low translational diffusivity for methanol confined in all FER systems, with D_s values in the range of 0.89–2.72 × 10⁻¹¹ m² s⁻¹ in the siliceous system and 0.26–1.65 × 10⁻¹¹ m² s⁻¹ in the Si/Al = 35 system, where the lower diffusivities in the Si/Al = 35 system are due to strong coordination between the Brønsted acidic hydrogen and the hydroxyl oxygen of the methanol, giving an average residence time of 2–3 ps over the measured temperature range. Notably, translational diffusion taking place at this rate would be on a timescale too slow to be sampled by the QENS spectrometer employed, hence we observe isotropic rotation. The rotational behaviour of the methanol molecules was also probed by directly reproducing QENS observables, such as the intermediate scattering function and the EISF. The calculated EISF was also best fit to an isotropic rotation model with varying mobile fractions ranging from 88–94% in the Si/Al = 35 systems, higher in the siliceous systems (96–98%). The rotational diffusion coefficients calculated range from 2.9 × 10¹¹ s⁻¹ to 6.6 × 10¹¹ s⁻¹ across both systems, but slightly higher in the Si/Al = 35 system than in its siliceous counterpart. The rotational dynamics extracted from the simulations take place at a similar rate to the experiment, at a factor of 2–5 times higher than the current QENS experiments and approximately 10 times higher than those reported from QENS experiments in ZSM-5, although the mobile fractions obtained at this loading are significantly lower.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC), grant no. EP/R513155/1 at the University of Bath and EP/K009567 at Cardiff University. NHdL, CHB and BKA also acknowledge the Royal Society and the UK Department for International Development for funding under the Africa Capacity Building Initiative (ACBI), which has supported this research. BKA would also like to acknowledge the Natural Environment Research Council for their funding through the grant NE/R009376/1. This work has made use of the Balena High Performance Computing (HPC) Service at the University of Bath and HPC Wales at Cardiff University. We would also like the thank Dr Gabriele Kociok-Kohn for running and maintenance of the PXRD instrument as well as the whole of MC² at the University of Bath. AJOM acknowledges Roger and Sue Whorrod for the funding of a Whorrod Fellowship. SKM would like to thank the UK Catalysis Hub for resources and support provided via our membership of the UK Catalysis Hub Consortium and funded by EPSRC grants: EP/R026939/1, EP/R026815/1, EP/R026645/1, EP/R027129/1. The ISIS neutron and muon source at the STFC Rutherford Appleton Laboratory are thanked for access to neutron beam facilities; the data from our experiment RB2010237 can be found at DOI: 10.5286/ISIS.E.RB2010237.

References

1. C. J. Maiden, in Studies in Surface Science and Catalysis, ed. D. M. Bibby, C. D. Chang, R. F. Howe and S. Yurchak, Elsevier, 1988, vol. 36, pp. 1–16.
2. M. Stöcker, Microporous Mesoporous Mater., 1999, 29, 3–48.
3. S. Matam, A. J. O'Malley, C. R. A. Catlow, P. Collier, A. Hawkins, A. Zachariou, D. Lennon, I. Silverwood, S. Parker and R. Howe, Catal. Sci. Technol., 2018, 8, 3304–3312.
4. D. Lesthaeghe, V. Van Speybroeck, G. B. Marin and M. Waroquier, Angew. Chem., 2006, 118, 1746–1751.
5. V. Van Speybroeck, K. De Wispelaere, J. Van der Mynsbrugge, M. Vandichel, K. Hemelsoet and M. Waroquier, Chem. Soc. Rev., 2014, 43, 7326–7357.
6. A. J. O'Malley, S. F. Parker, A. Chutia, M. R. Farrow, I. P. Silverwood, V. García-Sakai and C. R. A. Catlow, Chem. Commun., 2016, 52, 2897–2900.
7. E. Kianfar, S. Hajimirzaee, S. Mousavian and A. S. Mehr, Microchem. J., 2020, 156, 104822.
8. J. Lefevere, S. Mullens, V. Meynen and J. Van Noyen, Chem. Pap., 2014, 68, 1143–1153.
9. S. Wilson and P. Barger, Microporous Mesoporous Mater., 1999, 29, 117–126.
10. D. Chen, K. Moljord and A. Holmen, Microporous Mesoporous Mater., 2012, 164, 239–250.
11. P. Losch, A. B. Pinar, M. G. Willinger, K. Soukup, S. Chavan, B. Vincent, P. Pale and B. Louis, J. Catal., 2017, 345, 11–23.
12. I. Yarulina, A. D. Chowdhury, F. Meirer, B. M. Weckhuysen and J. Gascon, Nat. Catal., 2018, 1, 398–411.
13. U. Olsbye, S. Svelle, M. Bjørgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810–5831.
14. A. J. Porter and A. J. O'Malley, J. Phys. Chem. C, 2021, 125, 11567–11579.
15. E. Catizzone, A. Aloise, M. Migliori and G. Giordano, Appl. Catal., A, 2015, 502, 215–220.
16. E. Catizzone, S. V. Daele, M. Bianco, A. Di Michele, A. Aloise, M. Migliori, V. Valtchev and G. Giordano, Appl. Catal., B, 2019, 243, 273–282.
17. E. Catizzone, A. Aloise, M. Migliori and G. Giordano, J. Energy Chem., 2017, 26, 406–415.
18. C. Arcoumanis, C. Bae, R. Crookes and E. Kinoshita, Fuel, 2008, 87, 1014–1030.
19. J. Li, Y. Wei, G. Liu, Y. Qi, P. Tian, B. Li, Y. He and Z. Liu, Catal. Today, 2011, 171, 221–228.
20. E. B. G. Johnson and S. E. Arshad, Appl. Clay Sci., 2014, 97–98, 215–221.
21. B. Kwakye-Awuah, B. Sefa-Ntiri, E. Von-Kiti, I. Nkrumah and C. Williams, Water, 2019, 11, 1912.
22. C. Wang, J. Zhou, Y. Wang, M. Yang, Y. Li and C. Meng, J. Chem. Technol. Biotechnol., 2013, 88, 1350–1357.
23. Z. Qiang, X. Shen, M. Guo, F. Cheng and M. Zhang, Microporous Mesoporous Mater., 2019, 287, 77–84.
24. S. A. F. Nastase, A. J. O'Malley, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2019, 21, 2639–2650.
25. J. Andzelm, N. Govind, G. Fitzgerald and A. Maiti, Int. J. Quantum Chem., 2003, 91, 467–473.
26. F. Haase and J. Sauer, Microporous Mesoporous Mater., 2000, 35–36, 379–385.
27. P. Cnudde, R. Demuynck, S. Vandenbrande, M. Waroquier, G. Sastre and V. V. Speybroeck, J. Am. Chem. Soc., 2020, 142, 6007–6017.
28. P. Ferri, C. Li, R. Millán, J. Martínez-Triguero, M. Moliner, M. Boronat and A. Corma, Angew. Chem., Int. Ed., 2020, 59, 19708–19715.
29. A. J. O'Malley, V. García Sakai, I. P. Silverwood, N. Dimitratos, S. F. Parker and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2016, 18, 17294–17302.
30. T. Omojola, I. P. Silverwood and A. J. O'Malley, Catal. Sci. Technol., 2020, 10, 4305–4320.
31. H. Jobic, A. Renouprez, M. Bee and C. Poinsignon, J. Phys. Chem., 1986, 90, 1059–1065.
32. S. K. Matam, C. R. A. Catlow, I. P. Silverwood and A. J. O'Malley, Top. Catal., 2021, 1–8.
33. Y. Jiang, M. Hunger and W. Wang, J. Am. Chem. Soc., 2006, 128, 11679–11692.
34. W. Wang, Y. Jiang and M. Hunger, Catal. Today, 2006, 113, 102–114.
35. S. R. Blaszkowski and R. A. van Santen, J. Am. Chem. Soc., 1997, 119, 5020–5027.
36. A. J. O'Malley, S. F. Parker and C. R. A. Catlow, Chem. Commun., 2017, 53, 12164–12176.
37. H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50.
38. J. Armstrong, A. J. O'Malley, M. R. Ryder and K. T. Butler, J. Phys. Commun., 2020, 4, 072001.
39. C. H. Botchway, R. Tia, E. Adei, A. J. O'Malley, N. Y. Dzade, C. Hernandez-Tamargo and N. H. de Leeuw, Catalysts, 2020, 10, 1342.
40. M. T. Telling and K. H. Andersen, Phys. Chem. Chem. Phys., 2005, 7, 1255–1261.
41. R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. Tregenna-Piggott, C. M. Brown, J. R. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341.
42. O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
43. W. M. Meier, D. H. Olson and C. Baerlocher, Zeolites, 1996, 17, 1–229.
44. K.-P. Schröder, J. Sauer, M. Leslie, C. R. A. Catlow and J. M. Thomas, Chem. Phys. Lett., 1992, 188, 320–325.
45. M. J. Sanders, M. Leslie and C. R. A. Catlow, J. Chem. Soc., Chem. Commun., 1984, 1271–1273.
46. N. A. Ramsahye and R. G. Bell, J. Phys. Chem. B, 2005, 109, 4738–4747.
47. G. J. Kramer, N. P. Farragher, B. W. H. van Beest and R. A. van Santen, Phys. Rev. B: Condens. Matter, 1991, 43, 5068.
48. I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918.
49. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
50. D. F. Plant, G. Maurin and R. G. Bell, J. Phys. Chem. B, 2007, 111, 2836–2844.
51. D. Plant, G. Maurin and R. Bell, J. Phys. Chem. B, 2006, 110, 15926–15931.
52. C. Blanco and S. M. Auerbach, J. Phys. Chem. B, 2003, 107, 2490–2499.
53. P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins: Struct., Funct., Bioinf., 1988, 4, 31–47.
54. A. A. Shubin, C. R. A. Catlow, J. M. Thomas and K. I. Zamaraev, Proc. R. Soc. Lond. A: Math. Phys. Sci., 1994, 446, 411–427.
55. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
56. F. Volino and A. Dianoux, Mol. Phys., 1980, 41, 271–279.
57. M. Bee, Biology and Materials Science, Adam Hilger, Bristol, 1988, p. 193.
58. A. J. O'Malley and C. R. A. Catlow, in Experimental Methods in the Physical Sciences, ed. F. Fernandez-Alonso and D. L. Price, Academic Press, 2017, vol. 49, pp. 349–401.
59. A. J. O'Malley, M. Sarwar, J. Armstrong, C. R. A. Catlow, I. Silverwood, A. York and I. Hitchcock, Phys. Chem. Chem. Phys., 2018, 20, 11976–11986.
60. R. Mukhopadhyay, A. Sayeed, S. Mitra, A. V. Anil Kumar, M. N. Rao, S. Yashonath and S. L. Chaplot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061201.
61. D. Roy, S. Liu, B. L. Woods, A. R. Siler, J. T. Fourkas, J. D. Weeks and R. A. Walker, J. Phys. Chem. C, 2013, 117, 27052–27061.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cy02001c

---