Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrodeoxygenation of guaiacol over orthorhombic molybdenum carbide: a DFT and microkinetic study†
Kushagra
Agrawal
 ab,
Alberto
Roldan
ab,
Alberto
Roldan
 b,
Nanda
Kishore
a and
Andrew J.
Logsdail
b,
Nanda
Kishore
a and
Andrew J.
Logsdail
 *b
*b
aDepartment of Chemical Engineering, Indian Institute of Technology Guwahati, Guwahati, 781039, Assam, India
bCardiff Catalysis Institute, School of Chemistry, Cardiff University, Park Place, Cardiff CF10 3AT, Wales, UK. E-mail: LogsdailA@cardiff.ac.uk
First published on 17th December 2021
Abstract
The hydrodeoxygenation of guaiacol is modelled over a (100) β-Mo2C surface using density functional theory and microkinetic simulations. The thermochemistry of the process shows that the demethoxylation of the guaiacol, to form phenol, will be the initial steps, with a reaction energy of 29 kJ mol−1 (i.e. endothermic) and a highest activation barrier of 112 kJ mol−1. Subsequently, the dehydroxylation of the phenol, which has a rate-determining activation barrier of 145 kJ mol−1, will lead to the formation of benzene, with an overall reaction energy for conversion from guaiacol of −91 kJ mol−1 (i.e. exothermic). The sp2 and sp hybridized carbon atoms of the molecular functional groups are found to dissociate on the surface with minimum energy barriers, while the hydrogenation of the adsorbed molecules requires higher energy. The microkinetic modelling, which is performed considering typical reaction conditions of 500 to 700 K, and a partial pressure ratio for H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guaiacol of 1, shows quick formation and accumulation of phenol on the surface with increasing temperature, although high temperatures mitigate the guaiacol adsorption step. Based on simulated temperature programmed desorption (TPD), maximum conversion of guaiacol can be expected at 70% surface coverage of this species.
guaiacol of 1, shows quick formation and accumulation of phenol on the surface with increasing temperature, although high temperatures mitigate the guaiacol adsorption step. Based on simulated temperature programmed desorption (TPD), maximum conversion of guaiacol can be expected at 70% surface coverage of this species.
1. Introduction
In the quest for a viable renewable source of energy, biomass feedstocks have emerged as a strong contender because of the abundance of natural flora on the planet. The bio-oil obtained from the biomass, when properly treated, can be used as a direct substitute to fossil fuel;1,2 however, the cost of such treatment is currently preventive for commercial application. In particular, bio-oil obtained from the thermal treatment of biomass contains oxygen carrying compounds like guaiacol, anisole, and ferulic acid, and these oxy-compounds need to be reduced before being suitable as fuel.3 The reduction step is necessary because the oxygen carrying compounds are known to provide unfavorable properties to the crude bio-oil (such as low pH, high viscosity, etc.), and reduce its energy density.4The reduction of the oxy-compounds can be achieved through a process called hydrodeoxygenation (HDO), where molecular hydrogen is reacted at moderate temperature (300–500 °C) and high pressure (up to 30 bar) with the bio-oil,5 and oxygen is subsequently removed in the form of water. Unfortunately, the conditions outlined for HDO are economically prohibitive for scale-up;6 thus, catalysts are being actively sought to facilitate the reaction at milder conditions. Several different classes of metals have been tested as catalysts for the HDO process. While most of the transition metals are poor catalysts, due to low yield and high rates of char formation, the noble metals Ru, Pt and Pd have shown good performance;7 however, their low earth abundance and subsequent high cost prevents these materials being considered as commercial catalyst towards HDO.
To overcome the challenge of identifying effective and affordable catalysts, scientists are now considering cheaper materials with catalytically relevant characteristics similar to those of the noble metals. Nørskov et al.8 have shown that the performance of a catalyst is significantly influenced by the electronic structure at its surface, with the position of the d-band center, relative to the Fermi level, identified as a suitable indicator of the materials adsorption strength and catalytic activity.9 Such direct relation between the catalytic performance and the d-band position of the transition metal is due to the bonding and anti-bonding states formed when the adsorbate approaches the surface, where hybridization between the frontier orbitals of the adsorbate and s and d-orbital of the metal occurs; the adsorption strength is therefore dependent on the relative position of the metal states with respect to the Fermi level. The d-band theory has been quite successful in explaining, for instance, the trends observed in the oxygen reduction reactions (ORR),10–13 and the d-band center of catalytic materials has also been used as a descriptor for property prediction in transition-metal catalysed HDO studies.14–17 The transferability of the d-band approach is now of consideration for alternative composite catalysts, such as carbides and nitrides. As an example, molybdenum carbide (Mo2C) has similar d-band characteristics to the catalytically active noble metals (Ru, Pt and Pd), due to the carburization of molybdenum;18 specifically, the introduction of carbon between the Mo atoms increases their separation, which shifts the d-band center closer to the Fermi level, akin to the properties of the highlighted noble metals.
Considering the valorization of biomass, the crude bio-oil obtained after fast pyrolysis has a relatively high concentration of guaiacol (5–15% of the phenolic fraction).2 Guaiacol also contains both a methoxy and a hydroxyl functional group, which represents most of the oxygen-containing functional groups in bio-oils. In combination, these factors make guaiacol a convenient model molecule for studying the HDO of the bio-oil phenolic fraction. The upgrading of guaiacol over various catalysts, including the noble metals, and materials containing molybdenum and carbon with varying stoichiometries, has been considered in experimentation by several groups.19–28 Ma et al.29 upgraded guaiacol over α-MoC supported on activated carbon, with combined selectivity to phenols and alkylphenols of over 85%, and conversion at 87%. Similarly, Jongerius et al. obtained a combined selectivity of up to 87%, and a conversion greater than 99%, for the HDO of guaiacol over carbon nanofiber supported Mo2C;30 in this latter case, the upgrading was conducted at mild conditions of 5 bar of hydrogen pressure and temperatures of 300 to 375 °C. The Mo2C catalyst outperformed a tungsten carbide (WC) system with respect to yield of completely deoxygenated products, such as benzene. Indeed, Siaj et al.31 found acetaldehyde to dissociate selectively from the carbonyl bond over β-Mo2C surface in their experiments, with the mechanism explained subsequently by Martínez et al.32 Moreira et al.18 studied the efficacy of a Mo2C catalysts, supported again on carbon nanofiber, during the HDO of guaiacol, with phenol and cresol observed as the main products; the formation of phenol is proposed to have been initiated by the demethylation of guaiacol.
Experiments have clearly shown that Mo2C is a potentially effective and affordable catalyst for HDO reactions; however, the exact mechanism and the rate controlling parameters of the HDO process over the Mo2C surfaces remain unknown despite being necessary for catalyst design. Therefore, in this study, the reaction pathway for upgrading guaiacol over the Mo2C surface is investigated using density functional theory. A network of routes is proposed for guaiacol conversion to benzene, with important intermediates such as phenol and catechol included. The thermochemistry of all the proposed reactions is presented (Section 3) and subsequently, microkinetic modelling is applied to determine the kinetic parameters (Section 4) of the upgrading process.
2. Computational details
The orthorhombic (β) structure of molybdenum carbide was selected as base structure for our studies, as the excellent thermal stability of the material33 makes it suitable for catalytic applications over a wide temperature range. The (100) surface with a molybdenum termination shows favourable hydrogen adsorption properties,34 and has been reported as a suitable surface for HDO reactions in experimental works,29,35 and thus is considered herein. The Mo terminated (100) surface also has the highest surface metal density (0.130 atom per Å2) of all terminations of the (100) surface, resulting in a high coordination of surface Mo atoms. As a result, the electron-state fluctuations, which are involved in the breaking and formation of chemical bonds during catalytic reactions and are responsible for high turnover, are the highest at the Mo terminated surface.36 To simulate the β-Mo2C (100) surface, a 4-layer slab model with a 3 × 3 supercell was considered in a periodic environment (Fig. 1).All energy calculations were performed under the density functional theory (DFT) framework using the “Fritz Haber Institute ab initio molecular simulations” (FHI-aims) software package37 in combination with the “Atomic Simulation Environment” (ASE) Python package38 for geometry handling. After convergence testing with respect to surface energies, constraints were deemed appropriate for the bottom two layers of the slab, thus maintaining the long-range bulk structure, whilst the top two layers were unconstrained during all adsorption and reaction modelling. A 10 Å vacuum was added above and below the plane of the slab (i.e. total vacuum of 20 Å), which prevents spurious self-interaction errors. To counterbalance any dipole arising out of the imbalanced electric field at the surface, a dipole correction was also applied. A converged 5 × 5 × 1 k-grid was applied for the periodic condition calculations. The PBE39 functional with the Tkatchenko-Scheffler van der Waals correction40 was used for electronic structure calculations, along with the “light” basis set (version: 2010) of the FHI-aims package.41 In addition, zeroth order regular approximation (ZORA)37 scalar corrections were incorporated to account for relativistic effects. The choice of all these parameters is a result of a systematic study described previously.42
Geometry optimization of all the structures was conducted using the trust region method43 until the force on each atom was less than 0.01 eV Å−1. For the transition state calculations, a minimum of 7 images were used in the nudged elastic band (NEB) method calculations44 with the molecular dynamics based fast inertial relaxation engine (FIRE) optimization algorithm.45 The convergence criteria for the NEB calculations was set to a requirement of forces on each atom being less than 0.05 eV Å−1. This was followed by finite-difference frequency calculations with 0.01 Å displacement of atoms for the transition state structures to confirm their validity, with one imaginary frequency confirming a first-order saddle point. For cases where none or multiple imaginary frequencies were obtained, a more exhaustive machine-learning NEB method46 was used with 15 images to determine the correct transition state structure. In specific cases, where obtaining the transition state was challenging, a complementary approach was used: the distance, d, between atom A (or a group of atoms) that reacts with another atom B (or a group of atoms) was calculated, and then divided into n equal parts (n =20 in this case). Atom(/group) A is then placed at a distance of d/n from atom(/group) B, for all values of n, generating a pathway that contains n different geometry samples, and then structural optimization is performed for each geometry, with a cut-off force of 0.05 eV Å−1 on each atom, with the distance between A and B constrained. On plotting energy versus d for all the optimized geometries, the energy profile can then be used to identify the transition state structure. Once the transition state structure is obtained, again finite-difference frequency calculations were applied to confirm the nature of the first-order saddle point through identification of a single imaginary frequency.
The adsorption energy (Eads) of appropriate reaction processes was calculated as:
| Eads = EMo2C+Molecule − EMo2C − EMolecule | (1) |
The microkinetic modelling was conducted using our in-house code,47 with details outlined elsewhere.48 To describe briefly the details here: translations, rotations and vibrations were used to calculate the thermodynamic parameters, such as entropy, enthalpy and Gibbs free energy, based on a statistical thermodynamics approach.49 The derived energetic quantities were then used to calculate the rate constants for all the reactions using the transition-state theory (TST) approximation of Eyring, Evans and Polanyi50,51 as shown in eqn (2).
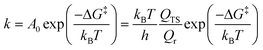 | (2) |
3. Results and discussions
The mechanism proposed herein initiates with the adsorption of guaiacol (GUA) on the catalyst surface. Guaiacol was considered interacting with the surface in three different orientations via: the aromatic ring, the methoxy group, or the hydroxyl group, as shown in Fig. 1(c). The adsorption was conducted on 5 different sites on the surface (atop, bridge, fcc, Mo-hcp and C-hcp, as illustrated in Fig. 1(a)), with the adsorbed structures and energetics shown in Tables S1–S3 of the ESI.†The strongest adsorption of guaiacol is via the aromatic ring over the C-hcp position of the surface, with an adsorption energy of −4.67 eV, which is at least 2.21 eV stronger than reported for the precious metal surfaces such as Ru (Eads = −2.46 eV),53 Pd (Eads = −1.43 eV)54 and Pt (Eads = −2.41 eV);55 the adsorption energy for guaiacol on tungsten carbide is closer to our calculated results, having been previously reported as −3.04 eV,56 though we note this is still 1.63 eV weaker than the molybdenum carbide. The difference in the adsorption energy could be a result of use of different functionals in different studies. In several cases during our investigation of orientations for guaiacol adsorption, such as interaction in the atop position with the methoxy group, and in the bridge position via the aromatic ring, the adsorbed molecule rearranges in the optimization process to a position over the C-hcp position and interacting via the aromatic ring. The preference of the hollow site (similar to the C-hcp site) for adsorption of aromatic species, including guaiacol, is well documented.57 As the C-hcp position was confirmed as the most stable adsorption site, all the subsequent calculations considering conversion of guaiacol were conducted at this position.
In order to validate the observations, calculations were conducted to obtain the sticking probability (σ(T)) of aromatic compounds as:
3.1. Energy profile of the upgrading routes
The HDO of guaiacol has been studied extensively over monometallic19,22,24,60 and bimetallic surfaces.21,27,61,62 Based on the reported literature, the possible pathway for upgrading could be guaiacol → catechol → phenol → benzene. Therefore, the proposed mechanism for hydrodeoxygenation involves the hydrogenation and subsequent deoxygenation of guaiacol in a series of elementary steps. Full saturation of the aromatic ring with hydrogen is reported as feasible at high hydrogen pressure and low temperature (<573 K) over noble metals;28 however, since completely saturated products are not desirable, and observed outside the standard HDO conditions, we focus on the upgrading of the adsorbed guaiacol beginning in two different ways: hydrogenation at the α- or the β-position of the aromatic ring (Fig. 2, structures 2 and 3), or dissociation of the the methoxy and hydroxyl groups from the molecule. In combination, there are therefore seven routes (R1–R7) by which the upgrading can initiate (Fig. 2).With respect to kinetic barriers, the dissociation of H from the hydroxyl group (R7) is the least energy demanding (0.62 eV), whereas thermodynamically, R6 is the most favourable reaction (ΔE = −2.29 eV). The deprotonation of the hydroxyl group was previously observed as having the lowest energy barrier among R1–R7 on noble metal surfaces,28,53 showing similarity to our results; the reported barrier over Pt (111) surface is 0.37 eV,28 and it is 0.29 eV over the Ru (0001) surface53 for the same reaction. The next most accessible reaction in our calculations is the cleavage of the methoxy group (R4), which has an activation energy (Ea) of 0.90 eV. The kinetic rate calculations show the rate constant for R7 to be 100 times faster than R4, suggesting faster production of structure 8 (6-methoxycyclohexa-2,4-dienone) over structure 5. The direct hydrogenation of the molecule via R1 and R2 is highly energy demanding with a kinetic barrier of 1.15 eV and 2.59 eV, respectively. Since the hydrogen cannot be transferred to the α- or β-position atom directly from the surface, due to steric hindrance, a concerted reaction mechanism is considered in these reactions. In the concerted process, a surface hydrogen migrates to the aromatic ring, and simultaneously a hydrogen from the ring shifts to the α- or β-position. Initially, the high activation barrier was suspected as arising due to hydrogen diffusion on the surface; however, R49 (Table 1), which describes the diffusion and association of hydrogen atoms to form molecular hydrogen on the surface, shows that the hydrogen diffusion is barrierless on the β-Mo2C(100) surface. Therefore, the activation energy observed is associated with the second step in the concerted process, i.e., the migration of H from the aromatic ring to the α- or β-position.
| Rxn. No | Reactions | E a (eV) | ΔE (eV) | 500 K | 600 K | 700 K | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A 0 | k f (s−1) | ΔG‡ (eV) | A 0 | k f (s−1) | ΔG‡ (eV) | A 0 | k f (s−1) | ΔG‡ (eV) | ||||
| a Reactions with transition state calculated by the complementary approach to NEB. | ||||||||||||
| Ads | GUA + * ≫ GUA* | — | −4.67 | 1.30 × 104 | 4.19 × 10−3 | −0.05 | 1.18 × 104 | 4.46 × 10−4 | −0.04 | 1.10 × 104 | 6.45 × 10−5 | −0.04 |
| R1 | 1r* > TS1 > 1p* | 1.15 | 0.64 | 4.47 × 1013 | 1.78 × 105 | 0.26 | 4.46 × 1013 | 2.15 × 105 | 0.25 | 4.39 × 1013 | 2.50 × 105 | 0.25 |
| R2 | 2r > TS2 > 2p* | 2.59 | 0.86 | 8.18 × 1013 | 1.78 × 10−4 | 0.33 | 9.37 × 1013 | 2.35 × 10−4 | 0.33 | 1.05 × 1014 | 3.13 × 10−4 | 0.33 |
| R3a | GUA* > TS3 > 3p* | 1.04 | −0.69 | 4.03 × 1013 | 4.82 × 106 | 0.96 | 4.69 × 1013 | 6.33 × 106 | 0.95 | 5.34 × 1013 | 8.36 × 106 | 0.95 |
| R4 | GUA* > TS4 > 4p* | 0.90 | 0.59 | 7.62 × 1013 | 9.65 × 107 | 0.82 | 8.67 × 1013 | 1.32 × 108 | 0.81 | 9.60 × 1013 | 1.79 × 108 | 0.80 |
| R5 | GUA* > TS5 > 5p* | 1.02 | −0.49 | 2.26 × 1013 | 6.76 × 106 | 0.91 | 2.47 × 1013 | 7.09 × 106 | 0.91 | 2.70 × 1013 | 7.78 × 106 | 0.91 |
| R6 | GUA* > TS6 > 6p* | 1.44 | −2.29 | 1.41 × 1015 | 1.33 × 106 | 1.25 | 2.09 × 1015 | 3.51 × 106 | 1.22 | 2.87 × 1015 | 9.13 × 106 | 1.18 |
| R7 | GUA* > TS7 > 7p* | 0.62 | −0.65 | 1.21 × 1013 | 2.01 × 109 | 0.52 | 1.13 × 1013 | 1.56 × 109 | 0.54 | 1.07 × 1013 | 1.24 × 109 | 0.55 |
| R8 | 1p* > TS8 > 8p* | 0.75 | −0.46 | 2.83 × 1013 | 4.32 × 108 | 0.67 | 2.93 × 1013 | 4.59 × 108 | 0.67 | 3.03 × 1013 | 4.98 × 108 | 0.66 |
| R9 | 1p* > TS9 > 9p* | 0.37 | −2.05 | 2.77 × 1014 | 3.68 × 1012 | 0.26 | 3.31 × 1014 | 6.24 × 1012 | 0.24 | 3.79 × 1014 | 1.04 × 1013 | 0.22 |
| R10 | 2p* ≫ 10p* | — | −2.16 | 2.68 × 1013 | 9.58 × 1028 | −2.16 | 3.04 × 1013 | 1.23 × 1029 | −2.17 | 3.37 × 1013 | 1.58 × 1029 | −2.18 |
| R11 | 11r* > TS11 >11p* | 0.97 | −0.29 | 7.06 × 1013 | 2.13 × 107 | −0.03 | 8.24 × 1013 | 3.07 × 107 | −0.03 | 9.31 × 1013 | 4.33 × 107 | −0.04 |
| R12 | 12r* > TS12 > S26* | 1.16 | −0.29 | 6.48 × 1013 | 7.57 × 105 | −0.02 | 7.50 × 1013 | 1.08 × 106 | −0.02 | 8.38 × 1013 | 1.49 × 106 | −0.03 |
| R13 | S6* > TS13 > 13p* | 0.79 | −0.22 | 1.86 × 1015 | 8.08 × 108 | 0.88 | 4.53 × 1015 | 9.85 × 109 | 0.79 | 1.04 × 1016 | 1.19 × 1011 | 0.69 |
| R14 | S6* > TS14 > 14p* | 0.82 | −1.58 | 5.70 × 1014 | 3.63 × 108 | 0.86 | 1.24 × 1015 | 3.05 × 109 | 0.78 | 2.64 × 1015 | 2.63 × 1010 | 0.69 |
| R15 | S6* > TS15 > 15p* | 0.49 | −2.08 | 5.63 × 1014 | 2.43 × 1010 | 0.61 | 1.20 × 1015 | 2.16 × 1011 | 0.52 | 2.48 × 1015 | 1.92 × 1012 | 0.43 |
| R16 | 16r* > TS16 > 16p* | 1.81 | 1.43 | 1.94 × 1014 | 8.80 × 101 | −0.03 | 2.30 × 1014 | 1.43 × 102 | −0.03 | 2.61 × 1014 | 2.27 × 102 | −0.03 |
| R17 | 17r* > TS17 > 17p* | 2.46 | 0.52 | 1.32 × 1013 | 1.11 × 10−4 | 0.58 | 1.33 × 1013 | 9.74 × 10−5 | 0.57 | 1.33 × 1013 | 8.60 × 10−5 | 0.57 |
| R18 | S7* > TS18 > 18p* | 1.03 | −1.19 | 8.30 × 1013 | 1.44 × 107 | 0.94 | 9.39 × 1013 | 2.00 × 107 | 0.93 | 1.04 × 1014 | 2.80 × 107 | 0.91 |
| R19 | S8* > TS19 > 19p* | 0.39 | −1.99 | 7.42 × 1013 | 5.60 × 1011 | 0.29 | 8.75 × 1013 | 7.82 × 1011 | 0.28 | 1.00 × 1014 | 1.09 × 1012 | 0.27 |
| R20 | S8* > TS20 > 20p* | 0.78 | −0.54 | 3.66 × 1013 | 7.88 × 108 | 0.65 | 4.12 × 1013 | 9.15 × 108 | 0.65 | 4.59 × 1013 | 1.10 × 109 | 0.64 |
| R21 | S9* ≫ 21p* | — | −1.94 | 1.06 × 1013 | 2.45 × 1027 | −1.99 | 1.15 × 1013 | 2.49 × 1027 | −1.99 | 1.23 × 1013 | 2.57 × 1027 | −1.99 |
| R22 | S11* > TS22 > 22p* | 1.02 | −0.52 | 2.57 × 1013 | 8.67 × 106 | 0.90 | 2.85 × 1013 | 9.34 × 106 | 0.90 | 3.14 × 1013 | 1.05 × 107 | 0.90 |
| R23 | S18* ≫ 23p* | — | −2.05 | 2.00 × 1013 | 2.97 × 1028 | −2.11 | 2.18 × 1013 | 3.33 × 1028 | −2.11 | 2.35 × 1013 | 3.73 × 1028 | −2.11 |
| R24 | 16p* > TS24 > 24p* | 0.18 | −1.12 | 6.01 × 1013 | 9.12 × 1012 | 0.11 | 6.83 × 1013 | 1.22 × 1013 | 0.10 | 7.60 × 1013 | 1.65 × 1013 | 0.09 |
| R25 | 25r* ≫ 25p* | — | 2.98 | 1.58 × 1013 | 1.73 × 10−8 | 0.47 | 1.55 × 1013 | 1.54 × 10−8 | 0.47 | 1.52 × 1013 | 1.37 × 10−8 | 0.46 |
| R26 | 17p* > TS26 > 26p* | 0.09 | −1.87 | 1.64 × 1013 | 4.40 × 1012 | 0.08 | 1.68 × 1013 | 4.56 × 1012 | 0.08 | 1.71 × 1013 | 4.73 × 1012 | 0.08 |
| R27 | 27r* > TS27 > S19* | 1.15 | 0.23 | 7.30 × 1013 | 9.72 × 105 | −0.65 | 8.63 × 1013 | 1.44 × 106 | −0.65 | 9.81 × 1013 | 2.07 × 106 | −0.66 |
| R28 | S12* ≫ 28p* | — | −2.31 | 1.87 × 1013 | 2.54 × 1030 | −2.38 | 2.09 × 1013 | 2.86 × 1030 | −2.38 | 2.30 × 1013 | 3.23 × 1030 | −2.38 |
| R29 | 29r* > TS29 > 25p* | 1.22 | 3.61 | 1.07 × 1013 | 5.05 × 105 | 0.24 | 1.20 × 1014 | 7.15 × 105 | 0.24 | 1.30 × 1014 | 9.89 × 105 | 0.23 |
| R30 | 30r* > TS30 > S26* | 2.19 | 1.41 | 5.97 × 1013 | 3.00 × 10−2 | −0.02 | 6.86 × 1013 | 4.11 × 10−2 | −0.03 | 7.64 × 1013 | 5.54 × 10−2 | −0.03 |
| R31 | 25p* ≫ 31p* | — | −4.47 | 1.96 × 1013 | 4.79 × 1044 | −4.36 | 2.19 × 1013 | 6.78 × 1044 | −4.37 | 2.40 × 1013 | 9.44 × 1044 | −4.39 |
| R32 | 32r* > TS32 > S7* | 2.28 | 1.69 | 1.89 × 1014 | 2.99 × 10−2 | 0.00 | 2.25 × 1014 | 4.95 × 10−2 | −0.01 | 2.58 × 1014 | 7.98 × 10−2 | −0.01 |
| R33a | S26* > TS33 > 33p* | 1.50 | −0.73 | 7.27 × 1013 | 6.05 × 103 | 1.40 | 8.62 × 1013 | 8.53 × 103 | 1.39 | 9.91 × 1013 | 1.20 × 104 | 1.38 |
| R34 | 34r* > TS34 > 34p* | 2.06 | 0.57 | 1.66 × 1014 | 5.05 × 10 | 0.89 | 1.98 × 1014 | 7.46 × 10 | 0.88 | 2.29 × 1014 | 1.12 × 101 | 0.87 |
| R35 | 35r* > TS35 > 35p* | 0.75 | −0.5 | 5.26 × 1013 | 5.33 × 108 | 0.46 | 6.09 × 1013 | 7.34 × 108 | 0.45 | 6.81 × 1013 | 9.88 × 108 | 0.45 |
| R36 | 34p* > TS36 >36p* | 0.5 | −1.94 | 1.83 × 1013 | 6.63 × 109 | 0.48 | 1.84 × 1013 | 6.39 × 109 | 0.48 | 1.84 × 1013 | 6.17 × 109 | 0.48 |
| R37 | 37r* > TS37 >  |
0.72 | 0.14 | 1.90 × 1013 | 1.08 × 108 | 0.27 | 1.92 × 1013 | 1.16 × 108 | 0.27 | 1.93 × 1013 | 1.22 × 108 | 0.26 |
| R38 | 38r* > TS38 >  |
1.56 | 1.25 | 7.62 × 1013 | 7.04 × 102 | 0.50 | 8.21 × 1013 | 9.37 × 102 | 0.49 | 8.62 × 1013 | 1.21 × 103 | 0.48 |
| R39 | 39r* > TS39 > H2O* | 2.15 | 1.65 | 9.33 × 1013 | 1.10 × 10−1 | 0.02 | 1.08 × 1014 | 1.58 × 10−1 | 0.02 | 1.21 × 1014 | 2.25 × 10−1 | 0.01 |
| R40 | 40r* > TS40 >  |
0.85 | 0.17 | 5.36 × 1013 | 3.87 × 107 | 0.12 | 5.91 × 1013 | 5.33 × 107 | 0.11 | 6.32 × 1013 | 7.04 × 107 | 0.10 |
| R41 | 41r* > TS41 > CH3OH* | 2.45 | 2.14 | 3.77 × 1014 | 6.27 × 10−3 | 0.04 | 4.75 × 1014 | 1.17 × 10−2 | 0.00 | 5.66 × 1014 | 2.14 × 10−2 | −0.04 |
| R42 | S26* ≫ phenol + * | — | 4.45 | 8.91 × 1024 | 3.49 × 101 | 3.25 | 8.24 × 1024 | 2.25 × 103 | 3.00 | 7.41 × 1024 | 1.43 × 105 | 2.74 |
| R43 | 16p* ≫ catechol + * | — | 4.26 | 9.24 × 1024 | 6.63 × 102 | 3.08 | 8.24 × 1024 | 4.40 × 104 | 2.82 | 7.20 × 1024 | 2.87 × 106 | 2.56 |
| R44 | S29* ≫ benzene + * | — | 4.06 | 2.18 × 1022 | 1.18 × 10 | 3.09 | 1.79 × 1022 | 2.54 × 101 | 2.90 | 1.46 × 1022 | 5.49 × 102 | 2.70 |
| R45 |
 ≫ CH4 + * ≫ CH4 + * |
— | 0.38 | 1.19 × 1019 | 5.16 × 1021 | −0.37 | 1.04 × 1019 | 4.18 × 1022 | −0.50 | 9.06 × 1018 | 3.51 × 1023 | −0.64 |
| R46 | CH3OH* ≫ CH3OH + * | — | 1.18 | 1.95 × 1022 | 1.31 × 1021 | 0.16 | 1.98 × 1022 | 3.82 × 1022 | −0.04 | 1.94 × 1022 | 1.13 × 1024 | −0.25 |
| R47 | H2O* ≫ H2O + * | — | 1.07 | 4.19 × 1020 | 6.31 × 1018 | 0.25 | 4.73 × 1020 | 1.22 × 1020 | 0.08 | 5.08 × 1020 | 2.33 × 1021 | −0.09 |
| R48 |
 ≫ H2 + * ≫ H2 + * |
— | 0.79 | 4.91 × 1018 | 5.82 × 1016 | 0.27 | 6.88 × 1018 | 8.09 × 1017 | 0.13 | 8.82 × 1018 | 1.08 × 1019 | −0.01 |
| R49 | H* + H* > TS49 >  |
— | 0.00 | 1.57 × 1013 | 1.38 × 1013 | 0.01 | 1.64 × 1013 | 1.55 × 1013 | 0.00 | 1.72 × 1013 | 1.76 × 1013 | 0.00 |
| R50 | s19* > TS50 > 37p* | 1.59 | −0.89 | 8.27 × 1013 | 1.21 × 103 | 1.51 | 9.67 × 1013 | 1.71 × 103 | 1.49 | 1.10 × 1014 | 2.41 × 103 | 1.48 |
| R51 | 61r* > TS51 > OH* | 1.97 | 1.16 | 3.77 × 1013 | 4.39 × 10−1 | 1.94 | 4.23 × 1013 | 5.61 × 10−1 | 1.93 | 4.61 × 1013 | 7.02 × 10−1 | 1.92 |
The methoxy group of structure 8 undergoes further dehydrogenation in R20, with a reaction barrier of 0.78 eV, to give structure 16; however, structure 16 decomposes rapidly to structure 23 (1,2-benzoquinone) via R28 in a barrierless exothermic step with reaction energy of −2.31 eV. Kinetic rate simulations give a rate constant of ∼1030 s−1, suggesting that the decomposition reaction is very fast. The carbene (CH2) that separates from structure 16 in R28 sits over a fcc site on the surface with the lowest carbon coordination (i.e., zero); Nagai et al.63 reported similar behaviour for carbon monoxide (CO), with the strongest CO adsorption occurring at the carbon deficient site (i.e., no neighbouring C atoms in the subsurface layer) on the β-Mo2C surface; experimental studies also report the surface to be selective to the cleavage of the C–O bond.31,64,65
An oxygen atom of structure 23 (1,2-benzoquinone) can be hydrogenated to produce structure 28 via R32, though a high energy barrier is calculated (Ea = 2.28 eV) and the rate constant for this conversion is low (∼10−2 s−1). Structure 28 can be formed from two more pathways: (i) the methyl radical from the guaiacol can directly cleave (R6) to form structure 7 (ketophenol) (which is equivalent to structure 28); or (ii) the methoxy group of guaiacol can lose a hydrogen (R5), to give structure 6, followed by the dissociation of a CH2 moiety (R15) to again produce structure 7/28 (ketophenol). The conversion via R6 is 0.42 eV more energy demanding than R5, and kinetically slower than the R5 and R15 (Table 1). Therefore, the formation of structure 7/28 (ketophenol) will occur predominantly via R5 and R15. The preference of dehydrogenation instead of deoxygenation in the methoxy group of guaiacol has also been reported by Lee et al.55 over a Pt (111) surface, with Ea = 0.75 eV for R5 with the help of Brønsted–Evans–Polanyi (BEP) correlation.
From structure 7/28 (ketophenol), there can be three possible reduction routes: in R16, hydrogenation yields structure 13, catechol, with an activation energy of 1.81 eV; in R17, the aromatic ring is hydrogenated with an activation energy of 2.46 eV; and in R18, the hydroxyl group is cleaved in a reaction with activation barrier of 1.03 eV. The kinetic rate modelling returns rate constants for R16 of ∼101 s−1 and for R18 of ∼107 s−1, which suggests that the formation of catechol from guaiacol is very slow; furthermore, the high barrier for R17 makes it unlikely. Thus, the reaction process can be concluded as proceeding via R27, with an energy barrier of 1.15 eV, to form structure 19/22, a phenoxyl radical.
The phenoxyl radical (structure 19/22) can also be formed via R2 and R3; the hydrogenation of the β-carbon of guaiacol (R2) has an activation energy of 2.59 eV, and is kinetically very slow (∼10−4 s−1), whereas R3 (condensation) has a barrier of only 1.04 eV and is kinetically faster. Thus, structure 4 will be formed and converted to structure 11, anisole, via re-hydrogenation of the aromatic ring (R11). Further dehydrogenation of the methoxy group (R22) requires only 1.02 eV of activation energy, which results in an unstable structure 18 that degrades to phenoxyl in a barrier-less exothermic step (ΔE = −2.05 eV).
From the cyclohexadienone, hydrogenation (R30) can yield phenol (Structure 10/26) in a very slow and energy demanding step (Ea = 2.19 eV). The prohibitively high reaction barrier in R30 is in contradiction to experimental studies, which report high selectivity and quick appearance of phenol over pure and supported molybdenum carbides.18,60,66 Therefore, phenol most likely forms by alternative route(s), of which two routes have been considered herein. One possibility is the direct methoxylation of guaiacol (R4, Ea = 0.90 eV) to give structure 5/20, which is then followed by hydrogenation (R12, Ea = 1.16 eV). The other possibility considered is the hydrogenation of guaiacol (R1) to form structure 2, which has an activation energy of 1.15 eV. The methoxy group can then directly cleave from structure 2 via R9, with a low activation energy of 0.37 eV, producing phenol. R9 is kinetically very favorable, with a rate constant of 3.68 × 1012 s−1 calculated for 500 K; however, structure 2 can also convert to structure 9 through an activation energy of 0.75 eV, with the unstable CH2 moiety in structure 9 leading to exothermic degradation (R21) to structure 17. The formation of structure 17 via R21 is kinetically favorable (2.45 × 1027 s−1 at 500 K) as the CH2 radical dissociates, with a thermodynamic energy change of −1.94 eV. Hydrogenation of structure 17 to structure 21/24 (R29, Ea = 1.22 eV) results in a molecule that decomposes in a highly exothermic step (R31, ΔE = −4.47 eV) to form structure 26, which is phenol. Alternatively, cyclohexadienone can be deoxygenated directly via R50 to obtain structure 25 with 1.59 eV of energy. Further hydrogenation of structure 25 yields benzene (R35).
Once formed, the desorption of phenol from the surface is kinetically slow (3.49 × 101 s−1 at 500 K) and energy demanding (Edes = 4.45 eV), which means it would be likely to accumulate on the surface. The adsorption energy, which can be calculated as the negative of the desorption energy, suggests that the adsorption of phenol on the surface is at least 2 eV stronger than that observed over transition metals.54,58,59,67,68 Thus, the accumulated phenol could convert further to benzene, which is considered further herein via two mechanisms. One possibility is the cleavage of the –OH group (R33) with an energy barrier of 1.50 eV, while alternatively the phenol α-position can be hydrogenated with an energy barrier of 2.06 eV to form structure 27 (R34). Kinetically, R34 is much slower than R33, with rate constants differing by ∼103 s−1. Therefore, the reaction will proceed via R33 to form structure 25, which will then be hydrogenated to form structure 29, benzene. The preference in our calculations towards dehydroxygenation of phenol rather than hydrogenation is in strong agreement with observations involving noble metal catalysts,28,53,69 and in non-catalytic works.70
The several smaller radicals formed during the outlined reaction mechanism have been considered, as they will react together to form stable entities and desorb from the surface. In our work, R37 and R38 describe the formation of methane from CH2; similarly, R40 and R41 describe the formation of methanol from OCH2; and R39 describes the formation of water from OH and H. To comprehensively complete the catalytic cycle, R37 to R49 are used in the microkinetic modelling.
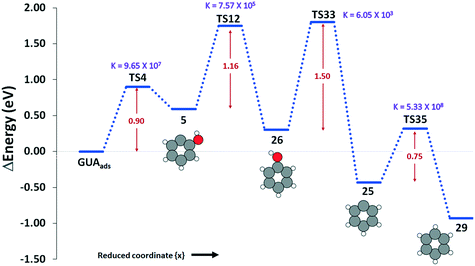
Overall, our results show that the most favorable pathway for the formation of benzene is via cleavage of the methoxy group in guaiacol (R4) to give structure 5/20, which is then hydrogenated (R12) to give phenol (Fig. 3). The hydroxyl group of the phenol is then cleaved (R33) with an energy barrier of 1.50 eV to yield structure 25, which is hydrogenated to give benzene. All the reactions become faster with increase in temperature, except the guaiacol adsorption on the surface.
To further summarise our findings, the overall activation energy for the formation of different important intermediates was calculated, as shown in Table 2. The formation of benzene via a reaction process of R4–R12–R33–R35 gives an activation energy of 1.75 eV, where reaction 33 is the rate limiting step with an activation energy of 1.50 eV. In the formation of catechol via reaction R5–R15–R16, the rate controlling step is reaction R5, and the overall activation energy for the conversion is 1.02 eV. The formation of anisole via reaction R3–R11 presents an overall barrier of 1.04 eV, which is associated with the dehydroxylation of guaiacol in reaction R3. Finally, the conversion of guaiacol to phenol is most feasible via reaction R1–R9 with an overall activation barrier of 1.15 eV during the hydrogenation of the adsorbed guaiacol.
| Overall reaction | Considered path | Activation energy (eV) | Pre-exponential factor (s−1) |
|---|---|---|---|
| Guaiacol → benzene | R4–R12–R33–R35 | 1.75 | 6.48 × 1013 |
| Guaiacol → catechol | R5–R15–R16 | 1.02 | 2.26 × 1013 |
| Guaiacol → anisole | R3–R11 | 1.04 | 4.03 × 1013 |
| Guaiacol → phenol | R1–R9 | 1.15 | 4.47 × 1013 |
3.2. Microkinetic modelling
Microkinetic modelling of the reaction network described in section 3.1 has been performed, considering specifically a batch reactor model at temperatures (T) ranging from 500 K to 700 K. The rate constants obtained from the thermochemical analyses were used to write the rate equation for 192 elementary reactions (Table S4, ESI†), and the set of coupled ordinary differential equations was solved. The initial ratio of hydrogen and guaiacol was set to unity, and in large excess with respect to the number of surface sites. The reaction profile was studied for the duration of 1 s from the initialization of the reaction (i.e. t = 0 s). At the atomic level in the DFT simulations, the reactions occur very quickly due to the absence of any heat and mass transfer resistance; furthermore, since the rate constants are first order (s−1), and because the magnitudes of the rate constants are much higher than the time scale considered herein, the total time considered in the study is sufficient to model the system.As the kinetics of formation of smaller species like water, methanol and methane are much higher than the kinetics of the formation of aromatic compounds, it is observed that methane, water, methanol and vacant sites cover 99% of the catalyst surface. The aromatic species like catechol, phenol and others, on the other hand, were present in very low coverage (<1%) at all times. The formation of the small species (water, methanol and methane) and the resultant loss in the carbon balance due to their difficult condensation has also been reported in experimental works.71 Moreover, such low coverage of the species of interest during the microkinetic modelling of guaiacol is not unique28 and, as the observed trends fairly representant the reactivity on the surface of the catalyst in DFT studies, they can be relied upon for insights into the surface reaction mechanism.
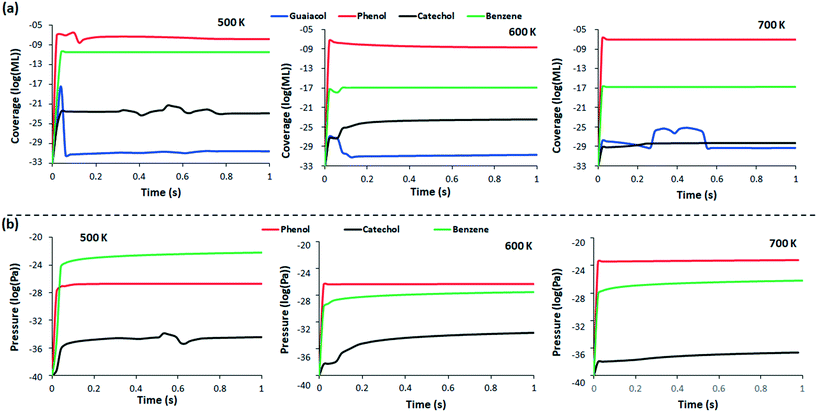
At 500 K, the concentration of guaiacol on the surface increases steeply at 0.02 s (Fig. 4), as the guaiacol is adsorbed on the surface, to reach 10−18 ML (monolayer). During the same time interval, the concentration of surface bound phenol increases to about 1010 times the concentration of the adsorbed guaiacol, suggesting that a large fraction of guaiacol immediately converts to phenol upon adsorption. The quick reaction occurs because the rate of formation of phenol is of the order 1012 s−1 in reaction 9 (Table 1), which leads to such high concentration of phenol forming in a short time interval. A corresponding increase of phenol is also observed in the gas phase, rising to 8.59 × 10−28 Pa in 0.02 s and maintaining a steady state thereafter. Since the catechol conversion kinetics competes with phenol formation, the catechol formation rate increases, to 5.85 × 10−23 ML at 0.32 s, while the phenol conversion attains a steady state (1.99 × 10−27 ML) after 0.18 s. Hydrogenation of phenol produces benzene, which appears on the surface in a lower concentration (3.39 × 10−11 ML) as the kinetics of reaction 33 and 34 are much slower than phenol formation. As more catechol, phenol and benzene are produced, the concentration of guaiacol declines to 4.38 × 10−32 ML at 0.06 s; thereafter, the concentration of guaiacol starts to decrease steadily by 0.5 × 10−1 ML per 0.01 s. However, as the smaller species like methanol and methane desorb from the surface due to fast kinetics (Table S4†), a slight increase in the production of catechol on the surface is observed from 0.30 s to 0.80 s. In the same duration, the concentration of catechol in gas phase increases by 10 times due to increased surface desorption. Thereafter, all species achieve steady state.
At 600 K, the concentration profile of all species exhibits less changes than at 500 K, due to the changes in the rate constants of all the reactions. Similar to 500 K, the concentration of phenol rises above all species at 0.02 s; however, the coverage (5.28 × 10−8 ML) is marginally lower than at 500 K. The lower guaiacol adsorption rate is because the rate of adsorption decreases with increase in temperature. As less guaiacol adsorbs to the surface, the concentration of products formed is also lower; at 0.02 s, guaiacol coverage is slightly elevated to 7.95 × 10−28 ML, which then slowly decreases by the order of 104 to achieve steady state at 0.30 s. The concentration of benzene is 4.09 × 10−18 ML at 0.02 s, due to quick phenol decomposition, but the concentration falls thereafter as the selectivity shifts towards catechol formation. After 0.08 s, the concentration of catechol starts to rise, coupled with a further decrease in the guaiacol concentration; the gas phase profile shows fluctuations in the benzene concentration at this time, suggesting that the rate of benzene desorption is competitive to the rate of formation of benzene on the surface. The concentration of catechol in gas phase has an increasing rate after 0.10 s, as a consequence of the increased formation on the surface. After 0.20 s, all the species start to attain steady state with the gas phase profiles of all products showing a steady marginal increase in production of value-added products after 0.5 s.
When the reaction is considered at 700 K, the concentration profile of all the compounds reach steady state very quickly. At 0.02 s, the concentration of guaiacol is expected to be much lower than at T = 500 or 600 K, due to decrease in the guaiacol adsorption rate constant (6.45 × 10−5 s−1); however, the concentration is calculated as 1.26 × 10−28 ML, which is only marginally lower than at 600 K. The higher surface coverage is because the reaction rate of almost all the reactions considered in the kinetic model increased at 700 K, leading to faster formation of products, and thus, faster product desorption from the surface. The quicker rate of reaction recreates vacant surface sites in a shorter time span than at lower T, and leads to a higher guaiacol adsorption. The higher product concentration observed in the gas phase at 0.02 s for 700 K, when compared to lower T, is the indicator of the quick desorption.
From t = 0 to t = 0.26 s, the concentration profile of guaiacol increases sharply to the maximum, and then declines steadily to 5.95 × 10−30 ML. After 0.26 s, a steady state is maintained until 0.38 s, from which time more products are desorbed from the surface, freeing surface sites and subsequently resulting in higher phenol, catechol and benzene formation. Further analysis of the selectivity of products shows that phenol will be the most likely product, with over 99% selectivity at all times, and this is consistent at all temperatures. The concentration of other products is very low in comparison, over the surface and in the gas phase. In the literature,72 high selectivity of benzene (35%) followed by phenol (30%) is reported among all other aromatic/cyclic products over Mo2C at 623 K and 27.48 bar. Blanco et al.73 report over 65% selectivity for phenol at 50 bar pressure and 623 K temperature over activated carbon supported Mo, which also has strong similarities to our modelled reaction process. The high hydrogen pressure in the experimental work could be the likely reason for the reported high selectivity of the fully hydrogenated benzene over phenol. Tran et al.71 also report phenol to desorb quickly after its formation on the same surface without undergoing further conversion. As the partial pressure of hydrogen is 0.5 in our study, a higher selectivity of phenol is obtained instead of full hydrogenation to benzene.
To determine the rate controlling step for the formation of each product in the gas phase, the degree of rate control was also analysed by the method proposed by Campbell,74 where the forward rate constants of each reaction is perturbed by 0.1% while keeping the equilibrium constant fixed, and the changes in the conversion of products are analysed. The degree of rate control for reaction i (XRC,i) was calculated as:
 | (3) |
The TPD model (Fig. 5) shows that the desorption of benzene occurs near 450 K at all coverages, after it is produced from phenol. Change in concentration of benzene has been reported at temperatures above 250 K for a different surface (Pt and Pt3Sn), at similar coverage,75 whilst benzene is known to desorb at temperatures as low as 150 K from graphene.76 Therefore, it is likely that the carbon-liking metal terminated surface investigated here binds the benzene strongly to the surface.77 Phenol, on the other hand, stays on the surface till 600 K and starts desorbing thereafter. The desorption of phenol is known to occur at above 450 K over other catalyst material surfaces.78–80 At high coverage (70%), the desorption of benzene from the surface is large, as more benzene is formed on the surface from phenol. At the same coverage, catechol desorption is also observed in large proportion after 500 K, due to its formation and accumulation on the surface. Further increasing the guaiacol coverage (100%) is detrimental to reaction rates, with the desorption rate of all species reduced due to lack of sites for the generation of species on the surface.
4. Conclusions
The HDO of guaiacol was studied over the (100) β-Mo2C surface. A network of reaction pathways was proposed to consider the mechanistic aspects of producing benzene from guaiacol, proceeding via phenol and catechol intermediates. The activation barriers and reaction energies were calculated using density functional theory. Through thermochemical analysis, increases in temperature were observed as being unfavorable for the surface adsorption of guaiacol, and the most favourable pathway for guaiacol HDO is initiated with demethoxylation, which is then followed by hydrogenation to yield phenol. From phenol, the most favourable pathway for benzene formation is initiated with dehydroxylation, followed by hydrogenation.Overall, the hydrogenation of molecules like guaiacol and phenol were observed to have higher energy barriers than the cleavage of functional groups. The carbon atoms of the functional group of the molecule, which were sp2 or sp hybridized, were also noted as dissociating spontaneously, with minimum energy barriers, and the dissociated moieties occupy carbon deficient sites on the surface.
Complementing the thermochemical analysis, microkinetic modelling of the system shows that although the adsorption of guaiacol decreases with increasing temperature, higher temperatures are more favorable for further upgrading of guaiacol into valuable products such as phenol and benzene. Simulation of temperature programmed desorption shows that the optimum surface coverage of guaiacol is ∼70%, as the change in the concentration of all the products was highest in the gas phase.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thanks Igor Kowalec for technical discussions. KA is a Commonwealth Scholar, funded by the UK government. The authors thank the U. K. High Performance Computing “Materials Chemistry Consortium” (EP/R029431/1) for access to the ARCHER National Supercomputing Service, Supercomputing Wales for access to the Hawk HPC facility, which is part-funded by the European Regional Development Fund via the Welsh Government, and GW4 and the UK Met Office for access to the Isambard UK National Tier-2 HPC Service (EP/P020224/1). AJL acknowledges funding by the UKRI Future Leaders Fellowship program (MR/T018372/1).References
- A. V. Bridgwater and G. V. C. Peacocke, Renewable Sustainable Energy Rev., 2000, 4, 1–73 CrossRef CAS.
- A. R. K. Gollakota, M. Reddy, M. D. Subramanyam and N. Kishore, Renewable Sustainable Energy Rev., 2016, 58, 1543–1568 CrossRef CAS.
- H. Wang, J. Male and Y. Wang, ACS Catal., 2013, 3, 1047–1070 CrossRef CAS.
- G. W. Huber, I. Sara and A. Corma, Chem. Rev., 2006, 2, 4044–4098 CrossRef PubMed.
- Y.-C. Lin and G. W. Huber, Energy Environ. Sci., 2009, 2, 68–80 RSC.
- P. M. Mortensen, J. D. Grunwaldt, P. A. Jensen, K. G. Knudsen and A. D. Jensen, Appl. Catal., A, 2011, 407, 1–19 CrossRef CAS.
- J. Han, J. Duan, P. Chen, H. Lou and X. Zheng, Adv. Synth. Catal., 2011, 353, 2577–2583 CrossRef CAS.
- H. Xin, A. Vojvodic, J. Voss, J. K. Nørskov and F. Abild-Pedersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115114 CrossRef.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- E. Toyoda, R. Jinnouchi, T. Hatanaka, Y. Morimoto, K. Mitsuhara, A. Visikovskiy and Y. Kido, J. Phys. Chem. C, 2011, 115, 21236–21240 CrossRef CAS.
- Y. Zhou, Z. Zhou, R. Shen, R. Ma, Q. Liu, G. Cao and J. Wang, Energy Storage Mater., 2018, 13, 189–198 CrossRef.
- F. Ando, T. Tanabe, T. Gunji, S. Kaneko, T. Takeda, T. Ohsaka and F. Matsumoto, ACS Appl. Nano Mater., 2018, 1, 2844–2850 CrossRef CAS.
- H. Tao, S. Liu, J.-L. Luo, P. Choi, Q. Liu and Z. Xu, J. Mater. Chem. A, 2018, 6, 9650–9656 RSC.
- J. Zhou, W. An, Z. Wang and X. Jia, Catal. Sci. Technol., 2019, 9, 4314–4326 RSC.
- Z. Chen, Y. Song, J. Cai, X. Zheng, D. Han, Y. Wu, Y. Zang, S. Niu, Y. Liu, J. Zhu, X. Liu and G. Wang, Angew. Chem., Int. Ed., 2018, 57, 5076–5080 CrossRef CAS PubMed.
- J. A. van Bokhoven and J. T. Miller, J. Phys. Chem. C, 2007, 111, 9245–9249 CrossRef CAS.
- F. Morteo-Flores, J. Engel and A. Roldan, Philos. Trans. R. Soc., A, 2020, 378, 20200056 CrossRef CAS PubMed.
- R. Moreira, E. Ochoa, J. L. Pinilla, A. Portugal and I. Suelves, Catalysts, 2018, 8(4), 127 CrossRef.
- R. N. Olcese, M. Bettahar, D. Petitjean, B. Malaman, F. Giovanella and A. Dufour, Appl. Catal., B, 2012, 115–116, 63–73 CrossRef CAS.
- T. Nimmanwudipong, R. C. Runnebaum, D. E. Block and B. C. Gates, Energy Fuels, 2011, 25, 3417–3427 CrossRef CAS.
- J. Sun, A. M. Karim, H. Zhang, L. Kovarik, X. S. Li, A. J. Hensley, J.-S. McEwen and Y. Wang, J. Catal., 2013, 306, 47–57 CrossRef CAS.
- D. C. Elliott and T. R. Hart, Energy Fuels, 2009, 23, 631–637 CrossRef CAS.
- C. Zhao, J. He, A. A. Lemonidou, X. Li and J. A. Lercher, J. Catal., 2011, 280, 8–16 CrossRef CAS.
- A. Gutierrez, R. K. Kaila, M. L. Honkela, R. Slioor and A. O. I. Krause, Catal. Today, 2009, 147, 239–246 CrossRef CAS.
- Y.-C. Lin, C.-L. Li, H.-P. Wan, H.-T. Lee and C.-F. Liu, Energy Fuels, 2011, 25, 890–896 CrossRef CAS.
- V. N. Bui, G. Toussaint, D. Laurenti, C. Mirodatos and C. Geantet, Catal. Today, 2009, 143, 172–178 CrossRef CAS.
- M. A. González-Borja and D. E. Resasco, Energy Fuels, 2011, 25, 4155–4162 CrossRef.
- J. Lu, S. Behtash, O. Mamun and A. Heyden, ACS Catal., 2015, 5, 2423–2435 CrossRef CAS.
- R. Ma, K. Cui, L. Yang, X. Ma and Y. Li, Chem. Commun., 2015, 51, 10299–10301 RSC.
- A. L. Jongerius, R. W. Gosselink, J. Dijkstra, J. H. Bitter, P. C. A. Bruijnincx and B. M. Weckhuysen, ChemCatChem, 2013, 5, 2964–2972 CrossRef CAS.
- M. Siaj, C. Reed, S. T. Oyama, S. L. Scott and P. H. McBreen, J. Am. Chem. Soc., 2004, 126, 9514–9515 CrossRef CAS PubMed.
- B. Martínez, F. Viñes, P. H. McBreen and F. Illas, J. Catal., 2021, 393, 381–389 CrossRef.
- T. Epicier, J. Dubois, C. Esnouf, G. Fantozzi and P. Convert, Acta Metall., 1988, 36, 1903–1921 CrossRef CAS.
- T. Wang, X. Tian, Y. Yang, Y.-W. Li, J. Wang, M. Beller and H. Jiao, Surf. Sci., 2016, 651, 195–202 CrossRef CAS.
- K. Xiong, W. Yu, D. G. Vlachos and J. G. Chen, ChemCatChem, 2015, 7, 1402–1421 CrossRef CAS.
- L. M. Falicov and G. A. Somorjai, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 2207–2211 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- K. Agrawal, A. Roldan, N. Kishore and A. J. Logsdail, Catal. Today, 2022, 384, 197–208 CrossRef.
- J. Nocedal and S. J. Wright, in Numerical Optimization, Springer New York, 2nd edn, 2006, pp. 66–100 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- J. A. Garrido Torres, P. C. Jennings, M. H. Hansen, J. R. Boes and T. Bligaard, Phys. Rev. Lett., 2019, 122, 156001 CrossRef CAS PubMed.
- A. Roldan, 2021, https://github.com/Roldan-Group/Kinetics.
- X. Lu, J. Zhang, W.-K. Chen and A. Roldan, Nanoscale Adv., 2021, 3, 1624–1632 RSC.
- I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, 2003 Search PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- K. W. Kolasinski, Surface Science, Foundations of Catalysis and Nanoscience, John Wiley & Sons, Ltd, Chichester, UK, 3rd edn, 2012 Search PubMed.
- J. Lu and A. Heyden, J. Catal., 2015, 321, 39–50 CrossRef CAS.
- A. M. Verma and N. Kishore, J. Mol. Model., 2018, 24, 254 CrossRef PubMed.
- K. Lee, G. H. Gu, C. A. Mullen, A. A. Boateng and D. G. Vlachos, ChemSusChem, 2015, 8, 315–322 CrossRef CAS PubMed.
- H. Fang, A. Roldan, C. Tian, Y. Zheng, X. Duan, K. Chen, L. Ye, S. Leoni and Y. Yuan, J. Catal., 2019, 369, 283–295 CrossRef CAS.
- C. Chiu, A. Genest, A. Borgna and N. Rösch, ACS Catal., 2014, 4, 4178–4188 CrossRef CAS.
- S. J. Carey, W. Zhao, Z. Mao and C. T. Campbell, J. Phys. Chem. C, 2019, 123, 7627–7632 CrossRef CAS.
- J. Lee, S. Ryu and S. K. Kim, Surf. Sci., 2001, 481, 163–171 CrossRef CAS.
- J. Chang, T. Danuthai, S. Dewiyanti, C. Wang and A. Borgna, ChemCatChem, 2013, 5, 3041–3049 CrossRef CAS.
- V. N. Bui, D. Laurenti, P. Afanasiev and C. Geantet, Appl. Catal., B, 2011, 101, 239–245 CrossRef CAS.
- M. V. Bykova, D. Y. Ermakov, V. V. Kaichev, O. A. Bulavchenko, A. A. Saraev, M. Y. Lebedev and V. Yakovlev, Appl. Catal., B, 2012, 113–114, 296–307 CrossRef CAS.
- M. Nagai, H. Tominaga and S. Omi, Langmuir, 2000, 16, 10215–10220 CrossRef CAS.
- J. R. McManus and J. M. Vohs, Surf. Sci., 2014, 630, 16–21 CrossRef CAS.
- W. S. Lee, Z. Wang, R. J. Wu and A. Bhan, J. Catal., 2014, 319, 44–53 CrossRef CAS.
- Z. Cai, F. Wang, X. Zhang, R. Ahishakiye, Y. Xie and Y. Shen, Mol. Catal., 2017, 441, 28–34 CrossRef CAS.
- F. Maldonado, L. Villamagua and R. Rivera, J. Phys. Chem. C, 2019, 123, 12296–12304 CrossRef CAS.
- A. M. Verma and N. Kishore, R. Soc. Open Sci., 2017, 4, 170650 CrossRef PubMed.
- M. Saleheen, A. M. Verma, O. Mamun, J. Lu and A. Heyden, Catal. Sci. Technol., 2019, 9, 6253–6273 RSC.
- K. Agrawal, A. M. Verma and N. Kishore, ChemistrySelect, 2019, 4, 6013–6025 CrossRef CAS.
- C.-C. Tran, O. Mohan, A. Banerjee, S. H. Mushrif and S. Kaliaguine, Energy Fuels, 2020, 34, 16265–16273 CrossRef CAS.
- C. C. Tran, Y. Han, M. Garcia-Perez and S. Kaliaguine, Catal. Sci. Technol., 2019, 9, 1387–1397 RSC.
- E. Blanco, C. Sepulveda, K. Cruces, J. L. García-Fierro, I. T. Ghampson and N. Escalona, Catal. Today, 2020, 356, 376–383 CrossRef CAS.
- C. T. Campbell, J. Catal., 2001, 204, 520–524 CrossRef CAS.
- B. M. Wong, G. Collinge, A. J. R. Hensley, Y. Wang and J.-S. McEwen, Prog. Surf. Sci., 2019, 94, 100538 CrossRef CAS.
- R. S. Smith and B. D. Kay, J. Phys. Chem. B, 2018, 122, 587–594 CrossRef PubMed.
- T. Mo, J. Xu, Y. Yang and Y. Li, Catal. Today, 2016, 261, 101–115 CrossRef CAS.
- E. Castillejos-López, D. M. Nevskaia, V. Muñoz and A. Guerrero-Ruiz, Carbon, 2008, 46, 870–875 CrossRef.
- B.-Q. Xu, T. Yamaguchi and K. Tanabe, Mater. Chem. Phys., 1988, 19, 291–297 CrossRef CAS.
- X. Xu and C. M. Friend, J. Phys. Chem., 1989, 93, 8072–8080 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available at DOI: 10.1039/d1cy01273h, including: Additional information is provided in a separate section containing details of the optimised configurations observed for all intermediates considered in the simulations, and the data derived from the microkinetic simulations. All structures calculated in this work have been uploaded to the NOMAD repository (DOI: 10.17172/NOMAD/2022.01.05-1). |
| This journal is © The Royal Society of Chemistry 2022 |