Open Access Article
Open Access ArticlePhotochemistry of transition metal carbonyls
James J.
Turner
*a,
Michael W.
George
 a,
Martyn
Poliakoff
a,
Martyn
Poliakoff
 a and
Robin N.
Perutz
a and
Robin N.
Perutz
 *b
*b
aSchool of Chemistry University of Nottingham, NG7 2RD, UK. E-mail: james.turner@nottingham.ac.uk
bDepartment of Chemistry, University of York, York, YO10 5DD, UK. E-mail: robin.perutz@york.ac.uk
First published on 16th June 2022
Abstract
The purpose of this Tutorial Review is to outline the fundamental photochemistry of metal carbonyls, and to show how the advances in technology have increased our understanding of the detailed mechanisms, particularly how relatively simple experiments can provide deep understanding of complex problems. We recall some important early experiments that demonstrate the key principles underlying current research, concentrating on the binary carbonyls and selected substituted metal carbonyls. At each stage, we illustrate with examples from recent applications. This review first considers the detection of photochemical intermediates in three environments: glasses and matrices; gas phase; solution. It is followed by an examination of the theory underpinning these observations. In the final two sections, we briefly address applications to the characterization and behaviour of complexes with very labile ligands such as N2, H2 and alkanes, concentrating on key mechanistic points, and also describe some principles and examples of photocatalysis.
Key learning points(1) On absorption of one UV/vis photon, binary metal carbonyls usually undergo loss of a single CO group in solution or matrices, but loss of several CO groups in the gas phase.(2) Photodissociation of CO normally occurs within <1 picosecond of light absorption, such that there is no time for excited states to equilibrate with their surroundings. (3) In substituted metal carbonyls and metal–metal bonded carbonyls, there are often two competing photochemical pathways and their relative quantum yields depend on the wavelength of irradiation, indicating the importance of careful selection of photolysis wavelengths. (4) The coordinatively unsaturated metal carbonyls formed by photodissociation are highly reactive and coordinate a solvent molecule, including alkanes and noble gases, within a few picoseconds. These alkane complexes act as stores of the fragments until the final photoproducts are formed; they also act as test-beds for understanding metal–ligand bonding. (5) Photodissociation of CO occurs by initial excitation into metal-to-CO charge-transfer excited states followed by rapid crossing into ligand-field (d–d) excited states. The excited states are typically spin-singlets but the ground states of some 3d transition metal fragments are spin-triplets. |
1. Introduction
1.1 Previous reviews and applications of metal carbonyl photochemistry
Transition metal carbonyls combine great photosensitivity and extraordinary reporters in the form of their CO-stretching bands with their structure sensitivity and exceptionally large absorption coefficients. In 1974, Mark Wrighton, one of the pioneers of the topic, published a review1 entitled “The Photochemistry of Metal Carbonyls” which summarised all aspects of the subject known at the time. A more recent review has emphasised the photophysical processes.2 The purpose of this Tutorial Review is to outline some of this basic photochemistry, draw out the principles, show how the advances in technology have increased our understanding of the detailed mechanisms, and to highlight how the simpler approaches used in early days can shed light on the more sophisticated modern problems.Photochemistry is applied in such areas as synthesis, photochemical CO-releasing molecules (photoCORMs), photocatalysis, photopolymerisation and photochemical modification of surfaces and glasses. In each of these examples, a basic understanding of the subtleties of metal carbonyl photochemistry is a prerequisite. It has also been crucial in understanding the ability of noble gases and alkanes to form labile bonds to transition metals.
A striking example of photosubstitution is the recent synthesis of a new boron complex by photolysis of (OC)5Cr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B(aryl) (aryl = 2,6-(2,4,6-iPr3C6H2)2C6H3) in the presence of diphenylacetylene (Scheme 1).3 The interesting feature of the product is that it contains the borirene group (isoelectronic with the cyclopropenium cation) attached to a single metal centre. Photosubstitution also provides a route to very labile complexes (Section 6) exemplified by the publication during revision of this review of a methane complex at low temperature that could be characterised by 13C and 1H NMR in a fluorocarbon solvent (Scheme 2).4
B(aryl) (aryl = 2,6-(2,4,6-iPr3C6H2)2C6H3) in the presence of diphenylacetylene (Scheme 1).3 The interesting feature of the product is that it contains the borirene group (isoelectronic with the cyclopropenium cation) attached to a single metal centre. Photosubstitution also provides a route to very labile complexes (Section 6) exemplified by the publication during revision of this review of a methane complex at low temperature that could be characterised by 13C and 1H NMR in a fluorocarbon solvent (Scheme 2).4
 | ||
| Scheme 1 Application of photosubstitution to synthesise borirene complex. Reproduced with permission from H. Braunschweig, R. D. Dewhurst, K. Radacki, C. W. Tate and A. Vargas, Angew. Chem., Int. Ed., 2014, 53, 6263–6266, copyright Wiley and Son 2014.3 | ||
 | ||
| Scheme 2 Formation of osmium methane complex4 by photosubstitution. | ||
Carbon monoxide is toxic but, surprisingly, it has very important biological functions.5 Current research focuses on how to make compounds which can release CO in the body in a controlled manner as a therapeutic agent. PhotoCORMs use transition metal carbonyls which can eject CO on photolysis.6 CO ejection usually requires UV light, which is somewhat dangerous, and anyway has low skin penetration. One way round this is to use a substituted species that absorbs in the visible such as (CO)5ReMn(CO)3(phenanthroline)7 which under deep-red photolysis splits the Re–Mn bond to give mononuclear radicals; normally these would simply recombine but in oxygenated media, species are formed which are much more labile towards CO release. In another example, MnBr(CO)3(L) (L = phenol substituted terpyridyl),8 the rate of photorelease can be regulated through deprotonation by F− that red-shifts the absorption dramatically. A different approach is to use a palladium porphyrin as a photosensitiser which on absorption at 635 nm converts to the excited triplet state, 3Pd(porph)*; the latter transfers energy to Mn2(CO)10 exciting it to a photolabile triplet state, releasing CO.9 This is intriguing because almost all photochemistry of metal carbonyls occurs from excited singlet states and triplet sensitisation is a rarity.
In photocatalysis, the photon energy can be used to drive the reaction uphill or to release (also described as “uncage”) the active catalyst (Section 7). Additionally, photochemical initiation of a reaction can elucidate the mechanism of a thermal catalytic reaction. A recent example concerns the reaction of 2-phenylpyridine (ppy) with alkynes to form alkenylated products, catalysed by manganese carbonyl complexes at elevated temperature and proceeding via cyclomanganated intermediates. The mechanism of the C–H bond functionalization is unravelled with time-resolved IR examination of the photochemistry of Mn(CO)4(ppy) (Scheme 3).10 Materials applications are illustrated by a study of a range of metal carbonyls in the radical photopolymerisation of vinylidene fluoride.11
 | ||
| Scheme 3 Above: Catalytic reaction. Below: Intermediates detected in the Mn(I) carbonyl-catalysed C–H bond functionalization of 2-phenylpyridine by TRIR spectroscopy. Adapted with permission from J. Am. Chem. Soc., 2021, 143, 1356–1364. Copyright 2021, American Chemical Society.10 | ||
Surface modification is illustrated by the photolysis of Cr(CO)6 in CH3CN on graphene proposed to lead via Cr(CO)3(CH3CN)3 to (η6-graphene)Cr(CO)3 with greatly increased conductivity compared to graphene.12 Look and Gafney have employed photolysis of W(CO)6 adsorbed on Vycor glass to generate photochromic tungsten oxides that are then used for photocatalytic reduction of CO2.13
This tutorial review concentrates on the binary carbonyls and cyclopentadienyl derivatives, M(CO)6 (M = Cr, Mo, W), Fe(CO)5, CpM(CO)n (M = Nb, Mn, Re, Co, Rh, Cp = η5-C5H5), Mn2(CO)10 and [CpFe(CO)2]2. Through restricting ourselves to these examples, we exemplify the fundamental principles of dissociative photochemistry. Alternative pathways of formation of equilibrated excited states are limited to certain substituted metal carbonyls and are mentioned only briefly.
To unravel the photochemistry, several approaches are usually needed. We first concentrate on identifying the initial products by looking at the behaviour in low-temperature glasses and matrices (Section 2), in the gas phase (Section 3) and in solution (Section 4). This is followed by a theory and dynamics section (Section 5) where we compare the predictions of theory and the experimental observations. The very first step in the photochemistry involves excited states and we consider how the photoproducts arise from specific excited states. Finally, we look at applications for the synthesis of photoproducts with very labile ligands (Section 6) and photocatalysis (Section 7).
1.2 Essential principles of IR spectroscopy
Much of the underpinning of metal carbonyl photochemistry is best served by the application of IR spectroscopy to C–O vibrations. These IR ν(C–O) bands are extremely intense, usually well-separated (at about 2000 cm−1) from other molecular vibrations and are narrow in solution in non-polar solvents, although in polar solvents they are broader.14 Two further aspects of the solvent need to be considered, namely its inherent reactivity and its own IR absorbance in the C–O stretching region.One approach that we introduced involves the use in metal carbonyl photochemistry, of liquefied noble gases, mostly Xe and Kr, as solvents at low temperature15 and as supercritical solvents16 near room temperature. These solvents have no IR absorptions, and hence allow the use of long pathlengths to compensate for the low solubility of the precursor complexes. The high solubility of CO, N2, H2 and other gases allows studies of reactivity with these species (see Section 6). With pressures up to 10 bar (Table 1), it is possible to cover a wide temperature range by use of liquid Ar, Kr and Xe. With supercritical solvents, it is even possible to reach room temperature. In principle such solvents should provide an “innocuous” environment, but, as we shall see, there can be interesting interactions.
| Noble gas | Melting point (K) | Temp. (K) of liquid with vapour pressure of 10 bar | Critical temp. (K) | Critical pressure (bar) |
|---|---|---|---|---|
| Ar | 84 | 116 | 151 | 49 |
| Kr | 116 | 159 | 209 | 55 |
| Xe | 161 | 219 | 290 | 58 |
The C–O frequencies can be interpreted by the Energy Factored Force Field (EFFF), which was first exploited by Cotton and Kraihanzel.17 A reminder of the principles is appropriate.18 In this approach, it is assumed that the C–O stretching vibrations can be treated separately from the other molecular vibrations. The spectra are strongly influenced by the electronic coupling between CO groups, but all other electronic and mechanical coupling can be ignored. When compared with a complete force constant analysis,19 the principal force constants (kCO) are very similar to the (anharmonic) full analysis constants (FCO); the major difference is in the interaction constants (kCO,CO compared with FCO,CO). This approximation had its critics,19 but the EFFF works amazingly well in applications to structure and bonding,20,21 as we shall see. Moreover, the patterns of CO-stretching frequencies give information about the symmetry of the molecule and the number of CO groups. Where the spectra with natural abundance isotopes do not resolve ambiguities, a decisive conclusion can be reached by isotopic substitution (13C16O or 12C18O). The EFFF is extremely powerful in conjunction with relative intensities (I) for estimation of C–M–C bond angles;18 for simple structures the angles are given by:
| M(CO)2: I(sym)/I(antisym) = tan2(θ/2) (θ = C–M–C angle) |
M(CO)3 (C3v): I(a1)/I(e) = [3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot2(θ/2) − 1]/4 (θ = C–M–C angle) cot2(θ/2) − 1]/4 (θ = C–M–C angle) |
M(CO)4 (C4v): I(a1)/I(e) = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan2 tan2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ (ϕ = angle of droop) ϕ (ϕ = angle of droop) |
How do the force constants, and hence frequencies, of metal carbonyls vary? In the light of both high-level and DFT approaches in recent years, the EFFF has become less fashionable. However, although modern theoretical calculations can predict structures and energetics reasonably well, they are less reliable, even with ‘adjustments’, when it comes to predicting frequencies. Thus we argue there is still a role for the simple approach.
As a reminder, Fig. 1 shows the bonding of CO to a transition metal in the Dewar–Chatt–Duncanson model. The σ donor orbital slightly C–O antibonding, and the π acceptor orbital is strongly C–O antibonding. The changes in the force constants determined by EFFF can be interpreted through this model. There can be considerable argument as to whether σ or π bonding is more important in affecting the C–O bond strength and hence the C–O force constant, but some general points remain.
The σ/π properties of other ligands will have an effect. For example in the classic work of Tolman,22 the a1 frequency of the CO groups in Ni(CO)3(phosphine) complexes increased from 2056 cm−1 in the essentially σ donating P(t-butyl)3 complex to 2111 cm−1 in the π-accepting ligand PF3 complex, where the back donation to PF3 relieves the back-bonding pressure on the CO groups, so that the C–O frequency increases. Force constants provide an effective way of comparing bond strengths that is independent of the molecular symmetry and number of CO groups. They are especially valuable for comparisons of π-acceptor properties of ligands. DFT calculations provide a direct route to estimating CO-stretching frequencies but the connection to force constants is usually lost and bond strength is approached in very different ways.
The Tolman approach was further developed by Gusev,23 who showed that there is a close correlation between experimental and DFT calculated frequencies for the Ni(CO)3L series, although the calculated frequencies were some 100 cm−1 different from the experimental. He also obtained a good correlation between experimental frequencies and DFT calculated C–O bond distances. The closely connected relationship between M–C and C–O distances has been analysed by Hocking and Hambley providing more detailed bonding indicators.24
We note that the ν(CO) will increase with:
(a) Positive charge on the complex (about 100 cm−1 per unit of charge);
(b) Increasing number of CO groups (about 30 cm−1 per added CO group);
(c) Oxidation state of the metal (about 20–40 cm−1 for an increase of 1 unit);
A very useful way of predicting the EFFF C–O force constants (kCO) – and hence ν(CO) – was introduced by John Timney (eqn (1)):25
| kCO = kd + ∑εθL | (1) |
| kCO = kNi + 2ε109.5CO + ε109.5PH3 | (2) |
1.3 Time-resolved infrared spectroscopy (TRIR)
Most modern Fourier Transform IR (FTIR) instruments have a spectral resolution of at least 0.5 cm−1, easily adequate for most purposes for ‘static’ or slowly changing systems, but alternative methods are required for systems that evolve in less than ca. 0.1 s. To follow photochemical changes, it is necessary to provide time-resolved spectra. The understanding of metal carbonyl photochemistry has been transformed by fast time-resolved IR spectroscopy (TRIR), enabled by a short pulse of pump light source to initiate a chemical reaction and to generate a high concentration of transient species. A second beam (the probe beam) passes through the sample to monitor changes that occur following the pump. Thus TRIR probes reaction dynamics and characterizes reactive intermediates on timescales that are inaccessible to conventional spectroscopy. Moreover, TRIR provides the structure sensitivity that is lacking in time-resolved UV/visible absorption. The first measurements in the mid-infrared used rapid-scan methods; the technique has continually advanced with new developments, particularly in lasers and computers, such that measurements can now be made right across the mid-IR on timescales from femtoseconds to milliseconds. Many approaches have been used for TRIR experiments and none has become uniformly adopted as the best because many different parameters need to be considered including: (i) the required wavenumber range; (ii) time-resolution; (iii) spectral resolution; (iv) sensitivity i.e., signal-to-noise required to observe the expected change in absorbance, Δabs, following irradiation.27This review includes examples spanning almost 40 years which illustrate the transformation in the key parameters. The fingerprint and other regions provide insights about other ligands bound to metal centres complementing information from the ν(CO) region.
The use of pump lasers, noise reduction techniques and computer-controlled IR scanning have resulted in commercial instruments based upon dispersive spectrometers which can record IR spectra with Δabs < 10−5 on nanosecond to millisecond timescales.29
 | ||
| Fig. 2 TRIR difference spectra of Fe(CO)5 in supercritical Xe (103 bar) doped with CO (2 bar) obtained at (a) 25 and (b) 200 ns after laser flash at 266 nm. The negative peaks correspond to loss of Fe(CO)5, the positive peaks to growth of products. The peaks are labelled according to the number of CO groups. The major products are: 34 = 3Fe(CO)4; 14-Xe = 1Fe(CO)4–Xe; 3 = Fe(CO)3. In addition, traces of Fe2(CO)88 and Fe2(CO)99 are formed. The inset shows the kinetics of (c) the formation of 14-Xe at 1961 cm−1 and (d) the decay of 34 overlapped with the growth of 14-Xe at 1990 cm−1. Reproduced with permission from J. Am. Chem. Soc., 2004, 126, 10713–10720. Copyright 2004, American Chemical Society.31 | ||
 | ||
| Fig. 3 (a) FTIR spectrum of Cr(η6-C6H6)(CO)3 in supercritical Xe at 298 K and 1500 psi in the presence of CO (30 psi). (b) Step scan FTIR spectra at various times between 1.0 and 2.1 μs after 355 nm laser excitation leading to the formation of Cr(η6-C6H6)(CO)2Xe. The time-resolved spectra depict the decay of the transient Cr(η6-C6H6)(CO)2Xe and recovery of Cr(η6-C6H6)(CO)3. Reproduced from ref. 32 with permission from the Royal Society of Chemistry. | ||
Since any imperfections in the interferogram generated in step-scan are transformed into the whole spectrum, this method is less forgiving of errors in repeatability than methods described above. Consequently, time-resolved step-scan FTIR has not been as widely implemented.
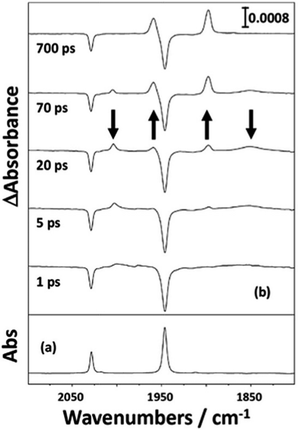 | ||
| Fig. 4 (a) FTIR spectrum of a solution of CpMn(CO)3 in n-heptane at room temperature; (b) selected picosecond TRIR spectra recorded at a series of time delays following 266 nm photolysis of the solution. Reproduced from ref. 33 with permission from the Royal Society of Chemistry. | ||
Advances in pump laser technology have enabled the gap between nanosecond measurements and the ultrafast measurements to be bridged by coupling high-repetition nanosecond lasers as the pump source to these probe systems allowing TRIR measurements from sub-picosecond to milliseconds on a single spectrometer.10
Applications and IR spectroscopy: key points(1) Applications: photosubstitution, photoCORMs, photocatalysis, photopolymerisation, photochemical surface modification, labile ligands.(2) IR spectra and ν(CO) bands. (3) Structure sensitivity: effects of charge, oxidation state, no of CO groups. (4) Liquefied and supercritical noble gases as solvents: low reactivity, IR transparency, solubility of added gases. (5) Energy factored force field for analysis of ν(CO). (6) TRIR spectroscopy, key parameters: pump wavelength, IR wavenumber range, time resolution, spectral resolution, sensitivity. |
2. Photochemistry in glasses and matrices
2.1 Metal hexacarbonyl photochemistry (metal = Cr, Mo, W)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 isopentane-methylcyclohexane were frozen to produce a colourless glass at ca. 90 K. UV irradiation led to the accumulation of new, yellow, species identified by the ν(CO) IR bands; for M = W at 2092 (w), 1952 (s) and 1924 (m) cm−1. By comparison with known W(CO)5L IR band patterns, the bands were confidently assigned to a C4v W(CO)5 fragment. There was some evidence that the species was observable even as the glass melted. It is very unlikely that a ‘naked’ M(CO)5 fragment would be so stable, implying that the species observed were actually M(CO)5(alkane) (eqn (3)), improbable though this seemed at the time.
4 isopentane-methylcyclohexane were frozen to produce a colourless glass at ca. 90 K. UV irradiation led to the accumulation of new, yellow, species identified by the ν(CO) IR bands; for M = W at 2092 (w), 1952 (s) and 1924 (m) cm−1. By comparison with known W(CO)5L IR band patterns, the bands were confidently assigned to a C4v W(CO)5 fragment. There was some evidence that the species was observable even as the glass melted. It is very unlikely that a ‘naked’ M(CO)5 fragment would be so stable, implying that the species observed were actually M(CO)5(alkane) (eqn (3)), improbable though this seemed at the time. | (3) |
Is it possible to generate the fragments in an environment less likely to coordinate with the solvent? We turn to the technique labelled ‘Matrix Isolation’ by its inventor, George Pimentel.36 In the photochemical application of this method, dilute gas mixtures of a precursor in a noble gas (Ne, Ar, Kr, Xe) are condensed onto a cold (10–20 K) IR transparent window (e.g. CsBr), and irradiated. In the first trial experiment37 with a metal carbonyl, HMn(CO)5 in Ar (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) was photolyzed with UV (229 nm) at 15 K. The resulting spectrum was readily assigned to HMn(CO)4, but the most interesting aspect of this experiment was that irradiation with λ > 285 nm reversed the reaction (eqn (4)). This had enormous significance for future experiments, although not understood at the time. A plethora of experiments of this type followed, but we concentrate on those of particular relevance to this Tutorial.
200) was photolyzed with UV (229 nm) at 15 K. The resulting spectrum was readily assigned to HMn(CO)4, but the most interesting aspect of this experiment was that irradiation with λ > 285 nm reversed the reaction (eqn (4)). This had enormous significance for future experiments, although not understood at the time. A plethora of experiments of this type followed, but we concentrate on those of particular relevance to this Tutorial.
 | (4) |
The first, partial, explanation of this reversal came in an experiment on W(CO)6 which monitored the UV/vis spectrum in addition to the IR (Fig. 5).38
 | ||
| Fig. 5 IR (left) and UV/visible (right) spectra (a) of W(CO)6 in argon (1/250) after depositing on to a KBr window at 20 K; (b) after 30 s photolysis with unfiltered UV light; (c) after 90 s irradiation with light >330 nm. 6 = W(CO)6, 5 = W(CO)5. Note the depletion of W(CO)5 and recovery of W(CO)6 in spectra (c). Reproduced from ref. 38 with permission from the Royal Society of Chemistry. | ||
The bands labelled 6 are assigned to W(CO)6; bands labelled 5 are assigned to W(CO)5. Clearly a species, easily assigned as W(CO)5,† is converted back to W(CO)6 when it absorbs radiation in its band at 435 nm (eqn (5)). An absorption band at much longer wavelength than that of the precursor turned out to be typical of coordinatively unsaturated metal carbonyls (see Section 5). What is not clear is how the recombination works; is it simply because the absorbed radiation is transferred to the matrix, warming it locally around the W(CO)5 fragment and hence causing a thermal back reaction, or is it a more specific photochemical process? One way to answer this question would be to warm the matrix and see if a back reaction occurs. However, one of the disadvantages of using frozen noble gases is that, in contrast to glasses, it is not possible to follow reactions over more than a small temperature range before the matrix gas boils off. We shall later briefly consider some methods which overcome this limitation.
 | (5) |
It is of course possible that the three C–O IR bands are wrongly assigned to W(CO)5; the only way to be sure of the assignment is to substitute some of the 12CO groups with 13CO. For the C4v M(CO)5 fragment there are three IR-active frequencies (a1, e and a1) but five EFFF constants: the principal kaxialCO, keqCO, and the interaction keq,eq(cis)CO,CO, keq,eq(trans)CO,CO and kax,eqCO,CO (Fig. 6). Thus the problem is underdetermined. However, with 13CO substitution, more frequencies are generated, but the force constants remain the same, and the problem is, if anything, overdetermined. Employing this approach, the photogenerated fragments were shown, unquestionably, to be M(CO)5 (M = Cr, Mo, W) with C4v structures39 in both Ar and CH4 matrices. Moreover, from the relative intensities of the IR bands, it was possible to estimate that the axial/equatorial Cax–M–Ceq bond angles were between 90° and 94°.
However, things are not so simple: the position of the visible absorption band is very sensitive to the matrix material.40 For example with Cr(CO)5, the bands occur at 624 (Ne), 533 (Ar), 518 (Kr), 492 (Xe), and at 489 nm (CH4); meanwhile the position of the IR bands is hardly affected. Experiments in mixed matrices, particularly of Ne and Xe, proved that two independent species were present and could be interconverted by selective photolysis; the shift in the visible band was caused by the interaction of the noble gas with the empty coordination site of the M(CO)5 fragment. This leads to the obvious conclusion that the noble gas is not an entirely innocent observer of the isolated fragment but interacts specifically with it, and we must write these species as M(CO)5Ng (Ng = noble gas). We return later to measurements of this interaction and the theory behind it. The wavelength selective photochemical experiments convert Cr(CO)5Xe to Cr(CO)5Ne and vice versa, by irradiation in the absorption band of the respective species (we assume that the interaction with Ne is very small).
To unravel more detail of the photochemistry, the use of polarised photolysis and polarised UV/vis/IR spectroscopy proved to be extremely valuable. Because M(CO)5 fragments are not spherically symmetrical, it is possible to select molecules for photolysis according to their orientation, and to examine the orientation of both product and residual reactant molecules.41,42 The first inference is that the visible band of M(CO)5Ng species must have the same symmetry as the e vibrational band; this limits the possible excited states for this transition. The second is that the excitation enables M(CO)5 to change from a C4v ground state to a D3h excited state and back again. The energy levels and structures are based on simple MO arguments; see Section 5. We now know what happens in the photochemistry of M(CO)6 in, say Ar. The excited D3h structure of M(CO)5, on collapsing to the C4v structure can do so in three orientations; in one of these, the “vacant site” faces the CO which has just been ejected and recombines with it; in the other two, the site faces an Ar atom and forms M(CO)5Ar (Fig. 7). This means that the quantum yield should be about 2/3; indeed in solution, the quantum yield was measured43 to be 0.67. In the reverse reaction, M(CO)5 + CO → M(CO)6, the pentacarbonyl is ‘stirred’ by absorption in the visible band and reorients until it finds a CO opposite the empty coordination site. In a mixed Ne/Xe matrix, the reorientation enables selective interconversion of M(CO)5Xe and M(CO)5Ne.
 | ||
| Fig. 7 Orbital energy level scheme, showing the generation of the C4v excited state and its conversion to the C4v ground state via the D3h intermediate, so executing a Berry pseudorotation. Adapted with permission from Inorg. Chem., 1978, 17, 147–154. Copyright 1978, American Chemical Society.41 | ||
Perhaps the most sophisticated example of unravelling complex photochemistry in a matrix involves W(CO)5CS.44,45 A combination of wavelength selective photolysis, 13CO isotopic enrichment, including (13CO)W(CO)4CS labelled specifically trans to the CS group, and polarised photolysis and spectroscopy, led to the interpretation shown in Scheme 4. Moreover, it was possible to demonstrate that following loss of CO, the W(CO)4CS fragment undergoes an excited state rearrangement. The relevance of these experiments to both gas phase and solution metal carbonyl photochemistry will be developed in succeeding sections.
 | ||
| Scheme 4 Photochemistry of W(CO)5(CS) in an argon matrix, adapted with permission from Inorg Chem., 1976, 15, 2892–2897. Copyright 1976, American Chemical Society.45 | ||
 | ||
| Scheme 5 Sequential CO photodissociation of M(CO)6 (M = Cr, Mo, W) in matrices and structures of photofragments. | ||
Thus molecules like W(CO)5Xe or Cr(CO)5(CH4) undergo different photochemical processes at different wavelengths. Long-wavelength visible radiation causes ejection of the extra ligand (here Xe or CH4), while short-wavelength UV radiation causes loss of CO to form a tetracarbonyl. Wavelength-dependent photochemistry is a critical characteristic.
Matrix isolation can answer an additional question about these reaction intermediates. The metal hexacarbonyls are air stable in the absence of UV irradiation, but why do they decompose rapidly in the presence of air and UV radiation forming metal oxides? The intermediates that are formed have been identified by photolysis in O2-doped matrices to be oxo species M(O)2(CO)4, M(O)2(CO)2 and peroxo species such as (η2-O2)M(CO)x (x = 3 or 4), prior to forming molecular oxides MO2 (M = Cr, Mo) and MO3 (M = Mo, W).47
In a recent interesting exploitation of this technique in combination with photochemistry, Wu et al.49 co-condensed a stream of laser-ablated Ca, Sr or Ba atoms with Ne doped with CO. The IR spectra showed, in each case, a single CO band, assigned via isotopic enrichment, to an M(CO)8 species. The strong back-bonding produced substantial shifts in the C–O frequencies. At lower concentrations of CO, M(CO)n (n = 2, 3, 4) were formed; their bands were distinguished from one another by their photochemical response.
2.2 Photochemistry of Fe(CO)5 and CpMn(CO)3
 | ||
| Scheme 6 (a) Photochemistry of Fe(CO)5 in matrices. (b) Formation and structures of Fe(CO)4 and its adducts. For notation, see text. | ||
Prolonged short wavelength photolysis of Fe(CO)5 in a low-temperature matrix generates the C3v fragment Fe(CO)3 with C–O bands at 2040.1 (a1) and 1930.4 (e) cm−1 in a CH4 matrix, and 2042/1935.6 cm−1 in an Ar matrix. From the relative intensities of the two bands, a C–Fe–C bond angle of 108 ± 3° was estimated.57 Thus Fe(CO)4 also exhibits wavelength-dependent photochemistry. Importantly, Burdett (see Theory section) calculated a bond angle of 111°, which demonstrates that the deviation from a naively expected trigonal D3h structure is real and not due to interaction with the matrix.
2.3 Photochemistry of Mn2(CO)10, HMn(CO)5 and [CpFe(CO)2]2
In neither case was there any evidence for Mn(CO)5.The reason is that any splitting of the Mn–Mn bond produces two radicals sitting next to each other, and they are too big to escape the surrounding glass/matrix cage, so they simply recombine. To establish the existence of Mn(CO)5 and determine its structure a slightly roundabout method is required.
Photolysis of HMn(CO)5 in a CO matrix leads to two processes: the major one is loss of CO to produce HMn(CO)4 (see above). In the minor process, loss of H occurs to produce Mn(CO)5 plus HCO. Because the HMn(CO)4 is sitting in a sea of CO, it readily recombines to form the parent, allowing the spectrum of Mn(CO)5 to be monitored. A combination of 13CO isotopic enrichment, polarised photolysis/spectroscopy, and intensity measurements confirmed that the product is indeed Mn(CO)5 with a C4v structure and an axial-equatorial angle of about 96°.62 EPR spectra following gamma-irradiation of HMn(CO)5 in krypton at 77 K, demonstrates the generation of Mn(CO)5Kr, (i.e. a species reminiscent of the M(CO)5Ng systems described earlier) and confirmed its C4v structure (Scheme 8).63
Once more, none of the proposed radical photoproduct, CpFe(CO)2, was identified in the matrix studies because of the cage effect. However, in an experiment significant for solution studies, (see later) it was demonstrated that prolonged photolysis of [CpFe(CO)2]2 in a 3-methylpentane glass at 98 K, yielded [CpFe(CO)]2, (ν(CO) = 1958 and 1904 cm−1; i.e. with no bridging CO group) presumably via photolysis of the triply bridged species.67
Matrix photochemistry: key points(1) Matrix isolation (10–20 K) in solid Ne, Ar, Kr, Xe or CH4 to observe ν(CO) IR bands of primary products of photodissociation. Product accumulates over time during irradiation and remains stable at conditions of measurement.(2) Alternatively, use hydrocarbon glasses, but less inert (77 K). (3) Coordinatively unsaturated metal carbonyls exhibit long-wavelength UV/vis absorption. (4) Reversibility of photodissociation on irradiation into this long-wavelength absorption. (5) Isotopes and energy-factored force fields (EFFF) to determine geometry of products of loss of one or two CO groups (e.g. Cr(CO)5, Fe(CO)4, Fe(CO)3). (6) OC–M–CO bond angles estimated from intensity ratios of ν(CO) IR bands. (7) Interaction of M(CO)5 (M = Cr, Mo, W) and Fe(CO)4 with Xe and CH4. (8) Wavelength selective photochemistry: recombination with CO vs. loss of further COs. (9) Cage effect prevents observation of M–M bond cleavage in the matrix. (10) Polarised photochemistry to probe photochemical mechanism. (11) Use of magnetic circular dichroism for evidence of paramagnetism of Fe(CO)4. |
3. Photochemistry in the gas phase
3.1 Formation of multiple fragments on single photon absorption
| Photolysis laser | Nd:YAG | KrF | ArF |
|---|---|---|---|
| Wavelength/nm | 355 | 248 | 193 |
| Photon energy/kcal mol−1 | 80.5 | 115.3 | 148.1 |
| Photofragment | Relative yields | ||
|---|---|---|---|
| Fe(CO) | 0.012 | ||
| Fe(CO)2 | 0.31 | 0.55 | 0.81 |
| Fe(CO)3 | 0.46 | 0.35 | 0.09 |
| Fe(CO)4 | 0.23 | 0.10 | 0.09 |
It will be evident from the identification of carbonyl fragments in low-temperature matrices by IR spectroscopy, that the undisputed identification of fragments in the gas phase would also benefit from IR spectroscopy. The problem, of course, is timescale; such fragments in the gas phase are expected to be very short-lived. Eric Weitz and colleagues were the first to tackle this problem.69 Various gas mixtures of Fe(CO)5/Ar/CO were photolysed with a pulsed KrF excimer laser (248 nm) and the change in IR transmitted intensity monitored at a series of different wavelengths with a CO laser. The identification of the Fe(CO)x fragments follows directly from the species identified in matrices,50 with slight shifts from matrix to gas of about 10 cm−1 (Fig. 8). It is important to note that at this gas pressure and over this timescale of several μs, the fragments are observed in their triplet ground states. The rate of recombination of Fe(CO)4 with added CO was (3.5 ± 0.9) × 1010 dm3 mol−1 s−1. A further feature of these gas phase spectra is that the band centres shift slightly to shorter wavelengths with time. As explained later, this shift is due to relaxation of ‘hot’ molecules.
 | ||
| Fig. 8 Comparison of IR difference spectra for Fe(CO)5 and Fe(CO)4 in gas phase with those in argon matrix. The bands of Fe(CO)5 appear negative whereas those of Fe(CO)4 appear positive. (a) TRIR spectra 3 μs after laser pump flash of Fe(CO)5 in the gas phase in presence of 100 torr CO; (b) FTIR spectra after photolysis of Fe(CO)5 in Ar matrix at 10 K. To aid comparison the wavenumber scales have been shifted 10 cm−1 relative to each other to compensate for the solvent effect of argon. Adapted with permission from Acc. Chem. Res., 1987, 20, 408–414. Copyright 1987, American Chemical Society.54 | ||
Weitz also observed that the gas phase IR spectra of the carbonyl fragments were very broad. How to overcome this? As explained by Tanaka et al.,70 vibrational cooling in supersonic jet expansion produces very narrow lines, for example, of the fragments Fe(CO) and Fe(CO)2, produced in their triplet ground states (3Σ− and 3Σg+, respectively) by ArF (193 nm) and KrF (248 nm) laser photolysis of Fe(CO)5. This method generated very high-resolution spectra and accurate rotational constants, leading to moments of inertia.
Studies by Weitz and colleagues,71 and by the groups of Rosenfeld and Rayner/Hackett allowed, largely on the basis of matrix IR data, the identification of a whole slew of metal carbonyl fragments, and determination of their reaction kinetics.
3.2 Alternative techniques for gas-phase photochemistry
In addition, UV/vis absorption spectra of MnL(CO)3·H+ and MnL(CH3CN)(CO)3·H+ were obtained by photodepletion of mass-selected ions with a tunable pulsed laser and the formation of photofragments was recorded as a function of excitation wavelength. These experiments reveal very strong dependence of the photofragmentation patterns of MnL(CO)3(CH3CN)·H+ on the excitation wavelength with CH3CN lost at the lowest photon energies, three CO groups lost at intermediate energies and both CH3CN and 3COs at the highest photon energies.73 In contrast to the gas phase, only one CO is lost from MnL(CO)3(CH3CN) in solution.75
Gas phase photochemistry: key points(1) Dissociation of multiple CO molecules on absorption of a single UV/vis photon.(2) Number of CO groups ejected increases with photon energy. (3) Measurements of kinetics of reaction of photoproducts with CO and other ligands. (4) Estimation of Ng–M(CO)5 (M = Cr, Mo, W) bond energies. (5) Photofragmentation patterns by mass spectrometry. (6) Time-resolved electron diffraction and photoelectron spectra of photofragments. |
4. Photochemistry in solution
4.1 Time-resolved UV/visible and infrared (TRIR) spectroscopy of M(CO)6 (M = Cr, Mo, W)
Can the initial products of photolysis be detected in solution? We start with a simple early experiment.78 Conventional UV/vis flash photolysis of Cr(CO)6 in cyclohexane, with a time resolution of about 3 μs, demonstrated the appearance of a transient with an absorption maximum at 503 nm. In a solution saturated under an atmosphere of CO, this transient regenerated Cr(CO)6 with a half-life of 25 μs. In a methane matrix (see above), Cr(CO)5(CH4) has a band at 489 nm. Given that both media involve saturated hydrocarbons it is reasonable to assign the solution transient to Cr(CO)5(cyclohexane).More evidence came from the first time-resolved IR experiments, also carried out by the Mülheim group.79 With very simple equipment, and employing the same conditions as in the UV/vis experiments, they detected a species with an IR band at 1962 cm−1 matching the most intense band of Cr(CO)5(CH4) in the methane matrix that appears at 1961 cm−1. It seemed reasonable to assign the band to Cr(CO)5(cyclohexane). The assignment was confirmed by irradiation of Cr(12CO)5(13CO) and analysis of the product bands due to Cr(12CO)5(cyclohexane) and Cr(CO)4(13CO)(cyclohexane) isotopologues.
In another significant early experiment, Bonneau and Kelly,80 again via conventional UV/vis flash photolysis, examined the behaviour of Cr(CO)6 in perfluoromethylcyclohexane solvent. They reasoned that the matrix data40 on Cr(CO)5L suggested that the interaction of Cr(CO)5 with the perfluoro solvent would be weaker than with cyclohexane (matrix data λmax Cr(CO)5(CF4) 547 nm compared with Cr(CO)5(CH4) 489 nm). The flash yielded a short-lived intermediate (half life ∼38 ns in CO-saturated solution), with an absorption centred at 620 nm, close to that of Cr(CO)5Ne at 624 nm. Both of these observations argue for the reactions in eqn (6) occurring in solution:
 | (6) |
“Naked” Cr(CO)5 was too short-lived to be detected (but see below). The reaction with CO is faster in the more weakly bound perfluoro solvent. Photochemistry in perfluoro solvents continues to play an important part in mechanistic studies, and we return to these solvents several more times.
The thermal displacement of cyclohexane in Cr(CO)5(cyclohexane) by heterocyclic ligands has also been followed by TRIR. The reactions occur by associative or interchange mechanisms with rates that are dependent on the entering ligand. For example, reaction with THF occurs within 10 μs at 0.02 M THF. These studies81 are important for understanding the mechanism of typical synthetic procedures for photochemical substitution that continue to be popular. Related studies82 have reported time-resolved absorption measurements to monitor the conversion of Cr(CO)5(η2-benzene) to Cr(CO)5(THF). These experiments, usually (but see later) show the loss of only one CO group. The accepted reason is that the ‘hot’ Cr(CO)5 rapidly loses excess energy to the surrounding solvent bath before any further CO groups are lost, in contrast to the gas phase behaviour, where multiple CO loss can occur.
In the time-resolved experiments described so far, the species detected is Cr(CO)5(solvent), not ‘naked’ Cr(CO)5; can the naked species be detected? Any attempt will involve much faster technology. On a very fast timescale with UV/vis detection, it was concluded83 that the dissociation of a CO group occurs within 300 fs and complexation to the solvent is complete within about 1 ps. This short timescale for dissociation reflects the studies in the gas phase.
There is a further complication. As mentioned in the gas phase studies, the C–O vibrational spectrum shifts slightly with delay time. What happens in solution? This is illustrated in elegant experiments by Dougherty and Heilweil.84Fig. 9 shows the TRIR spectra following laser photolysis of W(CO)6 in n-hexane. At the longest timescale (333 ps), the spectrum shows depletion of W(CO)6 at 1983 cm−1, and the formation of two bands at 1956 and 1928 cm−1. Comparing these to the bands in a CH4 matrix [W(CO)6, 1982 (t1u); W(CO)5, 1957 (e), 1926 (a1)] clearly establishes this species as W(CO)5(n-hexane). At 73.3 ps, there are two other bands in the spectrum at 1942 and 1908 cm−1 which disappear at the same rate and are thus assigned to the same species. The decay time is 160 ± 20 ps, which is reminiscent of the decay time for the v = 1 to v = 0 decay time of the t1u mode of W(CO)6 (140 ± 15 ps) in hexane established by IR pump-probe experiments. The −14 cm−1 shift of the e band of W(CO)5 (n-hexane) from 1956 to 1942 cm−1 similarly matches the −15 cm−1 from the fundamental v = 0 → v = 1 to the v = 1 → v = 2 mode of W(CO)6 corresponding to the anharmonicity.85 This strongly suggests that we are looking at the decay of vibrationally excited (v = 1) W(CO)5(n-hexane). The bands at 1942 and 1908 cm−1 are fully consistent with the vibrationally excited species, yielding anharmonic shifts of −14 and −20 cm−1. At the shortest timescale (1.67 ps), there is a hint of these four bands, but they are broadened almost beyond recognition. This broadening arises because of the coupling of the C–O stretches to lower vibrational modes which are in high vibrational states. Over some 40 ps, these vibrational modes relax to their ground states and the broadening vanishes. The importance of this broadening will depend on the system, and the shorter the wavelength of the photolysis laser, the more energy dumped in the fragment, and the greater the problem, as happens in the gas phase. This clearly makes assignment at very short times extremely difficult.
 | ||
| Fig. 9 Transient IR difference spectra for W(CO)6 in n-hexane following UV excitation. Reprinted from Chem. Phys. Lett., 1994, T. P. Dougherty and E. J. Heilweil, “Ultrafast transient infrared absorption studies of M(CO)6 (M = Cr, Mo or W) photoproducts in n-hexane solution”, 227, 19–25, Copyright 1994, with permission from Elsevier.84 | ||
Harris and colleagues have probed the photochemistry of the M(CO)6 (M = Cr, Mo, W) species on the even faster fs timescale.86 Not surprisingly, the analysis is complicated by the band broadening, but, in addition, coherent oscillations arising from the pump and probe pulses (free induction decay) present a problem. Nonetheless, they were able to conclude that hot Cr(CO)5 molecules react with ejected CO molecules which have not escaped the solvent cage in <300 fs. This geminate recombination is the analogue of the cage effect in matrices. The band broadening is also associated with the dynamics of rearrangement of the solvent coordination as is illustrated by a study of the Cr(CO)6 in alcohol solvents. The Cr(CO)5 moves along the alkyl chain of the solvent until it eventually coordinates to the hydroxyl group. The time constants for these processes vary according to the alkyl chain and range from ca. 200 to 2000 ps.87
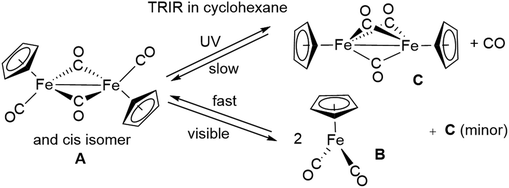
4.2 Photochemistry of Mn2(CO)10 and [CpFe(CO)2]2
 | ||
| Fig. 10 Transient difference spectra showing change in absorbance: (a) 5 μs, (b) 25 μs, and (c) 1.25 ms after the UV flash photolysis of [CpFe(CO)2]2 in cyclohexane solution under 1 atm pressure of CO. A = [CpFe(CO)2]2, B = CpFe(CO)2, C = CpFe(μ-CO)3FeCp. Reproduced from ref. 90 with permission from the Royal Society of Chemistry. | ||
Since this study, there have since been many investigations91 of the photochemistry of [CpFe(CO)2]2, over the time range ps to fs. Everyone agrees that on visible photolysis the initial product, generated in about 2 ps, is the radical CpFe(CO)2, and its subsequent reactions have been followed. UV photolysis produces some radical, and the triply-bridged [CpFe(μ-CO)3FeCp]. The majority of the [CpFe(μ-CO)3FeCp] is generated with time constant ca. 20 ps and decays over a relatively long time by reaction with, for example, MeCN92 or alkenes,93 to yield Cp(CO)Fe(μ-CO)2FeCp(L).
Although the radical is an obvious primary product, the same cannot be said for the triply-bridged species, and there have been many attempts to determine the primary step. The most recent effort91 suggests that one path with time constant 23 ps involves the expected [Cp(CO)Fe(μ-CO)2FeCp], formed by loss of a terminal CO but this intermediate has never been identified. The other route, providing ca. 16% of [CpFe(μ-CO)3FeCp] is more intriguing since it involves the one-photon loss of two CO groups, a very unusual event, but not unique. The assignment of this species relied on the study in glasses,67 and postulates that this species reacts with CO with time constant ca. 45 ns to form [CpFe(μ-CO)3FeCp].
4.3 Use of liquefied and supercritical noble gases
The use of liquefied noble gases (see Section 1.2) provided an opportunity for looking at the interaction between M(CO)5 fragments and noble gases. In the first experiment we were able to detect by FTIR, the species Cr(CO)5Xe, generated by photolysis of Cr(CO)6 in liquid Xe at −98 °C, with C–O bands almost identical to those in a solid Xe matrix, and with a lifetime of about 2 s.94 In an important development, Weiller95 repeated this experiment and in addition, by using rapid scan FTIR, monitored the kinetic behaviour of the species M(CO)5Ng (M = Cr, W; Ng = Xe, Kr) for reaction with CO over the temperature range 173 to 198 K. In this way he was able to obtain a minimum value‡ for the Xe–W(CO)5 bond dissociation of 8.4 ± 0.2 kcal mol−1, in remarkable agreement with Weitz's gas phase value.These experiments were conducted well below room temperatures, but even so required fairly high pressure cells. To conduct such experiments near room temperature, in the region where such solvents become supercritical (sc), requires apparatus operating at much higher pressures. George and colleagues96 studied the interaction between photochemically generated M(CO)5 species (M = Cr, Mo, W) and the solvents Xe and Kr at or above room temperature. Combining laser irradiation and IR diode laser detection, they obtained a value of 8.2 ± 0.2 kcal mol−1 for the Xe–W interaction. The Cr and Mo analogues reacted considerably faster, indicating lower Xe–M bond energies, in contrast to the numbers obtained by Weitz (Table 3). We shall come back to this point in due course. Of equal importance, by both TRIR and UV/vis detection, there was intriguing evidence in these room temperature solutions of interaction with Ar, although it was not possible to obtain any definitive assignment or bond energy numbers. To reduce carbonyl fragment-noble gas interactions further, one needs liquid Ne, corresponding to the Ne matrix experiments, but as far as we are aware, no one has attempted this.
4.4 Role of singlet and triplet structures for Fe(CO)4 and related complexes
In the early days of carbonyl photochemistry, it was assumed that the initial stage of CO loss led to singlet states of metal carbonyl fragments. However, the matrix experiments on Fe(CO)4, which demonstrated the importance of the triplet state, and subsequent experiments in the gas phase and solution, have shown that the photochemistry can be sensitive to the spin state. All the experiments show that there is no change of spin state prior to photodissociation but there may be a change in spin state after dissociation of CO. We now illustrate this with a few examples. | ||
| Scheme 10 Reactions of Fe(CO)5, Fe(CO)4 and Fe(CO)3. The major reactions are indicated by thick arrows. Reproduced with permission from J. Am. Chem. Soc., 2004, 126, 10713–10720. Copyright 2004, American Chemical Society.31 | ||
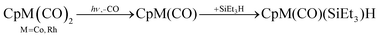 | (7) |
4.5 Combination of TRIR experiments with other techniques: NMR, RIXS and XFAS
Ball, George and colleagues have also demonstrated the power of this technique with Xe complexes. Once again TRIR provided clues. Photolysis102 of CpRe(CO)3 in supercritical Xe at room temperature and liquid Xe at 170 K generated CpRe(CO)2Xe, with a lifetime in the latter of about 3.5 min. Unfortunately CpRe(CO)3 was insufficiently soluble in liquid Xe for NMR investigation. However, a combination of NMR and IR positively identified106 the coordinated xenon of (iPrCp)Re(CO)(PF3)Xe on photolysis of (iPrCp)Re(CO)2(PF3) in liquid Xe via the couplings J(P–Xe), J(F–Xe) and the 129Xe chemical shift.
In a remarkable paper, Cho et al. reported the time-resolved XAFS and XANES spectra of Mn2(CO)10, so obtaining the corresponding spectra of Mn(CO)5 by difference (Fig. 11). The most significant change in the carbonyl geometry from Mn2(CO)10 to Mn(CO)5 was the increase in Cax–Mn–Ceq from 93.6 to 96.7°, respectively. (Unfortunately, no error bars are given.)109 It will be recalled that the angle for Mn(CO)5 determined from IR intensities62 was 96 ± 3°, gratifyingly close!
 | ||
| Fig. 11 XAFS spectra of Mn2(CO)10 and Mn(CO)5 in propan-2-ol 400 ps after laser excitation at 400 nm. The diagrams show the Fourier transform experimental (black solid line) and fitted (green solid line) spectra and contributions from the scattering nuclei. Reproduced with permission from Inorg. Chem., 2016, 55, 5895–5903. Copyright 2016, American Chemical Society.109 | ||
Using a combination of XAFS with TRIR to provide spectroscopic data, it has recently been possible to determine the structures of the short-lived species W(CO)5(heptane) and W(CO)5Xe.110 The most interesting parameter is the W–Xe bond length, 3.10 Å; a DFT calculation suggests a bond length of 3.15 Å. The same methods allowed determination of structural parameters for W(CO)5(n-heptane) (Fig. 12).
 | ||
| Fig. 12 Structures of W(CO)5Xe and W(CO)5(n-heptane) determined by EXAFS and DFT (LANL08 basis set for W and Xe, 6-311++G(d,p) for other atoms, M06 functional). Reproduced with permission from J. Am. Chem. Soc., 2019, 141, 11471–11480. Copyright 2019, American Chemical Society.110 | ||
Ultimately, one looks for single crystal X-ray diffraction to give accurate structures. This challenge was finally solved for alkane complexes by hydrogenation of a rhodium(diene) complex in a single crystal-to-single crystal transformation in which a single crystal of a diene complex is hydrogenated in the solid state to form the alkane complex while maintaining crystallinity.111 These studies have provided metrical details of linear and cyclic alkanes acting as chelating ligands through two η2-C,H linkages. Further information about alkane complexes is summarised in recent reviews.111,112
Solution photochemistry: key points(1) TRIR spectroscopy:(a) ns to ms for kinetics of reaction with substrates (b) fs to ps for: (i) initial photoproducts (ii) vibrational relaxation and geminate recombination (iii) reaction with solvent (iv) interconversion of product spin states (2) Application of liquefied and supercritical noble gases as solvents. (3) NMR, RIXS, XAFS provide direct evidence of coordination of Xe and alkanes. (4) Dissociation of one CO group per photon absorbed typical; rare examples of two CO groups. (5) Structures of unsaturated metal carbonyls in solution same as in matrices. (6) Kinetics of Xe and alkane complexes, bond dissociation energies. (7) Dinuclear metal carbonyls: CO loss and M–M cleavage as competing pathways with wavelength selective photochemistry. (8) Coordinatively unsaturated metal carbonyls with Mn, Fe and Co may exist in triplet and singlet forms with different structures and reactivity. |
5. Theory and gas-phase dynamics
How does theory relate to the structures and properties of the fragments generated by photolysis of metal carbonyls, and to the photochemical mechanisms? In this section we consider several questions: the shapes of carbonyl species; their energetics and C–O vibrational frequencies; the nature of excited states; the interaction with noble gases, and how photochemical excitation results in ultrafast and selective dissociation.5.1 Structures and properties of the fragments generated by photolysis of metal carbonyls.
 | ||
| Fig. 13 Wave function and energy changes along a Berry pseudorotation for M(CO)5. Reproduced with permission from Inorg. Chem., 1975, 14, 365–374. Copyright 1975, American Chemical Society.116 | ||
The invention of DFT methods has brought much more quantitative calculations within reach and has stimulated a great deal of theory on metal carbonyls and their photochemistry.120 Of particular relevance are calculations on the primary photoproducts of Cr(CO)6 and Fe(CO)5, i.e. Cr(CO)5 and Fe(CO)4.121 Full ab initio (e.g. CCSD(T)) calculations on large molecules are very expensive, but they are now within reach for some problems.122,123 As mentioned earlier, the problem with DFT calculations is that the results – especially bond angles and C–O stretching frequency – can be sensitive to the functional.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) in a neon matrix – compare the lowest energy absorption band of Cr(CO)6 at 340 nm (29
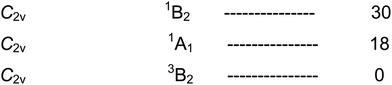
000 cm−1) in a neon matrix – compare the lowest energy absorption band of Cr(CO)6 at 340 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). Translated into electronic states, this is the transition from the ground 1A1 state to the excited 1E state (see Fig. 7). The reduced symmetry and reduced number of CO groups means that low-lying electronic transitions are ubiquitous for coordinatively unsaturated metal carbonyls.
000 cm−1). Translated into electronic states, this is the transition from the ground 1A1 state to the excited 1E state (see Fig. 7). The reduced symmetry and reduced number of CO groups means that low-lying electronic transitions are ubiquitous for coordinatively unsaturated metal carbonyls.
This analysis shows that – ignoring the triplet states, to which we will return – the lowest energy transition of Cr(CO)5 is from 1A1 to the 1E state. However, this C4v excited state is unstable with respect to D3h [(e′′)4(e′)2, i.e.1E′)]. In turn, this excited state is unstable in turn with respect to the ground state C4v structure [(b2)2(e)4; 1A1] (Fig. 7 and 13). Thus with this simple model we can explain why irradiation into the lowest absorption band of Cr(CO)5 in a matrix leads to a Berry pseudorotation (see Section 2).
A paper121 which is useful for providing earlier references, employs three popular DFT functionals (B3LYP, BP86, M06-L) to examine, among other systems, Cr(CO)5 and Fe(CO)4. We can summarise the energy level situation, in kcal mol−1, for Cr(CO)5 with approximate values based on a variety of calculations (Table 4).
| Symmetry | d orbital occupancy | Electronic state | Energy (kcal mol−1) |
|---|---|---|---|
| C 4v | [(b2)2(e)3(a1)1] | 1E | 45 |
| D 3h | [(e′′)4(e′)2] | 1E′ | 25 |
| C 4v | [(b2)2(e)3(a1)1] | 3E | 17 |
| D 3h | [(e′′)4(e′)2] | 3A1′ | 12 |
| C 4v | [(b2)2(e)4] | 1A1 | 0 |
Elian and Hoffmann pointed out that the mixing of the empty dz2 and pz orbitals of Cr(CO)5 generates a low-lying orbital, perfectly adapted for turning it into a powerful Lewis acid.114 Does this account for the formation of alkane complexes and noble gas complexes, probably yes for the former but perhaps not for the latter? Both ab initio and DFT calculations were carried by Ehlers et al. on M(CO)5Ng. This important work127 argued that the interaction involved van der Waals forces rather than genuine chemical bonds between the metal and the noble gas. A critical part of the original experimental evidence depended on the shifts in the energy of the excited 1E state with Ng. A further impressive part of this paper is that time-dependent DFT calculations of the 1A1 → 1E (e4a10 → e3a11) transitions in Ng–Cr(CO)5 match closely those observed in the matrix (Table 5).40 The match with the Mo and W complexes was much less impressive.
5.2 Mechanisms of photodissociation of M(CO)6 (M = Cr, Mo, W)
But how does the photochemistry of the parent proceed? There have been an enormous number of UV/vis absorption studies on transition metal carbonyls; for our present purposes, the important point is that it has now been demonstrated conclusively by time-dependent DFT methods128,129 that the ligand field (LF) excited states of M(CO)6 molecules are at higher energy than metal-to-ligand charge transfer states (MLCT), contrary to what was originally thought. Moreover, there is also strong support from experiment.130 Thus, UV irradiation will populate MLCT states. However, although LF states are expected to lead to dissociation of CO groups, this is not the case for MLCT states. Given the high quantum yield for CO dissociation, this is at first rather puzzling. The calculations showed that that the relative energies of states change as the molecules distort and the MLCT state formed initially crosses into a LF state which is dissociative. Notice that there is no change in spin state. Elegant gas-phase experiments by Fuss and colleagues offer a detailed explanation of this result.131With the hexacarbonyls M(CO)6 (M = Cr, Mo, W), pulsed UV lasers (270–345 nm; approx. lifetime 30 fs) excite the molecules and the resulting dissociation is probed with non-resonant ionization (810 nm; 20 fs). The cations M(CO)x+ are analysed in a time-of-flight mass spectrometer. The repulsive LF state ejects a CO, leading to C4v M(CO)5 in an excited 1E state (Fig. 14). What then follows, as the authors point out, matches the previous conclusions, in particular the matrix polarisation experiments.41
 | ||
| Fig. 14 Three different laser wavelengths (270, 318 and 345 nm) excite M(CO)6 into MLCT states. There is then extremely rapid crossing (12.5 fs) to the repulsive LF state. See the text for the next steps. Chem. Phys., 2008, S. A. Trushin, K. Kosma, W. Fuss and W. E. Schmid, “Wavelength-independent ultrafast dynamics and coherent oscillation of a metal–carbon stretch vibration in photodissociation of Cr(CO)6 in the region of 270–345 nm”, 347, 309–323, Copyright 2008, with permission from Elsevier.131 | ||
In other words, this is dissociative photochemistry with no time to form equilibrated excited states. This experiment confirms the matrix experiments which implied that the C4v1E excited state is unstable with respect to the D3h1E′ state distorted form of M(CO)5 and this, in turn, relaxes to the 1A1C4v ground state structure. Photodissociation dynamics calculations132 have fleshed out the details of formation of Cr(CO)5 in its 1E excited electronic state within ca. 80 fs of excitation of Cr(CO)6 and how it crosses through the conical intersection into the ground state creating oscillations between trigonal bipyramidal and square pyramidal geometries corresponding to the Berry pseudorotation, very much as postulated in qualitative form 24 years earlier.
There is an alternative pathway in the gas phase. There may be sufficient energy in the M(CO)5 fragment to lead to further loss of CO groups, the number depending on the original laser wavelength. The interesting fact is that the generation of M(CO)n fragments involves only one photochemical act, the loss of a single CO from the parent. The loss of multiple CO groups contrasts with what usually happens in solution, where rapid collisions disperse the excess energy before the molecule can further dissociate.
As we described earlier, Cr(CO)5L complexes (L = Xe, CH4, phosphine, etc.) undergo wavelength-selective photochemistry. On irradiation at long wavelength, only the ligand L is ejected, while at shorter wavelength CO ejection is dominant. Why do they show this behaviour which is quite unlike that of most organic molecules? Baerends and colleagues133 by time-dependent DFT have shown the lowest excited state of Cr(CO)5(PH3) to be MLCT in character while the LF state formed by population of the dz2 orbital lies above it. However, as soon as the Cr–P bond lengthens, the states undergo an avoided crossing which occurs within the Cr–PH3 and beyond the Cr–CO equilibrium distances. The result is PH3 dissociation but a barrier remains for CO dissociation. This dissociation generates the first excited state of Cr(CO)5, so the same dynamics will ensue as described for Cr(CO)6 photodissociation, albeit with less excess energy. The occurrence of wavelength dependent photochemistry for Cr(CO)5L and other examples below depends on dissociation on an ultrafast timescale before the molecule can equilibrate with its surroundings.
5.3 Electronic states of Fe(CO)4, role of singlets and triplets, photochemical mechanisms for Fe(CO)5
We now turn to Fe(CO)4, for which the calculated energy levels119 are shown in Scheme 11.The first interesting point to note is that there is an isomerisation process in Fe(CO)4 analogous to the Berry pseudorotation in Fe(CO)5. This process can be induced by IR laser irradiation in one of the C–O IR bands of 13CO-enriched Fe(CO)4 trapped in a low-temperature matrix.134,135 Moreover it was shown that the mechanism of this process involves the very rare non-Berry pseudorotation (Fig. 15). Since an IR frequency of 2000 cm−1 corresponds to an energy of 5.7 kcal mol−1, this value represents an upper limit for this process. On the other hand, in the presence of L = CH4 or Xe, the interaction energy is sufficient to cause reaction to the more stable 1[Fe(CO)4L], which is lower in energy than the 3B2 ground state of the ‘bare’ Fe(CO)4 (see Scheme 6). Whether the triplet or singlet states are experimentally observed, depends on timescales.
 | ||
| Fig. 15 A permutation of three ligands consistent with the non-Berry pseudorotation. Adapted with permission from J. Am. Chem. Soc., 1984, 106, 50–54. Copyright 1984, American Chemical Society.135 | ||
Both the ground triplet and the excited singlet states of Fe(CO)4 have C2v structures, but with different bond angles. The paper by Sun et al. reports calculated bond angles of Fe(CO)4 obtained with several functionals (Table 6). For the 1A1 state, there is an excellent match between the calculated121 and experimental52,56 values. For the 3B1 state, there is some discrepancy which will not be resolved until there is new experimental evidence.
We turn to the photochemistry of the parent, Fe(CO)5. It is more complex than Cr(CO)6 for two reasons: the initially excited states are mixed in character and the ground states of Fe(CO)4 and Fe(CO)3 are triplets. Nonetheless the overall pattern is very similar. Fig. 16 shows part of the proposed pathway.136 After loss of a CO, Fe(CO)4 is generated in an excited C2vsinglet (1B2), which via the tetrahedral 1T2 state, relaxes to the singletC2v1A1 state, which is still electronically excited. This is the state observed by Zewail by electron diffraction. Weitz and colleagues, following their early TRIR experiments in which they only observed the triplet ground state (3B2),69 were also able to detect the excited singlet state.137 The relaxation from singlet to ground state triplet (3B2) takes >500 ps, which is why it was not observed in Zewail's studies.55
 | ||
| Fig. 16 The photodissociation of Fe(CO)5; times in fs. Reproduced with permission from J. Phys. Chem A, 2000, 104, 1997–2006. Copyright 2000, American Chemical Society.136 | ||
The magnitude of the triplet-singlet gap is not known experimentally and is extremely hard to determine computationally. Reactions involving a change of spin-state such as 1[Fe(CO)4] → 3[Fe(CO)4] or 3[Fe(CO)4] +L → 1[Fe(CO)4L] (L = CO, Xe, H2) are enabled by spin–orbit coupling. One approach to obtaining the barrier is to calculate the potential energy surfaces of the reactant and product along the appropriate coordinates and hence determine the minimum energy crossing point between them. This method has had considerable success, but there are subtleties in putting it into practice.97,138 A multidimensional method reports better agreement with experiment for the reaction with H2 but does not calculate the rate constant.139
Baerends et al.133 have also addressed the preference for PH3 dissociation for ax-Fe(CO)4(PH3) and shown by quantum dynamics that there is a strong preference for dissociation of PH3 over CO on population of the lowest excited state, but the details are different from those described for Cr(CO)5PH3. The theory of H2 dissociation from Fe(CO)4(H)2 has been addressed by Daniel140 by CASSCF methods. There are two singlet excited states accessed by UV irradiation 1B1 (dyz to  ) and 1A1 (3dx2–y2 to
) and 1A1 (3dx2–y2 to  ) where
) where 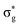 is Fe⋯H2 antibonding but H⋯H bonding. Elimination of H2 occurs within tens of femtoseconds in preference to dissociation of CO without intersystem crossing. The paper also addresses the reverse reaction on visible excitation of Fe(CO)4.
is Fe⋯H2 antibonding but H⋯H bonding. Elimination of H2 occurs within tens of femtoseconds in preference to dissociation of CO without intersystem crossing. The paper also addresses the reverse reaction on visible excitation of Fe(CO)4.
5.4 Photochemical mechanisms for Mn2(CO)10
The theory of the photochemistry of Mn2(CO)10 needs to explain why there are two competing dissociation processes with relative quantum yields that depend on irradiation wavelength and how the bridging ligand of Mn2(CO)9 is formed. Detailed DFT calculation by Baerends and colleagues141,142 have established an appropriate energy-level diagram and explained the photochemistry. A simplified diagram, based on Baerends’ work, is described in a later paper (Fig. 17).109 Low energy (337–355 nm) UV irradiation promotes the σ → σ* transition (1A1 → 1B2) which, via intersystem crossing, reaches the Mn–Mn dissociative 3B2 state; this produces two Mn(CO)5 radicals in their 2A1 ground states. To eject a CO group, higher energy UV is necessary, and the full picture is complex.141 The calculations suggest that the stable form of Mn2(CO)9 has the semibridging structure, (OC)4Mn(μ-CO)Mn(CO)4, as determined by the matrix isolation and TRIR experiments described earlier. However, as stated above, this cannot be the primary step in the photolysis. The authors suggest that the first step involves loss of an axial CO group, followed by the extremely fast rearrangement to the bridging structure. Cho et al. describe the time-resolved XANES and XAFS study of both Mn2(CO)10 and Mn(CO)5, irradiating at 400 nm in the long-wavelength edge of the band (Section 4.5.3).109 The XANES spectra are analysed by comparison with TD-DFT calculations to show details of the electronic structure of Mn(CO)5.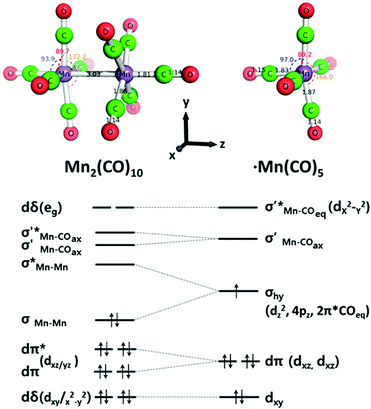 | ||
| Fig. 17 DFT optimised structures for Mn2(CO)10 in D4d and Mn(CO)5 radical in C4v symmetries with selected calculated bond angles and lengths. At the bottom are shown simplified MO diagrams with dominant metal contributions. Reproduced with permission from Inorg. Chem., 2016, 55, 5895–5903. Copyright 2016, American Chemical Society.109 | ||
5.5 Alternative types of metal carbonyl photochemistry
The principles of dissociative photochemistry outlined above can be extended to numerous substituted metal carbonyls but not to all. While cyclopentadienyl metal carbonyls follow the same pattern, there are some arene-substituted metal carbonyls and numerous diimine-substituted metal carbonyls that do not (diimine includes bipyridine, phenanthroline, etc.). The arene complexes (η6-arene)M(CO)3 (M = Cr, Mo) exhibit both CO dissociation and arene dissociation in different ratios according to solvent (see Fig. 3).32,143,144 Moreover, CO dissociation may be “delayed” for tens of picoseconds.2A further group of complexes exhibits dissociative photochemistry, but not of the CO ligands. Thus, irradiation of Ru(CO)(PPh3)3(H)2 results in reductive elimination of H2 and competing dissociation of PPh3 but there is no loss of CO.145 Similar behaviour has been observed for other metal monocarbonyl dihydride complexes.2
Diimine-substituted metal carbonyls usually exhibit quite different photochemical behaviour with long-lived (nanosecond) equilibrated excited states of charge-transfer character that are emissive and redox active. The application of [Re(CO)3(2,2′-bipy)L]+/0 complexes has proved exceptionally important.2 An early experiment146 showed that it was possible to probe, by TRIR, the long-lived excited state of [ClRe(CO)3(4,4′-bpy)2]; electron transfer from Re to the organic ligand results in an effective oxidation of the Re, and consequently an upward shift in the C–O IR bands. Since then there has been a plethora of experiments exploiting the application of a variety of time-resolved spectroscopies to excited states and corresponding investigation by theory.2,32,147 Recent examples of IR, Raman and X-ray methods also involve DFT calculations.148–150
Theory and dynamics: key points(1) Theoretical structures of metal carbonyl fragments M(CO)n agree with experiment and depend on n and the d-electron count.(2) CO stretching frequencies difficult to reproduce accurately by computation. (3) Lower symmetry and reduced n results in low-lying excited states for 16e and 14e-M(CO)n compared with 18e species. (4) Photodissociation of CO depends on excitation into MLCT excited state followed by ultrafast (femtosecond) crossing into dissociative LF state. (5) Dissociation proceeds through excited electronic states of the photoproduct. (6) The wavelength dependence of the photochemistry of Cr(CO)5L and Mn2(CO)10 depends on ultrafast branching leading to dissociation down competing channels. (7) The spin state may change after dissociation as in Fe(CO)4 but not before. (8) Femtosecond dissociation is not universal for metal carbonyls. Three classes of exception: (a) (η6-arene)M(CO)3 (M = Cr, Mo) lose CO more slowly (b) metal monocarbonyl dihydrides lose H2 on irradiation (c) complexes with low-lying excited states involving charge transfer to non-carbonyl ligands such as diimines exhibit equilibrated excited states |
6. Applications to synthesis of complexes with labile ligands
6.1 Importance of labile ligands.
We have already seen that reactive intermediates such as Cr(CO)5 coordinate solvent molecules on an ultrafast timescale and that their lifetime with respect to re-coordination of CO is strongly dependent on the coordinating ligand. Examples encountered so far include alkane complexes, noble-gas (Ng) complexes and the short-lived perfluoroalkane complexes. We have also seen the rapid conversion of Cr(CO)5(η2-benzene) to Cr(CO)5(THF). Thus, photodissociation of metal carbonyls is an excellent method for investigating the ability of these unusual ligands to form labile complexes. Are such complexes important? The alkane complexes have acted as paradigms for the development of σ-bond complexes,151 while the Cr(CO)5Xe and Fe(CO)4Xe were the first examples of the metal–Ng bond. These complexes also have a role in synthesis since they prolong the lifetime of the reaction intermediates giving them sufficient time to react with solutes that may be present in lower concentrations. The classic synthetic method of forming Cr(CO)5(THF) photochemically and then replacing THF with another ligand in a thermal reaction is an example of such a strategy but is limited to the formation of less labile complexes than Cr(CO)5(THF). In this section, we examine the photochemical method for the formation of N2 and H2 complexes as well as labile metal alkyl hydride complexes, concentrating on information that has not been obtained by conventional synthetic methods. Photochemistry in organic solvents is limited by the low solubility¶ of N2 and H2. This limitation is removed in liquefied noble gases under pressure where N2 and H2 have much higher solubility than in most conventional solvents under similar conditions.6.2 Examples of dinitrogen complexes
N2 is isoelectronic with CO, but the transition metal complexes with N2 as ligand are much less stable than metal carbonyls. The first metal carbonyl, Ni(CO)4, was synthesised in 1890 but it was a further 75 years before the first stable N2 complex, [Ru(N2)(NH3)5]2+, was made.152 The first successful attempt to form a dinitrogen complex by matrix photochemistry was Rest's generation of Ni(CO)3(N2) by photolysis of Ni(CO)4 in a 14N2 matrix (1/5000) at 20 K. As well as IR bands readily assigned to the Ni(CO)3 group, a band at 2266 cm−1, which shifted to 2193 cm−1 when the experiment was repeated in a 15N2 matrix, was clearly identified with the N–N stretching vibration.153 It proved possible to generate this unstable species by photolysis of Ni(CO)4 in N2-doped liquid Kr, and identify it by comparison with the matrix data. In the presence of added CO, the reverse reaction readily occurred and by monitoring this reaction over the temperature range 112–127 K, a Ni–N2 bond dissociation energy of at least ∼10 kcal mol−1 was estimated.154In a similar manner, by a combination of matrix isolation and liquefied noble gas solvents, it proved possible to generate all the species Cr(CO)6−x(N2)x (x = 1 to 5).155 As photolysis proceeds in N2-doped liquid Xe at 194 K, the degree of substitution increases. The assignment of the individual species was enormously helped by employing the EFFF approximation technique introduced by Timney.25 Even now, we know of no other solution observations of a complex with five N2 ligands.
The formation of Cr(CO)5(N2) has been examined by TRIR of Cr(CO)6 in N2-saturated cyclohexane at room temperature. As expected, the first identified transient is Cr(CO)5(cyclohexane) which converts to Cr(CO)5(N2) with a first order rate constant of ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1. At room temperature, the Cr(CO)5(N2) has a lifetime of about 1 s.156 By employing photoacoustic calorimetry, Walsh et al. estimated the Cr–N2 bond energy of Cr(CO)5(N2) as ∼19 kcal mol−1.157
000 s−1. At room temperature, the Cr(CO)5(N2) has a lifetime of about 1 s.156 By employing photoacoustic calorimetry, Walsh et al. estimated the Cr–N2 bond energy of Cr(CO)5(N2) as ∼19 kcal mol−1.157
Many other such photochemical reactions have been carried out to generate species of varying degrees of stability.158 In the most recent example, the photolysis of Mn(C^N)(CO)4 (C^N = bis-(4-methoxyphenyl)methanimine), was examined by ultrafast TRIR in both pure heptane, and in heptane under an atmosphere of N2. In pure heptane, at <2 ps, the spectra displayed the usual ‘hot’ features which relaxed to show at ∼10 ps C–O IR features readily assigned to Mn(C^N)(CO)3(heptane). Under N2, the species Mn(C^N)(CO)3(N2) was formed from the solvent complex in ∼20 ns.159
6.3 Examples of dihydrogen complexes.
Kubas’ discovery in 1984 that transition-metal compounds could not only bind hydrogen as hydride but also as dihydrogen ligands, marked a seminal moment in coordination chemistry.160,161 The photochemistry of metal carbonyls that include hydride ligands has been reviewed.162 Kubas’ original experiment reported the formation of W(CO)3(PR3)2(η2-H2) from thermal reaction of H2 with W(CO)3(PR3)2 (R = cyclohexyl, iPr). We describe some experiments which demonstrate the photochemical generation of dihydrogen complexes from metal carbonyls.Although photolysis of Cr(CO)6 in H2-doped Ar matrices provided strong evidence for the formation of an H2 species, there was scant information from any vibrations involving an attached H2 group.163 However, photolysis of Cr(CO)6 in H2- and D2-doped liquid Xe at 200 K, produced convincing evidence from the H–H and D–D stretching vibrations at 3030 and 2242 cm−1 respectively, of the formation of Cr(CO)5(H2).164 Moreover the position of the C–O bands was consistent with this species rather than the dihydride Cr(CO)5(H)2. The H–H and D–D stretching modes are broadened because of internal rotation of the dihydrogen ligand. Under the conditions of this experiment, the product is thermally quite stable although isotopic exchange of coordinated H2 occurs under D2. In contrast, TRIR of Cr(CO)6 in H2-saturated cyclohexane at room temperature, shows that Cr(CO)5(H2) decays with a rate constant of 2.5 s-1.165 Further experiments showed the generation of the corresponding Mo and W species as well as Cr(CO)4(H2)2.164 Subsequently, M(CO)5(H2) (M = Cr, W) complexes were characterised by NMR spectroscopy following photolysis of M(CO)6 at 195 K in several solvents under 1.5 atm H2.166 The role of dihydrogen complexes is illustrated by the unusual product distribution in the photocatalytic hydrogenation of norbornadiene (NBD) by Cr(CO)6 which proceeds initially via Cr(CO)4(η4-NBD). The latter is converted to two isomers of Cr(CO)3(η4-NBD)(solvent) followed by the corresponding dihydrogen complexes Cr(CO)3(η4-NBD)(H2), one of which generates norbornene and the other nortricyclene.167
The reactions of CpM(CO)4 with H2 in liquefied Xe are of particular interest because of the changes in product distribution. For M = V the only product is CpV(CO)3(H2), for M = Ta only the dihydride CpM(CO)3(H)2 is formed, while for M = Nb both dihydrogen and dihydride complexes are formed. The highest wavenumber a′ C–O stretch is shifted down ca. 30 cm−1 with respect to CpM(CO)4 for dihydrogen complexes whereas that of the dihydride complexes is shifted up by ca. 15 cm−1 in accord with the increased oxidation state The H–H stretching mode is observed as a broad band at ca. 2600 cm−1. The dihydrogen and dihydride complexes of niobium lie at rapid equilibrium, with a standard enthalpy of 3.5 ± 0.5 kJ mol−1 in favour of CpNb(CO)3(H2).168
6.4 The link between C–H oxidative addition and alkane coordination.
There was great excitement in 1982 when the activation of saturated hydrocarbons to produce alkyl complexes was demonstrated.169,170 The work by Hoyano and Graham (eqn (8)) is particularly relevant to this Review since it involved the photolysis of a metal carbonyl in neopentane to form the product of oxidative addition:170 | (8) |
Graham and colleagues even managed to activate methane, by photolysis of Cp*Ir(CO)2 in CH4-doped perfluorohexane to give Cp*Ir(CO)(H)(CH3).171 This was a clever experiment. Graham did not have the facilities for working in liquid or supercritical CH4, but from the matrix and liquid perfluoro experiments, it was known that the perfluoro solvent binds less strongly to a carbonyl fragment than a hydrocarbon, so the CH4 displaces the perfluoro solvent as ligand. These oxidative addition reactions are characteristic of the 4d and 5d metals of group 8 and 9 that form d8 reaction intermediates, with a few examples from group 7. The obvious route involves the photoactivated loss of CO to form the unsaturated Cp*Ir(CO) intermediate which then reacts with the hydrocarbon. By analogy with the oxidative addition of H2, it might be surmised that the mechanism involves a species in which a C–H bond forms an Ir(CH4) complex. As described in previous sections, there is plenty of evidence that metal carbonyl fragments interact quite strongly with saturated hydrocarbons such as cyclohexane.
Meanwhile, the question is: can an alkane complex be identified, and can its conversion to the alkyl hydride be observed and monitored? By analogy with earlier work, the matrix technique might be one method of following this. In matrix photolysis experiments on Cp*Ir(CO)2 in CH4 at 12 K, Rest et al. easily observed the activated species, i.e. Cp*Ir(CO)(H)(CH3). Moreover, oxidative addition of methane was also observed with CpIr(CO)2, Cp*Rh(CO)2 and CpRh(CO)2.172 Notably the reaction proceeded in much higher yield starting from CpIr(CO)(H)2, but evidence for CpIr(CO)(CH4) was not decisive.173 An ultrafast TRIR study on CpIr(CO)2 in cyclohexane showed that the risetime of the CpIr(CO)(cyclohexyl)(H) was as short as 2 ps and no cyclohexane complex was observed.174
In contrast, George et al.'s TRIR study on Cp*Re(CO)3 and CpRe(CO)3 in supercritical methane and ethane demonstrated formation of a methane complex prior to the corresponding methyl hydride complex.175 Irradiation of Cp*Re(CO)3 in sc CH4 shows Cp*Re(CO)2(CH4) after a few picoseconds together with vibrationally excited Cp*Re(CO)3. Monitoring over the subsequent nanoseconds shows the partial conversion (Fig. 18) of Cp*Re(CO)2(CH4) to Cp*Re(CO)2(CH3)H as an equilibrium mixture (k = (5 ± 2) × 108 s−1). Finally, these species react back with CO to Cp*Re(CO)3 over hundreds of microseconds. The position of equilibrium shifts toward the alkane complex with the Cp analogue and with use of ethane instead of methane. The spectra show very conspicuously that the ν(CO) bands of the Re(I) complexes lie ca. 50 cm−1 to high frequency of the isomeric Re(III) complexes.
 | ||
| Fig. 18 IR difference spectra recorded at the time delays shown after photolysis of indicated species in ethane (114 bar) or methane (276 bar) in the presence of CO at room temperature. Red and blue shaded areas indicate ν(CO) bands of CpRe(CO)2(alkane) and CpRe(CO)2(alkyl)(H), respectively. Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6933–6938, Copyright 2007 National Academy of Sciences.175 | ||
The formation of labile metal alkyl hydrides carries implications for the mechanisms of synthesis of stable products in hydrocarbon solution formed by oxidative addition, substitution or by formation of dinuclear products. All these processes require the intermediacy of metal alkyl hydrides in alkanes or metal aryl hydrides in arenes. Nowhere is this more conspicuous than in the cases of CpRh(CO)2 and Cp*Rh(CO)2. The initial stage is, as usual, immediate CO loss and formation of an alkane complex that then converts to the alkyl hydride complex. The reactions have been studied in liq Kr at low temperature176 and in liquid or supercritical alkanes177 at room temperature. The lifetime of linear alkane complexes is in the range 3-18 ns at room temperature and varies systematically with the length of the alkane chain as a consequence of subtle interplay between 1,2-shifts of the metal along the chain (chain walking) and oxidative cleavage of the primary C–H bond.176 Complexes of cyclic alkanes undergo oxidative cleavage more slowly than their linear counterparts.
Flash photolysis and TRIR spectroscopy in combination with matrix isolation demonstrated what happens next. The CpRh(CO)(cyclohexyl)H now acts as a long-lived store of the unsaturated intermediate.178 In the absence of other ligands, the symmetrical dimer [CpRh(μ-CO)]2 is formed over tens of milliseconds. The latter reacts with CO to yield the final stable product [CpRh(CO)]2(μ-CO) (k = (1.2 ± 0.1) × 103 dm3 mol−1 s−1). The structure of [CpRh(μ-CO)]2 was proved by polarised photochemistry in matrices. In the presence of added silane, Et3SiH, the CpRh(CO)(cyclohexyl)H reacts to form CpRh(CO)(SiEt3)H by complex kinetics|| with a limiting rate at high [Et3SiH] of 2.7 × 103 s−1.178
Applications to synthesis of complexes with labile ligands: key points(1) Labile ligands act as stores of reaction intermediates.(2) Matrix isolation, time-resolved spectroscopy and photolysis in liq and sc noble gases enable characterisation of metal carbonyl complexes with η2-H2, N2, alkane, noble-gas and silane ligands. (3) Kinetics of formation and their onward reactivity have been determined. (4) For some precursors, reaction with alkanes to form C–H oxidative addition products occurs within 2 ps of the initial laser pulse. For others, it is possible to detect alkane complexes as precursors to oxidative addition. (5) The C–H oxidative addition products may themselves be very labile. |
7. Photocatalysis
In a recent review on metal hydride photochemistry, Perutz and Procacci162 described the different types of photocatalysis following Wrighton1 and Hennig.179 The quantum yield, ϕ, is often the key measurement that distinguishes photoinduced catalysis from photoassisted catalysis. In the former, the photochemical act lies outside the catalytic cycle which consists of thermal reactions, ϕ may be greater than unity and the free energy of the catalytic reaction must be negative. In photoassisted catalysis, the photochemical act lies inside the cycle and ϕ ≤ 1, but the free energy may be positive. Photocatalysis may be achieved with the aid of a photosensitiser, though this is uncommon for metal carbonyls. Photosensitised catalysis requires transfer of either an electron or excitation energy from the sensitiser to an acceptor and can belong to either of the above classes.One early example of C–H activation of alkanes stands out. Goldman and colleagues observed catalytic dehydrogenation of cycloalkanes with Rh(PMe3)2(CO)Cl (0.1%) as photocatalyst with turnover numbers up to 5000 for cyclooctane. The quantum yield is inversely dependent on the pressure of added CO and independent of pressure of added H2.180 There is a large kinetic isotope effect when using cyclohexane and its deuterated analogues. Considering also that the free energy for this reaction is positive, this must be photoassisted catalysis. The evidence indicates that this reaction is driven by photochemical CO loss within the catalytic cycle, followed by alkane oxidative addition.180 That Rh(PMe3)2(CO)Cl undergoes photochemical CO loss has been confirmed by nanosecond TRIR.181 Time-resolved absorption suggests that there may be an excited state181 with time-constant ca. 40 ps preceding CO loss, but ultrafast IR data are lacking. Beller and colleagues have revisited this reaction and improved the conditions so that linear alkanes can also be dehydrogenated with good turnover numbers.182 With the benefit of DFT calculations and a thermodynamic cycle, their results indicate that reaction of the CO-loss product RhCl(PMe3)2 with octane is likely to be uphill. They therefore suggest that the reaction occurs from an excited state of Rh(PMe3)2(CO)Cl, but they did not explain the CO inhibition of the quantum yield.
The borylation of linear alkanes is a reaction with negative free energy and therefore could proceed by either photoassisted or photoinduced catalysis. Hartwig and colleagues demonstrated that Cp*Re(CO)3 (2.5%) under CO (2 bar) reacts photocatalytically with pentane and B2pin2 (pin = pinacolate) to form RBpin (R = pentyl) in 95% yield with respect to B2pin2 (i.e. 38 turnovers). The dicarbonyl Cp*Re(CO)2(Bpin)2 (mixture of cis and trans isomers) was isolated from the reaction and also acted as a photocatalyst, presumably via photochemical CO loss.183 More recently, CpFe(CO)2(Cu(IPr)) (IPr = N,N′-bis(2,6- diisopropylphenyl)imidazol-2-ylidene) has been used as the photocatalyst for arene borylation by HBpin. The catalytic cycle is postulated to involve formation of Cu(IPr)H and CpFe(CO)2(Bpin) which reacts photochemically with arene to form CpFe(CO)2H and Ar(Bpin).184 Similar photocatalytic reactions have been performed with Rh(PMe3)2(CO)Cl as photocatalyst, this time with the suggestion of CO photodissociation outside the cycle, i.e. photoinduced catalysis – surprising considering the alkane dehydrogenation.185
One of the most spectacular examples of photoinduced catalysis is the reaction of CpWH(CO)3 which undergoes CO substitution by PBu3 on UV irradiation via a radical chain reaction started by W–H homolysis (ϕ > 30). In the presence of small quantities of [CpW(CO)3]2, the quantum yield increased to about 1000.186 This reaction exploits the ability of metal hydride carbonyls to undergo photochemical homolysis of the M–H bond and the rapid thermal substitution of 17-electron species.
Photochemical reactions can also be used to identify short-lived intermediates in thermal catalytic reactions as exemplified in Scheme 3. Photochemical initiation benefits mechanistic investigation because the commencement of reaction is synchronised allowing the reaction sequence to be monitored at times from picoseconds to milliseconds in and beyond.
The mechanism of photocatalytic hydrogenation of norbornadiene by chromium carbonyls is considered in Section 6.3. Manganese and iron carbonyls continue to be used as photocatalysts for hydrosilation of ketones, aldehydes and carboxylic acids.187
Photocatalysis: key points(1) Catalytic reactions initiated by photochemical processes, e.g. ligand dissociation.(2) Photoinduced catalysis: light absorption outside catalytic cycle, ϕ unlimited, ΔGreaction negative. (3) Photoassisted catalysis: light absorption inside catalytic cycle, ϕ ≤ 1, ΔGreaction positive or negative. |
8. Conclusions and outlook
In this Tutorial Review, we have probed the subtlety of the photochemistry of transition metal carbonyls, emphasising the behaviour of the intermediates. We have shown the importance of metal carbonyl photochemistry to understanding fundamental principles of transition-metal chemistry and photochemistry, as well as to applications such as photocatalysis. In describing these results, we have delved into state-of-the art techniques, especially those of time-resolved spectroscopy. The principles that we have developed in each section have been summarised in text-boxes. The most important of these conclusions are brought together as Key Learning Points at the start of this review.Abbreviations
| CASSCF | Complete active space self-consistent field |
| CCSD(T) | Coupled-cluster with single and double and perturbative triple excitations |
| CORM | Carbon monoxide releasing molecule |
| DFT | Density functional theory |
| EFFF | Energy factored force field |
| EPR | Electron paramagnetic resonance |
| FTIR | Fourier transform infrared |
| IR | Infrared |
| MLCT | Metal-to-ligand charge transfer |
| Ng | Noble gas |
| NMR | Nuclear magnetic resonance |
| PFMCH | Perfluoromethylcyclohexane |
| PhotoCORM | Photochemical carbon monoxide releasing molecule |
| RIXS | Resonant inelastic X-ray scattering |
| sc | supercritical |
| THF | Tetrahydrofuran |
| TRIR | Time-resolved infrared |
| UV | Ultraviolet |
| XAFS | X-ray absorption fine structure |
| XANES | X-ray absorption near-edge structure |
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank all of our colleagues, students and coworkers who have contributed to the work described in this Review. We are grateful to the funders who have supported our work and to the generations of skilled technicians who built the equipment needed to perform our research.References
- M. S. Wrighton, Chem. Rev., 1974, 74, 401–430 CrossRef CAS.
- R. N. Perutz, O. Torres and A. Vlček, Jr., in Comprehensive Inorganic Chemistry II, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Oxford, 2013, vol. 8, ch. 8.06, pp. 229–253 Search PubMed.
- H. Braunschweig, R. D. Dewhurst, K. Radacki, C. W. Tate and A. Vargas, Angew. Chem., Int. Ed., 2014, 53, 6263–6266 CrossRef CAS PubMed.
- J. D. Watson, L. D. Field and G. E. Ball, Nat. Chem., 2022 DOI:10.1038/s41557-022-00929-w.
- B. E. Mann, Organometallics, 2012, 31, 5728–5735 CrossRef CAS.
- P. C. Ford, Coord. Chem. Rev., 2018, 376, 548–564 CrossRef CAS.
- Z. Li, A. E. Pierri, P.-J. Huang, G. Wu, A. V. Iretskii and P. C. Ford, Inorg. Chem., 2017, 56, 6094–6104 CrossRef CAS PubMed.
- R. Sakla, A. Singh, R. Kaushik, P. Kamur and D. A. Jose, Inorg. Chem., 2019, 58, 10761–10768 CrossRef CAS PubMed.
- S. H. C. Askes, G. U. Reddy, R. Wyrwa, S. Bonnet and A. Schiller, J. Am. Chem. Soc., 2017, 139, 15292–15295 CrossRef CAS PubMed.
- L. A. Hammarback, B. J. Aucott, J. T. W. Bray, I. P. Clark, M. Towrie, A. Robinson, I. J. S. Fairlamb and J. M. Lynam, J. Am. Chem. Soc., 2021, 143, 1356–1364 CrossRef CAS PubMed.
- C. P. Simpson, O. L. Adebolu, J.-S. Kim, V. Vasu and A. D. Asandei, Macromolecules, 2015, 48, 6404–6420 CrossRef CAS.
- M. Chen, A. Pekker, W. Li, M. E. Itkis, R. C. Haddon and E. Bekyarova, Carbon, 2018, 129, 450–455 CrossRef CAS.
- E. G. Look and H. D. Gafney, J. Phys. Chem., C, 2013, 117, 12268–12279 CrossRef CAS PubMed.
- For a review of bandwidths, see J. J. Turner, in Handbook of Vibrational Spectroscopy, ed. J. M. Chalmers and P. R. Griffiths, J. Wiley, Chichester, UK, 2002, vol. 1, pp. 101–127 Search PubMed.
- W. B. Maier II, M. Poliakoff, M. B. Simpson and J. J. Turner, J. Chem. Soc., Chem. Commun., 1980, 587–589 RSC.
- S. J. Barlow, M. W. George and M. Poliakoff, in Handbook of vibrational spectroscopy, ed. J. M. Chalmers and P. R. Griffiths, J. Wiley, Chichester, UK, 2002, vol. 4, pp. 3124–3136 Search PubMed.
- C. S. Kraihanzel and F. A. Cotton, Inorg. Chem., 1963, 2, 533–540 CrossRef CAS and references therein.
- For an excellent overall picture of metal carbonyl spectra, see P. S. Braterman, Metal Carbonyl Spectra, Academic Press, London, 1975 Search PubMed.
- L. H. Jones, Inorganic Vibrational Spectroscopy, Marcell Dekker, New York, 1971 Search PubMed.
- J. K. Burdett, R. N. Perutz, M. Poliakoff and J. J. Turner, Inorg. Chem., 1976, 15, 1245 CrossRef CAS.
- J. K. Burdett, M. Poliakoff, J. A. Timney and J. J. Turner, Inorg. Chem., 1978, 17, 948–952 CrossRef CAS.
- C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2953–2956 CrossRef CAS.
- D. G. Gusev, Organometallics, 2009, 28, 763–770 CrossRef CAS.
- R. K. Hocking and T. W. Hambley, Organometallics, 2007, 26, 2815–2823 CrossRef CAS.
- J. A. Timney, Inorg. Chem., 1979, 18, 2502 CrossRef CAS.
- J. A. Timney, Spectrochim. Acta, Part A, 1995, 53, 33–38 CrossRef.
- D. C. Grills and M. W. George, in Handbook of Vibrational Spectroscopy, ed. J. M. Chalmers and P. R. Griffiths, J. Wiley, Chichester, UK, 2002, vol. 1, pp. 677–693 Search PubMed.
- H. Hermann, F.-W. Grevels, A. Henne and K. Schaffner, J. Phys. Chem., 1982, 86, 5151–5154 CrossRef CAS.
- E. R. Kennehan, K. T. Munson, C. Grieco, G. S. Doucette, A. R. Marshall, M. C. Beard and J. B. Asbury, J. Am. Chem. Soc., 2021, 143, 13824–13834 CrossRef CAS PubMed.
- R. N. Sampaio, D. C. Grills, D. E. Polyansky, D. J. Szalda and E. Fujita, J. Am. Chem. Soc., 2020, 142, 2413–2428 CrossRef CAS PubMed.
- P. Portius, J. Yang, X.-Z. Sun, D. C. Grills, P. Matousek, A. W. Parker, M. Towrie and M. W. George, J. Am. Chem. Soc., 2004, 126, 10713–10720 CrossRef CAS PubMed.
- M. K. Kuimova, W. Z. Alsindi, J. Dyer, D. C. Grills, O. S. Jina, P. Matousek, A. W. Parker, P. Portius, X. Z. Sun, M. Towrie, C. Wilson, J. Yang and M. W. George, Dalton Trans., 2003, 3996–4006 RSC.
- X. Wu, Z. Liu, T. S. Murphy, X. Z. Sun, M. W.-D. Hanson-Heine, M. Towrie, J. N. Harvey and M. W. George, Faraday Discussions, 2019, 220, 86–104 RSC.
- I. W. Stolz, G. R. Dobson and R. K. Sheline, J. Am. Chem. Soc., 1962, 84, 3589–3590 CrossRef CAS.
- I. W. Stolz, G. R. Dobson and R. K. Sheline, J. Am. Chem. Soc., 1963, 85, 1013–1014 CrossRef CAS.
- See, e.g.: H. W. Brown and G. C. Pimentel, J. Chem. Phys., 1958, 29, 883–888 CrossRef CAS.
- A. J. Rest and J. J. Turner, J. Chem. Soc. D: Chem. Commun., 1969, 375–376 RSC.
- M. A. Graham, M. Poliakoff and J. J. Turner, J. Chem. Soc. A, 1971, 2939–2948 RSC.
- R. N. Perutz and J. J. Turner, Inorg. Chem., 1975, 14, 262–270 CrossRef CAS.
- R. N. Perutz and J. J. Turner, J. Am. Chem. Soc., 1975, 97, 4791–4799 CrossRef CAS.
- J. K. Burdett, J. M. Grzybowski, R. N. Perutz, M. Poliakoff, J. J. Turner and R. F. Turner, Inorg. Chem., 1978, 17, 147–154 CrossRef CAS.
- J. J. Turner, J. K. Burdett, R. N. Perutz and M. Poliakoff, Pure Appl. Chem., 1977, 49, 271–285 CAS.
- J. Nasielski and A. Colas, J. Organomet. Chem., 1975, 101, 215–219 CrossRef CAS.
- M. Poliakoff, Inorg. Chem., 1976, 15, 2022–2031 CrossRef CAS.
- M. Poliakoff, Inorg. Chem., 1976, 15, 2892–2897 CrossRef CAS.
- R. N. Perutz and J. J. Turner, J. Am. Chem. Soc., 1975, 97, 4800–4804 CrossRef CAS.
- M. J. Almond, J. A. Crayston, A. J. Downs, M. Poliakoff and J. J. Turner, Inorg. Chem., 1986, 25, 19–25 CrossRef CAS.
- M. Zhou, L. Andrews and C. W. Bauschlicher, Chem. Rev., 2001, 101, 1931–1961 CrossRef CAS PubMed.
- X. Wu, L. Zhao, J. Jin, S. Pan, P. Sudip, W. Li, J. Xiaoyang, W. Guanjun, Z. Mingfei and G. Frenking, Science, 2018, 361, 912–916 CrossRef CAS PubMed.
- M. Poliakoff and J. J. Turner, J. Chem. Soc., Dalton Trans., 1973, 1351–1357 RSC.
- M. Poliakoff and J. J. Turner, J. Chem. Soc., Dalton Trans., 1974, 2275–2285 Search PubMed.
- M. Poliakoff and J. J. Turner, Angew. Chem., Int. Ed., 2001, 40, 2809–2812 CrossRef CAS PubMed.
- T. J. Barton, R. Grinter, A. J. Thomson, B. Davies and M. Poliakoff, J. Chem. Soc., Chem. Commun., 1977, 841–842 RSC.
- M. Poliakoff and E. Weitz, Acc. Chem. Res., 1987, 20, 408–414 CrossRef CAS.
- H. Ihee, J. Cao and A. H. Zewail, Chem. Phys. Lett., 1997, 281, 10–19 CrossRef CAS.
- H. Ihee, J. Cao and A. H. Zewail, Angew. Chem., Int. Ed., 2001, 40, 1532–1535 CrossRef CAS PubMed.
- M. Poliakoff, J. Chem. Soc., Dalton Trans., 1974, 210–212 RSC.
- C. R. Kemnitz, E. S. Ball and R. J. McMahon, Organometallics, 2012, 31, 70–84 CrossRef CAS.
- T. J. Meyer and J. V. Caspar, Chem. Rev., 1985, 85, 187–218 CrossRef CAS.
- A. F. Hepp and M. S. Wrighton, J. Am. Chem. Soc., 1983, 105, 5934–5935 CrossRef CAS.
- I. R. Dunkin, P. Harter and C. J. Shields, J. Am. Chem. Soc., 1984, 106, 7248–7249 CrossRef CAS.
- S. P. Church, M. Poliakoff, J. A. Timney and J. J. Turner, J. Am. Chem. Soc., 1981, 103, 7515–7520 CrossRef CAS.
- S. A. Fairhurst, J. R. Morton, R. N. Perutz and K. F. Preston, Organometallics, 1984, 3, 1389–1391 CrossRef CAS.
- R. H. Hooker, K. A. Mahmoud and A. J. Rest, J. Chem. Soc. Chem. Commun., 1983, 1022–1024 RSC.
- A. F. Hepp, J. P. Blaha, C. Lewis and M. S. Wrighton, Organometallics, 1984, 3, 174–177 CrossRef CAS.
- J. P. Blaha, B. E. Bursten, J. C. Dewan, R. B. Frankel, C. L. Randolph, B. A. Wilson and M. S. Wrighton, J. Am. Chem Soc., 1985, 107, 4561–4562 CrossRef CAS.
- F. A. Kvietok and B. E. Bursten, J. Am. Chem. Soc., 1994, 116, 9807–9808 CrossRef CAS.
- G. Nathanson, B. Gitlin, A. M. Rosan and J. T. Yardley, J. Chem. Phys., 1981, 74, 361–370 CrossRef CAS.
- A. J. Ouderkirk, P. Werner, N. L. Schultz and E. Weitz, J. Am. Chem. Soc., 1983, 105, 3354–3355 CrossRef CAS.
- K. Tanaka, Y. Tachikawa, K. Sakaguchi, T. Hikida and T. Tanaka, J. Chem. Phys., 1999, 111, 3970–3977 CrossRef CAS and references therein.
- E. Weitz, J. Phys. Chem., 1994, 98, 11256–11264 CrossRef CAS.
- T. A. Seder, S. P. Church and E. Weitz, J. Am. Chem. Soc., 1986, 108, 7518–7524 CrossRef CAS PubMed.
- R. Cercola, K. C. Fischer, S. L. Sherman, E. Garans, N. G.-K. Wong, L. A. Hammerback, J. M. Lynam, I. J. S. Fairlamb and C. Dessent, Chem. – Eur. J., 2020, 26, 10297–10306 CrossRef CAS PubMed.
- A. B. Wolk, C. M. Leavitt, E. Garand and M. A. Johnson, Acc. Chem. Res., 2014, 47, 202–210 CrossRef CAS PubMed.
- B. J. Aucott, J. B. Eastwood, L. A. Hammerback, I. P. Clark, I. V. Sazanovich, M. Towrie, I. J. S. Fairlamb and J. M. Lynam, Dalton Trans., 2019, 48, 16426–16436 RSC.
- P. Wernet, T. Leitner, I. Josefsson, T. Mazza, P. S. Miedema, H. Schröder, M. Beye, K. Kunnus, S. Schreck, P. Radcliffe, S. Düsterer, M. Meyer, M. Odelius and A. Föhlisch, J. Chem. Phys., 2017, 146, 211103 CrossRef PubMed.
- T. Leitner, I. Josefsson, T. Mazza, P. S. Miedema, H. Schröder, M. Beye, K. Kunnus, S. Schreck, S. Düsterer, A. Föhlisch, M. Meyer, M. Odelius and P. Wernet, J. Chem. Phys., 2018, 149, 044307 CrossRef CAS PubMed.
- J. M. Kelly, H. Hermann and E. K. von Gustorf, J. Chem. Soc., Chem. Commun., 1973, 105–106 RSC.
- S. P. Church, F.-W. Grevels, H. Hermann and K. Schaffner, Inorg. Chem., 1985, 24, 418–422 CrossRef CAS.
- R. Bonneau and J. M. Kelly, J. Am. Chem. Soc., 1980, 102, 1220–1221 CrossRef CAS.
- L. Biber, D. Reuvenov, T. Revzin, T. Sinai, A. Zahavi and R. H. Schultz, Dalton Trans., 2007, 41–51 RSC.
- A. A. Bengali and T. F. Stumbaugh, Dalton Trans., 2003, 354–360 RSC.
- A. G. Joly and K. A. Nelson, J. Phys. Chem., 1989, 93, 2876–2878 CrossRef CAS.
- T. P. Dougherty and E. J. Heilweil, Chem. Phys. Lett., 1994, 227, 19–25 CrossRef CAS.
- S. M. Arrivo, T. P. Dougherty, W. T. Grubbs and E. J. Heilweil, Chem. Phys. Lett., 1995, 235, 247–254 CrossRef CAS.
- T. Lian, S. E. Bromberg, M. C. Asplund, H. Yang and C. B. Harris, J. Phys. Chem., 1996, 100, 11994–12001 CrossRef CAS.
- J. E. Shanoski, E. A. Glascoe and C. B. Harris, J. Phys. Chem. B, 2006, 110, 996–1005 CrossRef CAS PubMed.
- S. P. Church, H. Hermann, F.-W. Grevels and K. Schaffner, J. Chem. Soc., Chem. Commun., 1984, 785–786 RSC.
- J. Z. Zhang and C. B. Harris, J. Chem. Phys., 1991, 95, 4024–4032 CrossRef CAS.
- B. D. Moore, M. B. Simpson, M. Poliakoff and J. J. Turner, J. Chem. Soc., Chem. Commun., 1984, 972–974 RSC.
- C. M. Brookes, J. P. Lamont, S. C. Nguyen, J. A. Calladine, X.-Z. Sun, C. B. Harris and M. W. George, Polyhedron, 2014, 72, 130–134 CrossRef CAS and references therein.
- A. J. Dixon, M. A. Healy, M. Poliakoff and J. J. Turner, J. Chem. Soc, Chem. Commun., 1986, 994–996 RSC.
- C. J. Arnold, T.-Q. Ye, R. N. Perutz, R. E. Hester and J. N. Moore, Chem. Phys. Lett., 1996, 248, 464–469 CrossRef CAS.
- M. B. Simpson, M. Poliakoff, J. J. Turner, W. B. Maier Il and J. G. McLaughlin, J. Chem. Soc., Chem. Commun., 1983, 1355–1357 RSC.
- B. H. Weiller, J. Am. Chem. Soc., 2002, 114, 10910–10915 CrossRef.
- X.-Z. Sun, M. W. George, S. G. Kazarian, S. M. Nikiforov and M. Poliakoff, J. Am. Chem. Soc., 1996, 118, 10525–10532 CrossRef CAS.
- M. Besora, J.-L. Carreón-Macedo, A. J. Cowan, M. W. George, J. N. Harvey, P. Portius, K. L. Ronayne, X.-Z. Sun and M. Towrie, J. Am. Chem. Soc., 2009, 131, 3583–3592 CrossRef CAS PubMed.
- V. Bachler, F.-W. Grevels, K. Kerpen, G. Olbrich and K. Schaffner, Organometallics, 2003, 22, 1696–1711 CrossRef CAS.
- P. T. Snee, C. K. Payne, K. T. Kotz, H. Yang and C. B. Harris, J. Am. Chem. Soc., 2001, 123, 2255–2264 CrossRef CAS PubMed.
- H. Yang, M. C. Asplund, K. T. Kotz, M. J. Wilkens, H. Frei and C. B. Harris, J. Am. Chem. Soc., 1998, 120, 10154–10165 CrossRef CAS.
- J. W. Kee, Y. Y. Tan, B. H.-G. Swennenhuis, A. A. Bengali and W. Y. Fan, Organometallics, 2011, 30, 2154–2159 CrossRef CAS.
- X.-Z. Sun, D. C. Grills, S. M. Nikiforov, M. Poliakoff and M. W. George, J. Am. Chem. Soc., 1997, 119, 7521 CrossRef CAS.
- S. Geftakis and G. E. Ball, J. Am. Chem. Soc., 1998, 120, 9953–9954 CrossRef CAS.
- J. A. Calladine, S. B. Duckett, M. W. George, S. L. Matthews, R. N. Perutz, O. Torres and K. Q. Vuong, J. Am. Chem. Soc., 2011, 133, 2303–2310 CrossRef CAS PubMed.
- W. H. Bernskoetter, C. K. Schauer, K. I. Goldberg and M. Brookhart, Science, 2009, 326, 553–556 CrossRef CAS PubMed.
- G. E. Ball, T. A. Darwish, S. Geftakis, M. W. George, D. J. Lawes, P. Portius and J. P. Rourke, Proc. Nat. Acad. Sci. U. S. A., 2005, 102, 1853–1858 CrossRef CAS PubMed.
- P. Wernet, K. Kunuus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M.-F. de Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81 CrossRef CAS PubMed.
- K. Kunnus, I. Josefsson, I. Rajkovic, S. Schreck, W. Quevedo, M. Beye, C. Weniger, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, K. J. Gaffney, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M.-F. de Groot, S. Techert, M. Odelius, P. Wernet and A. Föhlisch, Struct. Dyn., 2016, 3, 043204 CrossRef CAS PubMed.
- H. Cho, K. Hong, M. L. Strader, J. H. Lee, R. W. Schoellein, N. Huse and T. K. Kim, Inorg. Chem., 2016, 55, 5895–5903 CrossRef CAS PubMed.
- S. A. Bartlett, N. A. Besley, A. J. Dent, S. Diaz-Moreno, J. Evans, M. L. Hamilton, M. W.-D. Hanson-Heine, R. L. Horvath, V. Manici, X.-Z. Sun, M. Towrie, L. Wu, X. Zhang and M. W. George, J. Am. Chem. Soc., 2019, 141, 11471–11480 CrossRef CAS PubMed.
- A. S. Weller, F. M. Chadwick and A. I. Mckay, Adv. Organomet. Chem., 2016, 66, 223–276 CrossRef.
- R. H. Crabtree, Struct. Bond., 2017, 171, 63–77 CrossRef CAS.
- J. K. Burdett, J. Chem. Soc., Faraday Trans. 2, 1974, 70, 1599–1613 RSC.
- M. Elian and R. Hoffmann, Inorg. Chem., 1975, 14, 1059–1076 CrossRef.
- J. K. Burdett, Inorg. Chem., 1975, 14, 375–382 CrossRef CAS.
- A. R. Rossi and R. Hoffmann, Inorg. Chem., 1975, 14, 365–374 CrossRef CAS.
- P. Portius, M. Bühl, M. W. George, F.-W. Grevels and J. J. Turner, Organometallics, 2019, 38, 4288–4297 CrossRef CAS.
- J. H. Jang, J. G. Lee, H. Lee, Y. Xie and H. F. Schaefer III, J. Phys. Chem. A, 1998, 102, 5298–5304 CrossRef CAS.
- Obtained by, among other techniques, the vacuum UV photolysis of Cr(CO)6 in low-temperature matrices: P. A. Breeze, J. K. Burdett and J. J. Turner, Inorg. Chem., 1981, 20, 3369–3378 CrossRef CAS.
- See J. Kim, J. Kim and H. Ihee, J. Phys. Chem. A, 2013, 117, 3861–3868 CrossRef PubMed for some relevant references.
- Z. Sun, H. F. Schaefer III, Y. Xie, Y. Liu and R. Zhong, J. Comput. Chem., 2014, 35, 998–1009 CrossRef CAS PubMed.
- For example: On Cr(CO)6/Cr(CO)5; L. A. Barnes, L. Bowen and R. Lindh, J. Chem. Phys., 1993, 98, 3978–3989 CrossRef CAS; A. W. Ehlers and G. Frenking, J. Am. Chem. Soc., 1994, 116, 1514–1520 CrossRef.
- On Fe(CO)5/Fe(CO)4; L. A. Barnes, M. Rosi and C. W. Bauschlicher, Jr., J. Chem. Phys., 1991, 94, 2031–2039 CrossRef CAS.
- J. Kim, T. K. Kim, J. Kim, Y. S. Lee and H. Ihee, J. Phys. Chem. A, 2007, 111, 4697–4710 CrossRef CAS PubMed.
- T. Witte, J. S. Yeston, M. Motzkus, E. J. Heilweil and K.-L. Kompa, Chem. Phys. Lett., 2004, 392, 156–161 CrossRef CAS.
- C. R. Baiz, P.-l McRobbie, J. M. Anna, E. Geva and K. J. Kubarych, Acc. Chem. Res., 2009, 42, 1395–1404 CrossRef CAS PubMed.
- A. W. Ehlers, G. Frenking and E. J. Baerends, Organometallics, 1997, 16, 4896–4902 CrossRef CAS.
- A. Rosa, E. J. Baerends, S. J.-A. van Gisbergen, E. van Lenthe, J. A. Groeneveld and J. G. Snijders, J. Am. Chem. Soc., 1999, 121, 10356–10365 CrossRef CAS.
- S. Villaume, A. Strich, C. Daniel, S. A. Perera and R. J. Bartlett, Phys. Chem. Chem. Phys., 2007, 9, 6115 RSC.
- P. Hummel, J. Oxgaard, W. A. Goddard, III and H. B. Gray, Inorg. Chem., 2005, 44, 2454 CrossRef CAS PubMed.
- S. A. Trushin, K. Kosma, W. Fuss and W. E. Schmid, Chem. Phys., 2008, 347, 309–323 CrossRef CAS . This paper also provides references to the appropriate UV/Vis studies, and also earlier similar work.
- M. J. Paterson, P. A. Hunt, M. A. Robb and O. Takahashi, J. Phys. Chem. A, 2002, 106, 10494–10504 CrossRef CAS.
- T. P.-M. Goumans, A. W. Ehlers, M. C. van Hemert, A. Rosa, E.-J. Baerends and K. Lammertsma, J. Am. Chem. Soc., 2003, 125, 3558–3567 CrossRef CAS PubMed.
- B. Davies, A. McNeish, M. Poliakoff and J. J. Turner, J. Am. Chem. Soc., 1977, 99, 7573–7579 CrossRef CAS.
- M. Poliakoff and A. Ceulemans, J. Am. Chem. Soc., 1984, 106, 50–54 CrossRef CAS.
- S. A. Trushin, W. Fuss, K. L. Kompa and W. E. Schmid, J. Phys. Chem. A, 2000, 104, 1997–2006 CrossRef CAS.
- R. J. Ryther and E. Weitz, J. Phys. Chem., 1992, 96, 2561–2567 CrossRef CAS.
- M. Besora, J. Carreón-Macedo, A. Cimas and J. N. Harvey, Adv. Inorg. Chem., 2009, 61, 573–623 CrossRef CAS.
- T. Takayanagi, Y. Watabe and T. Miyazaki, Molecules, 2020, 25, 882–891 CrossRef CAS PubMed.
- M. C. Heitz and C. Daniel, J. Am Chem. Soc., 1997, 119, 8269–8275 CrossRef CAS.
- A. Rosa, G. Ricciardi, E. J. Baerends and D. J. Stufkens, Inorg. Chem., 1995, 34, 3425–3432 CrossRef CAS.
- M. P. Wilms, E. J. Baerends, A. Rosa and D. J. Baerends, Inorg. Chem., 1997, 36, 1541–1551 CrossRef CAS PubMed.
- I. P. Clark, M. W. George, G. M. Greetham, E. C. Harvey, C. Long, J. C. Manton and M. T. Pryce, J. Phys. Chem. A, 2011, 115, 2985–2993 CrossRef CAS PubMed.
- M. W. George, C. Long, M. T. Pryce, X. Z. Sun and K. Q. Vuong, Organometallics, 2012, 31, 268–272 CrossRef CAS and references therein.
- B. Procacci, S. B. Duckett, M. W. George, M. W.-D. Hanson-Heine, R. Horvath, R. N. Perutz, X. Z. Sun, K. Q. Vuong and J. A. Welch, Organometallics, 2018, 37, 855–868 CrossRef CAS and references therein.
- P. Glyn, M. W. George, P. M. Hodges and J. J. Turner, J. Chem. Soc., Chem. Commun., 1989, 1655–1657 RSC.
- J. M. Butler, M. W. George, J. R. Schoonover, D. M. Dattelbaum and T. J. Meyer, Coord. Chem. Rev., 2007, 251, 492–514 CrossRef CAS.
- C. D. Windle, M. W. George, R. N. Perutz, P. A. Summers, X. Z. Sun and A. C. Whitwood, Chem. Sci, 2015, 5, 6847–6854 RSC.
- M. Pižl, A. Picchiotti, M. Rebarz, N. Lenngren, L. Yingliang, S. Záliš, M. Kloz and A. Vlček, J. Phys. Chem. A, 2020, 124, 1253–1265 CrossRef PubMed.
- A. El Nahhas, R. M. van der Veen, T. J. Penfold, V. T. Pham, F. A. Lima, R. Abela, A. M. Blanco-Rodriguez, S. Zalis, A. Vlcek, I. Tavernelli, U. Rothlisberger, C. J. Milne and M. Chergui, J. Phys. Chem. A, 2013, 117, 361–369 CrossRef CAS PubMed.
- R. N. Perutz, S. Sabo-Etienne and A. S. Weller, Angew. Chem., Int. Ed., 2022, 134, e202111462 CrossRef and references therein.
- A. D. Allen and C. V. Senoff, Chem. Commun., 1965, 621–622 RSC.
- A. J. Rest, J. Organomet. Chem., 1972, 40, C76–C78 CrossRef CAS.
- J. J. Turner, M. B. Simpson, M. Poliakoff and W. B. Maier II, J. Am. Chem. Soc., 1983, 105, 3898–3904 CrossRef CAS.
- J. J. Turner, M. B. Simpson, M. Poliakoff, W. B. Maier II and M. A. Graham, Inorg. Chem., 1983, 22, 911–920 CrossRef CAS.
- S. P. Church, F.-W. Grevels, H. Hermann and K. Schaffner, Inorg. Chem., 1984, 23, 3830–3833 CrossRef CAS.
- E. F. Walsh, V. K. Popov, M. W. George and M. Poliakoff, J. Phys. Chem., 1995, 99, 12016–12020 CrossRef CAS.
- See e.g., D. C. Grills, K.-W. Huang, J. T. Muckerman and E. Fujita, Coord. Chem. Rev., 2006, 250, 1681–1695 CrossRef CAS , and references therein.
- J. B. Eastwood, L. A. Hammarback, M. T. McRobie, I. P. Clark, M. Towrie, I. J.-S. Fairlamb and J. M. Lynam, Dalton Trans., 2020, 49, 5463–5470 RSC.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205 CrossRef CAS PubMed.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- R. N. Perutz and B. Procacci, Chem. Rev., 2016, 116, 8506–8544 CrossRef CAS PubMed.
- R. L. Sweany, J. Am. Chem. Soc., 1985, 107, 2374–2379 CrossRef CAS.
- R. K. Upmacis, M. Poliakoff and J. J. Turner, J. Am. Chem. Soc., 1986, 108, 3645–3651 CrossRef CAS.
- S. P. Church, F.-W. Grevels, H. Hermann and K. Schaffner, J. Chem. Soc., Chem. Commun., 1985, 30–32 RSC.
- S. L. Matthews and D. M. Heinekey, J. Am. Chem. Soc., 2006, 128, 2615–2620 CrossRef CAS PubMed.
- P. M. Hodges, S. A. Jackson, J. Jacke, M. Poliakoff, J. J. Turner and F.-W. Grevels, J. Am. Chem. Soc., 1990, 112, 1234–1244 CrossRef CAS and references therein.
- M. T. Haward, M. W. George, P. Hamley and M. Poliakoff, J. Chem. Soc., Chem. Commun., 1991, 1101–1103 RSC.
- A. H. Janowicz and R. G. Bergman, J. Am. Chem. Soc., 1982, 104, 352–354 CrossRef CAS.
- J. K. Hoyano and W. A. G. Graham, J. Am. Chem. Soc., 1982, 104, 3723–3725 CrossRef CAS.
- J. K. Hoyano, A. D. McMaster and W. A. G. Graham, J. Am. Chem. Soc., 1983, 105, 7190–7191 CrossRef CAS.
- A. J. Rest, I. Whitwell, W. A. G. Graham, J. K. Hoyano and A. D. McMaster, J. Chem. Soc., Dalton Trans., 1987, 1181–1190 RSC and references therein.
- P. E. Bloyce, A. J. Rest, I. Whitwell, W. A. G. Graham and R. Holmes-Smith, J. Chem. Soc. Chem. Commun., 1988, 846–848 RSC.
- J. B. Asbury, K. Hang, J. S. Yeston, J. G. Cordaro, R. G. Bergman and T. Lian, J. Am. Chem. Soc., 2000, 122, 12870–12871 CrossRef CAS.
- A. J. Cowan, P. Portius, H. K. Kawanami, O. S. Jina, D. C. Grills, X.-Z. Sun, J. McMaster and M. W. George, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6933–6938 CrossRef CAS PubMed.
- B. K. McNamara, J. S. Yeston, R. G. Bergman and C. B. Moore, J. Am. Chem. Soc., 1999, 121, 6437–6443 CrossRef CAS.
- M. W. George, M. B. Hall, O. S. Jina, P. Portius, X.-Z. Sun, M. Towrie, H. Wu, X. Yang and S. D. Zarić, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20178–20183 CrossRef CAS PubMed.
- S. T. Belt, F.-W. Grevels, W. E. Klotzbücher, A. McCamley and R. N. Perutz, J. Am. Chem. Soc., 1989, 111, 8373–8382 CrossRef CAS.
- H. Hennig, Coord. Chem. Rev., 1999, 182, 101–123 CrossRef.
- J. A. Maguire, W. T. Boese and A. S. Goldman, J. Am. Chem. Soc., 1989, 111, 7088–7093 CrossRef CAS.
- J. S. Bridgewater, T. L. Netzel, J. R. Schoonover, S. M. Massick and P. C. Ford, Inorg. Chem., 2001, 40, 1466–1476 CrossRef CAS PubMed.
- A. D. Chowdhury, J. Julis, K. Grabow, B. Hannebauer, U. Bentrup, M. Adam, R. Franke, R. Jackstell and M. Beller, ChemSusChem, 2015, 8, 323–330 CrossRef PubMed and references therein.
- H. Chen and J. F. Hartwig, Angew. Chem., Int. Ed., 1999, 38, 3391–3393 CrossRef CAS PubMed.
- T. J. Mazacano and N. P. Mankad, J. Am. Chem. Soc., 2013, 135, 17258–17261 CrossRef PubMed.
- C. B. Breeter, A. D. Chowhury, R. Adam, R. Jackstell and M. Beller, Org. Biomol. Chem., 2015, 13, 10336–10340 RSC.
- N. W. Hoffman and T. L. Brown, Inorg. Chem., 1978, 17, 613–617 CrossRef CAS.
- D. A. Valyaev, D. Wei, S. Elangovan, M. Cavailles, V. Dorcet, J.-B. Sortais, C. Darcel and N. Lugan, Organometallics, 2016, 35, 4090–4098 CrossRef CAS and references therein.
Footnotes |
| † Although the IR bands are very sharp – important in determining structure with 13CO enrichment (see below) – the single t1u band of W(CO)6 actually appears as a doublet. This ‘matrix splitting’ arises in many matrix spectra and is due to multiple or unsymmetric environments in the matrix. The effect is largely understood and can be accommodated in the interpretation of the spectra. |
| ‡ If the substitution mechanism is dissociative, the enthalpy of activation for substitution by CO can be equated to the bond energy. If there is an interchange mechanism, the actual BDE is higher than the measured value. |
| § Inaccuracies in vibrational frequencies also affect calculations of free energies via the third law of thermodynamics which require knowledge of the zero-point energy. |
| ¶ Solubilities of N2 and H2 in heptane 9.5 × 10−3 and 4.5 × 10−3 M at 1 atm, respectively. |
| || The quantum yield for formation of CpRh(CO)(SiEt3)H from CpRh(CO)2 is independent of [Et3SiH] as expected, but the quantum yield for photosubstitution of CpRh(CO)2 by PPh3 is dependent on [PPh3] implying that there is also another mechanism, probably a ring-slipped intermediate. The quantum yields for both reactions are strongly wavelength dependent. Dunwoody and Lees, Organometallics, 1997, 16, 5770. |
| This journal is © The Royal Society of Chemistry 2022 |