Open Access Article
Open Access ArticleShearing friction behaviour of synthetic polymers compared to a functionalized polysaccharide on biomimetic surfaces: models for the prediction of performance of eco-designed formulations†
Benjamin J.
Coscia
 a,
John C.
Shelley
a,
John C.
Shelley
 a,
Andrea R.
Browning
a,
Jeffrey M.
Sanders
a,
Andrea R.
Browning
a,
Jeffrey M.
Sanders
 b,
Robin
Chaudret
c,
Roger
Rozot
b,
Robin
Chaudret
c,
Roger
Rozot
 d,
Fabien
Léonforte
d,
Fabien
Léonforte
 *d,
Mathew D.
Halls
*d,
Mathew D.
Halls
 e and
Gustavo S.
Luengo
e and
Gustavo S.
Luengo
 *d
*d
aSchrödinger, Inc., Portland, OR 97204, USA
bSchrödinger, Inc., New York, NY 10036, USA
cSchrödinger, Inc., 80538 München, Germany
dL’Oréal Research and Innovation, Aulnay-Sous Bois, France. E-mail: gluengo@rd.loreal.com; fabien.leonforte@loreal.com
eSchrödinger, Inc., San Diego, California 92121, USA
First published on 22nd December 2022
Abstract
The substitution of natural, bio-based and/or biodegradable polymers for those of petrochemical origin in consumer formulations has become an active area of research and development as the sourcing and destiny of material components becomes a more critical factor in product design. These polymers often differ from their petroleum-based counterparts in topology, raw material composition and solution behaviour. Effective and efficient reformulation that maintains comparable cosmetic performance to existing products requires a deep understanding of the differences in frictional behaviour between polymers as a function of their molecular structure. In this work, we simulate the tribological behaviour of three topologically distinct polymers in solution with surfactants and in contact with hair-biomimetic patterned surfaces. We compare a generic functionalized polysaccharide to two performant polymers used in shampoo formulations: a strongly positively charged polyelectrolyte and a zwitterionic copolymer. Topological differences are expected to affect rheological properties, as well as their direct interaction with structured biological substrates. Using a refined Martini-style coarse-grained model we describe the polymer-dependent differences in aggregation behaviour as well as selective interactions with a biomimetic model hair surface. Additionally, we introduce a formalism to characterize the response of the solution to shear as an initial study on lubrication properties, which define the sensorial performance of these systems in cosmetics (i.e., manageability, touch, etc.). The tools and techniques presented in this work illustrate the strength of molecular simulation in eco-design of formulation as a complement to experiment. These efforts help advance our understanding of how we can relate complex atomic-scale solution behaviour to relevant macroscopic properties. We expect these techniques to play an increasingly important role in advancing strategies for green polymer formulation design by providing an understanding for how new polymers could reach and even exceed the level of performance of existing polymers.
1. Introduction
The future of sustainable cosmetic formulation development relies on a holistic approach to ingredient design and production which accounts for the environmental impacts of their whole lifecycle. In choosing ingredients, we must be vigilant of the sources of raw materials, ensuring fair trade practices that lead to positive societal impacts.1 Additionally, we must adhere to the principles of green chemistry which emphasize the use of renewable raw materials, safe, low-energy and low-waste processes, and minimal environmental and human health impacts.2At present, there is a well-established set of petrochemical-derived ingredients that are trusted to achieve the performance required by formulations used for washing and conditioning in the cosmetic and textile industries. For example, widely used cationic polymers and surfactants are very often of petrochemical origin.3,4 Due to the substantial quantity of these chemicals that are being used on an ongoing basis, they ultimately end up measurably accumulating in the environment.5
Depending on the application, there are a variety of molecular classes to choose from that may be suitable replacements to petrochemical-derived ingredients while satisfying the requirements of sustainable development. These can be used directly or as renewable raw materials. For example, biosurfactants are becoming increasingly popular alternatives to conventional surfactants.6,7 Lipids derived from natural fatty acids are useful emulsifiers in addition to providing skin protection and hydration.8 Polyols such as glycerine aid in skin hydration and elasticity preservation.9 Sorbitol, another polyol, can be used to synthesize vitamin C.10 Finally, plant-derived polysaccharides, studied in this work, find use in hair care formulations.
As we continue to gravitate towards more sustainable development, it is essential to maintain or improve product performance (i.e. texture, hair manageability, conditioning, etc.) to match consumer expectations.11 The complexity of these fluids, typically mixtures of surfactants, salt and polymers, makes it non-trivial to replace an ingredient and anticipate its effect on formulation properties. Bio-based polymers add further complexity as the material itself tends to be a mixture of varying molecular weights.12 The cosmetics industry is in need of an effective approach for intelligently probing and choosing from the ingredients accessible in the green chemical space described above.
In this work, we focus our efforts on strategies for reformulation of shampoos used in hair care. The authors believe that a successful reformulation is evaluated based in part on its ability to wash hair, but also its ability to provide conditioning effects that improve hair manageability and impart desirable tactile sensory features. Although a straightforward relationship between subjective consumer tactile perception and a particular ingredient in a formulation is far from being understood, it is well established that low adhesion and friction are desirable physicochemical characteristics.13,14 Therefore, tools which can be used to fundamentally understand these characteristics will be invaluable to reformulation.
Digital chemistry strategies may aid in this task and represent a useful addition to the sustainable development framework. Significant experimental effort has been devoted towards gaining experimental understanding of the conditioning effects of selected polymers with the surface of hair.15,16 By leveraging strategies at the intersection of data science and physics-based chemical simulation, we can quickly evaluate ingredient candidates prior to devoting significant resources to production of molecules.
There exists appreciable literature precedent applying various microscopic simulation techniques to study hair as well as interaction of polymers with surfaces. We can broadly classify these techniques into three main categories: Self-Consistent Mean Field Theory (SCF), Monte Carlo (MC) and Molecular Dynamics (MD).
SCF provides a computationally efficient theoretical framework that can be used to solve for equilibrium structural properties of simplified models. Researchers have applied SCF to determine the most thermodynamically probable structures of polymer–surfactant mixtures in bulk and in contact with surfaces.17–21 The assumptions needed to formulate these approximations of real systems tend to limit their interpretation.
MC allows structurally detailed simulations of systems that sample configurational space according to probabilities dictated by the system's energetics. Similar to SCF, MC provides information about equilibrium structural properties. Early MC implementations relied on lattice-based models which found use studying phase diagrams of surfactants22 as well as polymer adsorption.23 Advances in methodology soon led to implementations for moves in continuous space, opening the door to systems of increasing complexity, including polymer melts and polymers grafted to surfaces.24 However, steps in an MC simulation do not follow a physical process, which limits insight into mechanistic details of a system's behaviour.
MD simulation evolves a system deterministically through time according to Newton's equations of motion. One can derive equilibrium properties from time averages and dynamic properties from simulation trajectories. Mechanistic details enable lucid structure–property relationships. Due to the complete picture provided by an MD simulation, and the broad focus on development of efficient MD algorithms, it is our preferred method of simulation. However, we note that it is certainly conceivable that one could use MD in combination with SCF and/or MC to more thoroughly study structure alongside dynamics at equilibrium.
Ideally, we would use all-atom (AA) simulations to describe any system of interest because this approach incorporates all degrees of freedom that contribute to the system's classical Hamiltonian. Cheong et al. developed an AA model of hair by grafting 18-MEA to a graphene substrate and studying the structure of the 18-MEA layer as a function of their grafting density.25 Atomistic simulations of such large and complex systems are computationally intensive calculations, limiting their current applicability. Fortunately, we expect atomistic simulations of these types of systems, as well as more complex ones, to become more commonplace in tandem with the increasing accessibility and power of high-performance computing. However, there will likely always be value in studying larger and more complex systems with MD, which establishes the need for increased efficiency relative to AA systems.
Coarse grained (CG) simulations represent multiple atoms by a single atom-like particle, sacrificing some detail while enabling more efficient calculations and the study of larger collections of molecules. The reduction in the number of degrees of freedom in the system also results in faster collective evolution of the solutions. By moving to more massive coarse-grained particles, the simulation time increment can be increased, further decreasing the computer time needed relative to comparable atomistic simulations. Weiand et al. developed experimentally consistent CG models which enabled them to reproduce the wetting properties of healthy and damaged hair surfaces.26 One can further increase computational efficiency in CG systems by replacing all solvent molecules with an implicit solvent. Léonforte and Müller used a CG model in implicit solvent to study the surface-templated structure of adsorbed polymers.27 Morozova et al. used a similar approach to study polymer interactions with patterned substrates representative of hair under shear.28
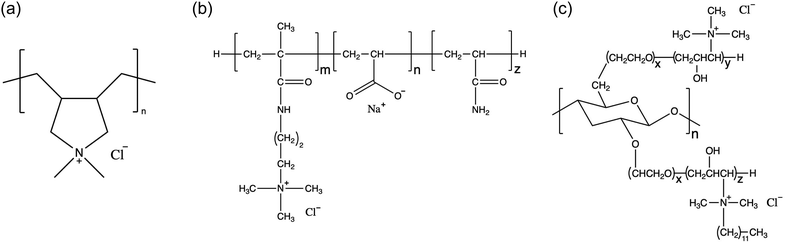
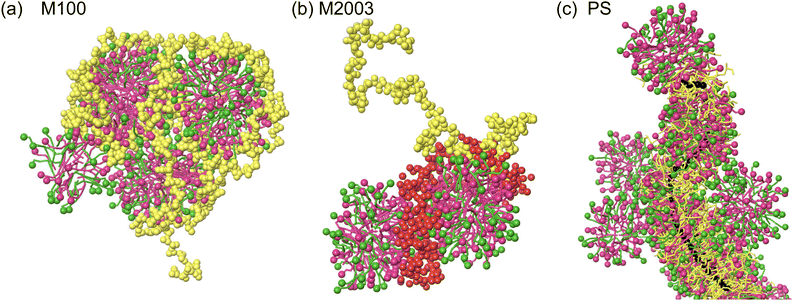
In this work, we use explicit-solvent CG MD simulations in order to build our chemical intuition around substitution of new ingredients in shampoo formulations. We develop a simulation framework for understanding the impact of substituting sustainably sourced polymers into shampoo formulations. We study three different polymers, shown in Fig. 1, in three separate types of systems: (1) poly(diallyldimethyl)ammonium chloride, a linear cationic homopolymer, often abbreviated PDADMAC, commercially known as Merquat 100™ and henceforth referred to as M10029 (2) a zwitterionic copolymer composed of acrylic acid, 3-trimethylammonium propyl methacrylamide chloride and acrylamide, known commercially as Merquat 2003™, henceforth referred to as M2003;30 and (3) an example of a generic amphiphilic charged polysaccharide called 2-(poly(ethyleneoxide)-block-poly(2-hydroxy-3-(N-dodecyl, N,N-trimethylammonium chloride)-propylene)-3-deoxy-6-deoxy-6-(poly(ethyleneoxide)-block-poly(2-hydroxy-3-(N,N,N-trimethylammonium chloride)-propylene)cellulose, a quaternized 3-deoxy-6-deoxy cellulose copolymer, henceforth referred to as PS.31 M100 and M2003 are both petroleum-based polymers while PS is a functionalized polysaccharide. PS adopts a cationic functionality to interact with oppositely charged damaged hair surfaces. PS also incorporates enhanced hydrophobic character through the addition of 12-carbon aliphatic chains to the cationic groups, prone to interactions with the hydrophobic, healthy surface. PS represents just one possible variation among the diverse structures accessible by functionalizing natural polysaccharides. We simulate the interaction of simplex shampoo formulations (polymer + surfactants) in bulk as well as with detailed molecular models of the outermost surface of hair cuticles, comparing aggregation behaviour and lubrication properties.
Perhaps the main drawbacks of CG simulation are the construction and reliability of the force field used to represent the valence and nonbonded interactions. The usefulness of a CG model depends on its ability to accurately model the interactions of the underlying system it is meant to represent. Due to decades of investment by many research groups, all-atom force fields tend to have more reliable “out-of-the-box” parameters which can be used to describe much of organic chemical space. CG force fields are relatively new and thus have not been as extensively parameterized or validated. Defining a general set of CG parameters is a very challenging task due to the diversity of atomic groups that can be represented by CG interaction centers. The Martini force field32 attempts to address this problem by using a relatively intuitive and easily implemented set of particle definitions for various kinds of atom groups. We increase the reliability of our CG model by optimizing a set of Martini-style parameters against AA simulations.
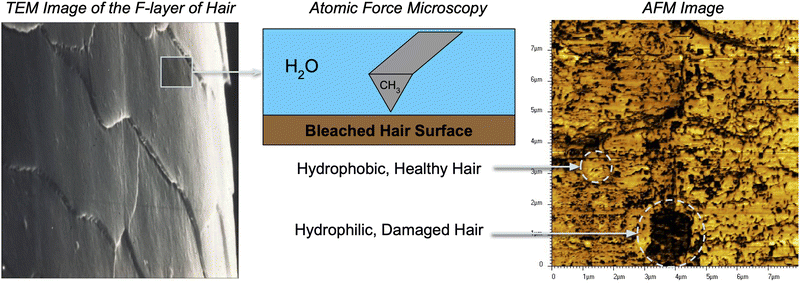
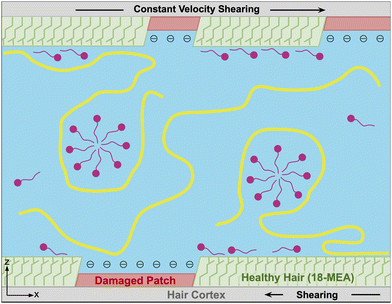
To effectively study interactions of a formulation with hair, it is important to incorporate a detailed understanding of the molecular structure of the hair surface. It is known that 18-methyl eicosanoic acid (MEA) coats the outer surface of healthy hair.33,34 When hair is damaged by chemical means such as bleaching, MEA is cleaved and oxidized at the thioester bond, leaving charged sulfonate groups on the surface. Imaging has shown that damage to hair typically occurs in localized patches (Fig. 2).35 Consistent with this understanding and other simulation studies,28 we study hair models of completely healthy hair, completely damaged hair and partially damaged hair represented with patches of damage among otherwise healthy hair (Fig. 3).
There are two primary outcomes of this work. First, we provide novel insight into the aggregation and friction behaviour of shampoo formulations with a model hair surface. We identify clear bulk and surface behavioural differences between two petroleum-derived polymers and a polysaccharide based on very different structures. Second, and more generally, we establish a framework for studying complex formulations in contact with biomimetic surfaces using both equilibrium and non-equilibrium MD simulations.
2. Methods
The computational studies in this paper build upon each other. We start by studying bulk formulations, then we introduce a model hair surface in contact with the solution, and finally apply shear to the model hair surface relative to the solution. All system builds, simulation setup and analysis were performed using Schrödinger Materials Science Suite (MSS) version 2021-4.36 Tools associated with MSS are emphasized with italics throughout the methods. All MD simulations were run using Desmond.37,382.1 Simulations of bulk formulations
The compositions of the systems studied are inspired by experimental formulations and are outlined in Table 1. As a baseline, the formulations are meant to represent diluted hair formulations, present at a concentration similar to that at the time of application in a hair care routine. We also studied more highly concentrated versions of the same systems in order to facilitate simulation of polymer chains closer to experimental molecular weight.| System | Polymer type | Composition (wt%) | Number of each component | |||||
|---|---|---|---|---|---|---|---|---|
| Polymer (%) | SLES + CAPB4 (%) | NaCl (%) | Monomers | Chains | Chain fraction of exp. MW | Total sites | ||
| M100-A | M100 | 0.50 | 1.00 | 0.70 | 910 | 2 | 0.73 | 409![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
| M100-B | M100 | 2.50 | 5.00 | 0.70 | 4850 | 7 | 1.11 | 443![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714 714 |
| M2003-A | M2003 | 0.25 | 1.00 | 0.70 | 550 | 2 | 0.10 | 407![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 674 |
| M2003-B | M2003 | 1.25 | 5.00 | 0.70 | 2904 | 2 | 0.52 | 439![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 650 |
| PS-A | PS | 0.20 | 1.00 | 0.30 | 30 | 2 | 0.01 | 418![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 405 |
| PS-B | PS | 2.00 | 10.00 | 0.30 | 341 | 2 | 0.13 | 470![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 775 |
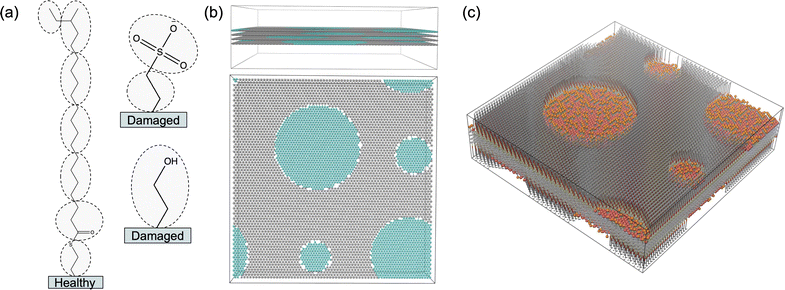
We built non-polymeric ingredients and polymer monomers using the Coarse-Grained Sketcher with bead definitions consistent with Fig. 4. We built polymers from monomer units using the Polymer Builder.
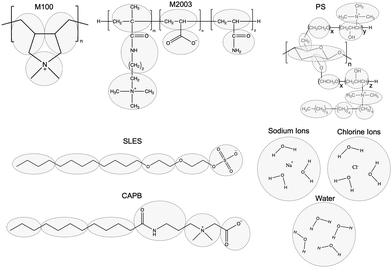 | ||
| Fig. 4 The particles of our coarse-grained model represent the highlighted groups from the associated all-atoms structures. The particle types were initialized consistent with Martini 2 standards and then optimized against measurements from all-atom simulations. Our choices of Martini 2 bead types are illustrated in Fig. S4 of the ESI.† | ||
With all ingredients except water as inputs, we built randomized initial configurations using the Disordered System Builder. This workflow placed molecules in a cubic unit cell of length 760 Å per side, except for the highly concentrated PS-B system where we increased the box size to 890 Å to aid the packing procedure. To give more reasonable starting configurations, all molecules with rotatable dihedrals, except PS, were grown according to a self-avoiding random walk with torsions drawn from a Boltzmann distribution at 300 K. For PS, it is necessary to enforce a 180-degree relative rotation between adjacent backbone monomers for consistency with the extended all-atom conformation. Therefore, we placed copies of the polymer in this conformation into the initial unit cell to preserve this configuration.
We solvated the system by overlaying copies of a pre-equilibrated box of Martini water which is a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of normal Martini water particles to antifreeze water particles.32 We deleted sites which overlapped the non-water components and then removed excess water sites in order to achieve the weight percentages listed in Table 1. When choosing which water sites to remove, we took care to preserve the ratio of antifreeze particles to normal water particles.
1 mixture of normal Martini water particles to antifreeze water particles.32 We deleted sites which overlapped the non-water components and then removed excess water sites in order to achieve the weight percentages listed in Table 1. When choosing which water sites to remove, we took care to preserve the ratio of antifreeze particles to normal water particles.
We used the Coarse-Grained Force Field Assignment tool to apply a Martini-derived force field to the initial configuration. Starting from an initial guess at Martini particle types for each particle as well as corresponding bond and angle parameters, we optimized our force field against analogous all-atom simulations. Details of the parameterization, along with the reference all-atom simulations, are described in Sections S1 and S2 of the ESI.† We represented bonds and angles by harmonic potentials and nonbonded interactions with shifted Lennard-Jones potentials.
We applied the following equilibration protocol to each parameterized initial configuration:
1. 100 ps Brownian dynamics, NVT ensemble, 10 K, 1 fs time step
2. 100 ps MD, NVT ensemble, 10 K, 1 fs time step
3. 100 ps MD, NVT ensemble, 300 K, 1 fs time step
4. 100 ps MD, NPT ensemble, 1 atm, 10 K, 1 fs time step
5. 2 ns MD, NPT ensemble, 10 bar, 300 K, 2 fs time step
6. 500 ps MD, NPT ensemble, 1 atm, 300 K, 15 fs time step
Lennard-Jones potentials used a GROMACS switching function39 with a cut-off distance of 12 Å and a shift radius of 9 Å. Electrostatics were treated using Particle Mesh Ewald sums with a real space cut-off of 12.0 Å. We applied a dielectric constant of 15, as is standard for Martini 2. A Langevin barostat and thermostat were used to control pressure and temperature with relaxation time constants of 6.0 and 3.0 ps respectively.
From the output of the equilibration, we ran 2000 ns production MD simulations in the NPT ensemble. Temperature and pressure were controlled with a Langevin thermostat and barostat with time constants of 10 ps and 50 ps respectively. We used a time step of 15 fs and recorded frames every 1 ns.
Our analysis of these simulations is based on observations after equilibration. We consider the systems to be equilibrated when the plot of total number of aggregates versus time reaches a plateau. To identify aggregates throughout the simulation, we use the MSS Cluster Analysis tool, which identifies clusters using the Density-based spatial clustering of applications with noise (DBSCAN) algorithm,40 with a periodic distance metric and maximum nearest-neighbour separation distance among cluster constituents of 6.5 Å. The chosen nearest-neighbour distance corresponds approximately to the outside edge of the first peak in the radial distribution functions characteristic of species in contact (see Fig. S7 for example, ESI†).
2.2 Simulations of formulations in contact with a model hair surface
We created a model hair substrate by adding functional groups to a base substrate made of stacked graphene-like layers. The lengths of each side of the square-shaped sheets were set to 39.6 nm, 39.8 nm and 33.2 nm for M100, M2003 and PS respectively. We stacked four sheets on top of each other, initially spaced 6.96 Å apart, in order to prevent interactions of solution components across the substrate in the z direction. We control the site density according to the type of surface being studied by changing the distance between hexagonally packed sites.We studied three different hair surface conditions: healthy, extremely damaged and partially damaged. We modelled healthy hair with a homogeneous layer of MEA molecules packed at a density of 4.79 molecules per nm2, corresponding to points packed hexagonally 0.425 nm apart. We modelled extremely damaged hair using a layer of tethered sulfone groups randomly distributed among similarly tethered alcohol groups with a total density of 6.4 molecules per nm2, achieved using a hexagonal packing distance of 0.491 nm. The sulfone groups represent oxidized cysteine sidechains from keratin and are packed at a density of 2.2 molecules per nm2. The remaining sites are functionalized with alcohol groups to represent exposed hydrophilic residues of the implicit underlying keratin protein. The choice of a single type of hydrophilic surface group is a simplification of the damaged surface which contains multiple types of hydrophilic residues besides cysteine. In the future, it may be worthwhile to reapply our parameterization technique to a more accurate atomistic model of the hair surface, such as that developed by Sanders et al.41
Partially damaged hair has been modelled previously via MD simulation in different ways. Weiand et al. modelled partially damaged hair by random removal of 18-MEA molecules from a healthy hair substrate.26 Morozova et al. mapped experimental AFM images to create an interacting surface with hydrophilic and hydrophobic zones.28 Based on the experimental descriptions of bleached hair (Fig. 2), we chose to model the partially damaged surface more in line with the patches modelled by Morozova et al. However, in contrast to Morozova et al., our partially damaged surface is a simplification of the highly non-uniform topology characteristic of the damaged patches to support system sizes accessible at the length scale of the current simulations.
Specifically, we modelled partially damaged hair as circular patches of damaged hair distributed throughout a healthy hair substrate (Fig. 5). We randomly placed four patches on each surface, targeting 30% coverage of the total surface area. We constrained the patch centers to be spaced apart from all others by at least 1.5 times the sum of their radii. We generated a randomized distribution of patch sizes by sampling their relative areas from a Dirichlet distribution with a concentration parameter, α = 10. We applied the same randomized patch-generation to each of the four sheets, even though only the outer two get functionalized. It was necessary to add patches to the middle sheets in order to give them deformation properties similar to the outer sheets, preventing unwanted strain that would lead to buckling.
For components confined between the two surfaces, we studied more concentrated versions of the formulations from the previous section, as outlined in Table 2. We chose to study higher concentrations for this portion of the work because we anticipated high levels of adsorption to the surfaces and because it allowed us to access polymer chain lengths similar in size to experiment. The number of water molecules was chosen in order to achieve a specific distance between the solvent-adjacent substrate surfaces after equilibration of the formulation (see Fig. S11 of the ESI†). We studied substrate separation distances of 10, 20 and 33 nm for M100, M2003 and PS, respectively.
| Polymer type | Hair type | Polymer characteristics | Number of components | Total sites | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Chains | Monomers/chain | Fraction of exp. MW | CAPB | SLES | Na | Cl | Water | |||
| M100 | Healthy | 9 | 605 | 0.97 | 851 | 1548 | 2697 | 6601 | 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 820 |
265![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341 341 |
| Damaged | 9 | 605 | 0.97 | 851 | 1548 | 9535 | 6601 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534 534 |
201![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874 874 |
|
| Partially | 9 | 605 | 0.97 | 851 | 1548 | 4725 | 6601 | 132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 708 |
286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 695 |
|
| M2003 | Healthy | 6 | 2871 | 1.02 | 1520 | 2766 | 6808 | 9215 | 203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 388 388 |
423![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
| Damaged | 6 | 2871 | 1.02 | 1520 | 2766 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 794 |
9215 | 210![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104 104 |
368![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
|
| Partially | 6 | 2871 | 1.02 | 1520 | 2766 | 8906 | 9215 | 228![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 239 |
429![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162 162 |
|
| PS | Healthy | 8 | 151 | 0.11 | 1491 | 2713 | 3863 | 5974 | 249![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 066 066 |
422![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
| Damaged | 8 | 151 | 0.11 | 1491 | 2713 | 8693 | 5974 | 255![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139 139 |
386![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602 602 |
|
| Partially | 8 | 151 | 0.11 | 1491 | 2713 | 5303 | 5974 | 253![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
413![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758 758 |
|
We built initial configurations by first placing all non-water ingredients in a unit cell on top of the model hair substrate. The x and y dimensions of the cell were determined by the dimensions of the substrate. The z dimension was chosen such that the density of the output “dry” configuration (not including the substrate) was 0.05 g cm−3 for M100 and PS and 0.03 g cm−3 for M2003. Due to the length of the M2003 polymer chains, it was more feasible to build the initial configuration with a slightly lower density than the other systems. The ingredients were placed in the cell using the Disordered System Builder in a manner similar to the bulk systems described in the previous section except that the build volume was bounded in the z-dimension by the substrate. We added the required number of waters according to the same procedure described in Section 2.1.
We expanded the coverage of the force field developed to describe bulk systems to include the hair substrates. We optimized our parameters relative to fully atomistic models of the hair substrates parameterized with OPLS4. In the spirit of Martini, we ensured transferability of the force field by only modifying nonbonded parameters involving the substrates. By doing this, we arrived at a single set of parameters that can be applied to both bulk and confined versions of the studied systems. In the future, the force field can be expanded to include additional ingredients by following the same procedure. See Section S2 of the ESI† for further discussion of our CG parameterization procedure.
We applied an equilibration protocol similar to that detailed in Section 2.1, with several modifications. We extended the Brownian dynamics stage to 500 ps in order to sufficiently relax the system prior to any MD stages. We replaced NPT stages with NPAT at steps 4 and 5 in order to allow the z dimension of the unit cell to collapse without risking serious perturbations, such as buckling to the substrate plane. In the last stage, we used an anisotropic barostat to allow the substrate to adjust. This was particularly important for the partially damaged surface which needed to relax the connections grafting the damaged patches to the healthy substrate.
Finally, we ran 2000 ns production simulations in the NPT ensemble at 300 K with anisotropic pressure coupling, and a 15 fs time step. Temperature and pressure were controlled with a Langevin thermostat and barostat with time constants of 50 ps and 10 ps respectively. Analogous to the bulk systems, we judged equilibration based on a plateau in the number of clusters versus time.
2.3 Simulations under shear
We modified the output of the surface simulations discussed in the previous section to create inputs to our shearing simulations. We added a 10 Å vacuum gap between the middle two substrate layers in order to eliminate friction caused by interactions between the substrate layers. We added mechanical strength to the outer layers by applying harmonic restraints between the outer layer and the adjacent middle layer. See Fig. S12 of the ESI† for a graphical illustration of this configuration.We applied shear to the systems by enforcing average velocities of constant magnitude but opposite direction to the outer sheets of the substrate, for a net relative velocity between the two pairs of sheets of 0.1 m s−1. To do so, we choose nine equally spaced particles on a rectangular grid from each of the two outer surfaces to be pulled. These particles are coupled to virtual sites, which were initially coincident with the particles, using harmonic potentials with an equilibrium distance of zero. Our constant velocity implementation biases the motion of the substrate by modifying the positions of the 9 virtual sites for each surface every 1 ps. We calculate the drag force from the force of the harmonic potentials between the virtual sites and real particles. The instantaneous values of drag force come with significant statistical noise, therefore we analysed 100 ns moving averages of the drag force.
In order to arrive at an intrinsic measure of friction, we calculated the coefficient of friction, μk. The coefficient of friction relates the force of friction Ff, which we equate to the drag force in the x direction measured in our simulations, to the normal force, FN:
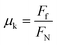 | (1) |
We measure the normal force by multiplying the value of the pressure tensor in the direction perpendicular to the xy plane, Pzz, by the area of the xy plane of the unit cell.
2.4 Additional simulation analysis
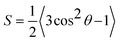 | (2) |
First, we centered the trajectory in the box frame-wise based on the average position of the water beads. To calculate S, we calculate the vector, n, orthogonal to the plane formed by each set of three adjacent beads along the polymer backbones. We calculate θ as the angle between n and the vector normal to the substrate (the z-axis). Simultaneously, we store the average z-position of the three beads used to define n. Finally, we discretized S based on its associated z-position. We used 100 bins with centers and widths defined by the average z-dimension of the unit cell over the trajectory.
3. Results and discussion
3.1 Simulations of bulk formulations
In order to establish a baseline understanding of the aggregation behaviour of the studied polymers and surfactants, we begin by characterizing bulk solutions. We observe distinct behaviour among polymers as a result of their chemical architecture.Spherical micelles form, composed only of CAPB and SLES. Micelles are composed of CAPB and SLES in a ratio approximately equal to their relative overall concentrations. As expected, surfactant tails point towards the center of mass of the micelles. Charged surfactant head groups line the solvent-adjacent surface of the micelle, giving them a net negative charge.
In systems containing M100, the polymers wrap around spherical micelles. The positively charged quaternary ammonium group of each M100 monomer distributes charge uniformly along the linear polymer. The positive charges associate with the negatively charged surfactant head groups (Fig. 6a) and combined with the length of the polymer, results in aggregates composed of multiple spherical micelles. These observations are consistent with previous SCF descriptions of a linear cationic polymer interacting with SLES micelles.17
In systems containing M2003, the two blocks of the polymer show distinct interactions with the solution components (see Fig. 6b). Like M100, the positively charged quaternary ammonium groups in the cationic block associate with the negatively charged head groups of SLES/CAPB micelles. The anionic block, which consists of a mixture of negatively charged carboxylate and neutral primary amide groups, exhibits more hydrophilic behaviour. Both groups in this block readily participate in hydrogen bonding, contributing to their preference for water. This preference is likely enhanced by electrostatic repulsion between the negatively charged carboxylate groups and negatively charged micelles.
Finally, in systems containing PS, we observe the same associative interaction of quaternary ammonium groups with micelles, in addition to a distinct behaviour characterized by the polymer backbone passing through the core of long worm-like micelles (see Fig. 6c). It appears that PS is saturated with surfactant leaving excess surfactant to form micelles in the bulk. Evidently, the environment created by the carbohydrate-like backbone, the long polyethylene oxide (PEO) branches and the 12-carbon alkyl chains attached to the quaternary ammonium sufficiently stabilizes the surfactants tails. Specifically, surfactants situate themselves with alkane tails pointing towards the hydrophobic PS backbone. The PEO branches are compatible with the SLES ethoxy groups and the hydrogen bond donating secondary amine group within CAPB. Surfactant head groups are stabilized by charged interactions between the pendant quaternary ammonium groups from the polymer as well as other surfactant head groups.
3.2 Simulations of formulations in contact with a model hair substrate
With an understanding of the behaviour of the formulation ingredients in bulk, we are now equipped to study their interactions with a model hair surface. In this section we study the interactions of the same formulations in contact with healthy, damaged and partially damaged surfaces. We choose to use M2003 in Fig. 7 to support our discussion, however we attempt to describe our observations in general terms, noting where differences between polymers exist. Analogous figures for M100 and PS are available in Fig. S13 and S14 of the ESI.†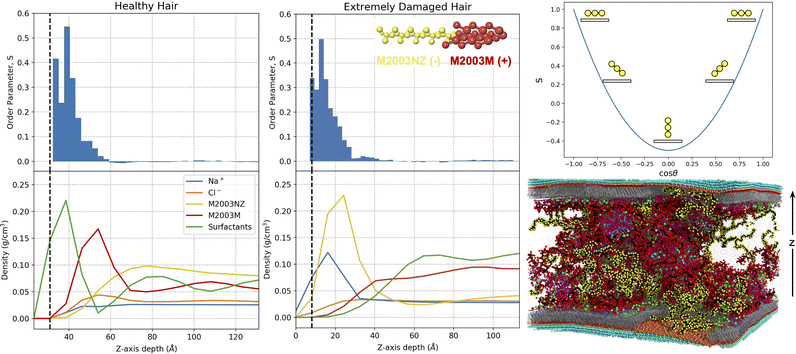 | ||
| Fig. 7 Density profiles aligned with z-dependent polymer order parameters, S, for healthy and extremely damaged model hair surfaces in contact with M2003 formulations. The upper right plot is present as a visual aid for relating S to polymer backbone configuration (yellow circles) relative to the surface (tan rectangles). The bottom right image is of a partially damaged system, chosen for display because it has structural features consistent with a mixture of the healthy and extremely damaged surfaces. In the density and order parameter plots, we define z = 0 at the center of the substrate. Vertical dashed black lines approximate the location of the surface/formulation interface based on the peak in the density profile of terminal (solvent-adjacent) beads of the appropriate surface components pictured in Fig. 5a. Since the systems are symmetric in the z-direction, profiles are mirrored and averaged about the center of the solvent region. For the density plots, we distinguish the density profiles of the two distinct sections of the M2003 polymer: M2003NZ-the hydrophilic region composed of primary amide and negatively carboxylate groups; M2003M-the brush-like region composed of positively charged quaternary ammonium groups. | ||
The density plots in Fig. 7 suggest that M2003 participates in surface interactions with only its positively charged block. The hydrophilic M2003 block extends out into the bulk and fills space relatively uniformly away from the surface. In addition to charged polymer–surfactant interactions, visual inspection clearly shows direct contact of PS with the surface (Fig. S14, ESI†) likely facilitated by favourable interactions between its 12-carbon alkane branches and the hydrophobic MEA surface.
Plots of the positionally-dependent order parameter, S, provide evidence that the healthy surfaces induce structuring of the polymers. The intermediate values of S near the surface are consistent with a loop and train mode of adsorption, as seen by Morozova et al. for adsorbing bead-spring polymer chains. That is, segments of monomers, or trains, adsorb flat near the layer of surfactant head groups (S = 1), while intermediate unadsorbed segments form semi-circular loops between trains (S < 1). For M100 and M2003, the observed structuring decays within about 20–30 Å of the surface at which point chains distribute randomly in solution. For PS, structuring extends well into the bulk which is a consequence of its high persistence length stemming from the relative rigidity of its bulky structure.
Although it has a net negative charge, the hydrophilic block of M2003 shows a high degree of association with the damaged surface. 80% of the monomers composing this block are uncharged primary amide groups with the ability to both donate and receive hydrogen bonds. These amide monomers have a natural affinity for the hydroxyl groups filling the space on the surface between sulfonate groups. The positioning of this M2003 block further suggests that sodium ions coordinated to the sulfonate groups play a role in stabilizing the negative charge of the carboxylate block components.
Finally, we observe a role played by chlorine in increasing the stability of the interface between bulk and the largely positively charged layer of sodium ions coordinated to surface sulfonate groups. The density of chlorine ions in damaged systems appears to plateau at a maximum slightly after the sodium ions’ peak density, relative to the surface. Rapid increases in polymer density (the positively charged block in the case of M2003) appear to coincide, with a small z-direction offset, with increasing chlorine density. All together, we believe our data suggests that sodium ions coordinated to sulfonate groups on the surface, further coordinate with chlorine from bulk and that these chlorine ions interact favourably with positively charged polymer groups. Thus, the role of chlorine is analogous to that played by the surfactants adsorbed on the healthy MEA regions.
At first glance, the order parameter plots appear quite similar to their healthy counterparts. For M2003, ordering (S > 0) coincides with high density of the polymer's hydrophilic block. This block appears to take on similar loop and train adsorption characteristics exhibited by the positively charged in the healthy hair system. However, unlike the healthy systems, the order parameter distributions of M100 and PS are close to zero near the surface (see Fig. S13 and S14 of the ESI†), before reaching peaks at intermediate distances from the surface. Aided by visualization of the trajectories, we believe that this is indicative of exclusion of the polymer from the region immediately adjacent to the damaged hair surface.
3.3 Exploratory tribological simulations of formulations in contact with a model hair substrate under shear
Using the structures output from the partially damaged hair simulations discussed in the previous section, we sheared the hair surfaces and calculated coefficients of friction (μk) as explained in Section 2.2 of the Methods. Here we emphasize that calculation of μk is not the main purpose of the current study. Rather we perform this calculation to probe its practicality and understand what additional work would be needed to get more useful values and comparisons.Although the distance between hair surfaces (Dsep) in our systems differ, we believe it is possible to make cautious comparisons of μk between systems. It is expected that, for a given system, the normal force will increase with a reduction in Dsep, because we expect further confinement of solution components to come with an energetic penalty. Kreer et al. showed that for surfaces sheared at a fixed velocity, frictional force increases linearly with increasing normal force (decreasing Dsep).42 Therefore, the ratio of frictional force to normal force, i.e. μk, is expected to remain constant in a well-behaved system. However, it's unclear whether the systems in this study can be considered well-behaved. The relationship shown by Kreer et al. was for a system of polymer-coated surfaces in direct contact. Currently it is unclear in what range, if any, this relationship holds for surfaces separated by structured polymer solutions, such as those in this study.
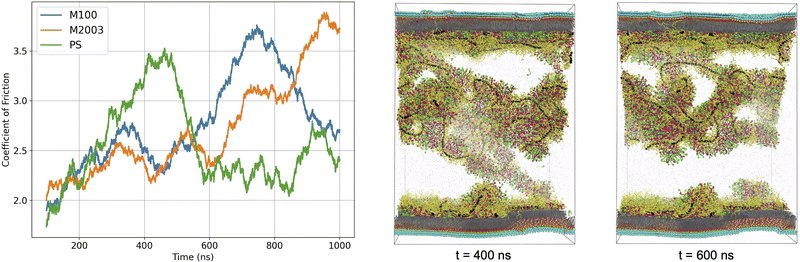
The curves in Fig. 8 display time-dependent measurements of μk for each system. Although we could interpret a macroscopic coefficient of friction based on the average of these curves, it is clear that averaging is an oversimplification on the timescales of our simulations. In all cases, the normal force remained approximately constant for the duration of the simulation (see Fig. S15 in the ESI†). Therefore, the fluctuations in μk evident in Fig. 8 are primarily due to fluctuations in the frictional forces induced by shearing.
The μk curves in Fig. 8 communicate the coefficient of friction for various simulation regimes. There is a slow rise in μk at the beginning of the simulation which may correspond to an increase in shearing force required as motion begins to propagate from components in direct contact with the surface to portions of aggregates that extend into solution. In the M100 and M2003 systems, μk appears to reach a plateau early in the simulation, before undergoing large increases. For PS, we see an initial increase in μk, followed by a rapid drop and plateau.
Deviations from the plateau values of μk are likely due to stretching of the polymers or aggregates in contact with both surfaces. In our simulations, we observe individual polymers in contact with both surfaces which we believe causes the increase in drag force as they slide further from each other causing the polymer to stretch before releasing. As illustrated in Fig. 8, the drop in the PS μk curve can be directly correlated to detachment of the dominant aggregate in solution from the bottom surface. The drop appears somewhat gradual due to our use of a 100 ns moving average on the time series data.
In agreement with experiment, our data suggests that the length of the polymer chain plays a role in lubrication properties.43–45 The ordering of the peak positions in each μk curve roughly corresponds to the relative lengths of the polymer chains used for each system (M2003 > M100 > PS). Depending on the stage of the wash cycle, it is possible that the distance between two hairs sliding past each other may not exceed the length of the polymers or polymer-containing aggregates. If this stick-slip behaviour continues, then μk as experienced by a user would become a strong function of the stick-slip frequency. This should be carefully considered in the design of future simulation experiments. Given that simulation of these systems is currently only feasible on timescales orders of magnitude smaller than those experienced by a user of these formulations, it is imperative that we sample stick-slip events with representative frequency. This will likely require even longer simulations and additional independent replicates.
The simulation data from this study suggests only that all three formulations, under the given simulation conditions, possess similar lubrication properties. The magnitude of the peak and plateau values of the μk curves are similar. There is considerable noise in the friction curves, masked somewhat by the use of moving averages. It is our expectation that the uncertainty of the quantitative μk estimates will benefit from measurements averaged over an ensemble of simulation replicas. However, we believe the simulations show that functionalization of polysaccharides beyond simple linear homopolymers is key to enabling performance that is comparable to petroleum-based polymer ingredients.
4. Conclusions
In this work we have demonstrated an approach to studying the interaction of complex polymer/surfactant formulations with biological substrates via MD simulations. We used detailed, experiment-inspired all-atom molecular models in order to parameterize coarse-grained simulations capable of portraying aggregation and adsorption behaviour. We believe our approach adds to the growing body of work surrounding simulations of complex formulations and biological substrates. We are confident that continued progress in this area will establish particle-based simulation as a viable technique for designing new eco-friendly formulations.The chemically detailed information provided by our study demonstrates the direct insight that simulation can provide. We identified clear differences in the interaction between each polymer and the surfactants in solution as well as with model hair surfaces. The quaternary ammonium groups common to all three polymers play an important role in bulk aggregation, as well as in interactions with surfactant-coated healthy hair surfaces. Deviations in polymer topology from this common structural feature showcase advantages of including alternate functionalities. In M2003, the hydrophilic block does not incorporate into aggregates, but it does adhere to the damaged surface, a quality not shown by the other polymers. In PS, the highly branched carbohydrate backbone offers a favourable environment for surfactants and may help increase surfactant solubility. Additionally, the 12-carbon alkane chains branching off each monomer makes it the only polymer that comes in direct contact with the hydrophobic healthy MEA surface. These insights may help inspire new polysaccharide variants that contain the favorable features displayed in our simulations.
Although exploratory, our friction studies take strides towards directly relating the observed polymer interactions to experimental observables. The majority of the current study helps us to build our chemical intuition relating polymer structure to microscopic behaviour. The full impact of simulation will be realized with the development of accurate and robust quantitative relationships between polymer structure and macroscopic observables. We believe that our exploratory measurements are promising in that they demonstrate that it is possible to quantify frictional coefficients of hair against complex formulations.
Large scale, systematic simulation studies that allow for more detailed comparisons between polymers of interest are a clear next step in advancing this area of study. In future work, we intend to examine friction as a function of variations to formulation compositions, polymer chain lengths, model hair surface topology, shear rate and distance between hair surfaces. It is critical that we design these studies in parallel with experiments aimed at providing evidence to support our conclusions. Provided sufficient agreement between simulation and experiment, our approach to force field parameterization and the workflows presented in this work can be used to study a large variation of formulations with considerable ease.
Author contributions
RR, FL, GSL, JCS, and ARB participated in conceptualization of the study. RR, FL and GSL were responsible for funding acquisition. RR and RC lead project administration. MDH and ARB provided supervision. BJC, ARB and JCS developed the methodology. BJC executed the investigation, developed software for system builds and formal analysis, generated visualizations, was responsible for data curation and wrote the original draft. All authors contributed to review and editing of the final manuscript.Conflicts of interest
RR, FL and GSL are full time employees of L’Oréal involved in basic research activities. BJC, JCS, ARB, JMS, RC and MDH are full time employees of Schrödinger, involved with scientific software development and basic research.Acknowledgements
We thank L’Oréal for financing this study.References
- M. Philippe, B. Didillon and L. Gilbert, Green Chem., 2012, 14, 952 RSC
.
- P. Anastas and N. Eghbali, Chem. Soc. Rev., 2010, 39, 301–312 RSC
.
- C. B. B. Farias, F. C. G. Almeida, I. A. Silva, T. C. Souza, H. M. Meira, R. D. C. F. Soares da Silva, J. M. Luna, V. A. Santos, A. Converti, I. M. Banat and L. A. Sarubbo, Electron. J. Biotechnol., 2021, 51, 28–39 CrossRef CAS
.
- Y. Zhu, C. Romain and C. K. Williams, Nature, 2016, 540, 354–362 CrossRef CAS
.
- J. Margot, L. Rossi, D. A. Barry and C. Holliger, Wiley Interdiscip. Rev.: Water, 2015, 2, 457–487 CrossRef CAS
.
- N. Baccile, C. Seyrig, A. Poirier, S. Alonso-de Castro, S. L. K. W. Roelants and S. Abel, Green Chem., 2021, 23, 3842–3944 RSC
.
- X. Vecino, J. M. Cruz, A. B. Moldes and L. R. Rodrigues, Crit. Rev. Biotechnol., 2017, 37, 911–923 CrossRef CAS
.
-
Skin moisturization, ed. J. J. Leyden and A. V. Rawlings, Marcel Dekker, New York, 2002 Search PubMed
.
- J. W. Fluhr, R. Darlenski and C. Surber, Br. J. Dermatol., 2008, 159, 23–34 CrossRef CAS
.
-
G. Pappenberger and H.-P. Hohmann, in Biotechnology of Food and Feed Additives, ed. H. Zorn and P. Czermak, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, vol. 143, pp. 143–188 Search PubMed
.
- G. S. Luengo, A.-L. Fameau, F. Léonforte and A. J. Greaves, Adv. Colloid Interface Sci., 2021, 290, 102383 CrossRef CAS
.
- J. L’Haridon, P. Martz, J.-C. Chenéble, J.-F. Campion and L. Colombe, Int. J. Cosmet. Sci., 2018, 40, 165–177 CrossRef PubMed
.
- A. Galliano, J. Y. Kempf, M. Fougere, M. Applebaum, L. J. Wolfram and H. Maibach, Int. J. Cosmet. Sci., 2017, 39, 653–663 CrossRef CAS
.
- S. Hendrickx-Rodriguez, S. Connetable, B. Lynch, J. Pace, R. Bennett-Kennett, G. S. Luengo, R. H. Dauskardt and A. Potter, Int. J. Cosmet. Sci., 2022, 44, 486–499 CrossRef CAS
.
- S. Llamas, E. Guzmán, F. Ortega, N. Baghdadli, C. Cazeneuve, R. G. Rubio and G. S. Luengo, Adv. Colloid Interface Sci., 2015, 222, 461–487 CrossRef CAS
.
- E. Guzmán, F. Ortega, N. Baghdadli, C. Cazeneuve, G. S. Luengo and R. G. Rubio, ACS Appl. Mater. Interfaces, 2011, 3, 3181–3188 CrossRef
.
- S. Banerjee, C. Cazeneuve, N. Baghdadli, S. Ringeissen, F. A. M. Leermakers and G. S. Luengo, Soft Matter, 2015, 11, 2504–2511 RSC
.
- M. Hernández-Rivas, E. Guzmán, L. Fernández-Peña, A. Akanno, A. Greaves, F. Léonforte, F. Ortega, R. G. Rubio and G. S. Luengo, Colloids Interfaces, 2020, 4, 33 CrossRef
.
- E. Guzmán, L. Fernández-Peña, G. S. Luengo, A. Rubio, A. Rey and F. Léonforte, Polymers, 2020, 12, 624 CrossRef PubMed
.
- L. Fernández-Peña, E. Guzmán, F. Leonforte, A. Serrano-Pueyo, K. Regulski, L. Tournier-Couturier, F. Ortega, R. G. Rubio and G. S. Luengo, Colloids Surf., B, 2020, 185, 110578 CrossRef
.
- P. Linse, Macromolecules, 1996, 29, 326–336 CrossRef CAS
.
- R. G. Larson, J. Chem. Phys., 1992, 96, 7904–7918 CrossRef CAS
.
- R. Zajac and A. Chakrabarti, J. Chem. Phys., 1996, 104, 2418–2437 CrossRef CAS
.
- V. G. Mavrantzas, Front. Phys., 2021, 9, 661367 CrossRef
.
- D. W. Cheong, F. C. H. Lim and L. Zhang, Langmuir, 2012, 28, 13008–13017 CrossRef CAS
.
- E. Weiand, J. P. Ewen, P. H. Koenig, Y. Roiter, S. H. Page, S. Angioletti-Uberti and D. Dini, Soft Matter, 2022, 18, 1779–1792 RSC
.
- F. Léonforte and M. Müller, Macromolecules, 2015, 48, 213–228 CrossRef
.
- T. I. Morozova, N. A. García, J.-L. Barrat, G. S. Luengo and F. Léonforte, ACS Appl. Mater. Interfaces, 2021, 13, 30086–30097 CrossRef CAS
.
- K. W. Mattison, P. L. Dubin and I. J. Brittain, J. Phys. Chem. B, 1998, 102, 3830–3836 CrossRef CAS
.
- L. Fernández-Peña, E. Guzmán, F. Ortega, L. Bureau, F. Léonforte, D. Velasco, R. G. Rubio and G. S. Luengo, Polymer, 2021, 217, 123442 CrossRef
.
- T. V. Drovetskaya, J. Cosmet. Sci., 2006, 14 Search PubMed
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS
.
- D. J. Evans and M. Lanczki, Text. Res. J., 1997, 67, 435–444 CrossRef CAS
.
- S. Breakspear, J. R. Smith and G. Luengo, J. Struct. Biol., 2005, 149, 235–242 CrossRef CAS
.
- M. Korte, S. Akari, H. Kühn, N. Baghdadli, H. Möhwald and G. S. Luengo, Langmuir, 2014, 30, 12124–12129 CrossRef CAS PubMed
.
- Materials Science Suite (2021-4 Release), Schrodinger Inc., New York, NY, 2021.
- K. J. Bowers, D. E. Chow, H. Xu, R. O. Dror, M. P. Eastwood, B. A. Gregersen, J. L. Klepeis, I. Kolossvary, M. A. Moraes, F. D. Sacerdoti, J. K. Salmon, Y. Shan and D. E. Shaw, in ACM/IEEE SC 2006 Conference (SC’06), IEEE, Tampa, FL, 2006, p. 43.
-
Schrödinger Release 2021-4: Desmond Molecular Dynamics System, D. E. Shaw Research, 2021 Search PubMed
.
-
W. F. van Gunsteren and H. J. C. Berendsen, Groningen Molecular Simulation (GROMOS) Library Manual, Biomos, Groningen, The Netherlands, 1987 Search PubMed
.
- M. Ester, H.-P. Kriegel and X. Xu, Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, 1996, pp. 226–231.
- J. Sanders, B. J. Coscia, A. Fonari, M. Misra, P. G. Mileo, D. J. Giesen, A. R. Browning and M. D. Halls, Exploring the effects of wetting and free fatty acid deposition on an atomistic hair fiber surface model incorporating Keratin Associated Protein 5-1, ChemRxiv. Cambridge: Cambridge Open Engage, 2022.
- T. Kreer, M. H. Müser, K. Binder and J. Klein, Langmuir, 2001, 17, 7804–7813 CrossRef CAS
.
-
G. S. Luengo, A. Galliano and C. Dubief, Aqueous Lubrication, Co-Published with Indian Institute of Science (IISc), Bangalore, India, 2011, vol. 3, pp. 103–144 Search PubMed
.
-
Intermolecular and Surface Forces, ed. J. N. Israelachvili, Academic Press, Boston, 3rd edn, 2011, p. iii Search PubMed
.
- M. Heuberger, G. Luengo and J. N. Israelachvili, J. Phys. Chem. B, 1999, 103, 10127–10135 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05465e |
| This journal is © the Owner Societies 2023 |