Disentangling reaction rate acceleration in microdroplets

Abstract

We have investigated the origin of the unexpected, recently discovered phenomenon of reaction rate acceleration in water microdroplets relative to bulk water. Acceleration factors for reactions of atmospheric and synthetic relevance can be dissected into elementary contributions thanks to the original and versatile kinetic model. The microdroplet is partitioned in two sub-volumes, the surface and the interior, operating as interconnected chemical reactors in the fast diffusion regime. Reaction rate acceleration and its dependence on reaction molecularity and microdroplet dimensions are explained by applying transition-state-theory at thermodynamic equilibrium. We also show that our model, in combination with experimental measurements of rate acceleration factors, can be used to obtain chemical kinetics data at the air–water interface, which has been a long-standing challenge for chemists.

---

Introduction

The discovery that unfavorable chemical reactions in bulk water solution are accelerated, or even spontaneously proceed in water microdroplets has attracted a lot of interest recently.^1–6 For instance, mass spectrometry using sprays, droplet levitation and other techniques have proven water microdroplets to be an efficient reaction medium that offers promising possibilities for the development of more environmentally friendly synthesis methods that reduce the need for organic solvents.^6–8 Reaction rate acceleration in water microdroplets can be considered as another manifestation of the on-water catalysis effect describing the dramatic rate enhancement obtained when insoluble reactants are stirred in a water solution.⁹

Experimental studies have suggested that rate acceleration in microdroplets is an interfacial phenomenon^2,10 that can be influenced by several factors.¹¹ Pioneering studies proposed that rate enhancement might be due to hydrogen-bonding with the water surface dangling protons,¹² but the ongoing discussion focuses on higher concentrations of the reactants and/or increased rate constants at the microdroplet surface.^2,3,11 The presence of strong electric fields^2,4,13 and the differential partial solvation of transition states and reactants at the air–water interface¹⁴ have been postulated as possible causes for the change in rate constant. The effect of strong Laplace pressure on reaction rates has also been pointed out, especially at the nanoscale.^15,16

However, the phenomenon remains incompletely understood. An open question for instance is the interplay between the reaction kinetics at the microdroplet surface and interior because even if the reactant concentrations and/or rate constants at the surface are larger, the involved volume is orders of magnitude smaller. Another unresolved question is the experimentally observed dependence of rate acceleration factors on reaction molecularity.¹⁰ Elucidating these issues experimentally is challenging due to the small size of the microdroplets and ultra-short lifetimes caused by quick evaporation.³ Thus, despite some efforts,^12,17,18 a general theory of reaction kinetics in water microdroplets is still missing. Here, we report a kinetic model based on transition-state-theory (TST) to rationalize the rate acceleration phenomenon and provide a tool for its quantitative assessment as a function of reaction molecularity, microdroplet size and interface–bulk partition constants. Moreover, our model allows the thermodynamic data at the air–water interface, otherwise difficult to access, to be obtained from experimentally observed acceleration factors in microdroplets.

Results and discussion

The microdroplet model used in our approach is shown in Fig. 1. The microdroplet is treated as a spherical system having two differentiated layers. At the microdroplet surface, we assume a 3-dimensional interfacial layer of thickness t and volume V_s. The microdroplet core or the “interior” layer has a volume V_i = V − V_s, where V is the total microdroplet volume. The chemical reaction can take place in either of the two layers with rate constants k_s, for the reaction at the interface, and k_i, for the reaction in the interior. Because the microdroplet size is much larger than the molecular size for the applications of interest here, we assume k_i ≃ k_bulk. We further assume that reaction rates are below the diffusion limit and that there is a fast mixing of the reactants at the interface and microdroplet interior leading to equilibrated concentrations. The conditions required for this hypothesis to be valid have been discussed previously.³ If required, diffusion effects can be incorporated into the model through Fick's second law at the cost of a more complex set of equations.^17,18 Finally, we assume that the reaction kinetics obeys TST, with comparable transmission coefficients in both microdroplet layers and bulk solution, and neglect cage effects.

Fig. 1 The microdroplet model used here. The model is a sphere with two sub-volumes, an interfacial layer of thickness t at the surface and the microdroplet interior. D is the microdroplet diameter assumed to be one to a few microns. The interface/interior differential solvation produces a modification of activation energies and rate constants, as illustrated in the scheme in the right part, where ΔG^X_si holds for the differential solvation free energy for species X. In the scheme shown here, all the species are assumed to be stabilized at the surface (surface accumulation) but it is not a requirement of the model, which can deal with a possible destabilization (surface depletion).

The rate acceleration factor (RAF) in a microscaled system has been defined as the ratio of the effective rate constant of the microscale reaction (in microdroplets here) relative to that of the corresponding bulk reaction at the same temperature:¹⁰

The details of our development are given in the ESI.† One starts with the rate equation, which for an irreversible monomolecular process reads as follows:

A → P

where n^A_s and n^A_i are the number of moles of species A at the interface and interior layers and [A] = (n^A_s + n^A_i)/V is the global concentration in the microdroplet. The concentration in the microdroplet interior [A]_i = n^A_i/V_i is related to [A] by:whereis the surface/interior partition constant. Conveniently substituting these expressions in the rate equation, and remembering that k_i ≃ k_bulk one obtains:where the TS partition constant K^TS_si can be written in terms of the rate constant ratio and the reactant partition constant as:

A similar treatment for bimolecular reactions leads to

A + B → P

withand extension to multimolecular reactions is trivial. Note that for D ≫ t,

These equations reveal the subtle dependence of the RAFs with the surface/interior partition constants of the reactants, the relative surface/interior rate constant value, and the microdroplet dimensions. A remarkable general finding is that significant rate acceleration (RAF ≫ 1) can only occur if one of the chemical species (reactants or transition state) is stabilized at the microdroplet surface by at least:

ΔG^X_si < −RT ln(V/V_s). (10)

This rule follows from the form of the 1 + (V_s/V)(K^X_si − 1) terms (see Fig. S1, ESI†) and establishes a quantitative prerequisite for rate acceleration to be experimentally observed. It links the droplet dimensions, which can be tailored experimentally, to thermodynamic data at the interface, which are not directly or easily accessible, and therefore, it constitutes one of the important outcomes of the present work. It must be emphasized, however, that (10) is a necessary but not a sufficient condition to get RAF ≫ 1. This is because of the dependence of RAF on k_s and k_i, and the partition constant(s) for the reactant(s). Further discussion on this point is done below.

The kinetic model provides a unique tool for obtaining rate constants at the air–water interface. As shown in eqn (5)–(8), k_s can be determined from the measured RAF if K^X_si for the reactants and the rate constant in bulk solution are known. In general, the latter can easily be obtained using standard techniques or computed with quantum chemical methods. The surface/bulk water partition coefficients for the reactants can be directly measured using surface-selective spectroscopic techniques or derived from measures of the Henry's law constant and air–water interface adsorption coefficients. For instance, Roth et al. used inverse gas chromatography to determine the air/interface partition coefficients of a large set of organic compounds.¹⁹ Partition coefficients can also be calculated through different theoretical approaches such as molecular dynamics simulations,^20,21 quantum chemical methods using dielectric models,^22–24 or simple correlations with various physicochemical indices (see ref. 22). Alternatively, K^X_si values can conveniently be tuned in experiments by appropriate modifications of the substituents in the reactants, e.g., by increasing the length of hydrophobic alkyl chains, leading to changes in RAF which can be analyzed in the light of the model to obtain kinetics information. This strategy offers valuable clues for the design of future experiments.

In the rest of the manuscript, we analyze the reaction rates for some selected chemical processes of synthetic relevance in microdroplets. But before moving on to applications of the model, it is worth mentioning that though the main objective of this work was to analyze the reaction kinetics in water microdroplets, the model developed does not presuppose the nature of the medium and can be used unchanged with other solvents or solvent mixtures.

As a first application, we have tried to clarify the RAF dependency of reaction molecularity observed experimentally in microdroplets for different organic reactions at ambient temperature and in different solvents.¹⁰ Reaction acceleration was observed to be on the order of 10⁴ or larger in the case of bimolecular reactions, but only minor changes were observed in unimolecular reactions. The results were qualitatively interpreted in terms of partial solvation at the interface, which should favor the decrease of the activation barrier of the bimolecular processes but not of the monomolecular ones. However, a complete understanding of this finding has not yet been achieved and it is unclear whether it has general validity. Our model provides additional insights into such an important phenomenon. To clarify the observed differences in RAF, we plot in Fig. 2 the predictions of the model for monomolecular and bimolecular reactions assuming V_s/V = 10⁻³. This factor is chosen as a reasonable approximation for the 8 μm droplets used in the experiments¹⁰ (consistent with an interface thickness of about 1.3 nm). For the sake of simplicity, bimolecular reactions of the type 2A → P are considered in Fig. 2 but the case of a general bimolecular reaction is presented in Fig. S2 (ESI†). The plots show RAF variations as a function of the partition constant K^A_si and the factor k_s/k_i. We have considered a large range of K^A_si data, assuming that concentrations are always sufficiently low to ensure ideal behavior. RAF values are close to one for small K^A_si, as expected from eqn (10), but display a fast increase as K^A_si becomes much larger than one. The limiting value is attained when the reactants can be considered to lay predominantly at the surface. More specifically, the figure shows that:

Fig. 2 Variation of RAF in monomolecular and bimolecular reactions. Values are given as a function of the partition constant K^A_si and rate constant ratio k_s/k_i. We assume V_s/V ∼ 0.001.

– In monomolecular reactions, rate acceleration in water microdroplets (RAF > 1) occurs if and only if the rate constant at the interface is larger than in the microdroplet interior (k_s/k_i > 1). Accumulation of the reactants at the interface can potentiate the effect but cannot lead to rate acceleration on its own. The limiting RAF value equals the factor k_s/k_i.

– In bimolecular reactions, rate acceleration occurs also when k_s/k_i > 1 but under some conditions, it can also occur when the rate constant at the interface is equal to or smaller than the rate constant in the microdroplet interior (k_s/k_i ≤ 1). This happens when reactant accumulation at the interface is significant because the RAF limiting value in this case is

which, in contrast to monomolecular reactions, depends on microdroplet dimensions.

The experimental observation that RAFs are much larger in bimolecular compared to monomolecular processes¹⁰ is therefore well predicted by the model. Moreover, the model supports the hypothesis about the effect of interfacial solvation on activation barriers since RAF values slightly larger than 1 in monomolecular reactions are consistent with a small increase of the k_s/k_i factor, while 10⁴-fold RAF values (or larger) for bimolecular processes indicate that there must be a strong rate constant increase (k_s/k_i > 10).

Getting more precise kinetic data for specific processes can be achieved by quantifying the surface/interior partition coefficients for the reactants, either experimentally or computationally, and this can be done using different methods, as explained above.

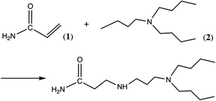
As an illustrative example showing how experimentally measured RAF values can be used to obtain kinetic constants at the microdroplet surface using our model, we will consider here the case of the aza-Michael addition reaction between 2-propenamide (1) and N′,N′-dibutylpropane-1,3-diamine (2) shown in Scheme 1.

Scheme 1 Aza-Michael addition reaction.

The measured acceleration factor for this reaction in microdroplets was reported as log(RAF) = 5.7 (using methanol as the solvent).¹⁰ According to the discussion above, such a strong RAF means that the reaction is significantly accelerated at the interface and that k_s/k_i > 10. This gives the minimum value for the barrier decrease, δΔG^‡_si < −1.4 kcal mol⁻¹. Furthermore, it follows from eqn (10) that at least one of the species has a stabilization energy at the surface verifying ΔG^X_si < −4.1 kcal mol⁻¹. To the best of our knowledge, values of ΔG^X_si for these reactants are not available in the literature but we have estimated them by computations using the conductor-like screening model (COSMO),²⁴ which allows much faster calculations than elaborated techniques such as molecular dynamics simulations. The free energies of transfer ΔG^X_si at 300 K are (see the calculation details in the ESI†) −3.05 kcal mol⁻¹ and −4.53 kcal mol⁻¹ for (1) and (2), respectively. As shown, ΔG^X_si for (2) fulfills the conditions given above. From these energies, one estimates the partition coefficients K⁽¹⁾_si 1.7 × 10² and K⁽²⁾_si = 2.0 × 10³, and using these data and eqn (7) and (8), one finally deduces (we assume V_s/V = 10⁻³):

The reaction in the microdroplet is therefore more than 3-orders of magnitude faster at the surface than in the core, and this result, together with reactant accumulation at the surface, produces the large RAF observed. The rate constant increase corresponds to a decrease of the activation barrier ΔG^‡_si by approximately −5.1 kcal mol⁻¹. Note that the measured RAF value 10^5.7 is not far from the limit value deduced from our model for this reaction, which is (see eqn (11)) 5.2 × 10⁶.

Finally, it is interesting to comment on the predictions of the model for the dependence of RAF on microdroplet diameter, D. An inverse proportionality between the apparent forward rate constant and the droplet diameter has been observed for the synthesis of a fluorescent imine from the reaction of an amine with an aldehyde and explained thanks to an adsorption–reaction–adsorption model.¹⁷ This behavior is predicted by our model too in a broad range of partition and kinetic constants, both for monomolecular and bimolecular reactions. However, due to the form of eqn (7), in the case of biomolecular reactions, the RAF dependence on D is such that for reactants with very large partition constants, it may display an initial increase with D before decreasing. These trends are illustrated in Fig. 3 with some examples. There may therefore be an optimum microdroplet size in such cases, which can be determined from the model if the partition constants are known.

Fig. 3 Variation of RAF in monomolecular (red) and bimolecular (blue) reactions with microdroplet diameter D in some illustrative examples. We assume k_s/k_i = 10³ and t = 1 nm in all cases.

Conclusions

To sum up, the kinetic equations reported here shed light on the subtle dependence of RAFs on reactant concentrations and reaction rate constants at the air–liquid interface of microdroplets. They contribute to rationalize the findings reported in recent experiments, in particular the strong dependence of RAFs on reaction molecularity.¹⁰ Both reactant accumulation and increased rate constants at the microdroplet surface depend on the degree of solvation of the reacting species and both affect the RAF. Our study is based on a simple water microdroplet reactor model having two sub-volumes in equilibrium. It uses common physicochemical properties such as partition coefficients and rate constants which can be measured or calculated using quantum chemical methods and statistical simulations. It complements previous models which were applied to study the equilibrium constant of a reversible reaction in monodisperse emulsions assuming compartmentalizations at the mesoscale, and were based on stochastic simulations¹⁸ or reaction–diffusion equations.¹⁷ This model might be valid for larger droplets when rapid exchange between the sub-volumes can still be reasonably assumed. For smaller droplets, curvature, Laplace pressure and other effects at the nanoscale may become important and so this model cannot be considered.

Real systems are certainly more complex where additional factors may be involved, such as a limited diffusion rate, non-ideal behaviour or significant ionic strength, for example. But the conclusions of the present work can provide valuable guidance for the theoretical study of such factors as well as for the design of new experiments. The most important conclusion is that the model proposed here together with a careful design of microdroplet experiments offers the possibility to obtain chemical kinetic data at the air–water interface, which are difficult to achieve otherwise and are fundamental to progress in this exciting field.

Author contributions

Conceptualization: MFRL and MTCMC. Methodology: MFRL and MTCMC. Investigation: MFRL and MTCMC. Visualization: MFRL and MTCMC. Funding acquisition: MFRL. Writing – original draft: MFRL. Writing – review & editing: MFRL and MTCMC.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the French TGCC (project gen5132) for providing computational resources. They also thank Dr Baptiste Sirjean (LRGP, University of Lorraine) for calculations with the COSMOtherm program.

Notes and references

1. M. Girod, E. Moyano, D. I. Campbell and R. G. Cooks, Chem. Sci., 2011, 2, 501–510.
2. X. Yan, R. M. Bain and R. G. Cooks, Angew. Chem., Int. Ed., 2016, 55, 12960–12972.
3. Z. Wei, Y. Li, R. G. Cooks and X. Yan, Annu. Rev. Phys. Chem., 2020, 71, 31–51.
4. J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19294–19298.
5. A. Gallo, N. H. Musskopf, X. L. Liu, Z. Q. Yang, J. Petry, P. Zhang, S. Thoroddsen, H. Im and H. Mishra, Chem. Sci., 2022, 13, 2574–2583.
6. C. Y. Liu, J. Li, H. Chen and R. N. Zare, Chem. Sci., 2019, 10, 9367–9373.
7. L. Zhao, X. Song, C. Gong, D. Zhang, R. Wang, R. N. Zare and X. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2200991119.
8. X. Yan, Int. J. Mass Spectrom., 2021, 468, 116639.
9. S. Narayan, J. Muldoon, M. G. Finn, V. V. Fokin, H. C. Kolb and K. B. Sharpless, Angew. Chem., Int. Ed., 2005, 44, 3275–3279.
10. L. Q. Qiu, Z. W. Wei, H. G. Nie and R. G. Cooks, ChemPlusChem, 2021, 86, 1362–1365.
11. M. F. Ruiz-Lopez, J. S. Francisco, M. T. C. Martins-Costa and J. M. Anglada, Nat. Rev. Chem., 2020, 4, 459–475.
12. Y. Jung and R. A. Marcus, J. Am. Chem. Soc., 2007, 129, 5492–5502.
13. H. Xiong, J. K. Lee, R. N. Zare and W. Min, J. Phys. Chem. Lett., 2020, 11, 7423–7428.
14. N. Narendra, X. S. Chen, J. Y. Wang, J. Charles, R. G. Cooks and T. Kubis, J. Phys. Chem. A, 2020, 124, 4984–4989.
15. M. Riva, J. Sun, V. F. McNeill, C. Ragone, S. Perrier, Y. Rudich, S. A. Nizkorodov, J. Chen, F. Caupin, T. Hoffmann and C. George, Environ. Sci. Technol., 2021, 55, 7786–7793.
16. S. S. Petters, Geophys. Res. Lett., 2022, 49, e2022GL098959.
17. A. Fallah-Araghi, K. Meguellati, J.-C. Baret, A. El Harrak, T. Mangeat, M. Karplus, S. Ladame, C. M. Marques and A. D. Griffiths, Phys. Rev. Lett., 2014, 112, 028301.
18. K. R. Wilson, A. M. Prophet, G. Rovelli, M. D. Willis, R. J. Rapf and M. I. Jacobs, Chem. Sci., 2020, 11, 8533–8545.
19. C. M. Roth, K.-U. Goss and R. P. Schwarzenbach, J. Colloid Interface Sci., 2002, 252, 21–30.
20. I. Benjamin, Annu. Rev. Phys. Chem., 1997, 48, 407.
21. M. Roeselova, P. Jungwirth, D. J. Tobias and R. B. Gerber, J. Phys. Chem. B, 2003, 107, 12690–12699.
22. C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2004, 108, 12882–12897.
23. K. Mozgawa, B. Mennucci and L. Frediani, J. Phys. Chem. C, 2014, 118, 4715–4725.
24. A. Klamt, Fluid Phase Equilib., 2016, 407, 152–158.

---

Footnote

† Electronic supplementary information (ESI) available: Details on the model development. Fig. S1 and S2. See DOI: https://doi.org/10.1039/d2cp04998h

---