Metallaaromaticity – a protean world

Abstract

The nature of magnetically induced current densities (MICD) of metallabenzenes and related compounds has been examined with relativistic DFT calculations to assess the magnetic aromaticity of the molecules. The origin of the total MICD has been analyzed in terms of individual molecular orbital (MO) contributions. Our study reveals that the σ-framework of the molecules always makes a diamagnetic contribution to the MICD. On the other hand, π-MOs and Craig–Möbius type π-MOs, i.e., MOs in which the d_xy/d_xz orbitals of the metal centers change the phase of the wave function akin to a Möbius twist, may not make a diatropic contribution. We have identified metallabenzenes with multiple magnetic aromaticities. In the case of iridabenzenes, σ-MICD has been found to decrease dramatically from Ir(III) to Ir(V) systems. Furthermore, a brief examination of some recently synthesized metallapolycycles has shown that the metal center in a given ring can strongly modulate the aromaticity of neighboring rings. Finally, the finding that relatively minor perturbations in the ligand environment of the metal can substantially influence the aromaticity of metallabenzenes and related molecules underscores the protean character of metallaaromaticity and the need for even wider-ranging investigations. Considering the conflicts between magnetic response and ground-state aromaticity criteria (energetic, structural, and electronic criteria), we propose that the term aromatic be used for labeling a molecule if and only if all criteria confirm aromaticity. In other words, neither magnetic nor ground-state criteria are necessary and sufficient conditions for labeling a molecule aromatic.

---

Introduction

The concept of metallaaromaticity arose from the proposal of Hoffmann and Thorn that a CH group in benzene could be replaced by an isolobal transition metal fragment.¹ Soon afterward, the first metallabenzenes, including 1 in Fig. 1, were synthesized and characterized by Roper and co-workers.² Since then the chemistry of metallacycles has developed substantially on both experimental and theoretical fronts.^3–7 Despite considerable advances on the experimental side, many simple questions regarding the nature of metallaaromaticity are not known. The first question concerns how many electrons in metallabenzenes are responsible for the aromaticity. This is a matter of dispute even for some of the simplest of metallaaromatics, including metallabenzenes. In their original work, Hoffmann and Thorn suggested that metallabenzenes, like benzene, are 6π-aromatic species obeying the Hückel (4n + 2) rule.¹ This notion was first challenged by Schleyer and Wang, as mentioned in a review by Bleeke⁴ referring to their personal communications. According to Schleyer and Wang's interpretation, which was later confirmed by a series of works by Zhu et al.,^8–10 metallabenzenes are 4n-π Craig–Möbius aromatic systems.¹¹ Zhu and his co-workers further extended the concept of metallaaromaticity to the σ-framework of organometallics, including metallacyclopropanes.^12–15 On the other hand, a recent analysis by Fernández and Frenking on a derivative of rhodabenzene suggests that at least that particular molecule is a 10π-electron Hückel-aromatic.¹⁶ In the latest study on the number of active electrons of the metallabenzenes, Boldyrev and his coworkers concluded on the basis of AdNDP analysis¹⁷ that six electrons are responsible for aromaticity, as expected from the Hückel rule and as suggested by Hoffman and Thorn.

Fig. 1 The structures of metallabenzenes studied; compounds 1 to 3 are osmabenzenes, 4 and 5 are iridabenzenes, and 6 and 7 are platinabenzenes. The charges of all systems are neutral except that of molecule 2 which is negatively charged and 6 which is positively charged. Roman superscripts indicate oxidation states on the metals.

In a recent study, we analyzed the patterns and the strengths of magnetically induced ring currents in a number of osmacycles at the scalar and 4-component relativistic levels.¹⁸ An unforeseen finding in that study was that osmabenzene 1 (Fig. 1) appears to sustain a strong σ-diatropic current despite the presence of the π-electrons of the benzene framework. This conclusion was drawn on the basis of the topology of the current density, a tool that was then applied for the first time to metallaaromatics. Given the continuing debate on the electronic structure of osmabenzene 1,^4,16,19–23 here we have dissected the contributions of individual molecular orbitals to the global ring current for a series of osmabenzenes, iridabenzenes, and platinabenzenes with different metal oxidation states²⁴ and d-electron counts (Fig. 1). We have also used the ring current criterion to briefly examine the effect of both 3d- and 5f-elements on the aromaticity and antiaromaticity of some polycyclic systems (Fig. 2), a hotly debated topic in the current literature.^25–28

Fig. 2 The structures of 8, an open-shell hexa lithio spiro vanadacycle,²⁹9, an open-shell urana-polycycle, and 10, its closed-shell thorium counterpart.³⁰ Hydrogens are removed for more clarity. Compound numerals are shown in boldface.

In this work, we aim to explore the nature and origin of magnetically induced electronic currents in metallacycles. We further propose a general definition for the aromaticity of these systems that can be extended to all aromatic molecules to unify all four criteria of aromaticity, i.e., energetic, electronic, structural, and magnetic, even though the origin of magnetic response properties are different from the other criteria of aromaticity.^31,32

Results and discussion

All results presented herein involve magnetically induced current densities, which provide the most accurate measure of aromaticity as far as the magnetic criterion of aromaticity is concerned. The ring current intensities were computed with DFT using the PBE0 functional, triple-ζ basis sets, and a fully relativistic Dirac–Kohn–Sham treatment for all species, as detailed in the Methods section.

How many active orbitals does a metallabenzene have?

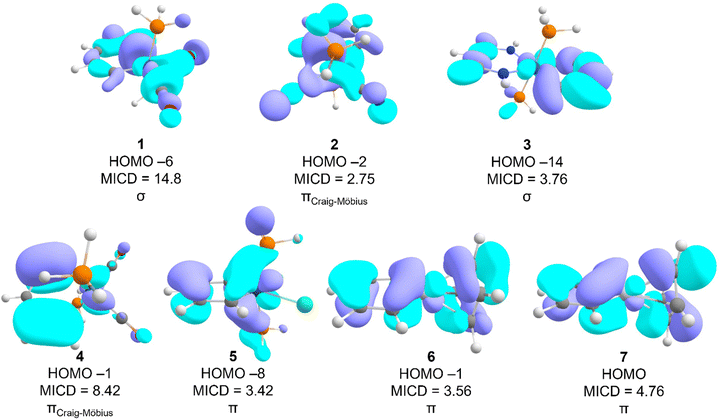
Table 1 lists the strength of the magnetically induced current density (MICD), the formal charge, and the number of electrons in the metal d orbitals in molecules 1–7 (Fig. 1). Comparing the total MICD of these molecules to that of benzene (12.2 nA T⁻¹)³³ suggests that the molecules are moderately to strongly magnetically-aromatic (MICDs between 5.7 and 12.4 nA T⁻¹). Besides MICD, the sum of the contributions of different valence MOs to the MICD and the number of MOs with diatropic currents are listed. The difference between the total MICD and the sum of valence shell contributions to the MICD is attributable to the contribution of the core electrons.

Table 1 Molecular charges, the number of d-electrons (dⁿ), the intensity of magnetically induced current density (MICD) in nA T⁻¹ and its orbital components, and the number of active diamagnetic orbitals (NADO)

Molecules	1	2	3	4	5	6	7
Charge	0	−1	0	0	0	+1	0
d ^n	4	4	4	6	4	6	6
MICD	9.05	6.84	9.46	12.07	5.71	5.73	8.39
MICDπ	—	−0.42	4.36	−1.54	0.26	4.68	5.98
MICDσ	9.50	1.32	1.88	4.74	1.41	1.95	1.79
MICDCraig–Möbius	3.74	5.82	3.26	8.90	4.74	−0.74	1.40
NADO	2πCM, 15σ	6πCM, 7σ	4πCM, 5π, 9σ	4πCM, 3π, 14σ	4πCM, 11σ	3π, 5σ	3π, 11σ

---

Table 1 indicates that the number of σ-MOs with diatropic character is generally significantly higher than the number of π- or Craig–Möbius type π-MOs. Craig–Möbius MOs are π-type MOs in which a d_π orbital of the metal center changes the phase of the wave function akin to a Möbius morphology and have an odd number of nodes along the ring.¹¹ A further general trend appears to be that the contribution of σ-MICD is non-zero and net-diatropic. On the other hand, the contribution of the π-MOs or the Craig–Möbius π-MOs¹¹ to the total current is zero or even paratropic in some cases. The net diatropic σ-current typically originates from small contributions of many σ-MOs. Thus, if one relies on the symmetry of MOs, the alleged magnetic aromaticity of metallobenzenes has multiple origins. If we arbitrarily set the bar for the definition of the magnetic aromaticity of a molecule equal to one-third of benzene's current intensity, i.e. ∼4 nA T⁻¹, then 1 would be classified as purely magnetically σ-aromatic, 2 and 5 would be classified as Craig–Möbius aromatic, 3, 6, and 7 would be classified as solely magnetically π-aromatic, and 4 would be classified as magnetically σ- and Craig–Möbius double-aromatic. The relative contribution of different types of MOs to the total MICD appears to vary fitfully from molecule to molecule, apparently defying any generalization.

As previously shown,¹⁸ molecule 1 sustains a strong σ-ring current. The diatropicity of Craig–Möbius MOs in 1 is more than 30% that of the σ-MOs, close to the chosen threshold of 4 nA T⁻¹ but not enough to unambiguously call the molecule magnetically double-aromatic. An examination of the relevant MOs reveals that a single σ-MO (HOMO−3) sustains a strong diatropic current of 14.8 nA T⁻¹ which is even larger than the total MICD (Fig. 3). It is worth repeating that the total current of benzene is about 12 nA T⁻¹ for comparison. Molecule 1 is unusual from another point of view as well: the core electrons are strongly paratropic. Although the total current of the majority of systems studied approximately equals the contributions from different valence MOs, the MICD due to the valence MOs of 1 is 4.19 nA T⁻¹ higher than the total MICD of the molecule. This finding suggests that the core orbitals are strongly active in a magnetic sense and sustain a paratropic MICD. The metal oxidation state in all the osmabenzenes studied is +IV and all the systems sustain diatropic σ-currents to some degree but in general not as strong as 1. Furthermore, except for 3, the contributions of the π-MOs to the MICD of the other osmabenzenes are essentially zero. Molecule 3 exhibits magnetic π-aromaticity (MICD_π = 4.36 nA T⁻¹) in addition to a notable diatropic contribution from its Craig–Möbius type π-MOs (MICD_CM = 3.26 nA T⁻¹) and a small contribution from the σ-framework (MICD_σ = 1.88 nA T⁻¹). Yet, the strongest diatropic contribution of a single MO of molecule 3 originates from a low-energy σ-MO (HOMO−14) and amounts to a current density of 3.76 nA T⁻¹ (Fig. 3). In contrast to 3, molecule 2 sustains a weak paramagnetic π-current (MICD_π = −0.42 nA T⁻¹). This current, however, is too weak for the molecule to qualify as a magnetically π-antiaromatic system. In spite of the same metal oxidation state in the various osmabenzenes examined, the current density of the σ-, π-, or Craig–Möbius MOs appear to exhibit rather capricious variations across the molecules and do not appear to evince any discernible trends.

Fig. 3 MOs with the largest contribution to the MICD of each molecule and their symmetry.

In iridabenzenes 4 and 5, the oxidation states of the metal atoms are different, +III and V, respectively. Although both systems are magnetically Craig–Möbius aromatic, the MICD of the Ir(III) complex 4 (MICD = 12.07 nA T⁻¹) is over twice that of the Ir(V) complex 5 (MICD = 5.71 nA T⁻¹), i.e., the lower metal oxidation state results in higher magnetic aromaticity. Furthermore, a single Craig–Möbius MO (HOMO−1, Fig. 3, MICD_CM = 8.42 nA T⁻¹) in 4 accounts for nearly 70% of the total current intensity of the molecule. In iridabenzene 5, the strongest diatropic current arises from a single π-type MO, a contribution of 3.42 nA T⁻¹, which is nearly 60% of the total MICD of the molecule. However, this strong diatropic current is masked by the strong paratropic currents from other π-MOs so π-MOs together make a negligible contribution (0.26 nA T⁻¹) to the total current density. The major insight from the iridabenzenes is that the metal oxidation state makes a key difference to overall MICD; the Ir(III) complex sustains a stronger MICD than the Ir(V) complex.

The metal oxidation state is the same in both platinabenzenes 6 and 7. The largest contribution of a single MO to the diatropic ring current originates from a higher-energy π-MO of similar topology in both platinabenzenes (the HOMO−1 in 6 and the HOMO in 7, see Fig. 2). Platinabenzenes 6 and 7 are chemically very similar, differing only in the point group symmetry and charge. Yet, they exhibit significant differences in aromatic behavior. C_2v6 sustains a moderately diatropic π-current (MICD_π = 4.68 nA T⁻¹) with a minor contribution from σ-MOs (MICD_σ = 1.95 nA T⁻¹), albeit with the Craig–Möbius π-MOs making a net paratropic contribution (MICD_CM = −0.24 nA T⁻¹). On the other hand, C_s7 exhibits a much stronger diatropic current (see Table 1) with a positive contribution also from the Craig–Möbius π-MOs. As a result, 7 sustains an overall stronger current density (8.39 nA T⁻¹) relative to its close relative 6 (MICD = 5.73 nA T⁻¹).

How do metals affect their neighboring rings?

Recently, two open-shell metallaaromatic systems^29,30 were characterized as aromatic on the basis of the NICS criterion.³⁴ NICS has proved unreliable in the case of transition metal and actinide compounds,^26,35,36 which has been attributed to interference from local paramagnetic currents around the metallic centers with the ring current. NICS cannot distinguish the former, a local effect, from the latter, the true measure of magnetic aromaticity. A key question now is how this local effect influences nearby rings in a polycyclic system. Here, we have computed the current density for three polycyclic systems – two open-shell molecules 8 and 9 and a closed-shell counterpart of 9, molecule 10 (Fig. 2 and Table 2).

Table 2 Magnetically induced current densities (MICD) in nA T⁻¹. Total MICDs computed via quantum theory of atoms in molecules (QTAIM)³⁷ analysis on scalar-relativistic wavefunctions are given in parentheses

Molecules	8(5-MR)	8(Benzene)	9(5-MR)	9(4-MR)	9(Benzene)	10(5-MR)	10(4-MR)	10(Benzene)
MICD	3.31	2.69	2.33	−8.27	3.92	5.43 (3.8)	−3.13 (−3.8)	8.28 (9.2)

---

The chiral molecule 8 was suggested to be a Craig–Möbius aromatic species by Huang et al. recently.²⁹ However, it sustains a weak diatropic current passing around the 5-membered vanadacycle that is consistent with simple nonaromaticity. Interestingly, the benzene rings of the system are nonaromatic as well! In this species, the large NICS values are the result of the local electronic current around the vanadium center, as previously discussed.^26,29,35,36

Molecules 9 and 10 have been suggested to contain an antiaromatic cyclobutadiene ring and an aromatic benzene ring, based on NICS computations.³⁰ The nature of the aromaticity in the metallacycles, however, was not discussed by the authors. The uranium-bearing ring of molecule 9 sustains a weak diamagnetic current indicative of nonaromaticity. The neighboring butadiene on the other hand sustains a ring current of −8.27 nA T⁻¹, consistent with the previous antiaromatic description. The benzene ring adjacent to the butadiene, however, is substantially dearomatized in response to the neighboring antiaromatic ring. The negative NICS values at the center of the benzene³⁰ thus appear to reflect the strong local paramagnetic currents around the uranium atom – a common occurrence in metallaaromatics – and the local effect of the cyclobutadiene's paramagnetic current outside the periphery of the ring.³⁸ The magnetically induced ring current of the closed-shell 10 is stronger than that of its counterpart 9. The thorium heterocycle and the phenyl ring in 10 thus sustain a sufficiently large diatropic current so as to qualify as weakly aromatic, but the central cyclobutadiene with a ring current of −3.1 nA T⁻¹ seems best described as borderline antiaromatic.²⁶ In 10, the benzene ring also conserves its magnetic aromaticity based on the diatropicity of the ring current that is 8.3 nA T⁻¹, ∼70% of the free benzene molecule.

When should we call a molecule aromatic?

A relevant discussion to the present work is the usefulness of the concept of aromaticity for metallic species and the relevance of the magnetic response properties to the aromatic character of a molecule. In recent years several researchers, including us, have criticized equating magnetic response properties to aromatic character because the presence of a ring current does not necessarily correlate with the stability of a molecule, especially for high-energy molecules.³² On the other hand, IUPAC defines aromaticity by energetic stability, structure, and the presence of induced ring current in a molecule.³⁹ We suggest calling a molecule aromatic if and only if it satisfies all criteria of aromaticity, i.e. both ground-state aromaticity criteria, i.e., energetic, structural, and electric, as well as the magnetic response properties. This means that each criterion is necessary but not sufficient for assessing a molecule as aromatic. Therefore, neither high-energy systems that sustain a diatropic ring current³² nor stable molecules that do not sustain a ring current²⁶ should be labeled as aromatic. This proposal will help to tighten the broad range of aromatic molecules that nowadays is like a zoo of exotic systems. The lack of induced current density eliminates molecules like 8 or 9 from the list of aromatic species as it does exotic systems such as [{Th(C₈H₈)Cl₂}₃]²⁻ despite their stability that permits their synthesis, separation, and characterization.²⁶ Nevertheless, these species can still benefit from resonance to be more stable compared to their other isomers.⁴⁰ On the other hand, molecules like the famous Al₄²⁻ which is the global minimum on its potential energy surface and sustains a strong ring current is unambiguously an aromatic species.⁴¹

Conclusions

In light of our reexamination of metallabenzenes and related molecules, metallaaromaticity emerges as a protean world, where the nature of magnetic aromaticity in metallabenzenes appears to vary willfully from one molecule to the next. We have identified all three possible types of magnetic aromaticity, i.e., σ-, π-, and Craig–Möbius aromaticity, within a small sample space of 7 molecules. While a comparison of two iridabenzenes emphasizes the importance of oxidation state, or d-electron count, on the nature and magnitude of the aromaticity, minor structural changes also appear to engender substantial changes in the aromaticity of osma- and platinabenzenes, even for a given metal oxidation state. A more extensive study thus seems clearly warranted so we might better understand the patterns and logic underlying this kaleidoscopic world.

We have analyzed the aromaticity of one closed-shell and two open-shell polycyclic metallacycles. We have shown that neither of the open-shell species sustains a strong enough ring current on any of their constituent rings to be described as aromatic. On the other hand, the cyclobutadiene ring in one of the open-shell polycyclics (9) is weakly antiaromatic. In contrast, the closed-shell molecule 10 harbors aromatic uranacycle and benzene rings with an intervening nonaromatic cyclobutadiene.

It is worth emphasizing that the divergent results on the number of active electrons contributing to the aromaticity of metallabenzenes reflect deep-seated differences among different aromaticity criteria.^{26,31,32,42,43} Two broad criteria center around ground-state (energetic, electronic, and structural) and response (magnetic) aromaticity.³¹ The present results once again confirm the validity of this distinction. However, here we suggest that neither ground-state criteria nor magnetic criteria of aromaticity are necessary and sufficient for describing a molecule as aromatic. We recommend calling a molecule aromatic if and only if it satisfies both the ground-state and the magnetic response (current density) criteria. We believe that this suggestion will effectively circumscribe the number of molecules that can be labeled “aromatic”.

Computational methods

All structures were optimized at the PBE0^44–47/def2-QZVPP⁴⁸ computational level with corresponding core potentials (ECPs) for the heavy metals using the Gaussian 09⁴⁹ suite of programs. The nature of local minima was identified via the Hessian of the energy and frequency analysis. The structures of molecules 8, 9, and 10 were taken from the relevant references with no additional optimization. The structures were used for analysis via the ReSpect (Relativistic Spectroscopy)⁵⁰ package version 5.2.0 (2019). To assess the nature of aromaticity, magnetically induced currents were computed using the PBE DFT level using all-electron basis sets ucc-pTVZ⁵¹ for light atoms and Dyall-VTZ⁵² for metal atoms. To compute the current density, preliminary SCF computations were performed using a one-component Kohn–Sham Hamiltonian with scalar one-electron relativistic second-order Douglas–Kroll–Hess (KS-DKH2)⁵³ corrections to generate an initial-guess wavefunction. The initial-guess SCF was then used in the four-component matrix Dirac–Kohn–Sham Hamiltonian (mDKS)⁵⁴ computations, which provided the final results for the magnetic response currents. In the MDKS calculations, the SO (spin–orbit coupling) integrals were switched off so only the mass-velocity and Darwin corrections of the relativistic effects were covered and thus the identity of the orbitals remained intact for further analysis.

The magnetically induced currents were computed with a magnetic field oriented perpendicular to the plane of the rings that encompass the metal atom. The contribution of the total current, as well as each molecular orbital, was computed by means of a rectangular plane of integration (10 Å × 10 Å) that originates approximately from the center of the ring and cuts through the C_α–C_β bond relative to the metal. The plane was defined as originating 5 Å below the ring to 5 Å above the ring of the molecules, where the electron density and hence the ring current are expected to be essentially zero.^42,55,56 Quantum theory of atoms in molecules³⁷ partitioning was used to measure the MICD in molecule 11 to compare the results of the choice of the integration plane. The results were found to be reasonably close, although the QTAIM analysis was performed on a scalar relativistic wavefunction. This analysis was performed using the AIMAll package.⁵⁷

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

AG acknowledges support from grant no. 324139 of the Research Council of Norway. CFN thanks the National Science Centre, Poland, for grant no 2020/39/B/ST4/02022. This research was also supported in part by PLGrid Infrastructure.

References

1. D. L. Thorn and R. Hoffmann, Nouv. J. Chim., 1979, 3, 39–45.
2. G. P. Elliott, W. R. Roper and J. M. Waters, J. Chem. Soc., Chem. Commun., 1982, 811–813.
3. D. Chen, Y. Hua and H. Xia, Chem. Rev., 2020, 120, 12994–13086.
4. J. R. Bleeke, Chem. Rev., 2001, 101, 1205–1228.
5. J. R. Bleeke, Acc. Chem. Res., 1991, 24, 271–277.
6. I. Fernández, G. Frenking and G. Merino, Chem. Soc. Rev., 2015, 44, 6452–6463.
7. D. Chen, Q. Xie and J. Zhu, Acc. Chem. Res., 2019, 52, 1449–1460.
8. J. Zhu, G. Jia and Z. Lin, Organometallics, 2007, 26, 1986–1995.
9. C. Zhu, M. Luo, Q. Zhu, J. Zhu, P. V. R. Schleyer, J. I.-C. Wu, X. Lu and H. Xia, Nat. Commun., 2014, 5, 3265.
10. C. Zhu, S. Li, M. Luo, X. Zhou, Y. Niu, M. Lin, J. Zhu, Z. Cao, X. Lu, T. Wen, Z. Xie, P. V. R. Schleyer and H. Xia, Nat. Chem., 2013, 5, 698–703.
11. D. P. Craig and N. L. Paddock, Nature, 1958, 181, 1052–1053.
12. C. Zhu, X. Zhou, H. Xing, K. An, J. Zhu and H. Xia, Angew. Chem., Int. Ed., 2015, 54, 3102–3106.
13. J. Wu, X. Liu, Y. Hao, H. Chen, P. Su, W. Wu and J. Zhu, Chem. – Asian J., 2018, 13, 3691–3696.
14. Zhou Xiaoxi, Wu Jingjing, Hao Yulei, Zhu Congqing, Zhuo Qingde, Xia Haiping and Zhu Jun, Chem. – Eur. J., 2017, 24, 2389–2395.
15. Y. Hao, J. Wu and J. Zhu, Chem. – Eur. J., 2015, 21, 18805–18810.
16. I. Fernández and G. Frenking, Chem. – Eur. J., 2007, 13, 5873–5884.
17. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
18. C. Foroutan-Nejad, J. Vícha and A. Ghosh, Phys. Chem. Chem. Phys., 2020, 22, 10863–10869.
19. M. A. Iron, A. C. B. Lucassen, H. Cohen, M. E. van der Boom and J. M. L. Martin, J. Am. Chem. Soc., 2004, 126, 11699–11710.
20. G. Periyasamy, N. A. Burton, I. H. Hillier and J. M. H. Thomas, J. Phys. Chem. A, 2008, 112, 5960–5972.
21. Y.-Z. Huang, S.-Y. Yang and X.-Y. Li, J. Organomet. Chem., 2004, 689, 1050–1056.
22. R. W. A. Havenith, F. D. Proft, L. W. Jenneskens and P. W. Fowler, Phys. Chem. Chem. Phys., 2012, 14, 9897–9905.
23. M. El-Hamdi, O. El Bakouri El Farri, P. Salvador, B. A. Abdelouahid, M. S. El Begrani, J. Poater and M. Solà, Organometallics, 2013, 32, 4892–4903.
24. G. Parkin, J. Chem. Educ., 2006, 83, 791.
25. J. T. Boronski, J. A. Seed, D. Hunger, A. W. Woodward, J. van Slageren, A. J. Wooles, L. S. Natrajan, N. Kaltsoyannis and S. T. Liddle, Nature, 2021, 598, 72–75.
26. B. J. R. Cuyacot and C. Foroutan-Nejad, Nature, 2022, 603, E18–E20.
27. J. T. Boronski, J. A. Seed, D. Hunger, A. W. Woodward, J. van Slageren, A. J. Wooles, L. S. Natrajan, N. Kaltsoyannis and S. T. Liddle, Nature, 2022, 603, E21–E22.
28. D. W. Szczepanik, Angew. Chem., Int. Ed., 2022, 61, e202204337.
29. Z. Huang, Y. Zhang, W.-X. Zhang, J. Wei, S. Ye and Z. Xi, Nat. Commun., 2021, 12, 1319.
30. J. K. Pagano, J. Xie, K. A. Erickson, S. K. Cope, B. L. Scott, R. Wu, R. Waterman, D. E. Morris, P. Yang, L. Gagliardi and J. L. Kiplinger, Nature, 2020, 578, 563–567.
31. Z. Badri and C. Foroutan-Nejad, Phys. Chem. Chem. Phys., 2016, 18, 11693–11699.
32. L. Zhao, R. Grande-Aztatzi, C. Foroutan-Nejad, J. M. Ugalde and G. Frenking, ChemistrySelect, 2017, 2, 863–870.
33. T. Janda and C. Foroutan-Nejad, ChemPhysChem, 2018, 19, 2357–2363.
34. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
35. C. Foroutan-Nejad, Theor. Chem. Acc., 2015, 134, 8.
36. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796.
37. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford; New York, 1990.
38. S. Radenković, J. Tošović, R. W. A. Havenith and P. Bultinck, Chem. Phys. Chem., 2015, 16, 216–222.
39. T. I. U. of P. and A. Chemistry (IUPAC), IUPAC – aromaticity (A00442), https://goldbook.iupac.org/terms/view/A00442, (accessed 21 February 2022).
40. X. Lin and Y. Mo, Angew. Chem., Int. Ed., 2022, e202209658.
41. X. Li, A. E. Kuznetsov, H.-F. Zhang, A. I. Boldyrev and L.-S. Wang, Science, 2001, 291, 859–861.
42. C. Foroutan-Nejad, S. Shahbazian, F. Feixas, P. Rashidi-Ranjbar and M. Solà, J. Comput. Chem., 2011, 32, 2422–2431.
43. C. Foroutan-Nejad, J. Phys. Chem. A, 2011, 115, 12555–12560.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
46. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
47. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
48. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, 2013.
50. M. Repisky, S. Komorovsky, M. Kadek, L. Konecny, U. Ekström, E. Malkin, M. Kaupp, K. Ruud, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2020, 152, 184101.
51. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
52. K. G. Dyall, Theor. Chem. Acc., 2004, 112, 403–409.
53. M. Reiher, Theor. Chem. Acc., 2006, 116, 241–252.
54. S. Komorovsky, M. Repisky, K. Ruud, O. L. Malkina and V. G. Malkin, J. Phys. Chem. A, 2013, 117, 14209–14219.
55. C. Foroutan-Nejad, S. Shahbazian and P. Rashidi-Ranjbar, Phys. Chem. Chem. Phys., 2010, 12, 12630–12637.
56. C. Foroutan-Nejad, Z. Badri, S. Shahbazian and P. Rashidi-Ranjbar, J. Phys. Chem. A, 2011, 115, 12708–12714.
57. T. A. Keith, 2019.

---

Footnote

† Electronic supplementary information (ESI) available: Valence molecular orbitals and their contribution to magnetically induced current density. Cartesian coordinates for all structures included in the paper (XYZ). See DOI: https://doi.org/10.1039/d2cp04846a

---