 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure and registry of the silica bilayer film on Ru(0001) as viewed by LEED and DFT†
Edmar A.
Soares
ab,
Joachim
Paier
c,
Leonard
Gura
b,
Kristen
Burson
de,
Catherine
Ryczek
 d,
Zechao
Yang
b,
Fernando
Stavale
fb,
Markus
Heyde
d,
Zechao
Yang
b,
Fernando
Stavale
fb,
Markus
Heyde
 b and
Hans-Joachim
Freund
b and
Hans-Joachim
Freund
 *b
*b
aDepartment of Physics, Federal University of Minas Gerais, Brazil
bFritz-Haber-Institute of the Max-Planck Society, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: freund@fhi-berlin.mpg.de
cInstitut für Chemie, Humboldt-Universität zu Berlin, 10099 Berlin, Germany
dHamilton College, Clinton, New York 13323, USA
eGrinnell College, Grinnell, Iowa 50112, USA
fCentro Brasileiro de Pesquisas Físicas, Rio de Janeiro, Brazil
First published on 28th November 2022
Abstract
Silica bilayers are stable on various metal substrates, including Ru(0001) that is used for the present study. In a systematic attempt to elucidate the detailed structure of the silica bilayer film and its registry to the metal substrate, we performed a low energy electron diffraction (I/V-LEED) study. The experimental work is accompanied by detailed calculations on the stability, orientation and dynamic properties of the bilayer at room temperature. It was determined, that the film shows a certain structural diversity within the unit cell of the metal substrate, which depends on the oxygen content at the metal-bilayer interface. In connection with the experimental I/V-LEED study, it became apparent, that a high-quality structure determination is only possible if several structural motifs are taken into account by superimposing bilayer structures with varying registry to the oxygen covered substrate. This result is conceptually in line with the recently observed statistical registry in layered 2D-compound materials.
1. Introduction
Silicon dioxide (SiO2) is one of the most abundant and yet still complex materials on earth. As an important raw material for modern technology, silica has been widely used in microelectronics and catalysis.1,2 Its function depends on many parameters, including structure.3,4 In order to shed light on the connection between function and structure, thin silica films supported on a metal substrate have been prepared. The quality of the created films, naturally, depends on structural parameters at the support interface and the formed oxide.5,6 Once well-structured systems have been prepared, they may be studied at the atomic level with spectroscopic and structure determining experimental tools, both in ultra-high vacuum (UHV) or under ambient conditions. Such tools include scanning tunnelling microscopy (STM), scattering experiments, vibrational and electronic spectroscopy, diffraction and scanning probe techniques.The acceptance of the general structure of the film as a silica network followed from a long history.7–16 In the present paper we are discussing the structure of a bilayer SiO2 film on Ru(0001) with the schemes as shown in Fig. 1 in top and side view.15,17,18 The structural models are based on density functional theory (DFT) calculations in combination with STM measurements.15 Each Si atom resides in the middle of a SiO4-tetrahedron and the tetrahedra are connected via oxygen bridges to form a hexagonal lattice structure. In each tetrahedron within the hexagonal arrangement one O atom is shared between a top and a bottom layer forming a so-called bilayer. This crystal structure has been shown to be consistent with results of a number of experimental techniques, including STM, X-ray photoelectron spectroscopy (XPS) and infrared spectroscopy. The bilayer may also be prepared in a vitreous form, representing amorphous silica, again verified through STM measurements.19,20 The crystalline silica bilayer is known from calculations to be bound to the substrate by dispersive forces only. This leaves a space of a few Ångström between the substrate and the film, where the distance depends on how much oxygen is adsorbed on the metal substrate. The latter information is up to today only available from theoretical calculations, as an analysis of the 3D structure of the system has, so far, not been reported. Due to the preparation procedure, there is always oxygen adsorbed at the interface. The oxygen concentration at the interface may be changed by heating. In a separate set of studies,21,22 this arrangement has been used to perform model studies on reactions in the confined space between the silica film, which is used as a membrane, and the metal substrate where an adsorbed reaction partner resides. Specifically water forms by exposing the system to hydrogen, which diffuses through the six-membered ring of the silica film and reacts with adsorbed oxygen on the metal support, i.e. Ru(0001) after dissociation at the surface. On the basis of the analysis of the observed kinetics, with the help of theoretical electronic structure calculations, it was suggested that the bilayer silica film allows for lateral and vertical motions during the reaction as the oxygen concentration at the interface varies while the reaction progresses. This consideration was leading to a consistent description of the observed apparent activation energy. The result triggered the idea to look into more detail of the 3D structure of the silica bilayer film on the metal support, which had not been carried out so far. In order to experimentally determine the structure, and, in particular, the distance between the film and the substrate, as well as its position with respect to the substrate, we here present a first low energy electron diffraction (I/V-LEED) study, together with a set of detailed DFT calculations.
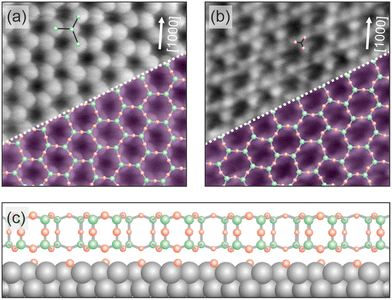 | ||
| Fig. 1 Structure of the 2D silica film on Ru(0001). Atomically resolved STM images of crystalline silica film regions are given in (a) and (b). The scan area of the two images is 3.5 nm × 3.5 nm. The images have been taken from ref. 23. (a) The imaging contrast reveals the position of Si atoms (VS = 3.0 V, IT = 100 pA), while in (b) a contrast towards the arrangement of O atoms is visible (VS = 100 mV, IT = 100 pA). White arrows indicate one crystallographic axis of the Ru(0001) substrate. In the lower right corner of (a) and (b) an atomic model of the topmost layer of the silica film is superimposed (green balls: Si atoms, red balls: O atoms). (c) A schematic side view of the silica film structure on the Ru(0001) substrate is plotted. | ||
The outcome of the present study reveals atomic level details, which connect not only to the results of the water formation study in confined space, but also to the recently discussed stacking disorder predicted, and observed, for three-dimensional compounds, consisting 2D-layers, where the layers are bound by dispersive forces.24 So far, often the structure of layered compounds, such as layered zeolites or layered covalent organic frameworks (LCOF), have been assumed to be characterized by fixed stacking of the layers based on X-ray diffraction. However, more recent detailed studies again using x-ray diffraction in combination with theoretical calculations, have revealed stacking disorder.21,25,26 Also, for graphene on Ni(111) co-existing structures been detected by XPS, where the graphene film is shifted with low activation energy between two positions on the metal surface.27 The experimental results, presented in this study, are paralleled and interpreted on the basis of extensive DFT calculations on the possible structural scenarios, as well as the phononic properties of those systems, augmented by molecular modelling calculations. The latter play a decisive role in understanding the details of the structure and revealed unexpected insight.
2. Theory
2.1 Structure optimizations and potential energy scans: computational details
Electronic and ionic structure optimizations have been carried out using the Vienna ab initio simulation package, VASP.28,29 Projector augmented wave method (PAW30,31) pseudopotentials for Ru include the 4s and 4p electrons of the Kr-core in the valence and were generated based on the electronic configuration 4s24p64d8 employing the Perdew, Burke, and Ernzerhof (PBE32) generalized-gradient approximation for exchange and correlation effects. Oxygen and silicon pseudopotentials use the valence electron configurations 2s22p4 and 3s23p2, respectively. These potentials correspond to the released version 5.4. A plane wave kinetic energy cut-off of 450 eV and a first order Methfessel–Paxton smearing of 0.1 eV has been used. This ensures minimal fictitious electronic entropy contributions of the order of 10 meV, well below the recommended value of 1 meV per atom. The break criterion for electronic relaxation was set to 10−5 eV. Structures were relaxed based on a maximum atomic force criterion of 0.02 eV Å−1. Brillouin zones of (2 × 2) surface unit cells were sampled using a Monkhorst–Pack33 grid of (6 × 6) k points. These k-point grids were tested, and deviations between total energies obtained using (6 × 6) and (8 × 8) grids are less than 0.01 eV per atom. A vacuum region of 12 Å between top- and bottom-most atoms of repeated slab models has been employed. Scans for the potential energy surfaces (PES) in lateral directions (parallel to the substrate surface) use (6 × 6) cells together with a (2 × 2) k-point sampling. Three Ru layers were used to model the metal substrate.21 Calculation of the average potential in the surface show that three-layer models suffice to describe the work function accurately (Fig. S1) as shown in the ESI.† PES scans vertical to the substrate surface (Table S1 and Fig. S2–S4, ESI†) use (2 × 2) unit cells with (6 × 6) k points. The distance of the silica bilayer to the metal surface is defined as the distance of the O atoms in SiO2 bilayer closest to the Ru surface and the average of the vertical positions, i.e., z-coordinates, of the optimized or relaxed Ru surface atoms.Regarding van der Waals-type dispersion interactions, this work employs Grimme's D2 approach34,35 to correct energies and gradients. Following previous work, for Ru atoms, the C6 coefficient of the noble gas Kr has been employed (Table S2, ESI†), i.e., considering core electron contributions only. Employing the C6 coefficient of a noble gas core, for instance Ne in Mg2+ ions, has been recently positively assessed for CO, CO2, and alkane adsorption on oxide surfaces, metal–organic frameworks, as well as zeolites.36 Herein, this ansatz is motivated by supposed complete delocalization of the valence electrons in Ru and will be referred to as DFT+D2′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,38 throughout this work. This means that seven 4d and one 5d valence electrons are supposed to be delocalized in metallic Ru. To check the impact of this approach, scans of the silica bilayer vertical to the Ru surface using default C6 values for Ru, i.e. 24.67 instead of 12.01 J nm6 mol−1, have been accomplished. Distances of oxygen atoms in SiO2 closest to surface Ru atoms corresponding to energy minima are shown in the first column of Table S1 (ESI†). These distances (PBE+D2) are ca. 5% shorter compared with PBE+D2′ results, and the effect is most pronounced for the clean Ru(0001) surface. For the 3O system, which is probably dominated by electrostatic interactions between SiO2 and the oxygen atoms (or ions) in the surface, varying C6 in Ru atoms affects the optimal film-metal distance less.
37,38 throughout this work. This means that seven 4d and one 5d valence electrons are supposed to be delocalized in metallic Ru. To check the impact of this approach, scans of the silica bilayer vertical to the Ru surface using default C6 values for Ru, i.e. 24.67 instead of 12.01 J nm6 mol−1, have been accomplished. Distances of oxygen atoms in SiO2 closest to surface Ru atoms corresponding to energy minima are shown in the first column of Table S1 (ESI†). These distances (PBE+D2) are ca. 5% shorter compared with PBE+D2′ results, and the effect is most pronounced for the clean Ru(0001) surface. For the 3O system, which is probably dominated by electrostatic interactions between SiO2 and the oxygen atoms (or ions) in the surface, varying C6 in Ru atoms affects the optimal film-metal distance less.
The actual values of van der Waals C6 coefficients and radii R0 employed for Ru, Si, and O are summarized in Table S2 (ESI†). The default global scaling factor, s6 = 0.75, being optimal for the PBE functional, has been employed.
Cross sections of the PES have been obtained by shifting or translating the silica bilayer across surfaces along six crystallographic directions as shown in Fig. S6 (ESI†). These cross sections, which are summarized in Fig. S7–S9 (ESI†), correspond to single points based on optimized structures (local minima). The height of the bilayer has been fixed to 3.18, 3.37, and 3.78 Å for the clean Ru(0001), the 1O, and the 3O substrate, respectively. For the clean surface and the 1O system, these values are 0.4 Å larger than those published in ref. 18, but have been chosen in view of the dynamics of the bilayer discussed in the following section. This dynamic behaviour suggests an average distance slightly off the global minimum, and cross sections were computed to represent the effective potential energy landscape “felt” by the bilayer on the surfaces at finite temperatures. Depending on directions, the bilayer has been shifted by two lattice constants. Along this shift, 20 single point structures have been obtained by linear interpolation between initial and final structures (Fig. S7–S9, ESI†). To test for possible relaxation effects, selected single points have been optimized. Based on these tests, relaxation effects are small. The energy lowering was found to be within 0.005–0.010 eV/(2 × 2)cell.
2.2 Molecular dynamics simulations: computational details
To accomplish molecular dynamics (MD) simulations of several tens of ps, machine learned force fields (MLFF) were employed. We use the MLFF implementation within VASP.6.39,40 These force fields were trained via NVT ensemble DFT-MD simulations employing PBE+D2′ at 300 K using a Nosé–Hoover thermostat.41,42 The training was done in a stepwise manner. First, a force field for the free silica bilayer has been trained using (2 × 2), (4 × 4), and (6 × 6) unit cells in order to provide an increasing number of atoms. Each training run consisted of 2000 steps of 1 fs. This has been sufficient to ensure Bayesian errors in the total energy/atom and forces to be less than defaulted thresholds. The so-called spilling factor43 has been three to four orders of magnitude smaller than the default value 0.02. After the successful training of the force fields for the free bilayer, the above procedure has been repeated for the Ru(0001) supported bilayer using again (2 × 2), (4 × 4), and (6 × 6) unit cells in repeated slab models. This force field had been used as a starting point for 1O and 3O structures. The training of corresponding force fields was again restarted using (2 × 2), (4 × 4), and (6 × 6) unit cells until Bayesian errors have been small enough to ensure accurate forces.During the actual MD runs based on the abovementioned force fields, desorption of the SiO2 bilayer from the Ru surface occurred occasionally. These desorption events were not observed in simulations based on PBE+D2′, which comprised approximately 9000 steps of 0.5 fs. We explain the desorption when using force fields by the missing dispersion interactions, which are responsible for bonding the film to the metal surface. Because the MLFF is based on a decomposition of the total energy in terms of local contributions, long-ranged dispersion-type of interactions cannot be accurately described by MLFF.39 Therefore, to prevent desorption of the bilayer during MD runs, a slab model with reduced vacuum height has been used during simulations. We repeated simulations at various distinctly larger vacuum gaps, but the trends or differences in findings reported below were unaffected. Herein reported calculations use a vacuum gap which is slightly larger than twice the equilibrium distance between bilayer and Ru surfaces, i.e., ca. 5–6 Å. For the simulations a (6 × 6) unit cell has been used. The temperature has been set to 300 K and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of 0.5 fs have been carried out. During these simulations of 50 ps, every 100th structure has been printed. In order to estimate atomic amplitudes of the bilayer during simulations, the following equation has been used
000 steps of 0.5 fs have been carried out. During these simulations of 50 ps, every 100th structure has been printed. In order to estimate atomic amplitudes of the bilayer during simulations, the following equation has been used
 | (1) |
To define these deviations or amplitudes the reference structure (superscript ref) corresponds to the last or final structure that has been printed. It is supposed that this structure relates to an equilibrated structure. The averaging over index i of length NX corresponds to the average over Si or O atoms in the bilayer.
The average squared amplitude, 〈u2〉, is defined as
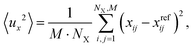 | (2) |
Analogous equations have been used to calculate y and z components of these average squared amplitudes.
3. Structural determination
3.1 Experimental details
The experiments were carried out in an ultra-high vacuum (UHV) chamber system (10−10 mbar range) equipped with STM and I/V-LEED instruments described in ref. 44. The Ru(0001) single crystal was cleaned by repeated cycles of annealing in oxygen atmosphere (2 × 10−6 mbar) for 30 min at 1250 °C, Ar+ bombardment, and annealing in UHV to 1250 °C for 1–2 min. Prior to the silica deposition, the ruthenium surface was covered with oxygen by exposing the clean Ru(0001) surface to molecular oxygen (5 × 10−6 mbar) at 930 °C for 10 min. Subsequently, silicon was evaporated in oxygen atmosphere (5 × 10−7 mbar) for 12 min. After the silicon deposition, the sample was heated to 860–870 °C for 15 min in 5 × 10−6 mbar O2. Based on previous studies and experiments, this optimal annealing temperature is chosen to minimize the coexistence of vitreous structures.45–47 When the sample is cooled down to room temperature in the same oxygen pressure, a final annealing step in UHV at lower temperatures of 630 °C was performed to clean the sample surface.The individual sample preparation procedures have been verified by using STM. Fig. 2 shows STM images of the resulting silica film recorded at room temperature with a beetle-type STM.44 The silica film exhibits a coverage of 1.8 monolyer (ML) and shows crystalline patches as shown in Fig. 2b. The characteristic ring structure is marked with green hexagons.
 | ||
| Fig. 2 STM images verifying the preparation of the silica bilayer on Ru(0001). (a) VS = 4.2 V, IT = 100 pA, scan area = 500 × 500 nm2. (b) VS = 3 V, IT = 350 pA, scan area = 2 × 2 nm2. | ||
After the final annealing step, I/V-LEED curves were recorded at room temperature using the experimental setup as described in ref. 48. Fig. 3 shows the LEED pattern recorded at electron energies of 100 eV. The absence of concentric ring patterns indicates the dominance of crystalline silica patches in the film system. Fig. 3b marks some of the distinct diffraction spots that are used to extract the experimental I/V-LEED curves. The corresponding color legend is shown on the right.
 | ||
| Fig. 3 LEED pattern of the silica bilayer on Ru(0001). (a) Diffraction pattern acquired at 100 eV and (b) with color coded diffraction spots. | ||
The tracking of the diffraction spot intensities as a function of electron energy was performed using a freely available software package described in ref. 49.
The I/V-LEED quantitative structural analysis was carried out using the method of symmetrized automated tensor LEED50 with the associated programs to calculate the scattering phase shifts using the approximation of the muffin-tin potential. The muffin-tin potential and the phase shifts were calculated using the Barbieri/Van Hove Phase Shift Package.50 In particular, a self-consistent Dirac–Fock approach was used to compute the atomic orbitals for each element. The muffin-tin potential was then evaluated following Mattheiss' prescription and the relativistic phase shifts were calculated by numerical integration of the Dirac equation.
4. Results and discussion
In this section we will first present the results of DFT calculations. They are discussed with respect to the question, which energies are necessary to shift the bilayer silica film parallel to the Ru(0001) substrate. Hereby, comparing the oxygen free interface with two oxygen covered surface configurations, i.e. the so-called 1O and the 3O surface. The first one contains one oxygen atom in the unit cell, the second one three oxygen atoms and represents saturation coverage. We then move to a discussion of the MD calculations before we discuss the experimental results of the present I/V-LEED study in light of theoretical results.4.1 Results and discussion of electronic structure calculations
Fig. 4 shows the PES cross section of the silica film when rigidly translated in [2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction (or in direction of any of the other rotationally equivalent base vectors, Fig. S6, ESI†). The structure shown in the beginning corresponds to a metastable state at +0.67 eV relative to the minimum energy structures. Vibrational characterization of this and the other metastable structures yield one imaginary mode in translational or shifting direction. It appears that the responsible structural feature of the bilayer relative to the Ru surface is the position of downward pointing O3 units of the SiO4 tetrahedra (triangular face). In high energy or metastable structures the oxygen atoms in O3 faces are close to or in atop position to Rusub atoms (triangle in Fig. 4), while Si atoms are close to or in atop position of Rusurf atoms. In contrast, the most stable structures are those with the oxygen atoms in the O3 face near Rusurf atoms and the Si atoms approximately bridging Rusurf atoms and hcp sites (Rusub). The above-mentioned energy barrier of 0.67 eV is estimated by taking the difference between highest and lowest energies found for the various structures shifting the (6 × 6) cell of SiO2 bilayer parallel to Ru(0001) surface in [2
0] direction (or in direction of any of the other rotationally equivalent base vectors, Fig. S6, ESI†). The structure shown in the beginning corresponds to a metastable state at +0.67 eV relative to the minimum energy structures. Vibrational characterization of this and the other metastable structures yield one imaginary mode in translational or shifting direction. It appears that the responsible structural feature of the bilayer relative to the Ru surface is the position of downward pointing O3 units of the SiO4 tetrahedra (triangular face). In high energy or metastable structures the oxygen atoms in O3 faces are close to or in atop position to Rusub atoms (triangle in Fig. 4), while Si atoms are close to or in atop position of Rusurf atoms. In contrast, the most stable structures are those with the oxygen atoms in the O3 face near Rusurf atoms and the Si atoms approximately bridging Rusurf atoms and hcp sites (Rusub). The above-mentioned energy barrier of 0.67 eV is estimated by taking the difference between highest and lowest energies found for the various structures shifting the (6 × 6) cell of SiO2 bilayer parallel to Ru(0001) surface in [2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction (06 in Fig. S7, ESI†). This is a relatively small barrier which may be overcome at room temperature, indicating that the film may easily be shifted under those conditions.
0] direction (06 in Fig. S7, ESI†). This is a relatively small barrier which may be overcome at room temperature, indicating that the film may easily be shifted under those conditions.
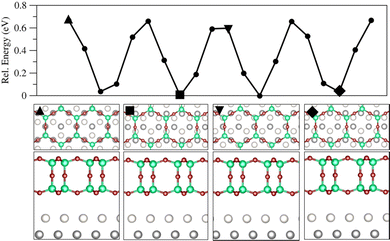 | ||
Fig. 4 Cross section of the PES for the bilayer on the clean Ru(0001) surface with an energy barrier of 0.67 eV obtained using PBE+D2′ (upper panel). The bilayer is translated along [2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] corresponding to direction 06 in Fig. S7 (ESI†). Below, top and side views for marked single points are shown. Colour code: Rusurf is light grey, Rusub is dark grey, Si is dark green, and O atoms in the bilayer are dark red. 0] corresponding to direction 06 in Fig. S7 (ESI†). Below, top and side views for marked single points are shown. Colour code: Rusurf is light grey, Rusub is dark grey, Si is dark green, and O atoms in the bilayer are dark red. | ||
The energy profiles shown in Fig. 5 and Fig. S8 (ESI†) for the bilayer translated on the 1O surface are substantially different compared to the profiles for the clean surface. Although bilayer heights with respect to Rusurf atoms are comparable (3.18 vs. 3.37 Å), energy barriers for the 1O system are 4.1 eV compared to 0.67 eV for the clean surface. Nonetheless, these cross sections of the PES reflect the symmetry of the surface. Note that the three-fold rotational symmetry of the clean Ru(0001) is preserved in case of the 1O overlayer structure. The scan starts at the low energy “O centred” structure, which means that Osurf is centred with respect to the ring of the bilayer (Fig. 5, first triangle). Regarding the Si atoms, one of the two per primitive unit cell is located at a Ru fcc site, and the second one is in an atop position to Rusurf. The downward pointing O3 units of individual SiO4 groups are collectively in the atop position to Rusub atoms. These energy barriers relate to structures where O ions of the bilayer are in atop position of surface O ions. The repulsive electrostatic interaction between these O ions causes the substantial destabilization. Normal mode analysis yields two orthogonal translational modes shifting the bilayer away from oxygen. Therefore, due to surface symmetry, the energy barrier corresponds to a second order saddle point. These modes are along the short and the long axis connecting interfacial or surface oxygen ions.
 | ||
Fig. 5 Cross section of the PES for the bilayer on the 1O-(2 × 2) surface with an energy barrier of 4.1 eV obtained using PBE+D2′ (upper panel). The bilayer is translated along [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 100] corresponding to direction 01 in Fig. S8 (ESI†). Below, top and side views for the marked single points are shown. Same colour code as in Fig. 4. Interfacial oxygen ions are light red. For the sake of clarity in top views, radii of these atoms have been notably increased. 100] corresponding to direction 01 in Fig. S8 (ESI†). Below, top and side views for the marked single points are shown. Same colour code as in Fig. 4. Interfacial oxygen ions are light red. For the sake of clarity in top views, radii of these atoms have been notably increased. | ||
Fig. 6 shows an energy profile for the bilayer translated on the 3O surface structure. The direction corresponds to [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] as displayed in Fig. S6 (ESI†) and features energy barriers of 0.70 eV, which are only slightly higher compared to the clean Ru support. Because of the higher O loading, it appears that some directions feature more and flatter potential wells in contrast to the clean Ru surface and the 1O overlayer structure. Like in previous structures, energy barriers are caused by repulsion of bilayer and interfacial oxygen ions when in atop positions. Conversely, stable structures avoid repulsive interactions among these aforementioned ions by adapting staggered instead of eclipsed configurations (second triangle, Fig. 6). Si atoms of SiO4 units occur in atop to Rusurf as well as in fcc hollow sites.
0] as displayed in Fig. S6 (ESI†) and features energy barriers of 0.70 eV, which are only slightly higher compared to the clean Ru support. Because of the higher O loading, it appears that some directions feature more and flatter potential wells in contrast to the clean Ru surface and the 1O overlayer structure. Like in previous structures, energy barriers are caused by repulsion of bilayer and interfacial oxygen ions when in atop positions. Conversely, stable structures avoid repulsive interactions among these aforementioned ions by adapting staggered instead of eclipsed configurations (second triangle, Fig. 6). Si atoms of SiO4 units occur in atop to Rusurf as well as in fcc hollow sites.
 | ||
Fig. 6 Cross section of the PES for the bilayer on the 3O-(2 × 2) surface with an energy barrier of 0.70 eV obtained using PBE+D2′ (upper panel). The bilayer is translated along [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2 2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] corresponding to direction 02 in Fig. S9 (ESI†). Below, top and side views for the marked single points are shown. Same colour code as in Fig. 4. For the sake of clarity in top views, radii of interfacial O ions have been notably increased. 0] corresponding to direction 02 in Fig. S9 (ESI†). Below, top and side views for the marked single points are shown. Same colour code as in Fig. 4. For the sake of clarity in top views, radii of interfacial O ions have been notably increased. | ||
4.2 Results and discussion of molecular dynamics
Fig. 7 shows results for amplitudes of the bilayer Si atoms in different directions evaluated according to eqn (1) for three systems: the clean Ru(0001) surface (black lines), 1O (red lines), and 3O (green lines). The amplitudes in z direction for the bilayer on the clean surface indicate an equilibration period within the first 20 ps. The amplitude of the entire bilayer is within a range of ±0.2 to ±0.3 Å. That the entire bilayer wiggles, can be shown by comparing the amplitudes of the bilayer oxygen atoms (Fig. S10, ESI†). These oxygen atoms show the same time evolution. Therefore, one can conclude that the centre of mass of the bilayer is subject to these oscillations normal to the surface. Beyond 20 ps of transient oscillations the amplitude in z-direction decreases and amounts to ±0.15 to ±0.2 Å approximately. Conversely, in x and y directions, parallel to the surface the bilayer drifts at least within 3–4 Å. This drift is not linear. It is akin to an ellipsoid motion.The amplitudes [uz] for the bilayer on 1O and 3O show distinct behaviour. Although a similar transient period of equilibration appears within the first 20 ps, these amplitudes are somewhat smaller. They are within ±0.1 to ±0.15 Å. Bilayer motions of these systems in directions parallel to the surfaces are noticeably smaller than corresponding motions on the clean Ru(0001) surface. This can be readily explained by the PES cross sections discussed in the previous section. As the SiO3 moieties are trapped by the substantial potential wells of ca. 4 eV depth, lateral mobility of the bilayer on the 1O surface structure is small. To quantify this mobility in a single number, we calculate average squared amplitudes following.51 These numbers, which have been computed according to eqn (2) are summarized in Table 1. It is apparent that Si atoms and O atoms show similar oscillatory or mobility characteristics. Furthermore, each system features distinct motional behaviour parallel to the surface. Consistent with the minimal energy barriers for the clean Ru(0001) support, corresponding amplitudes are one order of magnitude larger than respective numbers for 3O. The 1O surface relates to the smallest amplitudes, being another order of magnitude smaller than those for the 3O system. Consequently, the lateral SiO2 film motion or dynamics is largest on the Ru(0001) surface, it is one order of magnitude less pronounced for the 3O system and yet another order of magnitude smaller for the silica film on the 1O system. Therefore, the concentration of oxygen on the Ru(0001) surface affects the position of the entire bilayer film with respect to the metal underneath. These different stacking properties of the film depending on the different oxygen concentrations on the metal substrate has been observed in the experiments described below. These properties are the reason why different structures have to be combined in the LEED-I/V analysis.
| Si atoms | O atoms | ||
|---|---|---|---|
| Ru(0001) | 〈ux2〉 | 2.55 | 2.62 |
| 〈uy2〉 | 4.19 | 4.22 | |
| 〈uz2〉 | 0.0327 | 0.0402 | |
| 1O | 〈ux2〉 | 0.0481 | 0.0773 |
| 〈uy2〉 | 0.0368 | 0.0665 | |
| 〈u2z〉 | 0.0237 | 0.0271 | |
| 3O | 〈ux2〉 | 0.371 | 0.440 |
| 〈uy2〉 | 0.678 | 0.739 | |
| 〈uz2〉 | 0.0292 | 0.0374 | |
4.3 Results and discussion of I/V-LEED experimental studies and its structural analysis
Based on the results of the calculation, presented above, we considered the shift of the bilayer silica film by superimposing a variety of structures. 47 different structural models have been developed following the scheme depicted in Fig. 8. A complete table of the used models is given in the ESI† with further details. A (2 × 2) unit cell was used in the dynamical-LEED calculations. For each high-symmetry model, the distance between the topmost Ru layer and the bottom layer of the bilayer film (dSi–Ru) was varied from 2.2 Å up to 4.2 Å in steps of 0.2 Å. For each value dSi–Ru, all the atoms in the bilayer SiO2, the oxygen atoms at the interface layer and the Ru atoms down to the 2nd surface layer were allowed to fully relax respecting the symmetry constrains of each model. The Debye temperature of the Si (θSiD) atoms, of the O (θOD) atoms in the bilayer SiO2 and in the interface layer (θOinD) and of the surface Ru atoms (θRuD) were fitted, while the Debye temperatures of the Ru bulk layers were kept fixed at θBulkD 415 K.52 | ||
| Fig. 8 Scheme for the developed trial models considered in the I/V-LEED analysis. A complete list with the achieved RP factors is given in the ESI.† | ||
In the high-symmetry models the centre of the bilayer SiO2 hexagons lies on top of the high-symmetry substrate sites, namely fcc-hollow, hcp-hollow and top. For the fcc–hcp model the centre of the bilayer SiO2 hexagons are halfway between the fcc and hcp hollow sites. These models have then been developed with different amounts of oxygen at the interface. The labels (1O), (2O) and (3O) stands for the number of oxygen atoms in the (2 × 2) unit cell at the interface.
In the mixed-O coverage models the coexistence of different number of oxygen atoms in (2 × 2) unit cell at the interface was investigated for each individual high-symmetry model. The label convention adopted here is as follows: (1O + 2O) means that, in this particular model, the coexistence of the 1O and 2O phases was allowed at the interface. The relative amount of each phase was varied from 0% to 100% keeping the total concentration equal to 100%. This was done as following: 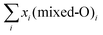 , where xi is the concentration of model (mixed-O)i, i is equal to 2 or 3 (if two or three models are mixed, respectively), and
, where xi is the concentration of model (mixed-O)i, i is equal to 2 or 3 (if two or three models are mixed, respectively), and  .
.
In the split-position model class (parallel to the surface), the split-position approach was introduced to simulate thermal vibrations with large amplitudes parallel to the surface for each high-symmetry models having the (3O) phase at the interface. The atoms were displaced from their equilibrium position by ±0.2 Å along the unit cell diagonals. The notation used here is: fcc(split) means that the split-position approach was introduced to the fcc(3O) model.
In the last class a stacking disorder plus split-position models have been introduced. Here the possibility of coexistence of different domains on the surface was investigated by mixing the high-symmetry models having the (3O) phase at the interface, after including large thermal vibrations through the split-position approach. The fraction of each domain on the surface was varied from 0% up to 100% always keeping the total concentration equal to 100%. This was done as following:  , where xi is the concentration of model (model)i, i is equal to 2, 3 or 4 (if two, three or four different models are mixed, respectively), and
, where xi is the concentration of model (model)i, i is equal to 2, 3 or 4 (if two, three or four different models are mixed, respectively), and 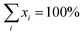 .
.
In all models where mixed domains were considered, the calculated spectra were derived from incoherently summing over the different terraces. In order to quantify the agreement between the experimental and theoretical I/V-LEED curves we have used the R-factor proposed by Pendry (RP).53
In order to include vibrations with large amplitudes, the split-position approach was used in some models where the bilayer is allowed to vibrate with an amplitude of ±0.2 Å with respect to the equilibrium position. The idea of split position is that the probability-density function describing the thermal vibrations can be approximated using a few distinct positions with an appropriate occupation factor.54–56
Fig. 9 shows the RP factors obtained for all the structural models evaluated in this work. A detailed list can be found in Table S2 of the ESI.† The first set of models analyzed here were the high-symmetry ones (from 1 to 16). All of them exhibited RP values higher than 0.44. For example, model 1–4, (01) fcc, (02) fcc(1O), (03) fcc(2O), (04) fcc(3O), RP decreases from ∼0.65 to ∼0.44 due to the change in oxygen coverage. It is also important to observe that the RP decreases when the oxygen coverage at the interface increases from 1 to 3 oxygen atoms in the (2 × 2) layer in the interface between the substrate and bilayer silica film (blue bars).
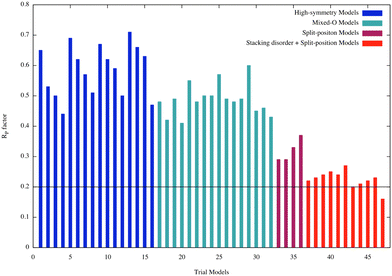 | ||
| Fig. 9 R P factors for all the trial models considered in the LEED analysis. An additional table of this graph is provided in the ESI.† | ||
Since these first models did not properly describe the experimental I/V-LEED curves, a second class was considered where we allowed the coexistence of domains with different number of oxygen atoms at the interface (mixed-O models: from 17 to 32). Once more, a poor agreement between theory and experiment was obtained as shown in Fig. 9 (turquoise bars) indicating that new structural models must be considered.
According to our DFT calculations the bilayer silica film interacts with the Ru(0001) substrate through van der Waals forces and is weakly bound to the substrate. This weak interaction would allow the bilayer silica easily to vibrate parallel and perpendicularly to the surface. If these vibration models had large amplitudes and low frequencies, as we realized via the above-discussed calculations, they could have a strong influence in the scattering processes undergone by the incident electrons in the LEED experiment. Molecular dynamic simulations performed in this work, and presented in the previous section, demonstrated that the centre of mass of the bilayer silica vibrates with relatively large amplitude. Guided by the facts just explained, the next class of models considered in this LEED analysis was built by allowing the high-symmetry models to have large amplitude vibrations parallel to the surface (split-position models: from 33 to 36). The RP factors obtained for this class of models are also presented in Fig. 9 (purple bars). An improvement in the agreement between the theoretical and experimental I/V-LEED curves is now observed as reflected by a decrease of the RP factors.
As revealed by our theoretical calculations, different adsorption sites may have similar adsorption energies and the film may easily be shifted. Therefore, different structures may coexist on the surface. Real-space STM images of domain boundaries have also emphasized several possible registries of the bilayer with the underlying metal substrate.57 To properly address this point, a new class of models was included in the LEED analysis (stacking disorder + split position models: from 37 to 47) and corresponding RP factors are shown in Fig. 9 (red bars). The assumption of presence of stacking disorder greatly improved the agreement between theory and experiment and reduce the RP factors from the range of 0.3 to 0.2. The lowest RP factor value achieved of 0.16 corresponds to model 47 having 22% of (top)split, 24% of (hcp)split, 32% of (fcc)split, and 22% (fcc–hcp)split domains covering the surface (Fig. 10 – top panel). A side view of the structure with the relevant structural parameters is presented in the lower panel of Fig. 9. The final structural parameters were calculated by averaging the corresponding structural parameters in the four different domains.
The uncertainty of Pendry R-factor is evaluated by calculating the  where Voi is the imaginary part of the inner potential and ΔE is total energy range defined by the experimental beams used in the structural determination. In this study, the imaginary part of the inner potential was set to 7.5 eV (after optimization) and the total energy range is 2.610 eV resulting in a RR = 0.1516. The final RP = Rmin (1 ± RR) = (0.16 ± 0.02). The final structural parameters and the respective error bars are presented in Fig. 10.
where Voi is the imaginary part of the inner potential and ΔE is total energy range defined by the experimental beams used in the structural determination. In this study, the imaginary part of the inner potential was set to 7.5 eV (after optimization) and the total energy range is 2.610 eV resulting in a RR = 0.1516. The final RP = Rmin (1 ± RR) = (0.16 ± 0.02). The final structural parameters and the respective error bars are presented in Fig. 10.
Fig. 11 shows the comparison between experimental (blue curves) and the theoretical (black curves) I/V-LEED curves corresponding to the best model is shown in Fig. 10. Most of the main features presented in the experimental curves are well reproduced in theory.
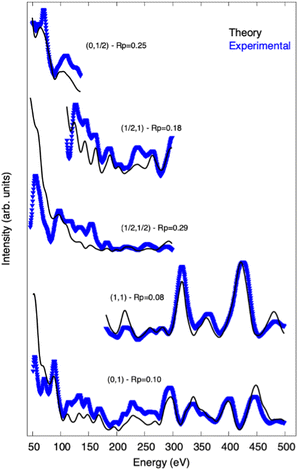 | ||
| Fig. 11 Experimental (blue) and theoretical (black) I/V-LEED curves for the best model (RP = 0.16) obtained from the LEED analysis. The (i, j) notation gives the index of the diffraction spots. The RP for each individual beam is also shown. I/V-LEED curves of additional diffraction spots are given in the ESI.† | ||
5. Summary and conclusions
Via a variety of surface science techniques in combination with theoretical electronic structure calculations, the structure of a silica bilayer on an oxygen covered Ru(0001) single crystal surface has been studied. It is shown that, since the bilayer is only bound by dispersive forces to the substrate, a detailed structure determination of all interatomic distances represents a challenge. Even though the STM data reveal a detailed structure of the top of the bilayer, the position of the entire bilayer with respect to the substrate is influenced by a number of parameters. In part, this became apparent when we tried to understand the kinetics of water formation at the interface between the bilayer and the substrate, used as model for a reaction in confined space. It was only possible to fit the observed apparent activation energy for the reaction, by assuming that the bilayer moves parallel and perpendicular to the surface without influencing the internal silica bilayer film structure, as the amount of oxygen at the interface changes during the reaction. This observation triggered the idea to perform the present I/V-LEED study.We find that for a given preparation of the silica film on the oxygen saturated Ru(0001) surface, a decent agreement between measured I/V-LEED data judged by the RP factor, and theoretical modelling of the intensity versus voltage curves, can only be obtained, if a combination of structural components is considered. Also, this finding is consistent with the calculated soft phonon modes moving the film parallel to the surface, which are documented through the molecular-dynamics simulations. Also, and foremost, the bilayer silica film shows almost the same activation energies for a full oxygen coverage as compared with the clean Ru(0001) surface, while an intermediate coverage, documented via calculations for an oxygen coverage of one oxygen atom per unit cell leads to a much-reduced mobility. The overall results are fully consistent with the concepts of statistical stacking of the layers in layered materials, and also with observations made for supported graphene.
Data availability statement
Further theoretical and experimental results supporting this article have been uploaded as part of the ESI.† Additional data supporting the findings is available from the authors upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Adrian Lewandowski, Earl Davis, and Helmut Kuhlenbeck for many helpful discussions. In addition, we would like to thank all members of the Group of Thomas Schmidt, especially Mauricio Prieto. We are grateful for discussions with Professor Marek Sierka, who has drawn our attention to the small energy barriers of silica films on the substrates discussed in the present work. JP would like to thank Professor Joachim Sauer for permission to use VASP.6 on his licence. EAS would like to thank CAPES for financial support. KMB gratefully acknowledges funding from the Alexander von Humboldt foundation. CNR acknowledges funding from the Hamilton College Summer Science Program. FS acknowledges the Brazilian financial support from CNPq and FABERJ. Open Access funding provided by the Max Planck Society.References
- F. J. Grunthaner and P. J. Grunthaner, Mater. Sci. Rep., 1986, 1, 65–160 CrossRef CAS.
- F. J. Himpsel, F. R. McFeely, A. Taleb-Ibrahimi, J. A. Yarmoff and G. Hollinger, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 6084–6096 CrossRef CAS PubMed.
- H.-J. Freund, Acc. Chem. Res., 2017, 50, 446–449 CrossRef CAS PubMed.
- J.-Q. Zhong and H.-J. Freund, Chem. Rev., 2022, 122, 11172–11246 CrossRef CAS PubMed.
- X. Yu, B. Yang, J. Anibal Boscoboinik, S. Shaikhutdinov and H.-J. Freund, Appl. Phys. Lett., 2012, 100, 151608 CrossRef.
- C. Zhou, X. Liang, G. S. Hutchings, J.-H. Jhang, Z. S. Fishman, R. Wu, A. Gozar, U. D. Schwarz, S. Ismail-Beigi and E. I. Altman, Nanoscale, 2019, 11, 21340–21353 RSC.
- X. Xu and D. W. Goodman, Appl. Phys. Lett., 1992, 61, 774–776 CrossRef CAS.
- X. Xu and D. W. Goodman, Surf. Sci., 1993, 282, 323–332 CrossRef CAS.
- K. Luo, D. Y. Kim and D. W. Goodman, J. Mol. Catal. A: Chem., 2001, 167, 191–198 CrossRef CAS.
- J. W. He, X. Xu, J. S. Corneille and D. W. Goodman, Surf. Sci., 1992, 279, 119–126 CrossRef CAS.
- T. Schroeder, M. Adelt, B. Richter, M. Naschitzki, M. Bäumer and H. J. Freund, Surf. Rev. Lett., 2000, 07, 7–14 CrossRef CAS.
- T. Schroeder, M. Adelt, B. Richter, M. Naschitzki, M. Bäumer and H. J. Freund, Microelectron. Reliab., 2000, 40, 841–844 CrossRef.
- T. Schroeder, A. Hammoudeh, M. Pykavy, N. Magg, M. Adelt, M. Baumer and H. J. Freund, Solid-State Electron., 2001, 45, 1471–1478 CrossRef CAS.
- T. Schroeder, J. B. Giorgi, M. Bäumer and H. J. Freund, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 165422 CrossRef.
- D. Löffler, J. J. Uhlrich, M. Baron, B. Yang, X. Yu, L. Lichtenstein, L. Heinke, C. Büchner, M. Heyde, S. Shaikhutdinov, H. J. Freund, R. Włodarczyk, M. Sierka and J. Sauer, Phys. Rev. Lett., 2010, 105, 146104 CrossRef PubMed.
- J. Weissenrieder, S. Kaya, J. L. Lu, H. J. Gao, S. Shaikhutdinov, H. J. Freund, M. Sierka, T. K. Todorova and J. Sauer, Phys. Rev. Lett., 2005, 95, 076103 CrossRef CAS PubMed.
- B. Yang, W. E. Kaden, X. Yu, J. A. Boscoboinik, Y. Martynova, L. Lichtenstein, M. Heyde, M. Sterrer, R. Włodarczyk, M. Sierka, J. Sauer, S. Shaikhutdinov and H.-J. Freund, Phys. Chem. Chem. Phys., 2012, 14, 11344–11351 RSC.
- R. Włodarczyk, M. Sierka, J. Sauer, D. Löffler, J. J. Uhlrich, X. Yu, B. Yang, I. M. N. Groot, S. Shaikhutdinov and H. J. Freund, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085403 CrossRef.
- L. Lichtenstein, C. Büchner, B. Yang, S. Shaikhutdinov, M. Heyde, M. Sierka, R. Włodarczyk, J. Sauer and H.-J. Freund, Angew. Chem., Int. Ed., 2012, 51, 404–407 CrossRef CAS PubMed.
- L. Lichtenstein, M. Heyde and H.-J. Freund, Phys. Rev. Lett., 2012, 109, 106101 CrossRef PubMed.
- M. J. Prieto, T. Mullan, M. Schlutow, D. M. Gottlob, L. C. Tănase, D. Menzel, J. Sauer, D. Usvyat, T. Schmidt and H.-J. Freund, J. Am. Chem. Soc., 2021, 143, 8780–8790 CrossRef CAS PubMed.
- M. J. Prieto, H. W. Klemm, F. Xiong, D. M. Gottlob, D. Menzel, T. Schmidt and H.-J. Freund, Angew. Chem., Int. Ed., 2018, 57, 8749–8753 CrossRef CAS PubMed.
- L. Lichtenstein, M. Heyde and H.-J. Freund, J. Phys. Chem. C, 2012, 116, 20426–20432 CrossRef CAS.
- N. Marom, J. Bernstein, J. Garel, A. Tkatchenko, E. Joselevich, L. Kronik and O. Hod, Phys. Rev. Lett., 2010, 105, 046801 CrossRef PubMed.
- M. Položij, H. V. Thang, M. Rubeš, P. Eliášová, J. Čejka and P. Nachtigall, Dalton Trans., 2014, 43, 10443–10450 RSC.
- Y. Zhang, M. Položij and T. Heine, Chem. Mater., 2022, 34, 2376–2381 CrossRef CAS.
- W. Zhao, S. M. Kozlov, O. Höfert, K. Gotterbarm, M. P. A. Lorenz, F. Viñes, C. Papp, A. Görling and H.-P. Steinrück, J. Phys. Chem. Lett., 2011, 2, 759–764 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097 CrossRef CAS PubMed.
- F. R. Rehak, G. Piccini, M. Alessio and J. Sauer, Phys. Chem. Chem. Phys., 2020, 22, 7577–7585 RSC.
- L. Gura, S. Tosoni, A. L. Lewandowski, P. Marschalik, Z. Yang, W.-D. Schneider, M. Heyde, G. Pacchioni and H.-J. Freund, Phys. Rev. Mater., 2021, 5, L071001 CrossRef CAS.
- S. Tosoni and J. Sauer, Phys. Chem. Chem. Phys., 2010, 12, 14330–14340 RSC.
- R. Jinnouchi, K. Miwa, F. Karsai, G. Kresse and R. Asahi, J. Phys. Chem. Lett., 2020, 11, 6946–6955 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2020, 101, 060201 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- N. Nilius, A. Corper, G. Bozdech, N. Ernst and H. J. Freund, Prog. Surf. Sci., 2001, 67, 99–121 CrossRef CAS.
- L. Lichtenstein, C. Büchner, B. Yang, S. Shaikhutdinov, M. Heyde, M. Sierka, R. Włodarczyk, J. Sauer and H.-J. Freund, Angew. Chem., Int. Ed., 2012, 51, 404–407 CrossRef CAS PubMed.
- H. W. Klemm, M. J. Prieto, F. Xiong, G. B. Hassine, M. Heyde, D. Menzel, M. Sierka, T. Schmidt and H.-J. Freund, Angew. Chem., Int. Ed., 2020, 59, 10587–10593 CrossRef CAS PubMed.
- K. M. Burson, H. J. Yang, D. S. Wall, T. Marsh, Z. Yang, D. Kuhness, M. Brinker, L. Gura, M. Heyde, W.-D. Schneider and H.-J. Freund, J. Phys. Chem. C, 2022, 126, 3736–3742 CrossRef CAS PubMed.
- A. L. Lewandowski, P. Schlexer, C. Büchner, E. M. Davis, H. Burrall, K. M. Burson, W.-D. Schneider, M. Heyde, G. Pacchioni and H.-J. Freund, Phys. Rev. B, 2018, 97, 115406 CrossRef CAS.
- A. Mayer, H. Salopaasi, K. Pussi and R. D. Diehl, Comput. Phys. Commun., 2012, 183, 1443–1447 CrossRef CAS.
- A. Barbieri and M. A. Van Hove, SATLEED and Phase Shift package, 1994, https://www.icts.hkbu.edu.hk/vanhove/VanHove_files/leed/leedpack.html Search PubMed.
- M. Baudin and K. Hermansson, Surf. Sci., 2001, 474, 107–113 CrossRef CAS.
- C. Y. Ho, R. W. Powell and P. E. Liley, J. Phys. Chem. Ref. Data, 1972, 1, 279–421 CrossRef CAS.
- J. B. Pendry, J. Phys. C: Solid State Phys., 1980, 13, 937–944 CrossRef CAS.
- T. Hertel, H. Over, H. Bludau, M. Gierer and G. Ertl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 8126–8129 CrossRef CAS PubMed.
- H. Over, W. Moritz and G. Ertl, Phys. Rev. Lett., 1993, 70, 315–318 CrossRef CAS PubMed.
- C. Stampfl, M. Scheffler, H. Over, J. Burchhardt, M. Nielsen, D. L. Adams and W. Moritz, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 4959–4972 CrossRef CAS PubMed.
- K. M. Burson, C. Büchner, M. Heyde and H. J. Freund, J. Phys.: Condens. Matter, 2017, 29, 035002 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04624e |
| This journal is © the Owner Societies 2022 |


