Radical-induced hetero-nuclear mixing and low-field ¹³C relaxation in solid pyruvic acid

Abstract

Radicals serve as a source of polarization in dynamic nuclear polarization, but may also act as polarization sink, in particular at low field. Additionally, if the couplings between the electron spins and different nuclear reservoirs are stronger than any of the reservoirs’ couplings to the lattice, radicals can mediate hetero-nuclear polarization transfer. Here, we report radical-enhanced ¹³C relaxation in pyruvic acid doped with trityl. Up to 40 K, we find a linear carbon T₁ field dependence between 5 mT and 2 T. We model the dependence quantitatively, and find that the presence of trityl accelerates direct hetero-nuclear polarization transfer at low fields, while at higher fields ¹³C relaxation is diffusion limited. Measurements of hetero-nuclear polarization transfer up to 600 mT confirm the predicted radical-mediated proton–carbon mixing.

---

1 Introduction

Nuclear magnetic resonance (NMR) spectroscopy and magnetic resonance imaging (MRI) are powerful tools in various fields of science and industry, but their versatility is limited by the weak nuclear polarization. The low sensitivity may be alleviated by dynamic nuclear polarization (DNP), where the large polarization of electron spins is transferred to nuclear spins. In dissolution-DNP,¹ this process is carried out at temperatures near 1 K and fields of several Tesla. Under these conditions, the electron spins are almost fully polarized, and it is possible to achieve near unity polarization also for nuclear spins. The hyperpolarized sample is then dissolved with a jet of hot solvent, and the solution is transferred to a second magnet for use in sensitized NMR spectroscopy^2–4 or MRI.^5–8

In bullet-DNP, the order of dissolution and transfer is reversed.^9,10 Here, the solid sample is transferred rapidly to the second magnet, and dissolved only near the NMR tube. This procedure limits dilution, avoids the use of hot solvents, and may be beneficial for hyperpolarization of moieties with a short T₁ in the liquid state.

During the bullet transfer at low field (100 ms at currently about 70 mT) the radical spins that are needed as a polarization source for DNP, however, may act as polarization sink. A previous study by Niedbalski et al. at low temperature in pyruvic acid doped with trityl between 0.9 and 9 T found a cubic field-dependence of the carbon T₁.¹¹ If this trend were to continue to lower fields, relaxation would be prohibitively fast for bullet-DNP. Indeed, we reported that the low-temperature low-field ¹H relaxation in pyruvic acid doped with trityl is linear in field, and showed that a spin temperature model (STM) by Wenckebach^12,13 yields a quantitative description of the proton relaxation data over two orders of magnitude in field.¹⁴ This STM indicated a significant heat-capacity of the electron Non-Zeeman reservoir, which suggests that the latter may be used to mediate hetero-nuclear polarization transfer.¹⁵

Here, we present ¹³C relaxation data as well as thermal mixing experiments in non-degassed neat 1-¹³C pyruvic acid (neat PA, °) and 1-¹³C pyruvic acid doped with 15 mM OX063 (doped PA, ^●) for fields up to 2 T. We find that the low-temperature low-field ¹³C relaxation time constant is linear in field, similar to that we reported for protons. The data show that in presence of trityl, relaxation during the low field transfer is not critical for either nuclear species in bullet-DNP.

The data are interpreted by extending the previously reported STM to account for the carbon Zeeman reservoir. This extended STM predicts an enhanced carbon relaxation due to effective trityl-mediated proton–carbon coupling from 20 mT to above 1 T.

For a quantitative description of the observed carbon relaxation, the extended STM takes into account enhanced low-field direct hetero-nuclear mixing due to trityl-induced nuclear line-broadening, and a field-dependent carbon spin diffusion process that limits relaxation at higher fields. Hetero-nuclear thermal mixing experiments confirm the predicted trityl-mediated polarization transfer at higher fields.

2 Fast-field-cycling experiments

2.1 Samples

One sample of neat 1-¹³C-pyruvic acid (CortecNet, FR), 14 M, referred to as neat PA, was measured during a single session. Two experimental sessions were required to record the data on 1-¹³C pyruvic acid doped with 15 mM OX063 (Oxford Instruments, UK), referred to as doped PA, and a fresh sample was prepared for each session. All samples were used without degassing and flash-frozen by insertion of the NMR probe into the cold variable temperature insert of the fast-field-cycling magnet.

2.2 Fast-field-cycling apparatus

The measurements were performed using a fast-field-cycling (FFC) setup^16,17 with a range of stable temperatures from 3 to 300 K and magnetic fields from 0 to 2.5 T, with an absolute error of 2 mT. In the experiments described here, the field is changed at a rate of 4 T s⁻¹. A Tecmag Apollo NMR spectrometer (Tecmag, TX) enables control of the magnet from within the NMR pulse sequence. We used a home-built NMR probe equipped with a solenoid tuned to a frequency of 22.83 MHz, which corresponds to resonant magnetic fields B_res of approximately 0.536 and 2.167 T for proton and carbon spins, respectively.

2.3 Fast-field-cycling NMR experiments

The field-dependence of the carbon relaxation time constant was measured using two variations of the sequence shown in Fig. 1. For field strengths of 0.5 T and higher a saturation recovery sequence is used. For fields up to 0.2 T the equilibrium polarization signal would be too small, and so a polarization decay sequence is used. This includes an additional polarization stage (stage II) of 70 s at 2 T.

Fig. 1 Fast-field-cycling experiments were performed in three variations of the displayed sequence. Polarization decay (⋯): for measurements of T₁ at evolution fields B_evo below 0.5 T the magnetization is saturated with a train of n π/2-pulses in stage I, to ensure reproducibility. Then in stage II the nuclei polarize at B_pol = 2 T (red dashed buildup curve). In stage III the field is changed to the evolution field B_evo and the magnetization relaxes (red dashed decay curve). In stage IV the NMR signal is read out at the resonant field B_res. Saturation recovery(—): for evolution fields of 0.5 T and higher only stages I, III and IV are used, i.e. stage II (highlighted) is dropped. For these fields the magnetization is saturated in stage I and recovers (blue buildup curve) in stage III at B_evo to the respective equilibrium value. In stage IV the NMR signal is read out. Thermal mixing(--): the sequence for thermal mixing is similar to saturation recovery, except that stage I lasts for t_sat = 70 s to ensure protons establish equilibrium polarization at 2.167 T while carbon spins are saturated.

Thermal mixing is measured using another variation of the sequence shown in Fig. 1. Here, stage I is prolonged (t_pol = 70 s ≫ T_1,H) such that the proton magnetization reaches thermal equilibrium at the ¹³C resonance field of 2.167 T, while the carbon spins are saturated. Stage II is skipped, such that for stage III the magnetic field is changed to the mixing field B_evo where no pulses are applied. In this period, carbon spins relax towards their thermal equilibrium polarization. Additionally, if fast direct or indirect proton–carbon exchange at B_evo is possible, thermal mixing leads to a transfer of spin polarization from proton to carbon spins. This gives rise to an observable maximum in carbon polarization or, if protons relax faster to the lattice, to carbon reaching equilibrium polarization faster than its spin-lattice relaxation could account for. In stage IV the NMR signal is read out at the ¹³C resonance field of 2.167 T.

3 Low-field ¹³C relaxation

3.1 Low-field ¹³C relaxation data

The field-dependence of the carbon relaxation time constant for doped PA for temperatures between 4.2 K and 40 K is shown in Fig. 2(a). At low fields, we find an approximately linear increase of with field. This low-field linearity holds up to 40 K, although expectedly decreases with increasing temperature.

Fig. 2 Field-dependent relaxation in 1-¹³C PA doped with 15 mM trityl (OX063). (a) ¹³C relaxation time constants for different temperatures together with 1.8 K data (gray) reproduced from ref. 11. The dashed gray line corresponds to a power law with an exponent α = 3.1 as reported by Niedbalski et al. based on measurements at 1.8 K and fields from 0.9 to 9 T. The dotted gray line is computed using T₁ = cB/(1 − P₀²), where c = 50 s T⁻¹, and P₀ = tan h(ħγ_SB/(2k_BT)) is the electron spin polarization. (b) The 4.2 K data on doped PA (solid symbols) plotted as rates together with ¹H data. For comparison the relaxation rates measured on neat PA (open symbols) are shown as well. The presence of OX063 increases the ¹³C relaxation rate throughout the observed field range, and causes faster ¹H relaxation up to approximately 200 mT. Also shown are EPR relaxation data reported by Lumata et al.¹⁸ near 4.2 K.

Also shown in Fig. 2(a) are data at 1.8 K recorded by Niedbalski, Lumata and co-workers.¹¹ They found that their data are well described by a power law T₁ = CB^α, with an exponent of α = 3.1, indicated by the dashed gray line. If persistent to lower fields, this trend would correspond to critical relaxation during the transfer in bullet-DNP (the transfer takes 0.1 s at 70 mT) marked in Fig. 2(a)). While we observe a linear rather than a cubic field dependence at lower fields, our data at 4.2 K between 1 and 2 T (corresponding to the upper limit of our field range) are nonetheless in good agreement with the data by Niedbalski et al. at 1.8 K (corresponding to the lower limit of their field range).

The steep increase in ¹³C , as observed by Niedbalski et al. at 1.8 K, may be attributed to the substantial electron spin polarization P₀ with increasing field, which leads to a suppression of triple-spin flips. As shown in Fig. 2(a), a corresponding correction of the observed linear dependence (dotted gray line) gives a satisfactory description over more than three orders of magnitude in field and more than four orders of magnitude in T₁.

To assess the effect of trityl radicals on nuclear relaxation, it is requisite to compare the relaxation of both ¹H and ¹³C nuclear spins in the presence of trityl to that in neat PA. Relaxation rates R₁ = 1/T₁ of both nuclei, recorded at 4.2 K, are shown for neat and doped PA in Fig. 2(b). We note for neat PA that the rates 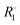of protons and carbons converge at low field, which is expected based on reports of direct low-field thermal mixing in neat PA.^17,19 This direct exchange is negligible for B > 10 mT but becomes relevant as the field approaches zero. The presence of trityl significantly accelerates the relaxation of carbon over the entire field range, while the effect on proton relaxation is only observable for fields below 200 mT.

In addition to the nuclear relaxation rates, Fig. 2(b) also shows electron spin-lattice relaxation rates reported by Lumata et al.¹⁸ for temperatures near 4.2 K. For our analysis below, we note that R_1,S(T = 4 K) ≈ 5 s⁻¹ is nearly independent of field, which is expected since trityl relaxes predominantly via oxygen.²⁰

3.2 Thermodynamic model

We have recently shown that the proton relaxation can be described quantitatively¹⁴ using a thermodynamic spin temperature model.^15,21,22 In this model, as indicated in the sketch in Fig. 3, the different nuclear spin species and radical electron spins are described as reservoirs with distinct inverse temperatures β_i = ħ/(k_BT_i) that couple to one another and the lattice. In particular, we showed that the relaxation of proton spins is described by their coupling to the electron Non-Zeeman (NZ) or dipolar reservoir. This exchange is via energy-conserving triple-spin flips (TSFs), in which a nuclear spin flip and an electron–electron flip-flop occur simultaneously.²³ The TSF rate was calculated from first principles,^12,13 after determining the NZ heat capacity from proton relaxation data. This lead to a nearly quantitative agreement between the model and the measured proton relaxation rates over two orders of magnitude in magnetic field.¹⁴

Fig. 3 Top: ¹³C relaxation is described by three reservoirs coupled to the lattice and each other. The vertical axis gives the reservoirs’ heat capacities at a field of 200 mT. (a) Heat capacities of nuclear Zeeman reservoirs grow quadratically with field, while the NZ heat capacity is field-independent. (b) Exchange rates used for modelling of nuclear relaxation rates. The TSF rates τ_NZ–H/C⁻¹ have previously been calculated¹⁴ and the electron T_1,S⁻¹ is known from literature data.¹⁸ Also shown are the calculated carbon core-bulk diffusion rate τ_C–C⁻¹ and the proton–carbon mixing rate τ_H–C⁻¹. (c) The resulting coefficient-weighted relaxation rates for protons describe ¹H data well.¹⁴ The predicted rate for carbon is slower than experimental rates for fields up to 30 mT and faster above. Between 0.1 and 1 T the high TSF rates for both nuclei cause the predicted relaxation rate for carbon to be tied to the proton relaxation rate. Taking into account faster low-field mixing with protons and carbon–carbon spin-diffusion, the ¹³C data are well described (dash-dot line).

In our previous analysis of the proton relaxation, the carbon reservoir could be ignored, as its heat capacity C_C is about times smaller than that of the proton reservoir C_H for pyruvic acid at any field, as shown in Fig. 3(a). We now extend the analysis to the carbon reservoir, which is coupled to the lattice with the rate 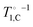measured in neat PA and to the NZ reservoir with the TSF rate τ_NZ–C⁻¹. The latter is calculated¹⁴ and compared to the TSF rate for protons in Fig. 3(b). The field-dependence of the carbon TSF rate is shifted relative to that of protons by a factor of γ_H/γ_C = 4 and its amplitude is approximately two orders of magnitude smaller.

Details on the extension of the previous analysis¹⁴ to three reservoirs and its numerical solution can be found in the ESI.† The relaxation of three coupled reservoirs to the lattice temperature is generally given by a tri-exponential decay. Since the experimental data do not warrant an extraction of three coefficients and three decay rates, we compare the experimental data in Fig. 3(c) with effective relaxation rates R_i,comb(t) = −[small beta, Greek, dot above]_i(t)/β_i(t), evaluated at the time of measurement 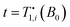. Further details are given in the ESI.†

3.3 Model vs. experimental data

As expected, the presence of the carbon reservoir does not affect the resulting proton relaxation (solid green line in Fig. 3(c)), i.e., the three-reservoir description traces the proton data for doped PA (full squares) as well as the previous analysis,¹⁴ which had considered only protons and the NZ reservoir.

The solution for the expected carbon rate (solid orange line in Fig. 3(c)) predicts accelerated relaxation throughout the field range, but does not describe the measured carbon rates well. At fields up to 20 mT, the predicted relaxation rates are smaller than the ones observed in experiment. For fields above 50 mT, the predicted relaxation rates are larger than the ones observed in experiment.

The discrepancy at low fields may be attributed to direct thermal mixing between the ¹H and ¹³C reservoirs. The rate for this process, denoted by τ_H–C⁻¹ in Fig. 3(b), is negligible above 20 mT but becomes significant at lower fields.¹⁷ Note that this direct mixing process causes the convergence, noted above, of the experimental carbon and proton relaxation rates at low fields in neat PA. Therefore, in neat PA below 20 mT, τ_H–C⁻¹ should correspond to the experimentally observed carbon relaxation rate. We find that the low-field relaxation rates of ¹³C in doped PA are well described by 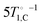, i.e. the direct proton–carbon relaxation rates scale with the neat rates, but are accelerated five-fold. We attribute this increase to nuclear line-broadening due to the presence of trityl in doped PA.

The discrepancy observed at fields above 50 mT may be attributed to carbon spin diffusion. In the model, the protons are in the fast thermal mixing limit in this field range, i.e., the NZ reservoir exchanges faster with the protons than with the lattice (τ_NZ–H⁻¹ ≫ T_1,S⁻¹) and the NZ heat capacity does not affect the proton reservoir relevantly (C_NZ ≪ C_H). Therefore the proton reservoir sets the temperature of the Non-Zeeman reservoir. As the field is increased, the carbon reservoir increasingly couples to the NZ reservoir, and so the model predicts the same spin temperatures and hence relaxation rates for both protons and carbons.

However, only a minute portion of nuclear spins in the radical vicinity, referred to as core spins, are in direct exchange with the electron NZ reservoir. Carbon spins in the bulk only exchange with the radicals indirectly via carbon spin diffusion. From our experiments we cannot distinguish whether a slow exchange between core and bulk carbon spins impedes the relaxation, or if the diffusion through the bulk is field-dependent, and we discuss both possibilities in Section 5.

As detailed in the ESI† and indicated in the sketch in Fig. 3, the relaxation model may be extended with a second carbon reservoir and a field-dependent carbon core-bulk time constant of 33 s T⁻¹. This leads to a satisfactory description (dash-dot line in Fig. 3(c)) of the experimental data.

In the following section we show that thermal mixing experiments are consistent with the predicted indirect proton–carbon coupling mediated by the NZ reservoir, as well as the inferred (i) five-fold accelerated direct hetero-nuclear exchange at low field, and (ii) the slowing of indirect hetero-nuclear coupling by a field-dependent carbon diffusion.

4 Hetero-nuclear mixing

In the thermal mixing experiments the carbon spins are saturated while the proton polarization is allowed to achieve thermal equilibrium at 2.167 T. The field is then ramped to the mixing field for the duration of the mixing delay, and subsequently the field is ramped back to 2.167 T, where the ¹³C spin polarization is read out. In the following thermal mixing data at 4.2 K are presented, further data are given in the ESI.†

4.1 Thermal mixing – neat vs. doped PA

In order to quantify the effectiveness of the thermal mixing step we define the thermal mixing efficiency η as the observed signal divided by the thermal equilibrium signal of ¹³C at 2.167 T. The heat load of the carbon reservoir on the protons is negligible, so that a thermal mixing efficiency of 100% implies that the carbon spins attain the spin temperature of the proton spins without any losses, which corresponds to the theoretical maximum attainable in absence of any relaxation. The dependences of TM efficiency on mixing delay at different fields measured in neat and doped PA at 4.2 K are shown in the Fig. 4(a and b), respectively.

Fig. 4 Thermal mixing in (a) neat and (b) doped PA at 4.2 K for fields from zero up to 100 mT and 600 mT, respectively. All data were normalized to the thermal equilibrium ¹³C signal at 4.2 K and 2 T (see ESI†), with the scale indicated for the respective zero-field data (lower left and right). TM efficiency is shown as a function of mixing delay. Also the measured ¹³C T₁ are indicated, where available, by white squares in the respective datasets.

For neat PA we find thermal mixing is most efficient well below 10 mT, in agreement with a previous study,¹⁷ and the converging s for protons and carbons pointed out above. We note, however, a limited polarization transfer to carbon in neat PA at fields up to 100 mT, cf. top of Fig. 4(a), corresponding to η ≈ 15%. This occurs even for the shortest mixing times and has similarly been observed in previous FFC experiments.¹⁷ We infer that this transfer occurs during the field ramp up to the resonance field, and it may be associated with exchange with quantized rotational states of the methyl group.^24,25

For doped PA in Fig. 4(b) we observe, as predicted, efficient thermal mixing also for fields above 20 mT. Maxima indicating hetero-nuclear mixing can be observed within the measured mixing time range for fields up to 400 mT.

We now consider the field-dependent maximum TM efficiency η_max and the corresponding mixing time t_max, displayed in Fig. 5(a and b), respectively.

Fig. 5 (a) The field-dependent maximum mixing efficiency η_max shows that trityl mediates hetero-nuclear mixing above 5 mT, since η_max is above equilibrium polarization throughout the investigated field range. (b) The corresponding times for TM maxima, t_max, show that trityl accelerates TM below 20 mT, uncertainty of neat t_max/5 (gray error bars) at corresponding fields (0, 5 and 10 mT) overlaps with uncertainty of t_max for doped PA. Above 20 mT t_max(B) for doped PA confirms TM, (orange dash-dot line). Also, for B ≥ 20 mT we find t_max grows with field, consistent with TM slowed down by diffusion. Beyond 200 mT the mixing process becomes slower than the proton relaxation, t_max > T_1,H (green dashed line), such that η_max in (c) only slightly above equilibrium can be achieved by TM for 400 and 600 mT.

For neat PA (open circles) we see that η_max in Fig. 5(a) falls from about 50% at zero field and levels off at η_max ≈ 15% for 10 mT and above. The corresponding mixing times Fig. 5(b) appear to be about 0.1 s rather independent of field.

For doped PA (full circles) in Fig. 5(a) we find mixing efficiency exceeds that of neat PA for B ≥ 5 mT, and for all fields values of η_max greater than or equal to equilibrium polarization (gray line in Fig. 5(a)) are achieved. These maxima are established at shorter mixing times than the measured spin-lattice relaxation could account for, i.e.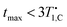 (orange dash-dot line in Fig. 5(b)), providing robust evidence for hetero-nuclear thermal mixing throughout the investigated field range.

4.2 Mixing data and relaxation model

For comparison with the results of our relaxation data analysis, it is instructive to consider relevant field domains marked in Fig. 5.

(I) Up to 20 mT, a five-fold accelerated direct hetero-nuclear exchange is attributed to radical induced line-broadening. In Fig. 5(b)t_max is indeed drastically reduced compared to neat PA, so much so that the actual mixing maxima appear to be reached for mixing times below our experimental range or even during the ramp, cf.Fig. 4(b).

(II) Above 20 mT, the relaxation model predicts efficient indirect proton–carbon mixing and we attribute the observed ¹³C relaxation to trityl-mediated hetero-nuclear exchange that is slowed down by field-dependent carbon core-bulk diffusion. The increase in t_max with field in Fig. 5(b) is consistent with this scenario, as is the broadening of mixing maxima with increasing field apparent in Fig. 4(b).

(III) Above 300 mT the observed indirect proton–carbon mixing becomes slower than the proton relaxation, (green dashed line in Fig. 5(b)), such that no pronounced maxima at 400 and 600 mT are observable, cf.Fig. 4, but rather η_max values slightly above thermal equilibrium, cf.Fig. 5(a). We can nonetheless distinguish the observed mixing from spin-lattice relaxation, since the maxima are achieved faster than spin-lattice relaxation could account for, (orange dash-dot line in Fig. 5(b)).

The TM data are qualitatively consistent with the results from the model used to describe the carbon relaxation. They show that the presence of trityl causes the predicted (indirect) mixing for fields above 20 mT. Additionally they indicate that (i) trityl accelerates (direct) mixing at low field, and that (ii) the (indirect) mixing above 20 mT slows down with increasing field.

5 Discussion

The relaxation data reported here explain the viability of bullet-DNP experiments.^9,10 Earlier work at fields down to 1 T indicated a scaling of ¹³C relaxation rates with field according to T₁ ∼ B³,¹¹ that would lead to very fast relaxation at low fields. Conversely, our data show that below 1 T the relaxation time constants scale only linearly with the applied field.

An extended STM predicts indirect proton–carbon exchange mediated by the NZ reservoir. Qualitatively, this is consistent with the observed enhanced carbon relaxation and with the enhanced mixing observed above 20 mT.

At fields up to 20 mT, a quantitative description of the carbon relaxation needs to include enhanced direct proton–carbon mixing. This is consistent with the shortened times t_max to attain maximum mixing in doped PA, and we attribute the enhanced direct hetero-nuclear mixing to nuclear line broadening due to the presence of trityl.

At fields above 50 mT, the experimentally observed relaxation rates are substantially smaller than those predicted. Here the model predicts efficient indirect coupling via the NZ reservoir such that carbon relaxation rates are equal to those of protons. Since only core ¹³C nuclei in the radical vicinity exchange directly with the NZ reservoir, we attribute this discrepancy to a field-dependent carbon diffusion process. This is also consistent with the thermal mixing data, where t_max increases with increasing field. A diffusion process that slows with increasing field is also compatible with long DNP build-up times at high field.²⁶ There are two different diffusion processes that may each limit the polarization exchange between carbon bulk spins and the radical NZ reservoir.

One possibility is that this reduction arises from slow carbon spin diffusion through the bulk. The carbon line in 1-¹³C PA has a contribution from chemical shift anisotropy (CSA),²⁷ and one may expect spin diffusion to limit the overall ¹³C relaxation as the field, and thereby the carbon linewidth, is increased.²⁸ It should be noted, however, that at the fields investigated in this study, the carbon line is dominated by dipolar interactions.

An alternative explanation of the observed slower carbon relaxation rates is that the proximity to the radicals causes a shift in the resonance frequency of the core spins, which in turn impedes diffusion to the bulk spins. The diffusion barrier separates the carbon spins into NMR-invisible core nuclei in the radical vicinity, and visible bulk nuclei outside the barrier. The diffusion among the bulk nuclei is fast, and so the carbon relaxation rate is limited by the exchange between core and bulk nuclei. As measured recently by Stern et al. on protons,²⁹ the core spins do nonetheless exchange polarization with the bulk spins. This exchange was modelled with two coupled reservoirs representing the core and bulk spins, respectively, where the diffusion barrier limits the exchange of Zeeman energy between these reservoirs.²⁹ The energy flow across the barrier is frequently attributed to dipolar interactions,^30–33 and it is conceivable that the coupling of the two reservoirs is field-dependent, since more Zeeman energy has to be transferred across the barrier at higher fields. However, for ¹³C no experimental studies of this coupling have have been presented to date.

6 Conclusion

In conclusion, we have found that at low fields and low temperatures the carbon T_1,C in pyruvic acid doped with 15 mM OX063 scales linearly with the applied field, and is long compared to the transfer times in bullet-DNP. The relaxation data may be described with a spin temperature model that predicts radical-mediated, triple-spin-flip driven hetero-nuclear polarization transfer at fields from 20 mT to beyond 1 T. The model comprises a carbon spin diffusion process that hampers polarization exchange between the radical and bulk carbon spins. Long build-up times in DNP of low-γ nuclei are a possible manifestation of this process, although its microscopic origin has yet to be determined.

Author contributions

HK performed experiments with help from DP, KK, ASK, AJH, JFM, JOB and BM. Experimental data were analysed by HK, BM and MJ. MJ and BM devised the thermodynamic description and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Tom Wenckebach for numerous discussions and assistance with the relaxation model. We thank Lloyd Lumata for discussions and for providing the high-field ¹³C T₁ data, and David Gadian for help with experiments. We thank Geoffrey Bodenhausen, Matthias Ernst and Malcolm Levitt for discussions. This work has been supported by the EPSRC (EP/R031959/1), by the “Impuls- und Vernetzungsfonds of the Helmholtz-Association” (grant VH-NG-1432), and by the DFG (grant number 454252029 - SFB 1527). This project has received funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreement No 951459).

References

1. J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163.
2. J. H. Ardenkjær-Larsen, Handbook of High Field Dynamic Nuclear Polarization, 2019, 239.
3. W. Köckenberger, in Dissolution Dynamic Nuclear Polarization, John Wiley & Sons, Ltd; 2014, pp. 161–170.
4. D. Kurzbach and S. Jannin, in Dissolution Dynamic Nuclear Polarization Methodology and Instrumentation, American Cancer Society; 2018, pp. 117–132.
5. S. J. Nelson, J. Kurhanewicz, D. B. Vigneron, P. E. Z. Larson, A. L. Harzstark, M. Ferrone, M. van Criekinge, J. W. Chang, R. Bok, I. Park, G. Reed, L. Carvajal, E. J. Small, P. Munster, V. K. Weinberg, J. H. Ardenkjær-Larsen, A. P. Chen, R. E. Hurd, L.-I. Odegardstuen, F. J. Robb, J. Tropp and J. A. Murray, Sci. Transl. Med., 2013, 5, 198ra108.
6. Z. J. Wang, M. A. Ohliger, P. E. Z. Larson, J. W. Gordon, R. A. Bok, J. Slater, J. E. Villanueva-Meyer, C. P. Hess, J. Kurhanewicz and D. B. Vigneron, Radiology, 2019, 291, 273–284.
7. F. A. Gallagher, R. Woitek, M. A. McLean, A. B. Gill, R. M. Garcia, E. Provenzano, F. Riemer, J. Kaggie, A. Chhabra, S. Ursprung, J. T. Grist, C. J. Daniels, F. Zaccagna, M.-C. Laurent, M. Locke, S. Hilborne, A. Frary, T. Torheim, C. Boursnell, A. Schiller, I. Patterson, R. Slough, B. Carmo, J. Kane, H. Biggs, E. Harrison, S. S. Deen, A. Patterson, T. Lanz, Z. Kingsbury, M. Ross, B. Basu, R. Baird, D. J. Lomas, E. Sala, J. Wason, O. M. Rueda, S.-F. Chin, I. B. Wilkinson, M. J. Graves, J. E. Abraham, F. J. Gilbert, C. Caldas and K. M. Brindle, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2092–2098.
8. R. Woitek, M. A. McLean, S. Ursprung, O. M. Rueda, R. M. Garcia, M. J. Locke, L. Beer, G. Baxter, L. Rundo, E. Provenzano, J. Kaggie, A. Patterson, A. Frary, J. Field-Rayner, V. Papalouka, J. Kane, A. J. Benjamin, A. B. Gill, A. N. Priest, D. Y. Lewis, R. Russell, A. Grimmer, B. White, B. Latimer-Bowman, I. Patterson, A. Schiller, B. Carmo, R. Slough, T. Lanz, J. Wason, R. F. Schulte, S.-F. Chin, M. J. Graves, F. J. Gilbert, J. E. Abraham, C. Caldas, K. M. Brindle, E. Sala and F. A. Gallagher, Cancer Res., 2021, 81, 6004–6017.
9. K. Kouřil, H. Kouřilová, S. Bartram, M. H. Levitt and B. Meier, Nat. Commun., 2019, 10, 1733.
10. K. Kouřil, M. Gramberg, M. Jurkutat, H. Kouřilová and B. Meier, Magn. Reson., 2021, 2, 815–825.
11. P. Niedbalski, Q. Wang, C. Parish, F. Khashami, A. Kiswandhi and L. Lumata, J. Phys. Chem. B, 2018, 122, 1898–1904.
12. W. Wenckebach, J. Magn. Reson., 2019, 299, 124–134.
13. W. Wenckebach, J. Magn. Reson., 2019, 299, 151–167.
14. M. Jurkutat, H. Kouřilová, D. Peat, K. Kouřil, A. S. Khan, A. J. Horsewill, J. F. MacDonald, J. Owers-Bradley and B. Meier, J. Phys. Chem. Lett., 2022, 13, 10370–10376.
15. S. F. J. Cox, V. Bouffard and M. Goldman, J. Phys. C: Solid State Phys., 1973, 6, L100–L103.
16. A. J. Horsewill and Q. Xue, Phys. Chem. Chem. Phys., 2002, 4, 5475–5480.
17. D. T. Peat, M. L. Hirsch, D. G. Gadian, A. J. Horsewill, J. R. Owers-Bradley and J. G. Kempf, Phys. Chem. Chem. Phys., 2016, 18, 19173–19182.
18. L. Lumata, Z. Kovacs, A. D. Sherry, C. Malloy, S. Hill, J. van Tol, L. Yu, L. Song and M. E. Merritt, Phys. Chem. Chem. Phys., 2013, 15, 9800.
19. M. L. Hirsch, N. Kalechofsky, A. Belzer, M. Rosay and J. G. Kempf, J. Am. Chem. Soc., 2015, 137, 8428–8434.
20. C. Hess, J. Herick, A. Berlin, W. Meyer and G. Reicherz, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 694, 69–77.
21. A. Abragam and W. G. Proctor, Phys. Rev., 1957, 106, 160–161.
22. A. Abragam and W. G. Proctor, Phys. Rev., 1958, 109, 1441–1458.
23. W. Wenckebach, Essentials of Dynamic Nuclear Polarization, Spindrift Publications, 2016.
24. A. Horsewill, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 35, 359–389.
25. B. Meier, Magn. Reson. Chem., 2018, 56, 610–618.
26. J. H. Ardenkjær-Larsen, S. Bowen, J. R. Petersen, O. Rybalko, M. S. Vinding, M. Ullisch and N. C. Nielsen, Magn. Reson. Med., 2018, 81, 2184.
27. S. Macholl, H. Jóhannesson and J. H. Ardenkjaer-Larsen, Phys. Chem. Chem. Phys., 2010, 12, 5804.
28. Y. Wang and K. Takeda, New J. Phys., 2021, 23, 073015.
29. Q. Stern, S. F. Cousin, F. Mentink-Vigier, A. C. Pinon, S. J. Elliott, O. Cala and S. Jannin, Sci. Adv., 2021, 7, eabf5735.
30. A. Z. Genack and A. G. Redfield, Phys. Rev. B: Solid State, 1975, 12, 78–87.
31. S. F. J. Cox, S. F. J. Read and W. T. Wenchebach, J. Phys. C: Solid State Phys., 1977, 10, 2917–2936.
32. A. E. Dementyev, D. G. Cory and C. Ramanathan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024413.
33. G. B. Furman, S. D. Goren, V. M. Meerovich and V. L. Sokolovsky, Appl. Magn. Reson., 2021, 52, 781–796.

---

Footnote

† Electronic supplementary information (ESI) available: T₁ measurements, additional TM data, multi-reservoir relaxation. See DOI: https://doi.org/10.1039/d2cp04535d

---