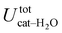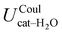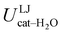Solvent effects on catechol's binding affinity: investigating the role of the intra-molecular hydrogen bond through a multi-level computational approach

Abstract

The subtle interplay between the inter-molecular interactions established by catechol with the surrounding solvent and the intra-molecular hydrogen bond (HB) characterizing its conformational dynamics is investigated through a multi-level computational approach. First, quantum mechanical (QM) calculations are employed to accurately characterize both large portions of the catechol's potential energy surface and the interaction energy with neighboring solvent molecules. The acquired information is thereafter exploited to develop a QM derived force-field (QMD-FF), in turn employed in molecular dynamics (MD) simulations based on classical mechanics. The reliability of the QMD-FF is further validated through a comparison with the outcomes of ab initio molecular dynamics, also purposely carried out in this work. In agreement with recent experimental findings, the MD results reveal remarkable differences in the conformational behavior of isolated and solvated catechol, as well as among the investigated solvents, namely water, acetonitrile or cyclohexane. The rather strong intramolecular HB, settled between the vicinal phenolic groups and maintained in the gas phase, loses stability when catechol is solvated in polar solvents, and is definitively lost in protic solvents such as water. In fact, the internal energy increase associated with the rotation of one hydroxyl group and the breaking of the internal HB is well compensated by the intermolecular HB network available when both phenolic hydrogens point toward the surrounding solvent. In such a case, catechol is stabilized in a chelating conformation, which in turn could be very effective in water removal and surface anchoring. Besides unraveling the role of the different contributors that govern catechol's conformational dynamics, the QMD-FF developed in this work could be in future employed to model larger catechol containing molecules, due to its accuracy to reliably model both internal flexibility and solvent effects, while exploiting MD computational benefits to include more complex players as for instance surfaces, ions or biomolecules.

---

1 Introduction

Despite its apparent simplicity, the simultaneous presence of an aromatic ring and two hydroxyl groups allows 1,2-dihydroxy-benzene (catechol) to establish a large variety of interactions with its surroundings, ranging from strong covalent bonds to more elusive non-covalent interactions.^1,2 Phenol, hydroquinone and resorcinol share with catechol the hydroxyl functional group, yet, the proximity of its two substituents, which can interchangeably act as both hydrogen donor or acceptor in an intra-molecular hydrogen bond (HB), and the consequent possibility to behave as a chelating agent, make catechol's chemistry more versatile, as witnessed by the continuously growing attention in the last decade.^1–8 Indeed, a plethora of chemical interactions exhibited by catechol containing species has recently stimulated continuous research aimed at the design of novel materials for application in several fields, including opto-electronic devices,⁹ biomedical nano-engineering,^10–13 smart polymers and functional materials,^6,14,15 and, preeminently, bio-inspired underwater adhesives.^16–23 In this latter field in particular, the strong yet versatile capability of catechol to interact with almost any kind of surface, and the possibility to tune such interactions by simply acting on extrinsic factors, as for instance the solvent²⁴ or the presence of ions,^8,25 is pivotal to its success in wet adhesion or water replacement.² In fact, recent studies have evidenced that the key role of catechol in adhesive materials^{8,11,20,21,23} is rooted in its exceptional ability to adapt to the absorbing surface, exploiting a network of very different chemical interactions, which may include covalent bonds, HBs, π–π stacking, and/or weaker cation–π interactions.²

Notwithstanding current progress in the design of efficient, catechol based adhesive materials,^{8,11,20,21,23} the effective mechanisms allowing this compound to overcome competing water molecules in an aqueous environment are still unclear, and the chemical details at an atomistic level remain largely unaddressed.² For instance, a fundamental feature currently under debate concerns the role of the formation/breaking of intra-molecular HBs. Both, calculations carried out at the quantum mechanical (QM) level and molecular dynamics (MD) simulations^26,27 suggested a strong relationship between the torsion governing the intramolecular HB and the versatility of catechol's chemistry. The hydroxyl groups can indeed effectively rotate with respect to the aromatic ring, allowing catechol to establish a stable HB network with the surroundings, find an optimal adsorption conformation, and eventually displace pre-adsorbed water molecules, bonding directly on the underlying surface.²⁷ Similarly, the augmented bidentate HB capacity, achieved by rotating one hydroxyl, has been connected to the longer binding lifetimes of catecholic peptides with respect to tyrosine analogues.¹⁷ Furthermore, the possible rotation of one or both hydroxyl groups was found to play an important role also in aggregate formation, with stacked catechol dimers being enforced by a network of several HBs, settled between the two monomers.²⁸ Finally, in more recent computational studies carried out by some of us,^29–31 the formation/breaking of internal HBs in catechol was found to be decisive in balancing cation–π and chelating σ-type interactions between catechol and neighboring metal and organic ions. As a matter of fact, even reducing the “dimensionality” of the problem to a single catechol molecule in the gas phase or solvated in a simple liquid, thus not considering other players as large bio-molecules, surfaces, ions and possible aggregates, the details of the interplay between solute's structure and solvation patterns remain not completely clear and therefore a subject of vibrant research. In very recent work, Bruckhuisen et al. reported³² a complete rotational and vibrational analysis of hydrogen bonded and free catechol's conformers in the gas phase, confirming the early findings of Caminati's group,³³ revealing through microwave spectroscopy that isolated catechol adopts only the planar structure, shown in Fig. 1a, which involves intramolecular HBs. Conversely, when the solvent is taken into account, the formation/breaking of such intramolecular HBs can be significantly altered, depending on the solvent's nature. Resorting to the pioneering work of Navarrete et al.,³⁴ who first studied the competition of catechol's “closed” and “open” conformers (see Fig. 1) in different solvents through Raman spectroscopy, Stavros and coworkers recently highlighted the critical role of the solvating environment in catechol's internal structure.^35,36 If, on the one hand, the early conclusion that catechol adopts a closed form in aprotic and less polar solvents as ether, benzene or cyclohexane^34,35 has been confirmed, on the other hand the behavior in polar and hydrogen accepting solvents as acetonitrile is still under debate. Although significant differences in the excited state lifetimes registered in cyclohexane and acetonitrile were first attributed to a conformational change between the closed and open conformer, respectively,³⁵ a more recent study by the same group,³⁶ contrary to previous interpretation,^34,35 has evidenced that catechol's monomer in acetonitrile should exist in the closed form. Finally, a recent combined experimental and theoretical study carried out on catechol-containing dopamine hydrochloride revealed that the intramolecular HB is lost in water.³⁷ However, notwithstanding its relevance, a detailed investigation of catechol conformational dynamics in water is, to our knowledge, still missing, as well as a systematic study comparing the closed/open inter-conversion in different solvents.

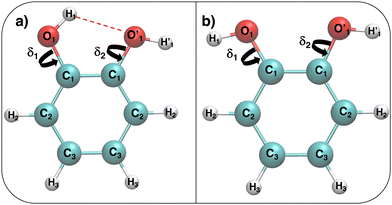Fig. 1 Catechol's optimized structures, atom types and dihedral definitions (δ₁ = H₁–O₁–C₁–C₁; 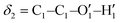). Note that both dihedral angles are defined following ref. 32 notation, which allows a convenient use of symmetry. (a) Closed conformer (local minimum at δ₁ = 0°, δ₂ = 180°) with the 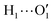HB evidenced with a red dashed line; (b) open conformer (global minimum at δ₁ = δ₂ = 180°) without any intramolecular HB.

This work is therefore aimed at finding a rationale of the interplay between intra-molecular HB and solute–solvent interactions. To this end, we will first resort to QM calculations to accurately characterize the catechol's monomer potential energy surface (PES), specifically focusing on the hydroxil rotation and comparing with the most recent work carried out in the gas phase.³² Thereafter we will attempt to describe, relying again on density functional theory (DFT), the solute and solvent structure and dynamics on small systems containing one catechol and a few (∼50) water molecules for 100 ps. Based on these QM results, we will then develop a model force-field (FF), and use it in MD simulations based on classical mechanics to overcome the limits of the QM description, thus investigating larger solvation shells (∼1000 molecules) and longer observation times (10 ns). Once validated for water, the MD study will be then extended to other solvents, namely, acetonitrile and cyclohexane, to assess the influence of solvent nature on the internal catechol conformation.

2 Computational details

2.1 QM calculations

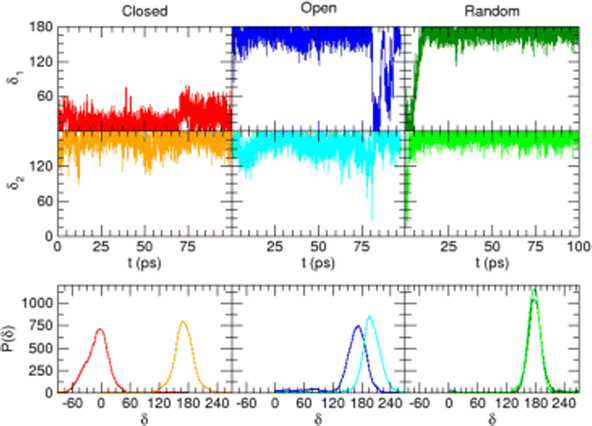
All QM calculations were performed resorting to DFT, employing the PBE functional³⁸ with the DZVP basis set.³⁹ This choice was made based on both (i) the functional availability in the Ab Initio Molecular Dynamics (AIMD) engine (vide infra) and (ii) the accuracy delivered in reproducing the results of few reference calculations (see for instance Fig. 4). The latter were carried out at a higher level of theory, employing coupled cluster with single, double, and perturbatively included connected triple excitations (CCSD(T)) with the cc-pvTz basis set.

Geometry optimization and torsional scans, point charges and the interaction energy with neighboring water molecules were obtained for catechol with the Gaussian16 suite of programs. The QM data required for the parameterization of the FF intra-molecular term, which only depends on the solute internal coordinates (see eqn (S1) and (S2) in the ESI†), were computed for the isolated monomer in the gas phase. Full geometry optimization was assessed by carefully checking all vibrational frequencies, whereas the relaxed torsional scans were carried out minimizing all degrees of freedom but the scanned dihedral δ₁ and δ₂ shown in Fig. 1. Point charges were derived through the RESP procedure by using the Antechamber suite,⁴⁰ employing catechol's electronic density computed at the monomer optimized geometry, yet accounting for the solvent (either water, acetonitrile or cyclohexane) through the polarizable continuum method (PCM).⁴¹ It might be worth noticing that this procedure allows the polarization effects induced by the different solvents to be partially included in catechol's point charges, and has been routinely adopted in similar QMD-FF parameterizations, previously reported by our group.^42–48 The catechol–water interaction energy curves were instead obtained using the standard super-molecule approach,

ΔE_{catechol⋯H2O}(R_k) = E_{catechol⋯H2O}(R_k) − (E_catechol + E_H2O), (1)

where E_catechol and E_H2O are the absolute energies of the isolated catechol and H₂O monomers, and E_{catechol⋯H2O}(R_k) refers to the catechol–H₂O complex at the kth geometry. The latter configurations were prepared by displacing the H₂O molecule along selected vectors (R_k) with respect to the center of catechol's aromatic ring, as displayed in Fig. 4. All the resulting interaction energies ΔE_{catechol⋯H2O} were eventually corrected with the standard CounterPoise correction⁴⁹ to take care of the basis set superposition error (BSSE).

AIMD was carried out with the CP2K code,⁵⁰ using the Quickstep module⁵¹ and orbital transformation⁵² for faster convergence. The electronic structure was calculated in the DFT framework, consistently using again the PBE³⁸ functional, with the explicit van der Waals terms according to the empirical dispersion correction (D3) by Grimme.⁵³ Basis sets belonging to the MOLOPT-DZVP-SR-GTH⁵⁴ family and GTH pseudopotentials^55,56 were applied; the time step chosen was 0.5 fs and the target temperature was set at 300 K using a Nosé–Hoover chain thermostat (tolerance 50 K) in the NVT ensemble. The systems were composed of one catechol monomer and 60 water molecules; AIMD runs have been carried out with PBC in a cubic cell of 12.42 Å, thus achieving a density of ∼1.00 g cm⁻³. Three different starting configurations were considered, differing for the initial conformation adopted by the solute, namely, the closed and open catechol structures shown in Fig. 1 and a “random” structure obtained by manually rotating the δ₁ and δ₂ dihedrals to 53° and 90°, respectively. The dynamics of all three systems was monitored for 100 ps, saving coordinates each 5 fs.

2.2 FFs and MD simulations

In all MD simulations, solvent molecules were described through literature FFs, employing the SPC/E model⁵⁷ for water, and OPLS parameters^58,59 for both acetonitrile and cyclohexane. Conversely, the FF parameters for catechol were specifically tuned as described in the following text.

(i) All the intra-molecular contributions concerning catechol, i.e., the bonding stretching, bending and dihedral terms and the non-bonded Lennard-Jones (LJ) parameters were derived with the Joyce code⁶⁰ from the computed QM data, following the standard procedure.^61–63 Further details and the complete list of all parameters are reported in Tables B–F in the ESI.†

(ii) The inter-molecular point charges, ruling the electrostatic interactions with the solvent, were derived through the RESP procedure from the QM electronic density of catechol, consistently computed at the PBE/DZVP level, accounting for the specific solvent at the PCM⁴¹ level, hence obtaining distinct set of charges for water, acetonitrile and cyclohexane, respectively. The final point charges are also listed for all solvents in Table A in the ESI.†

(iii) The intermolecular LJ parameters were directly transferred from the OPLS^58,59 database.

All MD runs were carried out with the GROMACS package,⁶⁴ in the NPT ensemble on three different systems, composed of the catechol monomer surrounded by 1199, 993 and 997 solvent molecules, for water, acetonitrile and cyclohexane. In all cases, temperature (T = 298 K) was kept constant through the v-rescale method,⁶⁵ while the Parrinello–Rahman algorithm⁶⁶ was employed to maintain pressure P at 1 atm, achieving densities of 1.009 ± 0.007 g cm⁻³, 0.736 ± 0.007 g cm⁻³, and 0.750 ± 0.004 g cm⁻³, respectively. A cut-off distance of 12 Å was employed for short-range interactions, and the standard correction for energy and virial⁶⁷ applied to LJ potentials, while long range electrostatic interactions were accounted for with the particle mesh Ewald (PME) method. During all simulations, the bond lengths were constrained to their equilibrium value through the LINCS algorithm,⁶⁸ setting the time step to 1 fs. All runs were monitored for 10 ns, storing all coordinates every 1 ps.

3 Results

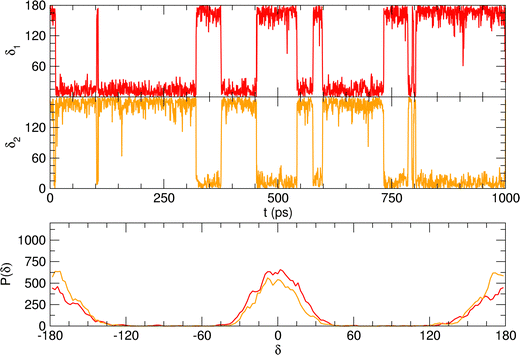
Considering the fairly rigid structure of its aromatic ring, catechol's intramolecular dynamics in water was monitored through AIMD simulations for 100 ps in terms of the most flexible coordinates, namely the δ₁ and δ₂ dihedrals, evidenced in Fig. 1. The top panels of Fig. 2 show the time evolution of the two dihedrals along different runs, each starting with the solute in a specific conformation. When catechol is initially placed in the closed conformation, the internal HB holds for all 100 ps, with δ₁ oscillating between 0° and 60°, while δ₂ is found in the [120–180°] range: the H₁ atom (see Fig. 1 for definition) is therefore always involved in the intra-molecular HB, whereas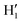 is continuously pointing toward the surrounding solvent. This picture is confirmed by the dihedral distributions displayed in the bottom left panel of Fig. 2, evidencing a single peak for each dihedral, broadened by ±60° but centered at either 0° or 180°. Conversely, when the initial geometry of catechol is the open conformation, both dihedrals oscillate around 180°, with the exception of an evident jump around 75 ps, where δ₁ shortly visits angles below 90°. However, the internal HB, established after ∼80 ps, only holds for few ps, and thereafter δ₁ is again found near 180° at the end of the AIMD run. The dihedral distributions are therefore very different from the previous case: the δ₂ peak is again centered at 180° with a similar broadening with respect to the closed conformation, but the maximum probability for δ₁ is now found near 180°, with only a broad, almost negligible band around 0°, indicating that a stable intra-molecular HB is never fully settled. Finally, when the catechol is initially placed out-of equilibrium, by displacing both δ₁ and δ₂ to random values (right panels with greenish lines), the solute quickly rotates both dihedrals to reach the open conformation, and both hydroxyl hydrogens point toward the embedding solvent for all the duration of the simulation, as confirmed by the almost superimposed dihedral distributions. A comparison among these three runs reveals that, despite the significant computational effort required by AIMD simulations explicitly accounting for 60 water molecules, 100 ps are neither sufficient to reliably assess the most stable conformation achieved by the catechol molecule nor to reach equilibrium.

Fig. 2 AIMD results for catechol in water, achieved for the closed (left), open (middle) and random (right) solute's starting conformation. Top panels: Time evolution of catechol's dihedrals δ₁ and δ₂ (see Fig. 1). Bottom panels: Corresponding dihedral distributions achieved in the AIMD runs.

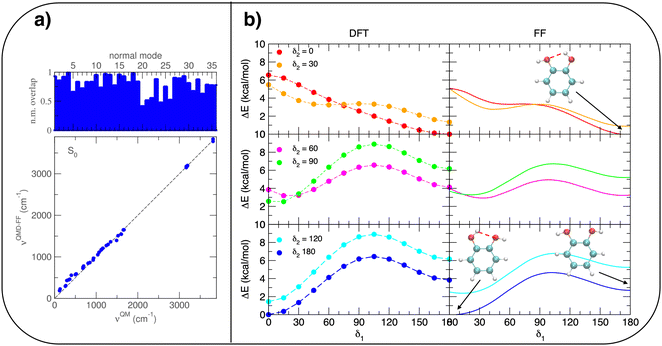
A possible solution to overcome this lack is therefore to resort to MD simulations based on classical mechanics, which allow for much longer observation times (and incidentally for a larger number of surrounding solvent molecules) with significant benefit in terms of computational effort. Nonetheless, the accuracy of MD predictions heavily relies on the adopted FF⁶⁷ and care should be taken to trust MD outcomes without some validation of the FF accuracy with respect to a more robust and reliable QM description. To this end, the intramolecular term⁶⁷ of the catechol's FF was specifically tailored on the PBE PES through the JOYCE procedure.^61,63 The results of the FF parameterization (see Sections A–C in the ESI† for details) are summarized in Fig. 3. Panel (a) displays the comparison between QM and FF vibrational frequencies and normal modes, obtained for the optimized geometry of isolated catechol. A good agreement between the two descriptions appears clearly, indicating that small distortions around the equilibrium structure are well accounted for by the FF. Fig. 3b instead compares the internal energy associated with the δ₁ and δ₂ rotations, with the aim of validating FF reliability in reproducing the QM PES for larger amplitude displacements. The left panels display the torsional profiles computed at the DFT (PBE) level. The curves are in good agreement with the very recent results of Bruckhuisen et al. (see also Fig. S1 in the ESI†), who have reported a two dimensional landscape computed at the B3LYP/aug-cc-pVTZ level for catechol in the gas phase.³² In fact, beside the two degenerate minima (0°/180° and 180°/0° for δ₁ and δ₂, respectively) found for the closed conformers, two additional local minima appear (blue, bottom panel of Fig. 3b), corresponding to the open structures without internal HB, their relative energy (∼4.0 kcal mol⁻¹) being close to the value (3.8 kcal mol⁻¹) found at the B3LYP level.³² More importantly, the FF profiles shown in the right panels of Fig. 3b agree well with that of their DFT counterparts, and the coupling between the two dihedrals is reliably reproduced, as confirmed by the saddle point (3.8 kcal mol⁻¹) found in both QM and FF descriptions point at δ₁/δ₂≃ 30° (orange, top panel of Fig. 3b), also reported in ref. 32 (3.7 kcal mol⁻¹).

Fig. 3 Summary of JOYCE parameterization results. (a) Comparison between QM and FF vibrational normal modes (top) and frequencies (bottom). (b) QM (left) and FF (right) relaxed torsional scans, obtained by scanning δ₁ while constraining δ₂ at different angles. In the insets, selected minima are shown for clarity.

Fig. 4 Validation of the intermolecular energy (ΔE (see eqn (1) for definition) of the catechol–water dimer in different configurations). H–π interactions (reddish lines), obtained by displacing the H₂O molecule along the R_H–π direction are reported with red full squares, orange empty circles and green dashed lines, for CCSD(T), PBE and FF, respectively. HB interactions are instead shown with red full triangles, magenta empty circles and blue dashed lines.

Once the reliability of the intra-molecular FF description has been assessed, before proceeding to MD simulation, it is important to validate the capability of the intermolecular term, which describes the catechol–water interactions, to reproduce the QM interaction energies with accurate and balanced predictions. To this end, several catechol–water configurations were prepared by displacing one H₂O molecule with respect to the center of the catechol's ring, as displayed in the insets of Fig. 4. Concretely, two possible kinds of catechol–water interaction were considered, i.e. H–π and HB. The former is evaluated at dimer geometries where the H₂O molecule lies on top of the aromatic ring, with an hydrogen atom pointing toward the phenyl center, and the oxygen is displaced along the R_H–π direction (see inset). HB interactions are instead sampled by shifting the water molecule within the ring plane, along the vector (R_HB) bisecting the phenyl carbon atoms bearing the hydroxyl groups. The comparison between CCSD(T) values, computed for few selected configurations, and PBE curves confirms the accuracy of the chosen DFT description, which nicely agrees with the higher-level values in all cases. The FF description is also fairly accurate, and the two curves appear to be well distinct and in the correct order. Although the HB interaction seem to be better described, with an almost quantitative agreement, larger discrepancies are found for the more elusive H–π interactions. However, the position of the H–π minimum is well reproduced, and the arising of the repulsive branch is shifted by only 0.4 Å with respect to the QM findings, making us confident on the overall reliability of the adopted FF description.

To further validate catechol's FF, a preliminary MD simulation was carried out on the isolated molecule for 1 ns, again monitoring the time evolution of the investigated dihedrals and their distributions. Fig. 5 displays the achieved results for catechol in the gas phase. In agreement with recent experimental findings,³² the most stable conformation adopted by the isolated catechol molecule is a closed structure, characterized by the intra-molecular HB. Yet, at difference with the short AIMD runs, the 1 ns MD run reveals a number of rather fast (∼5 ps) interconversions between the two degenerate minima, where δ₁ rotates from 0° to 180° while δ₂ accomplishes the opposite path, thus exchanging the 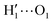HB with 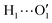. On the contrary, as confirmed by the dihedral distribution shown in the bottom panel of Fig. 5, the open conformation is never populated, due to the energy increase associated with the internal HB breaking.

Fig. 5 MD results for catechol in gas phase, collected over a 1 ns simulation. Top panels: Time evolution of catechol's dihedrals δ₁ (red lines) and δ₂ (orange lines). Bottom panel: Corresponding dihedral distributions.

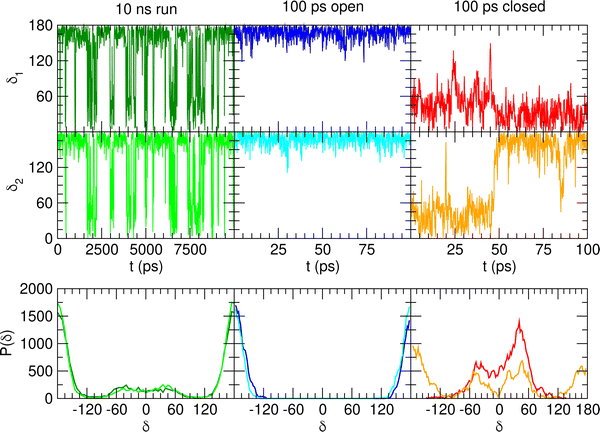
When catechol is solvated in water, MD simulations reveal a quite different picture. The left panels of Fig. 6 display the time behavior of the δ₁ and δ₂ dihedrals, evidencing important differences with the previously discussed AIMD results. First, when observed for 10 ns, i.e. two order of magnitudes longer than what allowed by AIMD, catechol shows several inter-conversions between closed and open conformers, also populating more distorted structures, where the H₁ and 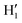hydrogens are found outside in the ring plane. Open to close conformational changes take place still rather quickly, yet slower with respect to the gas phase. Next, as evidenced by the distributions shown in the bottom panels, contrary to the AIMD findings, the two dihedrals share the same populations, as could be expected by the PES symmetry, indicating that equilibrium has been fully reached. More important, the peaks at ±180° are remarkably higher than the broad band resulting around 0°, clearly indicating that water solvation is able to break the internal HB, and the open conformer is now the most stable structure. To ease the comparison with the AIMD outcomes, the middle and right panels of Fig. 6 show the dihedral time evolution (top) and the consequent distributions (bottom) computed over selected 100 ps time intervals, extracted from the whole 10 ns trajectory in the [400–500 ps] and [1310–1410 ps] range. In the former case, catechol is always found in the open conformation, as clearly indicated by the two distribution peaks centered at 180°, which almost coincide with that found in the AIMD runs starting without the internal HB. On the contrary, the dihedral population distributions computed for the second interval are more similar to the ones achieved in the AIMD “closed” trajectory, δ₁ being peaked around 0° and the internal 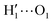maintained for all 100 ps. At difference with the the QM dynamics, δ₂ stays at 180° only in the last 50 ps, while it oscillates around the saddle point (∼30°) in the first half of the run, resulting in population distributions with non-negligible population in the central region of the explored dihedral range.

Fig. 6 MD outcomes for catechol in water. In the left panels are displayed the results achieved along the whole 10 ns trajectory, while the middle and right ones concern selected 100 ps intervals [400–500 ps] and [1310–1410 ps], respectively). Top panels: Time evolution of catechol's dihedrals δ₁ and δ₂. Bottom panels: Corresponding dihedral distributions achieved in the considered MD runs.

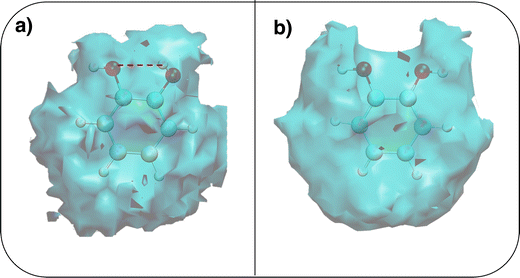
To gain a deeper insight into the solvent structure around the two different catechol conformers, ultimately responsible for the different intramolecular HB behaviors found with respect to the gas phase, the spatial density function (SDF) of the water proton (H_w) was computed along the two 100 ps intervals, and is displayed in Fig. 7. By comparing the (a) and (b) panels, where the SDF is, respectively, shown for the closed and open conformers, it is clear that the major differences are found in the region around the hydroxyl moieties, whereas the H_w density around the phenyl ring is almost indistinguishable. In fact, when the two hydroxyl hydrogens both point toward the solvent, a more symmetric distribution is obtained, with a significant reduction of the density in between the –OH groups and the concentration of water protons on top of the two oxygens, both free to act as acceptors thanks to the removal of the internal HB. Conversely, the H_w spatial distribution around the closed conformer displayed in panel (a) evidences a much less symmetric shape, as only 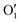is free to accept intermolecular HBs, as indicated by the remarkably larger density around it. This picture is confirmed by looking at the network of intermolecular HBs established in the two cases and the consequent solvation energies, all reported in Table 1. The average interaction energy between catechol and all the surrounding water molecules, 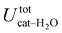, computed along the two 100 ps selected intervals, are reported in the last two columns. It is evident that the breaking of the internal HB characterizing the open conformer leads to stronger solute–solvent interactions, as indicated by the gain of about 4 kcal mol⁻¹ with respect to the closed conformer. Furthermore, when the charge–charge and LJ contributions to 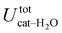are separately considered, it emerges that the larger stability of the solvated open conformer comes from the electrostatic contribution, whereas the H–π interactions involving the water interaction with the aromatic ring, mainly included in 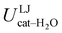, are nearly equal in the two considered intervals. The same conclusion can be drawn by computing the number of HBs established between catechol's hydroxyls and the surrounding water molecules: ∼4 HB are in average found for the open conformer, whilst only 3 can be settled when the intramolecular HB is maintained. Finally it should be noticed that, when the same properties are computed along the whole 10 ns (first column of Table 1), the resulting averages are very similar to those found for the open conformer, again indicating that this conformation is the most stable in water solvent.

Fig. 7 Spatial density functions (SDF) computed along the two 100 ps intervals extracted from the whole 10 ns MD trajectories. (a) H_w SDF around the closed conformer, where the intramolecular HB is evidenced with a dashed red line; (b) H_w SDF around the open conformer.

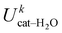Table 1 Total (tot), charge–charge (Coul) and LJ catechol–H₂O interaction energies (, kcal mol⁻¹) between catechol and all water molecules composing the system. Each term was computed according to eqn (S3) (ESI) and averaged either over the whole 10 ns MD trajectory (first column) or along the selected 100 ps intervals. The last row reports the number of intermolecular HBs (N_HB)

	Whole (10 ns)	Open (100 ps)	Closed (100 ps)
	−40.6 ± 0.3	−41.8 ± 0.8	−38.0 ± 1.2
	−35.1 ± 0.3	−36.6 ± 0.8	−32.3 ± 1.1
	−5.5 ± 0.1	−5.2 ± 0.1	−5.7 ± 0.2
N HB	3.7	3.8	3.4

---

A more detailed analysis of the solvent structure surrounding the hydroxyl groups in either the closed or open case, which also allows for a more direct comparison with the AIMD results, can be achieved by looking at the pair correlation functions computed between selected solute–solvent atom pairs. To this end, Fig. 8 shows the pair correlation functions computed, along both the AIMD and MD 100 ps runs, for the H₁–Ow, 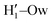, O₁–Hw and O'₁–Hw pairs. On the one hand, the excellent agreement achieved in all cases between the QM and FF functions confirms the reliability of the refined FF, which is able to predict solvent distributions almost superimposed on the ones computed for AIMD. On the other hand, a comparison between the pair correlation function computed for the closed and open conformers allows for gaining further insight into the mechanisms leading to the enhanced stability of the latter structure. Indeed, as revealed by the two intense peaks found for both the H₁–Ow and 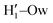pairs at ∼2 Å, the open conformer is able to establish two intermolecular HBs with the surrounding solvent, whereas the corresponding 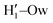peak appearing for the closed conformation is less intense, broader and shifted to larger distances, suggesting weaker interactions with the solvent. Moreover, a further stabilization of the open conformer also comes from the outer water shells; thanks to the more symmetric distribution of the neighboring water molecules (see also Fig. 7) achieved by the open conformer, the second solvation shell is more structured and stable with respect to the one around the closed structure, as indicated by the second H₁–Ow and 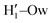peaks. Finally, It might be interesting to notice that the slight discrepancy between DFT and FF results found for the third peaks is probably due to the significantly smaller number of water molecules included in the AIMD simulations, which result in a smaller box, in which periodic boundary conditions may artificially induce a more structured solvent density.

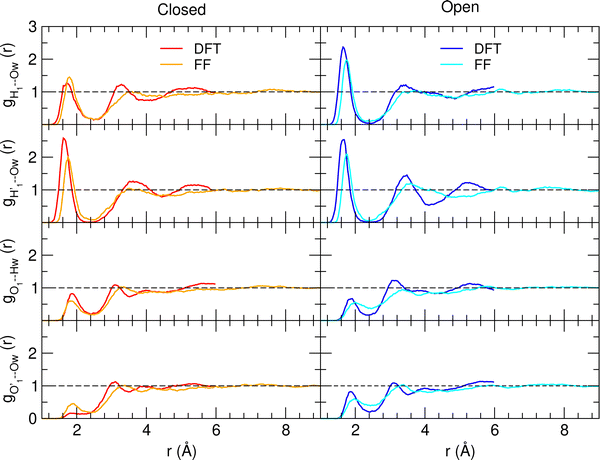Fig. 8 AIMD (DFT, red and blue lines) and MD (FF, orange and cyan) pair correlation functions, computed between selected solute–solvent atom pairs, for catechol in water.

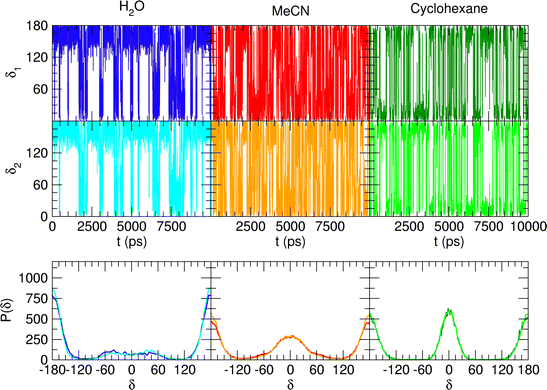
The encouraging results achieved with the refined FF description for the water solvent, as well as the their validation with respect to the higher level QM description, prompted us to adopt the same FF/MD protocol to investigate catechol's conformational behavior in two additional solvents, namely a polar, HB accepting species (acetonitrile) and an apolar one (cyclohexane). The time evolution of the δ₁ and δ₂ dihedrals and their distribution computed along the MD trajectories carried out in the three solvents are shown in Fig. 9, where a remarkably different behavior is registered by changing the solvent. With respect to water, both acetonitrile and cyclohexane show faster dihedral rotations, indicating that the internal HB is more easily broken and reformed (see also Fig. S4, ESI†). A more detailed analysis of the structure and dynamics of the internal HB (see Section G in the ESI†) confirms this finding, which is eventually revealed also by the comparison of the HB lifetime (τ_HB) computed in the three solvents and reported in Table 2. In fact, the largest lifetime is obtained for water, where, although the internal HB is more rarely settled, the stable network of intermolecular HBs established between catechol and the surrounding solvent and among the neighboring H₂O molecules requires more time to be altered, hence slowing down the internal HB dynamics. On the contrary, the weaker interactions with aprotic solvents allow for fast and frequent interchanges between the and internal HBs, eventually reflecting, similarly to the gas phase (see Fig. 5), in almost indistinguishable distributions of the δ₁ and δ₂ dihedrals. However, as clearly indicated in Fig. 9 by the intensity of the distribution peak centered at 0°, notwithstanding the faster dynamics of the δ₁ and δ₂ dihedrals, one of the two possible internal HBs is settled in the aprotic solvents much more often than in water. Indeed, as evidenced in Fig. S6 (ESI†) and in agreement with the experimental findings,^34,35 the internal HB in cyclohexane is almost always maintained, while the behavior registered in acetonitrile is intermediate between the one found in water and the one in cyclohexane. This latter finding is in line with the recent results reported by Stavros and co-workers;³⁶ in acetonitrile the closed conformer shows a not negligible population, as evidenced by the population distribution displayed in the central bottom panel of Fig. 8, although less intense than the one observed in vacuo or for cyclohexane. Nonetheless, as suggested in previous work of the same group³⁵ and confirmed by Fig. S6 in the ESI,† the open conformation, where both dihedrals oscillate around 180°, is also populated, even if to a lesser extent. This remarkable dependence of the internal HB structure and dynamics on both solvent polarity and proticity can be traced back, as evidenced in Fig. 10, to the different mean field potential energies (ΔU^pmf, see the ESI† for definition) exerted by each solvent on the δ dihedral around one C–OH bond. The rather flat shape of the ΔU^pmf computed for the apolar cyclo-hexane confirms the weak solute–solvent interactions, which, as already noted, almost do not alter the torsional profile obtained for the isolated molecule. Conversely, remarkable barriers are found for the other two solvents, centered in the planar closed conformation and whose intensity noticeably increases in going from acetonitrile to water, again indicating a much stronger interaction with the protic solvent.

Fig. 9 Comparison of catechol's conformational behavior in different solvents: from left to right water, acetonitrile and cyclohexane. Top panels: Time evolution of δ₁ and δ₂ dihedrals. Bottom panels: Corresponding dihedral distributions achieved in each MD run.

Table 2 Internal HB lifetimes (τ_HB), computed for the considered solvents according to eqn (S7) discussed in the ESI

Solvent	τ HB (ps)
Water	116
Acetonitrile	44
Cyclohexane	28

---

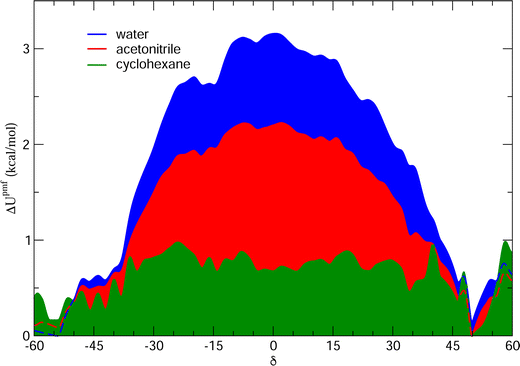Fig. 10 Potential mean field energy ΔU^pmf (δ exerted by each solvent on the δ dihedral). All curves were obtained according to the procedure described in more detail in Section H of the ESI.†

The above discussion is confirmed by both the average interaction energy, U_cat–solv, computed between the catechol and all the molecules of each considered solvent (see Table 3), and by the SDFs displayed in Fig. 11. By looking at U_cat–solv, it is evident that the larger values found for water are essentially due to the hydrogen bond network, which reflects in a higher charge–charge contributions, while at the opposite side the interaction with the apolar cyclohexane solvent mainly consists of LJ interactions, hence leaving catechol free to establish a strong an stable internal HB. As inferred by the pair correlation functions, acetonitrile behaves intermediately and both charge–charge and LJ contributions are present, indicating that both open and closed conformations are being populated. This is in agreement with the computed SDFs, shown for each solvent in Fig. 11. As far as the water solvent is concerned, the computed H_w distribution is very similar to the one displayed in Fig. 7 for the open conformer, confirming once more that the internal HB is lost in water solvent. In keeping with the weaker solute–solvent interaction energies, the SDF achieved for acetonitrile is slightly more extended, in particular in the region surrounding the hydroxyl groups. Furthermore, the density around the oxygen atoms is not perfectly symmetric, again suggesting that both open and closed structure might exist in this solvent. 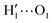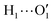Finally, due to the combination of the fast formation/breaking of the two and internal HBs with the weak interaction found for this solvent, the cyclohexane distribution around the closed catechol conformer is highly symmetric and more extended in space.

Table 3 Total (tot), charge–charge (Coul) and LJ catechol–solvent interaction energies, computed between catechol and all solvent molecules of the system according to eqn (S3) (ESI) and averaged along the 10 ns MD runs. All averages and error estimates are in kcal mol⁻¹

U cat–solv	Water	Acetonitrile	Cyclohexane
tot	−40.6 ± 0.3	−27.0 ± 0.5	−14.5 ± 0.1
Coul	−35.1 ± 0.3	−17.5 ± 0.5	+0.3 ± 0.1
LJ	−5.5 ± 0.1	−9.5 ± 0.1	−14.8 ± 0.1

---

Fig. 11 Spatial density functions (SDFs) computed along the 10 ns MD trajectories carried out in different solvents. (a) H_w SDF in water; (b) SDF in acetonitrile computed for the nitrogen atom; (c) SDF in cyclohexane computed for the carbon atom. Where present, the intramolecular HB is evidenced with a dashed red line.

4 Conclusions

MD simulations, carried out both in the gas phase and in different solvents, evidenced a strong relationship between solute–solvent interactions and the intra-molecular hydrogen bond that can be settled between catechol's vicinal hydroxyl groups. In agreement with recent experimental findings based on rotational and vibrational spectroscopy,³² the internal HB holds for catechol in the gas phase, where the closed conformer is always populated, although with fast interconversions, taking place between the two degenerate minima (0°/180° and 180°/0°) through either δ₁ or δ₂ rotations. When solvation is explicitly taken into account, catechol's conformational dynamics is strongly influenced by the kind and strength of the interactions that can be established with the surrounding solvent molecules. As suggested by both Raman spectroscopy³⁴ and femtosecond Transient Electronic (UV/visible) Absorption Spectroscopy (TEAS),³⁵ the dihedral distribution computed along MD trajectories confirms that in a weakly interacting solvent such as cyclohexane the behavior observed in vacuo remains unaltered, and the intramolecular HB always maintained. A remarkably different picture instead emerges in a protic, strongly interacting solvent such as water, where the internal HB is in average lost and the closed conformer seldom populated. Interestingly, when catechol is solvated in an aprotic yet polar medium, both conformers show a non-negligible population, suggesting a possible reason for the seemingly contrasting findings recently achieved through TEAS measures, which indicated either the open³⁵ or closed³⁶ conformer as the most stable species in acetonitrile.

The agreement with the previous experimental findings, as well as the one achieved with respect to first principles AIMD simulations, support the reliability of the MD predictions, which were therefore exploited to gain a deeper insight into the molecular mechanisms leading to the observed solvation patterns. Pair correlation and spatial density functions computed between catechol and the surrounding water molecules revealed that the remarkable stability of the open conformer is rooted in the favorable interaction with the first neighbors, achieved through the rotation of the δ₁/δ₂ dihedral, which breaks the internal HB, but allows the solvent to establish stabilizing HBs with both sides of the solute. Such stabilization of the HB network around catechol's hydroxyl groups in turn specifically strengthens the local H₂O⋯HO-interactions, and consequently slows down conformational dynamics, as indicated by the much lower frequency of 0° to 180° rotations observed with respect to the other cases. It might also be worth noticing that the breaking of the internal HB in favor of an open conformation makes catechol a more efficient chelating agent, as both oxygens are more exposed to the solvent and thus available for the formation of additional covalent and non-covalent bonds, with a clear benefit in terms of the interaction with surfaces or nearby ions.

In fact, notwithstanding this work deals with the simple catechol molecule, most of the physical/chemical observations allowed by the present computational approach most likely hold for many catechol containing species, as for instance those involved in a eumelanin structure or in under-water adhesive materials. In this framework, as all QMD-FF parameters are consistent with the standard FF expressions (see the ESI† for further details), the validation achieved for the here-employed FF paves the way to its usage in reliable MD simulations of larger systems, in which catechol containing species interact in a more complex environment, e.g. with surfaces, ions and/or other organic ligands bearing HB donors or acceptors.

Conflicts of interest

■■■■There are no conflicts to declare.

Acknowledgements

The authors are grateful to Prof. Marco D'Ischia for the many and useful discussions. We acknowledge support from Seal of Excellence (SoE) fellowship promoted by the University of Siena.

References

1. J. Yang, M. A. Cohen Stuart and M. Kamperman, Jack of all trades: versatile catechol crosslinking mechanisms, Chem. Soc. Rev., 2014, 43, 8271–8298.
2. J. Saiz-Poseu, J. Mancebo-Aracil, F. Nador, F. Busqué and D. Ruiz-Molina, The Chemistry behind Catechol-Based Adhesion, Angew. Chem., Int. Ed., 2019, 58, 696–714.
3. J. Sedó, J. Saiz-Poseu, F. Busqué and D. Ruiz-Molina, Catechol-Based Biomimetic Functional Materials, Adv. Mater., 2013, 25, 653–701.
4. J. Saiz-Poseu, J. Sedó, B. García, C. Benaiges, T. Parella, R. Alibés, J. Hernando, F. Busqué and D. Ruiz-Molina, Versatile Nanostructured Materials via Direct Reaction of Functionalized Catechols, Adv. Mater., 2013, 25, 2066–2070.
5. M. dIschia and D. Ruiz-Molina, Bioinspired Catechol-Based Systems: Chemistry and Applications, Biomimetics, 2017, 2, 25.
6. B. P. Lee, H. Birkedal and H. Lee, Editorial: Catechol and Polyphenol Chemistry for Smart Polymers, Front. Chem., 2019, 7, 883.
7. T. Priemel, R. Palia, M. Babych, C. J. Thibodeaux, S. Bourgault and M. J. Harrington, Compartmentalized processing of catechols during mussel byssus fabrication determines the destiny of DOPA, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 7613–7621.
8. M. Shin, Y. Park, S. Jin, Y. M. Jung and H. J. Cha, Two Faces of Amine-Catechol Pair Synergy in Underwater Cation–π Interactions, Chem. Mater., 2021, 33, 3196–3206.
9. M. D'Ischia, A. Napolitano, A. Pezzella, P. Meredith and T. Sarna, Chemical and structural diversity in eumelanins: unexplored bio-optoelectronic materials, Angew. Chem., Int. Ed., 2009, 48, 3914–3921.
10. Y. Liu, K. Ai and L. Lu, Polydopamine and its derivative materials: synthesis and promising applications in energy, environmental, and biomedical fields, Chem. Rev., 2014, 114, 5057–5115.
11. W. Zhang, R. Wang, Z. Sun, X. Zhu, Q. Zhao, T. Zhang, A. Cholewinski, F. K. Yang, B. Zhao, R. Pinnaratip, P. K. Forooshani and B. P. Lee, Catechol-functionalized hydrogels: biomimetic design, adhesion mechanism, and biomedical applications, Chem. Soc. Rev., 2020, 49, 433–464.
12. R. Pinnataip and B. P. Lee, Oxidation Chemistry of Catechol Utilized in Designing Stimuli-Responsive Adhesives and Antipathogenic Biomaterials, ACS Omega, 2021, 6, 5113–5118.
13. D. Wu, J. Zhou, M. N. Creyer, W. Yim, Z. Chen, P. B. Messersmith and J. V. Jokerst, Phenolic-enabled nanotechnology: versatile particle engineering for biomedicine, Chem. Soc. Rev., 2021, 50, 4432–4483.
14. M. A. Rahim, S. L. Kristufek, S. Pan, J. J. Richardson and F. Caruso, Phenolic Building Blocks for the Assembly of Functional Materials, Angew. Chem., Int. Ed., 2019, 58, 1904–1927.
15. Y. Na and C. Chen, Catechol Functionalized Polyolefins, Angew. Chem., Int. Ed., 2020, 59, 7953–7959.
16. B. P. Lee, P. Messersmith, J. Israelachvili and J. Waite, Mussel-Inspired Adhesives and Coatings, Annu. Rev. Mater. Res., 2011, 41, 99–132.
17. J. H. Waite, Mussel adhesion – Essential footwork, J. Exp. Biol., 2017, 220, 517–530.
18. M. V. Rapp, G. P. Maier, H. A. Dobbs, N. J. Higdon, J. H. Waite, A. Butler and J. N. Israelachvili, Defining the Catechol-Cation Synergy for Enhanced Wet Adhesion to Mineral Surfaces, J. Am. Chem. Soc., 2016, 138, 9013–9016.
19. M. A. Gebbie, W. Wei, A. M. Schrader, T. R. Cristiani, H. A. Dobbs, M. Idso, B. F. Chmelka, J. Herbert Waite and J. N. Israelachvili, Tuning underwater adhesion with cation–π interactions, Nat. Chem., 2017, 9, 473–479.
20. L. Xie, L. Gong, J. Zhang, L. Han, L. Xiang, J. Chen, J. Liu, B. Yan and H. Zeng, A wet adhesion strategy via synergistic cation–π and hydrogen bonding interactions of antifouling zwitterions and mussel-inspired binding moieties, J. Mater. Chem. A, 2019, 7, 21944–21952.
21. Q. Lyu, N. Hsueh and C. L. L. Chai, The Chemistry of Bioinspired Catechol(amine)-Based Coatings, ACS Biomater. Sci. Eng., 2019, 5, 2708–2724.
22. L. Xiang, J. Zhang, W. Wang, L. Gong, L. Zhang, B. Yan and H. Zeng, Nanomechanics of π-cation–π interaction with implications for bio-inspired wet adhesion, Acta Biomater., 2020, 117, 294–301.
23. D. Lee, H. Bae, J. Ahn, T. Kang, D. G. Seo and D. S. Hwang, Catechol-thiol-based dental adhesive inspired by underwater mussel adhesion, Acta Biomater., 2020, 103, 92–101.
24. L. B. Assis Oliveira, T. L. Fonseca, B. J. C. Cabral, K. Coutinho and S. Canuto, Preferential solvation and optical properties of eumelanin building blocks in binary mixture of methanol and water, J. Chem. Phys., 2021, 155, 174504.
25. S. Hong, Y. Wang, S. Y. Park and H. Lee, Progressive fuzzy cation–π assembly of biological catecholamines, Sci. Adv., 2018, 4, eaat7457.
26. S. A. Mian, X. Gao, S. Nagase and J. Jang, Adsorption of catechol on a wet silica surface: density functional theory study, Theor. Chem. Acc., 2011, 130, 333–339.
27. S. A. Mian, L.-M. Yang, L. C. Saha, E. Ahmed, M. Ajmal and E. Ganz, A Fundamental Understanding of Catechol and Water Adsorption on a Hydrophilic Silica Surface: Exploring the Underwater Adhesion Mechanism of Mussels on an Atomic Scale, Langmuir, 2014, 30, 6906–6914.
28. V. Barone, I. Cacelli, A. Ferretti and G. Prampolini, Noncovalent Interactions in the Catechol Dimer, Biomimetics, 2017, 2, 18.
29. G. Prampolini, M. D'Ischia and A. Ferretti, The phenoxyl group-modulated interplay of cation–π and σ-type interactions in the alkali metal series, Phys. Chem. Chem. Phys., 2020, 22, 27105–27120.
30. A. Ferretti, G. Prampolini and M. dIschia, Noncovalent interactions in catechol/ammonium-rich adhesive motifs: Reassessing the role of cation–π complexes?, Chem. Phys. Lett., 2021, 779, 138815.
31. A. Ferretti and G. Prampolini, Complexes of Alkaline and Ammonium Cations with Dopamine and Eumelanin Precursors: Dissecting the Role of Noncovalent Cation–π and Cation-Lone Pair (σ-Type) Interactions, J. Phys. Chem. A, 2022, 126, 2330–2341.
32. J. Bruckhuisen, G. Dhont, A. Roucou, A. Jabri, H. Bayoudh, T. T. Tran, M. Goubet, M.-A. Martin-Drumel and A. Cuisset, Intramolecular H-Bond Dynamics of Catechol Investigated by THz High-Resolution Spectroscopy of Its Low-Frequency Modes, Molecules, 2021, 26, 3645.
33. W. Caminati, S. D. Bernardo, L. Schäfer, S. Q. Kulp-Newton and K. Siam, Investigation of the molecular structure of catechol by combined microwave spectroscopy and AB initio calculations, J. Mol. Struct., 1990, 240, 263–274.
34. J. Navarrete and F. Ramírez, A study by Raman spectroscopy and the semiempirical AM1 method on several 1,2-dihydroxybenzene solutions, Spectrochim. Acta, Part A, 1993, 49, 1759–1767.
35. M. D. Horbury, L. A. Baker, W.-D. Quan, J. D. Young, M. Staniforth, S. E. Greenough and V. G. Stavros, Bridging the Gap between the Gas Phase and Solution Phase: Solvent Specific Photochemistry in 4-tert-Butylcatechol, J. Phys. Chem. A, 2015, 119, 11989–11996.
36. M. A. Turner, R. J. Turner, M. D. Horbury, N. D. Hine and V. G. Stavros, Examining solvent effects on the ultrafast dynamics of catechol, J. Chem. Phys., 2019, 151, 084305.
37. S. K. Callear, A. Johnston, S. E. McLain and S. Imberti, Conformation and interactions of dopamine hydrochloride in solution, J. Chem. Phys., 2015, 142, 014502.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78, 1396.
39. N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation, Can. J. Chem., 1992, 70, 560–571.
40. J. Wang, W. Wang, P. A. Kollman and D. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graphics Modell., 2006, 25, 247260.
41. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3094.
42. N. De Mitri, S. Monti, G. Prampolini and V. Barone, Absorption and Emission Spectra of a Flexible Dye in Solution: A Computational Time-Dependent Approach, J. Chem. Theory Comput., 2013, 9, 4507–4516.
43. I. Cacelli, A. Ferretti and G. Prampolini, Predicting light absorption properties of anthocyanidins in solution: a multi-level computational approach, Theor. Chem. Acc., 2016, 135, 156.
44. J. Cerezo, F. Santoro and G. Prampolini, Comparing classical approaches with empirical or quantum-mechanically derived force fields for the simulation electronic lineshapes: application to coumarin dyes, Theor. Chem. Acc., 2016, 135, 143.
45. G. Prampolini, F. Ingrosso, J. Cerezo, A. Iagatti, P. Foggi and M. Pastore, Short- and Long-Range Solvation Effects on the Transient UV-Vis Absorption Spectra of a Ru(II)-Polypyridine Complex Disentangled by Nonequilibrium Molecular Dynamics, J. Phys. Chem. Lett., 2019, 10, 2885–2891.
46. M. Campetella, N. De Mitri and G. Prampolini, Automated parameterization of quantum-mechanically derived force-fields including explicit Sigma holes: A pathway to energetic and structural features of halogen bonds in gas and condensed phase, J. Chem. Phys., 2020, 153, 044106.
47. J. Vilhena, L. Greff da Silveira, P. R. Livotto, I. Cacelli and G. Prampolini, Automated Parameterization of Quantum Mechanically Derived Force Fields for Soft Materials and Complex Fluids: Development and Validation, J. Chem. Theory Comput., 2021, 17, 4449–4464.
48. G. Prampolini, L. Greff da Silveira, J. Vilhena and P. R. Livotto, Predicting Spontaneous Orientational Self-Assembly: in Silico Design of Materials with Quantum Mechanically Derived Force-Fields, J. Phys. Chem. Lett., 2022, 13, 243–250.
49. S. Boys and F. Bernardi, The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors, Mol. Phys., 1970, 19, 553–566.
50. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al., CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103.
51. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128.
52. J. VandeVondele and J. Hutter, An efficient orbital transformation method for electronic structure calculations, J. Chem. Phys., 2003, 118, 4365–4369.
53. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
54. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
55. S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703.
56. C. Hartwigsen, S. Gœdecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641.
57. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271.
58. W. L. Jorgensen and J. Tirado-Rives, Potential Energy Functions for Atomic-Level Simulations of Water and Organic and Biomolecular Systems, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670.
59. L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands, Nucleic Acids Res., 2017, 45, W331–W336.
60. I. Cacelli, J. Cerezo, N. De Mitri and G. Prampolini, Joyce2.10, a Fortran 77 code for intra-molecular force field parameterization, 2013, https://www.iccom.cnr.it/en/joyce-2, last consulted September 2022.
61. I. Cacelli and G. Prampolini, Parametrization and Validation of Intramolecular Force Fields Derived from DFT Calculations, J. Chem. Theory Comput., 2007, 3, 1803–1817.
62. V. Barone, I. Cacelli, N. De Mitri, D. Licari, S. Monti and G. Prampolini, Joyce and Ulysses: Integrated and User-Friendly Tools for the Parameterization of Intramolecular Force Fields from Quantum Mechanical Data, Phys. Chem. Chem. Phys., 2013, 15, 3736–3751.
63. J. Cerezo, G. Prampolini and I. Cacelli, Developing accurate intramolecular force fields for conjugated systems through explicit coupling terms, Theor. Chem. Acc., 2018, 137, 80.
64. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, GROMACS 4.5: a High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit, Bioinformatics, 2013, 29, 845–854.
65. G. Bussi and M. Parrinello, Accurate sampling using Langevin dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 056707.
66. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190.
67. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon, Oxford, 1987.
68. B. Hess, B. Bekker, H. Berendsen and J. G. E. M. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04500a

---