Automated full-dimensional potential energy surface development and quasi-classical dynamics for the HI(X¹Σ⁺) + C₂H₅ → I(²P_3/2) + C₂H₆ reaction

Abstract

A full-dimensional spin–orbit-corrected analytical coupled-cluster-quality potential energy surface (PES) is developed for the HI(X¹Σ⁺) + C₂H₅ → I(²P_3/2) + C₂H₆ reaction using the ROBOSURFER program package, and a quasi-classical trajectory (QCT) study on the new PES is reported. The stationary-point relative energies obtained on the PES reproduce well the benchmark values. Our simulations show that in the 0.5–40 kcal mol⁻¹ collision energy (E_coll) range, the b = 0 reaction probability, where b denotes the impact parameter, increases first and then stays steady with increasing E_coll, reaching around 10% when E_coll = 5 kcal mol⁻¹. No significant E_coll dependence is observed in the range of 5–40 kcal mol⁻¹. The reaction probabilities decrease monotonically with increasing b, and the maximum b where the reactivity vanishes becomes smaller and smaller as E_coll increases. Scattering angle distributions show a forward scattering preference, indicating the dominance of the direct stripping mechanism, which is more obvious than in the case of HBr + C₂H₅ → Br + C₂H₆. The reaction clearly favors H-side attack over side-on HI and the least-preferred I-side approach, and favors side-on CH₃CH₂ attack marginally over CH₂-side and the least-preferred CH₃-side approach at high E_coll. At low E_coll, however, the dominant effect of H-side attack becomes weaker, while the side-on CH₃CH₂ attack becomes comparable with CH₂-side and the former is a little less favored when E_coll = 0.5 kcal mol⁻¹. It turns out that the initial translational energy is converted mostly into product recoil, whereas the reaction energy excites the C₂H₆ vibration. The vibrational and rotational distributions of the C₂H₆ product slightly blue-shift as E_coll increases, and none of the reactive trajectories violates the zero-point energy (ZPE) constraint. The energy transfer in the HI + C₂H₅ → I + C₂H₆ reaction is very similar to the case in the HBr + C₂H₅ → Br + C₂H₆ system that we investigated recently.

---

1. Introduction

As a class of elementary reactions, atom transfer or metathesis reactions of HX + C₂H₅ ↔ X + C₂H₆ (X = F, Cl, Br, I) have become benchmark systems to study the dynamics and mechanisms of post-six-atom polyatomic chemical reactions. These exothermic reactions have attracted a lot of attention from both experiment and theory for the forward processes (X = Br, I)^1–9 and backward processes (X = F, Cl),^10–34 whose activation energies have been found to have small positive or negative values.³⁵

The full-dimensional PESs and dynamics of X = F, Cl, Br have been theoretically investigated in our group: the vibrationally-resolved rotational state distributions of the HF product of the F + C₂H₆ reaction obtained from computations agree well with the single-collision experimental data for the v = 1, 2, and 3 states,³⁰ while the promoting effects of vibrational excitations, related to the slightly submerged barrier, are suppressed by the early-barrier-induced translational enhancement.³¹ A study on the Cl + C₂H₆ reaction provided unprecedented agreement with experiment for the rotational state distribution of the HCl product,³² and four out of five studied vibrational excitations clearly promote the slightly late-barrier Cl + C₂H₆ reaction.³³ Later, the impacts of rotational excitation on the reactivity, mechanism, and post-reaction distribution of energy of Cl + C₂H₆ were also investigated.³⁴ A full-dimensional spin–orbit-corrected analytical PES for the HBr + C₂H₅ reaction and a quasi-classical dynamics study on the new PES were reported very recently.⁹

Investigations of the HI + C₂H₅ → I + C₂H₆ reaction began with the measurement of rate constants as a function of temperature to determine the Arrhenius parameters in a tubular reactor coupled to a photoionization mass spectrometer.¹ Leplat et al.⁷ performed a reinvestigation of the absolute rate constants that led to the following Arrhenius expressions: k = 1.20(± 0.38) × 10⁻¹¹ exp(−7.12(± 1.059) kJ mol⁻¹/RT) in the temperature range of 293–623 K using a Knudsen reactor coupled to a single-photon photoionization mass spectrometer. They recommended the standard heat of formation of C₂H₅ to be 117.3 ± 3.1 kJ mol⁻¹, resulting from an average of “third law” evaluations using S_298°(C₂H₅) = 242.9 ± 4.6 J K⁻¹ mol⁻¹. Later, the same group extended the temperature range down to 213 K.⁸ They also applied ab initio quantum chemistry methods and canonical transition state theory for the reaction energy profiles and rate constants. Geometry optimizations of reactants, products, molecular complexes, and transition states were determined at the CCSD/cc-pVDZ level of theory. Subsequent single-point energy calculations employed the DK-CCSD(T)/ANO-RCC level. Further improvement of the electronic energies has been achieved by applying spin–orbit coupling corrections towards full configuration interaction and hindered rotation analysis of vibrational contributions. The resulting theoretical rate constants in the temperature range of 213–623 K lie in the range of 10⁻¹¹–10⁻¹² cm³ molecule⁻¹ s⁻¹; however, their experiments and theoretical modelling seem at great odds with each other.

In the present study we develop a full-dimensional ab initio PES for the title reaction. The spin–orbit coupling is taken explicitly into account in our computations. Using this PES, we carry out QCT simulations, and discuss the detailed dynamics results of the title reaction. The details of the PES development and the accuracy of the analytical PES are described in Section 2. The computational details and results of the QCT simulations are given and discussed in Section 3. The paper ends with conclusions in Section 4.

2. Potential energy surface

2.1. Initial geometry set

Following the same strategy applied previously for the HBr + C₂H₅ reaction,⁹ the initial candidate of the geometry set of the HI + C₂H₅ reaction is obtained by randomly displacing the Cartesian coordinates of the stationary points³⁵ in the 0–0.4 Å interval. In addition, the displaced reactants and products are randomly scattered around each other in the range of 3–8 Å. At these initial geometries single-point quantum chemical computations are performed at the ManyHF-based³⁶ RMP2³⁷/aug-cc-pVDZ³⁸ level of theory (for the I atom the small-core relativistic effective core potential (ECP)³⁹ and the corresponding aug-cc-pVDZ-PP basis set are used) using the MOLPRO program package.⁴⁰ We note that the ManyHF method and its utility are discussed in Section 2.4. The data set is then cut by excluding the geometries with a higher than 100 kcal mol⁻¹ relative energy with respect to the global minimum of the set. After the cut the initial data set consists of 6299 geometries.

For the fitting of the energy points of the PES we utilize the monomial symmetrization approach (MSA).⁴¹ Within this approach the PES is fitted using a full-dimensional analytical function which is inherently invariant under the permutations of like atoms. This function is an expansion of polynomials of the y_ij = exp(−r_ij/a) Morse-like variables, where r_ij is the inter-atomic distance and the a parameter, set to 2.0 bohr based on careful tests, controls the asymptotic behavior of the PES. The highest order of the polynomials is 5. The energy points are fitted using a least-squares fit with an E₀/(E + E₀) weighting factor, where E is the actual potential energy relative to the global minimum of the fitting set, and E₀ = 0.04 hartree.

2.2. Potential energy surface development

The above initial data set is used to start the PES development using the ROBOSURFER program package⁴² developed in our group. In the ROBOSURFER program a hard energy limit of 150 kcal mol⁻¹ relative to the energy of the free reactants is applied, above which no energy point is added. A hard energy limit of 60 kcal mol⁻¹ below the reactants is set to avoid spurious minima. A 0.5 kcal mol⁻¹ target accuracy of the fitting is set. These parameter values are chosen to obtain the best possible description of the HI + C₂H₅ reaction. The ManyHF-based RMP2/aug-cc-pVDZ (aug-cc-pVDZ-PP for the I atom) level of theory, the same as in Section 2.1, is used for the initial PES development, and consists of 141 ROBOSURFER iterations in total. During the PES development, QCT computations⁴³ are run to obtain new geometries, where E_coll is set from 1 to 60 kcal mol⁻¹, which is enough to cover the energies on the PES that we are interested in. We use both sides of the reaction, i.e., HI + C₂H₅ and I + C₂H₆, as the starting points of the QCTs. At the end we have 11 909 geometries.

2.3. Recalculation of energies

The energies of the above geometries are recomputed at the following composite level of theory: ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for the I atom), where “SO_corr” is the spin–orbit (SO) correction to each energy point. In free halogen atoms the non-relativistic ²P ground electronic state splits due to the relativistic spin–orbit interaction, and the relativistic ²P_3/2 ground state is lower by one-third of the splitting energy, which means 21.74/3 = 7.25 kcal mol⁻¹ for I (experimental value from NIST), with respect to the non-relativistic ground state. Thus, this energy-lowering effect is especially relevant in the exit (I + C₂H₆) channel of the reactive PES, where the I atom is far from and thus unbound to the ethane molecule. The SO correction is determined at the MRCI-F12+Q(5,3)/cc-pVDZ-F12(-PP)⁴⁴ level of theory for each geometry. The multireference computations utilize a minimal active space of 5 electrons on 3 spatial 5p-like orbitals, and the Q Davidson-correction⁴⁵ estimates higher-order correlation energy effects. The SO computations make use of a spin–orbit pseudopotential in the interacting-states approach,⁴⁶ where the SO eigenstates are determined by diagonalizing the 6 × 6 SO matrix whose diagonal elements are replaced by the Davidson-corrected MRCI energies. Our calculated absolute SO correction for the free iodine atom is 20.39/3 = 6.80 kcal mol⁻¹, which agrees with the experimental value (7.25 kcal mol⁻¹) within chemical accuracy. In the recalculation, 570 points failed in CCSD iteration, 406 points failed in MRCI iteration, and a few failed in ManyHF (for these points the default HF does not converge either), which leaves us with 10 921 geometries and the corresponding composite energies. We also checked that among these geometries, only 41 have T₁-diagnostic⁴⁷ values higher than 0.045, and none of them are higher than 0.06. Thus, it is safe to use the single-reference UCCSD(T)-F12a method.

The MSA is used again for the fitting of the geometries with new high-level energies. The root-mean-square (RMS) errors in the chemically interesting regions of the PES are 0.19, 0.53, and 0.98 kcal mol⁻¹ in the energy intervals of 0–20, 20–40, 40–100 kcal mol⁻¹ relative to the global minimum of the fitting set, respectively, which are within chemical accuracy.

2.4. ManyHF method

To test the validity and advantage of the ManyHF method recently developed in our group³⁶ for the title reaction system, we take 500 geometries randomly from the final geometry set, perform UCCSD(T)-F12a/cc-pVDZ-F12 (cc-pVDZ-PP-F12 for I atom) computations starting from the default Hartree–Fock (HF) calculation, and compare the results starting from the ManyHF method. We found that there are 29 geometries where the default HF could not converge while ManyHF succeeded, and 1 geometry where the default HF converged but the following CCSD did not converge while ManyHF gave a better reference energy lower than the default HF by 35 kcal mol⁻¹ and the following CCSD calculation worked. For all the other 470 points, the two methods give almost the same results (a difference of less than 0.01 kcal mol⁻¹, except for 1 geometry where the difference was about 0.5 kcal mol⁻¹). Therefore, it seems that the default HF does not produce unreasonably wrong energies for the title system, but the ManyHF method is more robust and ensures the convergence of more ab initio data, which is important for PES development.

2.5. Potential energy surface evaluation

The schematic energy diagram of the title reaction is shown in Fig. 1. The C_s-symmetry transition state (TS) structure with a 176° bent C–H–I arrangement and with a large H–C distance of 1.87 Å is clearly reactant-like.³⁵ A pre-reaction minimum is located very near to the TS. The reaction is exothermic, in accordance with its early-barrier nature.⁴⁸Fig. 1 also shows the comparison of the classical relative energies of the stationary points of the title reaction obtained on the newly-developed PES, the ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for the I atom) energies computed at the geometries optimized on the PES, and the previously determined benchmark results.³⁵ A comparison of the first two indicates low (0.1 kcal mol⁻¹) fitting errors of the full-dimensional PES, which is consistent with the small RMS values at the end of Section 2.3. The relative energies obtained on the PES reproduce well the benchmark values (<0.5 kcal mol⁻¹ difference). The intermediate complex of the reactants lies more shallowly while the TS lies deeper and releases more heat for the HI + C₂H₅ reaction compared with the HBr + C₂H₅ reaction.

Fig. 1 Schematic potential energy diagram of the HI + C₂H₅ → I(²P_3/2) + C₂H₆ reaction comparing the classical relative energies obtained on the present PES, the composite ab initio energies at geometries optimized on the PES, and the relativistic all-electron CCSDT(Q)/complete-basis-set-quality benchmark relative energies³⁵ of the stationary points, in kcal mol⁻¹.

The ZPEs of the reactants and product obtained on the present PES are 3.37 (HI), 37.40 (C₂H₅), and 47.13 (C₂H₆) kcal mol⁻¹, whereas the corresponding values at the CCSD(T)-F12b/aug-cc-pVDZ level are 3.79, 37.26, and 46.86 kcal mol⁻¹, respectively.³⁵

As we did for HBr + C₂H₅ (black and red lines in Fig. 2),⁹ to capture the properties near the TS, we take the TS geometry, and elongated and shortened the C–I distance, while the other degrees of the two parts, CH₃CH₂ and HI, were frozen. The one-dimensional potential energy curve as a function of the C–I distance obtained on the PES, compared with that obtained using the direct ab initio method, is shown in Fig. 2 (blue and pink lines). The asymptote in Fig. 2 is not the reactants in equilibrium, but is bent over a little, so its energy is higher than that of the reactants, leading to a deeper well with −8.6 and −7.8 kcal mol⁻¹ relative energies with respect to the asymptote in the case of the PES and the direct ab initio method, respectively. A comparison of the two minima indicates within-chemical-accuracy fitting error (0.8 kcal mol⁻¹) of the full-dimensional PES. The positions of the two minima are located at the same C–I distance of 3.02 Å, showing the good behavior of the analytical PES. The sub-barrier in the HI + C₂H₅ reaction is deeper than in the case of the HBr + C₂H₅ reaction, which is consistent with the benchmark values.³⁵

Fig. 2 One-dimensional potential energy curves for CH₃CH₂···HX (X = Br (ref. 9), I (this work)) as a function of the C–X distance, fixing the other coordinates at the TS values, obtained on the PES, compared with those obtained using the composite ab initio method.

3. Quasi-classical trajectory simulations

QCT simulations were carried out at E_coll = 0.5, 1, 5, 10, 20, and 40 kcal mol⁻¹ for the title reaction on the newly-developed PES. At the beginning of the trajectory, the ZPEs of HI and C₂H₅ were set via standard normal-mode sampling,⁴³ and the initial rotational angular momentum of each reactant was adjusted to zero. The spatial orientations of the reactants were randomly sampled. The initial distance between the center of mass of HI and the center of mass of C₂H₅ is (x² + b²)^1/2, where x = 28 bohr and the impact parameter is varied between 0 and b_max (where the reaction probability vanishes) with a step size of 0.5 bohr. 1000 trajectories were run at each b value. The trajectories were propagated with a 0.0726 fs time step until the largest interatomic distance became larger than the largest initial one by 1 bohr. At the end, less than 0.1% of the trajectories failed and gave unphysical results, which also indicated the good behavior of the newly-developed analytical PES.

3.1. Reaction probabilities and integral cross-sections

The opacity functions (reaction probabilities as a function of the impact parameter) obtained at the different E_coll values are shown in Fig. 3. No threshold energy above 0.5 kcal mol⁻¹ can be observed for the title reaction to proceed, in accordance with the negative barrier height relative to the reactants. It is clear that the opacity function at 0.5 kcal mol⁻¹E_coll has a much smaller reaction probability and much greater distance where the reaction can still occur than at larger collision energies. The b = 0 reaction probability increases with increasing E_coll, reaching around 10% when E_coll = 5 kcal mol⁻¹. No significant E_coll dependence is observed in the range of 5–40 kcal mol⁻¹. The reaction probabilities decrease monotonically with increasing b and the maximum b where reactivity vanishes decreases as E_coll increases. The b_max value is the largest (17 bohr) at 0.5 kcal mol⁻¹E_coll, presumably due to the fact that the dipole–dipole interaction between the reactants is the least counteracted by translational momenta. The smaller reaction probability at very low E_coll was also observed in other similar shallow sub-barrier reactions.^9,30,49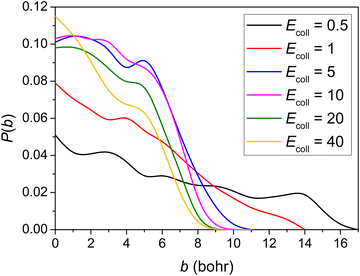

Fig. 3 Reaction probability as a function of the b impact parameter for the title reaction at different collision energies (given in kcal mol⁻¹).

The integral cross-section (σ) data are calculated using a b-weighted numerical integration of the P(b) opacity functions at each E_coll, as presented in Fig. 4 (red points). It shows an inhibition of the reaction by the increase in the initial translational energy from 5 to 40 kcal mol⁻¹. In the low E_coll range, however, the decreasing reaction probability and increasing b_max compete with each other, which results in the kink at around E_coll = 1 kcal mol⁻¹. The cross-section data of the HBr + C₂H₅ reaction from our previous work⁹ are also plotted in this figure as black points for comparison. It is clear that at very low E_coll, the promoting effect of increasing b_max suppresses the decreasing reaction probability, which gives a large σ for HI + C₂H₅, whereas it is reversed in the case of HBr + C₂H₅.

Fig. 4 Integral cross-section as a function of the collision energy for the HBr + C₂H₅ (ref. 9) and HI + C₂H₅ (this work) reactions.

3.2. Scattering and initial attack angle distributions

The scattering angle distributions were obtained by binning the cosine of the angle (θ) of the relative velocity vectors of the center of masses of the products and those of the reactants into 10 equidistant bins from −1 to 1. Here, cos(θ) = 1 (θ = 0°) corresponds to forward scattering, and cos(θ) = −1 (θ = 180°) corresponds to backward scattering. Differential cross-sections showing the scattering angle distributions of the title reaction are shown in Fig. 5. It is clear that forward scattering is favored, indicating the dominance of the direct stripping mechanism, with little E_coll dependence. The preference of forward scattering is more obvious in the HI + C₂H₅ reaction than in the HBr + C₂H₅ reaction.⁹

Fig. 5 Normalized scattering angle distributions for the title reaction at different collision energies (given in kcal mol⁻¹).

The initial attack angle distributions for the reactants were calculated by binning the cosine of the angle (α for HI and β for C₂H₅) of the velocity vector of the center of mass of the examined reactant and an interatomic vector that is considered as the I–H bond for HI and the C–C bond for C₂H₅. We also used 10 equidistant bins between −1 and 1, as in the case of the scattering angle distributions. HI cos(α) = −1 means that HI approaches with its I atom side, and in the situation of cos(α) = 1, HI goes with its H atom towards C₂H₅. Meanwhile, C₂H₅ cos(β) = −1 means that C₂H₅ approaches HI with its CH₃ side, and in the situation of cos(β) = 1, C₂H₅ goes with its CH₂ side towards the HI. Differential cross-sections that show the initial attack angle distributions of the title reaction at different E_coll values are shown in Fig. 6. The title reaction favors H-side attack over side-on HI and the least-preferred I-side approach, as expected, because an H–C bond forms in the abstraction process, and favors side-on CH₃CH₂ attack over CH₂-side and the least-preferred CH₃-side approach at high E_coll. At low E_coll, however, the dominant effect of H-side attack becomes weaker, while the side-on CH₃CH₂ attack becomes comparable with CH₂-side and the latter is even more favored when E_coll = 0.5 kcal mol⁻¹. The initial attack angle distributions of HI are similar to HBr while the CH₂-side attack has more advantage than in the HBr + C₂H₅ reaction.⁹

Fig. 6 Normalized initial attack angle distributions for the title reaction at different collision energies (given in kcal mol⁻¹). The attack angles are defined at the beginning of each reactive trajectory.

3.3. The post-reaction distribution of energy

Differential cross-sections showing the distribution of the relative translational energy of the products at different E_coll values are plotted in Fig. 7. It can be seen that the distributions become broader as the E_coll increases, and their maxima are shifted by almost the total increment of the E_coll, indicating that the major part of the initial translational energy ends up in translational recoil in all cases, which is very similar to the HBr + C₂H₅ reaction.⁹

Fig. 7 Normalized product relative translational energy distributions for the title reaction at different collision energies (given in kcal mol⁻¹).

Consistent with the above observation, the E_coll dependence of the internal energy distribution of ethane, plotted in Fig. 8, also suggests that only a small portion of the collision energy is transferred into the vibrational and rotational degrees of freedom of ethane, since the peaks of the distributions are less affected by the change in the initial translational energy than those of the product relative translational energy distributions. The internal energy excitations of the product ethane come mainly from the reaction energy. Considering that the ZPE of ethane is 47 kcal mol⁻¹, the classical vibrational energy of the C₂H₆ product is greater than its ZPE on the present PES for all 6139 reactive trajectories. It is clear that energy flow in the HI + C₂H₅ system is also very similar to the case in the HBr + C₂H₅ system, except that the reaction energy of HI + C₂H₅ is larger than that of HBr + C₂H₅ (35 vs. 19 kcal mol⁻¹, respectively).⁹ Rotational energy distributions are cold and are blue-shifted as E_coll increases. The corresponding rotational quantum numbers span ranges of about 0–60 and 0–120 at the lowest and highest collision energies, respectively, as Fig. 8 also shows. The fact that the low rotational energies correspond to relatively large J values originates from the large moments of inertia of the C₂H₆ molecule.

Fig. 8 Normalized internal energy (E_int), vibrational energy (E_vib), rotational energy (E_rot), and rotational quantum number (J) value distributions for the product ethane of the title reaction at different collision energies (given in kcal mol⁻¹). Rotational quantum numbers of C₂H₆ are obtained by rounding the lengths of classical rotational angular momentum vectors to the nearest integer values. Note that in the E_rot panel the curves for E_coll = 0.5 and 1 kcal mol⁻¹ are almost completely coincident with each other.

4. Conclusions

This work is a continuation of our previous studies on the analytical PES developments for the reactions HX + C₂H₅ ↔ X + C₂H₆ (X = F,^30,31 Cl,^32–34 Br⁹). In the present work we have developed a full-dimensional spin–orbit-corrected PES for the HI + C₂H₅ → I + C₂H₆ reaction using the ROBOSURFER program package and the MSA of the permutationally invariant polynomial method for fitting the ab initio energy points, and the dynamics of the title reaction were studied in detail by performing QCT simulations. The ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for the I atom) level of theory used for the PES development is necessary to correctly describe the reaction, and also reflects well the negative barrier height. We have shown that the use of the ManyHF method significantly improves the HF convergence, providing more successful ab initio computations compared with the default HF procedure, which is an important advance for PES development. The stationary-point energies on the PES agree well with the benchmark data. Quasi-classical dynamics simulations on this PES show substantial probabilities of this H-abstraction reaction for a wide range of collision energies. The preference of forward scattering is more obvious in the HI + C₂H₅ reaction than in HBr + C₂H₅.⁹ This finding indicates a direct stripping mechanism for HI + C₂H₅ at every E_coll. The title reaction favors H-side attack over side-on HI and the least-preferred I-side approach, as expected, because an H–C bond forms in the abstraction process, and favors side-on CH₃CH₂ attack over CH₂-side and the least-preferred CH₃-side approach at high E_coll. At low E_coll, however, the dominant effect of H-side attack becomes weaker, while the side-on CH₃CH₂ attack becomes comparable with CH₂-side and the former seems a little less favored when E_coll = 0.5 kcal mol⁻¹. The initial attack angle distributions of HI are similar to HBr, although the CH₂-side attack has more advantage than in the HBr + C₂H₅ reaction.⁹ Relative translational energy distributions of the products and internal energy distributions of ethane suggest that most of the E_coll ends up in product translational recoil, and only a small amount of the initial translational energy excites the rotational and vibrational modes of ethane. The substantial reaction energy excites the vibration of the product. The vibrational and rotational distributions of the C₂H₆ product are blue-shifted slightly as E_coll increases. The two systems, HBr + C₂H₅ → Br + C₂H₆ and HI + C₂H₅ → I + C₂H₆, show very similar energy transfer behavior. None of the reactive trajectories violates the ZPE constraint due to the high exothermicity of the title reaction. The present PES opens the door for vibrational and rotational mode-specific investigations and thermal sampling of the initial states, leading to rate constants.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Viktor Tajti and Tibor Győri for the tips and discussions. This work was supported by the National Research, Development and Innovation Office-NKFIH, K-125317; the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT; Project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences.

References

1. J. A. Seetula, J. J. Russell and D. Gutman, J. Am. Chem. Soc., 1990, 112, 1347.
2. Y. H. Chen and E. Tschuikow-Roux, J. Phys. Chem., 1993, 97, 3742.
3. J. A. Seetula, J. Chem. Soc., Faraday Trans., 1998, 94, 891.
4. J. A. Seetula, Phys. Chem. Chem. Phys., 2000, 2, 3807.
5. L. Sheng, Z. S. Li, J. Y. Liu, J. F. Xiao and C. C. Sun, J. Comput. Chem., 2004, 25, 423.
6. D. M. Golden, J. P. Peng, A. Goumri, J. Yuan and P. Marshall, J. Phys. Chem. A, 2012, 116, 5847.
7. N. Leplat, A. Wokaun and M. J. Rossi, J. Phys. Chem. A, 2013, 117, 11383.
8. N. Leplat, J. Federic, K. Sulkova, M. Sudolska, F. Louis, I. Cernusak and M. J. Rossi, Z. Phys. Chem., 2015, 229, 1475.
9. C. Yin, V. Tajti and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 24784.
10. O. Roberto-Neto and F. B. C. Machado, Chem. Phys. Lett., 2007, 449, 67.
11. E. S. Whitney, A. M. Zolot, A. B. McCoy, J. S. Francisco and D. J. Nesbitt, J. Chem. Phys., 2005, 122, 124310.
12. J. P. Layfield, A. F. Sweeney and D. Troya, J. Phys. Chem. A, 2009, 113, 4294.
13. J. Espinosa-Garcia, J. C. Corchado, M. Garcia-Chamorro and C. Rangel, Phys. Chem. Chem. Phys., 2018, 20, 19860.
14. S. A. Kandel, T. P. Rakitzis, T. Lev-On and R. N. Zare, J. Chem. Phys., 1996, 105, 7550.
15. S. A. Kandel, T. P. Rakitzis, T. Lev-On and R. N. Zare, Chem. Phys. Lett., 1997, 265, 121.
16. S. A. Kandel, T. P. Rakitzis, T. Lev-On and R. N. Zare, J. Phys. Chem. A, 1998, 102, 2270.
17. P. C. Samartzis, D. J. Smith, T. P. Rakitzis and T. N. Kitsopoulos, Chem. Phys. Lett., 2000, 324, 337.
18. O. Roberto-Neto and F. B. C. Machado, Theor. Chem. Acc., 2001, 107, 15.
19. M. J. Bass, M. Brouard, C. Vallance, T. N. Kitsopoulos, P. C. Samartzis and R. L. Toomes, J. Chem. Phys., 2003, 119, 7168.
20. R. L. Toomes and T. N. Kitsopoulos, Phys. Chem. Chem. Phys., 2003, 5, 2481.
21. A. Fernandez-Ramos, E. Martinez-Nunez, J. M. C. Marques and S. A. Vazquez, J. Chem. Phys., 2003, 118, 6280.
22. C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435.
23. S. Rudic, C. Murray, J. N. Harvey and A. J. Orr-Ewing, J. Chem. Phys., 2004, 120, 186.
24. C. Murray, J. K. Pearce, S. Rudic, B. Retail and A. J. Orr-Ewing, J. Phys. Chem. A, 2005, 109, 11093.
25. S. J. Greaves, J. Kim, A. J. Orr-Ewing and D. Troya, Chem. Phys. Lett., 2007, 441, 171.
26. S. J. Greaves, A. J. Orr-Ewing and D. Troya, J. Phys. Chem. A, 2008, 112, 9387.
27. C. S. Huang, W. Li and A. G. Suits, J. Chem. Phys., 2006, 125, 133107.
28. W. Li, C. S. Huang, M. Patel, D. Wilson and A. Suits, J. Chem. Phys., 2006, 124, 011102.
29. C. Rangel and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2018, 20, 3925.
30. D. Papp and G. Czakó, J. Chem. Phys., 2020, 153, 064305.
31. D. Papp and G. Czakó, J. Chem. Phys., 2021, 155, 154302.
32. D. Papp, V. Tajti, T. Győri and G. Czakó, J. Phys. Chem. Lett., 2020, 11, 4762.
33. D. Papp, J. Li, H. Guo and G. Czakó, J. Chem. Phys., 2021, 155, 114303.
34. D. Papp and G. Czakó, J. Phys. Chem. A, 2022, 126, 2551.
35. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
36. T. Győri and G. Czakó, J. Chem. Phys., 2022, 156, 071101.
37. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
38. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007.
39. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
40. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see https://www.molpro.net.
41. Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26.
42. T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51.
43. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley; New York, 1998, pp. 399–407.
44. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
45. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
46. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
47. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199.
48. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334.
49. D. Gao and D. Wang, Phys. Chem. Chem. Phys., 2021, 23, 26911.

---