Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent dependent triplet state delocalization in a co-facial porphyrin heterodimer†
Susanna
Ciuti
 a,
Jacopo
Toninato
a,
Antonio
Barbon
a,
Jacopo
Toninato
a,
Antonio
Barbon
 a,
Niloofar
Zarrabi
b,
Prashanth K.
Poddutoori
a,
Niloofar
Zarrabi
b,
Prashanth K.
Poddutoori
 *b,
Art
van der Est
*b,
Art
van der Est
 *c and
Marilena
Di Valentin
*c and
Marilena
Di Valentin
 *a
*a
aDipartimento di Scienze Chimiche, Università degli studi di Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: marilena.divalentin@unipd.it
bDepartment of Chemistry & Biochemistry, University of Minnesota Duluth, 1038 University Drive, Duluth, Minnesota 55812, USA. E-mail: ppk@d.umn.edu
cDepartment of Chemistry, Brock University, 1812 Sir Isaac Brock Way, St. Catharines, Ontario L2S 3A1, Canada. E-mail: avde@brocku.ca
First published on 21st November 2022
Abstract
The excited triplet state of a cofacial aluminum(III) porphyrin–phosphorus(V) porphyrin heterodimer is investigated using transient EPR spectroscopy and quantum chemical calculations. In the dimer, the two porphyrins are bound covalently to each other via a μ-oxo bond between the Al and P centres, which results in strong electronic interaction between the porphyrin rings. The spin polarized transient EPR spectrum of the dimer is narrower than the spectra of the constituent monomers and the magnitude of the zero-field splitting parameter D is solvent dependent, decreasing as the polarity of the solvent increases. The quantum chemical calculations show that the spin density of the triplet state is delocalized over both porphyrins, while magnetophotoselection measurements reveal that, in contrast to the value of D, the relative orientation of the ZFS axes and the excitation transition dipole moments are not solvent dependent. Together the results indicate that triplet state wavefunction is delocalized over both porphyrins and has a modest degree of charge-transfer character that increases with increasing solvent polarity. The sign of the spin polarization pattern of the dimer triplet state is opposite to that of the monomers. The positive sign of D predicted for the monomers and dimer by the quantum chemical calculations implies that the different signs of the spin polarization patterns is a result of a difference in the spin selectivity of the intersystem crossing.
1. Introduction
Tetrapyrroles are ubiquitous in nature as both chromophores and redox agents.1 The cyclic tetrapyrroles chlorophyll and heme are key components in photosynthesis and respiration, respectively. The importance of these structures in biochemical energy capture, storage and transport has spawned interest in the physical and chemical properties of porphyrins and their use in a broad range of applications.2–6 In particular, metalloporphyrins are widely used as chlorophyll mimics in artificial photosynthesis.7–12An important property of the cyclic tetrapyrroles is their ability to form co-facial dimers and oligomers. By tuning the strength of the excitonic coupling and the number of molecular units involved, the optical and redox properties can be tailored to meet specific needs. For example, the large J-aggregates found in chlorosomes have extraordinarily high extinction coefficients and allow the green photosynthetic bacteria to live under extremely low-light conditions.13 In purple bacteria, the excitonic coupling between the porphyrins is used to funnel excitation energy to the reaction center and to stabilize the radical cation created by the charge separation.14
The co-facial arrangement of the tetrapyrroles found in nature is controlled through protein-cofactor interactions and generating synthetic mimics is challenging.15–19 As a result, there are very few studies of the electronic and physical properties of co-facial porphyrin dimers.16,20,21 Recently, we reported the characterization of the co-facial porphyrin heterodimer AlPor–O–PPor·PF6 in which Al(III) porphyrin and P(V) porphyrin are linked via a μ-oxo bridge (Fig. 1a).16 The different oxidation states of the central elements cause a 0.9 V difference in the first oxidation potentials of the two porphyrins and optical absorption studies show that this leads to the formation of a singlet state with charge-transfer (CT) character when the complex is excited. In donor–acceptor systems, the lowest excited triplet state of the donor is also of interest because it has longer lifetime than the corresponding singlet state. Since the yield of electron transfer depends on the ratio of the electron transfer rate and the excited state decay rate, a longer excited state lifetime means the rate of electron transfer needed for a high yield can be lower and, hence, the electronic coupling to the acceptor can be weaker. In addition, charge recombination to the ground state is spin forbidden in the resulting radical pairs. Recently, we have shown that these two factors can be used to generate long-lived charge separation.22–24 Initial transient electron paramagnetic resonance (TREPR) spectroscopy measurements of AlPor–O–PPor·PF6 showed that the zero-field splitting (ZFS) parameter D of the dimer triplet state is smaller than that of the monomers and the sign of the electron spin polarization is opposite. This suggests that the lowest excited triplet state of the dimer is delocalized over both porphyrins and likely also has CT character.16 However, further study is required to fully understand the reasons for the differences in the ZFS parameters and the change in the sign of the polarization.
Here, we investigate the properties of the excited triplet states of AlPor–O–PPor·PF6 and its constituent monomers in more detail using a combination of magnetophotoselection TREPR measurements in a range of different solvent glasses and computational studies using density functional theory (DFT), complete active space self-consistent field theory (CASSCF) and N-electron valence state perturbation theory (NEVPT) approaches. Magnetophotoselection TREPR is an excellent method for quantitative determination of the relative orientation of the triplet state ZFS axes and the optical absorption transition moments.25–27 It also allows these axes to be fixed in the molecule if the orientation of one of them is known or can be determined in silico. The results confirm that the triplet state is indeed delocalized over both porphyrins of the dimer and that the excited states have CT character. The ZFS parameters are found to be solvent dependent and show that the CT character of the triplet state increases as the polarity of the solvent increases. However, the relative orientation of the ZFS axes and the excitation transition dipole moments is not solvent dependent and is the same in the monomers and dimer. We will show that this implies that the CT character of the excited wavefunctions represents only partial transfer of an electron and that multiple electronic transitions are likely involved in the excitation of the molecule. The sign of D is found to be positive in all three compounds. Thus, the difference in the sign of the polarization in the dimer compared to the monomers is not due to a change in the sign of D, which implies that it is a result of a change in the spin selectivity of the intersystem crossing.
2. Experimental section
2.1 Sample preparation
The synthesis of the heterodimer and the reference compounds have been described previously.16 Briefly, the two porphyrins were coupled using a condensation reaction between AlPor–CH3 and PPor–OH·PF6. Nucleophilic attack at the Al(III) center of AlPor–CH3 by the axial OH group of PPor–OH·PF6 and elimination of methane leads to the formation of the μ-oxo bridged heterodimer AlPor–O–PPor·PF6.2.2 EPR measurements
TREPR spectra were recorded on a Bruker ELEXSYS E580 spectrometer equipped with a dielectric resonator (ER4118X-MD5(W1)). The temperature was controlled using cold nitrogen gas and an Oxford CF900 cryostat. The signal coming from the detector (diode) was digitized using a LeCroy 9300 oscilloscope triggered by the laser flash. The spectrometer rise time has been estimated to be about 900 ns under these conditions. No modulation of the magnetic field was applied. The triplet spectra were recorded with a resolution of either 0.4 mT per point or 0.1 mT per point. A pulsed Nd:YAG laser (Quantel Brilliant) equipped with both second and third harmonic modules and an optical parametric oscillator (OPOTECH) for tunable irradiation in the visible was used to photoexcite the sample. Typical parameters were λ = 544 nm, pulse length = 5 ns, energy = ca. 3 mJ per shot, repetition rate = 10 Hz.2.3 EPR data processing and simulations
TREPR data were processed by subtracting: (i) the average baseline before the trigger event and (ii) a time profile taken at an off-resonance position. The spectra have been extracted from the 2D data set by numerically integrating over an appropriate time window. The simulations of the EPR spectra were performed using a home-written MATLAB program for triplet powder spectra26 and the “esfit” routine from EasySpin28 was used to extract the best-fit parameters. Simulation of the spectra obtained with polarized light takes into account the orientation of the excited transition dipole moments in the triplet ZFS reference frame, and a component of non-polarized light, which is characteristic for each experiment. More details are reported in the ESI.†2.4 Quantum chemical calculations
The absorption transition dipole moments, ZFS parameters and principal axes of AlPor–O–PPor and the reference compounds AlPor–OH and PPor–OMe+ were calculated using ORCA 5.0.2.29,30 The structures of the compounds were first constructed using the program Avogadro31 from the X-ray crystal structure data of related porphyrins17,32,33 and then subjected to energy minimization using the UFF force field.34 The geometries were then optimized in ORCA using the PBE functional35 and the def2-TZVP basis set.36 The optical transition dipole moments and oscillator strengths of the monomers were calculated using several different methods. First, by Time Dependent Density Functional Theory (TDDFT) using: (1) the PBE functional, the D3BJ dispersion correction and the def2-TZVP basis set36 and (2) the CAM-B3LYP functional37 and the 6-31G(d,p) basis set38,39 The resolution of identity approximation40 with the chain-of-spheres method41 RIJCOSX was used to speed up the calculations. Next, the complete active space self-consistent field (CASSCF) method was used. Natural orbitals from a second order Møller–Plesset perturbation theory (MP2) computation using the def2-TZVP basis set were used as the initial guess orbitals for the CASSCF computation. Finally, the CASSCF wavefunctions were used as a starting point for a strongly contracted N-electron valence state perturbation theory (NEVPT2) computation.42 Either a 4-orbital, 4-electron or an 8-orbital, 8-electron active space was used consisting of the doubly degenerate HOMO and LUMO orbitals or HOMO, HOMO−1, LUMO and LUMO+1 orbitals of the porphyrins. The ZFS parameters of the triplet states were calculated using CASSCF NEVPT2 computations as described for the ground state, except that the geometry was optimized in the triplet state and for the dimer the active space was expanded to 16 electrons and 12 orbitals. For the monomers, both the spin–spin and spin–orbit coupling contributions to the D and E values were calculated. However, the spin–orbit coupling contribution was found to be negligible. For the dimer the size of the molecule made calculation of the spin–orbit coupling contribution prohibitively expensive and only the spin–spin contribution was calculated.3. Results and discussion
3.1 UV/visible absorbance
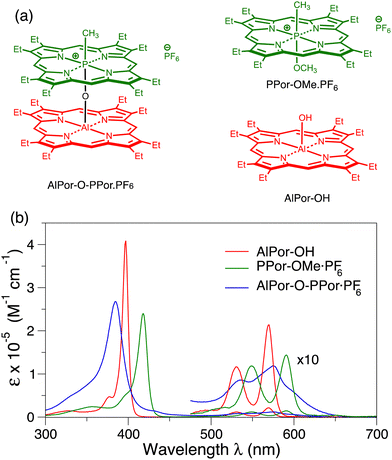
Fig. 1b shows the UV/visible absorbance spectra of AlPor–OH, PPor–OMe·PF6 and AlPor–O–PPor·PF6 in CH2Cl2. The spectra of the two monomers show the usual strong Soret band near 400 nm and weaker Q-bands between 500 and 600 nm. In PPor–OMe·PF6 the small size and high oxidation number of the phosphorus leads to puckering of the porphyrin ring that lifts the degeneracy of the two Soret transitions slightly. In the spectrum, this results in a red shift and broadening of the Soret band compared to AlPor–OH. In the dimer, the Soret band is broadened further and the interaction between the two porphyrins results in a blue shift compared to both monomers.The monomers AlPor–OH and PPor–OMe·PF6 each have two Q-bands separated by approximately 20 nm (680 cm−1) and 50 nm (1300 cm−1) in AlPor–OH and PPor–OMe·PF6, respectively. Computations of the vertical excitation energies of the Qx and Qy transitions (Table S1, ESI†) show that they are degenerate in both monomers. Thus, the Q-bands are ascribed to the first two transitions (ν00 and ν01) of a vibronic progression. For magneto-photoselection experiments it is important to know the orientation of the absorption transition dipole moments in the molecules. To evaluate the accuracy of different computational models in predicting the absorption properties, we made a comparison with the experimental excitation energies and oscillator strengths (Table S1, ESI†). Using time-dependent density functional theory and the Perdew–Burke–Ernzerhof functional (BPE),35 the oscillator strengths are badly underestimated, and the band positions are shifted compared to the experimental spectrum. Using the range separated CAM-B3LYP functional37 greatly improves the oscillator strengths but the band positions are blue shifted by 50–100 nm. Several other functionals and basis sets were also tried (data not shown) but none adequately reproduced the experimental spectrum and the predicted orientations of the transition dipoles depended on the functional and basis set that was used. The CASSCF method also gives reasonable values for the oscillator strengths, but all of the bands are still strongly blue shifted compared to the experimental spectrum. The NEVPT2 method overcorrects this but gives the best agreement with the experimental spectra with a comparatively small red shift. In AlPor–OH the Qx and Qy transition dipoles (Fig. S1, ESI†) are orthogonal to one another and lie in the plane of the molecule roughly along the Al–N bonds as expected. In PPor–OMe·PF6 the distortion of the porphyrin ring due to the small size of the P(V) centre results in a rotation of the transition dipoles so that they lie between the P–N bonds.
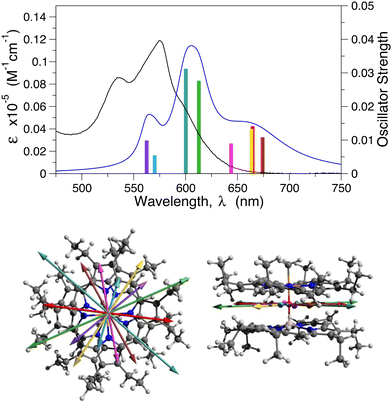
Having found a method that gives a reasonable description of the two monomers, we then applied it to the dimer. A comparison of the experimental and calculated Q-band region of the absorption spectrum of AlPor–O–PPor·PF6 is displayed in Fig. 2 along with the orientations of the transition dipole moments. The calculated spectrum obtained using the CASSCF-NEVPT2 method reproduces the relative band positions and intensities reasonably well, but it is red shifted by ∼20 nm compared to the experimental spectrum. The computations reveal that there are eight Q-band transitions in the dimer. As shown in the bottom part of Fig. 2, all of the corresponding transition dipole moments of the transitions are perpendicular to the Al–O–P axis.
The difference in the electron density between the excited state and the ground state for each of the eight transitions is displayed in Fig. 3. The density difference is plotted for an isosurface of 0.001 with green representing an increase of electron density in the excited state and red a decrease. The dimer is viewed with AlPor as the lower and PPor+ the upper of the two porphyrins. As can be seen, six of the eight transitions have CT character, with electron density being transferred from AlPor to PPor+. In particular, the two longest wavelength transitions have CT character, in agreement with the experimental observation that the intensity of the red edge of the spectrum is strongly solvent dependent.16 In contrast, the transitions at 663 nm and 644 nm show only very small density changes on PPor+ and AlPor respectively, indicating that the transitions are localized on one of the two porphyrins. The plots in Fig. 3 do not allow a quantitative determination of the CT character, but the small iso value used in generating them indicates that it is significantly less than one electron.
 | ||
| Fig. 3 Calculated density differences between the ground and excited states involved in the Q-band transitions of AlPor–O–PPor+. Green represents an increase and red a decrease in electron density. The density differences were calculated by subtracting the cube files of the electron densities of the states using Multiwfn 3.6.43 The resulting difference cube files were plotted using Avogadro31 with an iso value of 0.001. | ||
3.2 Triplet state TREPR spectra
Fig. 4 shows the TREPR spectra of AlPor–OH, PPor–OMe·PF6 and AlPor–O–PPor·PF6 measured in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 2-methyltetrahydrofuran (MeTHF) and CH2Cl2, which forms a transparent glass at 80 K. The spectra are the weighted sum (I‖ + 2I⊥) of spectra taken with the polarization of the excitation beam parallel (I‖) and perpendicular (I⊥) to the magnetic field to remove any photoselection effect.26 As can be seen, the widths of the spectra and their spin polarization patterns differ strongly. In particular, the sign of the polarization of the spectrum of the dimer is opposite to that of the two monomers. Such a change in sign can result either from a change in the sign of the ZFS parameters or from a change in the intersystem crossing rates to the three triplet sublevels as has been observed in other porphyrin model systems.44,45 However, without further information these two possibilities cannot be distinguished. A change in the sign of the ZFS would imply a large CT contribution to the triplet state. Because the ZFS, which determines the width of the spectrum, is dominated by the dipole–dipole interaction in porphyrin triplet states, a large CT contribution should also lead to narrowing of the spectrum. The width of the spectrum of the dimer is indeed narrower than the two monomer spectra, but the effect is not very large and so the extent of the charge transfer is not clear. Thus, we have carried out extensive additional TREPR measurements and computations to better understand the electronic structure of the dimer.
1 mixture of 2-methyltetrahydrofuran (MeTHF) and CH2Cl2, which forms a transparent glass at 80 K. The spectra are the weighted sum (I‖ + 2I⊥) of spectra taken with the polarization of the excitation beam parallel (I‖) and perpendicular (I⊥) to the magnetic field to remove any photoselection effect.26 As can be seen, the widths of the spectra and their spin polarization patterns differ strongly. In particular, the sign of the polarization of the spectrum of the dimer is opposite to that of the two monomers. Such a change in sign can result either from a change in the sign of the ZFS parameters or from a change in the intersystem crossing rates to the three triplet sublevels as has been observed in other porphyrin model systems.44,45 However, without further information these two possibilities cannot be distinguished. A change in the sign of the ZFS would imply a large CT contribution to the triplet state. Because the ZFS, which determines the width of the spectrum, is dominated by the dipole–dipole interaction in porphyrin triplet states, a large CT contribution should also lead to narrowing of the spectrum. The width of the spectrum of the dimer is indeed narrower than the two monomer spectra, but the effect is not very large and so the extent of the charge transfer is not clear. Thus, we have carried out extensive additional TREPR measurements and computations to better understand the electronic structure of the dimer.
An important initial consideration for such studies is whether the observed triplet spectra arise from a single species or are the sum of different components arising from different triplet states. In particular, in AlPor–O–PPor·PF6 several triplet states with differing amounts of CT character could be populated. In the monomers we expect only the lowest excited triplet to be populated, but coordination of the solvent to the Al center in AlPor–OH and porphyrin–porphyrin interactions could potentially result in triplet states with different ZFS parameters and optical properties. To investigate this possibility, we have measured the excitation wavelength and concentration dependence of the triplet spectra of all three samples. As can be seen in Fig. S2–S4 (ESI†) the TREPR spectra of the three compounds do not show any dependence on the excitation wavelength or concentration. Thus, we conclude that there are no aggregation effects present and that the spectra represent a single triplet species.
Isotropic TREPR spectra. The simulations of the X-band isotropic TREPR spectra of the triplet states of AlPor–OH and PPor–OMe·PF6 in 3
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeTHF
1 MeTHF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 at 80 K are also shown in Fig. 4 (dashed spectra). The corresponding experimental and simulated Q-band spectra are shown in Fig. S6 (ESI†). The parameters obtained from the simulations are presented in Table 1. Both AlPor–OH and PPor–OMe·PF6 are regular porphyrins with approximate D4h symmetry in which the central element does not have a significant effect on the excited state properties.46 For AlPor–OH, the ZFS tensor is nearly axial as expected based on the molecular symmetry. The ISC is accompanied by a change in the direction of the in-plane component of the orbital angular momentum. This is compensated for by the generation of in-plane spin angular momentum in the triplet state. As a result, the population rates px and py are equal and larger than pz. The ZFS parameters obtained from CASSCF calculations are given in parentheses in Table 1. The D-values are in reasonable agreement with the experimental parameters and show that D is positive. The smaller D-value in PPor–OMe·PF6 compared to AlPor–OH is also reproduced in the CASSCF calculations and is the result of the distortion of the porphyrin ring in PPor–OMe·PF6, which occurs because of the small size of the phosphorus centre. The solvent dependence of the TREPR spectra of AlPor–OH and PPor–OMe·PF6 is shown in Fig. S5 (ESI†) and only minor variations in the lineshape are seen with no change in the positions of the main features of the spectra.
CH2Cl2 at 80 K are also shown in Fig. 4 (dashed spectra). The corresponding experimental and simulated Q-band spectra are shown in Fig. S6 (ESI†). The parameters obtained from the simulations are presented in Table 1. Both AlPor–OH and PPor–OMe·PF6 are regular porphyrins with approximate D4h symmetry in which the central element does not have a significant effect on the excited state properties.46 For AlPor–OH, the ZFS tensor is nearly axial as expected based on the molecular symmetry. The ISC is accompanied by a change in the direction of the in-plane component of the orbital angular momentum. This is compensated for by the generation of in-plane spin angular momentum in the triplet state. As a result, the population rates px and py are equal and larger than pz. The ZFS parameters obtained from CASSCF calculations are given in parentheses in Table 1. The D-values are in reasonable agreement with the experimental parameters and show that D is positive. The smaller D-value in PPor–OMe·PF6 compared to AlPor–OH is also reproduced in the CASSCF calculations and is the result of the distortion of the porphyrin ring in PPor–OMe·PF6, which occurs because of the small size of the phosphorus centre. The solvent dependence of the TREPR spectra of AlPor–OH and PPor–OMe·PF6 is shown in Fig. S5 (ESI†) and only minor variations in the lineshape are seen with no change in the positions of the main features of the spectra.
| g xx | g yy | g zz | (px− py)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (py − pz) (py − pz) |
D (MHz) | E (MHz) | |
|---|---|---|---|---|---|---|
| AlPor–OH | 2.0040 | 2.0027 | 2.0020 | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5 |
1118 (1027) | 60 (290) |
| PPor–OMe·PF6 | 2.0035 | 2.0032 | 2.0039 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
837 (763) | 239 (48) |
| AlPor–O–PPor·PF6 | 1.9860 | 2.0163 | 2.0000 | 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.6 −0.6 |
606 (337) | 16 (19) |
Magnetophotoselection. To further characterize the monomer triplet states we have carried out magnetophotoselection experiments. Fig. 5 shows the TREPR spectra of AlPor–OH and PPor–OMe·PF6 with the plane of the laser polarization parallel to the magnetic field (red spectrum) and perpendicular to the field (blue spectrum). For both porphyrins, the relative intensities of the principal features are enhanced or suppressed depending on the polarization of the light. When the polarization of the light is parallel to the field direction, features of the spectrum corresponding to molecules in which the magnetic field direction lies in xy-plane of the ZFS tensor axis system are enhanced and those corresponding to the magnetic field along the z-direction are suppressed. When the polarization is perpendicular to the field, the situation is reversed and features corresponding to molecules with the ZFS z-axis parallel to the field are enhanced while those corresponding to the field in the xy-plane are suppressed. This suggests that the Qx and Qy absorption transition dipole moments are perpendicular to the ZFS z-axis as expected. Careful simulations of the spectra shown in Fig. 5 have been carried out using the parameters given in Table 1 and include the relative orientation of the ZFS axis system and the transition dipoles as variable parameters to determine the orientation of the transition dipole moments. Details of the simulation method are given in the ESI† and in Barbon et al.26 Because the Qx and Qy transitions cannot be excited separately in these porphyrins, it is only possible to determine that the plane defined by the two transitions dipoles is parallel to the XY plane of the ZFS reference frame for both AlPor–OH and PPor–OMe·PF6, in excellent agreement with the orientation of the transition dipole moments (Fig. S1, ESI†) and ZFS axes (Fig S8, ESI†) given by the CASSCF calculations.
Isotropic TREPR spectra. The experimental and simulated X-band TREPR spectra of AlPor–O–PPor·PF6 are shown in Fig. 4 and the corresponding Q-band spectra are presented in Fig. 6. As with the monomer spectra the weighted sum (I‖ + 2I⊥) has been taken to remove any photoselection effect. The parameters used in the simulations are given in Table 1. As is apparent when comparing Fig. 4 and 6, the shapes of the spectra are slightly different at X- and Q-band. The main difference is that the Q-band spectrum is asymmetric, with the high field half of the spectrum being wider than the low field half. This is indicative of g-anisotropy, with a large value of gyy as can be seen in the parameters obtained from the fit (Table 1). The sign of D cannot be determined from the simulations since identical spectra can be obtained with either sign of D using complementary population distributions. The simulations shown in Fig. 4 and 6 correspond to either a positive value of D and population primarily in the Tz zero-field level or a negative value of D and population in Tx and Ty. Because the CASSCF calculations show that D is positive, the simulations shown in Fig. 6 have been performed with D > 0 as indicated in Table 1.
 | ||
Fig. 6 Experimental and simulated Q-band transient EPR spectra of AlPor–O–PPor·PF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeTHF 1 MeTHF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 at 80 K and ∼1 μs ns after the laser flash (lex = 547 nm). CH2Cl2 at 80 K and ∼1 μs ns after the laser flash (lex = 547 nm). | ||
With the assumption of a positive value of D, the difference in the sign of the spin polarization in the dimer compared to the monomers is due to a difference in the spin selectivity of the intersystem crossing. In the dimer the population parameters follow the order pz > (px, py) while in the monomers (px, py) > pz. It is important to note that an appreciable spin–orbit coupling contribution to the ZFS is not expected for these porphyrins because they contain only light main group elements. In contrast to transition metal macrocycles in which mixing of the metal d-orbitals with the π-orbitals of porphyrin ring influences the value of D and the spin selectivity of the intersystem crossing,47 the central elements of the porphyrins here do not have filled d-orbitals and do not participate significantly in the active space molecular orbitals. Possible reasons for the different spin selectivity in the dimer will be discussed in the Conclusions section.
Solvent dependence. As discussed above, the CASSCF-NEVPT2 calculations show that the six of the eight excited states associated with the Q-band absorptions of AlPor–O–PPor·PF6 have CT character. Previous studies showed that the intensity of the bands on the red edge of the absorption spectrum is solvent dependent and is stronger in polar solvents.16 The fluorescence also displayed marked solvatochromism and the Stokes shift was found to be linearly dependent on the solvent polarity function in a Lippert–Mataga plot48 as expected for CT fluorescence. However, the CASSCF-NEVPT2 calculations show that the two next highest singlet states do not have CT character. Because the singlet–triplet energy gap depends on the distribution of the electrons, the ordering of the excited states is not necessarily the same in the triplet and singlet manifolds. Thus, it is unclear how large the CT character of the lowest triplet state is. Since the dipole–dipole part of the ZFS is also dependent on the spatial distribution of the two unpaired electrons, the TREPR spectrum of the triplet state reflects its CT character and becomes narrower as the CT character increases. Fig. 7 shows TREPR spectra of AlPor–O–PPor·PF6 in several solvents of differing polarity. Solvent mixtures were used to obtain a good glass at 80 K and because of the low solubility of the dimer in toluene. As is immediately apparent in Fig. 7, the width of the TREPR spectrum is solvent dependent and is largest in the lowest polarity solvent (6
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene
1 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2) and narrowest in the highest polarity solvent (9
CH2Cl2) and narrowest in the highest polarity solvent (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol). Corresponding spectra of the monomers, presented in Fig. S5 (ESI†), do not show any significant solvent dependence. Thus, the differences in the TREPR spectra of the triplet state of the dimer in different solvents are not due to specific solvent–solute interactions such as coordination of the solvent to the Al centre but are due to changes in the distribution of the unpaired electrons of the triplet state.
glycerol). Corresponding spectra of the monomers, presented in Fig. S5 (ESI†), do not show any significant solvent dependence. Thus, the differences in the TREPR spectra of the triplet state of the dimer in different solvents are not due to specific solvent–solute interactions such as coordination of the solvent to the Al centre but are due to changes in the distribution of the unpaired electrons of the triplet state.
 | ||
| Fig. 7 Solvent dependence of the isotropic X-band transient EPR spectrum of AlPor–O–PPor·PF6 at 80 K. The spectra were extracted from the full field/time dataset at ∼1 μs after the laser flash. | ||
Magnetophotoselection. Fig. 8 presents magnetophoto-selection TREPR spectra of AlPor–O–PPor·PF6 in three different solvents. As can be seen, features at the outer edges of the TREPR spectrum, which correspond to molecules with the ZFS z-axis parallel to the field, are enhanced when the polarization of the light is perpendicular to the magnetic field for all the solvents considered. From this, we can assess that the ZFS z-axis is roughly perpendicular to the transition dipole moment and does not depend on the solvent polarity. In agreement with this assessment, the CASSCF-NEVPT2 calculations predict that the z-axis of the ZFS tensor (Fig. S8, ESI†) is parallel to the Al–O–P bond in AlPor–O–PPor·PF6 and perpendicular to the transition dipoles shown in Fig. 2. The simulations of the spectra in Fig. 8 (dashed curves) provide quantitative values for the ZFS parameters, population rates and relative orientation of the ZFS axes and transition dipole moments. These values are summarized in Table 2. In each solvent the ZFS parameters do not depend much on the excitation wavelength indicating that the complex relaxes to the same (lowest) triplet state. The decrease in the value of |D| as the solvent polarity increases suggests that the triplet state wavefunction can be expressed as sum of at least two contributions with mixing coefficients dependent on the solvent polarity. With the wavefunction approximated as such a sum of contributions, the ZFS parameter D is given by:49–51
| D = c1D1 + c2D2 + ⋯ | (1) |
 | ||
Fig. 8 Magnetophotoselection transient X-band EPR spectra of AlPor–O–PPor·PF6 at 80 K in three different solvents. (a) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene 1 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 (b) 3 CH2Cl2 (b) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeTHF 1 MeTHF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 (c) 9 CH2Cl2 (c) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol 1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol. The red spectra were measured with the electric field E of the laser parallel to the magnetic field B. The blue spectra were taken with E perpendicular to B. The spectra were extracted from the full field/time dataset at ∼1 μs after the laser flash. (λex = 540 nm). The dashed spectra are simulations using the parameters given in Table 2. glycerol. The red spectra were measured with the electric field E of the laser parallel to the magnetic field B. The blue spectra were taken with E perpendicular to B. The spectra were extracted from the full field/time dataset at ∼1 μs after the laser flash. (λex = 540 nm). The dashed spectra are simulations using the parameters given in Table 2. | ||
| Solvent | λ ex (nm) | D (MHz) | E (MHz) | (px − py)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (py − pz) (py − pz) |
ω | ϕ |
|---|---|---|---|---|---|---|
Toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 3 CH2Cl2 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
539 | 657 | 44 | 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.6 −0.6 |
85° | 52° |
MeTHF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 3 CH2Cl2 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
477 | 606 | 16 | 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.6 −0.6 |
85° | 38° |
| 541 | 606 | 16 | 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.6 −0.6 |
87° | 42° | |
| 580 | 606 | 16 | 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.6 −0.6 |
90° | 48° | |
Methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol 9 glycerol 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
540 | 570 | 104 | 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.8 −0.8 |
90° | 42° |
| 575 | 570 | 104 | 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.8 −0.8 |
93° | 42° | |
| 615 | 570 | 104 | 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.8 −0.8 |
92° | 48° |
The orientation of the transition dipoles relative to the ZFS axes is described by the polar and azimuthal angles ω and ϕ. In the case of axial symmetry, the ZFS parameter E becomes zero and the orientation of the transition dipole is determined only by the angle ω because the x- and y-axes of the ZFS tensor are indistinguishable and hence the angle ϕ is undefined. In 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene
1 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 and 3
CH2Cl2 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeTHF
1 MeTHF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 the value of E is small (see Table 2) and hence, the orientation of the transition dipole in the xy plane is not well defined. The considerably larger value of E in 9
CH2Cl2 the value of E is small (see Table 2) and hence, the orientation of the transition dipole in the xy plane is not well defined. The considerably larger value of E in 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol may be due to coordination of the solvent to the Al center which is a good Lewis acid. In all solvents, the value of ω is close to 90°, meaning that the ZFS z-axis is roughly perpendicular to the transition dipole moment as predicted by the quantum chemical calculations. The values of the azimuthal angle ϕ are all close to 45°, in agreement with a quasi-axial symmetry of the molecule and excitation in both in-plane directions. This result is also in agreement with the presence of multiple transitions with similar energies and transition dipole moments distributed in the xy plane as predicted by quantum chemical calculations (Fig. 2). In this situation, it become difficult to distinguish the different in-plane directions and the value of ϕ represents an average of the different in-plane directions.
glycerol may be due to coordination of the solvent to the Al center which is a good Lewis acid. In all solvents, the value of ω is close to 90°, meaning that the ZFS z-axis is roughly perpendicular to the transition dipole moment as predicted by the quantum chemical calculations. The values of the azimuthal angle ϕ are all close to 45°, in agreement with a quasi-axial symmetry of the molecule and excitation in both in-plane directions. This result is also in agreement with the presence of multiple transitions with similar energies and transition dipole moments distributed in the xy plane as predicted by quantum chemical calculations (Fig. 2). In this situation, it become difficult to distinguish the different in-plane directions and the value of ϕ represents an average of the different in-plane directions.
4. Conclusions
The solvent dependence of the magnetic parameters obtained from the magnetophotoselection data combined with the quantum chemical calculations provides key information about the nature of the lowest excited states. The data clearly indicate that both the lowest excited singlet state as well as the lowest triplet state of the dimer have CT character. However, an important question is what fraction of the charge is actually transferred. This is difficult to answer quantitatively, but the iso value of 0.001 used for the plots of the density differences of the lowest excited singlet state (Fig. 3) is an order of magnitude less than is typically used for plotting molecular orbitals, which suggests that its CT character is relatively small. For the triplet state, the density difference is difficult to calculate, because the geometries of the singlet ground state and lowest triplet state differ slightly. However, if the triplet state density is calculated using the ground state geometry, the density difference surface shows CT character (Fig. S9, ESI†) but an even smaller iso value is required for the plot. The modest degree of CT character is also borne out by the fact that the value of D is only about 25% smaller in the dimer than in the PPor–OMe·PF6 monomer and remains positive. In a true radical pair triplet state, in which the two unpaired electrons are localized on different molecules, the ZFS is dominated by the dipole–dipole interaction and the D-value becomes negative. Thus, the positive D-value obtained in the CASSCF calculation, and the observed solvent dependence of D, suggest that the electrons are delocalized over both porphyrins but with some CT character. In agreement with this, the CASSCF computations predict that the spin density of the triplet state (Fig. S10, ESI†) is delocalized over both porphyrins.The magnetophotoselection experiments also point in the same direction, showing that the optical absorption transition dipole moments are perpendicular to the ZFS tensor z-axis, which lies along the Al–O–P bond axis. In the presence of a large CT contribution, the transition dipole moment and ZFS z-axis would be expected to be parallel and lie in the direction of the charge transfer. However, it is important to note that the TREPR experiments are carried out in frozen solution and that the solvent dependent CT character of the triplet state is likely larger in liquid solution. Indeed, the strong solvent dependence of the room temperature fluorescence suggests that the charge transfer is more strongly stabilized when the solvent molecules can re-orient.16
The spin polarization also provides insight into the pathway by which the triplet state is populated. The population parameters obtained from the simulations of the spectra show that the triplet state is formed by spin–orbit coupling mediated intersystem crossing and not by S–T0 mixing in the CT state. Rationalizing the difference in the ISC spin selectivity in the dimer compared to the monomers is complicated because of the large number of low-lying states in the dimer. For the monomers, there are two orbital states involved in the ISC and preferential population of the Tx and Ty sublevels occurs because it compensates for the change in the orbital angular momentum in the xy plane that occurs during the transition between the two orbital states. For the dimer, there are eight low-lying excited triplet states, and it is unclear which spin–orbit coupling matrix elements are most important for the ISC. However, it is known that in strongly coupled donor–acceptor complexes ISC between CT singlet states and localized triplet states can be accompanied by a change in orbital angular momentum. This change means that spin–orbit coupling is required for triplet recombination of the CT state to occur and thus, it is known as the spin–orbit charge-transfer intersystem crossing mechanism (SOCT-ISC).53–57 It occurs primarily in systems in which donor and acceptor are orthogonal to one another55 but has also been observed in cofacial stacked donor–acceptor systems.53 A comparison of the density difference plots of the lowest excited singlet (Fig. 1) and triplet (Fig. S9, ESI†) states shows that the triplet has lower CT character. Based on this difference, we speculate that the orbital motion in the triplet state is more confined to the xy plane than in the singlet state and as a result the ISC causes a change in the z-component of the orbital angular momentum. Thus, the triplet state would have to be formed with spin angular momentum in the z-direction to compensate for the change in the orbital angular momentum and the Tz level in the dimer would be preferentially populated as observed.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Grant-in-Aid (GIA No. 380228 to PPK) from the University of Minnesota Duluth and by an NSERC Discovery Grant (2015-04021) to AvdE. This work was made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: http://www.sharcnet.ca) and Compute/Calcul Canada. Financial support to MDV and AB (Biomolecular DSSCs Project from Interdepartmental Center Giorgio Levi Cases for Energy Economics and Technology) is gratefully acknowledged.Notes and references
- D. A. Bryant, C. N. Hunter and M. J. Warren, Biosynthesis of the modified tetrapyrroles-the pigments of life, J. Biol. Chem., 2020, 295, 6888–6925 CrossRef CAS PubMed.
- L.-L. Li and E. W.-G. Diau, Porphyrin-sensitized solar cells, Chem. Soc. Rev., 2013, 42, 291–304 RSC.
- H. A. Maddah, V. Berry and S. K. Behura, Biomolecular photosensitizers for dye-sensitized solar cells: recent developments and critical insights, Renewable Sustainable Energy Rev., 2020, 121, 109678 CrossRef CAS.
- H. He, Near-infrared emitting lanthanide complexes of porphyrin and BODIPY dyes, Coord. Chem. Rev., 2014, 273, 87–99 CrossRef.
- J. Rawson, P. J. Angiolillo, P. R. Frail, I. Goodenough and M. J. Therien, Electron spin relaxation of hole and electron polarons in π-conjugated porphyrin arrays: spintronic implications, J. Phys. Chem. B, 2015, 119, 7681–7689 CrossRef CAS PubMed.
- J. Zeng and K.-Q. Chen, A nearly perfect spin filter and a spin logic gate based on a porphyrin/graphene hybrid material, Phys. Chem. Chem. Phys., 2018, 20, 3997–4004 RSC.
- S. Fukuzumi, Y.-M. Lee and W. Nam, Mimicry and functions of photosynthetic reaction centers, Biochem. Soc. Trans., 2018, 46, 1279–1288 CrossRef CAS PubMed.
- S. Fukuzumi, K. Ohkubo and T. Suenobu, Long-Lived Charge Separation and Applications in Artificial Photosynthesis, Acc. Chem. Res., 2014, 47, 1455–1464 CrossRef CAS PubMed.
- J. Barber and P. D. Tran, From natural to artificial photosynthesis, J. R. Soc., Interface, 2013, 10, 20120984 CrossRef PubMed.
- A. C. Benniston and A. Harriman, Artificial photosynthesis, Mater. Today, 2008, 11, 26–34 CrossRef CAS.
- S. Berardi, S. Drouet, L. Francàs, C. Gimbert-Suriñach, M. Guttentag, C. Richmond, T. Stoll and A. Llobet, Molecular artificial photosynthesis, Chem. Soc. Rev., 2014, 43, 7501–7519 RSC.
- S. Fukuzumi, Y.-M. Lee and W. Nam, Bioinspired artificial photosynthesis systems, Tetrahedron, 2020, 76, 131024 CrossRef CAS.
- G. S. Orf and R. E. Blankenship, Chlorosome antenna complexes from green photosynthetic bacteria, Photosynth. Res., 2013, 116, 315–331 CrossRef CAS PubMed.
- R. E. Blankenship, M. T. Madigan and C. E. Bauer, ed., Anoxygenic Photosynthetic Bacteria, Springer, Netherlands, Dordrecht, 1995, vol. 2 Search PubMed.
- P. Mondal and S. P. Rath, Cyclic metalloporphyrin dimers: conformational flexibility, applications and future prospects, Coord. Chem. Rev., 2020, 405, 213117 CrossRef CAS.
- N. Zarrabi, B. J. Bayard, S. Seetharaman, N. Holzer, P. Karr, S. Ciuti, A. Barbon, M. Di Valentin, A. van der Est and F. D’Souza, et al., A charge transfer state induced by strong exciton coupling in a cofacial μ-oxo-bridged porphyrin heterodimer, Phys. Chem. Chem. Phys., 2021, 23, 960–970 RSC.
- G. Yamamoto, R. Nadano, W. Satoh, Y. Yamamoto and K. Akiba, Synthesis of μ-oxo-bridged group 15 element–aluminium heterodinuclear porphyrins [(oep)(Me) M–O–Al (oep)] ClO4 (M= P, As, Sb) and X-ray crystal structure of [(oep)(Me) As–O–Al (oep)] ClO4, Chem. Commun., 1997, 1325–1326 RSC.
- C. Schissler, E. K. Schneider, B. Felker, P. Weis, M. Nieger, M. M. Kappes and S. Bräse, A synthetic strategy for cofacial porphyrin-based homo- and heterobimetallic complexes, Chem. – Eur. J., 2021, 27, 3047–3054 CrossRef CAS PubMed.
- J.-M. Barbe, C. Stern, E. Pacholska, E. Espinosa and R. Guilard, Improved routes for the synthesis of face-to-face bismacrocycles in porphyrin and corrole series, J. Porphyr. Phthalocyan., 2004, 8, 301–312 CrossRef CAS.
- A. Langlois, J.-M. Camus, P.-L. Karsenti, R. Guilard and P. D. Harvey, Metal dependence on the bidirectionality and reversibility of the singlet energy transfer in artificial special pair-containing dyads, Inorg. Chem., 2017, 56, 2506–2517 CrossRef CAS PubMed.
- P. D. Harvey, C. Stern, C. P. Gros and R. Guilard, The photophysics and photochemistry of cofacial free base and metallated bisporphyrins held together by covalent architectures, Coord. Chem. Rev., 2007, 251, 401–428 CrossRef CAS.
- C. O. Obondi, G. N. Lim, B. Churchill, P. K. Poddutoori, A. van der Est and F. D’Souza, Modulating the generation of long-lived charge separated states exclusively from the triplet excited states in palladium porphyrin–fullerene conjugates, Nanoscale, 2016, 8, 8333–8344 RSC.
- D. R. Subedi, H. B. Gobeze, Y. E. Kandrashkin, P. K. Poddutoori, A. van der Est and F. D’Souza, Exclusive triplet electron transfer leading to long-lived radical ion-pair formation in an electron rich platinum porphyrin covalently linked to fullerene dyad, Chem. Commun., 2020, 56, 6058–6061 RSC.
- P. K. Poddutoori, Y. E. Kandrashkin, C. O. Obondi, F. D’Souza and A. van der Est, Triplet electron transfer and spin polarization in a palladium porphyrin–fullerene conjugate, Phys. Chem. Chem. Phys., 2018, 20, 28223–28231 RSC.
- A. J. Redman, G. Moise, S. Richert, E. J. Peterson, W. K. Myers, M. J. Therien and C. R. Timmel, EPR of Photoexcited Triplet-State Acceptor Porphyrins, J. Phys. Chem. C, 2021, 125, 11782–11790 CrossRef CAS PubMed.
- A. Barbon, M. G. Dal Farra, S. Ciuti, M. Albertini, L. Bolzonello, L. Orian and M. Di Valentin, Comprehensive investigation of the triplet state electronic structure of free-base 5,10,15,20-tetrakis(4-sulfonatophenyl) porphyrin by a combined advanced EPR and theoretical approach, J. Chem. Phys., 2020, 152, 034201 CrossRef CAS PubMed.
- S. Ciuti, A. Barbon, M. Bortolus, A. Agostini, E. Bergantino, C. Martin, M. Di Valentin and D. Carbonera, Neuroglobin provides a convenient scaffold to investigate the triplet-state properties of porphyrins by time-resolved EPR spectroscopy and magnetophotoselection, Appl. Magn. Reson., 2022, 53, 1031–1042 CrossRef CAS.
- S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 17 CAS.
- R. Guilard, A. Zrineh, A. Tabard, A. Endo, B. C. Han, C. Lecomte, M. Souhassou, A. Habbou, M. Ferhat and K. M. Kadish, Synthesis and spectroscopic and electrochemical characterization of ionic and σ-bonded aluminum(III) porphyrins. Crystal structure of methyl (2,3,7,8,12,13,17,18-octaethylporphinato)aluminum(III), (OEP)Al(CH3), Inorg. Chem., 1990, 29, 4476–4482 CrossRef CAS.
- Y. Yamamoto, R. Nadano, M. Itagaki and K. Akiba, Synthesis and structure of phosphorus(V) octaethylporphyrins that contain a σ-bonded element–carbon bond: Characterization of a porphyrin bearing an R–P
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and relation of the ruffling of the porphyrin core with the electronegativity of the axial ligands, J. Am. Chem. Soc., 1995, 117, 8287–8288 CrossRef CAS.
O bond and relation of the ruffling of the porphyrin core with the electronegativity of the axial ligands, J. Am. Chem. Soc., 1995, 117, 8287–8288 CrossRef CAS. - A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, 6-31G* basis set for atoms K through Zn, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, 6-31G* basis set for third-row atoms, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS.
- R. A. Kendall and H. A. Früchtl, The impact of the resolution of the identity approximate integral method on modern ab initio algorithm development, Theor. Chem. Acc., 1997, 97, 158–163 Search PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- C. E. Tait, P. Neuhaus, H. L. Anderson and C. R. Timmel, Triplet state delocalization in a conjugated porphyrin dimer probed by transient electron paramagnetic resonance techniques, J. Am. Chem. Soc., 2015, 137, 6670–6679 CrossRef CAS PubMed.
- L. Bolzonello, M. Albertini, E. Collini and M. Di, Valentin, Delocalized triplet state in porphyrin J-aggregates revealed by EPR spectroscopy, Phys. Chem. Chem. Phys., 2017, 19, 27173–27177 RSC.
- M. Gouterman, in The Porphyrins, ed. D. Dolphin, Academic Press, 1978, pp. 1–165 Search PubMed.
- M. Tanabe, H. Matsuoka, Y. Ohba, S. Yamauchi, K. Sugisaki, K. Toyota, K. Sato, T. Takui, I. Goldberg and I. Saltsman, Time-resolved electron paramagnetic resonance and phosphorescence studies of the lowest excited triplet states of Rh(III) corrole complexes, J. Phys. Chem. A, 2012, 116, 9662–9673 CrossRef CAS PubMed.
- E. Lippert, Dipolmoment und Elektronenstruktur von angeregten Molekülen, Z. Für Naturforschung Phys. Sci., 1955, 10, 541–545 CrossRef.
- T. Kamei, M. Terazima, S. Yamauchi and N. Hirota, Temperature and solvent dependences of the zero-field splittings and character of the triplet states of methylpyrazines, J. Phys. Chem., 1994, 98, 7963–7966 CrossRef CAS.
- N. Hirota and S. Yamauchi, Short-lived excited triplet states studied by time-resolved EPR spectroscopy, J. Photochem. Photobiol., C, 2003, 4, 109–124 CrossRef CAS.
- J. R. Norris, D. E. Budil, P. Gast, C. H. Chang, O. El-Kabbani and M. Schiffer, Correlation of paramagnetic states and molecular structure in bacterial photosynthetic reaction centers: the symmetry of the primary electron donor in Rhodopseudomonas viridis and Rhodobacter sphaeroides R-26, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 4335–4339 CrossRef CAS PubMed.
- M. Chen, J. Y. Shin, R. M. Young and M. R. Wasielewski, Tuning the charge transfer character of the multiexciton state in singlet fission, J. Chem. Phys., 2020, 153, 094302 CrossRef CAS PubMed.
- M. L. Williams, I. Schlesinger, R. M. Jacobberger and M. R. Wasielewski, Mechanism of ultrafast triplet exciton formation in single cocrystals of π-stacked electron donors and acceptors, J. Am. Chem. Soc, 2022, 144, 18607–18618 CrossRef CAS PubMed.
- F. Ema, M. Tanabe, S. Saito, T. Yoneda, K. Sugisaki, T. Tachikawa, S. Akimoto, S. Yamauchi, K. Sato and A. Osuka, Charge-transfer character drives Möbius antiaromaticity in the excited triplet state of twisted [28] hexaphyrin, J. Phys. Chem. Lett., 2018, 9, 2685–2690 CrossRef CAS PubMed.
- Z. E. Dance, S. M. Mickley, T. M. Wilson, A. B. Ricks, A. M. Scott, M. A. Ratner and M. R. Wasielewski, Intersystem crossing mediated by photoinduced intramolecular charge transfer: julolidine- anthracene molecules with perpendicular π systems, J. Phys. Chem. A, 2008, 112, 4194–4201 CrossRef CAS PubMed.
- H. Imahori, Y. Kobori and H. Kaji, Manipulation of charge-transfer states by molecular design: perspective from “Dynamic Exciton,”, Acc. Mater. Res., 2021, 2, 501–514 CrossRef CAS.
- H. Cao, I. Kurganskii, J. Pang, R. Duan, J. Zhao, M. Fedin, M.-D. Li and C. Li, Charge transfer, intersystem crossing, and electron spin dynamics in a compact perylenemonoimide-phenoxazine electron donor–acceptor dyad, J. Phys. Chem. B, 2021, 125, 12859–12875 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04291f |
| This journal is © the Owner Societies 2022 |