Osmolyte effect on enzymatic stability and reaction equilibrium of formate dehydrogenase†
Received
29th August 2022
, Accepted 3rd November 2022
First published on 3rd November 2022
Abstract
Osmolytes are well-known biocatalyst stabilisers as they promote the folded state of proteins, and a stabilised biocatalyst might also improve reaction kinetics. In this work, the influence of four osmolytes (betaine, glycerol, trehalose, and trimethylamine N-oxide) on the activity and stability of Candida bondinii formate dehydrogenase cbFDH was studied experimentally and theoretically. Scanning differential fluorimetric studies were performed to assess the thermal stability of cbFDH, while UV detection was used to reveal changes in cbFDH activity and reaction equilibrium at osmolyte concentrations between 0.25 and 1 mol kg−1. The thermodynamic model ePC-SAFT advanced allowed predicting the effects of osmolyte on the reaction equilibrium by accounting for interactions involving osmolyte, products, substrates, and water. The results show that osmolytes at low concentrations were beneficial for both, thermal stability and cbFDH activity, while keeping the equilibrium yield at high level. Molecular dynamics simulations were used to describe the solvation around the cbFDH surface and the volume exclusion effect, proofing the beneficial effect of the osmolytes on cbFDH activity, especially at low concentrations of trimethylamine N-oxide and betaine. Different mechanisms of stabilisation (dependent on the osmolyte) show the importance of studying solvent–protein dynamics towards the design of optimised biocatalytic processes.
Introduction
Biocatalysts (e.g., enzymes) have recently attracted attention for bringing biochemical reactions to industrial scale.1 The nature of enzymes generates highly favourable reaction conditions such as high specificity, high turnover numbers, biodegradability, and production from commodity chemicals to advanced pharmaceutical intermediates.2 However, some drawbacks must be addressed concerning the complex molecular structures of the enzymes. In that sense, different strategies have been used to increase the stability of enzymes in high-scale processes, such as chemical modifications, immobilization, mutagenesis, and the addition of chemicals, known as co-solutes or co-solvents.3
Although by far not all enzymes have the potential for industrial use, lipases, hydrolases, and oxidoreductases have shown promising results.4 Within the families of oxidoreductases, Candida boidinii formate dehydrogenase (cbFDH) is of interest since both reaction directions (NADH production vs. CO2 fixation) have industrial potential due to the low cost of the formate salts used as a substrate, the high price of the NADH product, and the ability to regenerate CO2.5,6cbFDH catalyses the oxidation of the formate ion to CO2 using the nicotinamide adenine nucleotide co-factors.6 The most significant shortcoming observed in the reactions of cbFHD is moderate thermal stability and low activity.7 High thermal stability of enzymes is a desired property in biotechnological processes since it enables the use of the enzyme at high temperatures.8 Process conditions such as pH, ionic strength, and the presence of co-solvent might affect the thermal stability of an enzyme.2 Even though there are kinetic studies on the cbFDH reactions, research on stability and reaction equilibrium is still scarce in the literature, especially in the presence of co-solvent.
In extreme conditions of temperature, pH, salinity, internal stress, and denaturants, the native conformation of an enzyme is usually stabilized in nature by means of osmolytes.9,10 Among osmolytes, common natural compounds are found, such as methylamines (betaine, sarcosine, trimethylamine n-oxide (TMAO)), polyalcohols (glycerol, sorbitol, xylitol), sugars (sucrose, glucose, fructose), and amino acids (alanine, proline, valine).11 Some studies on the osmolyte effect on different enzymes can be found in the literature: low concentrations of TMAO increased the stability of several enzymes.12–15 Previous studies on cbFDH have shown the impact of buffer and pH,16 expression in different bacteria,17 mutagenesis6 and cross-linked immobilization18 on enzyme stability. Further, notable increases in the denaturation temperature of enzymes have been reported upon osmolyte addition, i.e. sorbitol for RNase-A and hexokinase,19 glucose for RNase-A14, trehalose for lysosomes,20 and dimethylglycine for lactate dehydrogenase.21 Besides these observations, osmolytes also influence the kinetics and thermodynamics of enzyme-catalysed reactions.22–24
The multifaceted influence of osmolytes on the properties of enzymes and on the according thermodynamic and kinetic behaviours causes a huge experimental effort. Thus, predictive methods are desired to support developing bioprocesses by substantially reducing the number of trial and error experiments.25 From a theoretical perspective, equations of state and molecular simulations have been developed with a basis of realistic molecular models. Such tools are nowadays readily usable as predictive tools for process design.26 Perturbed-Chain Statistical Associating Fluid Theory (PC-SAFT) and its variations27–31 have been proven capable of predicting the physicochemical properties of different compounds and mixtures.32,33 PC-SAFT calculations have been successfully made in systems of varying complexity, such as amino acids,34 aromatics,35 electrolytes,29 proteins,36 reactive systems,37 and deep eutectic solvents.38 Molecular Dynamics (MD) has arisen as a reliable method to explore solvation of complex solutions.39–41 MD allows quantifying the solvent accumulation (or depletion) on the protein surface.41 The radial distribution functions (RDFs) are frequently used, but the interpretation is challenging, as preferential layers might not be detected correctly. Thus, researchers developed alternatives for the RDF to reduce the protein shape complexity42,43 by using the minimum-distance distribution function (MDDF). MDDF describes the structure of solutions based on the distance between the surfaces of the solute (e.g., enzyme) and the solvent (e.g., water) instead of the distance between each center of mass.44 In complement, the Kirkwood–Buff Integrals (KBI) profiles computed from MDDF reflect the excluded volume associated with the solute and solvent molecules at short distances.45
The main focus of this work is to study the osmolyte effects (kind of osmolyte and its concentration) on thermal stability and conformational stability of cbFDH, as well as the osmolyte effects on enzymatic activity, kinetics and thermodynamics of the cbFDH reaction. The osmolytes under consideration were betaine, TMAO, glycerol, and trehalose at molalities of 0.25, 0.5, and 1 mol kg−1. All investigations were done at 25 °C and 1 bar in a pH 8.5 Tris buffer. The experimental results were supported by a thermodynamic activity-based framework that predicts the effect of osmolytes on the reaction equilibrium using ePC-SAFT advanced28,29 as the equation of state. MD simulations were used to calculate MDDF and KBI profiles to explain the enzyme-solvent interactions in the solvation layer even at higher molalities than studied experimentally.
Materials and methods
Materials
Lyophilized powder of cbFDH (EC 1.17.1.9) was purified via dialysis to remove additives prior to all measurements. The other substances used in this work were used as obtained without further purification. Millipore water was used for the preparation of all aqueous buffer solutions. Solutions were prepared gravimetrically using a Sartorius CPA324S balance (Sartorius, Göttingen, Germany). All the chemicals used in this work are listed in Table 1. The pH value of the samples was measured with the pH meter GMH 3531 (GHM Messtechnik GmbH, Regenstauf, Germany). Molality given in this manuscript refers to moles of substance per kg of pure water. All the experiments in this work were performed in an aqueous 0.1 M Tris-buffer stock solution at pH 8.5. This pH ensures phase homogeneity as CO2 completely dissociates into bicarbonate at pH 8.5, as shown in Fig. S1 (ESI†).
cbFDH enzymatic activity in aqueous osmolytes solutions
As NADH is known to be unstable, the following conditions were chosen to avoid degradation along the reaction coordinate. Substrate molalities were fixed as 100 mmol kg−1 sodium formate and 0.1 mmol kg−1 NAD+. Both substrates were weighed gravimetrically in solutions of pure buffer or in osmolyte solutions with osmolyte molalities between 0.25 mol kg−1 and 1 mol kg−1. Enzyme stock solutions were prepared gravimetrically, with a final cbFDH concentration of 5 μmol kg−1, and stored in ice during the experiments. The reaction was followed using extinction measurements over time at 340 nm wavelength (extinction maxima of NADH) with an Eppendorf BioPhotometer® D30 (Eppendorf, Germany). The mixture concentrations used in this work are detailed in Table S1 (ESI†).
Table 1 Specifications of chemicals used in this work as molar mass (M), CAS number, supplier, and purity
| Chemical |
M/g mol−1 |
CAS |
Supplier |
Purity/wt% |
|
cbFDH |
40.000 |
9028-85-7 |
Roche GmbH |
— |
| Sodium formate |
68.007 |
141-53-7 |
VWR Chemicals |
>99.0 |
| NAD+ |
663.430 |
53-84-9 |
Sigma-Aldrich |
>96.5 |
| NADH |
665.441 |
58-68-4 |
Sigma Aldrich |
>97.0 |
| Betaine |
117.159 |
107-43-7 |
Sigma-Aldrich |
>99.0 |
| TMAO dihydrate |
75.11 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637-93-8 637-93-8 |
TCI |
>98.0 |
| Glycerol |
92.094 |
56-81-5 |
VWR Chemicals |
>99.5 |
| Trehalose dihydrate |
378.330 |
6138-23-4 |
Sigma-Aldrich |
>99.0 |
| Trizma base |
121.14 |
77-86-1 |
Sigma-Aldrich |
>99.9 |
| Trizma HCl |
157.60 |
1185-53-1 |
Sigma-Aldrich |
>99.0 |
cbFDH thermal stability in aqueous osmolytes solutions
Thermal stability assays were carried out using Prometheus NT.48 nanoDSF (NanoTemper, Germany) to determine the unfolding temperature of the cbFDH in pure buffer and under the influence of the different osmolytes at molalities of 0.25, 0.5, and 1 mol kg−1. For each sample, 10 μL of the solution was introduced in the capillary for high-throughput measurements. The heating rate was set to 0.7 K min−1 from 20 °C to 80 °C. The enzyme molality was 5 μmol kg−1, and the pH of the solutions was adjusted to 8.5. The software PR. ThermControl, version 2.1.2 was used to collect and process the data. All measurements were performed as triplets and are detailed in Table S2 (ESI†).
cbFDH reaction equilibrium measurements in aqueous osmolytes solutions
In order to study the equilibrium reaction, the same stock solutions as in the stability tests were used (aqueous TRIS buffer at pH = 8.5 with 100 mmol kg−1 sodium formate and 0.1 mmol kg−1 NAD+). Reactions were performed in pure buffer and in osmolyte solutions at an osmolyte molality of 0.5 mol kg−1. The reaction was carried out at 25 °C with an enzyme concentration of 20 μmol kg−1. The equilibrium concentration of NADH was measured after 30 minutes with Eppendorf BioPhotometer® D30 (Eppendorf, Germany), using a wavelength of 340 nm. This cut-off time was chosen because, as shown in Fig. S2 (ESI†), equilibrium was reached at this time. A summary of the studied systems can be found in Table S3 (ESI†).
Molecular dynamics simulations
The crystal structure of cbFDH complexed with NAD+ and azide was used to construct the initial configuration (PDB protein: 5DN9). Protonation states of all polar amino-acid residues were adjusted to pH 8.5, and the protonation states of the histidine residues were determined to match the hydrogen bonding patterns in the nearest environments according to ref. 46. The simulation systems were created by insertion of the cbFDH in the centre of a rhombic dodecahedron box. Each box was filled with 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules of water and the concentration of the osmolyte was fixed by adding these molecules. Additional sodium ions were used as counter ions to neutralize the protein net charge. The number of solvent molecules in each box is shown in Table S4 (ESI†). According to,44,45 the simulations were started with randomly produced solvent boxes and velocity distributions. This ensures that the cbFDH structure keeps its original conformation and acquires sufficient sampling of the solvent structure by executing a collection of 20 brief simulations (17 ns in total) instead of one large simulation for each system. MD simulations were carried out using GROMACS version 2021.2.47,48 The force field used to describe the cbFDH was OPLS-AA/M49 and the parameters for its ligands were retrieved from LigParGen.50 Water was modelled with TIP4P in all simulations51 For betaine and glycerol, OPLS parameters were retrieved from the validation realized by Monteiro et al.52 Shea force field was used for TMAO53 due to its compatibility with OPLS, and OPLS-AA for carbohydrates was used for trehalose.54 All these force fields are non-polarizable models, where electrostatic and van der Waals interactions are modelled using Coulomb potential and Lennard Jones potential, respectively. The cut-off radius was set to 1.2 nm and periodic boundary conditions were used in all directions. Electrostatic interactions were treated using the Particle-Mesh Ewald technique55 with an interpolation order set to four.
000 molecules of water and the concentration of the osmolyte was fixed by adding these molecules. Additional sodium ions were used as counter ions to neutralize the protein net charge. The number of solvent molecules in each box is shown in Table S4 (ESI†). According to,44,45 the simulations were started with randomly produced solvent boxes and velocity distributions. This ensures that the cbFDH structure keeps its original conformation and acquires sufficient sampling of the solvent structure by executing a collection of 20 brief simulations (17 ns in total) instead of one large simulation for each system. MD simulations were carried out using GROMACS version 2021.2.47,48 The force field used to describe the cbFDH was OPLS-AA/M49 and the parameters for its ligands were retrieved from LigParGen.50 Water was modelled with TIP4P in all simulations51 For betaine and glycerol, OPLS parameters were retrieved from the validation realized by Monteiro et al.52 Shea force field was used for TMAO53 due to its compatibility with OPLS, and OPLS-AA for carbohydrates was used for trehalose.54 All these force fields are non-polarizable models, where electrostatic and van der Waals interactions are modelled using Coulomb potential and Lennard Jones potential, respectively. The cut-off radius was set to 1.2 nm and periodic boundary conditions were used in all directions. Electrostatic interactions were treated using the Particle-Mesh Ewald technique55 with an interpolation order set to four.
The simulations were carried out as follows: (1) molecules were inserted randomly using PACKMOL,56 with the protein in the center of the box; (2) energy minimization using the steepest descent algorithm for 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, with all the heavy atoms (non-hydrogen atoms) of the protein and the ligand fixed; (3) 1 ns of equilibration using the canonical NVT ensemble, while retaining the previous position restrictions; (4) 5 ns of equilibration using the isothermal-isobaric NPT ensemble, while retaining the previous position restrictions; (5) 1 ns of equilibration using the NPT ensemble without positions restraints; (6) 10 ns of production using the NPT ensemble. The temperature of the system was maintained constant at 293 K using a velocity rescaling thermostat,57 with a time constant τT = 0.1 ps. The pressure was held at 1.0 bar using the Berendsen barostat58 for the equilibration step for τP = 2 ps, and Parrinello–Rahman barostat59,60 for the production step for τP = 2 ps. In all runs, equations of motion were integrated using the leapfrog algorithm61 for τT = 2 ps. Twenty independent simulations were performed for each system using the previous protocol. These short molecular simulations allow studying the solvation structures of the native state of the protein without denaturation effects or critical structural change.40 An open-source software “ComplexMixtures.jl”,41 implemented in Julia language62 was used to compute protein–solvent minimum-distance functions and KBI from the simulation results. To demonstrate the stability of the system in the simulation, root-mean-square deviation of atomic positions (RMSD), root-mean-square-fluctuation (RMSF), and radius of gyration (Rg) analysis are provided in ESI† (Fig. S3–S5).
000 steps, with all the heavy atoms (non-hydrogen atoms) of the protein and the ligand fixed; (3) 1 ns of equilibration using the canonical NVT ensemble, while retaining the previous position restrictions; (4) 5 ns of equilibration using the isothermal-isobaric NPT ensemble, while retaining the previous position restrictions; (5) 1 ns of equilibration using the NPT ensemble without positions restraints; (6) 10 ns of production using the NPT ensemble. The temperature of the system was maintained constant at 293 K using a velocity rescaling thermostat,57 with a time constant τT = 0.1 ps. The pressure was held at 1.0 bar using the Berendsen barostat58 for the equilibration step for τP = 2 ps, and Parrinello–Rahman barostat59,60 for the production step for τP = 2 ps. In all runs, equations of motion were integrated using the leapfrog algorithm61 for τT = 2 ps. Twenty independent simulations were performed for each system using the previous protocol. These short molecular simulations allow studying the solvation structures of the native state of the protein without denaturation effects or critical structural change.40 An open-source software “ComplexMixtures.jl”,41 implemented in Julia language62 was used to compute protein–solvent minimum-distance functions and KBI from the simulation results. To demonstrate the stability of the system in the simulation, root-mean-square deviation of atomic positions (RMSD), root-mean-square-fluctuation (RMSF), and radius of gyration (Rg) analysis are provided in ESI† (Fig. S3–S5).
ePC-SAFT advanced
In this work, the equation of state ePC-SAFT advanced28,29 was used to model the thermodynamic equilibrium of the cbFDH reaction. ePC-SAFT advanced represents an extension of the original PC-SAFT to handle electrolyte systems, which is important in this work caused by high concentrations of formate and bicarbonate, both of which were modelled as ionic species. PC-SAFT, which Gross and Sadowski developed in 2001,32 uses the residual Helmholtz energy as an explicit function of temperature, molar volume, and molar fraction of all the components to finally access the thermo-physical properties of a mixture. The residual Helmholtz energy is given as the sum of different contributions, each aiming to describe interactions arising from various physical features of the system components, as shown in eqn (1).| | | ares = aHC + adisp + aassoc + aDH + aBorn | (1) |
The hard-chain contribution aHC describes repulsive forces arising from actual molecules having their volume and form, which generally deviates from a perfect sphere. The dispersion contribution adisp describes isotropic short-range interactions such as weak dipolar or van der Waals forces. The association contribution aassoc describes short-range high-directional interactions, such as hydrogen bonding. The last two contributions describe intermolecular interactions in the presence of charged species in the system. The Debye–Hückel contribution aDH depicts long-range ion-ion electrostatic interactions in a dielectric medium. The modified Born contribution aBorn accounts for ion-dipole electrostatic interactions of the ions with the surrounding medium. Like the original PC-SAFT, ePC-SAFT advanced requires up to five pure-component parameters for each system component. Those are the segment number mi, the segment diameter σi, the dispersion energy ui, and for associating components, the association energy εAiBi and the association volume κAiBi. The parameters between components i and j in the mixture were expressed using the Berthelot–Lorentz combining rules. Furthermore, a binary interaction parameter kij was introduced as a linear function of the temperature according to eqn (2).
| | kij = kij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15K + kijT·(T/K − 298.15) 298.15K + kijT·(T/K − 298.15) | (2) |
Rational activity coefficients of all the species, referring to the infinite dilution in water, were accessed using mole-fraction based fugacity coefficients
φi at the desired composition and
φ∞i at infinite dilution in water according to
eqn (3).
| |  | (3) |
Note,
γ* becomes one at infinite dilution in water. The pure-component parameters of molecular compounds and ionic species were retrieved from the literature and are listed in Table S5 (ESI
†). All the binary interaction parameters used in this work (Table S6, ESI
†) were obtained from the literature and no parameters were fitted in this work.
Results
Effect of osmolytes on cbFDH activity
The effect of different osmolytes (betaine, glycerol, TMAO, and trehalose) on enzyme activity was measured at different osmolyte concentrations at 25 °C and 1 bar at pH 8.5. Enzymatic activity under osmolyte presence was expressed relative to the activity in the neat buffer and is shown in Fig. 1(A). Due to the relatively low concentration of the osmolytes (≤1 mol kg−1) in the studied aqueous solutions, there were no significant changes to the transport properties of the fluid, and therefore mass transfer limitations were not expected. At osmolyte concentrations of 0.25 and 0.5 mol kg−1, all the osmolyte solutions boosted enzyme activity, and TMAO exhibited the best performance by increasing the enzyme activity by 12% at 0.5 mol kg−1 compared to the buffer solution. This is not a surprise since it is known that TMAO interacts with the lysine and arginine residues on the protein surface,63 which preserve the solvation shell of the protein at moderate TMAO concentrations. Further, moderate hydrogen bond formation between the osmolytes and the cbFDH surface might allow higher diffusion of the substrate towards the active centre of cbFDH. However, at high TMAO concentrations, cbFDH-TMAO interactions are known to be strengthened, causing water to be excluded from the cbFDH surface and promoting a decrease in cbFDH enzymatic activity. This was found (cf.Fig. 1(A)) for all osmolytes at molalities greater than 0.5 mol kg−1. It can be observed that the strength of the negative volume exclusion of water on the protein surface that causes lower cbFDH activity relates to the molecular weight of the osmolytes.
 |
| | Fig. 1 Relative activity of cbFDH in different osmolyte aqueous solutions as function of (A) osmolyte concentration and (B) time at 25 °C, 1 bar, and pH = 8.5. TMAO (squares), betaine (circles), glycerol (triangles), and trehalose (stars). The black line represents the neat buffer value. Raw data is available in Table S1 (ESI†). | |
Fig. 1(B) shows the long-term activity of cbFDH upon the addition of 0.5 mol kg−1 of osmolyte over 16 days at 25 °C. Independent of the condition (buffer or co-solvent solution), enzyme activity was increased within the first days, reached a maximum, and then decreased. The behaviours of the buffer solution and of the TMAO solution are very similar. Further, glycerol and trehalose similarly influenced long-term cbFDH activity, showing advantages compared to the pure buffer solution only after day 7. Unlike TMAO, glycerol and trehalose interact strongly with the hydroxyl groups at the cbFDH surface through hydrogen bonding, enriching the first solvation layer of cbFDH. Most interestingly, unlike all other osmolytes, betaine maintained 80% of the activity after 10 days, a 3-fold value compared to the other osmolytes and to neat buffer. This promising result is possibly due to the interaction of betaine's carboxylate group with the surface of cbFDH and the stabilization of a second hydration layer of cbFDH due to the hydrophobic effect promoted by betaine's methyl groups. This lets conclude that keeping high cbFDH activity requires a balance between the stabilization of the first and of the second solvation layer around the cbFDH surface; this is detailed later by means of MD simulation results.
Effect of osmolytes on cbFDH on thermal denaturation
Unfolding temperatures (Tm) of cbFDH were measured to account for the change in thermal stability upon the addition of osmolytes. The Tm data in neat buffer (about 61 °C) agrees with previously reported data for cbFDH.16,36 For all the systems used in this work, Tm increased linearly with the osmolyte molality, as shown in Fig. 2. This indicates that osmolytes accumulation on the cbFDH surface have a protective role against thermal changes in the environment. The main driving force for this increased stability is the excluded volume effect. Excess trehalose on the cbFDH surface due to hydrogen bond interactions acts as a protective agent against temperature changes, reaching ΔTm = 3.2 °C at 1 mol kg−1 trehalose compared to buffer. This effect, known as macromolecular crowding, has been identified as an essential tool for the modulation of thermal stability of enzymes in general. Further increasing the osmolyte concentration above 1 mol kg−1 is not meaningful for enzyme catalysis due to the consequent loss of enzymatic activity (cf.Fig. 1A). This lets conclude that choosing an osmolyte (or a mixture of them) to tune biocatalytic reactions requires a compromise between thermal stability and enzymatic activity. Further investigations in this work showed that osmolytes effect also Tonset, which is defined as the threshold temperature at which denaturation begins. Note that the osmolytes did not cause aggregation of the cbFDH in the range of temperatures and concentrations under study.
 |
| | Fig. 2 Unfolding temperature (Tm) of cbFDH vs. osmolyte molality in aqueous solutions at pH = 8.5 and atmospheric pressure. TMAO (squares), betaine (circles), glycerol (triangles), and trehalose (stars). Black horizontal line represents the neat buffer value. Raw data is available in Table S2 (ESI†). | |
Effect of osmolyte on cbFDH solvation using molecular dynamics
A way to theoretically explain the stabilization of an enzyme induced by osmolytes is to analyse the surface of this enzyme. In this work, solvation analysis was performed using protein–solvent MDDF. These distributions have the advantage over the typical RDFs that they take into account the shape of the molecule. This is very important in the study of an enzyme since enzymes are highly non-spherical molecules.
Then, MDDFs allow a correct interpretation of the distance between the surface of the enzyme (p) and the surface of the solvent molecules (j). MDDF gmdpj was calculated as in eqn (4),41
| |  | (4) |
where
npj is the atoms-average number density of a solvent
j at a minimum distance from any protein p atoms, and

represents the same distribution but in the absence of protein p–solvent
j interactions, which was realized using a “phantom” protein that does not interact with the solvent. The calculations were made using the protein (p) as solute and water (w) + osmolyte (c) as the solvent.
Fig. 3(A) shows the distribution of minimum distances between cbFDH-osmolyte. It can be seen that there are two distinct peaks, which are two distances at which the osmolytes are deposited around the protein: 1.8 Å and 2.7 Å. The distinct peak at 1.8 Å indicates a hydrogen bond formation between cbFDH and the osmolytes. At this distance, the molecule density of both trehalose and glycerol is greater than that of betaine and TMAO, suggesting that the hydroxyl groups of trehalose and glycerol are mainly oriented toward the cbFDH surface to form hydrogen bonds. Betaine and TMAO are found primarily in a second solvation shell around 2.7 Å, which might be explained by the fact that their oxygen groups contribute much less to the hydrogen bonding zone compared to the OH groups of trehalose and glycerol.
 |
| | Fig. 3 Minimum-distance distribution functions of (A) osmolyte (c) relative to cbFDH (p) and (B) water (w) relative to cbFDH (p), for different osmolytes in 0.5 mol kg−1 aqueous solutions. Neat buffer (black), TMAO (orange), betaine (green), glycerol (light grey), and trehalose (blue). Standard errors computed from 20 independent runs are shown as shaded regions. Simulations at 25 °C and 1 bar. A system summary is available in Table S3 (ESI†). | |
The water dynamics on the surface of cbFDH was studied by using the protein-water minimum distance distributions shown in Fig. 3(B). It can be seen that the presence of TMAO increases the population density of water in both the first and second solvation layers of cbFDH, while trehalose excludes water from both layers. The increase of water density at the cbFDH surface caused by TMAO or betaine addition explains the observed increase in enzyme activity, while the exclusion of water molecules upon the addition of trehalose or glycerol on the cbFDH surface explains the protection of cbFDH against thermal denaturation. This lets conclude that the dynamics of water and osmolytes on the surface of cbFDH play fundamental roles in both, enzymatic activity and thermal stability.
Fig. S6 and S7 (ESI†) show the MDDFs for systems under the effect of different concentrations of the osmolytes on cbFDH–osmolyte interactions and on cbFDH–water interactions, respectively. In general, both distinct distances of the MDFF gpw decrease with increasing osmolyte concentration due to excess or saturation of osmolytes at the surface of cbFDH. Excess osmolyte causes water exclusion from cbFDH surface, which means less preferential protein-water interactions and less movement of water molecules towards the cbFDH surface.
To reflect the volume exclusion effect associated with protein–solvent interactions at short distances, the KBI profiles were computed for the systems in this work according to eqn (5),
| |  | (5) |
where
S(
r) is the surface area element at distance
r,
n atoms-average number density and
ρj is the molar density of the solvent
j in the bulk. As the integral term in
eqn (5) is dimensionless,
G is of the unit L mol
−1 as given by the cosolvent molar density.
Fig. 4 shows the KBI profiles for protein-osmolyte interactions, meanwhile, KBI profiles at different concentrations of osmolyte can be found in Fig. S8 (ESI
†). The very first peak is negative, which results from the volume exclusion effect caused by the osmolyte that consumes space previously available for the protein. The peak crosses the baseline (
GPC = 0) as soon as the osmolyte accumulation on the protein surface has compensated the excluded volume. As expected, a strong exclusion effect is observed for trehalose due to the marked accumulation at
cbFDH surface, withdrawing the hydration water of
cbFDH. Accordingly,
cbFDH is preferentially dehydrated in the presence of trehalose. This is different with TMAO, which accumulates at the
cbFDH surface much weaker than trehalose. This difference between
Gpc(TMAO) and
Gpc(trehalose) contributes to an explanation of the experimental observations on the thermal stability of
cbFDH (
cf.Fig. 2) through the preferential hydration parameters calculated according to
eqn (6):
| | | Γpc(R) ≈ ρc[Gpc(R) − Gpw(R)] | (6) |
while TMAO acts as a stabilizer being an excluder from the protein surface, trehalose acts as a macromolecular crowder, accumulating at the
cbFDH surface as shown in
Fig. 4(B). Trehalose and TMAO are the two extreme osmolytes in this study. The osmolytes glycerol and betaine have intermediate behaviours, exhibiting benefits for both
cbFDH activity and thermal stability, as mentioned above (
cf.Fig. 1 and 2). This is possible due to the fact that both osmolytes are found on
cbFDH surface and in the second layer, generating an advantageous environment for the catalytic process compared to the neat buffer solution.
 |
| | Fig. 4 (A) Kirkwood–Buff integrals of 0.5 mol kg−1 aqueous osmolytes solutions, relative to cbFDH and (B) preferential hydration parameter calculated with eqn (6). TMAO (orange square), betaine (green circles), glycerol (light grey triangles), and trehalose (blue stars) at 25 °C, atmospheric pressure, and pH = 8.5. Standard errors computed from 20 independent runs are shown as shaded regions. | |
Effect of osmolytes on cbFDH reaction equilibrium and yield
Thermodynamic modelling the effect of osmolytes on the equilibrium of the oxidation reaction of formate to CO2 requires an independent set of reactions that describe the underlying chemical equilibria. The reactions were carried out at pH = 8.5, and at this pH the bicarbonate anion HCO3− is the dominant species among the three species CO2, HCO3−, and CO32−. CO2 and CO32− are present only in traces, as shown in Fig. S1 (ESI†). Thus, two independent key reactions were defined in eqn (7)–(9), and the reaction of interest (eqn (7)) was reformulated based on the abundant species HCO3− instead of CO2.| | | For− + NAD+ + 2H2O ⇌ NADH + HCO3− + H3O+ | (7) |
| | | CO2 + 2H2O ⇌ HCO3− + H3O+ | (8) |
| | | HCO3− + H2O ⇌ CO32− + H3O+ | (9) |
The equilibrium constant for CO2 dissociation was taken from data available in the literature.64 The Kth of the NADH formation reaction, formulated in eqn (7), was calculated from the activities of reacting agents (i.e., equilibrium composition, pH, and the calculated activity coefficients) according to eqn (10):| |  | (10) |
where X represents the equilibrium molality ratio of all reacting agents except proton, Γ the respective activity coefficients ratio, and the activity of hydronium was accessed with the experimental pH by aH3O+ = 10−pH. The thermodynamic equilibrium constant Kth is independent of the solvent. Thus, the effects of osmolytes on X were predicted by accessing the change of the activity coefficients of the products and reactants upon osmolyte addition. In a first step, the experimental equilibrium concentration ratio X in neat buffer was used to calculate the equilibrium constant (Kth). Then, the effect of adding 0.5 mol kg−1 osmolyte was addressed with the change in the activity coefficient while keeping Kth constant. The iterative calculation delivered X as a result of osmolyte addition. The prediction results are compared to the experimental results in Fig. 5(A). As it becomes evident from the data, all osmolytes slightly decreased the equilibrium concentrations of NADH and bicarbonate. Molalities at equilibrium are independent of the enzyme, so substrate/product–osmolyte interactions govern the reaction. The predictions results obtained with ePC-SAFT advanced qualitatively agree with the experimental behaviour, cf.Fig. 5(A). No parameters were fitted to the shown experimental data, and only osmolyte–water binary parameters were used from the literature. Activity coefficients of the reacting agents were calculated to quantify the effect of added osmolytes (Fig. S9 and S10, ESI†). Fig. S9 (ESI†) illustrates that the activity coefficient of NADH increases exponentially upon adding osmolyte. That is, the higher the osmolyte concentration, the more the reaction equilibrium is shifted towards the reactants. This effect is partially counteracted by the effect of osmolyte on activity coefficient of NAD+, especially in the case of glycerol.| | 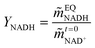 | (11) |
The yield of the reaction was calculated as shown in eqn (11), where ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) EQNADH represents the equilibrium molality of the product NADH and
EQNADH represents the equilibrium molality of the product NADH and  the initial molality of the limiting substrate NAD+. Fig. 5(B) shows the yield obtained by the reaction in a neat buffer and the aqueous osmolyte solutions. Interestingly, none of the osmolytes could increase the yield compared to the buffer solution. ePC-SAFT advanced allowed predicting the yield within max. 7% of error related to the experimental data.
the initial molality of the limiting substrate NAD+. Fig. 5(B) shows the yield obtained by the reaction in a neat buffer and the aqueous osmolyte solutions. Interestingly, none of the osmolytes could increase the yield compared to the buffer solution. ePC-SAFT advanced allowed predicting the yield within max. 7% of error related to the experimental data.
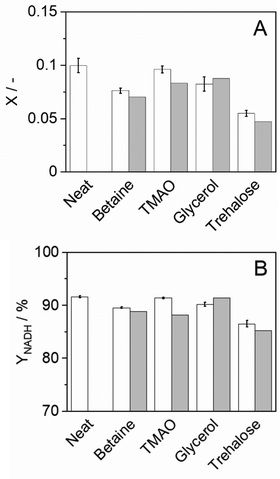 |
| | Fig. 5 Reaction equilibrium of cbFDH in 0.5 mol kg−1 osmolyte solutions at 25 °C and atmospheric pressure. (A) Equilibrium molality ratio X of all reacting agents except proton and (B) yield YNADH of NADH. Experimental (white bars) and ePC-SAFT predictions with parameters reported in Tables S5 and S6 (ESI†) (grey bars). | |
Conclusions
For the oxidation reaction catalysed by cbFDH, the effect of the different osmolytes on the enzyme activity, thermal stability, and reaction equilibrium were investigated. In addition to the experimental results, the systems were studied by means of thermodynamic modelling with ePC-SAFT advanced and by molecular dynamics.
The results showed that osmolytes increased enzyme activity at low osmolyte concentrations due to preferential interactions between cbFDH and water induced by the osmolytes. Only betaine maintained enzyme activity over long periods, probably due to hydrophobic interactions of the quaternary ammonium group with cbFDH. In contrast, the osmolytes with strong hydrogen bond interactions (trehalose and glycerol) with the cbFDH surface allowed greater protection against thermal denaturation, even at high osmolyte concentrations. However, excess osmolyte on the surface at high concentrations caused a depletion of hydration water in the protein environment, which explained the observed decreased enzymatic activity in the presence of trehalose. These results were confirmed with molecular dynamics simulations using minimum distance distribution functions where the distribution of the osmolytes on the protein surface was accessed. Thus, understanding the dynamics between water–osmolyte at the protein surface was studied with MD allows assisting the choice of suitable osmolytes for maximum enzyme stability or biocatalytic activity. Finally, osmolytes were found to have a slightly negative effect on the reaction equilibrium and yield of NADH. The influence of osmolytes on equilibrium was successfully predicted using a thermodynamic framework with ePC-SAFT advanced. Anyway, the impact on yield was not very pronounced at 0.5 mol kg−1 osmolyte. In sum, TMAO boosts enzyme activity, while trehalose protects cbFDH from thermal denaturation, and only glycerol and TMAO kept the equilibrium yield to values >90%. Thus, the use of the studied osmolytes on cbFDH is a compromise between their effect on yield, long-time activity, and thermal stability of cbFDH.
To conclude, this work shows the regulative effect of osmolytes on cbFDH by combining thermodynamic modelling, molecular dynamics simulations, and experiments. Such knowledge will help in the future to understand how the environment of proteins changes in the presence of different stimuli. This allows tuning the performance of catalytic reactions by combining experimental and theoretical methods.
Author contributions
The manuscript was written with the contributions of all authors. All authors have approved the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This study was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV. Nicolás Gajardo's work was supported by the German Academic Exchange Service (DAAD) under the Graduate School Scholarship Programme, 2020 (57516591). E. C.-K. acknowledges the scholarship from ANID, Chile. This research was partially supported by the supercomputing infrastructure of the Southern GPU Cluster – Fondequip EQM150134. The authors gratefully acknowledge the computing time provided on the Linux HPC cluster at TU Dortmund University (LiDO3), partially funded in the course of the Large-Scale Equipment Initiative by the German Research Foundation (DFG) as project 271512359.
References
- A. Schmid, J. S. Dordick, B. Hauer, A. Kiener, M. Wubbolts and B. Witholt, Industrial biocatalysis today and tomorrow, Nature, 2001, 409, 258–268 CrossRef CAS PubMed
 .
.
- U. T. Bornscheuer, G. W. Huisman, R. J. Kazlauskas, S. Lutz, J. C. Moore and K. Robins, Engineering the third wave of biocatalysis, Nature, 2012, 485, 185–194 CrossRef CAS PubMed
 .
.
- P. V. Iyer and L. Ananthanarayan, Enzyme stability and stabilization—Aqueous and non-aqueous environment, Process Biochem., 2008, 43, 1019–1032 CrossRef CAS
 .
.
- F. Xu, Applications of oxidoreductases: Recent progress, Ind. Biotechnol., 2005, 1, 38–50 CrossRef CAS
 .
.
- V. I. Tishkov and V. O. Popov, Catalytic mechanism and application of formate dehydrogenase, Biochemistry, Biokhimiia, 2004, 69, 1252–1267 CrossRef CAS
 .
.
- V. I. Tishkov and V. O. Popov, Protein engineering of formate dehydrogenase, Biomol. Eng., 2006, 23, 89–110 CrossRef CAS PubMed
 .
.
- H. Schüte, J. Flossdorf, H. Sahm and M. R. Kula, Purification and properties of formaldehyde dehydrogenase and formate dehydrogenase from Candida boidinii, Eur. J. Biochem., 1976, 62, 151–160 CrossRef PubMed
 .
.
- T. Wang and R. C. Wade, On the Use of Elevated Temperature in Simulations To Study Protein Unfolding Mechanisms, J. Chem. Theory Comput., 2007, 3, 1476–1483 CrossRef CAS PubMed
 .
.
- T. Arakawa and S. N. Timasheff, The stabilization of proteins by osmolytes, Biophys. J., 1985, 47, 411–414 CrossRef CAS PubMed
 .
.
- P. H. Yancey, Water Stress, Osmolytes and Proteins, Am. Zool., 2001, 41, 699–709 CAS
 .
.
- D. W. Bolen, Protein stabilization by naturally occurring osmolytes, Methods Mol. Biol., 2001, 168, 17–36 CAS
 .
.
- N. Zhadin and R. Callender, Effect of osmolytes on protein dynamics in the lactate dehydrogenase-catalyzed reaction, Biochemistry, 2011, 50, 1582–1589 CrossRef CAS PubMed
 .
.
- G. S. Sharma, S. Krishna, S. Khan, T. A. Dar, K. A. Khan and L. R. Singh, Protecting thermodynamic stability of protein: The basic paradigm against stress and unfolded protein response by osmolytes, Int. J. Biol. Macromol., 2021, 177, 229–240 CrossRef CAS PubMed
 .
.
- M. Ishrat, M. I. Hassan, F. Ahmad and A. Islam, Sugar osmolytes-induced stabilization of RNase A in macromolecular crowded cellular environment, Int. J. Biol. Macromol., 2018, 115, 349–357 CrossRef CAS PubMed
 .
.
- P. Cioni, E. Bramanti and G. B. Strambini, Effects of sucrose on the internal dynamics of azurin, Biophys. J., 2005, 88, 4213–4222 CrossRef CAS PubMed
 .
.
- H. Slusarczyk, S. Felber, M. R. Kula and M. Pohl, Stabilization of NAD-dependent formate dehydrogenase from Candida boidinii by site-directed mutagenesis of cysteine residues, Eur. J. Biochem., 2000, 267, 1280–1289 CrossRef CAS PubMed
 .
.
- A. M. Rojkova, A. G. Galkin, L. B. Kulakova, A. E. Serov, P. A. Savitsky, V. V. Fedorchuk and V. I. Tishkov, Bacterial formate dehydrogenase. Increasing the enzyme thermal stability by hydrophobization of alpha-helices, FEBS Lett., 1999, 445, 183–188 CrossRef CAS PubMed
 .
.
- M. H. Kim, S. Park, Y. H. Kim, K. Won and S. H. Lee, Immobilization of formate dehydrogenase from Candida boidinii through cross-linked enzyme aggregates, J. Mol. Catal. B: Enzym., 2013, 97, 209–214 CrossRef CAS
 .
.
- G. Xie and S. N. Timasheff, Mechanism of the stabilization of ribonuclease A by sorbitol: preferential hydration is greater for the denatured then for the native protein, Protein Sci., 1997, 6, 211–221 CrossRef CAS PubMed
 .
.
- S.-J. Jeong, J. Stitham, T. D. Evans, X. Zhang, A. Rodriguez-Velez, Y.-S. Yeh, J. Tao, K. Takabatake, S. Epelman, I. J. Lodhi, J. D. Schilling, B. J. DeBosch, A. Diwan and B. Razani, Trehalose causes low-grade lysosomal stress to activate TFEB and the autophagy-lysosome biogenesis response, Autophagy, 2021, 1–13 Search PubMed
 .
.
- K. Göller and E. A. Galinski, Protection of a model enzyme (lactate dehydrogenase) against heat, urea and freeze-thaw treatment by compatible solute additives, J. Mol. Catal. B: Enzym., 1999, 7, 37–45 CrossRef
 .
.
- A. Wangler, C. Held and G. Sadowski, Thermodynamic Activity-Based Solvent Design for Bioreactions, Trends Biotechnol., 2019, 37, 1038–1041 CrossRef CAS PubMed
 .
.
- M. Voges, C. Fischer, D. Wolff and C. Held, Influence of Natural Solutes and Ionic Liquids on the Yield of Enzyme-Catalyzed Reactions: Measurements and Predictions, Org. Process Res. Dev., 2017, 21, 1059–1068 CrossRef CAS
 .
.
- M. Knierbein, A. Wangler, T. Q. Luong, R. Winter, C. Held and G. Sadowski, Combined co-solvent and pressure effect on kinetics of a peptide hydrolysis: an activity-based approach, Phys. Chem. Chem. Phys., 2019, 21, 22224–22229 RSC
 .
.
- G. M. Kontogeorgis, R. Dohrn, I. G. Economou, J.-C. de Hemptinne, A. ten Kate, S. Kuitunen, M. Mooijer, L. F. Žilnik and V. Vesovic, Industrial Requirements for Thermodynamic and Transport Properties: 2020, Ind. Eng. Chem. Res., 2021, 60, 4987–5013 CrossRef CAS PubMed
 .
.
- E. Cea-Klapp, I. Polishuk, R. I. Canales, H. Quinteros-Lama and J. M. Garrido, Estimation of Thermodynamic Properties and Phase Equilibria in Systems of Deep Eutectic Solvents by PC-SAFT EoS, Ind. Eng. Chem. Res., 2020, 59, 22292–22300 CrossRef CAS
 .
.
- L. F. Cameretti and G. Sadowski, Modeling of aqueous amino acid and polypeptide solutions with PC-SAFT, Chem. Eng. Process., 2008, 47, 1018–1025 CrossRef CAS
 .
.
- M. Bülow, M. Ascani and C. Held, ePC-SAFT advanced – Part I: Physical meaning of including a concentration-dependent dielectric constant in the born term and in the Debye-Hückel theory, Fluid Phase Equilib., 2021, 535, 112967 CrossRef
 .
.
- M. Bülow, M. Ascani and C. Held, ePC-SAFT advanced – Part II: Application to Salt Solubility in Ionic and Organic Solvents and the Impact of Ion Pairing, Fluid Phase Equilib., 2021, 537, 112989 CrossRef
 .
.
- C. Held, T. Reschke, S. Mohammad, A. Luza and G. Sadowski, ePC-SAFT revised, Chem. Eng. Res. Des., 2014, 92, 2884–2897 CrossRef CAS
 .
.
- F. Tumakaka, J. Gross and G. Sadowski, Thermodynamic modeling of complex systems using PC-SAFT, Fluid Phase Equilib., 2005, 228–229, 89–98 CrossRef CAS
 .
.
- J. Gross and G. Sadowski, Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules, Ind. Eng. Chem. Res., 2001, 40, 1244–1260 CrossRef CAS
 .
.
- J. Gross and G. Sadowski, Application of the Perturbed-Chain SAFT Equation of State to Associating Systems, Ind. Eng. Chem. Res., 2002, 41, 5510–5515 CrossRef CAS
 .
.
- H. T. Do, S. Chakrabarty and C. Held, Modeling solubility of amino acids and peptides in water and in water + 2-propanol mixtures: PC-SAFT vs. gE models, Fluid Phase Equilib., 2021, 542–543, 113087 CrossRef CAS
 .
.
- N. F. Gajardo-Parra, H. T. Do, M. Yang, J. R. Pérez-Correa, J. Matías Garrido, G. Sadowski, C. Held and R. I. Canales, Impact of Deep Eutectic Solvents and their Constituents on the Aqueous Solubility of Phloroglucinol Dihydrate, J. Mol. Liq., 2021, 117932 CrossRef CAS
 .
.
- M. W. Jaworek, N. F. Gajardo-Parra, G. Sadowski, R. Winter and C. Held, Boosting the Kinetic Efficiency of Formate Dehydrogenase by Combining the Effects of Temperature, High Pressure and Co-solvent Mixtures, Colloids Surf., B, 2021, 112127 CrossRef CAS PubMed
 .
.
- M. Ascani, D. Pabsch, M. Klinksiek, N. Gajardo-Parra, G. Sadowski and C. Held, Prediction of pH in multiphase multicomponent systems with ePC-SAFT advanced, Chem. Commun., 2022, 58, 8436–8439 RSC
 .
.
- V. P. Cotroneo-Figueroa, N. F. Gajardo-Parra, P. López-Porfiri, Á. Leiva, M. Gonzalez-Miquel, J. M. Garrido and R. I. Canales, Hydrogen bond donor and alcohol chain length effect on the physicochemical properties of choline chloride based deep eutectic solvents mixed with alcohols, J. Mol. Liq., 2021, 116986 Search PubMed
 .
.
- P. Ganguly, J. Polák, N. F. A. van der Vegt, J. Heyda and J.-E. Shea, Protein Stability in TMAO and Mixed Urea-TMAO Solutions, J. Phys. Chem. B, 2020, 124, 6181–6197 CrossRef CAS PubMed
 .
.
- V. Piccoli and L. Martínez, Correlated counterion effects on the solvation of proteins by ionic liquids, J. Mol. Liq., 2020, 320, 114347 CrossRef CAS
 .
.
- L. Martínez, ComplexMixtures.jl: Investigating the structure of solutions of complex-shaped molecules from a solvent-shell perspective, J. Mol. Liq., 2022, 347, 117945 CrossRef
 .
.
- S.-C. Ou, J. A. Drake and B. M. Pettitt, Nonpolar Solvation Free Energy from Proximal Distribution Functions, J. Phys. Chem. B, 2017, 121, 3555–3564 CrossRef CAS PubMed
 .
.
- S.-C. Ou and B. M. Pettitt, Solute-Solvent Energetics Based on Proximal Distribution Functions, J. Phys. Chem. B, 2016, 120, 8230–8237 CrossRef CAS PubMed
 .
.
- L. Martínez and S. Shimizu, Molecular Interpretation of Preferential Interactions in Protein Solvation: A Solvent-Shell Perspective by Means of Minimum-Distance Distribution Functions, J. Chem. Theory Comput., 2017, 13, 6358–6372 CrossRef PubMed
 .
.
- I. P. de Oliveira and L. Martínez, The shift in urea orientation at protein surfaces at low pH is compatible with a direct mechanism of protein denaturation, Phys. Chem. Chem. Phys., 2019, 22, 354–367 RSC
 .
.
- Q. Guo, L. Gakhar, K. Wickersham, K. Francis, A. Vardi-Kilshtain, D. T. Major, C. M. Cheatum and A. Kohen, Structural and Kinetic Studies of Formate Dehydrogenase from Candida boidinii, Biochemistry, 2016, 55, 2760–2771 CrossRef CAS PubMed
 .
.
- H. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: A message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS
 .
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef
 .
.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, Improved Peptide and Protein Torsional Energetics with the OPLSAA Force Field, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed
 .
.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed
 .
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS
 .
.
- H. Monteiro, A. Paiva, A. R. C. Duarte and N. Galamba, Structure and Dynamic Properties of a Glycerol-Betaine Deep Eutectic Solvent: When Does a DES Become an Aqueous Solution?, ACS Sustainable Chem. Eng., 2022, 10, 3501–3512 CrossRef CAS PubMed
 .
.
- L. Larini and J.-E. Shea, Double resolution model for studying TMAO/water effective interactions, J. Phys. Chem. B, 2013, 117, 13268–13277 CrossRef CAS PubMed
 .
.
- W. Damm, A. Frontera, J. Tirado-Rives and W. L. Jorgensen, OPLS all-atom force field for carbohydrates, J. Comput. Chem., 1997, 18, 1955–1970 CrossRef CAS
 .
.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS
log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS  .
.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed
 .
.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 14101 CrossRef PubMed
 .
.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS
 .
.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
 .
.
- S. Nosé and M. L. Klein, Constant pressure molecular dynamics for molecular systems, Mol. Phys., 1983, 50, 1055–1076 CrossRef
 .
.
- R. Hockney, S. Goel and J. Eastwood, Quiet high-resolution computer models of a plasma, J. Comput. Phys., 1974, 14, 148–158 CrossRef
 .
.
- J. Bezanson, A. Edelman, S. Karpinski and V. B. Shah, Julia: A Fresh Approach to Numerical Computing, SIAM Rev., 2017, 59, 65–98 CrossRef
 .
.
- M. Gruebele, Protein folding and surface interaction phase diagrams in vitro and in cells, FEBS Lett., 2021, 595, 1267–1274 CrossRef CAS PubMed
 .
.
- D. Li and Z. Duan, The speciation equilibrium coupling with phase equilibrium in the H2O–CO2–NaCl system from 0 to 250 °C, from 0 to 1000 bar, and from 0 to 5 molality of NaCl, Chem. Geol., 2007, 244, 730–751 CrossRef CAS
 .
.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Harold
Akrofi-Mantey
a,
Harold
Akrofi-Mantey
 a,
Moreno
Ascani
a,
Moreno
Ascani
 a,
Esteban
Cea-Klapp
a,
Esteban
Cea-Klapp
 b,
José Matias
Garrido
b,
José Matias
Garrido
 b,
Gabriele
Sadowski
b,
Gabriele
Sadowski
 a and
Christoph
Held
a and
Christoph
Held
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637-93-8
637-93-8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules of water and the concentration of the osmolyte was fixed by adding these molecules. Additional sodium ions were used as counter ions to neutralize the protein net charge. The number of solvent molecules in each box is shown in Table S4 (ESI†). According to,44,45 the simulations were started with randomly produced solvent boxes and velocity distributions. This ensures that the cbFDH structure keeps its original conformation and acquires sufficient sampling of the solvent structure by executing a collection of 20 brief simulations (17 ns in total) instead of one large simulation for each system. MD simulations were carried out using GROMACS version 2021.2.47,48 The force field used to describe the cbFDH was OPLS-AA/M49 and the parameters for its ligands were retrieved from LigParGen.50 Water was modelled with TIP4P in all simulations51 For betaine and glycerol, OPLS parameters were retrieved from the validation realized by Monteiro et al.52 Shea force field was used for TMAO53 due to its compatibility with OPLS, and OPLS-AA for carbohydrates was used for trehalose.54 All these force fields are non-polarizable models, where electrostatic and van der Waals interactions are modelled using Coulomb potential and Lennard Jones potential, respectively. The cut-off radius was set to 1.2 nm and periodic boundary conditions were used in all directions. Electrostatic interactions were treated using the Particle-Mesh Ewald technique55 with an interpolation order set to four.
000 molecules of water and the concentration of the osmolyte was fixed by adding these molecules. Additional sodium ions were used as counter ions to neutralize the protein net charge. The number of solvent molecules in each box is shown in Table S4 (ESI†). According to,44,45 the simulations were started with randomly produced solvent boxes and velocity distributions. This ensures that the cbFDH structure keeps its original conformation and acquires sufficient sampling of the solvent structure by executing a collection of 20 brief simulations (17 ns in total) instead of one large simulation for each system. MD simulations were carried out using GROMACS version 2021.2.47,48 The force field used to describe the cbFDH was OPLS-AA/M49 and the parameters for its ligands were retrieved from LigParGen.50 Water was modelled with TIP4P in all simulations51 For betaine and glycerol, OPLS parameters were retrieved from the validation realized by Monteiro et al.52 Shea force field was used for TMAO53 due to its compatibility with OPLS, and OPLS-AA for carbohydrates was used for trehalose.54 All these force fields are non-polarizable models, where electrostatic and van der Waals interactions are modelled using Coulomb potential and Lennard Jones potential, respectively. The cut-off radius was set to 1.2 nm and periodic boundary conditions were used in all directions. Electrostatic interactions were treated using the Particle-Mesh Ewald technique55 with an interpolation order set to four.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, with all the heavy atoms (non-hydrogen atoms) of the protein and the ligand fixed; (3) 1 ns of equilibration using the canonical NVT ensemble, while retaining the previous position restrictions; (4) 5 ns of equilibration using the isothermal-isobaric NPT ensemble, while retaining the previous position restrictions; (5) 1 ns of equilibration using the NPT ensemble without positions restraints; (6) 10 ns of production using the NPT ensemble. The temperature of the system was maintained constant at 293 K using a velocity rescaling thermostat,57 with a time constant τT = 0.1 ps. The pressure was held at 1.0 bar using the Berendsen barostat58 for the equilibration step for τP = 2 ps, and Parrinello–Rahman barostat59,60 for the production step for τP = 2 ps. In all runs, equations of motion were integrated using the leapfrog algorithm61 for τT = 2 ps. Twenty independent simulations were performed for each system using the previous protocol. These short molecular simulations allow studying the solvation structures of the native state of the protein without denaturation effects or critical structural change.40 An open-source software “ComplexMixtures.jl”,41 implemented in Julia language62 was used to compute protein–solvent minimum-distance functions and KBI from the simulation results. To demonstrate the stability of the system in the simulation, root-mean-square deviation of atomic positions (RMSD), root-mean-square-fluctuation (RMSF), and radius of gyration (Rg) analysis are provided in ESI† (Fig. S3–S5).
000 steps, with all the heavy atoms (non-hydrogen atoms) of the protein and the ligand fixed; (3) 1 ns of equilibration using the canonical NVT ensemble, while retaining the previous position restrictions; (4) 5 ns of equilibration using the isothermal-isobaric NPT ensemble, while retaining the previous position restrictions; (5) 1 ns of equilibration using the NPT ensemble without positions restraints; (6) 10 ns of production using the NPT ensemble. The temperature of the system was maintained constant at 293 K using a velocity rescaling thermostat,57 with a time constant τT = 0.1 ps. The pressure was held at 1.0 bar using the Berendsen barostat58 for the equilibration step for τP = 2 ps, and Parrinello–Rahman barostat59,60 for the production step for τP = 2 ps. In all runs, equations of motion were integrated using the leapfrog algorithm61 for τT = 2 ps. Twenty independent simulations were performed for each system using the previous protocol. These short molecular simulations allow studying the solvation structures of the native state of the protein without denaturation effects or critical structural change.40 An open-source software “ComplexMixtures.jl”,41 implemented in Julia language62 was used to compute protein–solvent minimum-distance functions and KBI from the simulation results. To demonstrate the stability of the system in the simulation, root-mean-square deviation of atomic positions (RMSD), root-mean-square-fluctuation (RMSF), and radius of gyration (Rg) analysis are provided in ESI† (Fig. S3–S5).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15K + kijT·(T/K − 298.15)
298.15K + kijT·(T/K − 298.15)



 represents the same distribution but in the absence of protein p–solvent j interactions, which was realized using a “phantom” protein that does not interact with the solvent. The calculations were made using the protein (p) as solute and water (w) + osmolyte (c) as the solvent.
represents the same distribution but in the absence of protein p–solvent j interactions, which was realized using a “phantom” protein that does not interact with the solvent. The calculations were made using the protein (p) as solute and water (w) + osmolyte (c) as the solvent.




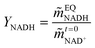
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) EQNADH represents the equilibrium molality of the product NADH and
EQNADH represents the equilibrium molality of the product NADH and  the initial molality of the limiting substrate NAD+. Fig. 5(B) shows the yield obtained by the reaction in a neat buffer and the aqueous osmolyte solutions. Interestingly, none of the osmolytes could increase the yield compared to the buffer solution. ePC-SAFT advanced allowed predicting the yield within max. 7% of error related to the experimental data.
the initial molality of the limiting substrate NAD+. Fig. 5(B) shows the yield obtained by the reaction in a neat buffer and the aqueous osmolyte solutions. Interestingly, none of the osmolytes could increase the yield compared to the buffer solution. ePC-SAFT advanced allowed predicting the yield within max. 7% of error related to the experimental data.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS
log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS .
.
.
.
.
.
.
.
.
.
