Torsional disorder and planarization dynamics: 9,10-bis(phenylethynyl)anthracene as a case study

Abstract

Conjugated molecules with phenylethynyl building blocks are usually characterised by torsional disorder at room temperature. They are much more rigid in the electronic excited state due to conjugation. As a consequence, the electronic absorption and emission spectra do not present a mirror-image relationship. Here, we investigate how torsional disorder affects the excited state dynamics of 9,10-bis(phenylethynyl)anthracene in solvents of different viscosities and in polymers, using both stationary and ultrafast electronic spectroscopies. Temperature-dependent measurements reveal inhomogeneous broadening of the absorption spectrum at room temperature. This is confirmed by ultrafast spectroscopic measurements at different excitation wavelengths. Red-edge irradiation excites planar molecules that return to the ground state without significant structural dynamics. In this case, however, re-equilibration of the torsional disorder in the ground state can be observed. Higher-energy irradiation excites torsionally disordered molecules, which then planarise, leading to important spectral dynamics. The latter is found to occur partially via viscosity-independent inertial motion, whereas it is purely diffusive in the ground state. This dissimilarity is explained in terms of the steepness of the potential along the torsional coordinate.

---

1 Introduction

Over the past few decades, conjugated polymers and oligomers have attracted increasing attention because of their electronic properties that make them important constituents of devices designed for a broad range of applications, including solar energy conversion,^1–5 molecular electronics and photonics.^6–10 A large number of these molecules contain phenylethene or phenylethylene building blocks that confer them significant torsional flexibility. They can, thus, exist with a relatively large distribution of a torsional angle at room temperature. In contrast, conjugation in the electronic excited state strongly reduces this torsional flexibility. Because of these very different potentials along the torsional coordinate in the ground and excited states and of the torsional disorder in the ground state, the electronic absorption spectra of these compounds generally consist of broad and structureless bands. On the other hand, the emission from the equilibrated S₁ state results in narrower and structured spectra and, thus, to a non-mirror-image relationship with the absorption spectrum.^11,12 Consequently, S₁ ← S₀ excitation of these molecules can be expected to be followed by substantial structural relaxation, mostly planarization, that should be accompanied by changes in the emission spectrum. Using time-correlated single photon counting with a 45 ps instrument response function, Sluch et al. could resolve the narrowing of the blue edge of the emission spectrum of a polyphenylethylnylene oligomer in chloroform with a 60 ps time constant.¹¹ Using electronic transient absorption (TA), Duvanel et al. found that the stimulated emission spectrum of a similar polyphenylethylnylene oligomer in toluene changes from broad to structured with a ∼30 ps time constant.¹² Roy et al. concluded from a transient absorption and Raman loss study of bis(phenylethynyl)benzene in acetonitrile that the central and terminal benzene rings relax on different timescales, ∼500 fs and ∼20 ps, respectively.¹³ They also observed that structural relaxation was negligible upon excitation on the red side of the absorption band. This is consistent with the observation of an excitation wavelength dependence of the fluorescence spectrum of this molecule in a low-temperature glass reported by Beeby and co-workers.¹⁴ Torsional dynamics of shorter molecules, such as tetraphenylethylene, were reported to be much faster and to occur on a sub-ps timescale in butyronitrile.¹⁵ Planarization dynamics were also observed using many multichromophoric systems, with a single bond connection,^16–18 or with conjugated bridges,^19–23 on timescales ranging from a few ps to several tens of ps.

Understanding torsional dynamics and its dependence on the environment is important for most applications of conjugated molecules. For example, charge and exciton transport in conjugated systems are most efficient with planar conformation and are, thus, strongly affected by torsional disorder.^24–26 Similarly, recently developed mechanosensitive probes have been shown to rely on the effect of torsion on conjugation.^27,28 Finally, torsion is often invoked as a crucial coordinate in charge separation processes.^29–32

Herein, we present our investigation of the torsional dynamics of 9,10-bis(phenylethynyl)anthracene (BPEA, Fig. 1A) in both the lowest singlet excited state and the ground state in liquids of different viscosities and in polymers, using a combination of fs broadband transient absorption (TA) and fluorescence up-conversion spectroscopy (FLUPS). BPEA is characterised by a high fluorescence quantum yield and is widely used as an emitter in chemiluminescence,^33,34 luminescent molecular liquids,³⁵ optoelectronics,^36–38 sensors,³⁹ triplet–triplet annihilation up-conversion,^40–42 and more recently as dye for singlet fission.^43–45 In solution, the S₁–S₀ absorption and emission bands of BPEA do not exhibit a mirror-image relationship: the absorption band is broad and structureless, whereas the emission band is structured.^46,47 Levitus and Garcia-Garibay as well as Beeby and co-workers attributed this to the coexistence of several conformations in the ground state.^46,48 From temperature-dependent measurements of the stationary electronic absorption spectrum and quantum-chemical calculations, we indeed show that the room-temperature spectrum of BPEA can be reproduced assuming a distribution of conformations with different dihedral angles of the phenyls relative to the anthracene core. Our FLUPS measurements with a sub-100 fs resolution reveal a strong time dependence of the emission spectral shape, which can mostly be attributed to planarization in the S₁ state. A significant excitation wavelength dependence of the spectral dynamics is observed in the TA data, indicating that distinct subpopulations of BPEA with different geometries can be selectively excited. The spectral dynamics in the bleach region gives access to the equilibration dynamics along the torsional coordinate in the electronic ground state. Our results reveal different viscosity dependence of the torsional motion in the S₁ and ground states.

Fig. 1 (A) Calculated (M06-2x/6-31G(d,p)) energy of the ground and excited states of BPEA along the torsional coordinate θ and thermal energy at room temperature. (B) S₁–S₀ absorption and emission bands of BPEA in CHX compared with the calculated gas-phase spectra and the main transitions shifted by 500 and 300 cm⁻¹, respectively.

2 Experimental

2.1 Samples

The dye, 9,10-bis(phenylethynyl)anthracene (BPEA), was purchased from Santa Cruz Biotechnology Inc. (99.9%) and was used without further purification. The solvents, cyclohexane (CHX), decaline (DEC), paraffin oil (PAR) and 2-methyltetrahydrofuran (MTHF) were of the highest commercially available purity and were used as received. To prepare the polyvinylbutyral (PVB, Mowital B60 H) and Zeonex (480R, Zeon) films, BPEA was added to polymer solutions in dichloromethane (PVB) or toluene (Zeonex). After evaporation of the solvent, the films were kept in a vacuum for one week. They were then slightly warmed up and compressed between two quartz windows. Their absorbance was between 0.1 and 0.2 at the maximum of the S₁ ← S₀ absorption band of BPEA.

2.2 Stationary spectroscopy

Electronic absorption spectra were recorded using a Cary 50 spectrometer. Room-temperature stationary fluorescence spectra were measured using a Horiba FluoroMax-4 spectrofluorometer, whereas temperature-dependent fluorescence spectra were recorded using a Cary Eclipse spectrofluorometer. The fluorescence spectra were corrected using a set secondary emissive standards.⁴⁹ Measurements at different temperatures were carried out using an Oxford OptistatDN cryostat.

2.3 Fluorescence up-conversion spectroscopy (FLUPS)

The setup for broadband fluorescence up-conversion spectroscopy (FLUPS) was described earlier⁵⁰ and was based on the design described in ref. 51. The pump pulses at 400 nm were generated by the frequency doubling part of the output of a Ti:Sapphire amplifier system (Spectra-Physics, Solstice Ace, 5 kHz). The pump pulses at 375 and 425 nm were produced using a TOPAS-Prime combined with a NirUVis module (Light Conversion). The gate pulses at 1340 nm were generated using an optical parametric amplifier (TOPAS C, Light Conversion) pumped at 800 nm. The polarization of the pump pulses was at magic angle relative to that of the detected fluorescence. The full width at half maximum of the cross-correlation of the pump and gate pulses was estimated from the Raman signal of the solvent to be less than 100 fs. The detection of the up-converted fluorescence was achieved using an Andor DV420A-BU CCD camera (Oxford Instruments) combined with a spectrograph and an optical fiber bundle. Photometric correction of the emission spectra was performed using secondary standards. The chirp was corrected using the rise of the fluorescence of BBOT solutions. The absorbance of the samples at the excitation wavelength did not exceed 0.2 in a 1 mm quartz cuvette. The FLUPS spectra were corrected for the reabsorption.

2.4 Electronic transient absorption (TA) spectroscopy

Transient absorption (TA) measurements were performed with a setup described in ref. 52 and 53 and based on an amplified Ti:Sapphire system (Solstice Ace, Spectra-Physics), producing 35 fs pulses centred at 800 nm with a 5 kHz repetition rate. In brief, the pump pulses were produced by a TOPAS-Prime combined with a NirUVis module (Light Conversion), and were compressed to 60–100 fs at the sample position. The pump intensity on the sample was ∼0.15–0.75 mJ cm⁻². For measurements with polymer films, the samples were continuously moved laterally and vertically according to Lissajoux functions to avoid the prolonged irradiation of the same spot. Probing was achieved from about 320 to 750 nm using white light pulses generated in a 3 mm CaF₂ plate. The polarisation of the pump pulses was at magic angle with respect to that of the probe pulses. The sample cell was 1 mm thick and the instrument response function had a full width at half maximum varying between 80 and 350 fs, depending on the probe wavelength.

2.5 Quantum-chemical calculations

All calculations were carried out at the density functional theory (DFT) or time-dependent (TD) DFT level in the gas phase, as implemented in the Gaussian16 (Rev. B) software.⁵⁴ Different functionals were tested with the 6-31G(d,p) basis set (see Table S1, ESI†). The M06-2x functional⁵⁵ was finally selected as the calculated S₁ ← S₀ transition energy was the closest to the experimental value. Calculations of the vibronic structure of the S₁–S₀ absorption and emission spectra were performed using the Franck–Condon–Herzberg–Teller method.⁵⁶ All vibration frequencies were multiplied by a correction factor of 0.95.⁵⁷

3 Results

3.1 Quantum-chemical calculations

Fig. 1A shows the energy of the ground and S₁ excited states of BPEA as a function of the dihedral angle θ between the two phenyls and anthracene. The energy of both states was optimised for each θ value. The ground state potential is shallow with a double minimum of around ±10°, and a negligibly small barrier, <10 cm⁻¹, in between. The excited state potential is significantly steeper with a clear minimum at the planar geometry. The potentials for the torsion of a single phenyl are similar to those shown in Fig. 1A but the barriers are twice as small. Consequently, at room temperature, θ can vary between ±40° in the ground state and between ±18° in the S₁ state. TD-DFT calculations suggest that the S₁ ← S₀ transition energy of BPEA increases by 0.1 eV (840 cm⁻¹) by varying θ from 0 to 40° (Fig. S1, ESI†). Therefore, the absorption band of BPEA can be expected to be inhomogeneously broadened at room temperature. The calculations also predict that this variation of θ should be accompanied by a decrease of the oscillator strength from 0.90 to 0.76 (Fig. S2, ESI†). This effect can be explained by the decrease of conjugation upon torsion.

Fig. 1B illustrates the calculated gas-phase absorption and emission spectra of BPEA with the vibronic structure. The calculated absorption transition energies were shifted by 500 cm⁻¹, whereas those for emission were shifted by 300 cm⁻¹. Considering that the measurements were performed in CHX at room temperature, the agreement between the experimental and calculated emission spectra is good. To achieve this, a Gaussian broadening function with a full width at half maximum of 200 cm⁻¹ was used. Applying the same broadening function for the absorption spectrum results in a close to mirror-image relationship in contrast to the experiments. The measured absorption spectrum can be approximately reproduced assuming a 650 cm⁻¹ wide broadening function. According to these calculations, the vibronic structure is dominated by three Franck–Condon (FC) active vibrations at 160, 382 and 1300 cm⁻¹.

3.2 Stationary spectroscopy

The absorption and fluorescence spectra of BPEA were measured in MTHF as a function of temperature down to 105 K. As illustrated in Fig. 2A, the S₁ ← S₀ absorption band at room temperature is broad and hardly structured as already observed before in other solvents.^46–48 As temperature is lowered, the vibronic structure becomes more visible, the band maximum shifts to lower energy and the band area increases. The change in the spectral shape is consistent with a narrower distribution of the torsional angle as thermal energy decreases. It should be noted that the spectrum does not change much below 137 K, the freezing point of MTHF. This suggests that the distribution of torsional angle cannot reach thermal equilibrium in a solid. Narrower absorption spectra were reported by Beeby and co-workers at 77 K in the ether–isopentane–ethanol mixture, which has a glass transition temperature below 100 K.⁴⁸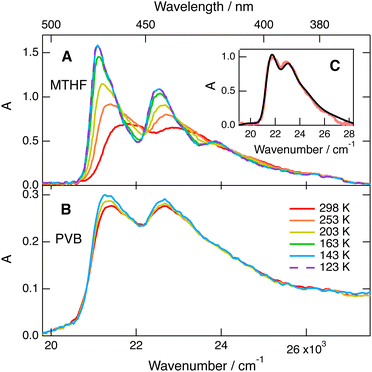

Fig. 2 (A and B) Temperature dependence of the stationary absorption spectrum of BPEA in methyltetrahydrofuran (MTHF) and polyvinylbutyral (PVB). (C) Best-fit of the convolution of the 143 K spectrum with eqn (1) to the room-temperature spectrum of BPEA in MTHF.

According to the calculated ground state potential for torsion (Fig. 1A), θ can vary between ±25° at 140 K. This corresponds to a change of S₁ ← S₀ transition energy of only 0.03 eV (240 cm⁻¹), hence to a significant decrease in inhomogeneous broadening. The small thermochromism of the band can be attributed to the temperature dependence of the refractive index, hence the increase of dispersion interactions upon decreasing temperature. Finally, the increase of the band area upon lowering the temperature is fully consistent with the increase of the oscillator strength upon planarization predicted by the quantum-chemical calculations. The low-temperature absorption spectrum is in much better agreement with that deduced from the quantum-chemical calculations assuming the same line width as for the emission.

Similar measurements in polymer films, PVB and Zeonex (Fig. 2B and Fig. S5, ESI†) point to a negligible temperature dependence of the absorption spectrum of BPEA. This confirms that, in the ground state, equilibration along the torsional coordinate is not possible in solids. This result contrasts with that reported by Levitus and Garcia-Garibay,⁴⁶ who found that the absorption spectrum of BPEA in polyethylene films was structured, indicative of a narrow distribution of the torsion angle. This difference probably arises from the fact that the dye molecules were adsorbed onto the polyethylene film, whereas in our case, BPEA and the polymers were co-dissolved.

These temperature-dependent measurements are consistent with a distribution of torsion angle and S₁ ← S₀ transition energy. To obtain a deeper insight into the nature of the broad absorption band of BPEA at room temperature, we used the potential along θ in the ground state shown in Fig. 1A to determine the Boltzmann distribution of θ and of the transition energy. We first reproduced the potentials for S₀ and S₁ (FC), i.e., S₁ at the ground state geometry, with the Pitzer potential⁵⁸ to obtain continuous functions of the S₁ (FC)–S₀ energy gap vs. θ. We then calculated the ground state population at each angle (Fig. S3, ESI†) to finally obtain the distribution of S₁ ← S₀ transition energies, which should reflect the inhomogeneous broadening of the absorption band at room temperature. As depicted in Fig. S4 (ESI†), this distribution can be well reproduced using an exponential function with a maximum at the lowest transition energy and a damping constant of β = 1.45 × 10⁻³ cm:

f([small nu, Greek, macron]) = H([small nu, Greek, macron] − [small nu, Greek, macron]₀)exp(−β([small nu, Greek, macron] − [small nu, Greek, macron]₀)), (1)

where H([small nu, Greek, macron] − [small nu, Greek, macron]₀) is the Heaviside step function and [small nu, Greek, macron]₀ is the lowest 0–0 transition energy, corresponding to the planar geometry. Fig. 2C reveals that the broad absorption spectrum of BPEA in room temperature MTHF can be reproduced by convolving the structured absorption spectrum at 143 K with eqn (1), using a damping constant of β = 2.4 × 10⁻³ cm. The significantly larger β value compared to that obtained from the quantum-chemical calculations can be explained, at least partially, by the fact that some inhomogeneous broadening is already present at 140 K. Therefore, eqn (1) with β = 2.4 × 10⁻³ cm corresponds to the additional broadening occurring when going from 140 K to room temperature, but not to the total broadening. Additionally, the decrease of the oscillation strength with increasing torsion angle was not taken into account. In the case of the structurally related bis(phenylethynyl)benzene, DFT calculations were found to overestimate the torsional barrier in the ground state.⁵⁹ Such a discrepancy for BPEA in both the ground and excited states could also explain different β values.

As illustrated in Fig. 3A, the fluorescence spectrum of BPEA in MTHF exhibits much weaker temperature dependence, in agreement with a steeper potential for torsion and, thus, a narrower distribution of θ and S₁ → S₀ transition energy. In polymer films, the emission spectrum (Fig. 3B and Fig. S6, ESI†) does essentially not depend on temperature, as was already found with the absorption. However, in contrast to the absorption, the fluorescence spectrum shows a clear vibronic structure, although it is significantly broader than in liquids. This absence of mirror-image symmetry in polymers independently of temperature reveals that, whereas torsional motion is ‘frozen’ in the ground state, it can still occur, at least partially in the excited state. This difference can be attributed to the steeper torsional potential in the S₁ state. Upon excitation to the S₁ state, a distorted molecule becomes so structurally strained that partial relaxation is most probably feasible without significant motion of the surrounding polymer molecules.

Fig. 3 Temperature dependence of the stationary fluorescence spectrum of BPEA in (A) methyltetrahydrofuran and (B) polyvinylbutyral upon 430 nm excitation.

3.3 Femtosecond broadband fluorescence up-conversion spectroscopy (FLUPS)

FLUPS measurements were carried out with BPEA in three non-polar solvents of increasing viscosity, η, namely cyclohexane (CHX, η (25 °C) = 0.9 cP), decaline (DEC, η (25 °C) = 2.4 cP) and paraffin oil (PAR, η (25 °C) ∼ 100 cP). Excitation was performed at 375, 400 and 425 nm. Because of the presence of cut-off filters after the sample to remove the scattered pump light, the blue side of the emission spectrum could not be measured upon longer-wavelength excitation. FLUPS spectra recorded at various time delays after 425 nm excitation of BPEA in CHX are presented in Fig. 4A. Global analysis assuming a series of four successive exponential steps with increasing time constants could appropriately reproduce these data. The resulting-evolution associated spectra (EAS) and time constants are shown in Fig. S7 (ESI†). These spectra cannot be necessarily attributed to a given state/species but allow for a visualisation of the spectral dynamics.^60,61 For the same reason, the time constants reflect the timescale of the spectral dynamics. The early emission spectrum is broad and structureless. In the transition dipole representation,⁶² it bears a strong resemblance with the mirror image of the absorption spectrum, as illustrated in Fig. 4B. This early spectrum suggests the onset of a shoulder above 22 400 cm⁻¹. The emission in this range is at a higher energy than the S₁ (v = 0) ← S₀ (v = 0) transition of planar molecules, which can be estimated to be around 21 800 cm⁻¹. It could thus arise from a vibrationally excited state, i.e. S₁ (v ≥ 1) → S₀ (v = 0), or from the S₁ (v = 0) → S₀ (v = 0) emission of strongly distorted molecules. According to the quantum-chemical calculations discussed above, the emission from distorted molecules should remain below 22 700 cm⁻¹ (i.e. 21 800 + 840 cm⁻¹) at room temperature. On the other hand, according to the vibrational progression of the fluorescence band, the S₁ (v = 1) → S₀ (v = 0) transition should be around 22 700 cm⁻¹. Most probably, both phenomena contribute this high-energy emission.

Fig. 4 (A) Transient fluorescence spectra recorded at various time delays after 425 nm excitation of BPEA in cyclohexane. (B) Comparison of the early transient fluorescence spectrum with the stationary fluorescence and absorption spectra in the transition dipole representation.

During the first ps, the high-energy side of the spectrum undergoes a significant narrowing and a vibronic structure starts to appear. During the next ∼10 ps, the spectrum becomes more structured and the band area increases. Afterwards, the spectral shape remains unchanged, and the intensity decreases slowly, in agreement with the nanosecond fluorescence lifetime of BPEA.⁴⁷ No significant difference in the FLUPS spectra could be observed upon 375 and 400 nm excitation (Fig. S8, ESI†).

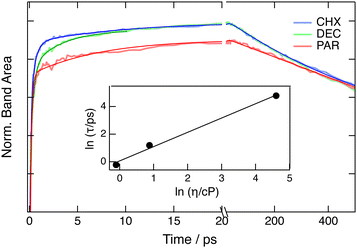
The FLUPS spectra measured in DEC and PAR show qualitatively the same dynamics as those in CHX. Global analysis reveals that the initial narrowing on the blue side of the spectrum occurs on a similar timescale in all three solvents (Fig. S9, ESI†). However, in PAR, the final stage of the spectral dynamics is associated with significantly slower time constants, of the order of 100 ps, than in CHX and DEC, where the spectrum reaches its final equilibrated shape with 5–10 ps time constants.

To try to better quantify these spectral dynamics and determine the effect of the viscosity and possibly of the excitation wavelength, two approaches were tested.

(i) The increase of the emission band area should reflect the increase of the oscillator strength upon planarization. As depicted in Fig. 5 with measurements upon 425 nm excitation, about 70% of the total rise occurs within 200 fs in all three solvents. Afterwards, the rise shows a distinct solvent dependence. Intensity normalisation of these time profiles by tail matching reveals that the kinetics in DEC merge with those in CHX after about 10 ps, while it takes more than 200 ps for those in PAR. Multiexponential analysis was performed to isolate the viscosity-dependent component of the rise. Its time constant varies from about 0.7 ps in CHX to more than 100 ps in PAR (Table S2, ESI†). A weak ≈10 ps rising component is also visible in all three solvents. It is tentatively assigned to vibrational cooling. The viscosity dependence of a time constant associated with large-amplitude motion is usually well reproduced using the following expression:⁶³

τ = Cη^α, (2)

where the exponent α ranges typically from 0.1 to 1. The inset of Fig. 5 shows a log–log plot of the solvent-dependent time constant vs. viscosity together with the best fit of eqn (2) with α = 1.03 ± 0.08. This result suggests that a large fraction of the structural relaxation of BPEA occurs via inertial motion, i.e. is independent of the solvent. This is consistent with the fluorescence data in polymers, showing that partial structural relaxation can occur even in a rigid environment. However, full equilibration requires the displacement of the surrounding solvent, hence diffusive motion. No significant excitation wavelength dependence of the band area dynamics could be detected.

Fig. 5 Time evolutions of the fluorescence band area measured upon 425 nm excitation in different solvents and normalised by tail matching with best multiexponential fits. Inset: log–log plot of the solvent-dependent rise time vs. viscosity and best fit of eqn (2). (CHX: cyclohexane; DEC: decaline; PAR: paraffin oil.)

(ii) The appearance of a vibronic structure in the emission spectrum reflects the decrease of the torsional disorder due to the steeper excited state potential, hence a decrease of inhomogeneous broadening. To quantify this process, the convolution of a late, >1 ns, FLUPS spectrum, corresponding to the equilibrated S₁ state, with the broadening function, f([small nu, Greek, macron]) (eqn (1)) was fitted to earlier FLUPS spectra. As illustrated in Fig. 6A with the data measured upon 425 nm excitation, the FLUPS spectra recorded after about 300 fs could be well reproduced using a fixed [small nu, Greek, macron]₀ value but a varying damping constant β. The fit to earlier FLUPS spectra was not as satisfactory and, consequently, these data were not considered. This disagreement is mostly due to the neglect of the emission from a vibrationally excited state, which appears at a shorter wavelength. Fig. 6B indicates that the damping parameter amounts initially to less than 2 × 10⁻³ cm and increases continuously above 8 × 10⁻³ cm. This change of β points to an important decrease of the inhomogeneous broadening upon excitation, as expected. In CHX, the increase of β could be well reproduced using an exponential function with a 3.1 ps time constant. The increase is significantly slower in DEC and PAR and required the sum of two or three exponential functions to be reproduced with average time constants of 7.1 and 135 ps, respectively. The analysis of the viscosity dependence of this average time constant using eqn (2) yields an α value of 0.80 ± 0.02 (Fig. S10, ESI†). In this case again, no significant dependence on the excitation wavelength could be observed.

Fig. 6 (A) Best fits of the convolution of a late FLUPS spectrum with eqn (1) to the FLUPS spectra recorded at early times upon 425 nm excitation of BPEA in cyclohexane. The spectra were vertically shifted for better visualisation. Inset: broadening function, f([small nu, Greek, macron]) (eqn (1)), used to reproduce the FLUPS spectra. (B) Time evolutions of the damping constant, β, used to reproduce the FLUPS spectra measured in cyclohexane (CHX), decaline (DEC) and paraffin oil (PAR) and best (multi)-exponential fits.

Both approaches result in similar α values. In the first one, only the solvent-dependent rising component of the band area is taken into account. The second one cannot be used for the early part of the spectral dynamics, because it presupposes that the Franck–Condon factors do not change with time, which is clearly not valid on timescales where vibrational relaxation is taking place. Therefore, neither of these approaches consider the inertial friction-independent part of structural relaxation.

3.4 Electronic transient absorption spectroscopy (TA)

TA spectra recorded in CHX at various delays upon 400 and 470 nm photoexcitation of BPEA are presented in Fig. 7A and B. Whereas 400 nm corresponds to the blue edge of the S₁ ← S₀ absorption band and should lead to the excitation of torsionally disordered molecules, 470 nm is at the red edge of the absorption band and should, in principle, result in the excitation of planar molecules only. The TA spectra are dominated by two positive bands which can be assigned to the excited state absorption (ESA), ESA_red between 500 and 600 nm, and ESA_blue between 350 and 400 nm, and by negative features in between, which arise from the S₁ → S₀ stimulated emission (SE) and ground state bleach (GSB). At time delays larger than about 50 ps, the TA spectra and their dynamics are the same at both excitation wavelengths: all bands decay on a ns timescale in agreement with the excited state lifetime of BPEA. Consequently, the ESA and SE bands can be assigned to the fully equilibrated S₁ state.

Fig. 7 Transient electronic absorption spectra recorded at various time delays after 400 nm (A and C) or 470 nm (B and D) excitation of BPEA in cyclohexane (A and B) and polyvinylbutyral films (C and D).

In contrast, significant dependence on the excitation wavelength can be observed in the early TA spectra. Upon 400 nm excitation, the negative band is initially broad and structureless. This band narrows rapidly and a vibronic structure coinciding with the fluorescence spectrum develops above 480 nm. In parallel, the intensity of ESA_red increases by about 50% whereas the low-energy side of ESA_blue narrows significantly. None of these initial spectral dynamics can be observed upon 470 nm excitation. However, a sharp negative feature is visible around 440 nm and decays on the 1 ps timescale, in parallel with a decrease of the main negative band around 470 nm. The TA spectra recorded in DEC and PAR are essentially the same as in CHX and exhibit an identical dependence on the excitation wavelength (Fig. S11 and S12, ESI†). The only difference is that the effect of the excitation wavelength vanishes at later time than that in CHX. TA measurements in DEC were also carried out upon 450 nm excitation, i.e. at the maximum of the S₁ ← S₀ absorption band. The resulting TA dynamics are very similar to those measured upon 400 nm excitation (Fig. S11, ESI†).

These differences in the early spectral dynamics can undoubtedly be attributed to the occurrence of vibrational and structural relaxation upon 400 nm excitation. The transformation of the negative band from broad to structured coincides with that observed by FLUPS and was, thus, not further investigated. On the other hand, about 60% of the increase of ESA_red occurs within the IRF in CHX, and the remaining part can be reproduced using the sum of two exponential functions with an amplitude-averaged time constant of 3 ps, in good agreement with that obtained from the analysis of the FLUPS spectra using approach (ii). These slower rising dynamics exhibit a distinct viscosity dependence as illustrated in Fig. 8, which can also be reproduced by a sum of exponential functions. The analysis of the amplitude-averaged time constant using eqn (2) gives an α value of 0.7 ± 0.1, in good agreement with those obtained from the analysis of the FLUPS data. The time evolution of the area of the low-energy side of ESA_blue requires the sum of at least three exponential functions to be appropriately reproduced. However, the total amplitude of this decay is too small to extract reliable time constants. As a consequence, it was not really possible to separate viscosity-dependent from viscosity-independent decay components.

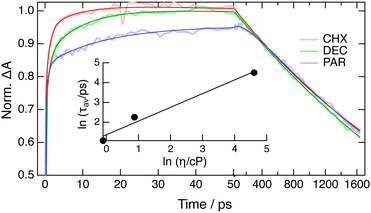Fig. 8 Time profiles of the band area of ESA_red in different solvents normalised by tail matching with best multiexponential fits. Inset: Viscosity dependence of the amplitude-averaged time constant and best fit of eqn (2). (CHX: cyclohexane; DEC: decaline; PAR: paraffin oil.)

The sharp negative feature at 440 nm present in the early spectra upon 470 nm excitation coincides with the first vibronic of the S₁ ← S₀ absorption spectrum recorded at low temperatures (Fig. S13A, ESI†). It can, thus, be attributed to the GSB of planar BPEA molecules. This sharp vibronic transforms rapidly into a broad shoulder, which overlaps well with the room temperature absorption spectrum (Fig. S13B, ESI†). This broad feature can be attributed to the GSB of torsionally disordered molecules. Consequently, these spectral changes of the GSB can be interpreted as the equilibration of the ground state population after the selective excitation of planar molecules. In other words, 470 nm excitation creates a hole in the distribution of ground state geometries, which partially refills upon re-equilibration. This is equivalent to the decay of a spectral hole by spectral diffusion.^64,65 Consequently, the dynamics of these GSB changes reflect the thermal fluctuations of the torsional angle in the ground state. In all three solvents, the decay of the 440 nm band area could be reproduced using a biexponential function, with both components slowing down with increasing viscosity (Fig. S14, ESI†). The analysis of this dependence with eqn (2) using the amplitude-averaged time constants yielded an α value of 1.05 ± 0.1. This suggests that ground state planarization is purely diffusive, in contrast to the same process in the S₁ state, which occurs partially via inertial motion.

TA measurements were also carried out in PVB and Zeonex films upon 400 and 470 nm excitation (Fig. 7C, D and Fig. S15, ESI†). Unfortunately, the scattering of the pump pulse could not be eliminated and, thus, the spectral region around the excitation wavelength is not available. Despite this, it is immediately clear that the effect of the pump wavelength on the early TA dynamics is significantly smaller than in liquids. For example, upon 400 nm excitation, the intensity of ESA_red increases by about 15% in films vs. 50% in liquids (Fig. 7A and C). Similarly, the spectral dynamics in the SE and GSB regions are still present in films but weaker than that in liquids. In liquids, the late spectra are the same at both excitation wavelengths, indicating full equilibration. In films, however, differences can still be noticed after 1.7 ns: the vibronic feature of the SE around 510 nm is more pronounced upon 470 than 400 nm excitation. This indicates that structural relaxation is only partial in films. This is consistent with the stationary spectra that show non-mirror-image relationship in films but a weaker vibronic structure in the emission compared to liquids.

Although the GSB band is largely hidden because of the scattering, the high-energy side of the 440 nm GSB vibronic is still visible. In contrast to the liquids, no spectral change can be observed in this region, suggesting that, in the ground state, structural reequilibration along the torsional coordinate is totally inhibited in polymer films.

A close inspection of the TA data in the negative band region reveals the presence of periodic oscillations of the TA intensity that can be assigned to vibrational coherence. They are the strongest at the two sides of the 470 nm band and disappear at the maximum. However, they can still be detected around 490 nm where the negative band is only due to SE and at 440 nm where it arises from GSB only. As shown in Fig. 9A, the oscillations on the red and blue sides of the main negative band are approximately π out-of-phase. Consequently, they can be attributed to vibrational coherences in both the electronic ground state and the excited states. They are present in all three solvents independently of the excitation wavelength. The signal-to-noise ratio in polymer films was not sufficient to resolve them. The Fourier-transform spectra point to two main vibrational modes, around 175 and 390 cm⁻¹. These two frequencies coincide well with those of the FC-active modes obtained from the quantum-chemical calculations at 160 and 382 cm⁻¹. As illustrated in Fig. 9B, they involve in-plane symmetric displacement of the two phenyl rings and distortion of the anthracene sub-units, respectively.

Fig. 9 (A) Residuals from a multiexponential analysis of the transient absorption data measured upon the 400 nm excitation of BPEA in CHX, averaged over the red and blue sides of the negative band at 470 nm. (B) Fourier-transform spectrum of the red side residuals together with the displacement vectors of two FC-active vibrations predicted from quantum-chemical calculations.

4 Discussion

The results described above converge towards a coherent picture of the effect of torsional disorder and planarization on the photocycle of BPEA in the condensed phase. The effect of temperature on the stationary absorption spectrum and the excitation wavelength dependence of the TA spectra, together with the quantum-chemical calculations are consistent with the coexistence of BPEA molecules in the electronic ground state with different dihedral angles of the phenyl groups relative to the anthracene moiety and distinct S₁–S₀ energy gaps. The strong spectral dynamics of the fluorescence, namely, the transition from a broad to a structured emission spectrum and the ability to reproduce most of these dynamics with a simple model based on eqn (1) indicate a significant reduction of the distribution of dihedral angles in the S₁ state, again in full agreement with the steeper potential for torsion in the excited state predicted by the quantum-chemical calculations.

The inhomogeneous nature of the S₁ ← S₀ absorption band implies that selective photoexcitation of subpopulations with distinct torsional angles should be possible. However, the FLUPS measurements did not show any significant excitation wavelength dependence between 375 and 425 nm. Similarly the TA dynamics are the same upon 400 and 450 nm excitation. An excitation wavelength dependence is only observed when excited at 470 nm, i.e. on the red-edge of the band. This result is fully consistent with previous investigations of the effect of the excitation wavelength on the excited state properties of organic molecules.^13,66–72 Red-edge irradiation ensures that only a single sub-population, with the smallest 0–0 transition energy, is excited. Higher-energy can excite the 0–0 transition of other sub-populations and vibronic transitions of sub-populations with smaller 0–0 gaps.

The results point to different viscosity dependence of planarization dynamics in the ground and excited states. It is a purely diffusive process in the ground state, whereas a large fraction of these dynamics in the S₁ state is ultrafast, independent of the solvent viscosity, and should, thus, involve inertial motion. This difference can be attributed to the S₀ and S₁ potentials along the torsional coordinate. This potential is very shallow in the ground state and, thus, the force experienced by a distorted molecule towards planarization is significantly smaller than the random forces due to interactions with the surrounding solvent. For this reason, the S₁ ← S₀ absorption band of BPEA in polymers does not show any significant change upon lowering the temperature. The forces toward planarization are too weak compared to friction for the distribution of the torsional angle to equilibrate to the new temperature.

In contrast, the steeper potential in the S₁ state implies that distorted molecules that were in thermal equilibrium in the ground state are far from equilibrium upon photoexcitation to the S₁ state. They are, thus, highly strained and experience strong forces toward planarization. Most probably, the latter enable for partial relaxation along the torsional coordinate with minor motion of the surrounding solvent molecules. This process is essentially independent of the solvent viscosity and can be considered as inertial.⁷³ As a consequence, this partial structural relaxation is also operative in polymer films as revealed by the TA measurements and the structured emission spectrum.

One could argue that the viscosity-independent part of the spectral dynamics is in fact due to vibrational relaxation (VR). Short-wavelength irradiation excites not only the 0–0 transition of distorted molecules but also vibronic transitions. VR can probably be observed in the early FLUPS spectra as the decay of the emission above 22 000 cm⁻¹. This decay is concurrent with the fastest rising component of the emission band area, which itself occurs on the similar timescale as the increase of the ESA_red intensity. However, these viscosity-independent dynamics can be largely attributed to structural relaxation for at least three reasons:

(1) Apart from the high energy shoulder, the early FLUPS emission spectrum is close to the mirror-image of the absorption spectrum. As a consequence, it can be assigned to the emission from an ensemble of excited molecules with essentially the same distribution of the torsion angle as that of the equilibrium ground state. The early spectral dynamics should, thus, be mostly related to a narrowing of this distribution.

(2) The FLUPS dynamics do not exhibit significant differences between 375 and 425 nm excitation, although this corresponds to an energy difference of about 3100 cm⁻¹. Similarly, the TA dynamics in DEC are essentially the same upon 400 and 450 nm excitation, despite an energy difference of about 2800 cm⁻¹. This indicates that apart from the decay of the high-energy shoulder of the fluorescence spectrum, VR is hardly visible in the emission and TA spectra. The most probable reason for this is that, according to the quantum-chemical calculations, only three among the 66 low-frequency vibrational modes of BPEA, <1000 cm⁻¹, show significant FC activity.

(3) In polymer films, where structural relaxation is only partial, the increase of the ESA_red intensity in the TA data just after excitation is much smaller than that in liquids. As VR is also operative in polymers, this implies that the increase of the ESA_red intensity reflects mostly structural relaxation.

5 Conclusions

We presented a detailed investigation of the excited state dynamics of BPEA in liquids and polymer films, which are dominated by structural relaxation. This can, thus, be considered a case study to better understand the role of torsional disorder, frequently encountered with conjugated molecules containing phenylethene or phenylethylene building blocks and multichromophoric systems. Using temperature-dependent measurements, we could establish that, at room temperature, the absorption spectrum is inhomogeneously broadened, in contrast to the emission spectrum from the equilibrated excited state. This allows for the selective photo-excitation of planar molecules through red-edge irradiation. These excited planar molecules exhibit little dynamics except for their return to the ground state on the ns timescale. In contrast, dynamics are observed in the ground state, because of the re-equilibration of the torsional disorder. This phenomenon gives access to the planarization dynamics of BPEA in the ground state. Shorter wavelengths excite torsionally disordered molecules, which exhibit significant spectral dynamics, giving access to the planarization of BPEA in the excited state. The nature of this planarization motion, i.e. purely diffusive or partially inertial, depends strongly on the steepness of the associated potential. One can anticipate that it should also depend on the size of the moving groups. Going to more bulky groups than phenyl can be expected to reduce the contribution of the inertial motion.

This excitation wavelength dependence of the excited state dynamics of this type of molecules, also observed by Roy et al.,¹³ makes them potential candidates for the exploration of non-Kasha photoinduced processes.^74,75 For example, intramolecular electron and energy transfer between the donor and the acceptor connected via a phenylethylene bridge are expected to depend on the dihedral angle between the two subunits.^76–78 To the best of our knowledge, the effect of the excitation wavelength on these dynamics has not been investigated so far.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Swiss National Science Foundation (grant 200020-184607) and the University of Geneva for financial support.

Notes and references

1. J. L. Delgado, P.-A. Bouit, S. Filippone, M. A. Herranz and N. Martín, Chem. Commun., 2010, 46, 4853–4865.
2. A. J. Heeger, Adv. Mater., 2014, 26, 10–28.
3. S. D. Dimitrov and J. R. Durrant, Chem. Mater., 2014, 26, 616–630.
4. O. Inganäs, Adv. Mater., 2018, 30, 1800388.
5. C. An, Z. Zheng and J. Hou, Chem. Commun., 2020, 56, 4750–4760.
6. J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539–541.
7. J. M. Tour, Acc. Chem. Res., 2000, 33, 791–804.
8. U. H. F. Bunz, Chem. Rev., 2000, 100, 1605–1644.
9. N. Robertson and C. A. McGowan, Chem. Soc. Rev., 2003, 32, 96–103.
10. M. R. Bryce, J. Mater. Chem. C, 2021, 9, 10524–10546.
11. M. I. Sluch, A. Godt, U. H. F. Bunz and M. A. Berg, J. Am. Chem. Soc., 2001, 123, 6447–6448.
12. G. Duvanel, J. Grilj, A. Schuwey, A. Gossauer and E. Vauthey, Photochem. Photobiol. Sci., 2007, 6, 956–963.
13. K. Roy, S. Kayal, V. Ravi Kumar, A. Beeby, F. Ariese and S. Umapathy, J. Phys. Chem. A, 2017, 121, 6538–6546.
14. A. Beeby, K. Findlay, P. J. Low and T. B. Marder, J. Am. Chem. Soc., 2002, 124, 8280–8284.
15. S. Kayal, K. Roy and S. Umapathy, J. Chem. Phys., 2018, 148, 024301.
16. Q. Verolet, A. Rosspeintner, S. Soleimanpour, N. Sakai, E. Vauthey and S. Matile, J. Am. Chem. Soc., 2015, 137, 15644–15647.
17. H. Song, H. Zhao, Y. Guo, A. M. Philip, Q. Guo, M. Hariharan and A. Xia, J. Phys. Chem. C, 2020, 124, 237–245.
18. J. García-Calvo, J. Maillard, I. Fureraj, K. Strakova, A. Colom, V. Mercier, A. Roux, E. Vauthey, N. Sakai, A. Fürstenberg and S. Matile, J. Am. Chem. Soc., 2020, 142, 12034–12038.
19. M.-H. Chang, M. Hoffmann, H. L. Anderson and L. M. Herz, J. Am. Chem. Soc., 2008, 130, 10171–10178.
20. F. V. A. Camargo, H. L. Anderson, S. R. Meech and I. A. Heisler, J. Phys. Chem. B, 2015, 119, 14660–14667.
21. F. V. A. Camargo, C. R. Hall, H. L. Anderson, S. R. Meech and I. A. Heisler, Struct. Dyn., 2016, 3, 023608.
22. K. H. Park, P. Kim, W. Kim, H. Shimizu, M. Han, E. Sim, M. Iyoda and D. Kim, Angew. Chem., Int. Ed., 2015, 54, 12711–12715.
23. P. Kim, K. H. Park, W. Kim, T. Tamachi, M. Iyoda and D. Kim, J. Phys. Chem. Lett., 2015, 6, 451–456.
24. R. J. Magyar, S. Tretiak, Y. Gao, H. L. Wang and A. P. Shreve, Chem. Phys. Lett., 2005, 401, 149–156.
25. R. Binder, D. Lauvergnat and I. Burghardt, Phys. Rev. Lett., 2018, 120, 227401.
26. R. Binder and I. Burghardt, J. Chem. Phys., 2020, 152, 204120.
27. M. Dal Molin, Q. Verolet, A. Colom, R. Letrun, E. Derivery, M. Gonzalez-Gaitan, E. Vauthey, A. Roux, N. Sakai and S. Matile, J. Am. Chem. Soc., 2015, 137, 568–571.
28. K. Straková, J. López-Andarias, N. Jiménez-Rojo, J. E. Chambers, S. J. Marciniak, H. Riezman, N. Sakai and S. Matile, ACS Cent. Sci., 2020, 6, 1376–1385.
29. M. M. Martin, P. Plaza, P. Changenet-Barret and A. Siemiarczuk, J. Phys. Chem. A, 2002, 106, 2351–2358.
30. Z. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4031.
31. G. Duvanel, J. Grilj, H. Chaumeil, P. Jacques and E. Vauthey, Photochem. Photobiol. Sci., 2010, 9, 908–915.
32. S. Sasaki, G. P. C. Drummen and G.-I. Konishi, J. Mater. Chem. C, 2016, 4, 2731–2743.
33. P. J. Hanhela and D. B. Paul, Aust. J. Chem., 1981, 34, 1701–1717.
34. J. Lukacs, R. A. Lampert, J. Metclafe and D. Phillips, J. Photochem. Photobiol., A, 1992, 63, 59–65.
35. S. S. Babu, M. J. Hollamby, J. Aimi, H. Ozawa, A. Saeki, S. Seki, K. Kobayashi, K. Hagiwara, M. Yoshizawa, H. Möhwald and T. Nakanishi, Nat. Commun., 2013, 4, 1969.
36. X. Cai, D. Ji, L. Jiang, G. Zhao, J. Tan, G. Tian, J. Li and W. Hu, Appl. Phys. Lett., 2014, 104, 063305.
37. J. Liu, J. Liu, Z. Zhang, C. Xu, Q. Li, K. Zhou, H. Dong, X. Zhang and W. Hu, J. Mater. Chem. C, 2017, 5, 2519–2523.
38. Z. Feng, T. Hai, Y. Liang, Q. Zhang and Y. Lei, Angew. Chem., Int. Ed., 2021, 60, 27046–27052.
39. D. Xiao, Y. Xian, L. Liu, Z. Gu and B. Wen, New J. Chem., 2014, 38, 902–905.
40. F. Zhong and J. Zhao, Dyes Pigm., 2017, 136, 909–918.
41. N. Nishimura, V. Gray, J. R. Allardice, Z. Zhang, A. Pershin, D. Beljonne and A. Rao, ACS Mater. Lett., 2019, 1, 660–664.
42. Y. Wei, Y. Li, Z. Li, X. Xu, X. Cao, X. Zhou and C. Yang, Inorg. Chem., 2021, 60, 19001–19008.
43. Y. J. Bae, G. Kang, C. D. Malliakas, J. N. Nelson, J. Zhou, R. M. Young, Y.-L. Wu, R. P. Van Duyne, G. C. Schatz and M. R. Wasielewski, J. Am. Chem. Soc., 2018, 140, 15140–15144.
44. B. Manna, A. Nandi and R. Ghosh, J. Phys. Chem. C, 2018, 122, 21047–21055.
45. S. Fan, W. Li, T. Li, F. Gao, W. Hu, S. Liu, X. Wang, H. Liu, Z. Liu, Z. Li, Y. Chen and X. Li, J. Photochem. Photobiol., A, 2022, 427, 113826.
46. M. Levitus and M. A. Garcia-Garibay, J. Phys. Chem. A, 2000, 104, 8632–8637.
47. A. Demeter, J. Phys. Chem. A, 2014, 118, 9985–9993.
48. A. Beeby, K. S. Findlay, A. E. Goeta, L. Porres, S. R. Rutter and A. L. Thompson, Photochem. Photobiol. Sci., 2007, 6, 982–986.
49. J. A. Gardecki and M. Maroncelli, Appl. Spectrosc., 1998, 52, 1179–1189.
50. Z. Szakacs, M. Tasior, D. Gryko and E. Vauthey, ChemPhysChem, 2020, 21, 1718–1730.
51. X.-X. Zhang, C. Würth, L. Zhao, U. Resch-Genger, N. P. Ernsting and M. Sajadi, Rev. Sci. Instrum., 2011, 82, 063108.
52. A. Aster, G. Licari, F. Zinna, E. Brun, T. Kumpulainen, E. Tajkhorshid, J. Lacour and E. Vauthey, Chem. Sci., 2019, 10, 10629–10639.
53. J. S. Beckwith, A. Aster and E. Vauthey, Phys. Chem. Chem. Phys., 2022, 24, 568–577.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Revision B, Gaussian Inc., Wallingford CT, 2016.
55. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
56. F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311.
57. D. J. I. Russell, NIST Computational Chemistry Comparison and Benchmark Database, Release 22, May 2022, http://cccbdb.nist.gov/.
58. K. S. Pitzer, Discuss. Faraday Soc., 1951, 10, 66–73.
59. S. J. Greaves, E. L. Flynn, E. L. Futcher, E. Wrede, D. P. Lydon, P. J. Low, S. R. Rutter and A. Beeby, J. Phys. Chem. A, 2006, 110, 2114–2121.
60. I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104.
61. J. S. Beckwith, C. A. Rumble and E. Vauthey, Int. Rev. Phys. Chem., 2020, 39, 135–216.
62. G. Angulo, G. Grampp and A. Rosspeintner, Spectrochim. Acta, Part A, 2006, 65, 727–731.
63. B. Bagchi, Chem. Phys. Lett., 1987, 138, 315–320.
64. J. Friedrich and D. Haarer, Angew. Chem., Int. Ed. Engl., 1984, 23, 113–140.
65. T. Basché, W. P. Ambrose and W. E. Moerner, J. Opt. Soc. Am. B, 1992, 9, 829–836.
66. W. C. Galley and R. M. Purkey, Proc. Natl. Acad. Sci. U. S. A., 1970, 67, 1116–1121.
67. K. Itoh and T. Azumi, J. Chem. Phys., 1975, 62, 3431–3438.
68. R. S. Fee, J. A. Milsom and M. Maroncelli, J. Phys. Chem., 1991, 95, 5170–5181.
69. M. Morgenthaler, S. Meech and K. Yoshihara, Chem. Phys. Lett., 1992, 197, 537–541.
70. P. K. Mandal, M. Sarkar and A. Samanta, J. Phys. Chem. A, 2004, 108, 9048–9053.
71. O. Nicolet, N. Banerji, S. Pagès and E. Vauthey, J. Phys. Chem. A, 2005, 109, 8236–8245.
72. R. Letrun and E. Vauthey, J. Phys. Chem. Lett., 2014, 5, 1685–1690.
73. Y. Zhang, M. I. Sluch, M. M. Somoza and M. A. Berg, J. Chem. Phys., 2001, 115, 4212–4222.
74. A. P. Demchenko, V. I. Tomin and P.-T. Chou, Chem. Rev., 2017, 117, 13353–13381.
75. T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939.
76. A. C. Benniston, A. Harriman, P. Li, P. V. Patel and C. A. Sams, Phys. Chem. Chem. Phys., 2005, 7, 3677–3679.
77. B. Albinsson and J. Mårtensson, J. Photochem. Photobiol., C, 2008, 9, 138–155.
78. O. S. Wenger, Acc. Chem. Res., 2011, 44, 25–35.

---

Footnote

† Electronic supplementary information (ESI) available: Results from quantum-chemical calculations, stationary spectroscopic data, FLUPS spectra and results from global analysis and TA spectra. All data can be downloaded from https://doi.org/10.26037/yareta:kludip3sovhwrmslm7grhjzboq. See DOI: https://doi.org/10.1039/d2cp03909e

---