Homogeneous freezing of water droplets for different volumes and cooling rates

Abstract

To understand the crystallization of aqueous solutions in the atmosphere, biological specimens, or pharmaceutical formulations, the rate at which ice nucleates from pure liquid water must be quantified. There is still an orders-of-magnitude spread in the homogeneous nucleation rate of water measured using different instruments, with the most important source of uncertainty being that of the measured temperature. Microfluidic platforms can generate hundreds to thousands of monodisperse water-in-oil droplets, unachievable by most other techniques. However, most microfluidic devices previously used to quantify homogeneous ice nucleation rates have reported high temperature uncertainties, between ±0.3 and ±0.7 K. We use the recently developed Microfluidic Ice Nuclei Counter Zurich (MINCZ) to observe the freezing of spherical water droplets with two diameters (75 and 100 μm) at two cooling rates (1 and 0.1 K min⁻¹). By varying both droplet volume and cooling rate, we were able to probe a temperature range of 236.5–239.3 K with an accuracy of ±0.2 K, providing reliable data where previously determined nucleation rates suffered from large uncertainties and inconsistencies, especially at temperatures above 238 K. From these data and from Monte Carlo simulations, we demonstrate the importance of obtaining a sufficiently large dataset so that underlying nucleation rates are not overestimated at higher temperatures. Finally, we obtain new parameters for a previous parameterisation by fitting to our newly measured nucleation rates, enabling its use in applications where ice formation needs to be predicted.

---

1. Introduction

The melting point of pure, bulk water at atmospheric pressure is 273.15 K (0 °C). This point is given by the thermodynamic requirement for the equality of chemical potentials between the solid and liquid phases at constant temperature and pressure. At atmospheric pressure and temperatures below 273.15 K, ice is the thermodynamically preferred state. However, a free energy barrier must be overcome for an ice phase to emerge out of liquid water.^1–5 It is the presence of this barrier that renders the liquid phase metastable and inhibits freezing even well below 273.15 K. A liquid in such a metastable state and below its melting point is termed supercooled. As temperature decreases and supercooling increases, the magnitude of the free energy barrier decreases, and the formation of the ice phase becomes statistically more likely. This statistical likelihood is quantified by the homogeneous nucleation rate, which describes how many nucleation events are expected to occur per unit of liquid volume per unit time.

Quantifying the nucleation rate of water is important in applications where ice nucleation is to be controlled or predicted. Controlling ice formation and/or growth is a concern in cryobiology,⁶ pharmaceutical science,^7–9 materials science,¹⁰ food preservation,¹¹ agriculture,¹² and construction.^13,14 In the atmosphere, predicting ice formation is important to determine the radiative balance of the Earth and the amount and frequency of continental precipitation.^15,16 Increasing the concentration of a soluble additive such as salt reduces water activity and lowers the freezing temperature of the aqueous solution (e.g., Koop et al.¹⁷). On the other hand, some soluble (e.g., macromolecules) and insoluble substances (e.g., mineral dust) are known to promote ice nucleation at temperatures greater than those observed for pure water.^15,18,19 In this case, the process is known as heterogeneous nucleation, since ice formation is catalysed by the presence of a substance other than water. As the volume of water decreases, however, it becomes more likely that there are no ice-promoting impurities in the water, rendering homogeneous nucleation the only pathway to ice. Micrometer-sized droplets found in the atmosphere, therefore, lack heterogeneous nucleation sites. In other applications where water is rarely devoid of ice-promoting impurities, the nucleation rate of pure water must be quantified before the magnitude of an additive's effect can be ascertained.

Despite the importance of ice nucleation across disciplines, the precise thermodynamic and kinetic contributions to its formation remain elusive, in part because experimental measurements have yielded nucleation rates that vary by orders of magnitude.^3,20,21 As stated by Ickes et al.,³ reducing the spread in measured nucleation rates would help to better constrain the thermodynamic and kinetic parameters used in classical nucleation theory (CNT) to describe homogeneous nucleation; in particular, there is a necessity for better experimental control and uncertainty estimation of temperature, droplet volume, and time. It has been shown that temperature uncertainty is the largest contributing factor to the spread in reported nucleation rates.²² Cold stage instruments and differential scanning calorimeters are typically associated with an accuracy in temperature near ±0.5 K.³ While the studies performed with an electrodynamic balance are able to detect temperature changes with a resolution of ±0.025 K, they estimate a factor-of-ten lower accuracy of ±0.25 K for droplet temperature.²³ The accuracy of droplet temperature is compromised because thermocouples are placed at a distance from the droplets, and there may be a difference in temperature between the thermocouple and droplet location.²³ Moreover, because droplets continuously evaporate (e.g., Krämer et al.²⁴ and Stöckel et al.²³), the droplet temperature is actually lower than the ambient temperature measured by the thermocouple; the estimation of this difference in temperature introduces an additional source of uncertainty to the accuracy of reported measurements.

Microfluidic devices represent a promising alternative for investigating nucleation rates. They allow the precise control of fluid flow through μm-sized channels to robustly generate monodisperse populations of water-in-oil droplets that can be used in a variety of applications.^25–27 However, microfluidic platforms previously developed for studying ice formation have used cold stages to control temperature,^28–30 with uncertainties in temperature remaining between ±0.3 K and ±0.7 K (as summarized by Tarn et al.²¹). Additionally, these instruments have typically been used to investigate only a narrow range of temperatures (the difference between minimum and maximum temperature ranging from 1 K²⁸ to 1.8 K^21,31). As a result of their temperature uncertainties, nucleation rates for the homogeneous freezing of water obtained using microfluidically-produced droplets on cold stages span orders of magnitude. To improve temperature accuracy, we recently developed and validated the Microfluidic Ice Nuclei Counter Zurich (MINCZ),³² which uses an ethanol bath to improve temperature equilibration, and thermocouples are placed in the same vicinity as the droplets (described in detail in Section 2.1).

As highlighted by Tarn et al.,²¹ there is a lack of dedicated studies that use microfluidic platforms to measure the homogeneous nucleation rate of water with accuracy and precision. Herbert et al.³³ further emphasised the lack of experimental data and consensus on the homogeneous nucleation rate of water specifically at temperatures greater than 238 K, citing the necessity of such data as inputs to climate and weather models. The goal of this study is to close this knowledge gap by providing an accurate and precise dataset over a wider temperature range using a single instrument: MINCZ.³² To widen the temperature range, we determine the nucleation rate of spherical water-in-oil droplets having diameters of 75 μm and 100 μm at two cooling rates (0.1 and 1 K min⁻¹). We evaluate previous measurements within their temperature uncertainties and constrain the nucleation rate across a range of 2.8 K from 236.5 K to 239.3 K that was previously characterised by discontinuous clusters of data from separate instruments. Additionally, we perform Monte Carlo simulations of droplets freezing in MINCZ to investigate the effect of droplet number on extracting the underlying nucleation rates that govern freezing behaviour. We use the insights gleaned from the Monte Carlo simulations to interpret our experimental results by combining independent experiments into a cumulative frozen fraction before calculating nucleation rates.

2. Methods

2.1. Experimental materials and methods

We employed the Microfluidic Ice Nuclei Counter Zurich (MINCZ), presented and described by Isenrich et al.³² A microfluidic device with a channel geometry previously reported in Isenrich et al.³² was used to generate spherical droplets with an average diameter of 75 μm. A new channel geometry was used to generate droplets having an average diameter of 100 μm, featuring different channel heights for droplet generation and droplet imaging (see ESI† for details). Microchannel circuits were drawn in AutoCAD® (Autodesk, San Rafael, USA) and patterned onto an SU-8 (Microchem Corporation, Westborough, USA) coated silicon wafer (10 mm diameter, 525 ± 25 μm thickness, 〈100〉 orientation, Siegert Wafer GmbH, Germany) using a mask aligner (UV-KUB3, Kloe, France) to align the two layers of different heights. Polydimethylsiloxane (PDMS) microfluidic devices with this design were fabricated using standard procedures, as outlined by Isenrich et al.³²

For all experiments, we used ultrapure water (molecular biology reagent grade, 0.1 μm filtered, Sigma-Aldrich, USA). Water-in-oil emulsions were stabilised by a fluorosurfactant (1% v/v 008-FluoroSurfactant (RAN Biotechnologies, USA)) in fluorinated HFE-7500 oil (3M™ Novec™ 7500, Interelec Electronics AG, Switzerland). The produced droplets left the chip from the outlet and flowed into a 50 cm length of high-purity perfluoroalkoxy alkane (PFA) tubing (360 μm OD, 75 μm or 100 μm ID, IDEX Health & Science LLC, USA), which was wrapped onto a polyether ether ketone (PEEK) holder. Three glass syringes (1 mL, Hamilton® syringe, Sigma-Aldrich) were each placed in a syringe pump (Aladdin AL1000-220Z, World Precision Instruments, USA) to control the flow rates of water, surfactant solution, and HFE-7500 spacer oil. Details of fluid flowrates used to obtain each individual population of droplets and the corresponding mean droplet diameters are included in the ESI.† Identification of potential variation in droplet diameter is limited by a measurement uncertainty of 5 μm. Within one droplet population, the droplet diameter varied within less than this measurement uncertainty.

As described by Isenrich et al.,³² the PFA tubing containing the droplets was immersed in an ethanol bath for cooling. The ethanol bath was cooled by a Peltier element (PKE 128A 0020 HR 150, Peltron GmbH, Germany) placed on an aluminium block through which heat was dissipated by an aqueous 55% v/v ethylene glycol (98% technical grade, Sigma-Aldrich, USA) solution circulated by a chiller (Huber KISS K6, Huber Kältemaschinenbau AG, Germany). Thermal paste ensured good contact and heat transfer between the aluminium block and the Peltier element. The Peltier element was driven by a power supply through a proportional controller implemented in Python. The Python-based interface allowed the user to prescribe a cooling rate and temperature range for each experiment. For experiments conducted at a rate of 1 K min⁻¹, the droplets were equilibrated to a temperature of approximately 248 K before controlled cooling was initiated; for experiments at a rate of 0.1 K min⁻¹, the equilibration temperature was approximately 243 K.

Two K-type thermocouples (0.5 mm OD, RS Components GmbH, Germany, and TC Direct, Germany) approximately 12 mm apart (see Fig. B1, ESI†) measured the temperature in the same plane as the droplets. The standard deviation of three measurements of the melting points of mercury and water with each thermocouple was 0.1 K.³² Over all the constant cooling rate experiments completed in the validation of our instrument³² and herein, the difference in the temperatures measured by the two thermocouples was 0.03 K with a standard deviation of 0.16 K. Droplet temperature is thus taken to be the average of the two thermocouple measurements, and we conservatively round the accuracy to 0.2 K for the droplet temperatures reported herein. There are two contributions to this accuracy. The first is that the inherent uncertainty of each thermocouple is ±0.1 K. The second is the possibility for slight variations in the positions of the thermocouples between independent experiments. To reduce the contribution of thermocouple position, the thermocouples are secured by two grooves in the PEEK tubing holder (Fig. B1, ESI†); nevertheless, it is possible for the thermocouple tips to move slightly. Since a vertical temperature gradient forms upon cooling, small variations in thermocouple position along the vertical axis could lead to slight differences in measured temperature. Overall, however, the positioning of both thermocouples in the same plane as the tubing immersed in the ethanol bath permits the accurate measurement of droplet temperature. We also confirm that there is no horizontal spatial bias in freezing behaviour, as shown in Fig. B2–B4 (ESI†).

A stereoscope (Nikon SMZ1270, 0.5× objective lens, fibre ring illuminator with LED light source) connected to a CMOS camera (iDS UI-3060CP-M-GL Rev. 2) was used during droplet generation and droplet cooling to obtain images. An image was saved every 3 s when cooling at 1 K min⁻¹ and every 30 s when cooling at 0.1 K min⁻¹, corresponding to a temperature interval of 0.05 K. Separate user interfaces facilitated the determination of droplet diameter and the semi-automated detection of droplet freezing, as described in Isenrich et al.,³² but with image processing parameters also tuned for analysing 100 μm diameter droplets.

2.2. Monte Carlo simulations

Homogeneous nucleation is described statistically as a Poisson process, so a droplet with volume V_d exposed to a temperature T for a duration Δt will have the following probability of freezing¹⁵

P = 1 − exp(−J_V(T)V_dΔt), (1)

where we calculated J_V with the parameterisation recommended by Ickes et al.³ Implemented in Python, each simulation was initialized by assigning a diameter to each droplet. A random number between 0 and 1 was generated from a uniform distribution for each droplet in the simulation, the value of which was compared to the probability of freezing for that droplet size. If the random number was less than or equal to P, then the droplet froze in the simulation; if the random number was greater than P, the droplet remained unfrozen. The number of unfrozen droplets was thus gradually depleted until the frozen fraction reached unity. The inputs to our simulations include: the initial number of unfrozen droplets (n), droplet volume, and Δt (3 s when cooling at 1 K min⁻¹ and 30 s when cooling at 0.1 K min⁻¹), and we select these variables to have the same values as those that were investigated in each experiment. Droplet volume and Δt are directly inserted into eqn (1) to calculate the probability of freezing for each unfrozen droplet.

3. Results and discussion

Using the MINCZ setup, we performed experiments to investigate the homogeneous nucleation of water-in-oil droplets with two distinct volumes. Fig. 1 shows the frozen fraction of droplets as a function of temperature for each population of droplets with mean droplet diameters of approximately (a) 75 μm and (b) 100 μm (see Table A1 in the ESI† for a summary of mean droplet diameters for each population). The frozen fraction is defined as f = n_frozen/n, where n_frozen is the number of frozen droplets and n is the total number of droplets in an experiment. We performed experiments on three independent droplet populations with cooling rates of 0.1 K min⁻¹ (labelled i, ii, and iii) and 1 K min⁻¹ (labelled a, b, and c). Experimental data for the cooling of 75 μm droplets at 1 K min⁻¹ (Fig. 1(a); labelled a, b, and c) are from the previous validation of the MINCZ setup.³² We also performed refreeze experiments in MINCZ, where we thawed droplets that were frozen at 0.1 K min⁻¹ and cooled them again at a rate of 1 K min⁻¹ (labelled r-i, r-ii, r-iii in Fig. 1). When analysing the refreeze experiments, droplets that had fused over the course of the thaw-cool process were excluded from further analysis, since the nucleation temperature would otherwise be skewed towards higher temperatures due to the increase in the droplet volume of these fused droplets.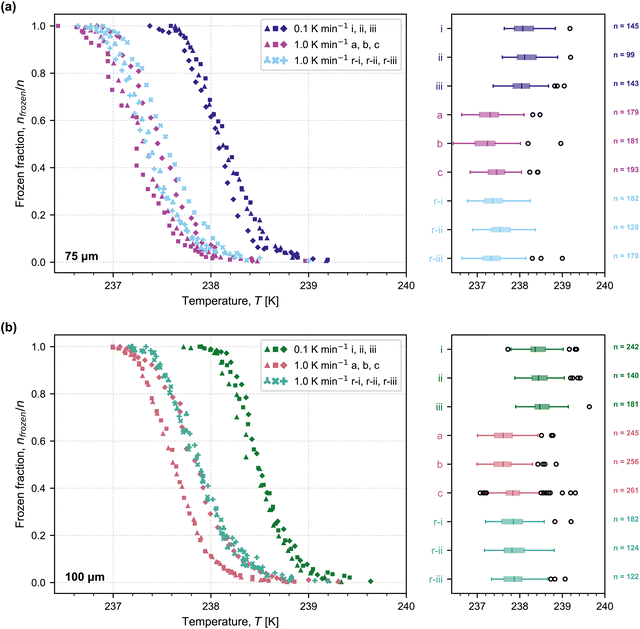

Fig. 1 Frozen fraction of droplets as a function of temperature for two droplet diameters, (a) ∼75 μm and (b) ∼100 μm, at two different cooling rates (0.1 K min⁻¹ and 1.0 K min⁻¹). Three independent droplet populations were cooled at 0.1 K min⁻¹ (labelled as i, ii, iii), which were subsequently thawed and refrozen at 1.0 K min⁻¹ (labelled as r-i, r-ii, and r-ii). Three other independent droplet populations were cooled at 1.0 K min⁻¹ (labelled as a, b, c); results for the 75 μm droplets at a cooling rate of 1.0 K min⁻¹ were obtained from Isenrich et al.³² Boxplots show the median freezing temperature (center line), interquartile range (box extending between the 25th and 75th percentiles), the maximum and minimum temperature range (whiskers), and outliers (open circles). The temperature accuracy is estimated to be ±0.2 K.

As expected, when droplets were cooled at the lower cooling rate of 0.1 K min⁻¹, freezing was observed at higher temperatures because more time was spent at each temperature interval, thus increasing the probability of ice nucleation. When the diameter of the spherical droplets increased from 75 μm to 100 μm, we also observed a shift of freezing to higher temperatures. This is also expected because a larger volume increases the statistical likelihood of an ice embryo forming and allowing a phase transition to occur. All populations of droplets of the same diameter cooled at 1 K min⁻¹, whether frozen immediately (a, b, and c) or refrozen (r-i, r-ii, and r-iii), froze reproducibly in the same temperature range within the accuracy of our temperature measurements. This means that, in future experiments, it would be sufficient to subject the same droplet population to different cooling rates rather than generate new droplet populations for each cooling rate of interest. It is interesting to note that the spread in nucleation temperature between experiments completed at 1 K min⁻¹ is wider than the spread between experiments completed at 0.1 K min⁻¹. This could be explained by the fact that the higher cooling rate induces a larger temperature gradient between the top and bottom of the ethanol bath, as energy is withdrawn at a higher rate by the Peltier element. As a result of the larger temperature gradient, small variations in the exact vertical position of the thermocouple tips could lead to slight offsets in measured temperature. With a lower cooling rate, this dynamic effect can be minimized, and measurement variability may decrease.

From the frozen fractions of droplets, the nucleation rate can be calculated, which describes the number of nucleation events per unit volume per unit time and is thus independent of droplet size and cooling rate. The homogeneous nucleation rate, J_V, can be calculated as a function of temperature using:²²

where t₂ − t₁ is the time elapsed between two images being saved (3 s when cooled at 1 K min⁻¹ and 30 s when cooled at 0.1 K min⁻¹, corresponding to a temperature interval of 0.05 K), T₂ is the temperature at time t₂, f₁ and f₂ are the frozen fractions at times t₁ and t₂, respectively, and V_d is the droplet volume calculated for a spherical droplet using the average diameter for each population (as listed in Table A1, ESI†). Eqn (2) is obtained by rearranging eqn (1) after substituting the probability of freezing with the frozen fraction (number of frozen droplets divided by the initial number of unfrozen droplets at time t₁).

Before analysing our experimental nucleation rates, we present and interpret Monte Carlo simulations of droplets freezing with our experimental parameters of droplet number, droplet diameter, cooling rate, and number of experiments. In this way, it is possible to better understand the contributions of experimental uncertainties and the inherent stochasticity of nucleation to the observed scatter in experimental nucleation rates. Assuming that the underlying nucleation rate is that recommended by Ickes et al.³ (see details of this parameterisation summarized in the ESI,† Section C), we simulate a frozen fraction for each experiment using eqn (1), and we calculate the nucleation rate as a function of temperature from each frozen fraction using eqn (2), summarized in Fig. 2(a). The scatter in the simulated nucleation rates is wider at the warmer temperatures, and there is a bias towards higher nucleation rates compared to the underlying nucleation rate (shown by the dashed line in Fig. 2(a)). To assess the impact of this bias on fitting parameters obtained from this simulated data, we refit the Ickes et al.³ parameterisation to the simulated nucleation rates by choosing the interfacial tension of ice–water to be a free variable, because it is a poorly constrained parameter at these supercooled temperatures.³ As done by Ickes et al.,³ we consider the ice–water interfacial tension, σ_iw(T), to vary linearly with temperature, i.e.,

where σ_iw,0 and dσ_iw/dT are fitting parameters corresponding to the ice–water interfacial tension at a temperature of 273.15 K and the slope with which the interfacial tension changes as a function of temperature, respectively. It is clear that the nucleation rate obtained by fitting to the simulated data of individual experiments (dotted blue line in Fig. 2(a)) overestimates the underlying nucleation rate at warmer temperatures (dashed line). Thus, due to the limited number of droplets in each experiment, σ_iw,0 and dσ_iw/dT derived from the simulated dataset are both lower than the values given in Ickes et al.³ that were used to create the simulated dataset (see parameters listed in Table 1).

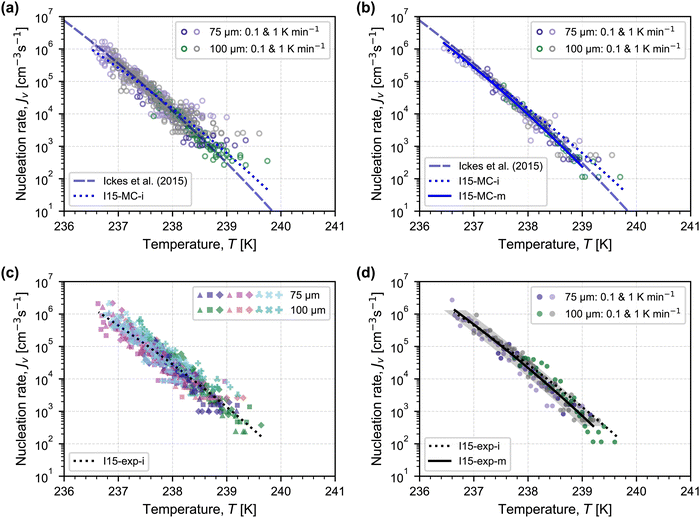Fig. 2 Nucleation rates calculated using eqn (2) with frozen fractions from: (a) Monte Carlo simulations for each experiment assuming that the underlying nucleation rate is described by the Ickes et al.³ parameterisation (dashed grey line); (b) merging the individual Monte Carlo simulations for each droplet diameter and cooling rate; (c) each individual experiment in Fig. 1; and (d) merging experiments completed for the same droplet diameter and cooling rate. In each panel, the Ickes et al.³ framework (I15) is fit to the illustrated dataset when the ice–water interfacial tension is a free variable with fitting parameters σ_iw,0 and dσ_iw/dT (dotted and solid lines in blue (to simulate data) and black (to experimental data)), the values of which are summarized in Table 1. In the bottom legend of each panel, “MC” and “exp” stand for Monte Carlo simulations and experimental data, while “i” and “m” correspond to the use of individual and merged frozen fractions, respectively, in obtaining the shown fit. In (d), the shaded grey region around the solid black line represents a temperature accuracy of ±0.2 K.

Table 1 Fitting parameters and 95% confidence intervals (CIs) for eqn (3) within the Ickes et al.³ parameterisation and as obtained by fitting to simulated (Monte Carlo) and experimental nucleation rates when the frozen fractions (FF) of each experiment are considered individually or merged for each droplet diameter and cooling rate. For nucleation rates calculated from merged frozen fractions, only frozen fractions (FF) greater than 0.01 were considered

Parameterisation name	Description	σ iw,0 ± 95% CI [mJ m^−2]	dσiw/dT ± 95% CI [mJ m^−2 K^−1]
I15	Ickes et al.^3 parameterisation	30	0.18
I15-MC-i	Monte Carlo individual	27.52 ± 0.20	0.1100 ± 0.0062
I15-MC-m	Monte Carlo merged and FF > 0.01	29.96 ± 0.24	0.1779 ± 0.0069
I15-exp-i	experimental individual	26.97 ± 0.23	0.0972 ± 0.0066
I15-exp-m	experimental merged and FF > 0.01	28.67 ± 0.34	0.1443 ± 0.0097

---

Therefore, to reduce this bias, we merge all simulations completed for the same droplet diameter and cooling rate into a single frozen fraction, from which nucleation rates are calculated using eqn (2). The nucleation rates with this approach are shown in Fig. 2(b). From these nucleation rates, we obtain fitting parameters for eqn (3) within the Ickes et al. parameterisation, while also only considering nucleation rates calculated from frozen fractions greater than 0.01. Merging the frozen fractions and excluding the first 1% of frozen droplets reduces the bias from droplets that nucleate at warmer temperatures, and the underlying nucleation rate is recovered (as shown by the overlap between the solid blue and dashed grey lines in Fig. 2(b) and by the coefficients in Table 1 between parameterisations I15 and I15-MC-m being the same). In the ESI,† we show the simulated effects of Gaussian distributions in droplet diameter and cooling rate (Fig. D1, ESI†), demonstrating that these effects are secondary to the number of droplets considered per frozen fraction.

As shown in Fig. 2(c) and (d), the nucleation rates obtained from experimental observations show a similar pattern between using each individual frozen fraction (Fig. 2(c)) and using merged frozen fractions (Fig. 2(d)). The scatter is reduced, and the fitting parameters for the interfacial tension in Fig. 2(d) indicate a larger value for σ_iw,0 and a steeper temperature dependence (dσ_iw/dT) compared to the fit in Fig. 2(c).

The values of the obtained fitting parameters are similar in magnitude to those in the literature summarized by Ickes et al.,³ where values of σ_iw,0 vary between 23.07 and 32 mJ m⁻² and dσ_iw/dT ranges from 0.1 to 0.25 mJ m⁻² K⁻¹ based on experimental data, whereas a narrower range of values is obtained in molecular simulations (when TIP4P-based models of water are used^34–36). In the parameterisation recommended by Ickes et al.,³ the suggested values of the fitting parameters are those obtained from molecular simulations by Reinhardt and Doye,³⁴ where σ_iw,0 = 30 mJ m⁻² and dσ_iw/dT = 0.18 mJ m⁻² K⁻¹. Based on the high temperature accuracy of the MINCZ platform, we recommend using the fit shown in Fig. 2(d) obtained from the merged experimental frozen fractions (I15-exp-m, with fitting parameters in the last row of Table 1) for predicting the homogeneous nucleation rate of ice for the freezing of micrometer-sized droplets. This fit is valid for temperatures between 236.5 K and 239.3 K, a range of 2.8 K.

Where do our measured nucleation rates lie in the context of previous literature? In Fig. 3(a), we compare our fit obtained from MINCZ data to measurements obtained using an electrodynamic balance,^23,24,37,38 an instrument type which is reported to have some of the lowest temperature uncertainties. Our measured nucleation rates are closest to those reported by Stöckel et al.,²³ both in absolute magnitude and in the temperature dependence of the nucleation rate. Stöckel et al.²³ noted that their reported temperatures were not identical to the temperatures of the droplets, because their droplets lose energy to the environment via evaporation. They estimated that their droplets were 0.2 K colder than the temperatures measured by the thermocouple in their instrument. Our nucleation rates would be in closer agreement with their results if this offset is considered (we plot the data in Fig. 3(a) as presented in the original paper without offset). The other three datasets obtained using electrodynamic balances,^24,37,38 however, suggest higher homogeneous nucleation rates for water. Krämer et al.²⁴ estimated that the effect of evaporation on droplet temperature in their instrument was to decrease the temperature by 0.1 K relative to the surrounding air. Accounting for this temperature offset, however, would not explain the discrepancy in nucleation rate compared to data from Stöckel et al.²³ and the data obtained herein. In general, the nucleation rates that have been observed in an electrodynamic balance are limited to temperatures below approximately 238 K, because above these temperatures, the levitated droplet evaporates to a size smaller than can be levitated before nucleation can be observed.²³ In contrast, we were able to investigate nucleation rates over a broader range and above 238 K.

Fig. 3 Homogeneous nucleation rate of water as a function of temperature from: (a) measurements using an electrodynamic balance;^23,24,37,38 (b) parameterisations based on observations of microfluidic or micron-scale droplets with associated temperature uncertainties represented by shaded regions (S09: Stan et al.³¹ data parameterised by Tarn et al.;²¹ E09: Edd et al.;³⁹ R13: Riechers et al.;²² W16: Weng et al.;⁴⁰ P16: Peckhaus et al.⁴⁴ data parameterised by Tarn et al.;²¹ T18: Tarn et al.;⁴⁵ R18: Reicher et al.;²⁸ H18: Häusler et al.⁴³ data parameterised by Tarn et al.;²¹ T21: Tarn et al.²¹); and (c) compared with CNT-based parameterisations by Ickes et al.³ and Koop and Murray,²⁰ where the blue shaded region corresponds to the uncertainty around the Koop and Murray parameterisation arising from a 95.4% confidence interval in the value for the self-diffusion of water.²⁰ In each panel, the solid black line illustrates the Ickes et al.³ parameterisation (I15) using the ice–water interfacial tension described by eqn (3) obtained by fitting to the merged experimental dataset obtained using MINCZ (the fit named I15-exp-m with σ_iw,0 = 28.67 mJ m⁻² and dσ_iw/dT = 0.1443 mJ m⁻² K⁻¹). The shaded grey region around the solid line represents the experimental temperature accuracy of ±0.2 K.

In Fig. 3(b), we place our parameterisation within the context of other microfluidic instruments and arrays of micron-sized droplets. As identified by Koop and Murray,²⁰ there is a general paucity of nucleation rate data at temperatures greater than 238 K, with only one dataset having been obtained between 2016 and the present day. Using MINCZ to study monodisperse droplets of two diameters with two cooling rates, we were able to obtain nucleation rates that span more than one degree below and above 238 K using one instrument with a high temperature accuracy of ±0.2 K. Below 238 K, our data agree in magnitude with the majority of data within the reported temperature uncertainties (excluding the data of Edd et al.³⁹ and Weng et al.,⁴⁰ both of which do not report a temperature uncertainty). Overall, a greater number of droplets per experiment is preferable for reducing scatter in nucleation rate, a result that has been reiterated throughout the nucleation and crystallization literature.^41,42 The effect of having relatively few droplets per experiment may be responsible for the shallowness of the slope reported by Tarn et al.²¹ when fitting the nucleation rate to frozen fraction data from Häusler et al.,⁴³ where only 25 droplets per experiment were investigated.

Fig. 3(c) compares our version of the Ickes et al.³ parameterisation (Table 1, I15-exp-m) to the physically constrained parameterisation provided by Koop and Murray.²⁰ A major difference between the two parameterisations is the assumed phase of ice, whether it is hexagonal (Ickes et al.³) or a metastable stacking disordered phase (Koop and Murray²⁰). In Ickes et al.,³ the data used for fitting at temperatures greater than 238 K span five orders of magnitude, while Koop and Murray²⁰ selected a subset of the data used in Ickes et al.³ based on criteria of minimal uncertainties and good reproducibility within a dataset, thus excluding all data above 238 K.

Our new semi-empirical fit based on data obtained with MINCZ agrees with the Ickes et al.³ parameterisation within experimental error, but the agreement becomes questionable at temperatures greater than 238 K. Our new data and fit suggest that the Ickes et al.³ parameterisation (I15) underestimates the homogeneous nucleation rate at temperatures greater than 238 K, which can be traced to a lack of good quality data that could be used to inform a parameterisation at these temperatures. There is broad agreement between our fit (I15-exp-m) and the parameterisation of Koop and Murray²⁰ within the uncertainty of our experimental measurements and the uncertainty in the self-diffusion of water in the parameterisation (illustrated by the blue shaded region in Fig. 3(c)). For the temperatures investigated experimentally, however, the most probable value of the Koop and Murray²⁰ parameterisation (the dash-dotted line) overestimates the homogeneous nucleation rate at temperatures less than 238 K and predicts a steeper slope at temperatures greater than 238 K.

With our newly-obtained data, we demonstrate that the homogeneous nucleation rate may in fact decrease less rapidly as temperature increases than predicted by previous parameterisations. In the atmosphere, this has important consequences, since ice would start to form homogeneously at higher temperatures than previously thought, which would in turn influence cloud evolution and microphysical properties such as ice particle size.

4. Conclusions

Although the homogeneous nucleation rate of ice formation in pure water is of interest across disciplines, previous measurements of its magnitude as a function of temperature vary across several orders of magnitude. This disagreement between measurements obtained using different instruments hinders progress in predicting or controlling ice nucleation in the variety of applications where it is pertinent. Therefore, in this study, we used the Microfluidic Ice Nuclei Counter Zurich (MINCZ) to obtain new data for the homogeneous nucleation rate of water with a high temperature accuracy of ±0.2 K to constrain the homogeneous nucleation rate within less than an order of magnitude over a temperature range of 2.8 K. To investigate a wide temperature range, we generated droplets with two volumes and cooled the droplets at two different rates. Importantly, we obtained data above 238 K, where rates have previously been challenging to access due to instrumental limitations. Nucleation rates were calculated as a function of temperature, and new parameterisations were obtained from these nucleation rates. To complement our experimental measurements, we performed Monte Carlo simulations of droplets freezing in the MINCZ setup. We showed that the stochasticity of freezing events resulting from the number of droplets in each independent droplet population can artificially flatten the apparent nucleation rate as a function of temperature. This observation justifies the need to merge frozen fractions from simulations or experiments completed for the same droplet diameter and cooling rate to accurately determine the underlying nucleation rate. Our experimental results suggest that nucleation rates may be shallower as a function of temperature for temperatures greater than approximately 238 K than those obtained using recommended parameterisations based on classical nucleation theory from Ickes et al.³ and Koop and Murray.²⁰ Practically, this means that ice may be more likely to nucleate at higher temperatures with potential consequences for the various applications where its formation or prevention is important—in the atmosphere, food preservation, and pharmaceutical products, for example.

Code and data availability

Plot data are compiled in the ETH Research Collection data repository at https://doi.org/10.3929/ethz-b-000581491. Python scripts are available upon request.

Author contributions

NS and FNI are co-first authors of the manuscript and contributed equally to the generation of data, data analysis, and writing of the original draft; as such, they may each list their name first in their CV. BW contributed to the generation of data. All authors contributed to project conceptualization, methodology, writing (review and editing), and have approved the final version of the manuscript.

Conflicts of interest

The authors declare that they have no conflict of interest.

Acknowledgements

We acknowledge technical support from Roland Walker and Michael Rösch who machined and 3D-printed portions of the instrument. NS acknowledges support from an ETH Postdoctoral Fellowship (20-1 FEL-46) and a Natural Sciences and Engineering Research Council of Canada (NSERC) Postdoctoral Fellowship.

References

1. M. Volmer and A Weber, Keimbildung in übersättigten Gebilden, Z. Phys. Chem., 1926, 119, 277–301.
2. R. Becker and W. Döring, Kinetische Behandlung der Keimbildurzg in übersättigten Dämpfen, Ann. Phys., 1935, 416, 719–752.
3. L. Ickes, A. Welti, C. Hoose and U. Lohmann, Classical nucleation theory of homogeneous freezing of water: Thermodynamic and kinetic parameters, Phys. Chem. Chem. Phys., 2015, 17, 5514–5537.
4. H. Vehkamäki, Classical Nucleation Theory in Multicomponent Systems, Springer, Berlin, 2006.
5. A. Laaksonen and J. Malila, Nucleation of Water: From Fundamental Science to Atmospheric and Additional Applications, Elsevier, Amsterdam, 2021.
6. K. Muldrew, J. Acker, J. Elliott and L. McGann, in Life in the Frozen State, ed. B. J. Fuller, N. Lane and E. E. Benson, CRC Press, Boca Raton, 2004, pp. 67–108.
7. L.-T. Deck, D. R. Ochsenbein and M. Mazzotti, Stochastic shelf-scale modeling framework for the freezing stage in freeze-drying processes, Int. J. Pharm., 2022, 613, 121276.
8. L.-T. Deck, D. R. Ochsenbein and M. Mazzotti, Stochastic ice nucleation governs the freezing process of biopharmaceuticals in vials, Int. J. Pharm., 2022, 625, 122051.
9. L. Goh, K. Chen, V. Bhamidi, G. He, N. C. S. Kee, P. J. A. Kenis, C. F. Zukoski and R. D. Braatz, A stochastic model for nucleation kinetics determination in droplet-based microfluidic systems, Cryst. Growth Des., 2010, 10, 2515–2521.
10. G. Graeber, T. M. Schutzius, H. Eghlidi and D. Poulikakos, Spontaneous self-dislodging of freezing water droplets and the role of wettability, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11040–11045.
11. Y. You, T. Kang and S. Jun, Control of ice nucleation for subzero food preservation, Food Eng. Rev., 2021, 13, 15–35.
12. J. D. Kalma, G. P. Laughlin, J. M. Caprio and P. J. Hamer, The Bioclimatology of Frost: Its Occurrence, Impact and Protection, Springer, Berlin, 1992.
13. R. Wang, Z. Hu, Y. Li, K. Wang and H. Zhang, Review on the deterioration and approaches to enhance the durability of concrete in the freeze–thaw environment, Constr. Build. Mater., 2022, 321, 126371.
14. N. Dalili, A. Edrisy and R. Carriveau, A review of surface engineering issues critical to wind turbine performance, Renewable Sustainable Energy Rev., 2009, 13, 428–438.
15. H. R. Pruppacher and J. D. Klett, Microphysics of Clouds and Precipitation, Springer, Dordrecht, 2010.
16. U. Lohmann, F. Lüönd and F. Mahrt, An Introduction to Clouds: From the Microscale to Climate, Cambridge University Press, Cambridge, UK, 2016.
17. T. Koop, B. Luo, A. Tsias and T. Peter, Water activity as the determinant for homogeneous ice nucleation in aqueous solutions, Nature, 2000, 406, 611–614.
18. Z. A. Kanji, L. A. Ladino, H. Wex, Y. Boose, M. Burkert-Kohn, D. J. Cziczo and M. Krämer, Overview of ice nucleating particles, Meteorol. Monogr., 2017, 58, 1.1–1.33.
19. R. Defay, I. Prigogine, A. Bellemans and D. H. Everett, Surface Tension and Adsorption, Longmans, London, 1966.
20. T. Koop and B. J. Murray, A physically constrained classical description of the homogeneous nucleation of ice in water, J. Chem. Phys., 2016, 145, 211915.
21. M. D. Tarn, S. N. F. Sikora, G. C. E. Porter, J. Shim and B. J. Murray, Homogeneous freezing of water using microfluidics, Micromachines, 2021, 12, 1–23.
22. B. Riechers, F. Wittbracht, A. Hütten and T. Koop, The homogeneous ice nucleation rate of water droplets produced in a microfluidic device and the role of temperature uncertainty, Phys. Chem. Chem. Phys., 2013, 15, 5873–5887.
23. P. Stöckel, I. M. Weidinger, H. Baumgärtel and T. Leisner, Rates of homogeneous ice nucleation in levitated H₂O and D₂O droplets, J. Phys. Chem. A, 2005, 109, 2540–2546.
24. B. Krämer, O. Hübner, H. Vortisch, L. Wöste, T. Leisner, M. Schwell, E. Rühl and H. Baumgärtel, Homogeneous nucleation rates of supercooled water measured in single levitated microdroplets, J. Chem. Phys., 1999, 111, 6521–6527.
25. G. M. Whitesides, The origins and the future of microfluidics, Nature, 2006, 442, 368–373.
26. A. R. Metcalf, S. Narayan and C. S. Dutcher, A review of microfluidic concepts and applications for atmospheric aerosol science, Aerosol Sci. Technol., 2018, 52, 310–329.
27. Y. Ding, P. D. Howes and A. J. DeMello, Recent advances in droplet microfluidics, Anal. Chem., 2020, 92, 132–149.
28. N. Reicher, L. Segev and Y. Rudich, The WeIzmann Supercooled Droplets Observation on a Microarray (WISDOM) and application for ambient dust, Atmos. Meas. Tech., 2018, 11, 233–248.
29. T. Brubaker, M. Polen, P. Cheng, V. Ekambaram, J. Somers, S. L. Anna and R. C. Sullivan, Development and characterization of a “store and create” microfluidic device to determine the heterogeneous freezing properties of ice nucleating particles, Aerosol Sci. Technol., 2019, 54, 79–93.
30. M. D. Tarn, S. N. F. Sikora, G. C. E. Porter, B. V. Wyld, M. Alayof, N. Reicher, A. D. Harrison, Y. Rudich, J. U. Shim and B. J. Murray, On-chip analysis of atmospheric ice-nucleating particles in continuous flow, Lab Chip, 2020, 20, 2889–2910.
31. C. A. Stan, G. F. Schneider, S. S. Shevkoplyas, M. Hashimoto, M. Ibanescu, B. J. Wiley and G. M. Whitesides, A microfluidic apparatus for the study of ice nucleation in supercooled water drops, Lab Chip, 2009, 9, 2293–2305.
32. F. N. Isenrich, N. Shardt, M. Rösch, J. Nette, S. Stavrakis, C. Marcolli, Z. A. Kanji, A. J. DeMello and U. Lohmann, The Microfluidic Ice Nuclei Counter Zürich (MINCZ): A platform for homogeneous and heterogeneous ice nucleation, Atmos. Meas. Tech., 2022, 15, 5367–5381.
33. R. J. Herbert, B. J. Murray, S. J. Dobbie and T. Koop, Sensitivity of liquid clouds to homogenous freezing parameterizations, Geophys. Res. Lett., 2015, 42, 1599–1605.
34. A. Reinhardt and J. P. K. Doye, Note: Homogeneous TIP4P/2005 ice nucleation at low supercooling, J. Chem. Phys., 2013, 139, 096102.
35. E. Sanz, C. Vega, J. R. Espinosa, R. Caballero-Bernal, J. L. F. Abascal and C. Valeriani, Homogeneous ice nucleation at moderate supercooling from molecular simulation, J. Am. Chem. Soc., 2013, 135, 15008–15017.
36. R. L. Davidchack, R. Handel, J. Anwar and A. V. Brukhno, Ice I_h-water interfacial free energy of simple water models with full electrostatic interactions, J. Chem. Theory Comput., 2012, 8, 2383–2390.
37. D. Duft and T. Leisner, Laboratory evidence for volume-dominated nucleation of ice in supercooled water microdroplets, Atmos. Chem. Phys., 2004, 4, 1997–2000.
38. D. Rzesanke, J. Nadolny, D. Duft, R. Müller, A. Kiselev and T. Leisner, On the role of surface charges for homogeneous freezing of supercooled water microdroplets, Phys. Chem. Chem. Phys., 2012, 14, 9359–9363.
39. J. F. Edd, K. J. Humphry, D. Irimia, D. A. Weitz and M. Toner, Nucleation and solidification in static arrays of monodisperse drops, Lab Chip, 2009, 9, 1859–1865.
40. L. Weng, S. N. Tessier, K. Smith, J. F. Edd, S. L. Stott and M. Toner, Bacterial ice nucleation in monodisperse D₂O and H₂O-in-oil emulsions, Langmuir, 2016, 32, 9229–9236.
41. G. M. Maggioni, L. Bosetti, E. Dos Santos and M. Mazzotti, Statistical analysis of series of detection time measurements for the estimation of nucleation rates, Cryst. Growth Des., 2017, 17, 5488–5498.
42. G. Vali, Quantitative evaluation of experimental results on the heterogeneous freezing nucleation of supercooled liquids, J. Atmos. Sci., 1971, 28, 402–409.
43. T. Häusler, L. Witek, L. Felgitsch, R. Hitzenberger and H. Grothe, Freezing on a Chip—A new approach to determine heterogeneous ice nucleation of micrometer-sized water droplets, Atmosphere, 2018, 9, 1–14.
44. A. Peckhaus, A. Kiselev, T. Hiron, M. Ebert and T. Leisner, A comparative study of K-rich and Na/Ca-rich feldspar ice-nucleating particles in a nanoliter droplet freezing assay, Atmos. Chem. Phys., 2016, 16, 11477–11496.
45. M. D. Tarn, S. N. F. Sikora, G. C. E. Porter, D. O’Sullivan, M. Adams, T. F. Whale, A. D. Harrison, J. Vergara-Temprado, T. W. Wilson, J. Shim and B. J. Murray, The study of atmospheric ice-nucleating particles via microfluidically generated droplets, Microfluid. Nanofluid., 2018, 22, 1–25.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03896j

---