Unexpected NMR shieldings of sp- and sp²-hybridized carbon atoms in graphyne systems

Abstract

Graphynes (GYs) are two-dimensional alloptropic forms of carbon consisting of periodically arranged sp- and sp²-hybridized carbon atoms in a planar structure. Graphynes can be formally created from graphene by inserting sp-hybridized carbon links into selected points of the graphene lattice. Depending on where the links are introduced, several forms of graphynes have been proposed with properties that make them potential candidates for new generation electronics or for applications in chemical processes. Since the applications of each form of GY depend on its structure, it is of interest to experimentally distinguish different forms of graphynes. In this paper we propose nuclear magnetic resonance (NMR) as a potential method of choice for such distinction. We computationally investigate on the DFT level the ¹³C-NMR chemical shifts for α-, β-, γ-, rhombic, and 6,6,12-graphynes, and α- and γ-graphdiynes. We perform the calculations both in periodic systems and with approximate finite models. The results show that NMR chemical shifts in graphynes are dependent on the structure and reflect the local bonding around the carbon nucleus. Interestingly, NMR shifts of several graphynes show anomalous values, differing significantly from shifts found in typical sp²-hybridized systems. We analyze these results in terms of local structural parameters and qualitatively investigate the possible origins of these anomalous NMR shifts. The results show that NMR is a viable method for determining the structure of graphynes and their finite precursor molecules.

---

1 Introduction

Carbon naturally occurs in significant quantities in two allotropic forms as diamond and as graphite. The structure of diamond is a three-dimensional network of sp³-hybridized carbon atoms forming a transparent, mechanically hard electric insulator. Graphite, on the other hand, is composed of stacked two-dimensional sheets of sp²-hybridized carbon atoms, and is a soft, dark material with good electric conductivity.

The contrast between the properties of diamond and graphite gives a glimpse into the range of different materials carbon can form. Due to the ability of carbon atoms to create energetically favorable single, double, and triple bonds, a wide variety of chemically stable structures can be formed. Many of these forms have been prepared or isolated in the laboratory and characterized, often showing interesting properties. Examples include fullerenes, nanotubes, nanoribbons, or carbon-based quantum-dots.

In recent years carbon allotropes forming two-dimensional (2D) structures with translational symmetry within a single plane have attracted considerable interest. The first such experimentally prepared system was graphene, which is essentially a single layer of graphite,¹ composed of fused six-member rings of sp²-hybridized carbons (Fig. 1).

Fig. 1 Structures of 2D carbon materials investigated in this study: graphene, α-graphyne, α-graphdiyne, β-graphyne, γ-graphyne, γ-graphdiyne, rhombic graphyne, and 6,6,12-graphyne. Circles indicate unique atoms, bars labelled a–h show unique bonds and the dashed regions denote unit cells. In the following discussion the sp² atoms are labeled “B” (branch) and sp atoms are labeled “L” (linkers). We note that each of these structures represents a single resonance form and the bonding situation should not be interpreted literally. In particular, benzene rings in graphene, γ-graphyne, γ-graphdiyne, and 6,6,12-graphyne should be interpreted in terms of typical benzene resonance structures, and the sp²-hybridized carbons in α-graphyne and α-graphdiyne as having three equivalent bonds due to the symmetry.

More complex two-dimensional structures can be created by formally inserting sp-hybridized acetylene links into the structure, creating so-called graphynes (GYs). Remarkably, graphynes were first proposed in 1987,² almost two decades before the experimental preparation of single-layer graphene.

Graphynes can occur in a variety of structures, depending on the number and position of the acetylene links inserted into the graphene lattice. Different graphynes have been shown to considerably differ in their properties. This variability of properties gives graphynes a wide range of applications. Thanks to their uniform pore sizes some graphynes were proposed as membranes for the separation of gases^3,4 or for water desalination.⁵ The large surface area of GYs allows them to efficiently adsorb metals, providing applications such as hydrogen storage materials,^6–8 electrode materials for lithium batteries,⁹ or removal of heavy metals from water.¹⁰ The graphynes also possess interesting electronic properties, such as carrier mobility even higher than graphene,¹¹ making them viable candidates for molecular electronics or spintronics.¹²

The large variety of possible arrangements of carbon atoms and correspondingly different properties and applications call for reliable ways to distinguish different graphyne structures. In this study we propose nuclear magnetic resonance (NMR) as a possible method of choice for such distinction. NMR is a convenient technique as it is non-destructive and can be performed for samples in both solid state as well as in solution. In addition, the NMR shielding constants are quite sensitive to the local molecular structure around the nucleus and thus can reveal both the bonding arrangements as well as interesting local electronic properties. ¹³C NMR has been shown to be a useful tool for studying different carbon allotropes, such as disordered carbon^13,14 or graphene^14–18 and its different spin states.^17,18

In this work we calculate NMR shielding for seven different graphyne systems shown in Fig. 1 both for periodic models and for finite models. The results show a wide range of values of nuclear shielding. In several cases the chemical shifts of sp- and sp²-hybridized carbon atoms switch order and the signals occur at values contrary to chemical intuition. We establish the correlation between the NMR shifts and local structural parameters such as hybridization of nearby carbon atoms, and rationalize the shifts by electron density analysis on finite models. The results show that NMR has potential for experimental identification of graphynes and their fragments, and that quantum-chemical modelling is vital for correct assignment of NMR signals in these structures.

2 Methods

2.1 Periodic calculations

Periodic lattice calculations were performed in Quantum Espresso 6.4.1.^19–22 All calculations were performed using the C.pbe-rrkjus-gipaw-dc pseudopotential²³ and the PBE²⁴ density functional on the Monkhorst-Pack grid.²⁵ The structures were optimized with dispersion correction (DFT-D3)²⁶ with energy cutoffs of 40 Ry and 400 Ry for wavefunction and charge density, respectively. The number of k-points in the grid was increased until the difference in all bond lengths between two calculations with n and n + 1 k-points was ≤0.1%. Detailed parameters for optimizations and geometric parameters of the optimized structures are given in the ESI.† For each optimized graphyne the band structure was calculated and compared with the literature to confirm the electronic state of the system. Good agreement was found in all cases (see the ESI†).

NMR nuclear shielding calculations were performed with the GIPAW method,^21,22 using identical pseudopotential and DFT functionals as in geometry optimization and with energy cutoffs for wavefunction and charge density 65 Ry and 650 Ry, respectively. The convergence of the nuclear shielding with respect to the number of k-points was tested by increasing the density of the grid with the criterion ≤0.2 ppm between two consecutive calculations used as a threshold. An exception is the system 6,6,12-GY, where this criterion was loosened because of its slower convergence (see the ESI†).

2.2 Finite system calculations

For comparison with the periodic systems we also investigated the behaviour of finite models, created by cutting out “flakes” from the graphyne sheet. The flakes were created by replication of the optimized unit cell from periodic calculation. Flakes of various sizes were created for all investigated systems, ranging from one to five unit cells across (see the ESI†). The structures were terminated at the edges by hydrogen atoms positioned 1.09 Å from the nearest carbon along the vector of the original carbon–carbon bond in the infinite lattice. The finite structures were not further optimized.

Gauge-including atomic orbitals (GIAO) NMR shielding calculations for finite systems were calculated using Turbomole 7.5^27,28 with PBE density functional using m4a numerical integration grid and resolution of identity approximation (RI). The PBE functional was chosen to allow as close as possible comparison with the results for the periodic system. The basis set was x2c-TZVPall-s²⁹ for the innermost atoms, for which the NMR parameters were calculated, and x2c-SVPall-s for the other carbon and hydrogen atoms to reduce the computational costs. This approach was shown to provide good results in previous works on graphene systems.¹⁶ We note that placing x2c-SVPall-s on all atoms produces differences in nuclear shieldings that are rather small, but sufficient to lead to a change of order of shifts in the 6,6,12-GY system, which has a crowded NMR spectrum with close lying lines. The relativistic x2c-{X}all-s basis sets were developed specifically for NMR shieldings and are expected to perform well also for non-relativistic calculations.

Additional nuclear shielding calculations were performed with a KT3 functional.³⁰ This functional provides generally good NMR parameters³¹ for light elements and was used to quantitatively verify trends of the results obtained with PBE. The obtained differences between values of NMR shifts calculated using PBE and KT3 were below 1 ppm for all cases except two. The largest difference was 2.8 ppm.

2.3 Reference molecules

The chemical shift δ_K for nucleus K was calculated with respect to benzene as

δ_K = σ_benzene − σ_K (1)

where σ_K and σ_benzene are isotropic nuclear shielding constants for the carbon nucleus K in graphyne and for carbon in benzene, respectively. All calculations for the molecule of benzene were performed in a cubic box with sides x = y = z = 20 Å with the molecule at the center parallel to the xy-plane. The number of k-points was 1 for both optimization and NMR as it satisfied the above convergence criteria for bond lengths and nuclear shielding; all other parameters were identical to those in the calculations of graphynes. Similarly, the reference shielding for finite systems was calculated in Turbomole at the same level of theory as the corresponding graphyne systems.

2.4 Analysis

Additionally, a set of small isolated organic molecules was optimized using identical parameters for geometry optimization. These were used for comparisons of bond lengths.

Difference densities of the electronic excited states were used for an analysis of paramagnetic nuclear shielding. These were obtained in Turbomole at the same level of theory as NMR calculations for flakes of the size of two unit cells and plotted using USCF Chimera.³²

3 Results and discussion

3.1 Periodic calculations

The results of NMR shielding calculations are presented in the left column of Fig. 2. The numerical values are in the ESI.† The sp²-hybridized carbon atoms are labeled B (branch atom) and the sp-hybridized carbons are labeled L (linker). Atoms L are connected directly to the B atoms, and atoms L′ in graphdiynes are in the middle of longer links, connected to the L atoms. The full numbering system of the atoms can be found in Fig. 1. The results show distinct differences in chemical shifts between the different graphyne systems. Fig. 2 also includes a representation of the closest structural motif near the B-type carbon atoms.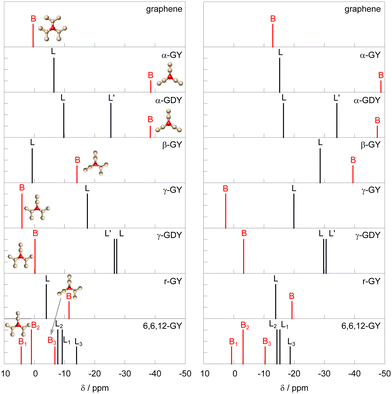

Fig. 2 Comparison of NMR shifts of carbon atoms in graphene and studied graphynes calculated in periodic systems at the PBE/pbe-rrkjus-gipaw-dc level of theory (left panel), and using the finite flake model (size = 4) at RI-PBE/x2c-SVPall-s(+x2c-TVPall-s on innermost cell) level of theory (right panel). For labeling of the atoms see the ESI† or Fig. 1. Local environments around the branched (B) carbon atoms are shown in the insets.

The α-graphyne shows two well-separated signals, both of them shielded compared to that of graphene. Interestingly, the ¹³C NMR signal of sp²-hydridized carbon (B) is shifted by about −39 ppm, while the sp signal (L) is closer to the signal of sp²-hybridized carbons of graphene. Introduction of another sp link (L′) in the α-graphdiyne leads to a new signal positioned between B and L, with only small shifts in shielding of B and L. The behaviour of the sp²-hybridized carbons B is rather peculiar as their shifts are lower than that of sp-hybridized carbons L and L′. This is in contrast to the usual ranges of chemical shifts, where sp²-hybridized carbons show higher chemical shifts than sp-hybridized carbon atoms.^33,34

In β-graphyne the signal of sp² carbon is shifted by about −14 ppm, while the signal of sp-hybridized carbon L is found close to the one of sp²-hybridized carbon in graphene.

The situation in γ-graphyne and γ-graphdiyne is quite different, and closer to the NMR of typical organic molecules, which exhibit higher ¹³C chemical shifts for sp²-hybridized carbons than for sp ones. The chemical shift of sp² (B) carbon is pushed to slightly higher values with respect to graphene, while the shifts of sp-hybridized carbons (L) move toward a lower chemical shift by about −18 ppm. This situation is in clear contrast to α and β structures, where the sp-hybridized carbons show higher chemical shifts compared to sp². In γ-graphdiyne signals of B and L shift by a few ppm, and the additional carbon link L′ gives rise to a new signal very close (<1 ppm) to the signal of L.

The rhombic graphyne r-GY has two signals quite close together in the region between 0 and −15, slightly shifted upfield compared to graphene. The sp-hybridized L carbon has a larger shift than the sp² one, showing a qualitatively similar anomaly as α-graph(di)yne and β-graphyne, i.e. reversed order of sp and sp²-hybridized carbons compared to typical values in organic molecules,^33,34 where sp carbons are found several tens of ppm lower than sp².

6,6,12-graphyne has six chemically distinct carbon sites. They are distributed rather closely in a pattern between 5 and −15 ppm. Similarly as in the case of γ-graphyne and γ-graphdiyne, the signals of sp² are all shifted toward a higher chemical shift compared to those of sp, consistently with typical ranges of ¹³C NMR. The position of B signals is not substantially different from the one in graphene, while L signals are shifted slightly toward negative values, in line with shifts in conventional organic molecules.

It is interesting to note that the shifts of the B carbons (sp²-hybridized) in all systems are related to the number of other B-type carbons bound to it. The carbons bound to three sp-hybridized carbons in α-GY and α-GDY show the smallest chemical shift. The chemical shift increases in β-GY and r-GY, which have one sp²- and two sp-hydridized neighboring atoms. The highest shift is in γ-GY and γ-GDY, which have two sp²-hybridized neighboring carbons. A similar situation is found for the B₁–B₃ in 6,6,12-GY. This is also consistent with the chemical shift of graphene, which can be described as a network of B atoms connected to three other sp² hybridized atoms. Accordingly, its chemical shift is found at the higher end of the chemical shift spectrum. The situation is illustrated with insets in Fig. 2.

Interestingly, the structures that conserve the benzene motif, such as γ-GY, γ-GDY, and 6,6,12-GY show chemical shifts close to the ones characteristic for sp- and sp²-hybridized atoms in isolated organic molecules with sp carbons having signals in the region of lower shifts compared to sp². On the other hand, graph(di)ynes in the family α feature an extended multicarbon hexagonal ring that is not usually found in organic molecules, and show a more interesting range of chemical shifts deviating from the typical values, swapping the relative positions of signals of the sp and sp²-hybridized carbon nuclei. Similarly, r-GY is a network of large elongated hexagons, which are not a typical feature in organic molecules. On the other hand, β-GY also features a “swap” of NMR signals, despite a lack of an obvious peculiarity in its structure. These swaps in positions can potentially lead to misinterpretation of the NMR spectra of graphynes when ¹³C signals are assigned based on experience with typical organic molecules. We will explore sources of this behaviour in later sections.

3.2 Finite models

In order to analyze the differences in the chemical shifts and their behaviour, we calculated NMR nuclear shielding for finite model “flakes” cut from the periodic structures. Calculations using these finite models allow for analysis of the NMR shielding in terms of molecular orbitals near the nuclei, giving insight into the local electronic structure. In addition, if the periodic systems can be to a good approximation modelled using a finite model, it opens possibilities for using different quantum chemical computational machinery for calculating their properties that is not available in software packages for periodic calculations (e.g., wider selection of DFT functionals, high level ab initio correlated methods such as MP2 or coupled cluster models, as well as relativistic effects including spin–orbit interactions). In order to evaluate the fidelity of the finite model, we calculated the NMR chemical shifts of flakes of different sizes and compared them with the values obtained from the periodic calculations.

As can be seen from Fig. 2, even small flakes qualitatively capture the order of chemical shifts observed in the periodic calculations for all systems. Notably, there is a significant shift in shielding for atoms in β-GY, which are more shielded by about 40 ppm compared to the periodic model. We note here that shifts of β-GY are the most sensitive to the size of the flake out of the studied systems, but their relative spacing is largely preserved (see the ESI†).

The overall consistency of the results with the periodic model allows us to use the finite model for further analysis of the NMR shielding constants.

3.2.1 Analysis of the NMR shielding components. Fig. 3 shows a comparison of the nuclear shielding constants expressed in terms of in-plane (IP; xx and yy) and out-of-plane (OOP; zz) components of the shielding tensor for both periodic systems and finite flakes. This allows us to get a more detailed picture of the origin of the chemical shifts and to evaluate similarity between atoms in different systems.

Fig. 3 Contributions of the in-plane ((xx + yy)/3) and out-of-plane (zz/3) components of the shielding tensor to the isotropic NMR shielding for periodic (left) and finite (right) systems. Flake size is 3 for β-GY, 4 otherwise.

We note here that the signs of some of the smallest components are dependent on the size of the flake (see the ESI†). Nevertheless, despite the apparent qualitatively different description, this does not significantly affect the results due to the overall smallness of these components. The exception to this is β-GY, which exhibits larger variation with flake size. Interestingly, this variation is mostly caused by sensitivity of the OOP component, while the IP one is rather constant (see the ESI†). For this reason the flake size of β-GY reported in Fig. 3 is 3, which corresponds to the closest agreements of the isotropic shifts with those in the periodic system. For the rest of the systems the flake sizes are 4.

It is apparent that there is a rather strong similarity of the ratio of the IP and OOP tensor elements between periodic and finite systems. This suggests similar physical origins of nuclear shielding and strengthens the argument that the agreement of the two models is not coincidental.

For α-GY and α-GDY we can see the unique character of the B-nucleus signals, which show almost equivalent proportions of both components. A similar composition is not found for any other nucleus and reflects the unique local structure of these systems. We will return to this further in the following section.

The composition of the shielding for L nuclei between the two systems is also very similar. The ratio of the IP/OOP components is also similar to that of L′, which just has an overall increase in intensity. Notably, with the increase in intensity the composition of this shielding resembles most closely that of the L′ nucleus in γ-GDY, underlining the similarity of their chemical neighborhood, despite the large difference in the other two signals.

The situation in β-GY is markedly different from α-GY and α-GDY. The shielding of the B-nucleus is composed mostly of the OOP component, with about 1/4 of IP contribution. This is qualitatively similar to the situation of B in r-GY and B₃ in 6,6,12-GY, which have only slightly smaller proportions of IP. The shielding of the L nucleus, on the other hand, is almost exclusively due to the IP component with a very small OOP part. A similar pattern is found for L in r-GY and L₁/L₂ in 6,6,12-GY. It is noteworthy that these similar nuclei in all three systems are part of the larger structural motif of “H”-shape where four linkers are connected via an sp²–sp² two-carbon bridge. These similarities are stronger in the periodic model, especially for β-GY, whose OOP component is sensitive to the size of the flake. We note that the very small OOP contribution in L₁ changes sign between the periodic and finite models.

A noteworthy feature here is that while the ratios of IP/OOP components are quite similar in all three systems, the shielding of the B₃ nucleus in 6,6,12-GY is weaker, pushing its chemical shift higher than its neighboring L₁/L₂. This means that the ordering of the chemical shifts in 6,6,12-GY is the same as in typical organic systems with δ(sp²) > δ(sp), in contrast to the anomalous order in β-GY and r-GY.

Another characteristic group of signals are B nuclei in γ-GY and γ-GDY together with B₁ and B₂ in 6,6,12-GY. These signals have a strong OOP contribution with a very small IP tensor component, which is in most cases negative, except for B₂ of 6,6,12-GY in finite system. As can be seen from Fig. 1, all of these atoms belong to the unbroken benzene ring. Moreover, this situation resembles that of graphene. However, in graphene both components are larger in magnitude, leading to a stronger overall shielding.

The L nucleus in γ-GY is opposite to the previous situation and is dominated by the IP component with very small negative OOP one. There is a strong similarity with the L₃ in 6,6,12-GY. Since both of these nuclei are links between two benzene rings, we can once again see a correlation with the local structure. The situation is also quite similar for L in γ-GDY. For L′ in γ-GDY the OOP component is slightly larger, and its overall composition becomes closer to the structurally similar linker atom L′ in α-GDY.

The shielding constants of both nuclei B and L in r-GY qualitatively reflect those of β-GY as discussed in the relevant paragraph above. This is related to their similar local environment.

Similarly, shieldings of nuclei in 6,6,12-GY show features analogous to that of β-GY and r-GY in the case of nuclei in the “H”-bridge, or that of γ-GY for nuclei of the benzene motifs and the link directly connecting them, as discussed above.

These results suggest that the NMR shielding tensor encodes the larger structural motifs of the system and can be used to identify building blocks of graphyne systems.

To validate the results more quantitatively, we also calculated NMR shifts using the KT3 DFT functional, which is generally considered a good functional for NMR parameters of light elements. The results show minimal changes with respect to results obtained using PBE. All trends are preserved and the largest change in chemical shift is less than 3 ppm (see the ESI†).

3.2.2 Relation to a local structure. As shown above, the trends of NMR shifts of periodic systems are reproduced in finite models. Moreover, similar structural features give rise to similar NMR shifts. This means that the origin of the anomalous NMR shifts is not a peculiar band structure of the periodic systems, but can be traced to some other influence in the local environment.

A simple measure of the electronic structure around the nucleus are the lengths of the adjacent bonds. An intuitive estimate of the “typical” bond order for graphynes (as shown in Fig. 1) can be determined based on the assumptions that (1) bonds have integer order; (2) the bond arrangements should have the highest possible symmetry allowed by the symmetry of the atomic lattice; (3) each carbon atom has eight electrons in its valence. Although such structures can be drawn for most of the investigated graphyne systems (Fig. 1), it is worth noting that each structure is only one of the possible resonance structures. To demonstrate this, we can compare the apparent bond orders as drawn in Fig. 1, where it follows the chemical intuition, to the ones from the optimized structures (Fig. 4).

Fig. 4 Comparison of the bond lengths in the studied systems with typical reference values for organic molecules. Color indicates the formal order of the bond with single bonds (green), double (blue), triple (red), aromatic (part of benzene ring, magenta) and the formally 4/3 order bonds in α-G(D)Y (black). Small letters indicate bond labels from Fig. 1.

The bond lengths in the periodic systems are plotted in Fig. 4, together with reference “typical” values for isolated organic molecules for comparison. The reference values were obtained from optimization of 2,2,3,3-tetramethylbutane, 2,3-dimethyl-but-2-ene, but-2-yne and coronene for single, double, triple and aromatic bond types. The coloring corresponds to the estimated bond orders as suggested in Fig. 1. The bonds in benzene rings are considered as typical aromatic ones, and the bonds a and b in α-graphyne can be thought of as having order 4/3 and 8/3, respectively, given as an average of their three equivalent resonance structures. The comparison shows that the bond lengths of the bonds appearing as single, double or as part of a benzene ring are all quite similar, suggesting that the π electrons in GYs are somewhat delocalized. Interestingly, formally single bonds are contrary to expectation somewhat shorter than the formally double ones, although these differences are minor. On the other hand, the triple bonds are significantly shorter and close to the typical values.

Interestingly, the values do not significantly change when the finite flakes are optimized (PBE/def2-TZVP in Turbomole). This suggests that even the rather anomalous bond lengths are results of the peculiar local arrangements of the carbons rather than a consequence of the infinite periodicity of the system and the loss of local molecular orbitals. Furthermore, this means that NMR could be also a viable method for identification of the structure of smaller fragments, which are employed as precursors in the synthesis of periodic graphyne structures³⁵ as they would exhibit similarly peculiar NMR signals.

Finally, we note here that the aim of this section was not to determine the exact bond order, e.g., from analysis of electronic structure calculation. While such calculations can be carried out, the purpose of this discussion is merely to point out possible challenges of applying common chemical intuition and drawings of structures such as those in Fig. 1 to the systems featuring unorthodox arrangements of carbon atoms.

3.2.3 Insights from local electron density. Finally, we can try to gain a qualitative insight into the origin of the NMR signals.

The nuclear shielding tensor component σ_λμ for Cartesian coordinates λ, μ can be separated into diamagnetic and paramagnetic parts^36,37 as

σ_λμ = σ_λμ^(d) + σ_λμ^(p) (2)

The diamagnetic part is related to the ground-state electron density around the nucleus, which is similar for the nuclei of the same type in a similar chemical environment. The paramagnetic part, on the other hand, couples the ground state to the manifold of excited states m through local paramagnetic nuclear spin – electron orbit operator ĥ^PSO and orbital Zeeman operator ĥ^OZ as

where E₀, E_n are energies of the ground and excited states n, respectively, and c.c is the complex conjugate of the previous term. The ĥ^PSO and ĥ^OZ operators include angular momentum that transforms as rotations and can produce non-zero matrix elements only in A_2g and E_1g symmetries, corresponding to out-of-plane and in-plane components of the shielding tensor, respectively.

The paramagnetic part is responsible for the differences in trends of NMR shielding for different atoms. Generally, the paramagnetic contribution is deshielding and, hence, increases chemical shift. Therefore, large matrix elements and small energy differences in eqn (3) will lead to more deshielding due to σ^(p), smaller total nuclear shielding, and larger chemical shift.

Since the ĥ^PSO operator has r⁻³ electron-nucleus distance dependence, it couples effectively only to the excited states n localized around the nucleus in question. The localization, and therefore the coupling strength, can be qualitatively estimated by visual inspection of spatial representations of the difference densities between the ground and the excited state n of the molecule.

The analysis is necessarily qualitative, as we are looking only at the first few excited states, and a combination of several different parameters plays a role: (a) relative energy of the excited states appearing in the denominator of eqn (3); (b) localization of the excited state around the nucleus (through ĥ^PSO operator) and (c) the strength of the magnetic transition dipole moment, m, between the ground and exited state n. The latter two are related to the size of the matrix elements in the numerator of eqn (3).

For a qualitative insight, we concentrate the analysis on the cases of α-GY and γ-GY that both have simple spectra of two lines with the opposite, abnormal and normal chemical shift ordering, respectively. The difference densities of the first five excited states, their energies and magnetic transition dipole moments in E_1g (IP shielding components) and A_2g (OOP) symmetries of the D_6h point group in α-GY and γ-GY are reported in Fig. 5.

Fig. 5 Difference densities between the ground and the first five excited states in α-GY (top two rows) and γ-GY (bottom two rows) in the inner-most cell. Green and red color represent an increase and decrease in electron density, respectively. Isodensity values are 4D-5, and the size of the flake is 4. The excitation energies and transition magnetic dipole moments m are also reported. The transitions in symmetry species A_2g (D_6h point group) correspond to out-of-plane (OOP) contributions to nuclear shielding and the transitions with E_1g symmetry to in-plane (IP) contributions.

First, from Fig. 3 we can see that the main difference in the ordering of the B and L signals is in the magnitude of the IP component (E_1g) for the B nucleus. It is large and positive in α-GY, but small and negative in γ-GY. From excited states data in E_1g symmetry displayed in Fig. 5, we can see that the excitation energies are quite similar, with γ-GY having only slightly larger energy differences with respect to the ground state. The γ-GY has clearly more pronounced positive difference densities compared to α-GY indicating that PSO “sees better” the excited states, i.e. the matrix elements of the PSO operator may be larger in γ-GY. While this is a qualitative prerequisite for the large paramagnetic deshielding contribution, the much larger downfield shift of the IP component in γ-GY is most clearly indicated by the about an order of magnitude larger magnetic transition dipole moments than in α-GY. Based on the discussion of eqn (3), the lack of strong magnetic dipole transition moments effectively prevents the existence of large paramagnetic contributions in the case of IP of the B signal in α-GY, which is consistent with the results in Fig. 3.

The large shielding in the IP (E_1g) and OOP (A_2g) components of the B signal in α-GY have different origins and two counteracting trends can be identified. The excited states in symmetry A_2g have lower energies and much larger transition magnetic dipole moments but have small positive difference densities and, hence, a qualitatively weaker PSO contribution. On the other hand, the E_1g states have more significant densities, but much smaller transition moments and somewhat larger energy separation. This means that neither set of excited states have a large paramagnetic contribution, leading to appreciable shielding in both symmetries.

In summary, the presence of a significant positive difference density, low excitation energies and non-negligible transition magnetic dipole moments can lead to large paramagnetic contributions and thus deshielding, but individually they are not indicative of that. It is important to note that the nuclear shielding is a sum of individual excitation terms that can add up in different ways, making their effect on the final shielding not easily predictable when only a few lowest excited states are considered. However, the current qualitative analysis provides explanation to the anomalous shift in α-GY. It is caused by small transition magnetic dipole moments in E_1g symmetry, which inhibits the paramagnetic contribution and, hence leads to a large nuclear shielding.

Based on these results it appears that in the case of graphynes the present simplified analysis of the NMR trends based on a few lowest excited states is not as straightforward as in the previous interpretation of NMR for graphene flakes.³⁸ The reason is that the previous study looked at larger changes in chemical shift trends in different regions (inner vs. outer rings) within the flakes with very different electronic structures caused by different edge defects, while in the present case more detailed information in similar chemical structures with smaller shift differences is explored.

The results are in principle not very surprising, as five states are a very rough approximation to the complete sum of eqn (3), especially considering that there is a significant density of states available for the coupling immediately above the investigated energy window (not shown here), making them potentially equally significant.

4 Conclusions

We have theoretically investigated the ¹³C nuclear magnetic resonance spectra of α-graphyne, α-graphdiyne, β-graphyne, γ-graphyne, γ-graphdiyne, rhombic graphyne and 6,6,12-graphyne. The results predict distinct NMR patterns for different graphynes.

Interestingly, some graphynes show peculiar ¹³C shifts, with sp²-hybridized carbons shifted toward smaller chemical shifts and sp-hybridized carbons shifted higher, in contrast to the NMR shifts usually observed in organic molecules. The chemical shifts are also related to the local structure of the systems and the peculiar increase of sp² carbon shielding is shown to follow the number of sp² neighbours.

It is noteworthy that these ¹³C-NMR patterns remain quite similar when calculated using both the periodic model and finite “flakes” of the graphynes. This suggests that the origin of the peculiar NMR shifts is determined by the local environment and not the band structure of the solid. This is supported by observing unconventional carbon–carbon bond lengths in both models.

The more detailed study of the roles of in-plane and out-of-plane components of the chemical shift helped to trace the anomalously small chemical shift of sp² carbon in α-graphyne to be due to large shielding in the in-plane component. Qualitative analysis of positive difference densities, excitation energies and magnetic transition dipole moments relates it to ineffective coupling between the ground and excited states. This produces a smaller than usual paramagnetic deshielding contribution to sp² carbons.

The current study highlights the opportunities for investigation of novel carbon nanomaterials using ¹³C NMR, as the spectra provide detailed fingerprints that is sensitively dependent on the local structure but also on detailed chemical bonding of individual carbon atoms. The results also showcase the risks of applying common chemical intuition to the interpretation of the novel carbon allotropes. Therefore, the first principles NMR modelling of these materials is necessary for correct interpretation of the experimental spectra.

Author contributions

P. Š.: calculations, data analysis, and manuscript writing. P. L.: project idea, study design, and manuscript writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the Academy of Finland (Grant 316180). The computational resources were provided by CSC – IT Center for Science (Espoo, Finland) and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533). The authors acknowledge the preliminary calculations by Antti Ilvesviita performed at the beginning of the project.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699.
3. S. W. Cranford and M. J. Buehler, Nanoscale, 2012, 4, 4587–4593.
4. Z. Meng, X. Zhang, Y. Zhang, H. Gao, Y. Wang, Q. Shi, D. Rao, Y. Liu, K. Deng and R. Lu, ACS Appl. Mater. Interfaces, 2016, 8, 28166–28170.
5. S. Lin and M. J. Buehler, Nanoscale, 2013, 5, 11801–11807.
6. Y. Guo, K. Jiang, B. Xu, Y. Xia, J. Yin and Z. Liu, J. Phys. Chem. C, 2012, 116, 13837–13841.
7. H. J. Hwang, Y. Kwon and H. Lee, J. Phys. Chem. C, 2012, 116, 20220–20224.
8. C. Li, J. Li, F. Wu, S.-S. Li, J.-B. Xia and L.-W. Wang, J. Phys. Chem. C, 2011, 115, 23221–23225.
9. H. Zhang, M. Zhao, X. He, Z. Wang, X. Zhang and X. Liu, J. Phys. Chem. C, 2011, 115, 8845–8850.
10. R. Liu, J. Zhou, X. Gao, J. Li, Z. Xie, Z. Li, S. Zhang, L. Tong, J. Zhang and Z. Liu, Adv. Electron. Mater., 2017, 3, 1700122.
11. J. Chen, J. Xi, D. Wang and Z. Shuai, J. Phys. Chem. Lett., 2013, 4, 1443–1448.
12. J. He, S. Y. Ma, P. Zhou, C. X. Zhang, C. He and L. Z. Sun, J. Phys. Chem. C, 2012, 116, 26313–26321.
13. A. R. Ambrozio, J.-M. Leyssale, R. J.-M. Pellenq, F. A. L. de Souza, G. L. Vignoles, W. L. Scopel and J. C. C. Freitas, J. Phys. Chem. C, 2020, 124, 12784–12793.
14. F. A. L. de Souza, A. R. Ambrozio, E. S. Souza, D. F. Cipriano, W. L. Scopel and J. C. C. Freitas, J. Phys. Chem. C, 2016, 120, 27707–27716.
15. S. Ikäläinen, P. Lantto, P. Manninen and J. Vaara, Phys. Chem. Chem. Phys., 2009, 11, 11404–11414.
16. J. Vähäkangas, S. Ikäläinen, P. Lantto and J. Vaara, Phys. Chem. Chem. Phys., 2013, 15, 4634–4641.
17. F. de Souza, F. Pansini, L. Filho, A. R. Ambrozio, J. Freitas and W. L. Scopel, Carbon, 2022, 191, 374–383.
18. J. Vähäkangas, P. Lantto, J. Mareš and J. Vaara, J. Chem. Theory Comput., 2015, 11, 3746–3754.
19. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
20. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
21. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
22. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
23. D. Ceresoli, https://sites.google.com/site/dceresoli/pseudopotentials.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
26. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
27. TURBOMOLE V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
28. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
29. Y. J. Franzke, R. Treß, T. M. Pazdera and F. Weigend, Phys. Chem. Chem. Phys., 2019, 21, 16658–16664.
30. T. W. Keal and D. J. Tozer, J. Chem. Phys., 2004, 121, 5654–5660.
31. C. J. Schattenberg and M. Kaupp, J. Chem. Theory Comput., 2021, 17, 7602–7621.
32. E. F. Pettersen, T. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and R. E. Ferrin, J. Comput. Chem., 2004, 13, 1605–1612.
33. P. W. Atkins and J. D. Paula, Physical Chemistry, Oxford University Press, 6th edn, 1998.
34. L. G. Wade, Organic chemistry, Pearson Prentice Hall, 6th edn, 2006.
35. X. Gao, H. Liu, D. Wang and J. Zhang, Chem. Soc. Rev., 2019, 48, 908–936.
36. N. F. Ramsey, Phys. Rev., 1950, 78, 695–699.
37. N. F. Ramsey, Phys. Rev., 1953, 91, 303–307.
38. N. Özcan, J. Vähäkangas, P. Lantto and J. Vaara, ChemPhysChem, 2014, 15, 1799–1808.

---

Footnote

† Electronic supplementary information (ESI) available: Benchmark results, geometry of optimized systems, electronic band structures, orbital analysis, and numerical results. See DOI: https://doi.org/10.1039/d2cp03837d

---